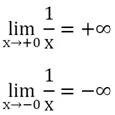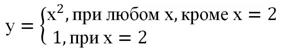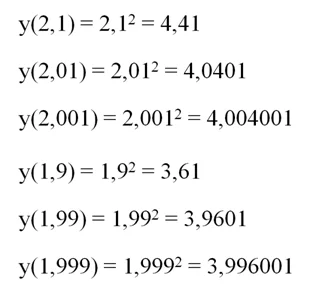Как найти приращение пути

Правила дифференцирования:

1. ;

2. , ;

3. , ;

4. ,
   если
   ,
   ;

5. ,
   если
   ,
   .

Определение.
Если функция задана уравнением
,
разрешенным относительно
,
то функция задана в
явном виде (явная функция).

Определение.
Неявная
функция одного
аргумента задается уравнением, связывающим
две переменные, причем уравнение не
разрешено относительно какой-либо из
них:

или
.

Определение.
Уравнение, связывающее три переменные,
задает неявную
функцию 2 аргументов:
,
или
,
или
.

Не
всегда легко, а иногда и невозможно
разрешить уравнение относительно

(например,

или
).

Если
неявная функция задана уравнением
,
то для нахождения производной от

по

нет необходимости разрешать уравнение
относительно
.
Нужно продифференцировать это уравнение
по
,
рассматривая при этом

как функцию
,
и полученное затем уравнение разрешить
относительно
.

Пример
Найти
производную функции
,
заданную уравнением:
.

Решение.
Функция

задана неявно. Продифференцируем
уравнение по
,
помня, что
:
.
Затем находим:
.

Рассмотрим дифференцирование функции, заданной параметрически.

Пусть
функция задана параметрически:

где
–
вспомогательная переменная, называемая
параметром.

Нужно
найти
.
Предположим, что

имеет однозначную обратную функцию
.
Продифференцируем уравнение

по
,
как сложную функцию, считая

промежуточным аргументом, зависящим
от
:
;
.
Так как
,
то получим:

. (4)

Пример
Пусть

Найти
.

Решение.
По формуле (4), получаем

Производную
функции одной переменной в некоторых
случаях можно найти значительно проще,
если функцию предварительно
прологарифмировать, такой метод
называется логарифмическое
дифференцирование.

Логарифмическое
дифференцирование обычно применяется
при отыскании производной от
степенно-показательной функции и от
произведения функций, т.е. в тех случаях,
когда обычными методами производную
нельзя найти, либо вычисление производной
очень громоздко. Конечно, эта операция
может применяться и в других случаях.

Определение.
Функция
,
у которых основание и показатель степени
есть функции независимых переменных,
называются степенно-показательными.

Производные
таких функций вычисляются только с
помощью логарифмического дифференцирования.

Пример
Дана
функция
.
Найти
.

Решение.
Прологарифмировав функцию
,
получим

.

Дифференцируем
полученное уравнение по
:


.
Из последнего равенства найдем
:

.

Дифференциал функции

Рассмотрим
функцию
,
имеющую в точке

отличную от нуля производную:
.
По теореме о связи функции, ее предела
и бесконечно малой функции, можно
записать
,
где

при
,
или
.
Приращение функции

представляет собой сумму двух слагаемых

и
,
являющихся бесконечно малыми при
.
Заметим, что

— бесконечно малая функция одного порядка
с
,
так как
,
а

— функция более высокого порядка, чем
:
.

Определение.
Слагаемое

называется главной
частью приращения
функции
.

Определение.
Дифференциалом
функции

в точке

называется главная
часть ее приращения, равная произведению
производной функции на приращение
аргумента, и обозначается

или
.
Заметим, что

. (5)

Определение.
Дифференциал

называется дифференциалом
первого порядка.

Дифференциал
независимой переменной равен приращению
этой переменной:

. (6)

В
самом деле, так как

и
,
то
.

Определение.
Дифференциал
функции
равен произведению производной этой
функции на дифференциал независимой
переменной:

. (7)

Так
как
,
то

– отношение дифференциалов

и
.

Пример
Найти
дифференциал функции
.

Решение.
По формуле

находим:

.

Пример
Найти полное
приращение функции

и ее дифференциал, сравнить их значения
при
.

Решение.
Полное приращение запишем в виде:

.
Преобразуем это выражение:
.
По определению найдем полный дифференциал:
.
Подставив
,
получим,

и
.

Геометрический
смысл дифференциала: Дифференциал
функции

в точке

равен приращению ординаты касательной
к графику функции в этой точке, когда

получит приращение.

Поясним
утверждение, для этого рассмотрим график
функции

(рисунок 4).

Проведем
к графику функции в точке

касательную
.
Рассмотрим ординату этой касательной
для точки
,
заметим, что
,
а
.
Рассмотрим прямоугольный треугольник
,
в котором
,
т.е.
.
Так как
–
геометрический смысл производной, то
.
Из формул:

и

получаем, что
.
Возможны три случая:
,

и

– если функция является постоянной.

Механический
смысл дифференциала: Дифференциал
пути равен приращению пути, полученному
в предположении, что, начиная с данного
момента времени
,
точка движется равномерно, сохраняя
приобретенную скорость.

Рассмотрим
неравномерное прямолинейное движение
точки, осуществляющееся по закону
,
где

— длина пути,

— время. Приращенному моменту времени

соответствует приращенное значение
пути:


.
Эта формула выражает истинное приращение
пути за промежуток времени
.

Вычислим
дифференциал пути. Так как

– скорость в момент
,
то


.

Поскольку
в выражение для дифференциала входит
производная, то правила его вычисления
используют правила
вычисления производной:

1. Если
   функция равна постоянной
   ,
   то ее дифференциал равен нулю, т.е.
   .

2. Дифференциал
   функции
   
   равен приращению этой функции:
   ;
   
   (дифференциал независимой переменной
   совпадает с ее приращением).

Отсюда
следует:
;
.

1. Дифференциал
   суммы:.

2. Дифференциал
   произведения:.

3. Дифференциал
   частного:
   .

Теорема
6.7 Дифференциал
сложной функции равен произведению
производной этой функции по промежуточному
аргументу на дифференциал этого
промежуточного аргумента:

Определение.


и

– форма дифференциала не изменилась
независимо от того, является ли ее
аргумент независимой переменной или
является функцией одного аргумента.
Такое свойство дифференциала называется
инвариантностью
(неизменностью)
формы первого дифференциала.

Таблица
дифференциалов

Пусть
,

– некоторые непрерывные функции
аргумента х.

1. ;

2. ,

   ;

3. ,

   ;

4. ,
   если
   ;

5. ,
   если
   
   и
   ;

6. ;

7. ;

8. ,
   ;

9. ,
   ;

10. ;

11. ;

12. ;

13. 

14. ;

15. ;

16. ;

17. ;

Приращение
любой дифференцируемой функции
приближенно с большой точностью можно
вычислить при помощи равенства:
.

Приращение

функции

в точке

можно представить в виде
,
где

при
.
Отбросим бесконечно малую

более высокого порядка, чем
,
получим приближенное равенство:
.
Чем меньше
,
тем точнее равенство.

Так
как
,
,
то из равенства

или

получим
формулу для вычислений приближенных
значений функци:

(8)

Пример
Вычислить
приближенно приращение функции

при изменении

от значения 2 к значению 2,02.

Решение.
Так как достаточно малых
:


().

Найдем
:
.
Вычислим
.
Итак,
.

Пример
Найти
приближенное значение
.

Решение.
Рассмотрим функцию
.
По формуле

имеем:

или
.
Так как
,
то при

и
,
получаем:

Так
как,
то
.
Приближенное равенство можно увидеть
из рисунка 4, дающего геометрическое
истолкование дифференциала. На графике
видно, что при уменьшении

все с большей относительной точностью
можно заменить приращение ординаты
кривой приращением ординаты касательной.

Рассмотрим
функцию одного переменного заданную
явно:
.

Производная
этой функции

зависит от координаты точки, в которой
она вычисляется, т. е. является также
функцией от
.
Поэтому от нее можно снова взять
производную.

Определение.
Производная,
взятая от первой, называется производной
второго порядка;
производная, взятая от производной
второго порядка, называется производной
третьего порядка
и т.д.:

;

;

.

Определение.
Производной
-го
порядка называется
производная, взятая от производной
-порядка.

Пример
Найти
производную
-го
порядка от функции
.

;

;

;

Пусть
функция

задана параметрическими
уравнениями:

Производная
функции
заданной параметрически также является
функцией заданной параметрически.
Вторую производную

можно найти и используя формулу (4), и по
формуле:

. (9)

Пример
Дано
параметрическое уравнение эллипса:
.

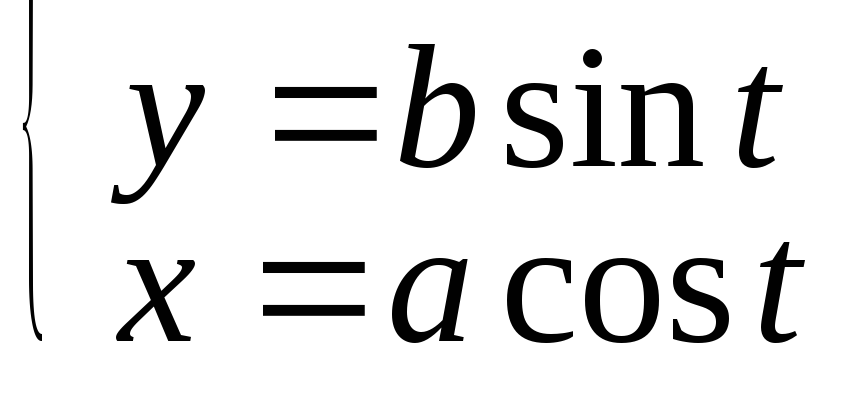
Найти

Решение.
По формуле (4), получаем

.

Чтобы
найти дифференциал второго порядка
нужно взять дифференциал от первого
дифференциала. Аналогично находят
дифференциал третьего порядка и т.д.
Рассмотрим функцию одного переменного
.
Найдем ее дифференциал второго порядка:

(
обозначает
).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  24.03.201514.79 Mб16Детские подвижные игры народов СССР.pdf

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Приращение — путь

Cтраница 1

Приращение пути dU движущейся точки за любой бесконечно малый промежуток времени всегда положительно.
 [1]

Это есть истинное приращение пути.
 [2]

После точки с приращение пути dS становится отрицательным, а вместе с тем tg Ф и скорости делаются также отрицательными. Это означает, что участку графика cd соответствует движение с возрастающей скоростью, но направленной в обратную сторону.
 [3]

Очевидно, что значения приращений пути на последующих участках могут быть приняты отличными от Афь и чем они мельче, тем точнее будет искомая кривая скорости.
 [5]

Таким образом, дифференциал пути равен тому фиктивному приращению пути, которое получится, если предположить, что, начиная с данного момента времени, точка движется равномерно, сохраняя приобретенную скорость.
 [6]

Какой величиной является в случае равномерного движения отношение приращения As пути s за любой промежуток времени к величине этого промежутка.
 [7]

Итак, величина скорости точки определяется как предел отношения приращения пути к соответствующему промежутку времени при стремлении последнего к нулю, а направление ее совпадает с касательной к траектории в данной точке.
 [8]

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути As к приращению времени At, когда приращение времени стремится к нулю.
 [9]

Так, например, обычная механическая работа равна произведению приложенной силы на приращение пути. Если две системы могут взаимодействовать, то они образуют одну общую систему, причем фактор емкости новой системы равен сумме факторов емкости составляющих ее частей при условии, если факторы интенсивности обеих исходных систем одинаковы.
 [10]

Покажите, пользуясь формулой (22.2), что для равноускоренного движения без начальной скорости приращения пути за любые равные промежутки времени, следующие друг за другом, равны двойному пути, проходимому точкой — за первый такой промежуток времени.
 [11]

Показать, пользуясь формулой (22.2), что для равномерно-ускоренного движения без начальной скорости приращения пути за любые равные промежутки времени, следующие друг за другом, равны двойному пути, проходимому точкой за первый такой промежуток времени.
 [12]

Показать, пользуясь формулой (22.2), что для равномерно-ускоренного движения без начальной скорости приращения пути за любые равные промежутки времени, следующие друг за другом, равны двойному пути, проходимому точкой за первый такой промежуток времени.
 [14]

Показать, пользуясь формулой (22.2), что для равномерно-ускоренного движения без начальной скорости приращения пути за любые равные промежутки времени, следующие друг за другом, равны двойному пути, проходимому точкой за первый такой промежуток времени.
 [15]

Страницы:  

   1

   2

План урока:

Предел функции на бесконечности

Предел функции в точке

Приращение аргумента и функции  

Средняя скорость изменения функции

Мгновенная скорость и понятие производной

Предел функции на бесконечности

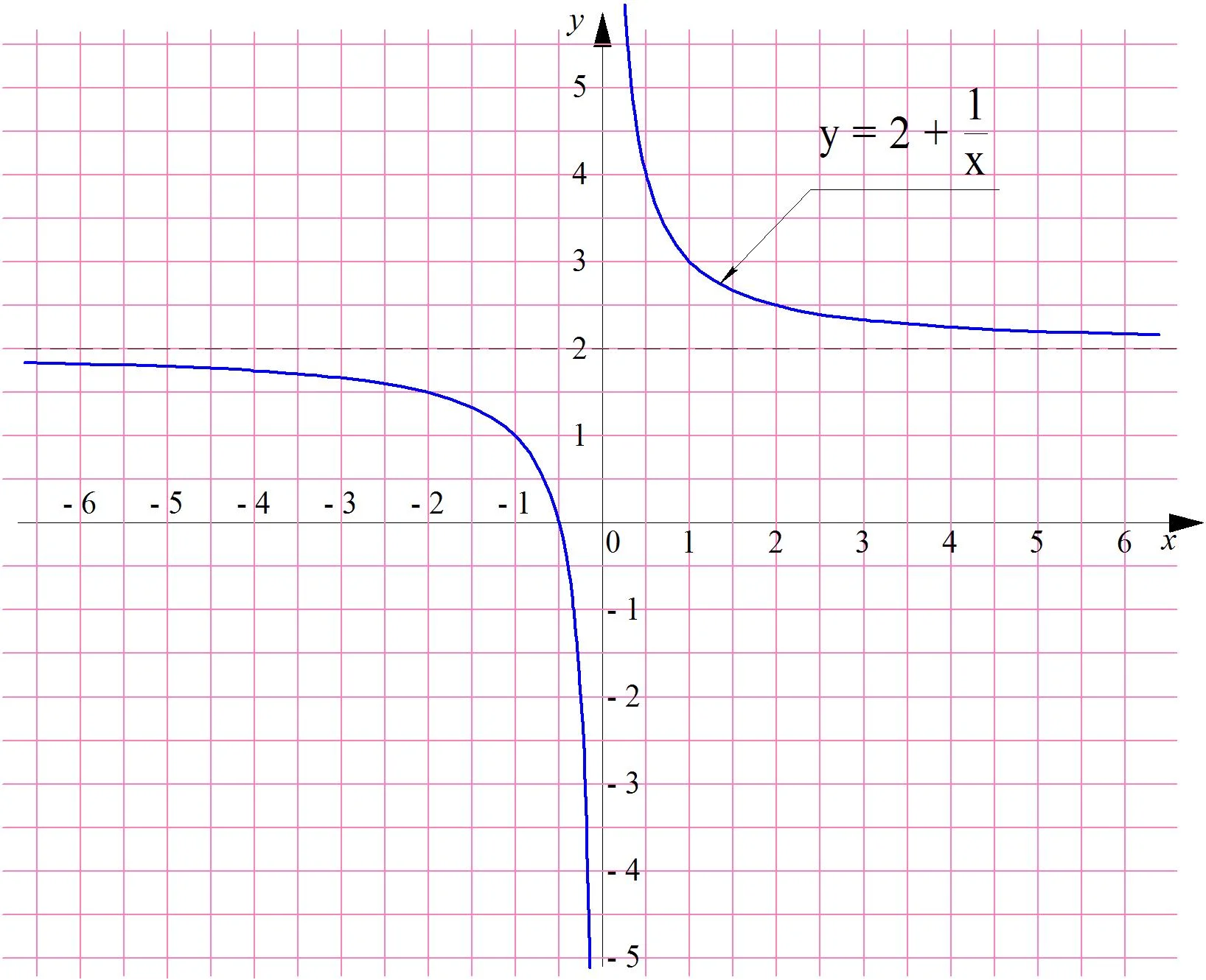
Рассмотрим довольно простую функцию

y = 1/x

Её график называется гиперболой и выглядит так:

Можно заметить, что при больших положительных значениях х график функции приближается к горизонтальной оси Ох, но не пересекает её. Действительно, если мы будем вычислять значение у при всё больших значениях х, то будем получать всё меньшие, но всё же положительные числа:

Получается, что при бесконечном росте аргумента х функция стремится к нулю. Можно ли эту особенность функции как-то записать, используя математические символы? Оказывается, можно, и выглядит это запись так:

которая означает, что х стремится к бесконечности. После символа lim записана сама функция 1/х. В целом вся запись читается так: «предел функции у = 1/х при х, стремящемся к бесконечности, равен нулю».

Вернемся к графику функции у = 1/х. Видно, что если мы будем брать всё меньшие отрицательные значения х, то функция также будет стремится к нулю. Действительно, попробуем подставлять в нее как можно меньшие значения аргумента:

Чтобы записать эту особенность функции, используется следующая запись:

который может быть получен параллельным переносом графика у = 1/х на две единицы вверх:

Очевидно, что пределы этой функции при х → + ∞ и х → – ∞ равны 2:

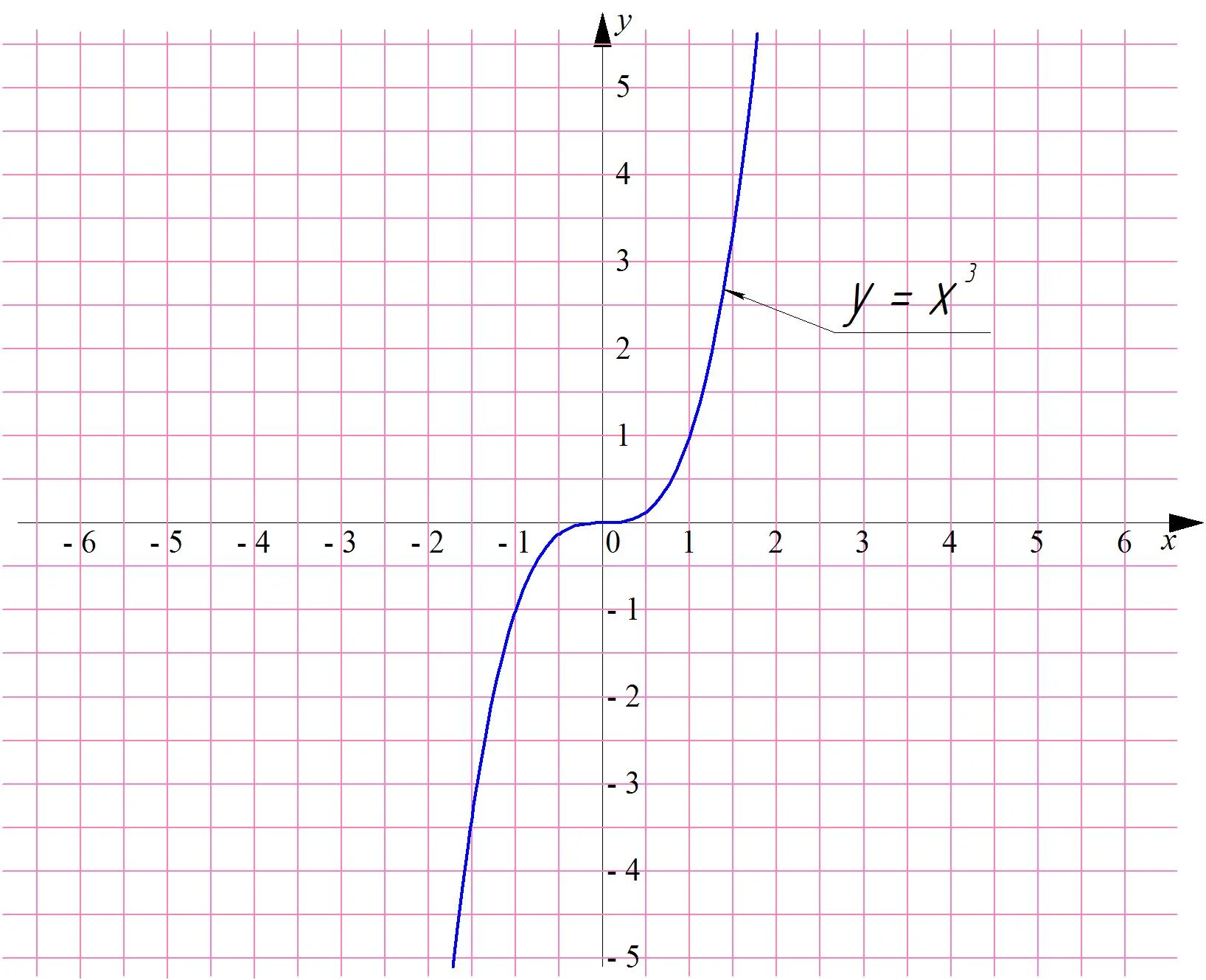
Возможны случаи, когда при бесконечном увеличении аргумента функции она не стремится к какому-то конкретному числу, а сама также неограниченно возрастает. Для примера посмотрим на график у = х³:

Видно, что при х → ∞ сама функция неограниченно растет, что можно показать расчетами:

Возникает вопрос – для всякой ли функции можно указать ее предел на бесконечности? Оказывается, что нет. Для примера рассмотрим тригонометрическую функцию у = sinx, графиком которой является синусоида:

С одной стороны, sinx явно не стремится к какому-то конкретному числу при увеличении х, он «колеблется» между числами 1 и (– 1). С другой стороны, нельзя и сказать, что он стремится к бесконечности. Получается, что у этой функции просто нет пределов на бесконечности.

Предел функции в точке

Порою нас интересует поведение функции не на бесконечности, а вблизи конкретной точки х₀. Конечно, в большинстве случае можно просто вычислить функцию в этой точке, однако иногда это невозможно сделать. Для примера рассмотрим функцию

Очевидно, что точка х = 2 не входит в ее область определения, ведь при подстановке этого значения в функцию знаменатель дроби обратится в ноль. Однако в любой другой точке значение функции будет равняться единице:

График такой функции будет выглядеть как прямая у = 1, у которой есть одна «выколотая точка», соответствующая х = 2:

Итак, функция не определена в точке х = 2, однако можно вычислить предел функции в точке х = 2. Действительно, при любом, сколь угодно близком к 2 значении х функция будет равна единице:

Попробуем также приблизиться к точке 2 с другой стороны, подставляя в функцию числа, меньшие двух:

Снова всё время получается единица. Поэтому мы можем уверенно записать, что

Значительно чаще приходится иметь дело с пределами в точке, которые равны бесконечности. Снова посмотрим на график функции у = 1/х:

Видно, график не пересекает ось Оу, ведь число х = 0 не входит в область определения функции. Однако можно заметить, что при приближении х к нулю функция неограниченно возрастает:

Обратите внимание, что под пределом мы использовали запись «х → + 0», а не «х → 0». Почему? Дело в том, что если мы будем приближаться к нулю с «противоположной» стороны, подставляя в функцию не положительные, а отрицательные числа, то функция будет стремится к – ∞:

Получается, что предел функции в точке х = 0 зависит от того, с какой стороны мы приближаемся к этой точке, слева или справа. В связи с этим в математике существует понятие односторонних пределов. Для обозначения пределов, получаемых при приближении к нулю справа, то есть со стороны бОльших чисел, перед ним ставят знак плюс, а при указании предела слева, то есть со стороны мЕньших чисел – знак минус:

Предел и односторонние пределы – это два разных понятия. Считается, что функция имеет предел в точке только тогда, когда оба односторонних предела в этой точке совпадают.

В качестве ещё одного примера предела функции в точке можно привести зависимость у = tg х, график которой выглядит следующим образом:

В точке х = π/2 функция не определена. Однако видно, что при приближении к этой точке слева функция неограниченно возрастает, а при приближении справа – неограниченно убывает. Это записывается следующим образом:

До этого мы вычисляли пределы функций в точках, где сами функции не определены. Однако пределы можно вычислять и в тех точках, где функция определена. В большинстве случаев (но не всегда) они как раз равны значению функции в этой точке. Например, найдем предел

В точке х = 2 значение функции будет равно 4:

Будут ли односторонние пределы в этой точке также равняться 4? Сначала проверим предел справа

Действительно, получаем значения у, всё более близкие к 4. Аналогично можно убедиться, что и предел слева также равен 4:

Приведем несколько искусственный пример функции, у которой предел в точке не совпадает со значением функции в этой точке. Пусть функция задается с помощью такого графика

Он представляет собой параболу у = х² с выколотой точкой (2; 4). При этом функция определена в точке х = 2, но имеет там значение, равное единице. Аналитически эту функцию можно описать так:

Понятно, что у(2) = 1, однако попытаемся приблизиться к точке х = 2 справа и слева и посмотрим, что получится:

Мы видим, что при х→2 функция и справа, и слева стремится к четверке, а не к единице. То есть получается, что предел функции в точке х = 2 не совпадает со значением функции этой функции в этой же точке. Такая ситуация произошла именно из-за того, что точка х = является выколотой.

Сразу заметим, что непосредственно в практических задачах пределы почти не используются. В связи с этим эта тема изучается в школьном курсе довольно поверхностно, не дается строгое определение предела функции (предполагается, что это понятие интуитивно понятно), а также не рассматриваются примеры на вычисление пределов функций. С другой стороны, на понятии предела построены почти все строгие рассуждения и доказательства в математическом анализе. В частности, определение понятие производной (которая имеет огромное практическое применение) дается именно с помощью предела. Поэтому полностью исключить пределы из школьного курса нельзя.

Приращение аргумента и функции

Часто нас интересует, как изменяется функция при изменении аргумента. Например, известно, что объем куба вычисляется по формуле

где а – ребро куба. Предположим, что мы провели измерения какого-то куба и выяснили, что длина его ребра равна 2 см. Тогда объем куба составит 2³ = 8 см³. Но ведь любое измерение производится не с абсолютной точностью, а с некоторой погрешностью. Как оценить погрешность вычисления объема, если известна погрешность измерения его ребра?

Пусть с учетом погрешности линейки, составляющей 0,1 см, известно, что длина ребра находится в диапазоне от 2 до 2 + 0,1 = 2,1 см. Тогда максимально возможный объем куба составит 2,1³ = 9,261 см³. Получается, что погрешность в измерении объема куба составляет 9,261 – 8 = 1,261 см³.

С точки зрения математического анализа мы в данном случае рассматривали поведение функции у = х³ в точке х = 2. Мы допустили некоторое изменение величины х, которое называют приращением аргумента и обозначают как ∆х. Далее мы высчитали, какое изменение величины у, или приращение функции, обозначаемое как ∆у, соответствует этому приращению аргумента. Выяснилось, что приращению ∆х = 0,1 соответствует приращение ∆у = 1,261.

В более общем случае произвольной функции у = f(x) можно дать некоторое приращение ∆х в некоторой точке х₀. В результате этого изменится и само значение f(x), причем величину этого изменения обозначают как ∆у. Это можно проиллюстрировать графически:

Задание. Дана функция у = 3х² + х + 4. Вычислите приращение функции в точке х₀ = 5, если ∆х = 1.

Решение. Сначала вычислим новое значение аргумента функции, с учетом данного ему приращения:

Далее вычислим значения функции, соответствующие старому и новому аргументу:

Задание. Радиус круга, измеренный с погрешностью не более 0,5 см в меньшую сторону, равен 10 см. Оцените погрешность вычисления его площади.

Решение. Площадь круга рассчитывается по формуле:

Средняя скорость изменения функции

Часто в физике и других естественнонаучных дисциплинах одни величины характеризуют изменение других величин. Классический случай – это скорость, которая характеризует, насколько быстро изменилось положение тела (или материальной точки в пространстве). Рассмотрим пример. Пусть пешеход движется по прямой улице с постоянной скоростью 2 м/с. Попытаемся построить график, который иллюстрирует зависимость пройденного пешеходом пути и его скорости от времени. Известно, что при равномерном прямолинейном движении пройденный путь можно найти по формуле:

S = v*t

Где s – путь;

V – скорость;

t – время.

Так как скорость равна 2 м/с, то зависимость пути от времени будет выглядеть так:

s(t) = 2t

которая является прямой пропорциональностью. Поэтому ее график будет прямой линией:

Так как скорость во время всего движения остается равной 2 м/с, то зависимость скорости от времени будет иметь вид v = 2, а выглядеть она будет как горизонтальная линия:

В данном случае найти зависимости s(t) и v(t) было очень легко. Но теперь усложним задачу. Пусть зависимость s(t) задается не прямой линией, а некоторой кривой:

Можно ли теперь что-то сказать о скорости движения пешехода?

Ясно, что в различные моменты времени скорость пешехода различна. Но мы можем найти среднюю скорость пешехода в какой-то момент времени. Например, рассмотрим промежуток времени со 2-ой по 10-ую секунду.

Его протяженность, очевидно, равна 10 – 2 = 8 секундам. Если первый момент времени обозначить как t₁, а второй как t₂, то протяженность этого промежутка времени (∆t) можно вычислить по формуле

Судя по графику, к моменту времени t₁ пешеход прошел только 1 метр, а на момент t₂он преодолел уже 9,5 м. Сколько же метров он прошел за промежуток времени ∆t? Если первое расстояние обозначить как s₁, а второе как s₂, то пройденное расстояние (∆s) можно рассчитать так:

Тогда средняя скорость на рассматриваемом участке можно вычислить, поделив ∆s на ∆t

В данной ситуации мы рассматривали функцию, которая задает зависимость между перемещением пешехода и временем. Средняя скорость характеризует, как быстро двигается пешеход, то есть как быстро функция s(t) меняет своё значение. Очевидно, что в данном случае величина ∆t – это некоторое приращение аргумента функции s(t), в то время как ∆s– это приращение самой функции. Получается, что с помощью приращений можно вычислять среднюю скорость объектов.

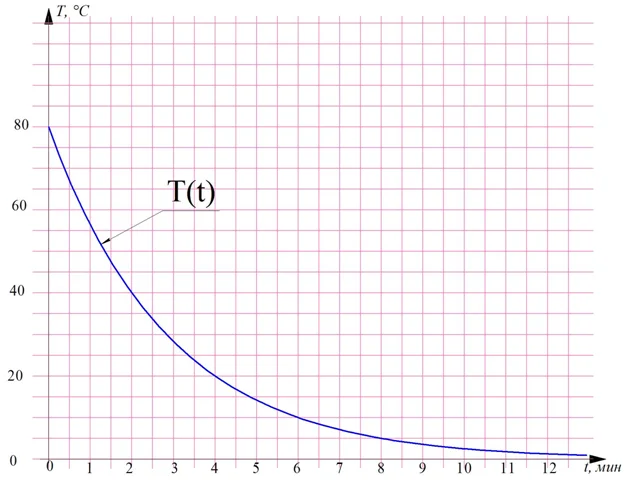
Однако в физике рассматривается не только скорость перемещения вточек пространстве. Например, можно говорить о скорости остывания горячего чайника. Пусть его температура меняется по закону, график которого представлен на рисунке:

Можно ли узнать, с какой средней скоростью остывал чайник на промежутках от 2-ой до 4-ой минуты? Да, для этого надо в точке t = 2 мин дать приращение аргумента ∆t = 2мин и посмотреть, какое приращение ∆T получит сама функция:

Пусть t₁ = 2 мин, а t₂ = 4 мин. Тогда

По графику видно, что в момент t₁ температура чайника составляет Т₁ = 40°С. Через две минуты она уже упала до отметки Т₂ = 20°С. Получается, что за промежуток ∆t функция T(t) получила приращение

Обратите внимание, что приращение оказалось отрицательным. Дело в том, что температура чайника падала, то изменялась в меньшую сторону. Знак минус указывает именно на направление изменения функции. Если бы чайник нагревался, то приращение оказалось бы положительным.

Теперь мы можем вычислить среднюю скорость остывания чайника на промежутке между 2-ой и 4-ой минутой:

Знак минус указывает на то, что температура на этом промежутке времени уменьшается, а не возрастает.

В более общем случае, когда у нас есть произвольная функция у = f(x), с помощью приращений можно вычислить среднюю скорость её изменения на каком-нибудь промежутке. Пусть первая точка промежутка обозначается как х₀, а его протяженность составляет ∆х. Тогда первой точке соответствует значение функции у(x₀), а концу промежутка – значение у(x₀ + ∆x):

Тогда средняя скорость изменения функции на промежутке [x₀;x₀ + ∆x] рассчитывается по формуле:

Мгновенная скорость и понятие производной

Итак, зная функцию, можно вычислить среднюю скорость ее изменения на любом промежутке. Но, когда автомобиль едет по шоссе, его спидометр показывает не среднее, а конкретное значение скорости в каждый момент времени. Другими словами, у автомобиля есть мгновенная скорость, и именно ее показывает спидометр. Как же узнать ее?

Пусть у нас есть функция s(t), определяющая пройденной машиной путь, и нам требуется найти мгновенную скорость в некоторый момент времени t₁. Мы можем дать функции s(t) приращение ∆t, а потом найти и среднюю скорость на промежутке [t₁; t₁ + ∆t]. Естественно, она будет являться лишь некоторым приближением, с помощью которого мы оцениваем мгновенную скорость в момент t₁. Однако далее мы можем уменьшить промежуток ∆t. Тогда у нас получится иное значение средней скорости, которое будет более близким к мгновенной скорости. Чем меньший промежуток ∆t мы возьмем, тем ближе к мгновенной скорости в точке t₀ будет полученное нами значение средней скорости.

Например, пусть путь, пройденный машиной, задается функций s = t². Нас интересует скорость автомобиля в момент t₁ = 5 сек. Мы можем найти среднюю скорость на интервале от 5-ой до 6-ой секунды. Так, к пятой секунде машина успеет проехать 5² = 25 метров, а к шестой секунде она проедет 6² = 36 метров. Получится, что за промежуток ∆t, равный 6 – 5 = 1 секунде, машина проедет путь ∆s = 36 – 25 = 11 метров. Тогда средняя скорость на промежутке составит

Теперь возьмем более короткий промежуток ∆t, равный всего лишь 0,1 с. То есть мы рассмотрим период времени между моментом t₁ = 5 cи t₂ = 5,1 c. Снова-таки, к 5-ой секунде машина проедет 25 метров, а к моменту 5,1 сона пройдет 5,1² = 26,01 м. То есть за 0,1 с автомобиль преодолеет 26,01 – 25 – 1,01 м, а средняя скорость при этом составит

Ещё раз уменьшим промежуток ∆t. Пусть теперь он составляет всего 0,01с. Тогда средняя скорость будет определяться так:

Видно, что при уменьшении промежутка ∆t средняя скорость стремится к величине 10 м/с. Поэтому логично считать именно эту величину мгновенной скоростью машины в момент времени t = 5 c. Однако возникает вопрос – уверены ли мы, что мгновенная скорость стремится именно к 10 м/с, а не, скажем, к 10,001 м/с? Как точно определить это число? Здесь как раз помогают пределы. Можно записать, что мгновенная скорость – это предел отношения ∆s/∆t при ∆t, стремящемся к нулю. То есть

Получили, что мгновенная скорость в момент t₁ = 5 действительно равна 10 м/с.

Задание. Вычислите мгновенную скорость разгоняющегося самолета через 10 секунд после начала разгона, если пройденное им расстояние задается законом s(t) = 5t².

Решение. За 10 секунд самолет успеет преодолеть

Дадим функции s(t) приращение ∆t и обозначим как t₁ момент времени, когда со старта прошло 10 секунд. Тогда к моменту t₁ + ∆t самолет успеет пройти

Решая данную задачу, мы дали функции s(t) приращение ∆t и записали отношение ∆s/∆t. Далее мы устремили величину ∆t к нулю и посмотрели, к какому числу устремится отношение ∆s/∆t. Это число и оказалось мгновенной скоростью. В более общем случае произвольной функции у = f(x)в точке х₀ можно дать приращение аргумента ∆х, которому будет соответствовать некоторое приращение функции ∆у. Далее можно вычислить предел отношения ∆у/∆х, который будет характеризовать, как быстро в точке х₀ функция меняет свое значение. Этот предел называют производной функции в точке х₀. Для обозначения производной над функцией ставят штрих.

В общем случае алгоритм вычисления производной в некоторой точке следующий:

1.Фиксируем точку х₀, вычисляем для нее значение функции у(х). Это значение будет конкретным числом

1. Даем функции приращение аргумента ∆х, переходим в новую точку х₀ + ∆х, вычисляем в ней значение функции у(х₀ + ∆х). Это значение будет не числом, а выражением, содержащим переменную ∆х.
2. Находим приращение функции ∆у, используя формулу

Это приращение также должно содержать величину ∆х.

1. Составляем соотношение ∆у/∆х.
2. Находим предел этого отношения при ∆х→0. Этот предел и есть значение производной.

Задание. Найдите производную функции у = 4х² + 7х в точке х₀ = 2.

Решение. Сначала вычислим значение функции в точке х₀:

Далее определяем величину у(х₀ + ∆х) (это будет не конкретное число, а некоторое выражение, содержащее переменную ∆х):

Задание. Найдите производную функции у = 1/х в точке х₀ = 5.

Решение. Высчитаем у(х₀):

Пусть у функции есть приращение ∆х, тогда в точке х₀ + ∆х ее значение составит:

В рассмотренных примерах для вычисления производной мы использовали ее определение. Однако на практике такой метод почти не используется. В будущем мы узнаем более эффективные способы для нахождения производной.

Мы уже убедились, что использование производной помогает находить мгновенную скорость тел. По этой причине понятие производной функции играет огромную роль в механике (разделе физике, изучающем движение). Однако этим ее практическое применение не ограничивается. По сути, она является основой для всей классической физики, и именно ее появление в XVII в. обеспечило выдающийся прогресс в науке вплоть до конца XIX в. При этом производная используется и в геометрии для анализа графиков функций. Более подробно ее применение будет также рассмотрено позже.

Как связаны путь и перемещение?

Путь и перемещение в общем случае не равны друг другу.

Рассмотрим траекторию движения тела из точки А в точку D:

За начало отсчета примем точку А.

За время t₁ точка проходит путь

S₁ = AB

а за время t₂ путь

S₂ = AC

Путь S от точки B до точки C равен AC минус AB

S = S₂ — S₁

Если расстояние от B до C мало, отрезок траектории практически совпадает с вектором перемещения (см. Связь траектории и вектора перемещения):

S = ±|r|

т.е. путь (очень малый его отрезок) равен модулю вектора перемещения, взятому с соответствующим знаком (на рисунке вектор показан укрупненно).

Обратите внимание, что мы рассматриваем не всю траекторию, а только очень маленький её участок. Утверждать, что весь путь от А до D равен модулю вектора перемещения R будет ошибкой. Правильное решение – это разбить путь на очень короткие участки и на них рассматривать вектор перемещения. Для таких участков путь можно приравнять к модулю вектора перемещения.

Итак, приращение пути (очень малое приращение) равно модулю соответствующего приращения вектора перемещения, взятому с соответствующим знаком.