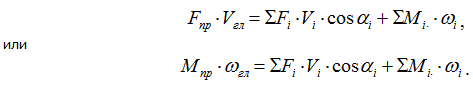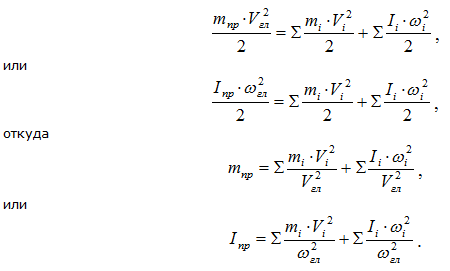Как найти приведенный момент инерции

3.1.9.1 Приведенные силы и моменты

При исследовании
движения механизма, находящегося под
действием заданных сил, удобно все силы,
действующие на звенья, заменять силами,
приложенными к одному из звеньев
механизма. Такие заменяющие силы получили
название приведенных сил.

Приведенная
силаилиприведенный момент– условная сила или момент пары сил,
которые приложены к звену приведения
и развивают мощность, равную сумме
мощностей, развиваемых звеньями. Т.е.:

Р_пр=∑N_i/υ_пр;
(3.41)

М_пр=∑N_i/ω_пр,
(3.42)

где N_i
— мощность, развиваемаяi-тымзвеном;υ_пр— линейная
скорость звена приведения,ω_пр– угловая скорость звена приведения.

Звено механизма,
к которому приложена приведенная сила,
называется звеном приведения.
Точка приложения приведенных сил
называетсяточкой приведения.
За звено приведения обычно принимается
звено, закон движения которого задан.
Таким звеном является кривошип.

Известно, что
мощность приведенных сил, есть производная
работы по времени

N_i
= dA/dt.
(3.43)

Работа есть
произведение силы на расстояние

dA/dt= (Р_прdS)/dt. (3.44)

Т.к. производная
расстояния по времени есть скорость
(dS/dt=υ_пр), то

dA/dt=Р_прυ_пр(3.45)

или, учитывая формулы (3.43) и
(3.45), имеем:

N_i
= Р_прυ_пр.
(3.46)

Работа вычисляется
по формуле (см. п. 3.1.6):

dA/dt=Р_ίυ_ίcosα_ί
+ М_ίω
_ί

или, учитывая уравнение (3.43),
получим:

N_i=
Р_ίυ_ίcosα_ί
+ М_ίω
_ί.
(3.47)

Приравнивая
равенства (3.46) и (3.47)

Р_прυ_пр
=Р_ίυ_ίcosα_ί
+ М_ίω
_ί

и, выразив приведенную силу,
получим выражение для Р_пр

.
(3.48)

Приведенный
момент и приведенная сила связаны между
собой зависимостью

М_пр=
Р_прℓ_ОА =
(Нм). (3.49)

Подставив формулу
Р_прв формулуМ_при, учитывая, чтоℓ_ОА=
υ_пр/ω_пр,
получим

.
(3.50)

Сравнивая формулы
(3.48) и (3.34) из п. 3.1.6, увидим идентичность
этих выражений. Поэтому имеет место
следующий вывод.

Рур А Рпр 1 О

Приведенная сила, также как и уравновешивающая, приложена перпендикулярно кривошипу (звену приведения), равна ей по величине, но противоположна по направлению, т.е.: Рпр=-Рур.

Поэтому, чтобы
определить приведенную силу, можно
воспользоваться соотношениями (3.34),
(3.48), использовать последовательный
силовой расчет механизма и ведущего
звена или применить «жесткий» рычаг
Н.Е. Жуковского.

3.1.9.2 Приведенные массы и приведенные моменты инерции.

Кинетическая энергия
механизма

Для начала
рассмотрим кинетическую энергиюмеханизма.

При поступательном движении
кинетическая энергия вычисляется по
формуле:

Т_пост==(Дж).

Для вращательного движения
формула кинетической энергии имеет
вид:

Т_вр==(Дж).

Для звена, имеющего сложное
(плоскопараллельное) движение, кинетическая
энергия будет вычисляться следующим
образом:

Т_сл=
=(Дж).

Кинетическая
энергия всего механизма будет равна
сумме кинетических энергий отдельных
его звеньев:

Т_мех =
=(Дж), (3.51)

где m_i
— массаi-того звена,υ_i —
скоростьi-того звена,
J_Si
— осевой момент инерцииi-того
звена,ω_i
— угловая скоростьi-того
звена.

Теперь определим,
как находятся приведенная масса и
приведенный осевой момент инерции. Для
начала дадим их определение.

Приведенная
масса(приведенный момент
инерции) – условная масса (условный
момент инерции), сосредоточенные в точке
приведения, кинетическая энергия которых
равна сумме кинетических энергий всех
звеньев механизма, т.е.:

m_пр==(кг); (3.52)

J_пр=
= (кгм²).
(3.53)

Подставляя
выражение (3.51) в формулы (3.52) и (3.53),
получим:

m_пр=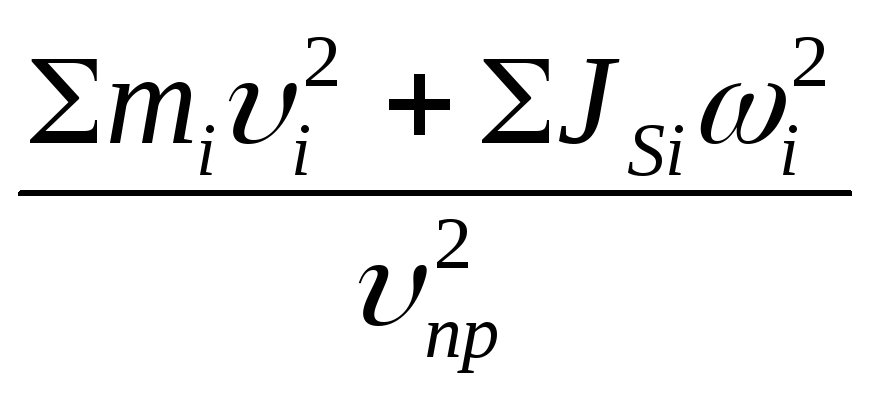=(кг);
(3.54)

J_пр
=
= (кгм²).
(3.55)

Приведенная
масса и приведенный момент инерции
связаны между собой соотношениями:

J_пр=
m_прℓ_ОА= (кгм²).
(3.56)

Сравнивая формулы
(3.51), (3.54) и (3.55), можно заметить, что
числители одинаковы. Поэтому, зная связь
между Т, J_приm_пр, можно
легко определить каждую из этих величин.

Вопросы
для самоконтороля

1. Дайте
   определение силе движущей, силе
   сопротивления.

2. Напишите
   формулу, по которой определяется модуль
   главного вектора силы инерции звена.
   Расскажите, как направлен этот вектор.

3. Расскажите
   о последовательности определения
   реакций в многозвенном механизме.

4. Расскажите
   о последовательности определения
   реакций в группе Ассура.

5. Расскажите,
   как с помощью рычага Н.Е. Жуковского
   определить уравновешивающую силу
   (уравновешивающий момент).

6. Что
   называют механической характеристикой
   машины? Индикаторной диаграммой
   двигателя?

7. Дайте
   определение приведенной силы (приведенного
   момента), приведенной массы (приведенного
   момента инерции звеньев механизма).

8. Докажите,
   что приведенный момент инерции звеньев
   механизма не зависит от угловой скорости
   звена приведения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

6. Динамика машин

Основными задачами этого раздела являются определение фактической угловой скорости ведущего звена и определение момента инерции маховика, необходимого для поддержания изменения угловой скорости в заданных пределах.

6.1. Вспомогательные задачи динамики машин

Динамическая модель машины

        В связи с необходимостью упрощения расчётной схемы и большей наглядности, а также сокращения расчётов реальную машину заменяют её моделью, сохраняющей те свойства машины, которые изучаются на данном этапе исследования. Такая модель представляет собой некоторый условный диск, вращающийся с кривошипом  как одно целое, т. е. с его угловой скоростью (рис. 6.1), обладающий так называемым приведённым моментом инерции. На этой основе кривошип или другое ведущее звено, с которым связан условный диск, называется звеном приведения. На диск  действуют приведённый момент движущих сил, направленный в сторону вращения, и приведённый момент сил сопротивления, направленный навстречу вращению.

На схеме рис. 6.1 обозначены  — приведённый момент инерции механизма,  — приведённый момент движущих сил и  — приведённый момент сил сопротивления.

Приведённый момент инерции

Приведённым моментом инерции механизма называется момент инерции условного диска, которым заменяется реальный механизм, обладающего кинетической энергией, равной сумме кинетических энергий всех звеньев механизма.

Кинетическая энергия условного диска , где , т. е. угловая скорость звена приведения, равная угловой скорости кривошипа.

Рекомендуемые материалы

Кинетическая энергия звена, совершающего поступательное движение, , где  – масса звена,  – скорость звена.

Кинетическая энергия звена, совершающего вращательное движение, , где  – момент инерции звена,  – угловая скорость звена.

Кинетическая энергия звена в плоскопараллельном движении , где  – масса звена, – скорость центра масс звена, – момент инерции звена относительно его центра масс,  – угловая скорость звена. Согласно определению имеем:

.

Подставив сюда записанные выше выражения кинетических энергий и, решая затем полученное равенство относительно , запишем

.

Как видно из этой формулы, приведённый момент инерции зависит от структуры механизма, от массовых характеристик звеньев, от положения механизма и не зависит от угловой скорости ведущего звена. Некоторые механизмы имеют постоянное значение приведённого момента инерции. Машины, в основе которых механизмы с , называются ротативными.

Приведённый момент сил сопротивления

Приведённым моментом сил сопротивления называется момент, приложенный к звену приведения, мгновенная мощность которого равна сумме мгновенных мощностей всех сил сопротивления, действующих в механизме.

Мгновенная мощность приведённого момента сопротивления  . Мгновенная мощность -той силы сопротивления  . Согласно определению , поэтому, подставив сюда соответствующие выражения, получаем , откуда

.

Если среди сил сопротивления имеются моменты, то их можно представить в виде пар сил с плечами, равными длинам соответствующих звеньев.

З а м е ч а н и е . Если во всех математических выражениях заменить силы сопротивления  движущими силами, то в результате получится приведённый момент движущих сил:                            

.

Зависимость приведённых моментов сил от угла поворота, скорости или времени называется механической характеристикой машины.

6.2. Характеристика режимов движения машин

Анализ динамики машин производится на основе теоремы об изменении кинетической энергии системы: изменение (приращение) кинетической энергии системы на её возможном перемещении равно сумме работ всех внешних и внутренних сил на этом перемещении, то есть

,

где   –кинетическая энергия системы в данный момент времени; – кинетическая энергия системы в последующий момент времени; – работа движущих сил при перемещении системы из -го до -го положения системы; – работа сил сопротивления на том же перемещении системы. Сумма работ в правой части равенства называется избыточной работой .

В зависимости от соотношения величин правой части этого равенства различают следующие режимы (виды) движения машин.

I. Неустановившийся режим

А) Пуск (разбег). Этот режим имеет место при соотношении работ   или . Тогда в левой части имеет место соотношение , т. е. кинетическая энергия машины возрастает, и возрастает угловая скорость . Графически это можно представить как на рис. 6.2.

Б). Остановка (выбег) имеет место при обратном соотношении работ, т. е.  и . При этом кинетическая энергия машины убывает, и угловая скорость также убывает. Графически этот режим представлен на рис. 6.3. Оба режима не являются рабочими, так как не могут продолжаться долго. Режим пуска заканчивается, когда угловая скорость начинает повторять свои значения, а режим остановки заканчивается полной остановкой машины. При исследовании этих режимов, кроме закона изменения угловой скорости, определяется время пуска или, соответственно, остановки.

II.Установившийся режим

А) Неравновесный. Режим характеризуется тем, что работа движущих сил то больше, то меньше работы сил сопротивления, т. е. в течение цикла имеют место следующие соотношения  и . Но за цикл работы машины эти величины  одинаковы , так что в начале  и в конце цикла .   

  В результате таких соотношений работ кинетическая энергия машины и угловая скорость ведущего звена в течение цикла изменяются периодически, причём средние значения как кинетической энергии, так и угловой скорости остаются постоянными. Графически характер изменения кинетической энергии и угловой  скорости представлен на рис. 6.4. Средняя угловая скорость определяется соотношением   . Величина, характеризующая отклонение максимальной и минимальной угловой скорости от её среднего значения, называется коэффициентом неравномерности . Численно коэффициент  равен .

Для поддержания изменения угловой скорости в заданных пределах в машинах применяют маховики, представляющие собой колёса с массивным ободом, устанавливаемые на вал ведущего звена и вращающиеся с его угловой скоростью.

Данный режим является рабочим, так как может продолжаться неопределённо долго. В этом режиме работают все машины циклического действия.

Б) Равновесный. Этот режим имеет место в тех машинах, в которых работа движущих сил постоянно равна работе сил сопротивления, т. е. . Избыточная работа в течение всего цикла равна нулю, . Кинетическая энергия и угловая скорость остаются постоянными (рис. 6.5).

Такой режим работы характерен для ротативных машин.

6.3. Уравнения движения машин

Уравнение движения в интегральной форме

Основой для вывода уравнения служит соотношение между работой и энергией, вытекающее из теоремы об изменении кинетической энергии системы: , которое можно представить в виде равенства . В этом равенстве: – текущее значение кинетической энергии, – начальное значение кинетической энергии, – работа движущих сил, выполненная от начального до текущего момента времени, – работа сил сопротивления, выполненная за то же время.

Величины энергий и работ определяются следующими равенствами:

,  , , .

Подставляя эти выражения в вышезаписанное равенство, получаем окончательный вид уравнения:

.

В правой части уравнения подынтегральные выражения представляют собой функции от угла поворота кривошипа, т.е. перемещения. Это значит, что данные функции могут быть определены, только если внешние силы также зависят от перемещений. Данное обстоятельство определяет область применения уравнения в интегральной форме.

Уравнение в дифференциальной форме

Внешние силы, действующие в машинах, могут зависеть не только от перемещений, но и от скоростей, и от времени. В этих случаях уравнение в интегральной форме неприменимо. Для исследования динамики таких машин применяют более универсальное уравнение –уравнение в дифференциальной форме. Оно может быть получено из уравнения в интегральной форме путём дифференцирования по .

.

Сделав замену  и затем, выполнив несложные преобразования, получим  окончательно   .

Первое слагаемое левой части представляет собой момент сил инерции, как следствие изменения . Второе слагаемое представляет также момент сил инерции,  но как результат изменения .

6.4. Назначение и приближённое определение

момента инерции маховика

Маховик служит для уменьшения колебаний величины угловой скорости ведущего звена, уменьшения угловых ускорений и, в конечном итоге, инерционных воздействий. Этот эффект, называемый кинематическим, тем больше, чем больше момент инерции маховика. Кинематический эффект тесно связан с динамическим, который заключается в том, что маховик выступает как аккумулятор кинетической энергии. Он накапливает кинетическую энергию в те промежутки времени, когда возрастает его угловая скорость, принимая на себя часть избыточной работы, которая в этом случае не тратится на разгон машины. При уменьшении угловой скорости маховик отдаёт часть накопленной энергии, помогая движущим силам выполнять полезную работу и препятствуя существенному уменьшению угловой скорости. Некоторые машины, например машины ударного  действия, без такой помощи не смогли бы функционировать.

       Для расчёта момента инерции маховика примем допущение, что максимальный перепад   кинетической энергии машины, численно равный максимальному перепаду избыточной работы, поглощается маховиком. Для иллюстрации этого служит рис. 6.6. Допущение здесь заключается в том, что часть кинетической энергии поглощается звеньями механизма, чем мы пренебрегаем.  Обозначим перепад избыточной работы . Согласно принятому допущению эта величина   составляет разность   между максимальным и минимальным значениями кинетической энергии маховика:                                   ,

то есть                                                      .

Максимальная величина кинетической энергии маховика вычисляется по формуле

,

минимальная величина вычисляется по формуле

.

 Поэтому  разность этих величин даёт выражение

.

Разложив разность квадратов в скобках на множители и заменив последние их выражениями, полученными из приведенных выше формул для вычисления  и , получаем                                                                                                       

                            .

Объединяя  результаты выкладок, запишем  и , откуда окончательно получаем

.

Как видно из этой формулы, достичь полного постоянства угловой скорости невозможно, так как для этого необходимо иметь бесконечно большой маховик (требуется ). Ясно также, что увеличение скорости вращения маховика ведёт к уменьшению его массы и размеров, поэтому целесообразно маховик устанавливать на более быстроходный вал.

Вопросы для самопроверки

1. Какие задачи решаются при исследовании динамики машин?

2. Что представляет собой динамическая модель машины?

3. Что называется приведённым моментом инерции механизма?

4. Что называется приведённым моментом сил?

5. Какая теорема механики положена в основу уравнений динамики машин?

6. Как записать кратчайшую форму уравнения динамики?

7. Какие существуют виды (режимы) движения машин?

8. Чем характеризуются пуск, остановка и установившийся режим работы машин?

В лекции «1.8 Направляющие косинусы вектора» также много полезной информации.

9. Что такое коэффициент неравномерности движения машины?

10. Как определяется средняя величина угловой скорости ведущего звена?

11. Для чего предназначен маховик в машине?

12. Какое допущение принято для приближённого определения момента инерции маховика?

13. В чём заключается кинематический и динамический эффект действия маховика?

14. Как определяется момент инерции маховика?

 Приведенный момент сил и приведенный момент инерции.

Условный момент, приложенный к звену приведения, называется моментом приведения (приведенным моментом сил). Момент приведения равен совокупности всех моментов и сил, приложенных к звеньям механизма. Приведенный момент движущих сил M, приложенный к звену приведения, определяется из условия равенства мгновенных мощностей. Мощность, развиваемая M, равна сумме мощностей, развиваемых силами и моментами сил, действующих на звенья машинного агрегата.

Условный момент инерции звена приведения называется приведённым моментом инерции. Для каждого положения механизма приведенный момент инерции звеньев находится по формуле:

где m_i – масса звена i, J_si – момент инерции звена i относительно оси, проходящей через центр масс S_i звена, w_i – угловая скорость звена i, V_si – скорость центра масс звена i.

Приведенным моментом сил называется момент (М_пр), приложенный к звену приведения и развивающий мощность, равную сумме мощностей всех сил и моментов сил, приложенных к звеньям механизма.

Приведенный момент инерции J_np представляет собой момент инерции звена приведения, обладающий кинетической энергией, равной сумме кинетических энергий всех движущихся звеньев механизма.

1. Уравнения движения машинного агрегата в энергетической и дифференциальной формах.

Для определения законов движения начальных звеньев за заданными силами используются уравнения, которые называются уравнениями движения механизма. Число этих уравнений равняется числу степеней подвижности механизма.

Уравнения движения механизма могут быть представлены в разных формах. Для механизмов с одной степенью вольности одна из самых простых форм уравнений получается на основе теоремы об изменении кинетической энергии: изменение кинетической энергии механизма на некотором перемещении равняется сумме работ всех сил, которые действуют на звенья механизма на этом самом перемещении. Данный закон в виде уравнения: Т-Т₀=∑А (1), где Т – кинетическая энергия механизма в произвольном положении; Т₀ – кинетическая энергия механизма в положении, которое принимается за начальное; ∑А – сумма работ всех сил и моментов, которые прилагаются к механизму на некотором перемещении. Работу осуществляют все активные силы и моменты и силы трения во всех кинематических парах механизма. Уравнение движения в энергетической форме. Сведем все силы и моменты механизма с одной степенью вольности к одному звену возведения, то есть заменим рассматриваемый механизм его динамической моделью. Поскольку вся нагрузка, прилагаемая к модели, выражается возведенным моментом М_ЗВ, то правая часть уравнения (1) равняется:

 (2)

 а именноуравнение (1), учитывая, можно записать в виде

(3)

Уравнение (3) называют уравнением движения механизма в энергетическом виде, или – в форме уравнения кинетической энергии.

Уравнение движения механизма в дифференциальном видесодержит вторые производные от координат по времени. Изменение кинетической энергии механизма равно приращению работ сил действующих на механизм:

В случае если начальное звено совершает вращательное движение:   , тогда