Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ — это общий член ряда. $n$ — это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ — первый член прогрессии, а $q$ — основание. В данном случае сумма равна $S = frac{1}{1 — frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |
Признаки сходимости числовых рядов
На
практике часто не столь важно найти
сумму ряда, как ответить на вопрос о
сходимости ряда. Для этой цели используются
признаки сходимости, основанные на
свойствах общего члена ряда.
Необходимый признак сходимости ряда
ТЕОРЕМА
1
Если
ряд
сходится, то его общий член
стремится к нулю при
,
т.е.
.
Кратко:
если ряд сходится, то его общий член
стремится к нулю.
Доказательство.
Пусть ряд сходится и его сумма равна
.
Для любого
частичная сумма
.
Тогда
.
Из
доказанного необходимого признака
сходимости вытекает достаточный
признак расходимости ряда:
если при
общий член ряда не стремится к нулю, то
ряд расходится.
Пример
4. Исследовать
на сходимость ряд
Решение
Для
этого ряда общий член
и
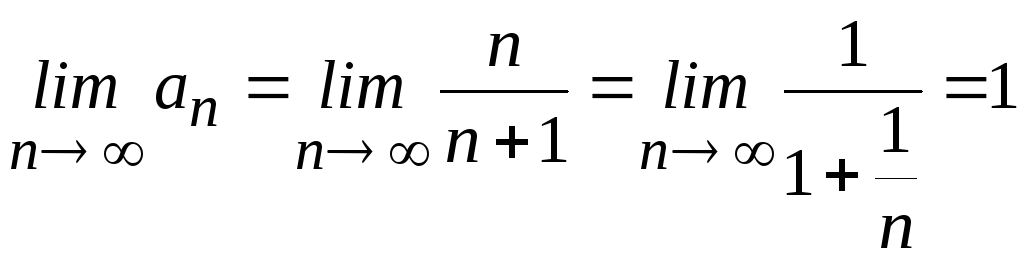
Следовательно,
данный ряд расходится.
Пример
5. Исследовать
на сходимость ряд
Решение
Очевидно,
что общий член этого ряда, вид которого
не указан ввиду громоздкости выражения,
стремится к нулю при
,
т.е. необходимый признак сходимости
ряда выполняется, однако этот ряд
расходится, так как его сумма
стремится к бесконечности.
Знакоположительные числовые ряды
Числовой
ряд, все члены которого положительны,
называется знакоположительным.
ТЕОРЕМА
2 (Критерий сходимости знакоположительного
ряда)
Для
сходимости знакоположительного ряда
необходимо и достаточно, чтобы все его
частичные суммы были ограничены сверху
одним и тем же числом.
Доказательство.
Так как для любого
,
то,
т.е. последовательность– монотонно возрастающая, поэтому для
существования предела необходимо и
достаточно ограничение последовательности
сверху каким-либо числом.
Эта
теорема в большей степени имеет
теоретическое, чем практическое значение.
Далее приведены другие признаки
сходимости, имеющие большее применение.
Достаточные признаки сходимости знакоположительных рядов
ТЕОРЕМА
3 (Первый признак сравнения)
Пусть
даны два знакоположительных ряда:
(1)
и
(2)
причем,
начиная с некоторого номера
,
для любоговыполняется неравенство
Тогда:
-
из
сходимости ряда
следует сходимость ряда
;
-
из
расходимости ряда
следует расходимость ряда
.
Схематическая
запись первого признака сравнения:
сход.сход.
расх.расх.
Доказательство.
1) Так как отбрасывание конечного числа
членов ряда не влияет на его сходимость,
докажем теорему для случая
.
Пусть для любогоимеем
, (3)
где
и
—
соответственно частичные суммы рядов
(1) и (2).
Если
ряд (2) сходится, то существует число
.
Поскольку
при этом последовательность
— возрастающая, ее предел больше любого
из ее членов, т.е.
для
любого
.
Отсюда
из неравенства (3) следует
.
Таким
образом, все частичные суммы ряда (1)
ограничены сверху числом
.
Согласно
теореме 2 этот ряд сходится.
2)
Действительно, если бы ряд (2) сходился,
то по признаку сравнения сходился бы и
ряд (1).
Для
применения этого признака часто
используют такие ряды-эталоны, сходимость
или расходимость которых известна
заранее, например:
-
—
геометрический
(он сходится при
и расходится при
);
-
–гармонический
(он расходится);
3)
— ряд
Дирихле (он сходится при
и расходится при
).
Кроме
этого часто используют ряды, которые
можно получить с помощью следующих
очевидных неравенств:
,
,
,
.
Рассмотрим
на конкретных примерах схему исследования
знакоположительного ряда на сходимость
с помощью первого признака сравнения.
Пример
6. Исследовать
ряд
на сходимость.
Решение
Шаг
1. Проверим знакоположительность ряда:
для
Шаг
2. Проверим выполнение необходимого
признака сходимости ряда:
.
Так как,
то
(если
вычисление предела вызывает трудности,
то этот шаг можно пропустить).
Шаг
3. Используем первый признак сравнения.
Для этого подберем для данного ряда
ряд-эталон. Так как
,
то в качестве эталона можно взять ряд,
т.е. ряд Дирихле. Этот ряд сходится, так
как показатель степени.
Следовательно, согласно первому признаку
сравнения сходится и исследуемый ряд.
Пример
7.
Исследовать ряд
на сходимость.
Решение
1)
Данный ряд знакоположительный, так как
для
2)
Необходимый признак сходимости ряда
выполняется, ибо
.
3)
Подберем ряд-эталон. Так как
,
то в качестве эталона можно взять
геометрический ряд
.
Этот ряд сходится, следовательно,
сходится и исследуемый ряд.
ТЕОРЕМА
4 (Второй признак сравнения)
Если
для знакоположительных рядов
и
существует отличный от нуля конечный
предел
,
то
ряды
сходятся или расходятся одновременно.
Доказательство.
Пусть ряд (2) сходится; докажем, что тогда
сходится и ряд (1). Выберем какое-нибудь
число
,
большее,
чем
.
Из
условия
вытекает
существование такого номера
,
что для всех
справедливо неравенство
,
или,
что то же,
(4)
Отбросив
в рядах (1) и (2) первые
членов (что не влияет на сходимость),
можно считать, что неравенство (4)
справедливо для всех
Но ряд с общим членом
сходится
в силу сходимости ряда (2). Согласно
первому признаку сравнения, из неравенства
(4) следует сходимость ряда (1).
Пусть
теперь сходится ряд (1); докажем сходимость
ряда (2). Для этого следует просто поменять
ролями заданные ряды. Так как
то,
по доказанному выше, из сходимости ряда
(1) должна следовать сходимость ряда
(2).
Если
при
(необходимый признак сходимости), то из
условия,
следует, чтои
– бесконечно малые одного порядка
малости (эквивалентные при).
Следовательно, если дан ряд
,
где
при
,
то для этого ряда можно брать ряд-эталон
,
где общий член
имеет тот же порядок малости, что и общий
член данного ряда.
При
выборе ряда-эталона можно пользоваться
следующей таблицей эквивалентных
бесконечно малых при
:
1)
; 4)
;
2)
; 5)
;
3)
; 6)
.
Пример
8.
Исследовать на сходимость ряд
.
Решение
Данный
ряд знакоположительный, так как
для любого
.
Так
как
,
то возьмем в качестве ряда-эталона
гармонический расходящийся ряд.
Поскольку предел отношения общих членови
конечен и отличен от нуля (он равен 1),
то на основании второго признака
сравнения данный ряд расходится.
Пример
9.
Исследовать на сходимость ряд
по двум признакам сравнения.
Решение
Данный
ряд знакоположительный, так как
,
и.
Поскольку,
то в качестве ряда-эталона можно брать
гармонический ряд.
Этот ряд расходится и следовательно,
по первому признаку сравнения, исследуемый
ряд также расходится.
Так
как для данного ряда и ряда-эталона
выполняется условие
(здесь использован 1-й замечательный
предел), то на основании второго признака
сравнения ряд– расходится.
ТЕОРЕМА
5 (Признак Даламбера)
Если
для знакоположительного ряда
существует конечный предел
,
то ряд сходится прии расходится при
.
Доказательство.
Пусть
.
Возьмем какое-либо число,
заключенное
между
и
1:
.
Из условия
следует,
что начиная с некоторого номера
выполняется
неравенство
;
;
(5)
Рассмотрим
ряд
(6)
Согласно
(5) все члены ряда (6) не превосходят
соответствующих членов бесконечной
геометрической прогрессии
Поскольку
,
эта прогрессия является сходящейся.
Отсюда в силу первого признака сравнения
вытекает сходимость ряда
Случай
рассмотрите самостоятельно.
Замечания:
-
Если
,
теорема 5 не дает ответа на вопрос о
сходимости ряда и поэтому необходимо
использовать другие признаки сходимости. -
Признак
Даламбера дает оценку и остатка ряда.
Из неравенства
,
следует,
что остаток ряда
.
-
Признак
Даламбера удобен на практике тогда,
когда общий член ряда содержит
показательную функцию или факториал.
Пример
10.
Исследовать на сходимость ряд
по признаку Даламбера.
Решение
Данный
ряд знакоположительный и
.
(Здесь
при вычислении дважды применено правило
Лопиталя).
Так
как
то
по признаку Даламбера данный ряд
сходится.
Пример
11. Исследовать
на сходимость ряд
.
Решение
Данный
ряд знакоположительный и
.
Поскольку
,
то
данный ряд сходится.
ТЕОРЕМА
6 (Признак Коши)
Если
для знакоположительного ряда
существует
конечный предел
,
то приряд сходится, а при
ряд расходится.
Доказательство
аналогично теореме 5.
Замечания:
-
Если
,
теорема 6 не дает ответа на вопрос о
сходимости ряда и поэтому необходимо
использовать другие признаки сходимости. -
Если
,
то ряд расходится.
Пример
12. Исследовать
на сходимость ряд
.
Решение
Данный
ряд знакоположительный, так как
для любого
.
Поскольку вычисление пределавызывает определенные трудности, то
проверку выполнимости необходимого
признака сходимости ряда опускаем.
Так
как
,
то
по признаку Коши данный ряд расходится.
ТЕОРЕМА
7 (Интегральный признак сходимости
Маклорена — Коши)
Пусть
дан ряд
(7)
члены
которого положительны и не возрастают:
Пусть,
далее
—
функция, которая определена для всех
вещественных
,
непрерывна, не возрастает и
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
Признаки сходимости числового ряда (Таблица)
Необходимый признак сходимости числового ряда
Если сходится, то
Следствие. Если , то
расходится.
Достаточные признаки сходимости знакоположительных рядов
|
Название признака |
Определение |
|
|
Первый признак сравнения |
Если аn ≤ Ьn ∀n то: 1) из сходимости ряда 2) из расходимости ряда |
|
|
Второй признак сравнения |
1) при 0 < c < ∞ 2) при c = 0 из сходимости 3) при с = ∞ из расходимости |
|
|
Признак Даламбера |
|
р < 1, ряд сходится; р > 1, ряд расходится; p = 1, признак не работает |
|
Радикальный признак Коши |
|
|
|
Интегральный признак Коши |
Пусть ƒ(х) — положительная, непрерывная и убывающая функция на [1,∞), такая, что а1 = ƒ(1), а2 = f(2), …, an= ƒ(n), …. Если соответствующий несобственный интеграл |
Рекомендации к использованию признаков сравнения
Рекомендации к использованию признака Даламбера
Признак целесообразно применять, когда общий член содержит n!(n! = 1 · 2 · 3 · 4 · … · n — n-факториал). При n→∞ для приближенного вычисления n! используется формула Стирлинга:
Сходимость знакопеременных рядов
|
Виды сходимости |
Определение |
|
Абсолютная сходимость |
Знакопеременный ряд |
|
Условная сходимость |
Знакопеременный ряд |
|
Достаточный признак сходимости для знакочередующегося ряда |
Теорема (признак Лейбница). Знакочередующийся ряд 1) последовательность абсолютных величин членов ряда монотонно убывает, т.е. ∀n: аn ≥ an+1; 2) |

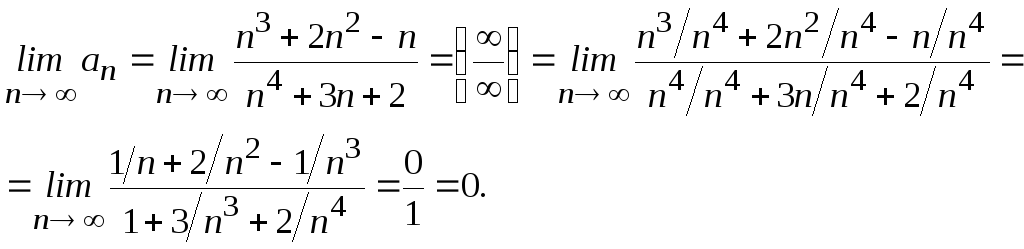
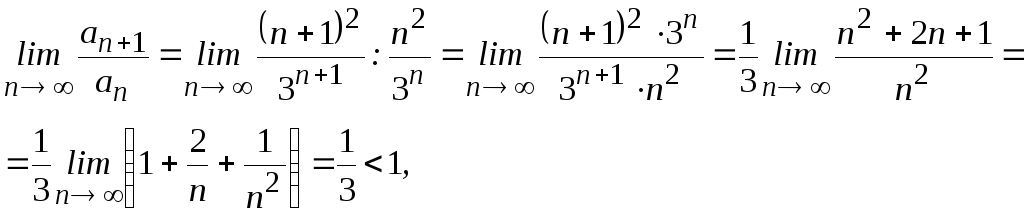
 сходится (расходится), то и ряд
сходится (расходится), то и ряд 
