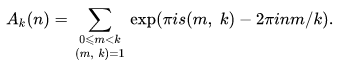Ваш вопрос — наш ответ
Добрый день, решаем с сыном пример к самостоятельной работе к урокам 4-6(задание 2), 1 класс, 2 часть
Вопрос:
Добрый день, решаем с сыном пример к самостоятельной работе к урокам 4-6(задание 2), 1 класс, 2 часть
«Составь выражения и запиши признак разбиения».
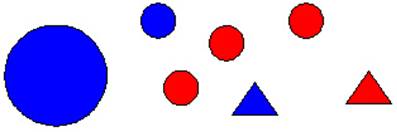
Ни я, ни сын не можем понять, что там нужно делать и по какому принципу разбивать? Там даны кружочки, треугольники.
Ответ:Уважаемый родитель,
По всей видимости, Ваш ребенок или не занимается по программе Л.Г. Петерсон, а Вы занимаетесь с ним дополнительно, или пропустил очень важную тему.
Данная тема является ключевой на подготовительном этапе обучения в 1-ом классе, так и при изучении смысла действий сложения, вычитания. В дальнейшем эти знания помогают ученикам решать задачи.
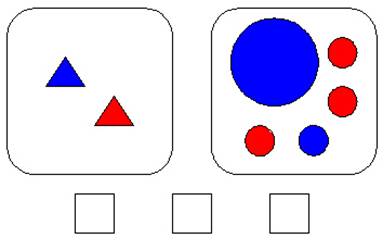
Смысл данного задания в том, что одни и те же фигуры разбиты на группы по разным признакам.
Так, в первом случае отдельно выделены все треугольники (4), отдельно все круги (3). То есть признак разбиения – форма фигур. На примере данного рисунка можно составить выражение на сложение, в котором нужно найти количество всех фигур: 4+3=7.
Во втором случае признак разбиения — цвет фигур, так ка в одну группу выделены белые фигуры, в другую все синие. На примере данного рисунка можно составить выражение на сложение, в котором нужно найти количество всех фигур: 5+2=7.
И в третьем случае признак разбиения — размер фигур, так ка в одну группу выделены большие фигуры, в другую все маленькие. На примере данного рисунка можно составить выражение на сложение, в котором нужно найти количество всех фигур: 1+6=7.
Успехов Вам и Вашему сыну в освоении математики!
С уважением, старший методист ЦСДП «Школа 2000…»,
Посполита Наталья Владимировна
Математика 5 — 9 классы 
03.05.19
Решено
172
ОТВЕТЫ
Признак разбиения — цвет фигур
2+1=3
4+2=6
8-4=4
7-2=5
Признак разбиения :формы фигурок:1+4=5;1+3=4;5-1=4;4-1=3
161
Отв. дан
2019-03-05 01:54:07
Для написания вопросов и ответов необходимо зарегистрироваться на сайте
Другие вопросы в разделе — Математика
Михайлович
Вася купил 5 карандашей по 23 руб. и 2 …
2019-03-05 09:36:08
Vizamev
71638:38?))))))))))))) …
2019-03-05 09:36:06
Кирсан
1) Складіть рівняння прямої, яка проходить через точки D …
2019-03-05 09:36:04
Русланович
Длина прямоугольника 18,2 дм, а ширина в 2 раза …
2019-03-05 09:36:00
I. Актуализация знаний
1) На доске записи:
3 + 5 6 – 2 1 + 6 4 – 1
Учитель: Как назвать записи на доске?
Ученик: Математические выражения.
Учитель: Найти значения выражений и составить математические предложения.
Ученик: Сумма трех и пяти равна восьми.
Учитель выставляет под выражением карточку с числом 8.
Ученик: Разность шести и двух равна четырем.
Учитель выставляет под выражением карточку с числом 4.
Появляются карточки 8, 4, 7, 3.
Учитель сдвигает карточки и предлагает продолжить ряд чисел.
Ученик: 6, 2, 5, 1, 4, 0.
На доске числа 8, 4, 7, 3, 6, 2, 5, 1, 4, 0.
Учитель: Придумать выражения с числами 6, 2, 0.
Учитель: Какие числа остались?
Ученик: 5, 1, 4.
Учитель предлагает составить с этими числами задачу.
Ученики придумывают задачи, «одевают» схемы, обосновывают выбор арифметического действия и решают их устно.
2) Работа с геометрическими фигурами.
Игра «Угадай признаки разбиения фигур».
Учитель показывает равенства, дети читают их и называют признаки разбиения.
2 + 5 = 7 – по форме
4 + 3 = 7 – по цвету
1 + 6 = 7 – по размеру.
Учитель: Разложите фигуры в мешки по форме
У детей на карточках аналогичный рисунок. Возможна работа в группах.
Учитель просит придумать задание для ребят.
Ученик: Сравнить число треугольников с числом кружков.
Один ученик выполняет задание у доски, остальные – на карточках: определяет количество фигур в каждом мешке, устанавливают взаимно однозначное соответствие между фигурами в большем по численности мешке, выделяют часть фигур, вошедших в пару.
Учитель: Какие выводы можно сделать?
Ученик: Две меньше пяти
И другие: Пять больше двух, пять больше двух на три, две меньше пяти на три.
II. Постановка учебной задачи.
Учитель предлагает выполнить аналогичное задание по другой иллюстрации, где в каждом мешке фигур очень много.
Проблема: Задание выполнить сложно, нужен новый способ сравнения.
III. Решение учебной задачи.
1) Учитель предлагает вернуться к первой иллюстрации, где предметов немного.
Учитель: Что можно сказать об оставшихся без пары фигурах?
Ученик: Их три. Они составляют часть.
Учитель: Загляните во второй мешок и составьте равенство, которое показывает, как найти эту часть.
Ученик: 5 – 2 = 3.
Учитель: Что показывает 5?
Ученик: Число кружков.
Учитель: Что показывает 2?
Ученик: Число треугольников.
Учитель: Что показывает 3?
Ученик: Это разность (разница) чисел 5 и 2. 3 показывает, на сколько 5 больше 2.
Учитель: По какому правилу определяем, на сколько 5 больше 2?
Ученик: Из большего числа 5 вычитаем меньшее число 2.
2) Сравнение чисел с помощью полосок.
У каждого ребенка на столе по 2 полоски разной длины.
Учитель: Возьмите красную полоску. Какое число она может обозначать?
Ученик: Большее число.
Учитель: Почему?
Ученик: Она длиннее.
Учитель: Что обозначает зеленая полоска?
Ученик: Она будет обозначать меньшее число.
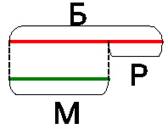
Учитель просит на красной полоске поставить букву «Б», а на зеленой – «М».
Учитель: Как сравнить полоски?
Ученик: Наложить одну полоску на другую.
Учитель: Отметьте на большей полоске часть, равную меньшей. Как называется вторая часть?
Ученик: Разность (разница).
Появляется схема.
Учитель: Как найти разность?
Ученик: Б – М = Р
Учитель: Какие еще равенства можно составить?
Ученик: М + Р = Б, Б – Р = М.
На доске появляются карточки.
Дети проговаривают правила: чтобы узнать, насколько одно число больше или меньше другого, надо из большего числа вычесть меньшее.
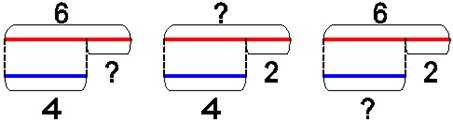
3) Составление и решение обратных задач на сравнение по иллюстрации: красных шаров 6, синих – 4. На сколько красных шаров больше, чем синих?
IV. Подведение итогов.
Какой новый способ сравнения чисел узнали? Рассказать или повторить правило.
Привет, Вы узнаете про разбиение числа, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
разбиение числа, разбиением числа, диаграммы юнга, диаграмма юнга, пентагональная теорема , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
разбиение числа — это представление
в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие от композиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В канонической записи разбиения части перечисляются в невозрастающем порядке.
Число разбиений натурального числа
является одним из фундаментальных объектов изучения в теории чисел.
Примеры
Например, {3, 1, 1} или {3, 2} — разбиения числа 5, поскольку 5 = 3 + 1 + 1 = 3 + 2. Всего существует разбиений числа 5:
{1, 1, 1, 1, 1},
{2, 1, 1, 1},
{2, 2, 1},
{3, 1, 1},
{3, 2},
{4, 1},
{5}.
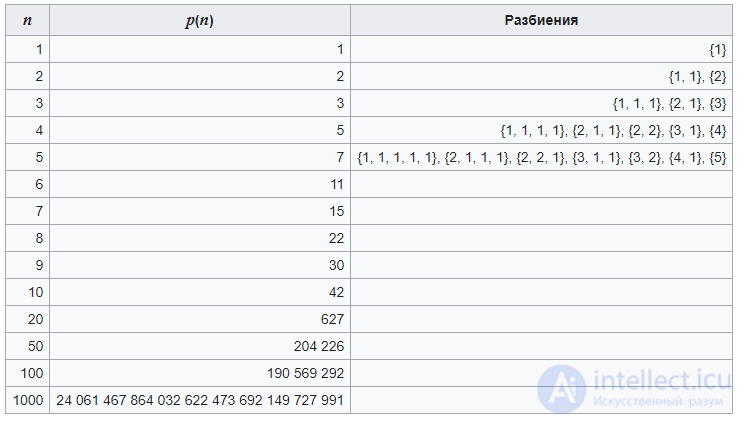
Некоторые значения числа разбиений приведены в следующей таблице :
Число разбиений
Производящая функция
Последовательность числа разбиений имеет следующую производящую функцию:
Эта формула была открыта Эйлером в 1740 году.
пентагональная теорема Эйлера
Изучая производящую функцию последовательности , Эйлер сосредоточил внимание на ее знаменателе, то есть, на произведении
. Это бесконечное произведение при раскрытии скобок приобретает следующий вид:
Показатели степеней в правой части — числа вида
где
— целое число, а знак при }
равен
. Об этом говорит сайт https://intellect.icu . Для натуральных
:
— это пятиугольные числа.[2]
Согласно этому наблюдению, Эйлер предположил, что должна быть верна Пентагональная теорема:
.
Впоследствии эта теорема была доказана Эйлером. Она позволяет вычислять числа разбиений при помощи деления формальных степенны́х рядов.
Асимптотические формулы
Асимптотическое выражение для количества разбиений было получено Харди и Рамануджаном в 1918 году и независимо от них российским математиком Успенским в 1920 году
при
Это выражение дает, например, .
Впоследствии Харди и Рамануджан нашли более точное выражение в виде суммы, и, наконец, Радемахер нашел для асимптотического представления числа разбиений сходящийся ряд.
где
Здесь суммирование ведется по , взаимно простым с
, а
— сумма Дедекинда. Ряд сходится очень быстро.
Рекуррентные формулы
Количество разбиений числа на слагаемые, не превышающие
, удовлетворяет рекуррентной формуле:
с начальными значениями:
для всех
При этом количество всевозможных разбиений числа равно
.
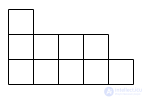
диаграммы юнга
диаграмма юнга разбиения 10 = 5 + 4 + 1.
Разбиения удобно представлять в виде наглядных геометрических объектов, называемых диаграммами Юнга, в честь английского математика Альфреда Юнга[en]. Диаграмма Юнга разбиения — подмножество первого квадранта плоскости, разбитое на ячейки, каждая из которых представляет собой единичный квадрат. Ячейки размещаются в строки, первая строка имеет длину
, над ней расположена строка длиной
, и т. д. до
-й строки длины
. Строки выровнены по левому краю.
Более формально, диаграмма Юнга — это замыкание множества точек таких, что
и
где обозначает целую часть
.
В англоязычной литературе диаграммы Юнга часто изображают отраженными относительно оси абсцисс.
Схожий объект, называемый диаграммой Феррерса, отличается тем, что
- вместо ячеек изображаются точки;
- диаграмма транспонируется: ряды и столбцы меняются местами.
Применение
Разбиения естественным образом возникают в ряде математических задач. Наиболее значимой из них является теория представлений симметрической группы, где разбиения естественно параметризуют все неприводимые представления. Суммы по всем разбиениям часто встречаются в математическом анализе.
Вау!! 😲 Ты еще не читал? Это зря!
- Композиция
- Биномиальный коэффициент
- Теорема Хаусдорфа
В общем, мой друг ты одолел чтение этой статьи об разбиение числа. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое разбиение числа, разбиением числа, диаграммы юнга, диаграмма юнга, пентагональная теорема
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но емко про разбиение числа