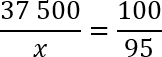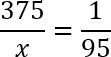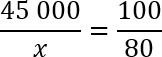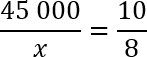|
Один из способов решения задач на проценты — это использование пропорций. Как правильно составлять и решать подобные пропорции? Существует много практических задач, использующих понятие процентов. Часто для их решения используется понятие пропорции. В простых случаях можно решать вот таким образом: все мы знаем, что 50% это половина от числа, 25% — это его четвёртая часть, 20% — это пятая часть, 10% -это 10 часть , 5 % — 20 часть, 1% — 100 часть. Итак, найти один процент от 2000 это 2000/100=20. Найти 50 % от 60 это 60/2=30. А можно использовать универсальный способ — понятие пропорции. Предположим надо найти 13% от 180. Тогда составим: 180 — 100% Х — 13 % Мы должны числа писать под числами, проценты под процентами. Далее раскрывает пропорцию крест накрест. То с чем икс не в паре перемножаем, а с чем в паре по диагонали — делим. У нас получаем 180*13/100=23,4 система выбрала этот ответ лучшим Ксарфакс 4 года назад Пропорция с процентами составляется по следующему принципу:
Вот как выглядет такая пропорция: A / B = 100% / p% Например: 1000 / 50 = 50% / 5%. Или можно записать по-другому: 1000 — 100%. 50 — 5%. При решении задач на проценты с помощью пропорции неизвестный её член (а здесь может быть 3 варианта) обычно обозначается за x. Решить пропорцию (то есть найти неизвестный член) можно благодаря её основному свойству: произведение крайних членов пропорции равно произведению средних (другими словами, нужно перемножить члены пропорции крест-накрест).
Далее рассмотрим несколько простых примеров. Пример 1. Зарплата составляет 30000 рублей, а премия — 10% от зарплаты. Нужно определить размер премии. 30000 — 100%. x — 10%. Вспоминаем, что произведение крайних членов равно произведению средних: 30000 * 10 = 100 * x. x = (30000 * 10) / 100 = 3000. Значит, премия равна 3000 рублей. Пример 2. Сделано 20 выстрелов, 4 из них — мимо мишени. Нужно определить процент попадания. 20 — 100%. 4 — x%. Умножаем крест-накрест и приравниваем: 20 * x = 100* 4. x = (100 * 4) / 20 = 20. Здесь нужно учесть, что 20% — это процент выстрелов мимо мишени (так как рядом с неизвестным x были записаны именно промахи). Процент попадания в свою очередь равен 100% — 20% = 80%. Пример 3. За месяц было продано 30 ноутбуков, что составляет 20% от всего количества ноутбуков, имеющихся в продаже. Нужно найти, сколько всего ноутбуков было в магазине изначально. x — 100%. 30 — 20%. Умножаем крест-накрест: 20 * x = 100 * 30. x = (100 * 30) / 20 = 150. Таким образом, изначально в продаже было 150 ноутбуков. Zummy out off 3 года назад Я как-то со школы запомнила принцип пропорции и способ ее решения называю «крест-накрест», не помню, кто это мне подсказал. Никогда не нахожу проценты по принципу умножения на сотую часть, мне не удобно, всегда использую свой «крест», единственное неудобство — нужно наглядно записывать это. Это не страшно — бумага всегда под рукой. Составляю пропорцию по условию, одно из значений неизвестное обозначаю Х. Затем решаю: перемножаю цифры, расположенные «на углах» слева и справа от Х, делю на число, расположенное на противоположном углу от Х. Пример: нужно найти 5% от числа 420. Пишу пропорцию. 420 — 100 % Х — 5 % Х = 5 • 420 : 100 = 21% Вот моя запись с крестом Ещё пример: сколько процентов от 200 составляет число 20. Составляю пропорцию. 200 — 100 % 20 — Х % Решение: X = 20 • 100 : 200 = 10% Алиса в Стране 3 года назад Странно, конечно, для таких простых задач составлять какие-то дополнительные пропорции, они решаются в уме и очень быстро, но способ такой есть, давайте его рассмотрим, возможно, кому-то он пригодится. Допустим, нам надо найти сколько процентов составляет число 18 от числа 90, в принципе, мы и так сразу видим что 18 это одна пятая, то есть 20 процентов от числа 90, но давайте составим пропорцию, приняв за х искомое количество процентов, пропорция у нас будет такая: 90 — 100 % 18 — х %, откуда х = 100 х 18 / 90 = 20 процентов. Еще один пример для закрепления материала, найдем, сколько процентов составляет 24 от 250, пропорция: 24 — х 250 — 100 х = 24 х 100 /250 = 9,6 %. Go Green 3 года назад Для определения процентного соотношения от числа нужно иметь представление об основных простых процентных соотношениях и о принципе вычисления любых из них. Для простоты давайте приведем примеры с числом 100. 1 % от ста — это одна сотая часть или один процент. 2% от ста — две сотых части от ста. 7% от ста — семь сотых части от ста и так далее. То есть сначала нам нужно узнать, сколько составляет один процент любого числа, разделив его на сто, а затем узнавать заданное процентное соотношение. Например, нам нужно найти, сколько будет равно 7 процентам от 200. Делим 200 на 100. Получится 2. Умножим 2 на 7, получится 14. Итого: 7% от 200 будет равняться числу 14. СТА 1106 3 года назад Всегда любила задачки на пропорции. Главное- правильно ее составить, а потом все просто, крест на крест и решение готово. Простейший пример. Найти на сколько процентов цех выполнил план по сборке за смену, если общий план 250 механизмов( штук), а всего за смену было собрано 262 ? Итак решаем. 250 штук — 100 % 262 штуки — х % Решение: 262 × 100:250= 104,8 %. Пример 2. Выяснить, сколько столовой нужно картофеля на год, если 20 тонн закрывают потребность лишь на 82%. Решение. Опять пропорция, где известно доля от потребности и в тоннах и процентах. Общая потребность , разумеется берется за 100. 20 тонн — 82 % Х тонн — 100 %. 20 × 100:82= 24,4 тонны. Бекки Шарп 3 года назад Допустим по условию задачи нам известно сколько всего было единиц (1000 кг яблок) и надо узнать сколько единиц (кг сухого вещества) составляют 18%. Составляем пропорцию, в которой 1000 — это 100%, а неизвестной х — 18 %. То есть в пропорции у нас есть единицы и проценты. Соотносим соответственно кг к кг и проценты к процентам. это обязательное условие пропорции. Пропорция будет выглядеть так: Бархатные лапки 3 года назад Обычно в таких задачах задано общее число единиц, кг, км и нужно узнать сколько этих единиц составит определенное количество процентов. Или наоборот сколько процентов составляет количество единиц. То есть даны два известных, но мы помним что есть еще проценты, что общее количество чего-то это всегда 100%. Например нам нужно узнать сколько процентов составляет 38 рублей от 40 рублей. Составим пропорцию: 40/38=100/х, где 40 рублей это 100%, х — сколько рублей 38%. Из пропорции находим х = 95 %. Точно в цель 3 года назад Посчитать пропорцию с процентами очень легко. В задачах на пропорции с процентами нам нужно посчитать проценты от числа. Для решения задачи нам нужно знать, что 50% — это половина от числа, 25% — одна четвертая от числа. То есть для того, чтобы найти пропорцию с процентами, нам нужно разделить число на 100 и умножить на процент. Например, мне нужно найти 20 процентов от числа 230. Сначала я 230 делю на 100, получается 2.3, а затем умножаю его на 20 — получаю 46. 50 процентов является половиной от числа, 25 является четвертой частью, 20 — пятой, 10 — 10, 5 является 20, а 1 процент — 100 часть. Один процент от 2000 найти не сложно. 2000 делим на 100 получим 20. Для того чтобы найти 50 процентов от 60 вам потребуется поделить на 2 = 30. Если нужно найти 13 процентов от 180 то 180 = 100 процентам , х = 14 получится 180 умножим на 13 делим на 100 и получаем 23,4. [пользователь заблокирован] 4 года назад Всё очень просто. Всегда нужно начинать с того, что процент — это одна сотая часть. Ну, а далее — пропорция составляется исходя из этой посылки. Знаете ответ? |
Метод решения задач с процентами
Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции
Данные задачи на проценты можно записать в виде следующих соотношений:
все — 100% часть — часть в %
которые можно записать в виде пропорции
Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.
Примеры решения задач на проценты
30 соответствует 100% x соответствует 15%
решим полученное уравнение
Ответ: 15% от 30 равно 4.5.
20 соответствует 100% 35 соответствует x
решим полученное уравнение
Ответ: 35 составляет 175% от 20.
x соответствует 100% 20 соответствует 5%
решим полученное уравнение
Ответ: 400.
При изучении процентов вам также будут полезны:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Задачи на проценты: стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X — 95%
Нужно составить пропорцию и найти x . Получаем:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x — 80%
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x :
x = 45 000 · 8 : 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Решение задач на проценты
В обычной жизни нам часто необходимы знания, которые мы получили в школе. Но согласитесь, что порой мы не детально разобрались в том или ином вопросе школьной программы. Наиболее замысловатым многие школьники считают проценты. Сложным для большинства становится не только решение, но и толкование условия. Не стоит расстраиваться в данном случае. Даже не подозревая, мы сталкиваемся в обычной жизни с задачами на проценты и удачно с ними справляемся. В этом случае с ними проще справиться, так как они напрямую связаны с нашей реальной жизнью.
Сложности у многих при изучении этого раздела будут возникать до тех пор, пока в учебниках не появятся примеры из реальной жизни. Ниже будут приведены примеры, которые помогут вам разобраться в этом аспекте раз и навсегда. В качестве ситуаций будут приведены варианты из обычных жизненных ситуаций, которые встречаются ежедневно. Простое и понятное объяснение решения задач на проценты расставит все на свои места, и больше не будет вызывать вопросов.
Проценты и их использование в повседневной жизни
Если внимательно присмотреться к упаковкам продуктов, которые мы покупаем, то там указываются проценты. Еще чаще знак «%» можно увидеть на рекламных плакатах, обозначающий в них скидку. Именно это значение становится решающим для шопоголиков. Неприятные эмоции у каждого человека вызывает этот символ при просмотре новостей о количестве смертей, поднятии стоимости коммунальных услуг или прочих платежей. Для того, чтобы понимать, что подразумевает под собой это значение, необходимо знать, как им оперировать.
Для того, чтобы не стать жертвой рекламных акций, особенно в периоды «огромных» скидок, необходимо знать, как высчитать сумму скидки и будет ли конечная цена со скидкой ниже стоимости без скидки. Знание правил исчисления задач с процентами поможет разобраться с банковскими услугами. Особенно если речь идет о кредитах или ипотеке. Чаще всего данные о процентах указывают мелким шрифтом. Решив задачу с процентом, можно четко понять, сколько вам придется вернуть дополнительно собственных денег за то, что вы воспользовались услугами банка.
В сезонный период повышения заболеваний мы можем увидеть статистику количества людей, которые стали жертвами вируса. Именно в данных можно встретить специальный знак. Это значение определяет превышен ли эпидемиологический порог. Прекрасным вариантом включения процентов для показания информации может стать сведения о подаче документов от абитуриентов на ту или иную специальность университета. Процент заявлений определяет конкурс, а относительно этого и шансы каждого поступающего.
Суть понятия — процент
Чаще всего этот термин представлен десятичной дробью. Чаще всего для сравнения в привычной жизни мы сравниваем целое с частями. Наиболее распространенными значениями выступают:
В учебном году присутствует такое понятие как «четверть». Оно привычно для каждого. Но многие забывают о том, что оно подразумевает четвертую часть учебного процесса. Большинство людей отмечает, что исчисление удобнее всего вести в сравнении сотых долей. Именно так и пришло значение «процент».
Для обозначения на письме значения процента, можно использовать специальный символ «%». Кроме этого, доступно применять десятичные дроби или натуральное число. Получают его при разделе на 100: 0,1 или наоборот в процессе умножения на 100%.
Основные варианты задач на проценты
Давайте определимся, что упражнения с %– это нахождение дроби. Именно таким положением мы и будем дальше пользоваться.
Вариант 1: Определение процента (дроби) от общего числа.
- Задача. В магазин завезли 200 кг огурцов. 10% из общего количества имели признаки испорченности и не годились для реализации. Сколько килограмм огурцов были непригодны для продажи?
- Решение. Вам требуется найти 10% от всего объема привезенных огурцов (200). 10% = 0,1. 200*0,1= 20. 20 кг из всего количества огурцов не могут быть проданы из-за низкого качества.
Вариант 2: Вычисление числа по его проценту (дроби).
- Задача. Ученику на летний период дали прочитать определенное количество художественных книг. Он прочел 42 книги. Это составляет 25% от общего количества заданного материала. Сколько всего необходимо прочитать книг за летние каникулы?
- Решение. Для нас неизвестно число книг, которые были заданы ученику. Зато в условии нам дано, что 42 книги составляют 25% от общего количества. Значит, нам стоит перевести 25% в дробь и это будет 0,25. После этого известную нам величину делим на данный указатель. 42/0,25 =42*100/25=168. 168 книг нужно прочесть ученику на летних каникулах.
Вариант 3: Ищем соотношение двух чисел в процентах (часть от общего количества).
- Задача. В группе детского сада 28 детей. 14 мальчиков. Сколько процентов мальчиков в группе?
- Решение. Чтобы понять процентное соотношения чисел между собой, вам необходимо значение, которое вы ищите, разделить на общий объем и после перемножить на 100%. Пример: 14/28*100% =1/2*100% = 1*100%/2 = 50%. В группе 50% мальчиков.
Вариант 4: Увеличение числа на процент.
- Задача. Стоимость пиджака выросла на 20%. Какая цена его теперь, если перед повышением цены она составляла 2400 рублей?
- Решение. Ищем 20% от 2400. Для поиска 20% от 2400, вам потребуется перемножить 2400 на 0,2: 2400*0,2 = 480. Пиджак стоил 2400 р, возрастание ценника составило 480 р, сегодня ценник составляет 2400+ 480 = 2880р.
Вариант 5: Уменьшение числа на процент.
- Задача. За ночь в комнату залетело 30 комаров. До утра их стало меньше на 40%. Сколько насекомых в помещении осталось на утро?
- Решение. Для получения правильного ответа нам необходимо уменьшить значение на 40%, т. е. умножить 30 на (1−40/100)=1−0,4=0,6(1−40/100)=1−0,4=0,6. 30*0,6 = 18. В комнате на утро было 18 комаров.
Вариант 6: Использование простых процентов в упражнениях.
- Задача. Произведите дисконтирование 800 долларов за 8 месяцев по простой ставке 12% за год.
- Решение. Т.к. исчисление процентов идет за год, то первым делом вам ее нужно определить в месяц. В году 12 месяцев и 12 процентов, а значит 1% в месяц. Чтобы получить результат, воспользуйтесь формулой с включением предоставленных данных: P=800, I=0,01, T=8 месяцев. Она будет выглядеть так: А=800*(1+0,01*8)=864 долларов. Спустя 8 месяцев размер дисконта равен 864 доллара.
Вариант 7: Упражнения со сложными процентами.
- Задача. Клиент взял в банке ссуду на 9000 евро на 3.5 года под 20% в год с условием зачисления процентов каждые 6 месяцев. Вычислите размер суммы при сложны процентах.
- Решение. Формула с использованием сложных процентов:
J = 20% = 0.2 — ставка процентов
n = 3.5 года — продолжительность срока выдачи ссуды
P – 9000 евро — изначальный размер вклада
m = 2 – разы, когда будут начислены проценты за период использования
S = 9000 * (1+0.2/2)2*3.5 = 17538.5 евро.
Ответ: сумма по ставке со сложными процентами равна 17538,5 евро.
Для более удобного решения простых задач на проценты, можно использовать пропорцию. Данный метод очень доступен. Вы можете выбирать тот вариант, который вам нравится больше. Итак, решим задачу, составив пропорцию.
- Задача. На клумбе растет 45 роз. Красных – 18. Какое процентное соотношение красных роз ко всем остальным?
- Решение. Чтобы было удобнее, давайте искомое число обозначим х. Общее количество цветов в таком случае будет составлять 100%. Пропорция составляется крест накрест. Она будет выглядеть следующим образом:
Чтобы решить уравнение стоит умножить левую и правую части накрест. В результате мы получим: 45*х=18*100. Отсюда будет следовать, что х=18*100/45=40% Ответ: процентное соотношение красных роз к остальным составляет 40%.
Способы решения задач на проценты
Для получения правильного результата, стоит полностью разобраться в способа решения условий с процентами. Тщательная работа над ними даст уверенность в собственных силах. Чем больше практики будет, тем лучше будет усвоен материал. При необходимости вы автоматически составите пропорция в уме.
Задача 1.
Стоимость куртки составляет 16000р. Впервые она увеличилась на 20%, затем на следующий день — снизилась на 20%. Она по прежнему стоит 16000 р., не так ли?
Решение. Нет. Если коротко, то: 16000*1,2*0,8 = 15360р — теперь вещь стоит эту сумму.
Развернутое решение. Сперва ценник увеличился на 20%, т. е. на 16000*0,2 = 3200р. Новая стоимость 16000+ 3200 = 19200 (р). Через день произошло снижение на 20%. Тут стоит понимать, что эта сумма отнималась не от 16000, а от 19200: 0,2*19200 = 3840 р. 19200 — 3840 = 15360 (р). Именно поэтому конечный результат составил 15360 р.
Задача 2.
Оба платья были по 14000 р. Цена одного из них возросла на 10%, а затем — еще на 10%. Цена второго сразу поднялась на 20%. Какое платье теперь более дорогое?
Решение. Чтобы понять, нужно сперва разобраться в проблеме. Первая вещь дорожала дважды по 10%, а соответственно сумма увеличилась в 1,1 раза: 14000*1,1*1,1 = 16940 (р). Вторая вещь изначально повысилась в цене на 20%, а точнее в 1,2 раза. Произведем расчеты: 14000*1,2 = 16800. Если сравнить обе цены, то первое платье стало намного дороже.
А почему нельзя сразу приплюсовать проценты? и после совершать расчеты. Все заключается в том, что 10% сперва отсчитывается от 14000 р, а далее — исчисление производиться уже от повышенной стоимости. По расчетам это выглядит так: 14000 + 1400 = 15400 (р). Далее переписывание ценника будет таким: 15400*0,1 = 1540 (р). Складываем 1540 и 15400 — получаем окончательную цену куртки — 16940 р.
Задача 3.
Цена на квартиру в новостройке в январе составляла 12000000 р. Через месяц она возросла на 5%, в еще через месяц — упала на 3%. Апрель показал возрастание на 7%, а в мае — снижение на 10%. Определите стоимость сейчас?
Решение. На основе вышеприведенных задач, уже точно можно сказать, что нельзя плюсовать все процентные значения в единое целое. Вариант: 5% — 3% + 7% — 10% = -1%. Будет неправильным. Все исчисления нужно проводить относительно новой суммы после очередного действия.
Толкование подробного решения:
Первое увеличение цены — это 5% от 12 000 000 = 600 000 (р).
12 000 000 + 600 000 = 12 600 000 (р).
Далее — это 3% от 12 600 000 = 378 000 (р).
12 600 000 — 378 000 = 12 222 000 (р).
Затем возрастание — это 7% от 12 222 000 = 855 540 (р).
12 222 000 + 855 540 = 13 077 540 (р).
Окончательный спад на 10% — это 10% от 1 307 7540 = 1 307 754 (р).
13 077 540 — 1 307 754 = 11 769 786.
Чтобы упростить задачу и не писать много лишнего, распишите данные в строку:
12 000 000*1,05*0,97*1,07*0,9 = 11 769 786 (р).
Чаще всего используется именно первый вариант. Хотя стоит постепенно переходить к более простому варианту, отказываясь от длительного рассуждения.
Задача 4.
Есть 5% раствор кислоты. Его масса 3,8 кг. Туда добавили 1,2 кг дистиллированной воды. Какой стала концентрация раствора (в процентах)?
Решение. Чтобы определить конечный результат, узнайте, сколько кислоты находиться в растворе. Из 3,8 кг 5% — это кислотная составляющая, а значит в растворе 0,05⋅3,8=0,19 кг 0,05⋅3,8=0,19 кг кислоты
После просчитайте вес нового раствора: 3,8 кг + 1,2 кг = 5 кг. Так как в воде нет кислоты, то значение осталось неизменным. А это значит, что концентрация кислоты стала равна 0,19/5=0,038 Для перевода в проценты выполните следующие действия — 0,038*100%=3,8%
Задача 5.
Мокрая губка содержала 80 % воды, а после выжимания только 20%. Чему была равна масса мокрой губки, если масса губки после выжимания стала 100 грамм? Ответ дайте в граммах.
Решение. Первый способ: В выжатой губке 100%−20%=80% сухого вещества, тогда после выжимания масса сухого вещества губки стала составлять 0,8*100=80 грамм. Но и до выжимания она была такой же, при этом до выжимания она составляла только 100−80=20% массы мокрой губки, значит масса мокрой губки была 80:0,2=400 грамм. Второй способ: Пусть x кг – масса мокрой губки, тогда г x/100*20 г – масса сухого вещества. После выжимания масса сухого вещества стала составлять 100−20=80% от массы выжатой губки (то есть 80 грамм), тогда x/100*20=80, откуда x=400 грамм. Ответ: 400 г.
Заключение
Из всего выше перечисленного можно сказать, что решать задачи на проценты не так уж и сложно. Разбор и запоминание основных правил позволит вам решать их максимально просто и быстро.
Для закрепления пройденного материала, было бы лучше самостоятельно составить задачу и решить ее. Можете проверить ваши способности на друзьях или близких. Поверьте, решать задачи на проценты вам придется неоднократно не только в школе, но и в повседневной жизни. Именно поэтому важно тщательно и детально изучить эту тему.
источники:
http://www.berdov.com/ege/percent/standartnii-metod-proporcii/
http://brainhouse.com.ua/reshenie-zadach-na-proczenty/
Задачи на проценты: стандартный расчет с помощью пропорций
12 ноября 2013
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X — 95%
Нужно составить пропорцию и найти x. Получаем:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
x = 375 · 95
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
x = 35 625
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x — 80%
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x:
x = 45 000 · 8 : 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
x = 4500 · 8
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Смотрите также:
- Процент: налоги и зарплата. Считаем с помощью коэффициентов
- Задачи на проценты: считаем проценты с помощью пропорции
- Тест к уроку «Что такое числовая дробь» (легкий)
- Тест: простейшие показательные уравнения (1 вариант)
- Изюм и виноград (смеси и сплавы)
- ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
Содержание материала
- Проценты в обыкновенную дробь
- Видео
- Проценты: правила
- Нахождение одного процента от числа
- Составление пропорции
- Соотношения чисел
- Второй способ нахождения процента
- Сколько процентов составляет одно число от другого?
- Онлайн-сервисы для вычислений
- На сколько процентов одно число больше другого
- Прибавить проценты к числу
- Как найти процентное соотношение чисел
- Отнять от числа проценты
Проценты в обыкновенную дробь
Чтобы представить проценты в виде обыкновенной дроби нужно проценты представить в виде десятичной дроби. Затем десятичную дробь преобразовать в обыкновенную дробь.
Преобразовать 25% в обыкновенную дробь
25%100%
=
0.25
=
25100
=
1 × 25 4 × 25
=
14
Проценты: правила
Рассмотрим четыре известных способа поиска процентов.
Нахождение одного процента от числа
Найти процент от числа можно несколькими способами.
Первый способ
-
Найдем, чему равен 1%.
-
Умножим полученное значение на количество искомых процентов.
Пример: найти 12% от числа 48.
-
48 : 100 = 0,48.
-
0,48 × 12 = 5,76.
Второй способ
-
Переведем проценты в десятичную дробь.
-
Умножим число на полученную десятичную дробь.
Давайте снова найдем 12% от 48, но другим способом.
-
12 : 100 = 0,12.
-
48 × 0,12 = 5,76.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Как решаем:
- Переведем 15% в рубли:
250 : 100 = 2,5 — это 1% от стоимости шоколада,
значит, 2,5 × 15 = 37,5 — это 15%.
- Вычислим цену со скидкой 15%: 250 − 37,5 = 212,5.
- 212,5 < 225.
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
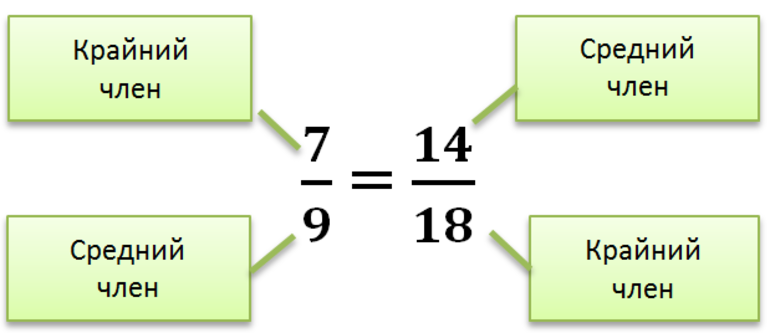
Равенство двух отношений называют пропорцией.
a : b = c : d или a/b = c/d
- a, d — крайние члены
- b, c — средние члены
Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Как решаем:
Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:
1390 руб. = 100% x руб. = 14%
Перемножим крест-накрест и найдем x:
x = 1390 × 14 : 100 x = 194,6
Ответ: выгода по скидке составила 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
- 100% — 25% = 75%,
значит, нужно заплатить 75% от первоначальной цены.
- Используем правило соотношения чисел:
75% — это 3/4 от числа, значит, 8500 : 4 × 3 = 6375 (рублей).
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Видео
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись 

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Сколько процентов составляет одно число от другого?
Чтобы вычислить процентное отношение двух чисел, нужно вычислить их отношение и умножить его на 





То есть число 




Решение. Зарплата сотрудника составляет от зарплаты начальника
Зарплата начальника составляет
от зарплаты сотрудника.
Сколько процентов составляет число от числа от числа = неопределённость
Округлять до знаков после запятой.
Онлайн-сервисы для вычислений
В нахождении нужных процентов могут помочь различные сервисы-калькуляторы, работающие в режиме онлайн. Например, популярный сайт имеет в своём функционале различные инструменты, помогающие, в том числе, высчитать процент от любого числа.
Порядок действий:
- Перейдите на .
- Введите искомые показатели в соответствующие клетки.
- Нажмите на «Рассчитать». Вы сразу же получите искомый результат.
Также указанный калькулятор позволяет высчитать какую долю от 1 составляет 2, прибавить % к числу или вычесть из него. Всё очень быстро и удобно.
На сколько процентов одно число больше другого
Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на 100 и вычесть 100.
Вычислим, на сколько процентов число 20 больше числа 5: 205 · 100 — 100 = 4 · 100 — 100 = 400 — 100 = 300% Число 20 больше числа 5 на 300%. Например, зарплата начальника равна 50000 рублей, а сотрудника — 35000 рублей. Найдем, на сколько процентов зарплата начальника больше: 5000035000 · 100 — 100 = 1,43 * 100 — 100 = 143 — 100 = 43% Таким образом, зарплата начальника на 43% выше зарплаты сотрудника.
Прибавить проценты к числу
Чтобы прибавить к числу p процентов, нужно умножить это число на (1 + p100)
Прибавим 30% к числу 200: 200 · (1 + 30100) = 200 · 1,3 = 260 200 + 30% равняется 260. Например, абонемент в бассейн стоит 1000 рублей. Со следующего месяца обещали поднять цену на 20%. Вычислим, сколько будет стоить абонемент. 1000 · (1 + 20100) = 1000 · 1,2 = 1200 Таким образом, абонемент будет стоить 1200 рублей.
Как найти процентное соотношение чисел
Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.
Для определения такого результата существуют следующая формула:
B / A * 100 =
К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.
Используя приведённую формулу, выполняем несложные арифметические операции:
85 / 500 * 100 = 17%
Таким образом, число 85 составляет 17% от 500.
Проверяем полученное число по формуле первого способа:
500 / 100 * 17 = 85.
Всё сошлось.
Отнять от числа проценты
Давайте отнимем 



Чтобы отнять от числа 
Уменьшить число на % — 0% =
Округлять до знаков после запятой.
Теги
Задачи на проценты: стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X — 95%
Нужно составить пропорцию и найти x . Получаем:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x — 80%
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x :
x = 45 000 · 8 : 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Как решать пропорции — правила, методы и примеры вычислений
Общие сведения
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.
Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.
Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.
Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:
- Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
- Перемножение «крест-накрест»: x * z = y * v.
- Перестановка: x / v = y / z и v / x = z / y.
- Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
- Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.
Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.
В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
- Записать функцию.
- Рассмотреть составные части.
- Если простой тип, перейти к 5 пункту.
- Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
- Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
- Определить тип линейности, построив график.
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
- Записать соотношение пропорции.
- Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
- Применить свойство умножения «крест-накрест».
- Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
- Решить уравнение.
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
- Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
- При D равном 0 (один): р = (-b) / 2a.
- Если D 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
http://nauka.club/matematika/proportsii.html
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami