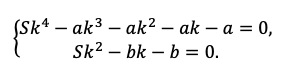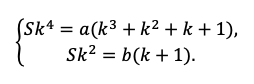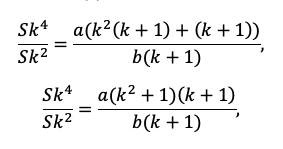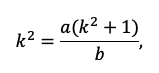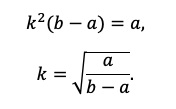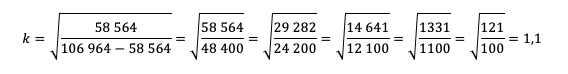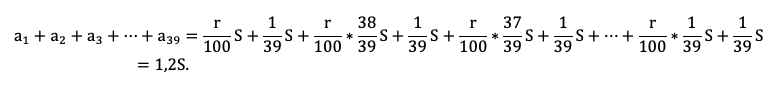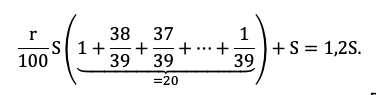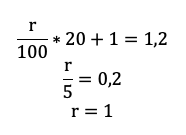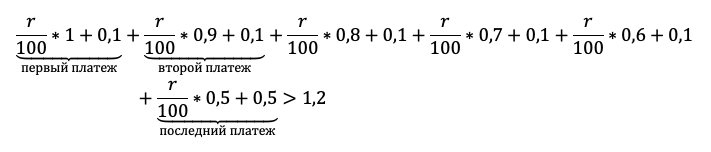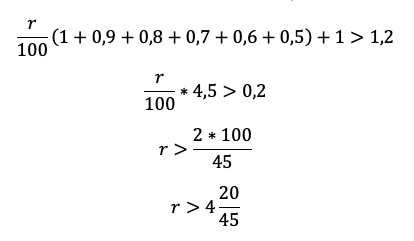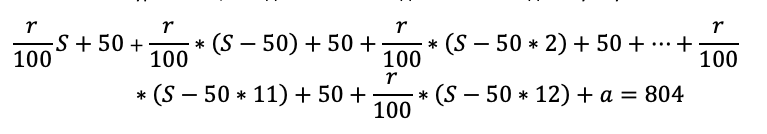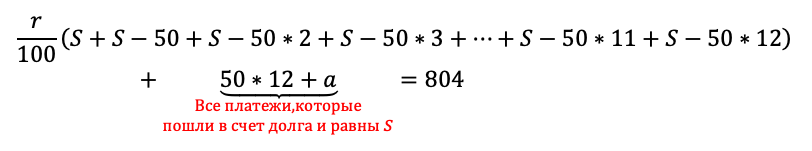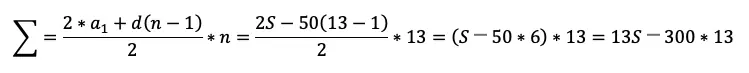Как найти процент в задаче на кредиты - Исправление недочетов и поиск решений вместе с Examum.ru

В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!

Как научить школьника решать экономическую (банковскую) задачу в ЕГЭ по математике

Прототипы для 17-го номера делятся на три большие группы:

банковские задачи,
на ценные бумаги,
задачи на оптимальный выбор.

В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

Как работает процент по кредиту?
На какую сумму начисляется?
Из каких частей состоит платеж?
Как уменьшается долг?

На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!

Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.

С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике

Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:

Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.

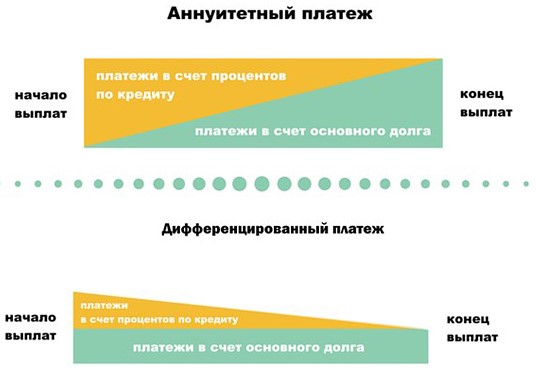
Как научить школьника решать любую банковскую задачу

Экономическая задача ЕГЭ по математике в реальной жизни

Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.

Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.

Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.

Тип 1. Равные платежи

Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

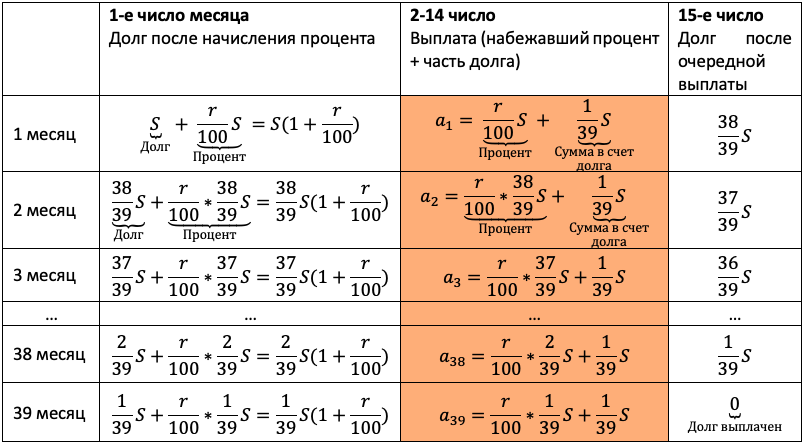
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!

Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.

Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.

Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!

Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.

Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:

Наше решение не зависит от суммы кредита, S сокращается.

По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:

Пожалуй, все, проще уже некуда. Подставляем значения!

Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.

Вспоминаем, что k=1+r/100, а найти нам надо r.

Ответ: 10%.

Не забудьте после решения расставить акценты в задаче:

Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.

Тип 2. Равномерно убывающий долг

В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.

15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)

Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.

Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:

Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:

Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:

Приведем подобные, вынесем общий множитель за скобку:

Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:

Ответ: 1%.

И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.

Тип 3. Долг, убывающий согласно табличке

Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг(в млн рублей)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.

Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.

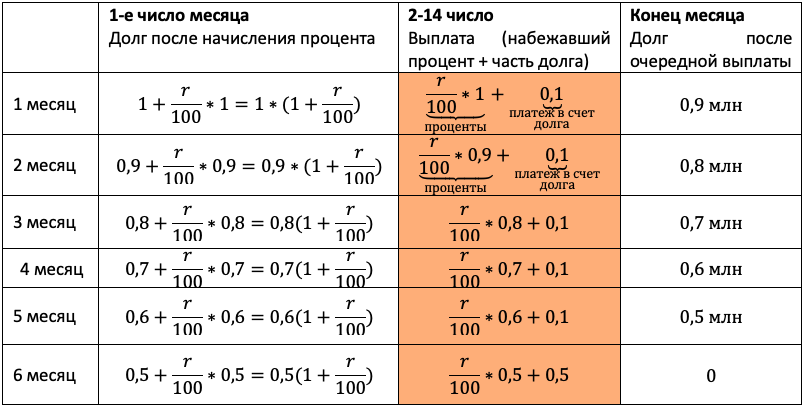
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:

Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.

Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.

«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:

Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.

Приведем подобные и вынесем общие множители за скобку:

Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.

Ответ: 5%.

Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.

Тип 4. Погашение кредита в два этапа.

По сути, это та же прошлая задача, но месяцев больше

В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!

15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?

И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.

Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.

Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.

Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:

Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:

Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.

Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:

Посчитаем эту сумму:

Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!

Ответ: 700 тысяч.

Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.

Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике

Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:

Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
Повторите типы задач и механизм распределения платежа на проценты и долг;
Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
Проговорите, что математическая модель должна точно отражать условие задачи.

Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.

За что дают баллы?

Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.

17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.

Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.

Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:

А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.

Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.

Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.

Источник

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Источник

Основные формулы в задачах на вклады и кредиты

12 марта 2015

Сегодня мы немного отвлечемся от стандартных логарифмов, интегралов, тригонометрии и т.д., а вместе этого рассмотрим более жизненную задачу из ЕГЭ по математике, которая имеет прямое отношение к нашей отсталой российской сырьевой экономике. А если быть точным, мы рассмотрим задачу про вклады, проценты и кредиты. Потому что именно задачи с процентами с недавних пор добавлены во вторую часть единого государственного экзамена по математике. Сразу оговорюсь, что за решение этой задачи согласно спецификациям ЕГЭ предлагается сразу три первичных балла, т. е. экзаменаторы считают эту задачу одной из самых сложных.

Вместе с тем, для решения любой из указанных задач из ЕГЭ по математике необходимо знать всего лишь две формулы, каждая из которых вполне доступна любому школьному выпускнику, однако по непонятным мне причинам эти формулы начисто игнорируются как школьными учителями, так и составителями всевозможных задач для подготовки к ЕГЭ. Поэтому сегодня я не просто расскажу вам, что это за формулы и как их применять, а выведу каждую из этих формул буквально у вас на глазах, взяв за основу задачи из открытого банка ЕГЭ по математике.

Поэтому урок получился довольно объемный, довольно содержательный, поэтому устраивайтесь поудобнее, и мы начинаем.

Вкладываем деньги в банк

Прежде всего, хотелось бы сделать небольшое лирическое отступление, связанное с финансами, банками, кредитами и вкладами, на основании которых мы и получим те формулы, которые будем использовать для решения данной задачи. Итак, давайте немного отвлечемся от экзаменов, от предстоящих школьных проблем, и посмотрим в будущее.

Допустим, вы выросли и собираетесь покупать квартиру. Допустим, вы собираетесь покупать не какую-то плохую квартиру на окраине, а хорошую качественную квартиру за 20 миллионов рублей. При этом также предположим, что вы устроились на более-менее нормальную работу и зарабатываете по 300 тысяч рублей в месяц. В этом случае за год вы сможете отложить примерно три миллиона рублей. Разумеется, зарабатывая по 300 тысяч рублей в месяц, за год у вас получится чуть большая сумма — 3600000 — но эти 600000 пусть будут потрачены на еду, на одежду и на прочие ежедневные бытовые радости. Итого вводные данные таковы: необходимо заработать двадцать миллионов рублей, у нас же в распоряжении имеется лишь три миллиона рублей в год. Возникает естественный вопрос: сколько лет нам необходимо откладывать по три миллиона, чтобы получить эти самые двадцать миллионов. Считается это элементарно:

[frac{20}{3}=6,….to 7]

Однако как мы уже с вами отмечали, вы зарабатываете 300 тысяч рублей в месяц, это значит, что вы умные люди и не будете откладывать деньги «под подушку», а отнесете их в банк. И, следовательно, ежегодно на те вклады, которые вы принесете в банк, будут начисляться проценты. Допустим, вы выберете надежный, но при этом более-менее прибыльный банк, и поэтому ваши вклады ежегодно будут расти на 15% годовых. Другими словами можно сказать, что сумма на ваших счетах ежегодно будет увеличиваться в 1,15 раза. Напомню формулу:

[Ktext{%} to 1+frac{K}{100}]

Давайте посчитаем, сколько денег будет на ваших счетах после каждого года:

В первый год, когда вы только начнете откладывать деньги, никакие проценты не накопятся, т. е. в конце года вы отложите три миллиона рублей:

[3m]

В конце второго года на те три миллиона рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года вы также доложили еще три миллиона рублей. Разумеется, на эти три миллиона еще не были начислены проценты, потому что к концу второго года эти три миллиона только появились на счету:

[3mcdot 1,15+3m]

Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15. И опять же, в течение всего года вы усердно работали и еще отложили три миллиона рублей:

[left( 3mcdot 1,15+3m right)cdot 1,15+3m]

Давайте рассчитаем еще четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще три миллиона, потому что в течение четвертого года вы также работали и также откладывали деньги:

[left( left( 3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m]

А теперь давайте раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:

[begin{align}& left( left( 3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m= \& =left( 3mcdot {{1,15}^{2}}+3mcdot 1,15+3m right)cdot 1,15+3m= \& =3mcdot {{1,15}^{3}}+3mcdot {{1,15}^{2}}+3mcdot 1,15+3m= \& =3mleft( {{1,15}^{3}}+{{1,15}^{2}}+1,15+1 right)= \& =3mleft( 1+1,15+{{1,15}^{2}}+{{1,15}^{3}} right) \end{align}]

Как видим, в скобках у нас стоят элементы геометрической прогрессии, т. е. у нас стоит сумма элементов геометрической прогрессии.

Напомню, что если геометрическая прогрессия задана элементом ${{b}_{1}}$, а также знаменателем $q$, то сумма элементов будет считаться по следующей формуле:

[{{S}_{n}}={{b}_{1}}cdot frac{{{q}^{n}}-1}{q-1}]

Эту формулу обязательно нужно знать и четко применять.

Обратите внимание: формула n-го элемента звучит следующим образом:

[{{b}_{n}}={{b}_{1}}cdot {{q}^{n-1}}]

Из-за этой степени многие ученики путаются. В сумме у нас стоит просто nдля суммы n-элементов, а сам n-й элемент имеет степень $n-1$. Другими словами, если мы сейчас попытаемся посчитать сумму геометрической прогрессии, то нужно учитывать следующее:

[begin{align}& {{b}_{1}}=1 \& q=1,15 \end{align}]

Теперь мы можем посчитать сумму:

[{{S}_{4}}=1cdot frac{{{1,15}^{4}}-1}{1,15-1}]

Посчитаем числитель отдельно:

[{{1,15}^{4}}={{left( {{1,15}^{2}} right)}^{2}}={{left( 1,3225 right)}^{2}}=1,74900625approx 1,75]

Итого, возвращаясь к сумме геометрической прогрессии, мы получим:

[{{S}_{4}}=1cdot frac{1,75-1}{0,15}=frac{0,75}{0,15}=frac{75}{15}=5]

В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится не в четыре раза, как если бы мы не клали деньги в банк, а в пять раз, т. е. пятнадцать миллионов. Давайте запишем это отдельно:

4 года → 5 раз

Забегая вперед, скажу, что если бы мы копили не четыре года, а пять лет, то в итоге наша сумма накоплений увеличилась бы в 6,7 раза:

5 лет → 6,7 раз

Другими словами, к концу пятого года мы бы получили на счету следующую сумму:

[6,7cdot 3=20,1]

Т. е. к концу пятого года накоплений с учетом процентов по вкладу мы бы уже получили свыше двадцати миллионов рублей. Таким образом, общий счет накоплений за счет банковских процентов снизился бы с почти семи лет до пяти лет, т. е. почти на два года.

Таким образом, даже, несмотря на то, что банк начисляет достаточно низкий процент на наши вклады (15%), уже через пять лет эти самые 15% дают прибавку, существенно превышающую наш ежегодный заработок. При этом основной мультипликационный эффект приходится на последние годы и даже, скорее, на последний год накоплений.

К чему я это все писал? Разумеется, не к тому, чтобы агитировать вас нести деньги в банк. Потому что если вы действительно хотите приумножить свои сбережения, то вкладывать их нужно не в банк, а в реально действующий бизнес, где эти самые проценты, т. е. рентабельность в условиях российской экономики редко опускается ниже 30%, т. е. вдвое больше банковских вкладов.

А вот что действительно полезно во всех этих рассуждениях, так это формула, которая позволяет нам найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк. Так и запишем:

[text{Vklad}=text{platezh}frac{{{text{%}}^{n}}-1}{text{%}-1}]

Сам по себе % считается по следующей формуле:

[Ktext{%}to 1+frac{K}{100}]

Эту формулу также необходимо знать, как и основную формулу суммы вклада. А, в свою очередь, основная формула способна значительно сократить вычисления в тех задачах с процентами, где требуется посчитать именно вклад.

Почему стоит пользоваться формулами, а не таблицами?

У многих наверняка возникнет вопрос, а к чему вообще все эти сложности, нельзя ли просто расписать каждый год в табличке, как это делают во многих учебниках, посчитать отдельно каждый год, а затем посчитать общую сумму вклада? Конечно, можно вообще забыть про сумму геометрической прогрессии и все считать с помощью классических табличек — так сделано в большинстве сборников для подготовки к ЕГЭ. Однако, во-первых, резко увеличивается объем вычислений, а во-вторых, как следствие, увеличивается вероятность допустить ошибку.

Да и вообще, использовать таблицы вместо этой замечательной формулы — это то же самое, что на стройке копать траншеи руками вместо того, чтобы использовать стоящий рядом и полностью работающий экскаватор.

Ну, или то же самое, что умножить пятерку на десятку не с помощью таблицы умножения, а складывать пятерку с самой собой десять раз подряд. Впрочем, это я уже отвлекся, поэтому еще раз повторю самую главную мысль: если есть какой-то способ упростить и сократить вычисления, то именно этим способом и надо воспользоваться.

Проценты по кредитам

С вкладами мы разобрались, поэтому переходим к следующей теме, а именно — к процентам по кредитам.

Итак, пока вы копите деньги, скрупулезно планируете свой бюджет, думаете о своей будущей квартире, ваш одноклассник, а нынче простой безработный, решил жить сегодняшним днем и просто взял кредит. При этом он еще будет подкалывать и смеяться над вами, мол, у него кредитный телефон и подержанный автомобиль, взятый в кредит, а вы до сих пор ездите на метро и пользуетесь старым кнопочным телефоном. Разумеется, за все эти дешевые «понты» вашему бывшему однокласснику придется дорого расплатится. Насколько дорого — вот это именно сейчас мы и посчитаем.

Для начала краткая вводная информация. Допустим, ваш бывший одноклассник взял два миллиона рублей в кредит. При этом согласно договору он должен платить xрублей в месяц. Допустим, что кредит он взял по ставке 20% годовых, что в нынешних условиях выглядит вполне прилично. Кроме того, предположим, что срок кредита составляет всего три месяца. Давайте попробуем связать все эти величины в одну формулу.

Итак, в самом начале, как только ваш бывший одноклассник вышел из банка у него в кармане два миллиона, и это и есть его долг. При этом не год прошел, и не месяц, а это только самое начало:

[2m]

Затем спустя один месяц на сумму задолженности будут начислены проценты. Как мы уже знаем для вычисления процентов достаточно умножить исходную задолженность на коэффициент, который считается по следующей формуле:

[Ktext{%}to 1+frac{K}{100}]

В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:

[1+frac{20}{100}=1,2]

Это коэффициент суммы, которая будет начисляться в год. Однако наш одноклассник не очень умный и он не читал договор, и на деле кредит ему выдали не под 20% в год, а под 20% в месяц. И уже к концу первого месяца на эту сумму будут начислены проценты, и она увеличится в 1,2 раза. Сразу после этого человеку будет необходимо оплатить оговоренную сумму, т. е. xрублей в месяц:

[2mcdot 1,2- x]

Далее к концу второго месяца уже на эту сумму будут вновь начислены проценты:

[left( 2mcdot 1,2- xright)cdot 1,2-x]

И вновь наш паренек вносит платеж в размере $x$ рублей.

Затем к концу третьего месяца сумма его задолженности еще раз увеличивается на 20%:

[left( left( 2mcdot 1,2- xright)cdot 1,2- xright)1,2- x]

И по условию за три месяца он должен полностью расплатиться, т. е. после внесения последнего третьего платежа его объем задолженности должен быть равен нулю. Мы можем записать такое уравнение:

[left( left( 2mcdot 1,2- xright)cdot 1,2- xright)1,2 — x=0]

Давайте решать:

[begin{align}& left( 2mcdot {{1,2}^{2}}- xcdot 1,2- xright)cdot 1,2- x=0 \& 2mcdot {{1,2}^{3}}- xcdot {{1,2}^{2}}- xcdot 1,2- x=0 \& 2mcdot {{1,2}^{3}}=cdot {{1,2}^{2}}+cdot 1,2+ \& 2mcdot {{1,2}^{3}}=left( {{1,2}^{2}}+1,2+1 right) \end{align}]

Перед нами вновь геометрическая прогрессия, а точнее, сумма трех элементов геометрической прогрессии. Давайте перепишем ее в порядке возрастания элементов:

[2mcdot {{1,2}^{3}}=left( 1+1,2+{{1,2}^{2}} right)]

Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Давайте запишем:

[begin{align}& {{b}_{1}}=1; \& q=1,2 \end{align}]

Теперь найдем сумму геометрической прогрессии:

[{{S}_{3}}=1cdot frac{{{1,2}^{3}}-1}{1,2-1}]

Следует напомнить, что сумма геометрической прогрессии с такими параметрами $left( {{b}_{1}};q right)$ считается по формуле:

[{{S}_{n}}={{b}_{1}}cdot frac{{{q}^{n}}-1}{q-1}]

Вот этой формулой мы только что и воспользовались. Подставляем эту формулу в наше выражение:

[2mcdot {{1,2}^{3}}=cdot frac{{{1,2}^{3}}-1}{1,2-1}]

Для дальнейших вычислений нам следует узнать, чему равна ${{1,2}^{3}}$. К сожалению, в этом случае мы уже не можем расписать как в прошлый раз в виде двойного квадрата, но зато можем посчитать так:

[begin{align}& {{1,2}^{3}}={{1,2}^{2}}cdot 1,2 \& {{1,2}^{3}}=1,44cdot 1,2 \& {{1,2}^{3}}=1,728 \end{align}]

Переписываем наше выражение:

[2mcdot 1,728=cdot frac{0,728}{0,2}]

Это классическое линейное выражение. Давайте вернемся к следующей формуле:

[2cdot {{1,2}^{3}}=cdot frac{{{1,2}^{3}}-1}{1,2-1}]

По сути, если обобщить ее, то мы получим формулу, связывающую проценты, кредиты, платежи и сроки. Формула звучит следующим образом:

[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]

Вот она, самая главная формула сегодняшнего видеоурока, с помощью которой считается не менее 80% всех экономических задач из ЕГЭ по математике во второй части.

Чаще всего в реальных задачах у вас будет спрашиваться платеж, либо чуть реже кредит, т. е. общая сумма задолженности, которая была у нашего одноклассника в самом начале платежей. В более сложных задачах вас попросят найти процент, ну а совсем сложных, которые мы разберем в отдельном видеоуроке от вас попросят найти сроки, в течение которых при данных параметрах кредита и платежа наш безработный одноклассник сможет полностью расплатится с банком.

Возможно, кто-то сейчас подумает, что я являюсь яростным противником кредитов, финансов и вообще банковской системы. Так вот, ничего подобного! Напротив, я считаю, что кредитные инструменты очень полезны и крайне необходимы нашей экономике, но только при условии, что кредит берется на развитие бизнеса. В крайнем случае, можно взять кредит на покупку жилья, т. е. ипотеку либо на неотложное медицинское лечение — все, других причин взять кредит просто не существует. А всевозможные безработные, которые берут кредиты на покупку «понтов» и при этом совершенно не задумываются о последствиях в итоге и становятся причиной кризисов и проблем в нашей экономике.

Возвращаясь к теме сегодняшнего урока, хотел бы отметить, что знать эту формулу, связывающую кредиты платежи и проценты, также необходимо как и сумму геометрической прогрессии. Именно с помощью этих формул решаются реальные экономические задачи из ЕГЭ по математике. Ну, а теперь, когда вы все это прекрасно знаете, когда понимаете, что такое кредит и почему его не стоит брать, переходим к решению реальных экономических задач из ЕГЭ по математике.

Решаем реальные задачи из ЕГЭ по математике

Пример № 1

Итак, первая задача:

31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т .е. увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (т .е. за четыре года)?

Итак, это задача про кредит, поэтому сразу записываем нашу формулу:

[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]

Кредит нам известен — 9282000 рублей.

С процентами мы сейчас разберемся. У нас речь идет о 10% в задаче. Следовательно, мы можем их перевести:

[10text{%}to 1+frac{10}{100}=1,1]

Мы можем составить уравнение:

[9289000cdot {{1,1}^{4}}=xcdot frac{{{1,1}^{4}}-1}{1,1-1}]

У нас получилось обычное линейное уравнение относительно $x$, хотя с достаточно грозными коэффициентами. Давайте попробуем его решить. Для начала найдем выражение ${{1,1}^{4}}$:

$begin{align}& {{1,1}^{4}}={{left( {{1,1}^{2}} right)}^{2}} \& 1,1cdot 1,1=1,21 \& {{1,1}^{4}}=1,4641 \end{align}$

Теперь перепишем уравнение:

[begin{align}& 9289000cdot 1,4641=xcdot frac{1,4641-1}{0,1} \& 9282000cdot 1,4641=xcdot frac{0,4641}{0,1}|:10000 \& 9282000cdot frac{14641}{10000}=xcdot frac{4641}{1000} \& frac{9282cdot 14641}{10}=xcdot frac{4641}{1000}|:frac{4641}{1000} \& x=frac{9282cdot 14641}{10}cdot frac{1000}{4641} \& x=frac{2cdot 14641cdot 1000}{10} \& x=200cdot 14641 \& x=2928200 \end{align}][]

Все, наша задача с процентами решена.

Разумеется, что это была лишь самая простая задача с процентами из ЕГЭ по математике. В настоящем экзамене такой задачи, скорее всего, не будет. А если и будет, то считайте, что вам очень повезло. Ну, а для тех, кто любит считать и не любит рисковать, переходим к следующим более сложным задачам.

Пример № 2

31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20% годовых. Схема выплаты кредиты следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е.) увеличивает долг на 20%), затем Степан производит в банк платеж. Весь долг Степан выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа.

Перед нами задача про кредиты, поэтому записываем нашу формулу:

[][kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]

Что нам известно? Во-первых, нам известен общий кредит. Также нам известны проценты. Давайте найдем коэффициент:

[20%to 1+frac{20}{100}=1,2]

Что касается $n$, то нужно внимательно прочитать условие задачи. Т. е. сначала нам необходимо посчитать, сколько он заплатил за три года, т. е. $n=3$, а затем выполнить еще раз те же самые действия но рассчитать платежи за два года. Давайте запишем уравнение для того случай, когда платеж выплачивается за три года:

[4004000cdot {{1,2}^{3}}=xcdot frac{{{1,2}^{3}}-1}{1,2-1}]

Давайте решать это уравнение. Но для начала найдем выражение ${{1,2}^{3}}$:

[begin{align}& {{1,2}^{3}}=1,2cdot {{1,2}^{2}} \& {{1,2}^{3}}=1,44cdot 1,2 \& {{1,2}^{3}}=1,728 \end{align}]

Переписываем наше выражение:

[begin{align}& 4004000cdot 1,728=xcdot frac{1,728-1}{0,2} \& 4004000cdot frac{1728}{1000}=xcdot frac{728}{200}|:frac{728}{200} \& x=frac{4004cdot 1728cdot 200}{728} \& x=frac{4004cdot 216cdot 200}{91} \& x=44cdot 216cdot 200 \& x=8800cdot 216 \& x=1900800 \end{align}]

Итого, наш платеж составит 1900800 рублей. Однако обратите внимании: в задаче от нас требовалось найти не ежемесячный платеж, а сколько всего Степан заплатит за три равных платежа, т. е. за все время пользования кредитом. Поэтому полученную величину необходимо еще раз умножить на три. Давайте посчитаем:

[3x=5702400]

Итого за три равных платежа Степан заплатит 5702400 рублей. Вот во сколько ему обойдется пользование кредитом в течение трех лет.

Теперь рассмотрим вторую ситуацию, когда Степан поднапрягся, собрался и выплатил весь кредит не за три, а за два равных платежа. Записываем все ту же нашу формулу:

[begin{align}& 4004000cdot {{1,2}^{2}}=xcdot frac{{{1,2}^{2}}-1}{1,2-1} \& 4004000cdot frac{144}{100}=xcdot frac{11}{5}|cdot frac{5}{11} \& x=frac{40040cdot 144cdot 5}{11} \& x=3640cdot 144cdot 5=3640cdot 720 \& x=2620800 \end{align}]

Но это еще не все, потому что сейчас мы посчитали лишь один из двух платежей, поэтому всего Степан заплатит ровно в два раза больше:

[2x=5241600]

Прекрасно, вот теперь мы и приблизились к окончательному ответу. Но обратите внимание: ни в коем случае мы еще не получили окончательный ответ, потому что за три года платежей Степан заплатит 5702400 рублей, а за два года платежей он заплатит 5241600 рублей, т. е. чуть-чуть поменьше. Насколько меньше? Чтобы это узнать, нужно из первого размера платежей вычесть второй размер платежей:

[5702400-5241600=460800]

Итого окончательный ответ — 460800 рублей. Именно сколько сэкономит Степан, если будет платить не три года, а два.

Как видите, формула, связывающая проценты, сроки и платежи, существенно упрощает вычисления по сравнению с классическими таблицами и, к сожалению, по непонятным причинам в большинстве сборников задач, тем не менее, до сих пор используются именно таблицы.

Отдельно хотел бы обратить ваше внимание на срок, на который взят кредит, и размером ежемесячных платежей. Дело в том, что эта связь напрямую не просматривается из тех формул, которые мы записали, однако ее понимание необходимо для быстрого и эффективного решения настоящих задач на экзамене. На самом деле эта связь очень проста: чем на больший срок берется кредит, тем меньшая сумма будет в ежемесячных платежах, но тем большая сумма накопится за все время пользования кредитом. И наоборот: чем меньше срок, тем больше ежемесячный платеж, однако при этом меньше итоговая переплата и меньше общая стоимость кредита.

Разумеется, все эти утверждения будут равны лишь при условии, что сумма кредита и процентная ставка в обоих случаях одна и та же. В общем, пока просто запомните этот факт — он будет использоваться для решения самых сложных задач на эту тему, а пока мы разберем более простую задачу, где как раз и требуется найти общую сумму исходного кредита.

Пример № 3

Итак, еще одна задача на кредит и по совместительству последняя задача в сегодняшнем видеоуроке.

31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 13% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 13%), затем Василий переводит в банк 5 107 600 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (за два года)?

Итак, в первую очередь, эта задача вновь про кредиты, поэтому записываем нашу замечательную формулу:

[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]

Посмотрим, что нам известно из условия задачи. Во-первых, платеж — он равен 5107600 рублей в год. Во вторых проценты, поэтому мы можем найти коэффициент:

[13%to 1+frac{13}{100}=1,13]

Кроме того, согласно условию задачи Василий взял в банке кредит на два года, т.е. выплатил двумя равными платежами, следовательно, $n=2$. Давайте все подставим и также заметим, что кредит нам неизвестен, т.е. та сумма, которую он взял, и обозначим ее за $x$. Получим:

[xcdot {{1,13}^{2}}=5107600cdot frac{{{1,13}^{2}}-1}{1,13-1}]

Знаменатель мы можем тут же посчитать — это будет 1,13, а вот в числителе, а также слева перед переменной $x$ у нас стоит коэффициент ${{1,13}^{2}}$. Предлагаю посчитать данное выражение отдельно:

[{{1,13}^{2}}=1,2769]

Перепишем наше уравнение с учетом этого факта:

[begin{align}& xcdot frac{12769}{10000}=5107600cdot frac{1,2769-1}{0,13} \& xcdot frac{12769}{10000}=frac{5107600cdot 2769}{1300}|:frac{12769}{10000} \& x=frac{51076cdot 2769}{13}cdot frac{10000}{12769} \& x=4cdot 213cdot 10000 \& x=8520000 \end{align}]

Все, это и есть окончательный ответ. Именно такую сумму Василий взял в кредит в самом начале.

Теперь понятно, почему в этой задаче нам предлагается взять кредит лишь на два года, потому что здесь фигурируют двузначные проценты, а именно 13%, которые в квадрате дают уже довольно «зверское» число. Но и это еще не предел — в следующем отдельном уроке мы рассмотрим более сложные задачи, где будет требоваться найти срок кредита, а ставка будет составлять один, два или три процента.

В общем, учитесь решать задачи на вклады и кредиты, готовьтесь к экзаменам и сдавайте их «отлично». А если что-то непонятно в материалах сегодняшнего видеоурока, то не стесняйтесь — пишите, звоните, и я постараюсь вам помочь.

Смотрите также:

Задача на производительность труда
ЕГЭ по математике 2016: задача про кредиты с фиксированным платежом
Тест к уроку «Что такое логарифм» (тяжелый)
Комбинированные задачи B12
Как решать задачи про летающие камни?
Задача C1: тригонометрия и показательная функция — 1 вариант

Источник

Задание 15 Профильного ЕГЭ по математике – это задача с экономическим содержанием.

Это может быть задача на кредиты и вклады. Или на нахождение наибольшего (наименьшего) значения какой-либо функции (прибыли, зарплат, времени работы). Мы разберем и те, и другие.

Начнем с задач о кредитах и вкладах. Прежде чем браться за реальные задания ЕГЭ из Банка заданий ФИПИ, подумаем – как вообще работает банк?

Доход банка образуется в виде разницы между процентом кредита и процентом вклада. Например, клиент банка положил на свой сберегательный счет 100 тысяч рублей под 10 % годовых – то есть открыл вклад. Через год он может получить в банке 110 тысяч рублей. Другому клиенту, наоборот, нужны 100 тысяч рублей. Банк выдает ему кредит под 30 % годовых, и теперь этот клиент должен вернуть банку 130 тысяч рублей. Таким образом, прибыль банка составит 130 – 110 = 20 (тысяч рублей).

Конечно же, процентные ставки банка по кредиту выше, чем процентные ставки по вкладу.

Вспомним формулы из темы «Проценты». Без них задачи на кредиты и вклады не решить!

Сначала — несколько контрольных вопросов:

1. Что принимается за 100%?

2. Величина х увеличилась на p%. Как это записать?

3. Величина y дважды увеличилась на р%. Как это записать?

И ответы на вопросы:

1. за 100% мы принимаем ту величину, с которой сравниваем.

2. если величину x увеличить на p процентов, получим $xcdot left ( 1+frac{p}{100} right )$ ;

если величину x уменьшить на p процентов, получим
$xcdot left ( 1-frac{p}{100} right )$ ;

если величину x увеличить на p процентов, а затем уменьшить на q процентов, получим $xcdot left ( 1+frac{p}{100} right )cdot left ( 1-frac{q}{100} right )$ ;

3. если величину x дважды увеличить на p процентов, получим $xcdot left ( 1+frac{p}{100} right )^{2}$ ;

4. если величину x дважды уменьшить на p процентов, получим $xcdot left ( 1-frac{p}{100} right )^{2}$ .

Вот простая подготовительная задача.

Клиент А. сделал вклад в банке в размере 7700 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Еще ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 847 рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?

Пусть банк начисляет p% в год.

У клиента А после начисления процентов через год сумма вклада станет равной $7700left ( 1+frac{p}{100} right )$ . Соответственно, через два года эта сумма станет равной $7700left ( 1+frac{p}{100} right )^{2}$

Клиент В сделал вклад позже, чем клиент А, на год. У него сумма вклада через год станет равной $7700left ( 1+frac{p}{100} right )$ .

Так как клиент А получил на 847 рублей больше клиента В, то
$7700left ( 1+frac{p}{100} right )^{2}-7700left ( 1+frac{p}{100} right )=847$

Вынесем 7700 за скобки:
$7700left (left ( 1+frac{p}{100} right )^{2}-left ( 1+frac{p}{100} right ) right )=847$

Чтобы не получить квадратное уравнение с огромными коэффициентами, сократим обе части уравнения на 77.

$100left (left ( 1+frac{p}{100} right )^{2}-left ( 1+frac{p}{100} right ) right )=11$

Сделаем замену $1+frac{p}{100}=k$
$100left ( k^{2}-k right )=11$

$100k^{2}-100k=11$

$100k^{2}-100k-11=0$

Его корни $x_{1}=-0,1$ и $x_{2}=1,1$ . Отрицательный корень нам не подходит, поэтому x=1,1 .

Сделав обратную замену, получим

$1+frac{p}{100}=1,1$

Отсюда p = 10%.

Ответ: 10.

Еще одна задача – на этот раз о кредите.

2. Костя оформил кредитную карту на 244 тысячи рублей под 25% годовых и расплачивался ею при каждой покупке. Через неделю деньги на карте кончились, и Костя обнаружил, что обязан погасить долг тремя равными ежегодными платежами. Сколько собственных денег Костя выплатит банку сверх суммы, взятой в кредит?

Обозначим сумму кредита , где рублей.

Проценты начисляются ежегодно, и после первого начисления процентов сумма долга равна
$left ( 1+frac{25}{100} right )S=frac{5}{4}S=kS$ .

Переменная — коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов;
$k=1+frac{p}{100}$ , где – процентная ставка банка.

Костя обязан ежегодно выплачивать банку рублей. После первой выплаты сумма долга равна $frac{5}{4}S-X=kS-X$ рублей.

Банк снова начисляет р процентов, и сумма долга становится равна
рублей, где $k=1,25=frac{5}{4}$ . Костя снова перечисляет в банк рублей.

Теперь сумма долга равна
рублей.

Банк в третий раз начисляет проценты, и сумма долга равна
рублей.

И снова Костя переводит в банк рублей. Теперь его долг равен нулю.

Выразим Х (ежегодный платеж Кости) из этого уравнения. Раскрыв скобки, получим:
$Sk^{3}-Xleft ( k^{2}+k+1 right )=0$ ;
$X=frac{Sk^{3}}{k^{2}+k+1}$ .Осталось подставить числовые данные.

Будем вести расчеты в тысячах рублей, а значение возьмем равным $frac{5}{4}$ . Это удобнее для расчетов, чем 1,25 .

$X=frac{Sk^{3}}{k^{2}+k+1}=frac{244cdot 5^{3}}{4^{3}left ( left ( frac{5}{4} right )^{2}+frac{5}{4}+1 right )}=frac{244cdot 125}{64left ( frac{25}{16} +frac{5}{4}+1right )}=frac{244cdot 125}{100+80+64}=125$ тысяч рублей.

Всего Костя выплатит банку 3X=375 тысяч рублей, что на 375 – 244 = 131 тысячу рублей больше суммы, взятой в кредит.

Вот задача на вклады, где надо составить, упростить и решить систему уравнений. Постарайтесь справиться самостоятельно.

3. В начале года $frac{5}{6}$ некоторой суммы денег вложили в банк А, а то, что осталось — в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у. е. (условных единиц), к концу следующего — 749 у. е. Если бы первоначально $frac{5}{6}$ суммы было вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у. е. Определите сумму вкладов по истечении второго года в этом случае.

Пусть первоначальная сумма равна – чтобы удобнее было записать $frac{1}{6}$ и $frac{5}{6}$ этой суммы.

Пусть банк A начисляет p процентов годовых. Тогда сумма, внесенная на счет в банке А, за год увеличивается в $1+frac{p}{100}=k$ раз, а за 2 года в $k^{2}$ раз.

Банк Б начисляет q процентов годовых. За год сумма, внесенная на счет в банке Б, увеличивается в $1+frac{q}{100}=m$ раз, а за 2 года в $m^{2}$ раз.

Надо найти $Sk^{2}+5Sm^{2}$ . Составим систему уравнений:

$left{begin{matrix}5Sk+Sm=670 ;;;;(1)\5Sk^{2}+Sm^{2}=749 ;;(2)\Sk+5Sm=710;;;;;(3)end{matrix}right.Leftrightarrowleft{begin{matrix}6Sleft ( m+k right )=1380\4Sleft ( m-k right )=40\5Sk^{2}+Sm^{2}=749end{matrix}right.Leftrightarrow$
$Leftrightarrowleft{begin{matrix}m+k=frac{230}{S}\m-k=frac{10}{S}\5Sk^{2}+Sm^{2}=749end{matrix}right.Leftrightarrowleft{begin{matrix}2m=frac{240}{S}vspace{2mm}\2k=frac{220}{S}vspace{2mm}\5Sk^{2}+Sm^{2}=749end{matrix}right.Leftrightarrowleft{begin{matrix}m=frac{120}{S} vspace{2mm}\k=frac{110}{S} vspace{2mm}\5Sk^{2}+Sm^{2}=749end{matrix}right.$

Подставим значения m и k в третье уравнение:

$Sleft ( 5cdot frac{110^{2}}{S^{2}} +frac{120^{2}}{S^{2}}right )=749$

$frac{100}{S}cdot left ( 5cdot 121+144 right )=749$

$frac{100}{S}cdot749=749$

S=100 .

Осталось вычислить $Sk^{2}+5Sm^{2}$ .

Ответ: 841.

Пора переходить к реальным задачам ЕГЭ о кредитах (задачи на вклады решаются похожим способом).

Запомним – есть всего две схемы решения задач на кредиты.

Первая – когда выплаты производятся равными платежами. Или есть информация о платежах.

Вторая – когда сумма долга уменьшается равномерно. Или есть информация о том, как уменьшается сумма долга.

Начнем с первой схемы.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задача 15 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Уметь правильно и быстро решать текстовые задачи на проценты необходимо не только учащимся, которым предстоит сдача ЕГЭ по математике базового или профильного уровня, но и всем взрослым, поскольку подобные задания постоянно встречаются в повседневной жизни. Повышение цен, планирование семейного бюджета, выгодное вложение финансовых средств и множество других вопросов невозможно уладить без данных навыков. При подготовке к сдаче аттестационного испытания обязательно нужно повторить, как решать задачи на проценты: в ЕГЭ по математике они встречаются как в базовом, так и в профильном уровне.

Необходимо запомнить

Процент — это (frac{1}{100})
часть от какого-либо числа. Обозначает долю чего-либо по отношению к целому. Письменный символ — (%)
. При подготовке к ЕГЭ по теме «Проценты» школьникам как в Москве, так и в других точках РФ необходимо запомнить следующую формулу:

Как ее применить?

Для того чтобы решить простое задание с процентами в ЕГЭ по математике, нужно:

Разделить имеющееся число на (100)
.
Умножить полученное значение на то количество (%)
, которое нужно найти.

Например, для того чтобы вычислить (10%)
от числа (300)
, нужно найти (1)
процент, разделив (300:100=3)
. И полученное от предыдущего действия число (3cdot10=30)
. Ответ: (30).

Это простейшие задания. Учащиеся 11 класса в ЕГЭ сталкиваются с необходимостью выполнить решение сложных задач на проценты. Как правило, речь в них идет о банковских вкладах или платежах. Ознакомиться с формулами и правилами их применения вы можете, перейдя в раздел «Теоретическая справка». Здесь вы сможете не только повторить основные определения, но и познакомиться с вариантами решения сложных задач на проценты по банковскому кредиту, а также с упражнениями из других разделов алгебры, например,

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Теория по теме: «Решение задач на проценты».

Тип 1: Перевод процентов в десятичную дробь. проценты  дробь А%  А разделить на 100 Задачи:20%;75%;125%;50%;40%;1%;70%;35%;80%…. Заполните таблицу 1% 5% 10% 20% 25% 50% 75% 100%

Тип 2:Перевод дроби в проценты. число  проценты А  А умножить на 100 % Переведите дроби в проценты: 3/4; 0,07; 2,4. (ГИА, тематические задания) Соотнесите дроби, которые выражают доли некоторой величины, и соответствующие им проценты. А.1/4 ; Б)3/5 ; В) 0,5; Г) 0,05 1) 5%; 2) 25%; 3) 50%; 4) 60% Ответ: А Б В Г

Тип 3: Находим процент от числа. Х% от А 1)Х% представляем в виде десятичной дроби 2) Число А умножаем на десятичную дробь. Задача — образец. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества? Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20 % = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло контроль качества.

Тип 4: Находим число по его проценту. А это Х% : 1) Х% представляем в виде десятичной дроби 2) А делим на десятичную дробь. Задача — образец. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 25% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки? Решение. Мы не знаем, сколько всего задач в пособии. Но зато нам известно, что 38 задач это 25% от общего их количества. 25 %=0,25 38/0,25 = 152. 152 задачи в этом сборнике.

Тип 5: Находим процентное отношение двух чисел. А и В числа. Сколько % составляет В от А? 1)В/А 2) Полученное частное умножить на 100% Задача — образец. В классе 30 учеников. 15 из них – девочки. Сколько процентов девочек в классе? Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 1)15 /30=0,5 2)0,5*100%=50% Задача — образец. За 1 час станок-автомат изготовлял 240 деталей. После реконструкции этого станка он стал изготовлять в час 288 таких же деталей. На сколько процентов повысилась производительность станка? Решение. Производительность станка повысилась на 288-240=48 деталей в час. Нужно узнать, сколько процентов от 240 деталей составляют 48 деталей. Для того чтобы узнать, сколько процентов число 48 составляет от числа 240 нужно число 48 разделить на 240 и результат умножить на 100%. 48/240 *100% =20% Ответ: производительность станка повысилась на 20%

Тип 6: Увеличиваем число на процент. Уменьшаем число на процент. А- число; увеличиваем на Х% то оно увеличилось в (1 + х /100) раз. : 1)число А умножаем на 2) (1 + х /100) . Задача — образец. . На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году? Решение. 140 * (1 + 15/100) = 161. А- число; уменьшаем на Х% то оно уменьшилось в (1 — х /100) раз. : 1)число А умножаем на 2) (1 — х /100) . Задача — образец. Год назад школу закончили 100 ребят. А в это году выпускников на 25 % меньше. Сколько выпускников в этом году? Решение. 100 * (1 – 25/100) = 75.

Тип7: Концентрация раствора. Задача — образец. Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)(Петерсон 6 кл.) Решение 1)Масса растворенного вещества 1 кг 2)Масса всего раствора 1+9=10(кг) 9 кг — масса воды в растворе (не путать с общей массой раствора) 3)1/10*100%=10% 10% — концентрация раствора

Тип 8:Процентное содержание металла в сплаве. Задача – образец 1. Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы получившийся сплав содержал 40% меди? Решение.1)12 . 0,45= 5,4 (кг) — чистой меди в первом сплаве; 2) 5,4: 0,4= 13,5 (кг)- вес нового сплава; 3) 13,5- 12= 1,5 (кг) олова. Ответ: надо 1,5 кг олова.

Задача – образец 2. Имеется два сплава, состоящие из меди, цинка и олова. Известно, что первый сплав содержит 40% олова, а второй- 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалась 30% цинка. Определите, сколько килограммов олова содержится в получившемся новом сплаве. Так как процентное содержание цинка в первом и втором сплавах одинаково и в третьем сплаве оказалось 30%, то в первом и втором сплавах процентное содержание цинка 30%. 250*0,3= 75 (кг)- цинка во втором сплаве; 250 * 0,26= 65 (кг)- меди во втором сплаве; 250-(75+65)= 110 (кг) олова во втором сплаве; 150 . 0,4= 60 (кг)- олова в первом сплаве; 110+60= 170(кг)- олова в третьем сплаве. Ответ: 170 кг. 1 сплав 2сплав Новый сплав (3) Медь 26 % Цинк 30% 30% 30% Олово 40% ?кг масса 150кг 250кг 150+250=400

Тип 9: На «сухое вещество ». Практически любой продукт – яблоки, арбузы, грибы, картофель, крупа, хлеб и т.д. состоит из воды и сухого вещества. Причём, воду содержат как свежие, так и сушёные продукты. В процессе высыхания испаряется только вода, а масса сухого вещества не изменяется. А.Г. Мордкович “Математика 6” Задача № 362 Задача — образец. Свежий гриб содержит 90% воды, а сушеный – 15%. Сколько получится сушеных грибов из 17кг свежих? Сколько надо взять свежих грибов, чтобы получить 3,4кг сушеных? Решение. Составим таблицу: 1 часть задачи: вещество Масса вещества (кг) Процентное содержание воды Процентное содержание сухого вещества Масса сухого вещества (кг) Свежий гриб 17кг 90% 10% 17*0,1=1,7 Сушеный гриб Х кг 15% 85% Х*о,85=0,85х Так как масса сухого вещества в сухих и свежих грибах остается неизменной, получим уравнение: 0,85х = 1,7, х = 1,7: 0,85, х = 2.

2 часть задачи: Вещество Масса вещества (кг) Процентное содержание воды Процентное содержание воды Масса сухого вещества (кг) Свежий гриб х 90% 10% 0,1х Сушеный гриб 3,4 15% 85% 3,4*0,85=2,89 0,1х = 2,89, х = 2,89: 0,1, х = 28.9. Ответ: из 17кг свежих грибов получится 2кг сушеных; чтобы получить 3,4кг сушеных грибов, надо взять 28,9кг свежих.

Тип задания: 11
Тема:
Задачи на проценты

Условие

Елена сделала вклад в банк в размере 5500
рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Спустя год Наталья положила такую же сумму в этот же банк и на тех же условиях. Ещё через год Елена и Наталья одновременно закрыли вклады и забрали деньги. В результате Елена получила на 739,2
рубля больше, чем получила Наталья. Найдите, какой процент годовых начислял банк по вкладам?

Показать решение

Решение

Пусть процент годовых будет x
, тогда через год вклад Елены составил:

5500 + 0, 01x cdot 5500 = 5500(1 + 0,01x)
рублей, а ещё через год — 5500(1 + 0,01x)^2
рублей. Вклад Натальи лежал в банке только год, потому он равен 5500(1 + 0,01x)
рублей. А разность между получившимися вкладами Елены и Натальи составила 739,2
рубля.

Составим и решим уравнение:

5500(1+ 0,01x)^2-5500(1+0,01x)=
739,2,

(1+0,01x)^2-(1+0,01x)=0,1344,

x^2+100x-1344=0,

x_1=-112,enspace x_2=12.

Банк начислял 12%
годовых.

Ответ

Тип задания: 11
Тема:
Задачи на проценты

Условие

Предприниматель Петров получил в 2005
году прибыль в размере 12,000
рублей. Каждый следующий год его прибыль увеличивалась на 110%
по сравнению с предыдущим годом. Сколько рублей заработал Петров за 2008
год?

Показать решение

Решение

В 2005
году прибыль составляла 12,000
рублей, каждый следующий год она увеличивалась на 110%
, то есть становилась 210%
= 2,1
от предыдущего года. Через три года она будет равна 12,000 cdot 2,1^3 = 111,132
рубля.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема:
Задачи на проценты

Условие

Имеется два сплава. Первый сплав содержит 12%
железа, второй — 28%
железа. Масса второго сплава больше массы первого на 2
кг. Из этих двух сплавов изготовили третий сплав с содержанием железа 21%
. Найдите массу третьего сплава. Ответ дайте в килограммах.

Показать решение

Решение

Обозначим массу первого сплава через x
кг. Тогда масса второго сплава (x + 2)
кг. Содержание железа в первом сплаве равно 0,12x
кг, во втором сплаве — 0,28(x + 2)
кг. Третий сплав имеет массу x + x + 2 = 2x + 2
(кг), и в нём содержание железа равно 2(x + 1) cdot 0,21 = 0,42(x + 1)
кг.

Составим и решим уравнение:

0,12x+ 0,28(x + 2) = 0,42(x+1),

6x + 14(x + 2) = 21(x + 1),

X = 7.

Третий сплав имеет массу 2 cdot 7 + 2 = 16
(кг).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема:
Задачи на проценты

Условие

Цена телевизора в магазине ежеквартально (в квартале — три месяца) уменьшается на одно и то же число процентов от предыдущей цены. Известно, что телевизор, стоимостью 50 000
рублей был продан спустя два квартала за 41 405
рублей. Найдите, на сколько процентов ежеквартально уменьшалась стоимость телевизора.

Показать решение

Решение

Цена телевизора первоначально была 50 000
руб. Через квартал она стала 50,000-50,000cdot0,01x = 50,000(1-0,01x)
рублей, где x
— количество процентов, на которые уменьшается ежеквартально цена телевизора. Через два квартала его цена стала

50,000(1-0,01x)(1-0,01x)=50,000(1-0,01x)^2.

Составим и решим уравнение:

50,000(1-0,01x)^2=41,405,

(1-0,01x)^2=0,8281,

1-0,01x=0,91,

x=9.

Итак, на 9
процентов уменьшалась цена телевизора ежеквартально.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема:
Задачи на проценты

Условие

В 2005
году в посёлке проживало 55 000
человек. В 2006
году, в результате строительства новых домов, число жителей увеличилось на 6%
, а в 2007
году — на 10%
по отношению к 2006
году. Найдите, число жителей посёлка в 2007
году.

Показать решение

Решение

В 2006
году число жителей посёлка выросло на 6%
, т.е. стало 106%
, что равно 55,000 cdot 1,06 = 58,300
(жителей). В 2007
году число жителей посёлка выросло на 10%
(стало 110%
) по сравнению с 2006
годом, т.е. число жителей посёлка стало 58,300 cdot 1,1 = 64,130
человек.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема:
Задачи на проценты

Условие

Показать решение

Решение

В 3
литрах 14%
-ного водного раствора содержится 3cdot0,14=0,42
л. некоторого вещества. Добавили 4
литра воды, стало 7
литров раствора. В этих 7
литрах нового раствора — 0,42
л некоторого вещества. Найдём концентрацию нового раствора: 0,42:7cdot100=6
%
.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема:
Задачи на проценты

Условие

Строительные фирмы учредили компанию с уставным капиталом 150
млн рублей. Первая фирма внесла 20%
уставного капитала, вторая фирма — 22,5
млн рублей, третья — 0,3
уставного капитала, четвертая фирма внесла оставшуюся часть.

Процент – это сотая доля числа.

Процент обозначается символом $%$.

Чтобы проценты представить в виде десятичной дроби, надо значение разделить на $100$.

$35%={35}/{100}=0.35$.

Чтобы найти процент от числа, надо заданное число разделить на $100$ и умножить на величину процента.

$n%$ от $а={а⋅n}/{100}$

Сколько градусов содержит угол, если он составляет $5%$ от развернутого угла?

Развернутый угол равен $180°$.

Найдем $5%$ от $180°$, для этого ${180°⋅5}/{100}=9°$.

Ответ: $9°$.

Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на $100$.

Найдите число, $20%$ которого составляют $80$.

Число, $20%$ которого составляют $80$, находим так:

${80⋅100}/{20}=400$.

Ответ: $400$.

Задачи на скидки

Скидка — это снижение цены товара или услуги. Чаще всего скидку указывают в процентах.

Чтобы найти цену товара с учетом скидки необходимо:

Из $100%$ вычесть процент скидки.
Найти полученный процент от полной стоимости товара.

Зимняя куртка стоит $4500$ рублей. Сезонная скидка составляет $20%$. Сколько надо заплатить за куртку с учетом скидки?

Найдем, какой процент от начальной стоимости будет составлять стоимость куртки со скидкой:

Посчитаем, сколько составляет $80%$ от $4500$ рублей. Чтобы найти процент от числа, надо заданное число разделить на $100$ и умножить на величину процента.

${4500·80}/{100}=3600$ — стоимость куртки с учетом скидки.

Задачи на вклады, кредиты, наценки

Чтобы найти сумму денег с учетом годовой ставки, необходимо:

К $100%$ прибавить годовой процент вклада.
Найти полученный процент от изначального количества денег.

Клиент положил в банк 150000 рублей под $12%$ годовых. Какую сумму он сможет снять через год?

$100%+12%=112%$ — это процент, который составляет сумма денег клиента через год относительно первоначальной суммы.

Найдем $112%$ от $150000$ рублей:

${112⋅150000}/{100}=168000$ рублей.

Ответ: $168000$.

В некоторых задачах на проценты удобно использовать пропорцию, например:

Мешок картошки стоил $200$ рублей. После повышения цены он стал стоить $250$ рублей. На сколько процентов была повышена цена на мешок картошки?

Возьмем за $100%$ изначальную стоимость товара (так как именно с ней мы будем сравнивать стоимость после повышения цены):

Пусть $х%$ — столько процентов составляет новая цена относительно старой.

С этими данными составим и решим пропорцию:

${100%}/{х%}={200}/{250}$.

Произведение крайних членов пропорции равно произведению средних членов пропорции:

$200⋅х=100⋅250$.

$х={100⋅250}/{200}=125%$.

Новая стоимость мешка с картошкой составляет $125%$ относительно начальной цены.

Цена увеличилась на $125%-100%=25%$.

Ответ: $25$.

Рабочая тетрадь по математике стоит $65$ рублей. Сколько тетрадей может купить ученик на $450$ рублей, если действует скидка $8%$?

Найдем, сколько процентов составляет стоимость тетради с учетом скидки:

Найдем $92%$ от $65$ рублей и получим стоимость $1$ тетради со скидкой:

${450}/{59.8}={4500}/{598}≈7.5$

Дробное число тетрадей мы купить не можем, на восемь тетрадей денег не хватит, поэтому ученик сможет купить только $7$ тетрадей.

Ответ: $7$.

Для решения некоторых задач необходимо быть знакомым с термином «сложные проценты»
, который часто нужен для решения задач о вкладах, кредитах и пр. Простыми словами, «сложные проценты» возникают тогда, когда мы начисляем проценты на проценты. Давайте разберем на примере.

Допустим мы положили в банк $X$ рублей под $N%$ годовых. И оставили деньги в банке не на один, а на два года. Это значит, что в конце первого года мы смогли бы забрать $X + X*{N/100} = X(1+{N/100})$ рублей, но мы их не забираем, а оставляем на второй год. И теперь как бы сумма нашего «нового» вклада на второй год под $N%$ составляет уже не $X$, а $X(1+{N/100})$ рублей. То есть в течение второго года проценты будут начисляться в том числе на проценты, накопленные за первый год. Итого под конец второго года мы сможем забрать $X(1+{N/100}) + X(1+{N/100})*{N/100} = X(1+{N/100})(1+{N/100}) = X(1+{N/100})^2$.
Если бы мы сделали вклад не на два, а на $Y$ лет, то в конце получили бы $X(1+{N/100})^Y$ рублей.

Вкладываем деньги в банк

[frac{20}{3}=6,….to 7]

Давайте посчитаем, сколько денег будет на ваших счетах после каждого года:

[left(3mcdot 1,15+3m right)cdot 1,15+3m]

[left(left(3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m]

[begin{align}& left(left(3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m= & =left(3mcdot {{1,15}^{2}}+3mcdot 1,15+3m right)cdot 1,15+3m= & =3mcdot {{1,15}^{3}}+3mcdot {{1,15}^{2}}+3mcdot 1,15+3m= & =3mleft({{1,15}^{3}}+{{1,15}^{2}}+1,15+1 right)= & =3mleft(1+1,15+{{1,15}^{2}}+{{1,15}^{3}} right) end{align}]

Эту формулу обязательно нужно знать и четко применять.

Обратите внимание: формула n
-го элемента звучит следующим образом:

[{{b}_{n}}={{b}_{1}}cdot {{q}^{n-1}}]

Из-за этой степени многие ученики путаются. В сумме у нас стоит просто n
для суммы n-
элементов, а сам n
-й элемент имеет степень $n-1$. Другими словами, если мы сейчас попытаемся посчитать сумму геометрической прогрессии, то нужно учитывать следующее:

[begin{align}& {{b}_{1}}=1 & q=1,15 end{align}]

[{{S}_{4}}=1cdot frac{{{1,15}^{4}}-1}{1,15-1}]

Посчитаем числитель отдельно:

[{{1,15}^{4}}={{left({{1,15}^{2}} right)}^{2}}={{left(1,3225 right)}^{2}}=1,74900625approx 1,75]

Итого, возвращаясь к сумме геометрической прогрессии, мы получим:

[{{S}_{4}}=1cdot frac{1,75-1}{0,15}=frac{0,75}{0,15}=frac{75}{15}=5]

4 года → 5 раз

5 лет → 6,7 раз

Другими словами, к концу пятого года мы бы получили на счету следующую сумму:

[text{Vklad}=text{platezh}frac{{{text{%}}^{n}}-1}{text{%}-1}]

Сам по себе % считается по следующей формуле:

Почему стоит пользоваться формулами, а не таблицами?

Проценты по кредитам

С вкладами мы разобрались, поэтому переходим к следующей теме, а именно — к процентам по кредитам.

В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:

[left(2mcdot 1,2- xright)cdot 1,2-x]

И вновь наш паренек вносит платеж в размере $x$ рублей.

Затем к концу третьего месяца сумма его задолженности еще раз увеличивается на 20%:

[left(left(2mcdot 1,2- xright)cdot 1,2- xright)1,2- x]

[left(left(2mcdot 1,2- xright)cdot 1,2- xright)1,2 — x=0]

Давайте решать:

[begin{align}& left(2mcdot {{1,2}^{2}}- xcdot 1,2- xright)cdot 1,2- x=0 & 2mcdot {{1,2}^{3}}- xcdot {{1,2}^{2}}- xcdot 1,2- x=0 & 2mcdot {{1,2}^{3}}=cdot {{1,2}^{2}}+cdot 1,2+ & 2mcdot {{1,2}^{3}}=left({{1,2}^{2}}+1,2+1 right) end{align}]

Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Давайте запишем:

[begin{align}& {{b}_{1}}=1; & q=1,2 end{align}]

Теперь найдем сумму геометрической прогрессии:

[{{S}_{3}}=1cdot frac{{{1,2}^{3}}-1}{1,2-1}]

Следует напомнить, что сумма геометрической прогрессии с такими параметрами $left({{b}_{1}};q right)$ считается по формуле:

[{{S}_{n}}={{b}_{1}}cdot frac{{{q}^{n}}-1}{q-1}]

Вот этой формулой мы только что и воспользовались. Подставляем эту формулу в наше выражение:

[begin{align}& {{1,2}^{3}}={{1,2}^{2}}cdot 1,2 & {{1,2}^{3}}=1,44cdot 1,2 & {{1,2}^{3}}=1,728 end{align}]

Переписываем наше выражение:

Это классическое линейное выражение. Давайте вернемся к следующей формуле:

Решаем реальные задачи из ЕГЭ по математике

Пример № 1

Итак, первая задача:

31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (т.е. за четыре года)?

Итак, это задача про кредит, поэтому сразу записываем нашу формулу:

Кредит нам известен — 9282000 рублей.

С процентами мы сейчас разберемся. У нас речь идет о 10% в задаче. Следовательно, мы можем их перевести:

Мы можем составить уравнение:

$begin{align}& {{1,1}^{4}}={{left({{1,1}^{2}} right)}^{2}} & 1,1cdot 1,1=1,21 & {{1,1}^{4}}=1,4641 end{align}$

Теперь перепишем уравнение:

[begin{align}& 9289000cdot 1,4641=xcdot frac{1,4641-1}{0,1} & 9282000cdot 1,4641=xcdot frac{0,4641}{0,1}|:10000 & 9282000cdot frac{14641}{10000}=xcdot frac{4641}{1000} & frac{9282cdot 14641}{10}=xcdot frac{4641}{1000}|:frac{4641}{1000} & x=frac{9282cdot 14641}{10}cdot frac{1000}{4641} & x=frac{2cdot 14641cdot 1000}{10} & x=200cdot 14641 & x=2928200 end{align}][]

Все, наша задача с процентами решена.

Пример № 2

Перед нами задача про кредиты, поэтому записываем нашу формулу:

[]

Давайте решать это уравнение. Но для начала найдем выражение ${{1,2}^{3}}$:

[begin{align}& {{1,2}^{3}}=1,2cdot {{1,2}^{2}} & {{1,2}^{3}}=1,44cdot 1,2 & {{1,2}^{3}}=1,728 end{align}]

Переписываем наше выражение:

[begin{align}& 4004000cdot 1,728=xcdot frac{1,728-1}{0,2} & 4004000cdot frac{1728}{1000}=xcdot frac{728}{200}|:frac{728}{200} & x=frac{4004cdot 1728cdot 200}{728} & x=frac{4004cdot 216cdot 200}{91} & x=44cdot 216cdot 200 & x=8800cdot 216 & x=1900800 end{align}]

[begin{align}& 4004000cdot {{1,2}^{2}}=xcdot frac{{{1,2}^{2}}-1}{1,2-1} & 4004000cdot frac{144}{100}=xcdot frac{11}{5}|cdot frac{5}{11} & x=frac{40040cdot 144cdot 5}{11} & x=3640cdot 144cdot 5=3640cdot 720 & x=2620800 end{align}]

Пример № 3

Итак, еще одна задача на кредит и по совместительству последняя задача в сегодняшнем видеоуроке.

Итак, в первую очередь, эта задача вновь про кредиты, поэтому записываем нашу замечательную формулу:

[{{1,13}^{2}}=1,2769]

Перепишем наше уравнение с учетом этого факта:

[begin{align}& xcdot frac{12769}{10000}=5107600cdot frac{1,2769-1}{0,13} & xcdot frac{12769}{10000}=frac{5107600cdot 2769}{1300}|:frac{12769}{10000} & x=frac{51076cdot 2769}{13}cdot frac{10000}{12769} & x=4cdot 213cdot 10000 & x=8520000 end{align}]

Все, это и есть окончательный ответ. Именно такую сумму Василий взял в кредит в самом начале.

Типы задач на проценты и способы их решения в заданиях ОГЭ и ЕГЭ

Авторы
Руководители
Файлы работы
Наградные документы

Павлов А.А. 1

1МБОУ «ООШ № 12» Асбестовского городского округа

Самофалова В.В. 1

1МБОУ «ООШ № 12»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

В настоящее время людям часто приходится встречаться с понятием «процент». Современный человек должен уметь вычислять скидку на интересующий его товар; решать задачи на смеси, сплавы, растворы, в которых без процентов не обойтись. Например, нужно знать, как правильно приготовить маринад для консервирования, как смешать клей для обоев, как приготовить раствор для заливки фундамента дома, как разбавить уксусную кислоту для употребления в пищу. На этикетках продуктов питания часто указывается массовая доля вещества, например, жира, выраженная в процентах. Задачи на проценты встречаются на ОГЭ и ЕГЭ базового и профильного уровней. Это, как правило, практико-ориентированные задания. Поскольку мне тоже предстоит сдавать экзамен по математике, я решил рассмотреть задачи на проценты и способы их решения в задачах ОГЭ и ЕГЭ. Так как будущую профессию я хочу связать с экономической специальностью, руководствуясь примером моей мамы, которая работает в банке, я быстро определился с практической частью моего проекта. Я провел интервью с сотрудником банка, которому задал интересующие меня вопросы.

Цель проекта: исследовать типы задач на проценты и способы их решения в заданиях ОГЭ и ЕГЭ.

Задачи проекта:

Изучить историю возникновения процентов.

Проанализировать информационные источники по теме: «Типы задач на проценты и способы их решения в заданиях ОГЭ и ЕГЭ».

Разобрать решение задач на проценты из ОГЭ и ЕГЭ.

Провести интервьюирование сотрудника и клиентов банка ПАО КБ «УБРиР» города Асбеста с целью понять, как начисляются проценты на кредиты и вклады.

Разработать анкету и провести анкетирование среди обучающихся основной школы №12, обработать результаты.

Объект исследования: задачи на проценты.

Предмет исследования: типы задач на проценты и способы их решения.

Гипотеза: опираясь на знания по математике, полученные в 5-6 классах по теме «Проценты», можно решить любую задачу на проценты из банка задач ОГЭ и ЕГЭ.

Методы исследования:

Изучить литературу по данной теме.

Решение задач на проценты из ОГЭ и ЕГЭ.

Интервьюирование сотрудника и клиентов банка ПАО КБ «УБРиР» города Асбеста.

Анкетирование и обработка его результатов.

Теоретическая часть

1. Истрия возникновения процентов

Слово «процент» происходит от латинского «pro centum», что буквально означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотых долях. Это даёт возможность упрощать расчёты и легко сравнивать части между собой и целыми. Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась ещё в древности у вавилонян, которые пользовались шестидесятеричными дробями. Уже в клинописных табличках вавилонян содержатся задачи на расчет процентов. До нас дошли составленные ими таблицы, которые позволили быстро определять сумму процентных денег. Были известны проценты и в Индии. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией. Они умели производить более сложные вычисления с применением процентов[19, 3].

Денежные расчёты с процентами были особенно распространены в Древнем Риме. Они называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Римский сенат даже должен был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.

В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т.е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислении процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы[5].

Впервые опубликовал таблицы для расчёта процентов в 1584 г. Симон Стевин — инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий, в том числе — особой записи десятичных дробей.

Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчётах, статистике, науке и технике. Ныне процент — это частный вид десятичных дробей, сотая доля целого, принимаемого за единицу [8].

Знак «%» происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения в скорописи буквы t в наклонную черту произошёл современный символ для обозначения процента. Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошёл в результате нелепой опечатки, совершенной наборщиком. В 1685 году в Париже была опубликована книга — руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %. После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.

Иногда применяют и более мелкие доли целого — тысячные, т.е. десятые части процента. Их называют «промилле» (от латинского pro mille — «с тысячи»), обозначаемые ‰ по аналогии со знаком %. Изобретение математических знаков и символов значительно облегчило изучение математики и способствовало ее дальнейшему развитию.

Таким образом, появились проценты далеко в прошлом и в настоящее время понятие «процент» очень активно используется в банковской системе, в торговле (скидка на товар, различные акции в магазинах и пр.), экономике (налогообложении и пр.), статистике и др. Также понятие процент встречается на ОГЭ по математике.

2. Типы задач на проценты и способы их решения

В настоящие время задачи на проценты в заданиях ОГЭ встречаются под номерами 1-5 и 22, причём в одной задаче сочетаются сразу несколько типов задач на проценты. Также задачи на проценты встречаются в заданиях ЕГЭ базового и профильного уровней. Рассмотрим некоторые из них.

Тип 1: Находим процент (дробь) от числа.

Способ решения: что бы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?

Решение. Нужно найти 20% от общего количества изготовленных приборов. 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.

Тип 2: Находим число по его проценту (дроби).

Способ решения: Что бы найти число от данного числа процентов, нужно количество процентов записать десятичной дробью, а затем умножить число равное количеству процентов на проценты, записанные десятичной дробью.

Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?

Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 23% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

Способ решения: Число процент, которого нужно узнать, надо сначала разделить на второе число, затем умножить на сто.

Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?

Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, процент которого требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.

Тип 4: Увеличиваем число на процент.

Способ решения: нужно к данному числу прибавить это же число делённое на сто и умноженное на количество процентов, на которое должно увеличиться число.

Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?

Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.

Тип 5: Уменьшаем число на процент.

Способ решения: нужно из данного числа вычесть это же число, делённое на сто и умноженное на количество процентов, на которое должно уменьшиться число.

Задача. Год назад школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?

Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.

Тип 6: Задачи на простые проценты.

Способ решения: формула для расчета простых процентов:

A=P*(1+IT), где

T-количество периодов;

I-процентная ставка;

P-вкладываемая сумма;

A-получаемая сумма.

Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?

Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку:

S = 5000 · (1 + 12 · 0,15) = 14000.

Тип 7: Задачи на сложные проценты.

Способ решения: формула для начисления сложного процента:

S=A*(1+R)^T

A- СУММАВКЛАДА;

R- СТАВКА ПРОЦЕНТА;

T- КОЛИЧЕСТВО ПЕРИОДОВ;

S- ПОЛУЧАЕМАЯ СУММА.

Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.

Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% — процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)^у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)³ = 38021,875 – искомая сумма.

Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще.

Таким образом, мною выделено семь типов задач на проценты, подробно описан способ их решения и также приведены конкретные примеры.

Практическая часть.

3. Решение задач на проценты из ОГЭ и ЕГЭ.

Мною в теоретической части проекта было выделено семь типов задач на проценты, теперь подробнее рассмотрим решение задач из ОГЭ и ЕГЭ базового и профильного уровней.

Тип 1: Находим процент (дробь) от числа.

Задача из ЕГЭ по математике базового уровня.

Задание 3 № 26631

В городе N живет 200 000 жителей. Среди них 15% детей и подростков. Среди взрослых жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает?

Решение: Численность детей в городе N составляет 200 000 0,15 – это 30 000. Численность взрослого населения 200 000 − 30 000 = 170 000 человек. Из них не работает 170 000*0,45 = 76 500 человек. Значит, работает 170 000 − 76 500 = 93 500 человек.

Ответ: 93 500.

Тип 2: Находим число по его проценту.

Задача из ЕГЭ по математике базового уровня.

Задание 3 № 77340

В школе 124 ученика изучают французский язык, что составляет 25% от числа всех учеников. Сколько учеников учится в школе?

Решение: Разделим 124 на 0,25:

Значит, в школе учится 496 учеников.

Ответ: 496.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

Задача из ОГЭ по математике.

Вариант №11

Задача№3 На сколько процентов сократилась посевная площадь после того, как земледелец устроил терассы. Ответ округлите до десятых.

Решение:

По теореме Пифагора найдём сторону AB

AB²=AC²+BC²=12²+35²=144+1225=1369

AB = 37

2. Найдём посевную площадь

S=40*37=1480 м²

3. Найдём посевную площадь после устройства терасс

S=35*40=1400

4. Составим пропорцию

1480-100%

1400-x%

X=(1400*100)/1480=94.6

5.100-94.6=5.4

Ответ: 5.4

Тип 4: Увеличиваем число на процент.

Задача из ЕГЭ по математике базового уровня.

Задание 3 № 26619

Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?

Решение: После повышения цены ручка станет стоить 40 + 0,1·40 = 44 рубля. Разделим 900 на 44:

Значит, можно будет купить 20 ручек.

Ответ: 20.

Тип 5: Уменьшаем число на процент.

Задание из ОГЭ по математике.

Вариант №6. Задача №4. Доставка печи из магазина до участка стоит 500 рублей. При покупке печи ценой свыше 20000 рублей магазин делают 3% скидку на товар и 35% процентов скидку на доставку. Сколько будет стоить доставка печи «кентавр» вместе с доставкой на этих условиях?

Решение:

1. Найдём сколько составляет 3% от 25000.

25000*0,03=750 рубля

2. Вычисляем стоимость печи со скидкой 3%

25000-750=24250 рубля

3. Найдём сколько составляет 35% от 500.

500*0,35=175 рубля

4.Вычисляем стоимость доставки со скидкой 35%.

500-175=325 рубля

5. 24250+375=24575 рубля

Ответ: 24575

Тип 6: Задачи на простые проценты.

Задание из ОГЭ по математике.

Задание 5 № 367104

В таблице даны условия банковского вклада в трех различных банках. Предполагается, что клиент кладет на счет 10 000 рублей на срок 1 год. В каком банке к концу года вклад окажется наибольшим? В ответе укажите сумму этого вклада в рублях.

Банк	Обслуживание счета *	Процентная ставка (% годовых) **
Банк А	40 руб. в год	2
Банк Б	8 руб. в месяц	3,5
Банк В	Бесплатно	1,5

* В начале года или месяца со счета снимается указанная сумма в уплату за ведение счета
** В конце года вклад увеличивается на указанное количество процентов.

Решение.

Рассмотрим все варианты.

В банке A после снятия суммы в уплату за ведение счета на счету останется 10 000 − 40 = 9 960 руб. К концу года на счету окажется 9 960 + 0,02 · 9 960 = 10 159,2 руб.

В банке Б в качестве платы за ведение счета за год снимается со счета 12 · 8 = 96 руб. Таким образом, проценты начисляются на сумму 10 000 − 96 = 9 904 руб. К концу года на счету окажется 9 904 + 0,035 · 9 904 = 10 250,64 руб.

В банке В плата за ведение счета не взимается, таким образом, проценты будут начисляться на первоначальную сумму. К концу года на счету окажется 10 000 + 0,015 · 10 000 = 10 150 руб.

Ответ: 10 250,64.

Тип 7: Задачи на сложные проценты.

Задача из сборника: Математика. Профильный уровень 50 вариантов, под ред. И.В.Ященко, М.:Экзамен, 2018

31 декабря 2016 года Василий взял в банке 5460000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Василий переводит в банк х рублей. Какой должна быть сумма х, чтобы Василий выплатил долг тремя равными платежами (то есть за три года)?

Решение:Sо=So*a=So(1+a)=5460000(1+0,2)=5460000*1,2, где So-сумма кредита, a-процентная ставка, x-определенная сумма ежегодного платежа.

Составляем уравнение

(((5460000*1,2-х)*1,2-х)*1,2-х)=0

((5460000*1,2²-2,2х)*1,2-х)=0

5460000*1,2³-3,64х=0

3,64х=5460000*1,2³

Х==2592000 рублей.

Ответ: 2592000 рублей-сумма ежегодного платежа.

Таким образом, мною было выделено семь типов задач на проценты, рассмотрены задачи с сайтов решу ОГЭ и решу ЕГЭ, сборников под ред. И.В.Ященко Математика: ОГЭ, ЕГЭ базовый и профильный уровень.

Опрос клиентов и сотрудника банка ПАО КБ «УБРиР»

города Асбеста

Для того, что бы узнать, как проценты влияют на банковские операции, мною проведено интервьюирование сотрудника банка ПАО КБ «УБРиР». Также, чтобы узнать владеют ли клиенты банка информацией об операциях с процентами, мною был проведён опрос среди клиентов данного банка. Для этого я разработал сценарий интервью, который представлен в Приложении 1.

В ходе интервью мы выяснили, что в банке предоставляются два вида

платежей по кредитам:

1. Аннуитетный платеж – представляет собой равные ежемесячные транши (платежи), растянутые на весь срок кредитования. В сумму транша включены: часть ссудной задолженности и начисленный процент. При этом, в первые месяцы (или годы) кредита большую часть транша составляют проценты, а меньшую – погашаемая часть основного долга. Ближе к концу кредитования пропорция меняется: большая часть транша идет на погашение «тела» кредита, меньшая – на проценты. При этом общий размер транша всегда остается одинаковым[6, 7].

2. Дифференцированный платеж – представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Наибольшие платежи – в первой четверти срока, наименьшие – в четвертой четверти. «Срединные» платежи обычно сравнимы с аннуитетом. Ежемесячно тело кредита уменьшается на равную долю, процент же насчитывается на остаток задолженности. Поэтому сумма транша меняется от выплаты к выплате. Если в задаче присутствуют слова «равными платежами» или «долг уменьшается на одну и ту же величину», то речь идет о дифференцированном платеже.

В ходе интервью сотрудник банка ПАО КБ «УБРиР» представил мне график погашения кредита дифференцированными платежами, который представлен ниже.


Параметры сделки:
Сумма кредита — 1 200 000 руб.
Срок кредита — 12 месяцев
Процентная ставка — 13 %

График погашения кредита дифференцированными платежами

Месяц	Ежемесячный платеж (руб.)	Погашение процентов (руб.)	Погашение основного долга (руб.)	Остаток основного долга (руб.)
1	113 000,00	13000	100 000	1 200 000
2	111 916,67	11917	100 000	1 100 000
3	110 833,33	10833	100 000	1 000 000
4	109 750,00	9750	100 000	900 000
5	108 666,67	8667	100 000	800 000
6	107 583,33	7583	100 000	700 000
7	106 500,00	6500	100 000	600 000
8	105 416,67	5417	100 000	500 000
9	104 333,33	4333	100 000	400 000
10	103 250,00	3250	100 000	300 000
11	102 166,67	2167	100 000	200 000
12	101 083,33	1083	100 000	100 000
ИТОГО:	1 284 500,00	84500,00	1 200 000

Для расчёта доли процентов в дифференцированных платежах использовалась следующая формула:

In – сумма, которая идёт на погашение процентов по кредиту в данный расчётный период;

Sn – остаток задолженности по кредиту;

p – годовая процентная ставка.

Действительно, рассчитаем долю процентов в дифференцированных платежах за первый платёж: .

Расчёт остатка ссудной задолженности:

Sn = 1 200 000 – 100 000 = 1 100 000 руб.

Расчёт начисленных процентов:

I n = 1 100 000 * 13 % / 12 = 11 917 руб.

В процессе интервью сотрудник банка ПАО КБ «УБРиР» также предоставил информацию, как вычисляется доходность по вкладу. На сайте банка представлены виды вкладов (Приложение 2).

Используя полученные данные, получены следующие расчёты:

Параметры вклада следующие:

Сумма вклада – 200 000 руб.

Срок – 210 дней

Процентная ставка – 6 % годовых.

Для расчета размера дохода по вкладу используем формулу простых процентов.

Первоначальную сумму вклада нужно умножить на годовую процентную ставку и разделить на число дней в текущем году.

Таким образом я узнал, сколько процентов будет начисляться в день.

Затем полученную сумму необходимо умножить на срок вклада.

Например, вы размещаете на вклад 200 000 руб.

Находим, сколько процентов будет начислено в день:

200 000 * 6% / 365 = 32 ,88 руб.

Полученную сумму умножаем на срок вклада – 210 дней.

32,88 * 210 = 6905 руб.

Чтобы узнать, какую сумму выдаст банк при снятии вкладанеобходимо прибавить к ним первоначальную сумму вклада.

В нашем случае – 200 000 руб.

200 000 + 6905 = 206 905 руб.

Таким образом, в ходе интервью с сотрудниками и клиентами банка ПАО КБ «УБРиР» я получил подробную информацию о том, как вычисляются доходность по вкладу и задолженность по кредиту.

5. Анкетирование

Мною была разработана анкета для обучающихся шестых, седьмых и девятых классов:

1.Умеешь ли ты решать задачи на процент?

_____________________________________________________________

2.Решал ли ты задачи на процент на сайте Решу ОГЭ?

_____________________________________________________________

3.Где по-твоему могут встретиться проценты в жизни?

_____________________________________________________________

4.Планируешь ли ты в будущем взять кредит или оформить вклад?

_____________________________________________________________

5.Сможешь ли ты рассчитать переплату по кредиту или доходность по вкладу?

Проанализировав результаты анкетирования, получил следующую информацию:

Опрошены обучающиеся шестого, седьмого, девятого классов основной школы № 12. Всего участвовало в анкетировании 72 человека. Результаты представлены ниже:

6 класс	Да	Нет
1 вопрос	86%	14%
2 вопрос	28%	72%
3 вопрос	магазин 72% банк-18% незнаю-10%
4 вопрос	21%	79%
5 вопрос	22%	78%

7 класс	Да	Нет
1 вопрос	85%	15%
2 вопрос	50%	50%
3 вопрос	магазин 57% банк-43%
4 вопрос	21%	79%
5 вопрос	50%	50%

9 класс	Да	Нет
1 вопрос	85%	15%
2 вопрос	98%	2%
3 вопрос	магазин 62% банк-38%
4 вопрос	76%	24%
5 вопрос	86%	14%

Для наглядности результатов изобразим результаты в виде диаграмм.

1. Умеешь ли ты решать задачи на проценты?

2. Решал ли ты задачи на проценты на сайте «Решу ОГЭ»?

4. Планируешь ли ты в будущем взять кредит или оформить вклад?

5. Сможешь ли ты рассчитать переплату по кредиту или доходность по вкладу

Таким образом, можно сделать вывод, что большинство школьников умеют решать задачи на процент и смогут рассчитать переплату по кредиту или доходность по вкладу. Задачи на процент лучше умеют решать ученики из 9 класса, так как скоро им предстоит сдавать ОГЭ, половина учеников седьмого класса начинает готовиться к ОГЭ, а в шестом классе задачи данного типа интересуют меньшие количество обучающихся.

Заключение

В современной жизни очень важно уметь правильно выполнять операции с процентами. Для того чтобы понять, как решаются задачи на проценты, а так же как рассчитать доходность по вкладу или переплату по кредиту, я решил исследовать эту тему.

Работая над проектом, я научился находить информацию, обрабатывать ее и выделять в ней главное. Выяснил, что появились проценты давно, и в настоящее время понятие «процент» очень активно используется в банковской системе, в торговле (скидка на товар, различные акции в магазинах и пр.), экономике (налогообложении и пр.), статистике и др. Также задачи на проценты встречается на ОГЭ и ЕГЭ базового и профильного уровней по математике.

Сегодня трудно найти экономически развитую страну, где отсутствуют кредитные продукты и вклады. В настоящее время существует различные виды кредитов и вкладов. В своей работе я подробно рассмотрел кредит с дифференцированным платежом, а также изучил расчет доходности по вкладу, используя метод простых процентов. В ходе работы выделил наиболее выгодный способ для погашения кредита – с помощью дифференцированного платежа.

Проведя анкетирование среди обучающихся шестых, седьмых, девятых классов основной школы № 12, я выяснил, что не все школьники умеют решать задачи на проценты и смогут рассчитать переплату по кредиту или доходность по вкладу. Задачи на проценты лучше умеют решать только ученики из 9 класса, так как скоро им предстоит сдавать ОГЭ, половина учеников седьмого класса начинает готовиться к ОГЭ, а в шестом классе задачи данного типа интересуют меньшее количество людей.

Я рассмотрел 7 прототипов задач из ЕГЭ базового и профильного уровня. Все задачи подробно разобраны и дается полное объяснение их решения. При разборе заданий я использовал знания по математике 5 и 6 класса. Но для меня пока сложными являются задания № 17 ЕГЭ по «Финансовой математике». Я уверен, что работа над проектом, полученные знания и умения пригодятся мне на ОГЭ и ЕГЭ по математике. Также я считаю, что эти знания и умения обязательно пригодятся мне в повседневной жизни. Думаю, что без труда смогу научить своих одноклассников решать задачи на проценты. Материал моего проекта будет полезен для обучающихся выпускных классов как пособие для подготовки к ОГЭ и ЕГЭ, к олимпиадам по экономике и математике.

Таким образом, можно сделать вывод, что поставленные задачи

решены и цель достигнута, гипотеза подтвердилась.

Свою будущую профессию я хочу связать с экономической специальностью. Работа над проектом для меня была интересной и увлекательной. И это еще раз подтвердило, что направление моей будущей профессиональной деятельности выбрано правильно.

Список литературы

1. Абчук В. «Занимательная экономика и бизнес», С-П: Тригон,1998.

2. Банковское дело. Справочное пособие. Под ред. Ю. А. Бабичевой- М.:

«Экономика», 1994.

3. Буслаев А.“Сложные проценты”. Газета “Математика” №30. 2002. стр.29

4. Вигман С.Л. Финансы, кредит, деньги в вопросах и ответах: учеб. пособие.-

М: ТК Велби, Изд-во Проспект, 2010

5.Вигдорчик Е., Нежданова Т. Элементарная математика в экономике и

бизнесе.- М., 1997.

6. Демин Ю. Все о кредитах. Понятно и просто. – СПб.: Питер, 2007

7. Ершов Ю.С. «Финансовая математика в вопросах и ответах», Новосибирск:

Сибирское соглашение, 1999.

8. Кац М. “Проценты”. Газета “Математика” №20. 2004. стр.22; №22. 2004.

стр.29; №23. 2004. стр.28

9. Колягин Ю. М., Ткачёва М. В. и др. Алгебра 7 класс: учебник для общеобразовательных организаций- М.: Просвещение, 2018

10. Лаврушин О.И. Деньги, кредит, банки: Учебник. — М.: Финансы и

статистика, 2000

11. Липцис И.В. «Экономика без тайн», Москва, изд. «Вита» 2004г.

12. Математика. ЕГЭ Профильный уровень 50 вариантов, под ред. И.В.Ященко,

М.:Экзамен, 2020

13. Математика. ЕГЭ Базовый уровень 50 вариантов, под ред. И.В.Ященко,

М.:Экзамен, 2020

14. Математика. ОГЭ по математике 50 вариантов, под ред. И.В.Ященко,

М.:Экзамен, 2020

15. Процентные вычисления. 10-11кл.:Учеб.метод.пособие/Г.В.Дорофеев,

Е.А.Седова. — М.: Дрофа, 2003

16. Петрова И.Н.. Проценты на все случаи жизни. М.: «Просвещение», 2006.

17. Савицкая Е.В., Серегина С.Ф. Уроки экономики в школе. – М.: Вита-Пресс,1999.

18. Седова Е.А. Проценты в X классе общеобразовательного направления. //

журнал «Математика в школе».-1994-№4.

19. Энциклопедия для детей. Т. 11. Математика/Глав. Ред. М.Д. Аксенова. М.: Аванта+, 2001.

20. Сайт решу ОГЭ математика [https://math-oge.sdamgia.ru/]

21. Сайт решу ЕГЭ математика базовый уровень[https://mathb-ege.sdamgia.ru/]

22. Сайт решу ЕГЭ математика профельный уровень[https://math-ege.sdamgia.ru/]

23. Сайт ПАО КБ «УБРиР» [https://www.ubrr.ru/]

Приложение 1

Сценарий интервьюирования сотрудника и

клиентов банка ПАО КБ «УБРиР».

Я на крыльце банка.

Очень часто люди обращаются в банк по разным причинам. В большинстве случаев, для оформления кредита или вклада. В основе данных банковских продуктов лежит начисление процентов. Правильно рассчитать стоимость кредита и доходность по вкладу помогут мне сотрудники Асбестовского офиса Уральского банка реконструкции и развития.

В юридическом отделе спрашиваю у клиента:

— Добрый день. Подскажите, пожалуйста, с какой целью вы посетили банк?

Клиент банка отвечает.

Я:

— На что вы обращаете внимание при выборе того или иного кредита?

Клиент банка отвечает.

В юридическом отделе спрашиваю старшего специалиста по кредитованию юридических лиц:

— Здравствуйте. Пожалуйста, объясните, что такое кредит?

Кредитный специалист отвечает.

Я:

— Клиенты при выборе кредитного продукта, особое внимание обращают на размер процентной ставки и способ начисления процентов. Расскажите, как начисляются проценты в вашем банке при кредитовании?

Кредитный специалист отвечает.

Я:

— Подскажите, возможно ли рассмотреть пример начисления процентов?

Кредитный специалист отвечает.

Я:

— На сайте вашего банка очень большой выбор кредитных продуктов. На мой взгляд, наиболее выгодные условия кредитования предлагаются по кредиту «Бизнес-привилегия». Давайте рассмотрим дифференцированные платежи по данному кредиту.

Специалист банка отвечает.

Я:

— Спасибо большое! Теперь я понял, как начисляются проценты на кредит. А этот график я приложу к своему проекту.

Я спрашиваю у клиента:

— Добрый день. Подскажите, пожалуйста, для чего вы посетили банк?

Клиент банка отвечает.

Я:

— Чем Вы будете руководствоваться, выбирая вклад?

Клиент банка отвечает.

Я подхожу к специалисту банка и спрашиваю:

— Здравствуйте, на сайте банка я познакомился с различными видами вкладов для физических лиц. Меня привлек вклад «Мобильный Он-Лайн». Не могли бы Вы рассказать, как начисляются проценты по этому вкладу? Например, я бы хотел оформить вклад на 200 000 рублей на срок 210 дней.

Специалист отвечает.

Я:

— Действительно, очень легко. Теперь я понял принцип начисления процентов по вкладам. А как узнать какую сумму выдаст банк при снятии вклада?

Специалист отвечает.

Я:

— Спасибо! Теперь я знаю, что такое доходность вклада.

Приложение 2

Просмотров работы: 1236

18 ноября 2015

В закладки

Обсудить

Жалоба

17 заданий с решениями.

→ Нахождение количества лет выплаты кредита
→ Вычисление процентной ставки по кредиту
→ Нахождение суммы кредита
→ Нахождение ежегодного транша
и другие.

banks.docx

Минпросвещения вводит исполнение гимна России во всех школах с 1 сентября

Образование | Сегодня, 15:00

Исполнение гимна РФ и поднятие государственного флага в начале учебной недели будут проводиться в каждой школе с 1 сентября следующего учебного года, заявил во вторник глава министерства просвещения Сергей Кравцов на первом всероссийском школьном историческом форуме «Сила в правде!» в Музее Победы.

Консультация по биологии

Биология | Сегодня, 14:58

Разработчики экзаменационных материалов, учителя и выпускники, расскажут, как подготовиться к экзамену, об особенностях заданий в ЕГЭ и ответят на вопросы старшеклассников.

Консультация по английскому языку

Английский | Сегодня, 10:14

Решение задач по математике на применение основных понятий о процентах.

Задачи на проценты учат решать с 5 класса.

Решение задач этого типа тесно связано с тремя алгоритмами:

нахождение процента от числа,
нахождение числа по его проценту,
нахождение процентного отношения.

На уроках с учениками разбирают, что сотая часть метра — это сантиметр, сотая часть рубля – копейка, сотая часть центнера — килограмм. Люди давно заметили, что сотые доли величин удобны в практической деятельности. Потому для них было придумано специальное название – процент.

Значит одна копейка – один процент от одного рубля, а один сантиметр – один процент от одного метра.

Один процент – это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.

Определение одного процента можно записать равенством: 1 % = 0,01 • а

5%=0,05, 23%=0,23, 130%=1,3 и т. д.

Как найти 1% от числа?

Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.

Пример. Найти: 25% от 120.

Решение:

25% = 0,25;
120 . 0,25 = 30.

Ответ: 30.

Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?

Решение:

Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах – 25%.

Ответ: производительность труда токаря повысилась на 25%.

Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.

Пример. При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?

Решение:

66 : 60 = 1,1 — такую часть составляют изготовленные автомобили от количества автомобилей по плану. Запишем в процентах =110%.

Ответ: 110%.

Пример. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?

Решение:

6+ 34 =40 (кг) – масса всего сплава.
34 : 40 = 0,85 = 85 (%) – сплава составляет медь.

Ответ: 85%.

Пример. Слонёнок за весну похудел на 20%, потом поправился за лето на 30%, за осень опять похудел на 20% и за зиму прибавил в весе на 10%. Остался ли за этот год его вес прежним? Если изменился, то на сколько процентов и в какую сторону?

Решение:

100 – 20 = 80 (%) – после весны.
80 + 80 • 0,3 = 104 (%) – после лета.
104 – 104 • 0,2 = 83,2 (%) – после осени.
83,2 + 83,2 • 0,1 = 91,52 (%) – после зимы.

Ответ: похудел на 8,48%.

Пример. Оставили на хранение 20 кг крыжовника, ягоды которого содержат 99% воды. Содержание воды в ягодах уменьшилось до 98%. Сколько крыжовника получится в результате?

Решение:

100 – 99 = 1 (%) = 0,01 – доля сухого вещества в крыжовнике сначала.
20 • 0,01 = 0,2 (кг) – сухого вещества.
100 – 98 = 2 (%) = 0,02 – доля сухого вещества в крыжовнике после хранения.
0,2 : 0,02 = 10 (кг) – стало крыжовника.

Ответ: 10 кг.

Пример. Что произойдет с ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%?

Решение:

Пусть цена товара х руб., тогда после повышения товар стоит 125% прежней цены, т.е. 1,25х, а после понижения на 25% , его стоимость составляет 75% или 0, 75 от повышенной цены, т.е.

0,75 •1,25х= 0,9375х,

тогда цена товара понизилась на 6, 25 %, т.к.

х — 0,9375х = 0,0625х;
0,0625 • 100% = 6,25%

Ответ: первоначальная цена товара снизилась на 6,25%.

Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (А : В) • 100%.

Пример. Найти число, если 15% его равны 30.

Решение:

15% = 0,15;
30 : 0,15 = 200.

Или

х — данное число;
0,15 • х = 300;
х = 200.

Ответ: 200.

Пример. Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480кг волокна?

Решение:

Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби).
480 : 0,24= 2000 кг = 2 т

Ответ: 2 т.

Пример. Сколько кг белых грибов надо собрать для получения 1 кг сушеных, если при обработке свежих грибов остается 50% их массы, а при сушке остается 10% массы обработанных грибов?

Решение:

1 кг сушеных грибов – это 10% или 0, 01 часть обработанных, т.е.
1 кг : 0,1=10 кг обработанных грибов, что составляет 50% или 0,5 собранных грибов, т.е.
10 кг : 0,05=20 кг.

Ответ: 20 кг.

Пример. Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?

Решение:

22 • 0,1 = 2,2 (кг) — грибов по массе в свежих грибах; (0,1 это 10% сухого вещества);
2,2 : 0,88 = 2,5 (кг) — сухих грибов, получаемых из свежих (количество сухого вещества не изменилось, но изменилось его процентное содержание в грибах и теперь 2,2 кг это 88% или 0,88 сухих грибов).

Ответ: 2,5 кг.

Правило 4. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.

В задачах на банковские расчёты обычно встречаются простые и сложные проценты. В чём же состоит разница простого и сложного процентного роста? При простом росте процент каждый раз исчисляется, исходя из начального значения, а при сложном росте он исчисляется из предыдущего значения. При простом росте 100% – начальная сумма, а при сложном 100% каждый раз новые и равны предыдущему значению.

Пример. Банк платит доход в размере 4% в месяц от величины вклада. На счет положили 300 тысяч рублей, доход начисляют каждый месяц. Вычислите величину вклада через 3 месяца.

Решение:

100 + 4 = 104 (%) = 1,04 – доля увеличения вклада по сравнению с предыдущим месяцем.
300 • 1,04 = 312 (тыс. р) – величина вклада через 1 месяц.
312 • 1,04 = 324,48 (тыс. р) – величина вклада через 2 месяца.
324,48 • 1,04 = 337,4592 (тыс. р) = 337 459,2 (р)-величина вклада через 3 месяца.

Или можно пункты 2-4 заменить одним, повторив с детьми понятие степени: 300•1,043 =337,4592(тыс. р) = 337 459,2 (р) – величина вклада через 3 месяца.

Ответ: 337 459,2 рубля

Пример. Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10% за каждый месяц. На сколько процентов выросли цены за 3 месяца?

Пример. Деньги, вложенные в акции известной фирмы, приносят ежегодно 20% дохода. Через сколько лет вложенная сумма удвоится?

Далее в 6 классе решают подобного типа задачи уже с применением пропорции. На эту базу знаний и опираются, готовя учеников к итоговым экзаменам в 9 и 11 классах.

Рассмотрим подобного плана задачи на конкретных примерах.

Пример. (Вариант 1 № 16. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 -80с)

Спортивный магазин проводит акцию. Любой джемпер стоит 400 рублей. При покупке двух джемперов – скидка на второй джемпер 75%. Сколько рублей придется заплатить за покупку двух джемперов в период акции?

Решение:

Согласно условию задачи получается, что первый джемпер покупается за 100 % его исходной стоимости, а второй за 100 – 75 = 25 (%), т.е. всего покупатель должен заплатить 100 + 25 = 125 (%) от исходной стоимости. Далее можно рассмотреть решение тремя способами.

1 способ.

400 рублей принимаем за 100 %. Тогда в 1% содержится 400 : 100 = 4 (руб.), а в 125 %
4 • 125 = 500 (руб.)

2 способ.

Процент от числа находится умножением числа на дробь, соответствующую проценту или умножением числа на данный процент и делением на 100.
400 • 1,25 = 500 или 400 • 125/100 = 500.

3 способ.

Применение свойства пропорции:
400 руб. – 100 %
х руб. – 125 %, получим х = 125 • 400 / 100 = 500 (руб.)

Ответ: 500 рублей.

Пример. (Вариант 4 № 16. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 -80с)

Средний вес мальчиков того же возраста, что и Гоша, равен 57 кг. Вес Гоши составляет 150 % среднего веса. Сколько килограммов весит Гоша?

Решение:

Аналогично примеру, рассмотренному выше можно составить пропорцию:

57 кг – 100 %
х кг – 150 %, получим х = 57 • 150 / 100 = 85,5 (кг)

Ответ: 85,5 кг.

Пример. (Вариант 7 № 16. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 — 80с)

После уценки телевизора его новая цена составила 0,52 старой. На сколько процентов уменьшилась цена в результате уценки?

Решение:

1 способ.

Найдем сначала долю уменьшения цены. Если исходную цену принять за 1, то 1 – 0,52 = 0,48 составляет доля уменьшения цены. Тогда получаем, 0,48 • 100 % = 48 %. Т.е. на 48 % уменьшилась цена в результате уценки.

2 способ.

Если исходную стоимость принять за А, то после уценки новая цена телевизора будет равняться 0,52А, т.е. она уменьшится на А – 0,52А = 0,48А.

Составим пропорцию:
А – 100%
0,48А – х %, получим х = 0,48А • 100 / А = 48 (%).

Ответ: на 48 % уменьшилась цена в результате уценки.

Пример. (Вариант 9 № 16. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 — 80с)

Товар на распродаже уценили на 15%, при этом он стал стоить 680 рублей. Сколько рублей стоил товар до распродажи?

Решение:

До понижения цены товар стоил 100%. Цена на товар после распродажи уменьшилась на 15%, т.е. стала 100 – 15 = 85 (%), в рублях эта величина равна 680 рублей.

1 способ.

680 : 85 = 8 (руб.) – в 1%
8 • 100 = 800 (руб.) – стоил товар до распродажи.

2 способ.

Это задача на нахождение числа по его проценту, решается делением числа на соответствующий ему процент и путем обращения полученной дроби в проценты, умножением на 100, или действием деления на дробь, полученную при переводе из процентов.
680 : 85 • 100 = 800 (руб.) или 680 : 0,85 = 800 (руб.)

3 способ.

С помощью пропорции:
680 руб. – 85 %
х руб. – 100 %, получим х = 680 • 100 / 85 = 800 (руб.)

Ответ: 800 рублей стоил товар до распродажи.

Решение задач на смеси и сплавы, с использованием понятий «процентное содержание», «концентрация», «% -й раствор».

Самые простые задачи этого типа приведены ниже.

Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.

Решение:

10 • 0,15 = 1,5 (кг) соли.

Ответ: 1,5 кг.

Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором (например, 15%-й раствор соли).

Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?

Решение:

Процентное содержание вещества в сплаве — это часть, которую составляет вес данного вещества от веса всего сплава.

10 + 15 = 25 (кг) — сплав;
10 : 25 • 100% = 40% — процентное содержание олова в сплаве;
15 : 25 • 100% = 60% — процентное содержание цинка в сплаве.

Ответ: 40%, 60%.

В задачах этого типа основным является понятие «концентрация». Что же это такое?

Рассмотрим, например, раствор кислоты в воде.

Пусть в сосуде содержится 10 литров раствора, который состоит из 3 литров кислоты и 7 литров воды. Тогда относительное (по отношению ко всему объему) содержание кислоты в растворе равно . Это число и определяет концентрацию кислоты в растворе. Иногда говорят о процентном содержании кислоты в растворе. В приведенном примере процентное содержание будет таково: . Как видно, переход от концентрации к процентному содержанию и наоборот весьма прост.

Итак, пусть смесь массы М содержит некоторое вещество массой m.

Тогда:

концентрацией данного вещества в смеси (сплаве) называется величина ;
процентным содержанием данного вещества называется величина с×100%;

Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c×M.

Задачи на смеси (сплавы) можно разделить на два вида:

Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества, равными соответственно с1 и с2. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c1m1+c2m2, а концентрация .
Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.

При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом добавлении смеси. В результате такого контроля получаем разрешающее уравнение. Рассмотрим конкретные задачи.

Если концентрация вещества в соединении по массе составляет P%, то это означает, что масса этого вещества составляет P% от массы всего соединения.

Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 261 г.

Решение:

300 • 0,87 = 261 (г).

В этом примере концентрация вещества выражена в процентах.

Отношения объема чистого компонента в растворе ко всему объему смеси называется объемной концентрацией этого компонента.

Сумма концентраций всех компонентов, составляющих смесь, равна 1.

Если известно процентное содержание вещества, то его концентрация находится по формуле:
К = P/100%,
где К — концентрация вещества;
P — процентное содержание вещества (в процентах).

Пример. (Вариант 8 № 22. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 — 80с)

Свежие фрукты содержат 75% воды, а высушенные – 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов?

Решение:

Если в свежих фруктах содержится 75% воды, то сухого вещества будет 100 – 75 = 25 (%), а высушенные – 25%, то сухого вещества в них будет 100 – 25 = 75 (%).

При оформлении решения задачи, можно использовать таблицу:

Общая масса, кг | Концентрация сухого вещества | Масса сухого вещества

Свежие фрукты х 25% = 0,25 0,25 • х

Высушенные фрукты 45 75% = 0,75 0,75 • 45 = 33,75

Т.к. масса сухого вещества для свежих и высушенных фруктов не меняется, то получим уравнение:

0,25 • х = 33,75;
х = 33,75 : 0,25;
х = 135 (кг) – требуется свежих фруктов.

Ответ: 135 кг.

Пример. (Вариант 8 №11. ЕГЭ-2016. Математика. Типов. тест. зад. ред Ященко 2016 -56с)

Смешав 70 % -й и 60 % -й растворы кислоты и добавив 2 кг чистой воды, получили 50 % -й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90 % -го раствора той же кислоты, то получили бы 70 % -й раствор кислоты. Сколько килограммов 70 % -го раствора использовали для получения смеси?

Решение:

Общая масса, кг | Концентрация сухого вещества | Масса сухого вещества
I х 70% = 0,7 0,7 • х
II у 60% = 0,6 0,6 • у
вода 2 – –
I + II + вода х + у + 2 50 % = 0,5 0,5 • ( х + у + 2 )
III 2 90 % = 0,9 0,9 • 2 = 1,8
I + II + III х + у + 2 70 % = 0,7 0,7 • ( х + у + 2)

Используя последний столбик из таблицы составим 2 уравнения:

0,7 • х + 0,6 • у = 0,5 • ( х + у + 2 ) и 0,7 • х + 0,6 • у + 1,8 = 0,7 • ( х + у + 2).

Объединив их в систему, и решив ее, получим, что х = 3 кг.

Ответ: 3 килограмма 70 % -го раствора использовали для получения смеси.

Пример. (Вариант 2 №11. ЕГЭ-2016. Математика. Типов. тест. зад. ред Ященко 2016 -56с)

Три килограмма черешни стоят столько же, сколько пять килограммов вишни, а три килограмма вишни – столько же, сколько два килограмма клубники. На сколько процентов килограмм клубники дешевле килограмма черешни?

Решение:

Из первого предложения задачи получаем следующие равенства:

3ч = 5в,
3в = 2к.
Из которых можно выразить: ч = 5в/3, к = 3в/2.

Таким образом можно составить пропорцию:
5в/3 – 100%
3в/2 – х %, получим х = (3 • 100 • в •3)/(2 • 5 • в), х = 90% составляет стоимость килограмма клубники от стоимости килограмма черешни.

Значит, на 100 – 90 = 10 (%) – килограмм клубники дешевле килограмма черешни.

Ответ: на 10 процентов килограмм клубники дешевле килограмма черешни.

Решение задач на «сложные» проценты, с использованием понятия коэффициента увеличения (уменьшения).

Чтобы увеличить положительное число А на р процентов, следует умножить число А на коэффициент увеличения К = (1 + 0,01р).

Чтобы уменьшить положительное число А на р процентов, следует умножить число А на коэффициент уменьшения К = (1 – 0,01р).

Пример. (Вариант 29 № 22. ОГЭ-2015. Математика. Тип. экзаменационные варианты: 36 вариантов/ под ред. Ященко, 2015 — 224с)

Цена товара была дважды снижена на одно и то же число процентов. На сколько процентов снижалась цена товара каждый раз, если его первоначальная стоимость 5000 рублей, а окончательная 4050 рублей?

Решение:

1 способ.

Т.к. цена товара снижалась на одно и то же число %, обозначим число % за х. Пусть в первый и второй раз цена товара была понижена на х %, тогда после первого понижения цена товара стала (100 – х ) %.

Составим пропорцию
5000 руб. – 100%
у руб. – (100 – х)%, получим у = 5000 • (100 – х) / 100 = 50 • (100 – х) рублей – стоимость товара после первого понижения.

Составим новую пропорцию уже по новой цене:
50 • (100 – х) руб. – 100%
z руб. – (100 – х)%, получим z = 50 • (100 – х) (100 – х) / 100 = 0,5 • (100 – х)2 рублей – стоимость товара после второго понижения.

Получим уравнение 0,5 • (100 – х)2 = 4050. Решив его, получим, что х = 10 % .

2 способ.

Т.к. цена товара снижалась на одно и то же число %, обозначим число % за х, х % = 0,01 х.

Используя понятие коэффициента уменьшения, сразу получаем уравнение:
5000 • (1 – 0,01х)2 = 4050.

Решив его, получим, что х = 10 %.

Ответ: на 10 % снижалась цена товара каждый раз.

Пример. (Вариант 30 № 22. ОГЭ-2015. Математика. Тип. экзаменационные варианты: 36 вариантов/ под ред. Ященко, 2015 — 224с)

Цена товара была дважды повышена на одно и то же число процентов. На сколько процентов повышалась цена товара каждый раз, если его первоначальная стоимость 3000 рублей, а окончательная 3630 рублей?

Решение:

Т.к. цена товара повышалась на одно и то же число %, обозначим число % за х, х % = 0,01 х.

Используя понятие коэффициента увеличения, сразу получаем уравнение:
3000 • (1 + 0,01х)2 = 3630.

Решив его, получим, что х = 10 %.

Ответ: на 10 % повышалась цена товара каждый раз.

Пример. (Вариант 4 №11. ЕГЭ-2016. Математика. Типов. тест. зад. ред Ященко 2016 -56с)

В четверг акции компании подорожали на некоторое число процентов, а в пятницу подешевели на то же самое число процентов. В результате они стали стоить на 9% дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?

Решение:

Пусть акции компании дорожали и дешевели на х %, х % = 0,01 х, а исходная стоимость акций была А. Используя все условия задачи, получаем уравнение:

(1 + 0,01 х)(1 – 0,01 х)А = (1 – 0,09)А,
1 – (0,01 х)2 = 0,91,
(0,01 х)2 = (0,3)2,
0,01 х = 0,3,
х = 30 %.

Ответ: на 30 процентов подорожали акции компании в четверг.

Решение «банковских» задач в новой версии ЕГЭ-2016 по математике.

Пример. (Вариант 2 №17. ЕГЭ-2016. Математика. 50 типов. вар. ред. Ященко 2016)

15-го января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:

1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?

Решение:

1) Пусть А – сумма кредита, 1 % = 0,01.

Тогда 1,01А долг после первого месяца.

Со 2-го по 14-е число производится выплата А/15 +0,01А.

После чего сумма долга составит 1,01А – А/15 – 0,01А = 14А/15.

При такой схеме долг становится на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Через 2 месяца получаем: 1,01• 14А/15.

Второй платеж А/15 + 0,01• 14А/15.

Тогда долг после второго платежа 13А/15.

Аналогично получаем, что восьмая выплата будет иметь вид:

А/15 + 0,01• 8А/15 = А/15 • (1 + 0,08) = 1,08А/15.

А по условию она равна 108 тыс. рублей. Значит, можно составить и решить уравнение:

1,08А/15 = 108,

А=1500 (тыс. руб.) – исходная сумма долга.

2) Чтобы найти сумму, которую нужно вернуть банку в течение всего срока кредитования, мы должны найти сумму всех выплат по кредиту.

Сумма всех выплат по кредиту будет иметь вид:

(А/15 + 0,01А) + (А/15 + 0,01• 14А/15) + (А/15 + 0,01• 13А/15) + … + ( А/15 + 0,01• А/15) = А + 0,01А/15 (15+14+13+12+11+10+9+8+7+6+5+4+3+2+1) = А + (0,01• 120А)/15 = 1,08А.

Значит, 1,08 • 1500 = 1620 (тыс. руб.) = 1620000 рублей нужно вернуть банку в течение всего срока кредитования.

Ответ: 1620000 рублей.

Пример. (Вариант 6 №17. ЕГЭ-2016. Математика. 50 типов. вар. ред. Ященко 2016)

15-го января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:

1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что за первые 12 месяцев нужно выплатить банку 177,75 тыс. рублей. Какую сумму планируется взять в кредит?

Решение:

1) Пусть А – сумма кредита, 1 % = 0,01.

Тогда 1,01А долг после первого месяца.

Со 2-го по 14-е число производится выплата А/24 +0,01А.

После чего сумма долга составит 1,01А – А/24 – 0,01А = А – А/24 = 23А/24.

При такой схеме долг становится на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Через 2 месяца получаем: 1,01• 23А/24.

Второй платеж А/24 + 0,01• 23А/24.

Тогда долг после второго платежа 1,01• 23А/24 – А/24 – 0,01• 23А/24 = 23А/24(1,01 – 0,01) – А/24 = 23А/24 – А/24 = 22А/24.

Таким образом получаем, что за первые 12 месяцев нужно выплатить банку следующую сумму:
А/24 +0,01А • 24/24 + А/24 + 0,01• 23А/24 + А/24 + 0,01• 22А/24 + … + А/24 + 0,01• 13А/24 =12А/24 + 0,01А/24 (24+23+22+21+20+19+18+17+16+15+14+13) = А/2 + 222А/2400 = 711А/1200.

А по условию она равна 177,375 тыс. рублей. Значит, можно составить и решить уравнение:
711А/1200 = 177,75,
А=300 (тыс. руб.) =300000 рублей – планируется взять в кредит.

Ответ: 300000 рублей.

В помощь учителю

Уважаемые коллеги! Опубликуйте свою педагогическую статью или сценарий мероприятия на Учительском портале и получите свидетельство о публикации методического материала в международном СМИ.

Для добавления статьи на портал необходимо зарегистрироваться.

Конкурсы

Диплом и справка о публикации каждому участнику!

Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни.

Пока такие задачки остаются оторванными от реальности строчками в учебнике, их бывает сложно понять и тем более решить. Чтобы стало понятнее, мы вам сейчас покажем примеры из обычной жизни, где вам могут встретиться проценты. А еще просто и доступно объясним, как решать задачи на проценты. И все у вас станет на свои места.

Задачи про проценты вокруг нас

Давайте оглядимся по сторонам: значения в процентах указаны на упаковках с любыми продуктами. Значок процента «%» смотрит на нас с рекламных плакатов скидок и распродаж. В новостях проценты сразу бросаются в глаза, когда речь идет о повышении цен на товары или коммунальные услуги. Разве вы сможете расшифровать все эти послания, если не научитесь решать задачи с процентами? Но вы, конечно, научитесь – мы в вас верим.

А вот такая ситуация: вы купили что-нибудь через интернет и получили извещение от ближайшего почтового отделения. Или сами собираетесь послать подарок другу в другой город. Вам обязательно надо уметь разбираться с процентами, чтобы узнать, сколько денег почта захочет получить за свои услуги по пересылке.

Или возьмем банковские кредиты и ипотеку. Банки в договорах всегда пишут мелкими буквами всякие вещи, которые полезно понимать. Например, какой процент по кредиту придется заплатить банку кроме тех денег, которые вы у него «одолжили» и обязаны вернуть.

А самый близкий школьникам пример связан с ЕГЭ. Каждый год после экзаменов публикуют официальную статистику. В которой немало задействованы и проценты. И эти проценты имеют прямое отношение к будущим выпускникам. Например, процент ребят, сдавших экзамен по математике на «хорошо» и «отлично» косвенно говорит о том, сколько абитуриентов с высокими баллами могли подать документы в вузы на технические специальности. А еще на программирование, прикладную математику и т.п. Чем их больше, тем выше конкурс. Если сравнивать их результаты со своими оценками, можно прикинуть собственные шансы на поступление.

Что такое процент?

Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.

Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.

Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.

Типы задач на проценты

Раз мы уже договорились, что задачи на проценты – это задачи на дроби, такой тактики будем придерживаться и дальше.

Тип 1: Находим процент (дробь) от числа.

Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.

Тип 2: Находим число по его проценту (дроби).

Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.

Тип 4: Увеличиваем число на процент.

Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.

Тип 5: Уменьшаем число на процент.

Задача. Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.

Тип 6: Задачи на простые проценты.

Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.

Тип 7: Задачи на сложные проценты.

Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% — процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)^у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)³ = 38021,875 – искомая сумма.

Решение. Обозначим искомый процент девочек в классе как х, общее количество учеников примем за 100%. Пропорция выглядит так:

30 – 100%
14 – х%

Перемножим крест накрест левую и правую части пропорции и получим, что 30* х = 14 * 100 («30 относится к х также, как 14 относится к 100»). Откуда найти х уже совсем несложно: х = 14 * 100/30 = 47%.

Задачи на проценты с решением

Давайте решим несколько задач для подготовки к ЕГЭ. Как вы сами видите, решать их совсем несложно. Сейчас просто закрепим материал.

Задача 1. После открытия торгов на бирже в понедельник акции некой компании выросли в цене на неизвестное количество процентов. А во вторник на то же самое количество процентов упали в цене. В итоге они подешевели на 4% по отношению к своей первоначальной стоимости в понедельник. На какой процент акции этой компании поднимались в цене в понедельник?

Решение. Пускай первоначальная стоимость акций это 1. В понедельник акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х). После чего они стали дешевле на 4%, т.е. стали стоить 0,96.

Отсюда 1 + х – х * (1 + х) = 0,96 ↔1 – х² = 0,96 ↔ х² = 0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.

Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте, на сколько процентов пять пар брюк стоят дороже, чем одно пальто.

Решение. Исходя из условия задачи, стоимость четырех пар брюк – это 92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это 23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 = 115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.

Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.

Решение. Из условия следует, что общий доход семьи находится в прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100% – 67% – 6% = 27%.

Задача 4. В емкости находится 5 литров водного раствора с концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды. Раствор какой концентрации (с каким процентным содержанием вещества) получился после этого?

Решение. Опишем концентрацию вещества в растворе такой формулой: С = Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6 литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости увеличился. Но концентрация вещества понизилась (его объем остался неизменным). Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% = 0,6 /12 * 100% = 5%.

Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Решение. Исходя из условия, в абрикосах 10% питательного вещества, а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять 19/0,1 = 190 килограммов свежих абрикосов.

Заключение

Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить воображение, вы сможете щелкать такие задачки как орешки.

Вы даже можете составить задачу на проценты сами по нашим образцам. Кстати, будет очень хорошо, если вы так и поступите. Можете оставить нам свои задачи в комментариях – пускай другие наши читатели решат ваши задачи. А вы сможете решить те, что придумают они. Чтобы задач для подготовки к экзаменам получилось больше, расскажите про эту статью своим друзьям в социальных сетях.

Вот увидите, задачи на проценты вам придется решать еще много раз даже после того, как вы закончите школу. Они встречаются в физике, химии, биологии. Да и в повседневной жизни умение решать их может не раз пригодится. Не бойтесь сложных задач – мы всегда поможем вам найти к ним ключ.

Источник