Percent deviation measures the degree to which individual data points in a statistic deviate from the average measurement of that statistic. To calculate percent deviation, first determine the mean of the data and the average deviation of data points from that mean.
Calculate the Mean
Calculate the average, or mean of your data points. To do this, add the values of all data points, then divide by the number of data points. Say you have four melons, with weights of 2 pounds, 5 pounds, 6 pounds and 7 pounds. Find the sum: 2 + 5 + 6 + 7 = 20, then divide by four, since there are four data points: 20 / 4 = 5. So your potatoes have a mean weight of 5 pounds.
Calculate Average Deviation
Once you know the mean of your data, calculate the average deviation. Average deviation measures the average distance of your data points from the mean.
First, calculate the distance of each data point from the mean: the distance, D, of a data point equal to the absolute value of the data point’s value, d, minus the mean, m: D = |d — m| Absolute value, represented by the | |, signifies that if the result of the subtraction is a negative number, convert it into a positive number. For example, the 2-pound melon has a deviation of 3, since 2 minus the mean, 5, is -3, and the absolute value of -3 is 3. Using this formula, you can find that the deviation of the 6-pound melon is 1, and the 7-pound melon is 2. The 5-pound melon’s deviation is zero, since its weight is equal to the mean.
Once you know the deviations of all your data points, find their average by adding them, and dividing by the number of data points. The deviations are 3, 2, 1 and zero, which have a sum of 6. If you divide 6 by the number of data points, 4, you get an average deviation of 1.5.
Percent Deviation from Mean and Average
The mean and average deviation are used to find the percent deviation. Divide the average deviation by the mean, then multiply by 100. The number you get will show the average percentage that a data point differs from the mean. Your melons have a mean weight of 5 pounds, and an average deviation of 1.5 pounds, so:
percent deviation = 1.5 / 5 x 100 = 30 percent
So on average, your data points are distant from your mean by 30 percent of the mean’s value.
Percent Deviation From a Known Standard
Percent deviation can also refer to how much the mean of a set of data differs from a known or theoretical value. This can be useful, for instance, when comparing data gathered from a lab experiment to a known weight or density of a substance. To find this type of percent deviation, subtract the known value from the mean, divide the result by the known value and multiply by 100.
Suppose you did an experiment to determine the density of aluminum, and came up with a mean density of 2,500 kilograms per meter squared. The known density of aluminum is 2,700 kilogram per meter squared, so you can use these two numbers to calculate by how much your experimental mean differs from the known mean. Subtract 2,700 from 2,500, divide the result by 2,700, then multiply by 100:
percent deviation = (2,500 — 2,700) / 2,700 x 100 = -200 / 2,700 x 100 = -7.41 percent
The negative sign in your answer signifies that your mean is lower than the expected mean. If the percent deviation is positive, it signifies your mean is higher than expected. So your mean density is 7.41 percent lower than the known density.
Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.
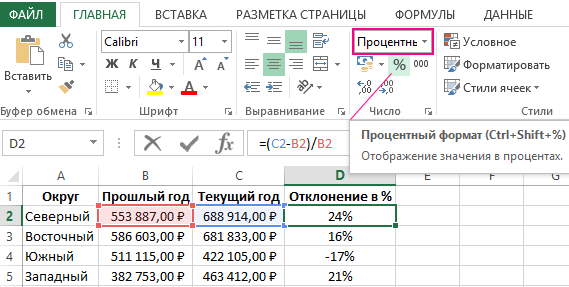
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
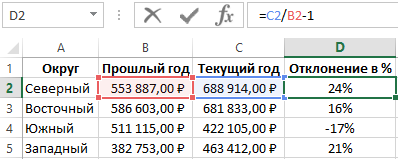
Альтернативная формула для вычисления процента отклонения в Excel
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.
Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.
Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.
Как рассчитать процентили от среднего и стандартного отклонения
17 авг. 2022 г.
читать 2 мин
Вы можете использовать следующую формулу для расчета процентиля нормального распределения на основе среднего значения и стандартного отклонения:
Процентное значение = μ + zσ
куда:
- мк : Среднее
- z : z-оценка из таблицы z , которая соответствует значению процентиля
- σ : стандартное отклонение
Следующие примеры показывают, как использовать эту формулу на практике.
Пример 1. Вычисление 15-го процентиля с использованием среднего значения и стандартного отклонения
Предположим, что вес определенного вида выдр распределен нормально со средним значением μ = 60 фунтов и стандартным отклонением σ = 12 фунтов.
Каков вес выдры на 15-м процентиле?
Чтобы ответить на этот вопрос, мы должны найти z-оценку, ближайшую к значению 0,15 в таблице z.Это значение оказывается равным -1,04 :
Затем мы можем подставить это значение в формулу процентиля:
- Процентное значение = μ + zσ
- 15-й процентиль = 60 + (-1,04) * 12
- 15-й процентиль = 47,52
Выдра в 15-м процентиле весит около 47,52 фунтов.
Примечание.Мы также можем использовать калькулятор процентиля для Z-показателя , чтобы определить, что точный z-показатель, соответствующий 15-му процентилю, равен -1,0364.
Подставив это значение в формулу процентилей, мы получим:
- Процентное значение = μ + zσ
- 15-й процентиль = 60 + (-1,0364) * 12
- 15-й процентиль = 47,5632
Пример 2. Вычисление 93-го процентиля с использованием среднего значения и стандартного отклонения
Предположим, что экзаменационные баллы по определенному тесту нормально распределены со средним значением μ = 85 и стандартным отклонением σ = 5.
Какова оценка на экзамене учащегося, набравшего 93-й процентиль?
Чтобы ответить на этот вопрос, мы должны найти z-оценку, ближайшую к значению 0,93 в таблице z.Это значение оказывается равным 1,48 :
Затем мы можем подставить это значение в формулу процентилей:
- Процентное значение = μ + zσ
- 93-й процентиль = 85 + (1,48) * 5
- 93-й процентиль = 92,4
Студент, набравший 93-й процентиль, получит на экзамене около 92,4 балла.
Примечание.Мы также можем использовать калькулятор процентиля для Z- значения, чтобы определить, что точное значение z-показателя, соответствующее 93-му процентилю, составляет 1,4758.
Подставив это значение в формулу процентилей, мы получим:
- Процентное значение = μ + zσ
- 93-й процентиль = 85+ (1,4758)*5
- 93-й процентиль = 92,379
Дополнительные ресурсы
Как использовать таблицу Z (с примерами)
Как преобразовать Z-баллы в процентили в Excel
Содержание материала
- Как посчитать относительно отклонение?
- Как вычислить стандартное отклонение в Excel?
- Среднеквадратическое отклонение
- Как рассчитать отклонение показателей?
- Абсолютное отклонение
- Отклонение в процентах при отрицательных величинах
- Как посчитать отклонение от среднего?
- Селективное отклонение
- Как рассчитать процент выполнения плана?
Как посчитать относительно отклонение?
А относительное отклонение — соотношение тех же показателей друг к другу, только выраженное в процентах. Показатели текущего периода надо разделить на показатели базового периода и умножить на 100. Так мы получаем в процентах относительное отклонение.
Метод 3 Вычисление стандартного отклонения
- Поставьте курсор в ячейку ниже последнего введенного значения. Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. …
- Введите знак равенства. …
- Наберите «СТАНДОТКЛОН». …
- Укажите диапазон данных. …
- Нажмите кнопку «Enter «.
19 окт. 2018 г.
Среднеквадратическое отклонение
Для превращения дисперсии в логично понятные баллы, килограммы или доллары используется среднеквадратическое отклонение, которое представляет собой квадратный корень из дисперсии. Давайте вычислим его для нашего примера:
S = sqrt(D) = sqrt(2,78) = 1,667
Мы получили баллы и теперь можем использовать их для связки с математически ожиданием. Наиболее вероятный результат выстрела в этом случае будет выражен как 7,75 плюс-минус 1,667. Этого достаточно для ответа, но так же мы можем сказать, что практически наверняка стрелок попадет в область мишени между 6,08 и 9,41.
Стандартное отклонение или сигма — информативный показатель, иллюстрирующий разброс величины относительно ее центра. Чем больше сигма, тем больший разброс демонстрирует выборка. Это хорошо изученный коэффициент и для нормального распределения известно занимательное правило трех сигм. Установлено, что 99,7 % значений нормально распределенной величины лежат в области плюс-минус трех сигм от среднего арифметического.
Как рассчитать отклонение показателей?
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%.
Абсолютное отклонение
Как рассчитать абсолютное отклонение? Абсолютным отклонением можно назвать разницу, получаемую при вычитании одной величины из другой, этот способ является выражением сложившихся положений вещей между плановым и фактическим параметрами.
Известно, что определенную проблему обычно вызывает такой показатель, как знак абсолютного отклонения. Обычно считается, что отклонение, которое позитивно сказывается на прибыли предприятия, считается положительным, и в вычислениях его ставят со знаком «+». Что же касается банальной математики, такой подход считается не совсем корректным, а это, в свою очередь, вызывает конфликты и разногласия среди специалистов. Исходя из этого, на практике вычисления абсолютного отклонения зачастую пользуются не базовой экономической, а математической моделью. Математическая модель заключается в том, что повышение фактического оборота в сравнении с запланированным обозначается знаком «+», а уменьшение фактических издержек в сравнении с плановыми обозначается знаком «-«.
Отклонение в процентах при отрицательных величинах
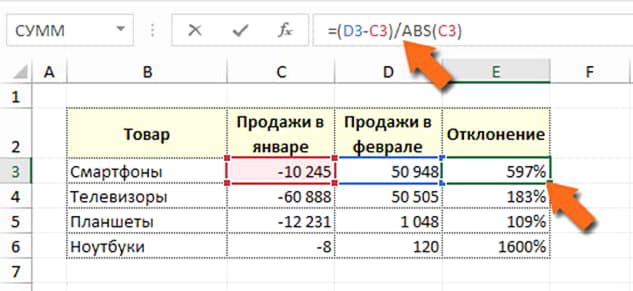
Что будет с изменением прибыли, если какие-то товары имеют отрицательное старое значение? Пусть в нашем примере в январе мы продавали в убыток и прибыль была негативной. А ведь это не такой уж и редкий случай!
Фактически, прибыль выросла, а по расчётам – нет. Исправим формулу, нужно знаменатель взять по модулю (отбросить знак минус). Это распространенный подход, многие его используют. Применим функцию ABS, которая возвращает модуль числа:
Проблема исправлена, этими результатами можно пользоваться. Однако, хочу вас предостеречь. Результаты могут быть недостаточно корректными. Взгляните на картинку еще раз. Прибыль от смартфонов выросла на 60 тысяч, и это 597%. А прибыль от телевизоров – на 110 тысяч, и это лишь 183%. Я использую такие результаты лишь для поверхностной оценки. Или можно не выводить отклонение для таких случаев.
Как посчитать отклонение от среднего?
Вычисление стандартного отклонения
- вычисляем среднее арифметическое выборки данных
- отнимаем это среднее от каждого элемента выборки
- все полученные разницы возводим в квадрат
- суммируем все полученные квадраты
- делим полученную сумму на количество элементов в выборке (или на n-1, если n>30)
12 авг. 2020 г.
Селективное отклонение
Как рассчитать отклонение такого рода? Этот способ расчета отклонения подразумевает сравнение контролируемых величин на определенном промежутке времени, это может быть такой показатель времени, как квартал или месяц, иногда даже это бывает день. Сравнивание интересующих нас величин за определенный промежуток времени (к примеру, месяц, давайте возьмем май) текущего года с тем же маем предыдущего года может дать нам более информативное сравнение с предыдущим месяцем, который рассматривается в плановом периоде.
Селективное отклонение актуальны для фирм, которые занимаются поставкой сезонных услуг. Далее будут описаны еще несколько видов отклонений, знание которых может существенно облегчить вашу жизнь.
Как рассчитать процент выполнения плана?
Для того, чтобы рассчитать процент выполнения плана, нужно воспользоваться формулой: %плана = (факт / план) * 100%. Эти показатели могут быть выражены как в количественных, так и в стоимостных единицах, а также складываться из нескольких компонентов.
Теги
Вычисление среднего отклонения может быть эффективным способом анализа изменчивости в наборе данных. Независимо от точного характера собранных данных, знание их среднего отклонения может помочь вам в их интерпретации. Знание того, как рассчитать среднее отклонение — ценный навык, но он требует изучения и практики. В этой статье мы обсудим, что такое среднее отклонение, как его рассчитать, а также различия между абсолютным и средним отклонением, средним средним и средним отклонением от среднего и стандартным отклонением в сравнении со средним отклонением.
Что такое среднее отклонение?
Среднее отклонение набора данных — это среднее значение всех отклонений от заданной центральной точки. Это статистический инструмент для измерения расстояния от среднего значения или медианы, где среднее значение — это среднее значение всех чисел в наборе данных, а медиана — это точное среднее число, когда мы упорядочиваем набор данных от самого низкого до самого высокого числа. Среднее отклонение набора данных также называется средним абсолютным отклонением (MAD) или средним абсолютным отклонением.
Хотя при работе с относительно небольшими наборами данных вы можете рассчитать среднее отклонение вручную, для больших наборов данных обычно требуется специальное программное обеспечение, которое выполняет расчеты за вас после ввода исходных данных.
Как рассчитать среднее отклонение
Рассмотрим эти шаги при расчете среднего отклонения набора данных:
1. Рассчитать среднюю медиану
Первый шаг — вычисление среднего значения. Вы можете сделать это, сложив все значения в наборе данных и разделив полученную сумму на общее количество значений.
Также можно вычислить медиану, если вы хотите использовать ее вместо среднего значения. Расположите все числа в числовом порядке и подсчитайте, сколько их всего. Затем, если общее число нечетное, разделите его на два и округлите, чтобы найти положение медианы. Если общее число четное, разделите его на два и сделайте среднее между числом в этой позиции и числом в следующей более высокой позиции.
2. Рассчитайте отклонение от среднего значения
После расчета среднего значения можно рассчитать отклонение от среднего для каждого значения в наборе данных. Вычислите разницу между ранее рассчитанным средним и каждым значением в наборе данных и запишите абсолютное значение получившихся чисел. Абсолютное значение числа — это его модуль или неотрицательное значение. Поскольку направление каждого отклонения не имеет значения при расчете среднего отклонения, все результирующие числа положительны.
3. Вычислите сумму всех отклонений
После вычисления отклонения от среднего значения для каждого значения в наборе данных необходимо сложить их вместе. Поскольку это операция с абсолютным значением, каждое значение должно быть положительным числом.
4. Вычислить среднее отклонение
Наконец, рассчитайте среднее отклонение вашего набора данных, разделив ранее рассчитанную сумму всех отклонений на общее количество отклонений, которые вы сложили вместе. Полученное число — это среднее отклонение от среднего.
Пример
Рассмотрите этот пример при расчете среднего отклонения от среднего значения.
Баскетболист сыграл 5 игр в этом сезоне. Числа очков в каждой игре: 23, 30, 31, 15 и 46.
Первый шаг — вычисление среднего значения. Вы делаете это, складывая очки и деля результат на пять игр.
23+30+31+15+46=145
1455=29
Теперь, когда вы определили, что игрок набирал в среднем 29 очков за игру, вам нужно рассчитать отклонение от среднего значения для каждой игры.
23-29=6
30-29=1
31-29=2
15-29=14
46-29=17
Далее необходимо вычислить сумму всех вариаций.
6+1+2+14+17=40
Среднее отклонение — это сумма всех отклонений, деленная на общее количество записей.
Среднее отклонение=405=8
Среднее отклонение от среднего значения по очкам, набранным в первых пяти играх сезона, составляет 8.
Абсолютное отклонение vs. среднее отклонение
Вычисление абсолютного отклонения является важным шагом для определения среднего отклонения. Абсолютное отклонение — это разница между средним значением набора данных и каждым значением в соответствующем наборе данных. Название абсолютного отклонения происходит от того, что все полученные числа записываются как абсолютные числа. Мера выражает расстояние между средним и каждым значением, поэтому отрицательное или положительное число не имеет значения.
После расчета абсолютного отклонения для каждого значения в наборе данных можно рассчитать среднее отклонение, сложив их все вместе и разделив на общее количество значений в наборе данных.
Среднее значение против. среднее отклонение от среднего
Вычисление среднего значения также является важным шагом для определения среднего отклонения от среднего значения. Среднее среднее — это просто сумма всех значений, включенных в набор данных, деленная на общее количество значений. Вычисление среднего значения помогает определить отклонение от среднего путем вычисления разницы между средним и каждым значением. Далее разделите сумму всех ранее рассчитанных значений на количество отклонений, сложенных вместе, и в результате получите среднее отклонение от среднего.
Стандартное отклонение против. среднее отклонение
Стандартное отклонение также является мерой изменчивости в наборе данных, так как оно показывает размер отклонения между всеми значениями в наборе данных. Основное различие между ними заключается в том, что значения, полученные в результате вычитания среднего из значения каждой точки данных, записываются как абсолютные только при вычислении среднего отклонения. Чтобы рассчитать стандартное отклонение, полученные значения записываются не в абсолютных величинах, а в квадрате. Затем необходимо вычислить среднее арифметическое всех квадратных значений. Квадратный корень из этого среднего значения является стандартным средним значением.
Стандартное отклонение чаще всего используется для измерения изменчивости, являясь очень популярным инструментом для расчета волатильности финансовых инструментов и потенциальной инвестиционной доходности. Более высокая волатильность обычно означает, что существует повышенный риск того, что инвестиции принесут убытки. Это означает, что инвестор, который берет на себя риск высоковолатильной ценной бумаги, обычно ожидает от нее высокой доходности. Среднее отклонение также используется в качестве финансового инструмента, но, как правило, реже, чем стандартное отклонение.