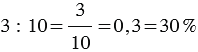Как найти процентное отношение чисел пример

Проценты

  • Нахождение процентов от числа
  • Нахождение числа по его процентам
  • Процентное отношение двух чисел
  • Перевод процентов в десятичную дробь

Процент — это одна сотая часть числа. Отсюда следует, что два процента — это две сотых, двадцать процентов — двадцать сотых и так далее.

Слово  процент  обозначается знаком  %.  Так,  43%  какого либо числа означает  43 процента,  то есть  тема процентов по математике  этого числа. Однако стоит обратить внимание, что в вычислениях знак  %  не пишется, он может быть записан в условии задачи и в окончательном результате.

Величина, от которой вычисляются проценты (например, цена, длина, количество конфет и т. д.), составляет  100  своих сотых долей, то есть  100%.

Чтобы найти один процент от числа, надо разделить это число на  100.

Пример 1. Найти один процент от числа  300.

Решение:

300 : 100 = 3.

Ответ: Один процент от  300  равен  3.

Пример 2. Найти один процент от числа  27,5.

Решение:

27,5 : 100 = 0,275.

Ответ: Один процент от  27,5  равен  0,275.

Нахождение процентов от числа

Чтобы найти некоторое число процентов от данного числа, нужно данное число разделить на  100  и умножить на число процентов.

Задача 1. В том году в магазине к новому году купили  200  ёлок. В этом году количество купленных ёлок увеличилось на  120%.  Сколько ёлок купили в этом году?

Решение: Сначала надо найти  120%  от  200,  для этого  200  надо разделить на  100,  так мы найдём  1%,  а затем полученный результат умножить на  120:

(200 : 100) · 120 = 240.

Число  240  — это  120%  от  200.  Значит, в этом году количество проданных ёлок увеличилось на  240  штук. То есть, количество ёлок, проданных в этом году равно:

200 + 240 = 440 (ёлок).

Ответ: В этом году купили  440  ёлок.

Задача 2. В коробке  28  конфет,  25%  конфет с клубничной начинкой. Сколько конфет с клубничной начинкой в коробке?

Решение:

как посчитать проценты от числа

Ответ: В коробке  7  конфет с клубничной начинкой.

Нахождение числа по его процентам

Чтобы найти число по данной величине его процентов, нужно эту величину разделить на число процентов и умножить на  100.

Задача. Цена метра сукна снизилась на  24 руб.,  что составило  15%  цены. Сколько стоил метр сукна до снижения?

Решение:

задачи по математике на проценты

Ответ: Метр сукна стоил  160  рублей.

Процентное отношение двух чисел

Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на  100.

Задача. Завод по годовому плану должен выпустить продукции на сумму  1 250 000 руб.  За 1-ый квартал он выпустил её на сумму  450 000 руб.  На сколько процентов выполнен заводом годовой план за 1-ый квартал?

Решение:

решение задач на проценты

Ответ: За 1-ый квартал план выполнен на  36%.

Перевод процентов в десятичную дробь

Чтобы перевести проценты в десятичную дробь, надо количество процентов разделить на  100.

Пример 1. Представить  25%  в виде десятичной дроби.

Решение:

25 : 100 = 0,25.

Ответ:  25%  — это  0,25.

Пример 2. Выразить  100%  десятичной дробью.

Решение:

100 : 100 = 1.

Ответ:  100%  — это  1.

Пример 3. Выразить  230%  десятичной дробью.

Решение:

230 : 100 = 2,3.

Ответ:  230%  — это  2,3.

Из данных примеров следует, что для перевода процентов в десятичные дроби, надо в числе, стоящем перед знаком  %,  перенести запятую на два знака влево.

Источник

Процентное отношение двух чисел

Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.

Процентное отношение двух чисел можно записать следующей формулой: R_% = frac{N1}{N2}times{100_%}

Пример процентного отношения

Например есть два числа: 750 и 1100.

Процентное отношение 750 к 1100 равно R_% = frac{750}{1100}times{100%} = 68.18%

Число 750 составляет 68.18% от 1100.

Процентное отношение 1100 к 750 равно R_% = frac{1100}{750}times{100%} = 146.67%

Число 1100 составляет 146.67% от 750.

Пример-задача 1

Норма завода по производству автомобилей составляет 250 машин в месяц. Завод собрал за месяц 315 машин. Вопрос: на сколько процентов завод перевыполнил план?

Процентное отношение 315 к 250 = 315:250*100 = 126%.

План выполнен на 126%. План перевыполнен на 126% — 100% = 26%.

Пример-задача 2

Прибыль компании за 2011 год составила 126 млн $, в 2012 году прибыль составила 89 млн $. Вопрос: на сколько процентов упала прибыль в 2012 году?

Процентное отношение 89 млн к 126 млн = 89:126*100 = 70.63%

Прибыль упала на 100% — 70.63% = 29.37%

9 оценок

Категории

НаукаМатематика

Читайте также

  • ГНОМ ГНОМ СКАЛА
  • ДОМ ВОДА ДАЧА
  • Спряжение глагола «to relate» (Английский язык)

Комментарии

Источник

Содержание материала

  1. Проценты в обыкновенную дробь
  2. Видео
  3. Проценты: правила
  4. Нахождение одного процента от числа
  5. Составление пропорции
  6. Соотношения чисел
  7. Второй способ нахождения процента
  8. Сколько процентов составляет одно число от другого?
  9. Онлайн-сервисы для вычислений
  10. На сколько процентов одно число больше другого
  11. Прибавить проценты к числу
  12. Как найти процентное соотношение чисел
  13. Отнять от числа проценты

Проценты в обыкновенную дробь

Чтобы представить проценты в виде обыкновенной дроби нужно проценты представить в виде десятичной дроби. Затем десятичную дробь преобразовать в обыкновенную дробь.

Преобразовать 25% в обыкновенную дробь

25%100%

=

0.25

=

25100

=

1 × 25 4 × 25

=

14

Проценты: правила

Рассмотрим четыре известных способа поиска процентов.

Нахождение одного процента от числа

Найти процент от числа можно несколькими способами.

Первый способ

  1. Найдем, чему равен 1%.

  2. Умножим полученное значение на количество искомых процентов.

Пример: найти 12% от числа 48.

  1. 48 : 100 = 0,48.

  2. 0,48 × 12 = 5,76.

Второй способ

  1. Переведем проценты в десятичную дробь.

  2. Умножим число на полученную десятичную дробь.

Давайте снова найдем 12% от 48, но другим способом.

  1. 12 : 100 = 0,12.

  2. 48 × 0,12 = 5,76.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем:

  • Переведем 15% в рубли:

    250 : 100 = 2,5 — это 1% от стоимости шоколада,

    значит, 2,5 × 15 = 37,5 — это 15%.

  • Вычислим цену со скидкой 15%: 250 − 37,5 = 212,5.
  • 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Равенство двух отношений называют пропорцией.

a : b = c : d или a/b = c/d

  • a, d — крайние члены
  • b, c — средние члены

Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.

Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем:

Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:

1390 руб. = 100% x руб. = 14%

Перемножим крест-накрест и найдем x:

x = 1390 × 14 : 100 x = 194,6

Ответ: выгода по скидке составила 194,6 рубля.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.

Процент Дробь Как найти % от числа a
10% 1/10 a : 10
20% 1/5 a : 5
25% 1/4 a : 4
50% 1/2 a : 2
75% 3/4 a : 4 × 3

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем:

  • 100% — 25% = 75%,

    значит, нужно заплатить 75% от первоначальной цены.

  • Используем правило соотношения чисел:

    75% — это 3/4 от числа, значит, 8500 : 4 × 3 = 6375 (рублей).

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Видео

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись Теперь для нахождения 50% от 300, достаточно будет , а если перевести эти Теперь для нахождения 50% от 300, достаточно будет в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

300 × 0,5 = 150

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Сколько процентов составляет одно число от другого?

Чтобы вычислить процентное отношение двух чисел, нужно вычислить их отношение и умножить его на . Например, давайте посчитаем, сколько процентов число Пример. Зарплата сотрудника равна , а зарплата его составляет от числа Пример. Зарплата сотрудника равна , а зарплата его. Для этого мы делим Пример. Зарплата сотрудника равна , а зарплата его на Пример. Зарплата сотрудника равна , а зарплата его и умножаем результат на Пример. Зарплата сотрудника равна , а зарплата его:

То есть число Пример. Зарплата сотрудника равна , а зарплата его есть Пример. Зарплата сотрудника равна , а зарплата его от числа Пример. Зарплата сотрудника равна , а зарплата его Пример. Зарплата сотрудника равна Сколько процентов составляет чи, а зарплата его начальника — Решение. Зарплата сотрудника составляет о Найти, сколько процентов составляет зарплата сотрудника от зарплаты начальника и наоборот.

Решение. Зарплата сотрудника составляет от зарплаты начальника

Зарплата начальника составляет

Зарплата начальника составляет

от зарплаты сотрудника.

от зарплаты сотрудника.

Сколько процентов составляет число от числа от числа = неопределённость

Округлять до знаков после запятой.

Онлайн-сервисы для вычислений

В нахождении нужных процентов могут помочь различные сервисы-калькуляторы, работающие в режиме онлайн. Например, популярный сайт имеет в своём функционале различные инструменты, помогающие, в том числе, высчитать процент от любого числа.

Порядок действий:

  1. Перейдите на .
  2. Введите искомые показатели в соответствующие клетки.
  3. Нажмите на «Рассчитать». Вы сразу же получите искомый результат.

Также указанный калькулятор позволяет высчитать ка

Также указанный калькулятор позволяет высчитать какую долю от 1 составляет 2, прибавить % к числу или вычесть из него. Всё очень быстро и удобно.

На сколько процентов одно число больше другого

Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на 100 и вычесть 100.

Вычислим, на сколько процентов число 20 больше числа 5: 205 · 100 — 100 = 4 · 100 — 100 = 400 — 100 = 300% Число 20 больше числа 5 на 300%. Например, зарплата начальника равна 50000 рублей, а сотрудника — 35000 рублей. Найдем, на сколько процентов зарплата начальника больше: 5000035000 · 100 — 100 = 1,43 * 100 — 100 = 143 — 100 = 43% Таким образом, зарплата начальника на 43% выше зарплаты сотрудника.

Прибавить проценты к числу

Чтобы прибавить к числу p процентов, нужно умножить это число на (1 + p100)

Прибавим 30% к числу 200: 200 · (1 + 30100) = 200 · 1,3 = 260 200 + 30% равняется 260. Например, абонемент в бассейн стоит 1000 рублей. Со следующего месяца обещали поднять цену на 20%. Вычислим, сколько будет стоить абонемент. 1000 · (1 + 20100) = 1000 · 1,2 = 1200 Таким образом, абонемент будет стоить 1200 рублей.

Как найти процентное соотношение чисел

Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.

Для определения такого результата существуют следующая формула:

B / A * 100 =

К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.

Используя приведённую формулу, выполняем несложные арифметические операции:

85 / 500 * 100 = 17%

Таким образом, число 85 составляет 17% от 500.

Проверяем полученное число по формуле первого способа:

500 / 100 * 17 = 85.

Всё сошлось.

Отнять от числа проценты

Отнять от числа проценты

Давайте отнимем Чтобы отнять от числа процентов, нужно это число от числа Чтобы отнять от числа процентов, нужно это число Это значит, что нужно найти Чтобы отнять от числа процентов, нужно это число от числа Чтобы отнять от числа процентов, нужно это число и вычесть их из него:

Чтобы отнять от числа процентов, нужно это число умножить на

Уменьшить число на % — 0% =

Округлять до знаков после запятой.

Теги

Источник
  1. Главная
  2. Справочники
  3. Справочник по математике 5-9 класс
  4. Отношения и пропорции
  5. Отношения

Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.

Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.

Например:

14 : 7 — отношение числа 14 к числу 7;

6 : 25 — отношение числа 6 к числу 25;

  — отношение числа к числу ;

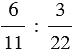
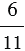
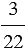
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.

Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число  составляет от числа .

Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .

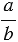
Основное свойство отношения:

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Запишем отношение числа 3 к числу 10 и найдем его значение:

То есть отношение двух чисел можно выразить в процентах.

Процентное отношение двух чисел — это их отношение, выраженное в процентах.

Процентное отношение показывает, сколько процентов одно число составляет от другого.

Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Пример:

Сколько процентов составляет число 5 от числа 10?

51021·100%=12·100%=1002%=50%.

Ответ: 50% составляет число 5 от числа 10.

Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.

Например:

Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.

1 м = 100 см;

Отношение длины прямоугольника к его ширине равно 12 : 100 =  .

Отношение ширины прямоугольника к его длине равно 100 : 12 = .

Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).

Например:

Пусть на карте задан масштаб 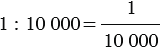, то есть карта сделана в масштабе одна десятитысячная.

Найдем, какой длине на местности соответствует отрезок 5 см на карте.

Для решения обозначим через  длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:

5 : = 1 : 10 000;

Решаем данное уравнение:

= 510 000;

= 50 000;

50 000 см = 500 м = 0,5 км.

Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.

Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.

Для решения обозначим через  длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности:  : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:

: 9,5 = 1 : 10 000;

Решаем данное уравнение:

= 9,5 : 10 000;

= 0,00095;

0,00095 км = 0,95 м = 95 см.

Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.

Советуем посмотреть:

Пропорции

Прямая и обратная пропорциональные зависимости

Длина окружности и площадь круга

Отношения и пропорции


Правило встречается в следующих упражнениях:

6 класс

Номер 581,
Мерзляк, Полонский, Якир, Учебник

Номер 604,
Мерзляк, Полонский, Якир, Учебник

Номер 669,
Мерзляк, Полонский, Якир, Учебник

Номер 686,
Мерзляк, Полонский, Якир, Учебник

Номер 693,
Мерзляк, Полонский, Якир, Учебник

Номер 7,
Мерзляк, Полонский, Якир, Учебник

Номер 5,
Мерзляк, Полонский, Якир, Учебник

Задание 753,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 757,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 816,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 146,
Мерзляк, Полонский, Якир, Учебник

Номер 149,
Мерзляк, Полонский, Якир, Учебник

Номер 150,
Мерзляк, Полонский, Якир, Учебник

Номер 198,
Мерзляк, Полонский, Якир, Учебник

Номер 229,
Мерзляк, Полонский, Якир, Учебник

Номер 230,
Мерзляк, Полонский, Якир, Учебник

Номер 405,
Мерзляк, Полонский, Якир, Учебник

Номер 426,
Мерзляк, Полонский, Якир, Учебник

Номер 847,
Мерзляк, Полонский, Якир, Учебник

Номер 943,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 303,
Мерзляк, Полонский, Якир, Учебник

Источник

Понравилась статья? Поделить с друзьями:
  • Как мне найти схему нашего дома
  • Как хороший завтрак найти
  • Пропал документ ворд как найти
  • Как найти площадь треугольника в мм2
  • Как найти размер критерия