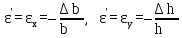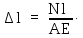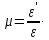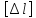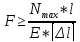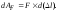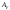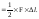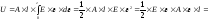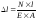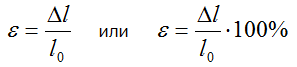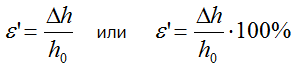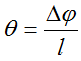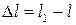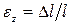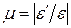Как найти продольные относительные деформации

Выделим
из стержня на участке, где действует
постоянная продольная
сила N,
некоторую его часть длиной l
и шириной b
(см. рис. 4.3, а). Опыты показывают,
что при растяжении резинового стержня
его длина увеличивается, а ширина
уменьшается. Пусть
l₁
и b₁ –
длина и ширина стержня после деформации
соответственно.

Изменение
длины стержня при растяжении (сжатии)
называется абсолютной продольной
деформацией и определяется по формуле

∆l
= l₁
– l₂.

Отношение
абсолютной продольной деформации к
первоначальной длине стержня называется
относительной продольной деформацией
и определяется по формуле

.

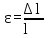
По
аналогии с продольными деформациями
имеем:

∆b
= b₁
– b,
∆h
= h1
– h
– абсолютные
поперечные деформации;

– относительные
поперечные деформации.

При
растяжении: N

0, ∆l

0, ε

0, ∆b
< 0, ε^‘
<
0; при сжатии:

N
< 0, ∆l
< 0, ε
<
0, ∆b

0, ε^‘

0.

Закон
Гука –
относительная продольная деформация
прямо пропорциональна нормальному
напряжению, а именно:

,

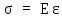
где
Е
– модуль
Юнга или модуль упругости первого рода
(кН/см²,
МПа).

Используя
зависимости
,
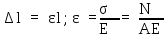
получим

Абсолютная
продольная деформация прямо пропорциональна
продольной силе в пределах участка
длиной l
при
постоянных N
и
EА,
где EА
– жесткость поперечного сечения при
растяжении (сжатии).

Коэффициент
Пуассона 
– безразмерная величина, характеризующая
упругие свойства и способность материала
деформироваться в поперечном направлении
при его растяжении или сжатии в продольном
направлении.

Для
реальных материалов коэффициент Пуассона
изменяется в очень узких пределах: 
= 0…0,5.

Значение

для некоторых
материалов:

—
пробка –
;

—
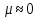
резина –
;

—
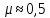
сталь –
;

—
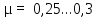
свинец –
;

—
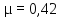
бетон –
;

—
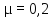
каучук – 

0,5.

Значение
коэффициента Пуассона определяется
опытным путем в результате специальных
испытаний материала.

4.4. Условия прочности и жесткости

Условие
прочности элементов конструкций и
сооружений рассмотрено в главе 3.

В
некоторых случаях для обеспечения
нормальной работы машин, конструкций
и сооружений требуется проектировать
размеры деталей и элементов таким
образом, чтобы обеспечивалось условие
жесткости:

,

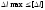
где

– допускаемое удлинение, задается
техническими условиями.

Удлинение
ступенчатых стержней, а также когда
внешние силы приложены в разных точках
продольной оси стержня, определяется
суммированием удлинений отдельных
участков.

,

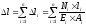
где
N_i,
l_i,
E_i,
А_i
– нормальная сила, длина, модуль упругости
и площадь поперечного сечения і—го
участка соответственно.

Условие
жесткости позволяет выполнять три вида
расчетов:

1)
проверочный:
;

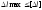
2)
проектировочный: 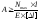(стержень
постоянного сечения);

3)
расчет грузоподъемности или несущей
способности:

.

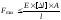
4.5. Потенциальная энергия упругой деформации

Внешние
силы, приложенные к упругому телу и
вызывающие изменение его геометрии,
совершают работу А_F
на соответствующих перемещениях. В
упругом теле накапливается потенциальная
энергия деформации U.
При действии динамических нагрузок
часть работы внешних сил превращается
в кинетическую энергию движения частиц
тела К.

Уравнение
баланса энергии можно записать в
следующем виде:

А_F = U + K.

При
статическом нагружении упругого тела
работа внешних сил полностью преобразуется
в потенциальную энергию деформации,
следовательно, А_F = U.
При разгрузке тела производится работа
за счет потенциальной энергии деформации,
накопленной телом. При этом упругое
тело является аккумулятором энергии.
Это свойство упругого тела широко
используется в заводных пружинах часовых
механизмов, в конструкции лука и т. д.
Для вывода необходимых расчетных
зависимостей потенциальной энергии
деформации рассмотрим простейший случай
– растяжение стержня.

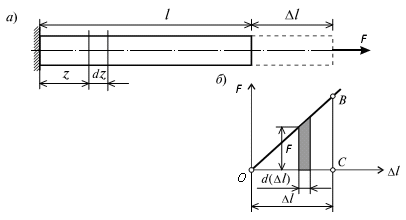
На
рис. 4.5, а изображен стержень,
растягиваемый силой F,
удлинение которого соответствует l.
График изменения величины удлинения
стержня l
в зависимости от силы F
показан на рис. 4.5, б.
В соответствии
с законом Гука этот график носит линейный
характер.

Рис.
4.5. а
– схема растягиваемого стержня; б
– график зависимости F
– ∆l

Пусть
некоторому значению силы F соответствует
удлинение стержня l.
Дадим некоторое приращение силе
F  соответствующее
приращение удлинения составит d (l ).
Элементарная работа на этом приращении
удлинения составит:

.

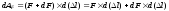
Вторым
слагаемым, в силу его малости, можно
пренебречь, и тогда

Полная
работа равна сумме элементарных работ,
тогда при линейной зависимости работа
внешней силы F
на перемещении l
будет равна площади треугольника ОСВ
(рис. 4.5, б), т. е.

Если
напряжения 
и деформации 
распределены по объему тела V
равномерно, то потенциальную энергию
деформации стержня можно записать в
следующем виде:

,

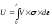
где
V = А l,
F = 
 A,
 = Е ;

А
– площадь поперечного сечения стержня.

Тогда
окончательно

.

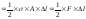
С
учетом

для
однородного стержня с постоянным
попе­речным сечением при F = const
получим:

.

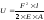
В общей физике и теоретической механике мы предполагали, что тело абсолютно твердое. То есть расстояние между любыми точками равно вне зависимости от ситуации. Однако в самом фундаменте курса сопромата мы уже выяснили, что материалы выдерживают внешние (и внутренние, но об этом позже) воздействия именно за счет изменения расстояния между молекулами: химические связи стремятся вернуть самое оптимальное для них расстояние. Это стремление материала к занятию определенной формы называется напряжением, и в прошлой статье мы поговорили о том, как его искать. Пора нам научиться численно оценивать, чему равна деформация продольного растяжения.

Деформация продольного растяжения

Как мы уже говорили, то, с какой силой атомы конкретного материала будут притягиваться друг к другу зависит от расстояния между атомами. Вопрос силы связи с точки зрения химии мы рассматривать не будем и возьмём силы противодействия внешним усилиям как данность, экспериментальные данные которые мы будем использовать при расчётах, а не пытаться их интерпретировать.

Если мы измерим силу взаимодействия между атомами в зависимости от расстояния между ними, то мы получим следующую картину:

По графику видно, что есть достаточно существенный отрезок, на котором сила изменяется линейно. Более того, забегая вперёд скажу также что именно этот участок для нас наиболее интересен, так как на нем не происходят неупругие (т.е. когда после снижения нагрузки материал не возвращается в первоначальное положение) деформации. И очень велик соблазн попытаться найти формулу, по которой изменяется сила в зависимости от изменения расстояния.

И именно это и сделал Гук, обобщив интуитивное предположение «это должна описывать какая-то формула», имеющуюся теорию и экспериментальные данные.

Продольные деформации: закон Гука

Итак, действие равно противодействию, а противодействие зависит от изменения формы. А как вычислить силу сопротивления материала имея только измененный размер? Или, наоборот, увидев насколько велика будет деформация продольного растяжения, сказать через сколько он порвётся?

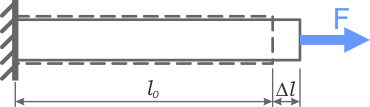
Разумеется, провести эксперимент! Возьмём цилиндрический предмет из некоторого материала (условная сталь). С одной стороны его закрепим, а с другой приложим усилие. Разумеется, перед проведением эксперимента, мы измерим изначальную длину образца. Затем посмотрим, насколько образец увеличится в длину. Или, как это принято обозначать в сопромате, «измерим длину образца под нагрузкой».

Обычно этих данных достаточно, но могут быть особые случаи, когда нам необходимо знать и то, как изменяется брусок в диаметре, поэтому эти данные мы тоже померим.

Соответственно, под нагрузкой наш цилиндр становится на какие-то доли миллиметра длиннее (dl). И отношение этого приращения к изначальной длине (l) называется относительной продольной деформацией (общается ε, эпсилон): ε=dl/l. Иными словами, если умножить длину бруска до нагрузки на относительную продольную деформацию (ε), мы получим его длину под нагрузкой.

Для чего это нужно? 

Представим себе железную дорогу Санкт-Петербург–Москва. Это 634 км. по прямой. И вот случается перепад температур, зима сменилась летом, сталь расширилась. И, казалось бы, что эта пара миллиметров на несколько километров сделают. А потом считаем все как следует и оказывается, что увеличение длины в сумме составляет около 100 метров. И все, вокзал переезжает два раза в год на олимпийскую дистанцию. Разумеется, рельсы закреплены жёстко и двигаться никуда не будут. Однако очевидно, что такие нагрузки (представьте равномерно распределенную между Санкт-Петербургом и Москвой нагрузку и какое суммарное продольное напряжение получится) не способствуют долговечности конструкций. 

Температурное расширение мы будем разбирать позже, но от того, внутренние ли силы или внешние силы воздействуют на материал, суть разговора не меняется. Просто если мы сейчас разбираем случаи, когда мы приложили усилия к бруску и начали менять в нем расстояния между молекулами, то сейчас, наоборот, идеальное расстояние между молекулами изменилось, и оно оказывает влияние на внешний мир. 

История, между прочим, абсолютно реальная. И для решения этой проблемы между рельсами могут оставлять небольшой зазор, чтобы при температурных перепадах рельсы не находились под нагрузкой и не теряли микроструктуру. 

Гораздо очевиднее будет пример монтажа конструкций: пока все детали изделия находятся на бумаге, они взаимодействуют правильно. Однако когда на объект начинает действовать сила тяжести, из-за расстяжения отверстие и заклепка могут оказаться на совершенно разных высотах. И несмотря на то, что нагрузки конструкция выдерживает, за счет изменения ее габаритов смонтировать ее становится на порядок сложнее. Если изменения не учитывать при проектировании, будет увеличена трудоемкость монтажа.

Точно также можно найти относительную поперечную (в ширину) деформацию: ε_п=Δd/d

Отношение продольной и поперечной деформации обычно одинаково под любой нагрузкой и оно уже давно экспериментально установлено для каждого конкретного материала.  В справочниках искать коэффициент Пуассона:

μ=|ε_п/ε|

Остается только выяснить, насколько удлинится конкретный стержень при определенной нагрузке.

И, как ни странно, все необходимое для таких вычислений у нас уже есть. А именно, у нас есть некоторая нагрузка, длина и ширина стержня. Логично предположить, что чем больше сила (P), тем больше растяжение. Также логично предположить, что чем больше длина (l), тем легче растягивать: вспомните, ведь более длинную пружину проще растянуть, нежели короткую. В то же время, чем больше площадь, тем сложнее нечто растягивать: чем больше площадь, тем больше в ней связей между атомами. Помимо прочего для связей каждого материала должна быть своя константа, которая будет обозначать силу сопротивления на единицу материала. Называется она модулем Юнга (E) и для большинства материалов уже найдена.

Итого, изменение длины (dl) стержня длиной l, площадью сечения F, с модулем Юнга этого материала E под воздействием силы P:

dl=Nl/EF

Это выражение называется Законом Гука.

На практике для расчетов используется напряжение, которое можно из этой формулы вывести. σ=N/F. следовательно, dl=σl/E. ε=dl/l. Следовательно:

σ=εE

Деформация продольного растяжения под нагрузкой

Какая техническая наука возможна без экспериментов? Я лично таких не припомню. 

Попробуем экспериментально проверить, насколько будет удлиняться образец под нагрузкой.

Так как оборудования у меня под рукой нет, я предоставлю перерисованный график без численных значений оставшийся у меня с лабораторных работ в Санкт-Петербургском Политехническом Университете.

Жёстко закрепляем стальной стержень и пытаемся его растянуть:

До определенной точки график действительно линеен и деформация продольного растяжения полностью отвечает теоретическим значениям. Однако в точке А график «скругляется» и значения начинают отличаться от полученных через формулу закона Гука. При этом, если нагрузку убрать до того, как удлинение достигнет точки B, образец вернётся в первоначальное состояние. Однако точка B (предел упругости) является граничной: все что будет после неё – это неупругие, пластичные деформации, которые для конструкций недопустимым.

Затем при увеличении нагрузки происходит резкий скачок удлинения. На графике это практически плоская линия BC, а называется площадкой текучести (напряжение же возникающее на площадке: предел текучести).

Если мы снимем нагрузку, то образец будет иметь не первоначальную длину, а изменится на определённую величину (её можно приблизительно найти проведя из нашей точки на графике линию параллельную линии AB до нуля нагрузки).

Затем на промежутке упрочнения CD деформация продольного растяжения требует увеличения усилия: под нагрузкой кристалическая решётка перестроилась, избавилась от микродефектов, повысилась прочность стержня. 

Затем (на промежутке DE) нагрузку необходимо снижать, так как из-за уменьшения площади сечения образец в состоянии выдерживать все меньшие усилия.

Однако, по мере удлинения стержня, он, со временем, всё-таки порвётся.

График напряжения в зависимости от относительного продольного удлинения можно увидеть ниже:

Резюмируем. Деформация продольного растяжения под нагрузкой делится на основных этапов:

1. Упругое пропорциональное растяжение OA (σ_у)
2. Упругое непропорциональное растяжение AB (или предел упругости σ_п.у.)
3. Скачок растяжения BC (напряжение – предел текучести (σ_т), отрезок – площадка текучести) 
4. Упрочнение CD (напряжение максимальное временное в точке D σ_в)
5. Снижение несущей способности из-за уменьшения поперечного сечения DE (разрыв в точке E (σ_р))

Изменение длины под воздействием внешних сил

Возвращаемся от стержня конкретного к стержню абстрактному и попробуем рассчитать его удлинение при разных приложенных нагрузках.

Самый простой способ мы, по сути, уже разобрали. К некоторому невесомому стержню диаметра F и длины l жёстко закрепленному одним концом приложили силу P.  Из таблицы мы знаем Модуль Юнга E. 

Для удобства мы строим эпюру, из которой становится понятно, что продольные напряжения в каждом из сечений равны, а значит и изменяться длина будет достаточно равномерно:

По сути, теперь нам остаётся только подставить в закон Гука все значения и получить удлинение стержня:

dl=Pl/EF

При необходимости мы также можем найти и изменение диаметра, так как коэффициент Пуассона (μ=|ε_п/ε|) никто у нас не забирал из справочной литературы. Необходимо только рассчитать относительное продольное удлинение, домножить на константу материала и получить относительное поперечное сужение.

Также возможны ситуации, когда конструкция будет составной и (или) к ней будут приложены разные силы в разных точках. Тогда потребуется точно также построить эпюры и вычислить требуемые значения для каждого участка. 

В случае с распределенными нагрузками ситуация сложнее, но не сильно. 

Фактически вся проблема сводится к тому, что мы ищем функцию распределения нагрузки, её подставляем в формулу и таким образом получаем функцию распределения удлинения по всему стержню. При необходимости интегрируем и получаем суммарное удлинение стержня.

dl= ₀∫^lNdx/EF

Опасное напряжение и коэффициент запаса

Ширина и длина у образцов может быть разная, а нам бы хотелось вычислить заранее, достаточно ли прочный для данной нагрузки у нас стержень. 

Экспериментально мы уже померили относительные продольные деформации и знаем, при каких значениях материал испытывает упругие деформации, а когда его структура меняется навсегда. Компетентные органы тоже испытания провели и в соответствующей документации уже отсортировали напряжения, которые приняты опасными и их и следует использовать как граничных. 

Вообще, “опасные” напряжения определяются прежде всего нормативной документацией и справочной информацией. И считать их самостоятельно не только не надо, но и нельзя (главные друзья инженера — это не умение считать в уме и идеальная память, а калькулятор и справочник).

Методика расчета мне не известна, но могу предположить, что она учитывает в себе как экспериментальные данные по исследованию материалов (в частности, предел текучести обычно понимается под опасным напряжением), так и статистику по практике эксплуатации (аварии и т.д.).

Примечание: в науках изучающих материалы принято разделение на пластичные и хрупкие материалы. Пластичные одинаково хорошо выдерживают как растяжение, так и сжатие, хрупкие нет. Надо понимать, что разделение довольно условно, так как “степень пластичности”, если можно так назвать соотношение предельных нагрузок перед необратимой деформацией для сжатия и растяжения различается не только для материалов, но и для разных условий. Например сталь, пластичная в нормальных условиях, при низких температурах будет становиться более хрупкой. Среди влияний можно выделить как температуру, так и радиационное излучение, если мы говорим о проектировании конструкций ядерных реакторов, сталкивающихся с большим нейтронным потоком, или космических аппаратов, бомбардируемых космическим излучением.

Для пластичных материалов опасное напряжение примерно равно как на сжатие (σ_оп.сж.), так и на растяжение (σ_оп.рас.). Однако в ряде материалов опасное напряжение для сжатия и разрыва будет разным.

Помимо прочего, предельные нагрузки будут отличаться в зависимости от условий, таких как температура.

Во время проектирования конструкций важны две вещи:

1. Надежность
2. Экономичность

Ни у кого нет желания рассчитывать конструкцию «впритирку», так как возможны и брак и нецелевое использование и просто непредвиденные ситуации. Но и материал надо беречь, всё-таки это ваши деньги и труд других людей. 

По этой причине используются коэффициенты запаса прочности (k). Разделив на некоторую величину опасное напряжение можно найти предельно допустимое напряжение в конструкции, которое можно оставлять в материале: 

[σ]=σ/k

Находить коэффициенты необходимо в справочной и нормативной документации.

Нормативная и справочная документация специфична для разных отраслей. Например, в строительстве искать значения опасных напряжений следует в СП, а коэффициенты запаса прочности в СНиП-ах.

Автор: Овчинников К.А.
Фактчекер и редактор: Сабуров Д.А.

4 327

Коэффициент Пуассона. Связь продольной и поперечной деформации

Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины

называется абсолютным удлинением стержня.

Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением (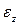 – эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации:

При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.

Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:

.

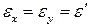
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона или коэффициентом поперечной деформации, вычисляется по формуле:

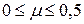
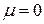
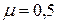
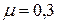
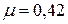
Для различных материалов коэффициент Пуассона изменяется в пределах . Например, для пробки , для каучука , для стали , для золота .

Лекция 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ – СЖАТИЕ

Внутренние силы в поперечных сечениях стержня. Построение эпюр
внутренних сил от действия внешних сил. Напряжения в поперечных сечениях
стержня. Деформации продольные и поперечные, коэффициент Пуассона.
Закон Гука. Модуль упругости. Определение перемещений поперечных сечений
стержня. Построение эпюр напряжений и перемещений. 

Растяжение – сжатие. Растяжение и сжатие – это наиболее простые
и часто встречающиеся виды деформации. На растяжение и сжатие работают
многие элементы конструкций: стержни ферм, колонны, канаты лебедок,
штоки паровых машин, лонжероны крыла самолетов. Растяжение и сжатие –
это наиболее простые виды деформации, поэтому изучение курса сопромата
начинается именно с изучения этих видов деформации.

Внутренняя продольная сила (или нормальная сила). При растяжении
или сжатии в поперечных сечениях бруса возникает только один внутренний
силовой фактор – внутренняя продольная сила N (рис. 5). Брус имеет два
характерных участка. Для определения продольной силы N воспользуемся
методом сечения. На расстоянии y1 проведем сечение на первом участке
и рассмотрим равновесие отсеченной части. Продольную силу будем всегда
показывать от сечения, что будет соответствовать растяжению бруса.

Составим условие равновесия на ось y

N₁ – F = 0,

откуда

N₁ = F.

Проведем на втором участке сечение на расстоянии y2. Рассматривая
равновесие отсеченной части, получаем N2 = F. Строим эпюру продольных
сил.

Нормальные напряжения. Исходя из определения напряжения, можно записать

(1)

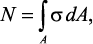
где σ – нормальное напряжение в произвольной точке сечения.

Согласно гипотезе плоских сечений (гипотезаБернулли) все
продольные волокна бруса деформируются одинаково, а это означает, что
напряжения в поперечных сечениях одинаковы, т.е. σ = const.

 

 

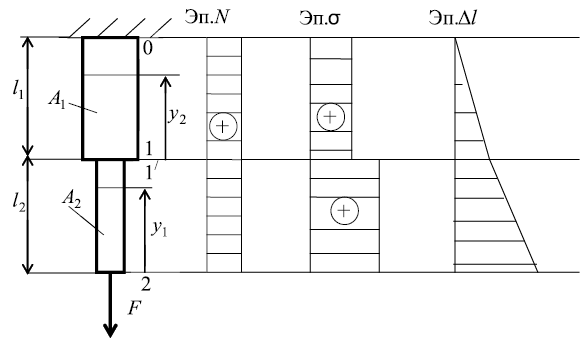
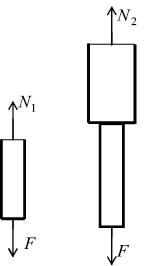
Рис. 5. Построение эпюр N, σ_т, Δl

В этом случае получаем

 

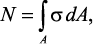
откуда .

 

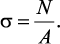
Рассчитывая напряжения в каждом сечении, строим эпюру нормальных напряжений (рис. 5).

 

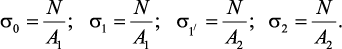
Деформации и перемещения.

Величина, на которую изменится длина бруса (или одного из его
участков) под действием продольных сил, называется продольной
деформацией (рис. 6). Относительная продольная деформация – отношение
абсолютной продольной деформации Dl к первоначальной длине стержня l:

ε = Dl/l₀

Величина Δа (Δb), на которую изменится размерпоперечного сечениябруса а (b) под действием продольной силы, называется поперечной деформацией.

Отношение абсолютной поперечной деформации, Dа (Db)
к первоначальному размеру сечения бруса а (b), называется относительной
поперечной деформацией:

 

 

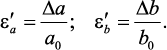
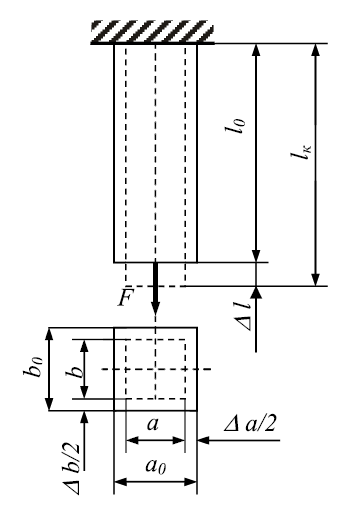
Рис. 6. Схема деформирования стержня