В этой статье мы рассмотрим концепцию уравнения прямой прямой. Мы попытаемся понять общее уравнение прямой, формулу прямой, способ нахождения уравнения прямой и откроем для себя другие интересные аспекты этого. Попробуйте свои силы в решении нескольких интересных примеров и вопросов для лучшего понимания концепции.
Определение
Уравнение прямой — может быть записано в различных формах. Прямая линия -это двумерная геометрическая фигура, которая простирается на обоих своих концах до бесконечности.
Для того чтобы освоить описанные приемы, необходимо много практиковаться, чтобы они стали привычными.
После прочтения информации по этой теме вы должны уметь:
- находить уравнение прямой прямой, учитывая ее наклон и пересечение с осью y;
- находить уравнение прямой, учитывая ее наклон и одну точку, лежащую на ней;
- найти уравнение прямой, учитывая две точки, лежащие на ней;
- дать уравнение прямой в любой из форм y = mx + c или ax + by + c = 0
Уравнения прямых могут принимать различные формы в зависимости от фактов, которые мы знаем о прямых. Итак, для начала предположим, что у нас есть прямая линия содержащая точки из следующего списка.
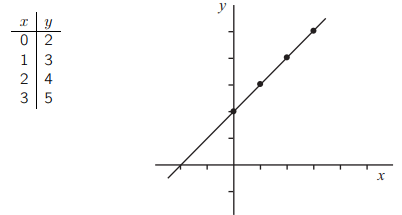
На прямой есть еще много точек, но уже достаточно, чтобы увидеть закономерность. Если мы возьмем любое значение x и прибавим 2, мы получим соответствующее значение y: 0 + 2 = 2, 1 + 2 = 3, 2 + 2 = 4, и так далее. Между координатами x и y любой точки на прямой существует фиксированная зависимость, и уравнение y = x + 2 всегда верно для точек на прямой. Мы можем обозначить прямую, используя это уравнение.
Уравнение прямой, проходящей через начало координат с заданным коэффициентом
Предположим, что у нас есть прямая с уравнением y = x. Тогда для каждой точки на прямой координата y должна быть равна координате x. Таким образом, прямая будет содержать точки из следующего списка.
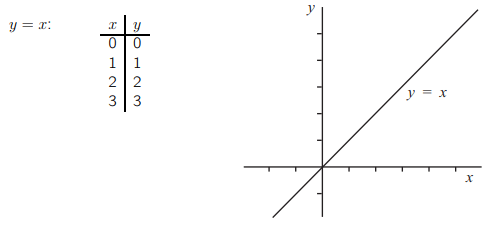
Мы можем найти коэффициент прямой, используя формулу для нахождения коэффициента:
[ m=frac{y 2-y 1}{x 2-x 1} ]
Далее следует подставить первые два набора значений из таблицы. Получаем:
[ m=frac{1-0}{1-0}=1 ]
Таким образом, коэффициент этой прямой равен 1.
А как насчет уравнения y = 2x? Оно также представляет собой прямую линию, и для всех точек на y в два раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующем списке.
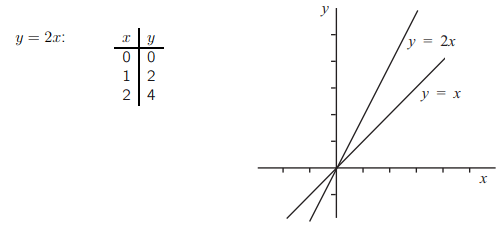
Если мы вычислим коэффициент прямой y = 2x, используя первые два набора значений в таблице, то получим:
[ m=frac{2-0}{1-0}=2 ]
Таким образом, коэффициент этой прямой равен 2.
Теперь возьмем уравнение y = 3x. Оно также представляет собой прямую линию, и для всех точек на прямой. Каждая точка y в три раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующего списка.
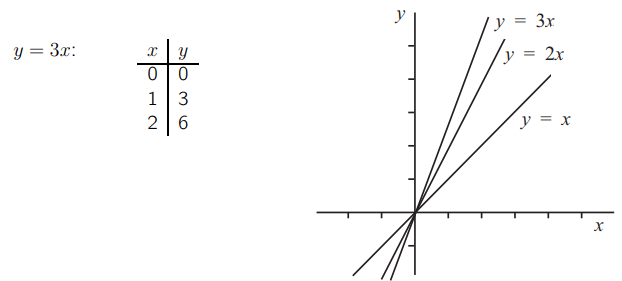
Если мы вычислим коэффициент прямой y = 3x, используя первые два набора значений в таблице, мы получим:
[ m=frac{3-0}{1-0}=3 ]
Следовательно, коэффициент этой прямой равен 3.
Мы можем начать видеть здесь закономерность. Все эти прямые имеют уравнения, где y равно некоторому числу, умноженному на x. И в каждом случае линия проходит через начало координат, а коэффициент прямой равен m.
Таким образом, если бы у нас была прямая с уравнением y = 13x, то мы бы указали, что коэффициент прямой будет равен 13. Аналогично, если бы у нас была прямая с уравнением y = -2x, то коэффициент будет равен -2. Таким образом, в общем случае уравнение y = mx представляет собой прямую линию, проходящую через начало координат с коэффициентом m.
Важно
Уравнение прямой с коэффициентом m, проходящей через начало координат, имеет вид:
[y = mx]
Пересечение прямой y
Рассмотрим прямую линию с уравнением y = 2x + 1. Это уравнение имеет несколько иную форму в отличие от тех, которые мы видели ранее. Чтобы нарисовать график прямой, мы должны вычислить некоторые значения.
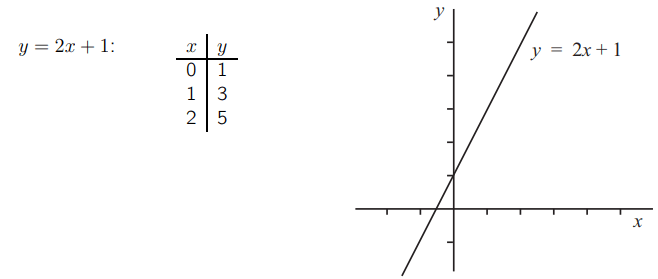
Обратите внимание, что при x = 0 значение y равно 1. Значит, эта прямая пересекает ось y в точке y = 1.
А как насчет прямой y = 2x + 4? Мы снова можем вычислить некоторые значения.
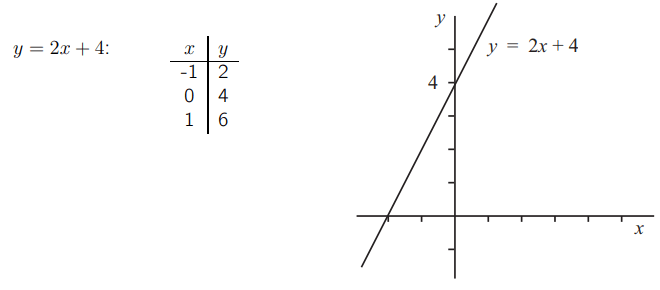
Эта линия пересекает ось y в точке y = 4.
А как насчет прямой y = 2x — 1? Мы снова можем вычислить некоторые значения.
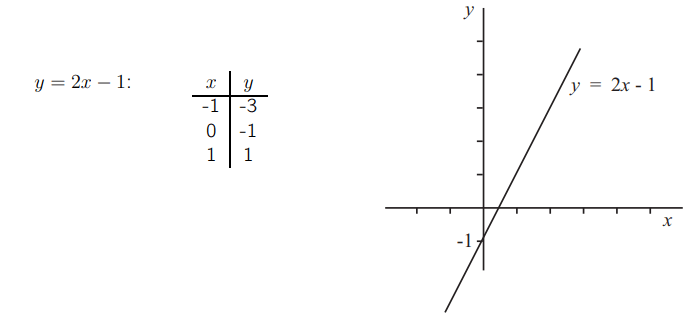
Эта линия пересекает ось y в точке y = — 1.
Общее уравнение прямой — y = mx + c, где m — коэффициент, а y = c — значение на оси у, при через которое проходим прямая.
Это число c является пересечением с осью y.
Важно
Уравнение прямой с коэффициентом m и точкой пересечения c на оси y имеет вид:
[y = mx + c]
Иногда нам задают уравнение прямой в другой форме. Предположим, у нас есть уравнение 3y — 2x = 6. Как показать, что оно представляет собой прямую линию, и найти ее коэффициент и значение точки пересечения с осью y?
Мы можем использовать алгебраическую перестановку, чтобы получить уравнение в виде y = mx + c:
3y — 2x = 6,
3y = 2x + 6,
[y=frac{2}{3} x+2]
Теперь уравнение находится в стандартной форме, и мы видим, что коэффициент равен [frac{2}{3}], а значение точки пересечения с осью y равно 2.
Мы также можем работать в обратном направлении. Предположим, мы знаем, что прямая имеет коэффициент [frac{1}{5}] и имеет вертикальное пересечение в точке y = 1. Каким будет ее уравнение?
Чтобы найти уравнение, достаточно подставить нужные значения в общую формулу y = mx + c.
Здесь m равно [frac{1}{5}], а c — 1, поэтому уравнение равно y =[frac{1}{5}]x + 1. Если мы хотим убрать дробь, мы можем также привести уравнение к виду 5y = x + 5, или 5y — x — 5 = 0.
Уравнение прямой прямой с заданным коэффициентом, проходящее через заданную точку на оси у
Предположим, что мы хотим найти уравнение прямой с коэффициентом [frac{1}{3}], которое проходит через точку (1, 2). Здесь, хотя мы знаем коэффициент, мы не знаем значение точки пересечения с осью у, оно равно c.
Начнем с общего уравнения прямой y = mx + c.
Мы знаем, что коэффициент равен [frac{1}{3}], именно поэтому мы можем сразу подставить это значение на место m. Это дает: [y=frac{1}{3} x+c]
Теперь мы используем тот факт, что прямая проходит через (1, 2). Это означает, что когда x = 1, y должно быть равна 2. Подставляя эти значения, находим:
[2=frac{1}{3}(1)+c]
так что
[c=2-frac{1}{3}=frac{5}{3}]
Таким образом, уравнение прямой имеет вид:
[y=frac{1}{3} x+frac{5}{3}]
Мы можем вывести общую формулу для задач такого типа, используя тот же метод. Мы возьмем общую прямую с коэффициентом m, проходящую через фиксированную точку [mathrm{A}left(x_{1}, y_{1}right)].
Начнем с общего уравнения прямой y = mx + c. Теперь мы используем тот факт, что прямая проходит через точку [mathrm{A}left(x_{1}, y_{1}right)]. Это означает, что при x = [x_{1}], y должно быть [y_{1}]. Подставляя эти значения, находим:
[y_{1}=m x_{1}+c]
так что
[mathrm{c}=y_{1}-mathrm{m} x_{1}]
Таким образом, уравнение прямой имеет вид y = mx + [y_{1}-mathrm{m} x_{1}].
Мы можем записать его в альтернативной форме
[mathrm{y}-y_{1}=mathrm{m}left(mathrm{x}-x_{1}right)]
Тогда это прямая с уклоном m, проходящая через точку [left(x_{1}, y_{1}right)]. Таким образом, эта общая форма полезна, если вы знаете коэффициент и одну точку на прямой.
Важно
Уравнение прямой с коэффициентом m, проходящей через точку [left(x_{1}, y_{1}right)], имеет вид:.
[y-y_{1}=mleft(x-x_{1}right)]
Например, мы знаем, что прямая имеет коэффициент -2 и проходит через точку (-3, 2).
Мы можем воспользоваться формулой [y-y_{1}=mleft(x-x_{1}right)] и сразу подставить значения:
y — 2 = -2(x — (-3))
y — 2 = -2(x + 3)
y — 2 = -2x — 6
y = -2x — 4 .
Упражнение 1
Найдите уравнение описанных ниже прямых (приведите уравнение в виде y = mx + c):
(1) коэффициент 3, проходящей через (1, 4);
(2) коэффициент -2, проходящей через (2, 0);
(3) коэффициент [frac{2}{5}], проходящий через (5, -1);
(4) коэффициент 0, проходящий через (-1, 2);
(5) коэффициент -1, проходящий через (1, -1).
Нет времени решать самому?
Наши эксперты помогут!
Уравнение прямой проходящей через две заданные точки
Что нужно сделать, если мы хотим найти уравнение прямой, проходящей через две точки (-1, 2) и (2, 4)?
Здесь мы не знаем коэффициент прямой, поэтому кажется, что мы не можем использовать ни одну из формул, которые мы знаем на данный момент. Но мы знаем две точки на прямой, и поэтому можем использовать их для определения коэффициента.
Следует просто использовать формулу [mathrm{m}=frac{left(y_{2}-y_{1}right)}{left(x_{2}-x_{1}right)}].
Получаем: [m=frac{4-2}{2-(-1)}=frac{2}{3}].
Таким образом, коэффициент прямой равен [frac{2}{3}].
Нам известны две точки на прямой, поэтому мы можем использовать одну из них в формуле y — y1 = m(x — x1). Если мы возьмем точку (2, 4), то получим:
y — 4 = [frac{2}{3}](x — 2)
3y — 12 = 2x — 4
3y = 2x + 8
[y=frac{2}{3} x+frac{8}{3}]
Как и в предыдущих случаях, будет полезно найти общую формулу, которую можно использовать для примеров такого рода.
Итак, предположим, что общая прямая проходит через две точки [mathrm{A}left(x_{1}, y_{1}right) text { и } mathrm{B}left(x_{2}, y_{2}right)]. Пусть общая точка на прямой будет P(x, y).
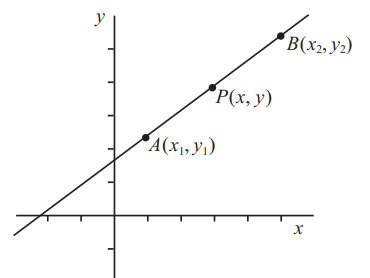
Теперь мы знаем, что коэффициент AP должен быть таким же, как коэффициент AB, так как все три точки лежат на одной прямой. Но коэффициент AP равен:
[mathrm{mAP}=frac{left(y_{2}-y_{1}right)}{left(x_{2}-x_{1}right)}]
тогда как коэффициент AB равен:
[mathrm{mAB}=frac{left(y_{2}-y_{1}right)}{left(x_{2}-x_{1}right)}]
Тогда mAP = mAB, поэтому мы имеем:
[ frac{left(y-y_{1}right)}{left(mathrm{x}-mathrm{x}_{1}right)}=frac{left(y_{2}-y_{1}right)}{left(mathrm{x}_{2}-mathrm{x}_{1}right)} ]
Эта формула довольно сложна, но ее легче запомнить, если все члены с участием y находятся на одной стороне, а все члены с участием x — на другой. Если мы будем преобразовывать эту формулу, сначала мы сможем получить:
[mathrm{y}-y_{1}=mathrm{x}-mathrm{x}_{1} frac{left(y_{2}-y_{1}right)}{left(mathrm{x}_{2}-mathrm{x}_{1}right)}]
а затем
[frac{left(y-y_{1}right)}{left(y_{2}-y_{1}right)}=frac{left(x-x_{1}right)}{left(x_{2}-x_{1}right)}]
Запомнить эту формулу вам поможет замечание, что закономерность в левой части, с участием y, такая же, как и с участием x в правой части.
Важно
Уравнение прямой, проходящей через две точки (x1, y1) и (x2, y2), имеет вид:
[frac{left(y-y_{1}right)}{left(y_{2}-y_{1}right)}=frac{left(x-x_{1}right)}{left(x_{2}-x_{1}right)}]
Теперь мы можем использовать эту формулу для решения примеров. Предположим, что мы хотим найти уравнение прямой, проходящей через две точки (1, -2) и (-3, 0).
Попробуем подставить в формулу и решить:
[frac{(y-(-2))}{(0-(-2))}=frac{(x-1)}{(-3-1)}]
[frac{y+2}{2}=frac{x-1}{-4}]
[ y+2=frac{x-1}{-2} ]
[ y+2=-frac{1}{2}(x-1) ]
-2y — 4 = x — 1
-2y = x + 3
[ y=-frac{1}{2} x-frac{1}{2} ]
Таким образом, прямая имеет коэффициент — [frac{1}{2}], а значение и точку пересечения с осью [y-frac{1}{2}].
Мы также можем преобразовать уравнение, чтобы получить 2y = -x — 3, или 2y + x + 3 = 0.
Упражнение 2
Найдите уравнение описанных ниже прямых (приведите уравнение в виде y = mx + c):
(1) проходящей через (4, 6) и (8, 26),
(2) проходящей через (1, 1) и (4, -8),
(3) проходящий через (3, 4) и (5, 4),
(4) проходящий через (0, 2) и (4, 0),
(5) проходящий через (-2, 3) и (2, -5).
Общее уравнение прямой прямой
Существует еще одна форма уравнения прямой, которая иногда бывает необходима. Это уравнение: ax + by + c = 0 .
Мы уже писали уравнения в этой форме для некоторых наших примеров. Мы можем увидеть некоторые особые случаи этого уравнения, установив либо a, либо b равными нулю.
Если a = 0, то получаются прямые с общим уравнением by + c = 0, то есть y = [-frac{c}{b}].
Эти прямые горизонтальны, то есть параллельны оси x.
Если b = 0, то получаются две прямые с общим уравнением ax + c = 0, следовательно есть x = [frac{c}{a}].
Эти прямые вертикальны, то есть параллельны оси y. Уравнение вертикальной прямой не может быть записано в виде y = mx + c. Уравнение ax + by + c = 0 является наиболее общим уравнением для прямой и может использоваться там, где другие формы уравнения не подходят.
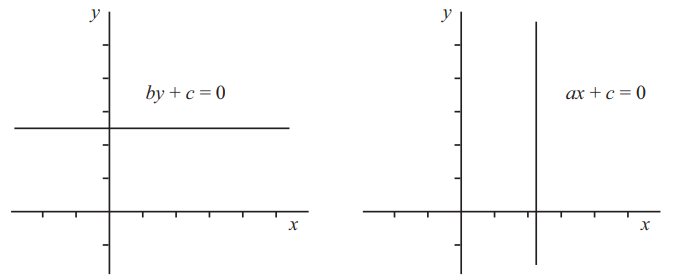
Важно
Общим уравнением прямой прямой является уравнение:ax + by + c = 0.
Если a = 0, то линия горизонтальна, а если b = 0, то линия вертикальна.
Упражнение 3
Найдите уравнение описанных ниже прямых (приведите уравнение в виде
ax + by + c = 0, где a, b и c — целые числа и a > 0):
(1) прямая из упражнения 2 (2)
(2) прямая в упражнении 2 (5)
(3) прямая в упражнении 3 (3)
(4) прямая в упражнении 4 (2)
(5) прямая в упражнении 4 (4)
(6) прямая в упражнении 4 (5)
(7)прямая , проходящая через (3, -2) и (3, 2)
(8) вертикальная прямая, проходящая через точку (0, [frac{2}{3}]).
Упражнение 1
(1) y = 3x + 1,
(2) y = -2x + 4,
(3) y =x — 3,
(4) y = 2,
(5) y = — x.
Упражнение 2
(1) y = 5x — 14,
(2) y = -3x + 4,
(3) y = 4,
(4) y = —x + 2,
(5) y = -2x — 1.
Упражнение 3
(1) 2x + y + 1 = 0,
(2) 3x + 4y — 2 = 0,
(3) 2x — 5y — 15 = 0,
(4) 3x + y — 4 = 0,
(5) x + 2y — 4 = 0,
(6) 2x + y + 1 = 0,
(7) x — 3 = 0,
(8) x = 0.
Как найти k и b по графику линейной функции?
В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):
В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.
Способ 1
Первый способ основывается на трех фактах:
Линейная функция пересекает ось (y) в точке (b).
Примеры:
Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.
Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).
Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac<4><4>=1,b=1). (f(x)=x+1).
Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:
Вычтем второе уравнение из первого, чтоб убрать (b):
(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
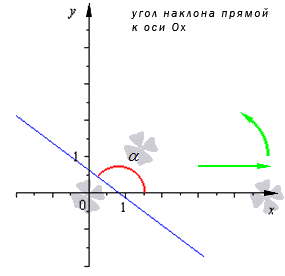
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
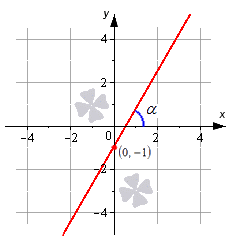
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Как найти коэффициенты уравнения прямой по графику
Неверно введено число.
Точки должны быть разными.
Уравнение прямой по двум точкам
Введите координаты точек:
Количество знаков после разделителя дроби в числах:
Общее уравнение прямой:
Теория
Уравнение прямой, проходящей через две заданные точки (x1,y1) и (x2,y2), имеет вид:
или в общем виде
Т.е. получили общее уравнение прямой линии на плоскости в декартовых координатах:
источники:
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-prjamoj-s-uglovym-koeffitsientom/
http://www.math.by/geometry/eqline.html
Загрузить PDF
Загрузить PDF
В двумерном пространстве две прямые пересекаются только в одной точке,[1]
задаваемой координатами (х,y). Так как обе прямые проходят через точку их пересечения, то координаты (х,y) должны удовлетворять обоим уравнениям, которые описывают эти прямые. Воспользовавшись некоторыми дополнительными навыками, вы сможете находить точки пересечения парабол и других квадратичных кривых.
-
1
Запишите уравнение каждой прямой, обособив переменную «у» на левой стороне уравнения. Другие члены уравнения должны размещаться на правой стороне уравнения. Возможно, данное вам уравнение вместо «у» будет содержать переменную f(x) или g(x); в этом случае обособьте такую переменную. Для обособления переменной выполните соответствующие математические операции на обеих сторонах уравнения.
-
2
Приравняйте выражения, расположенные с правой стороны каждого уравнения. Наша задача — найти точку пересечения обеих прямых, то есть точку, координаты (х,у) которой удовлетворяют обоим уравнениям. Так как на левой стороне каждого уравнения находится переменная «у», то выражения, расположенные с правой стороны каждого уравнения, можно приравнять. Запишите новое уравнение.
-
3
Найдите значение переменной «х». Новое уравнение содержит только одну переменную «х». Для нахождения «х» обособьте эту переменную на левой стороне уравнения, выполнив соответствующие математические операции на обеих сторонах уравнения. Вы должны получить уравнение вида х = __ (если это невозможно, перейдите в конец этого раздела).
-
4
Используйте найденное значение переменной «х» для вычисления значения переменной «у». Для этого подставьте найденное значение «х» в уравнение (любое) прямой.
-
5
Проверьте ответ. Для этого подставьте значение «х» в другое уравнение прямой и найдите значение «у». Если вы получите разные значение «у», проверьте правильность ваших вычислений.
-
6
Запишите координаты (х,у). Вычислив значения «х» и «у», вы нашли координаты точки пересечения двух прямых. Запишите координаты точки пересечения в виде (х,у).
-
7
Вычисления в особых случаях. В некоторых случаях значение переменной «х» найти нельзя. Но это не значит, что вы допустили ошибку. Особый случай имеет место при выполнении одного из следующих условий:
Реклама
-
1
Определение квадратичной функции. В квадратичной функции одна или несколько переменных имеют вторую степень (но не выше), например,
или
. Графиками квадратичных функций являются кривые, которые могут не пересекаться или пересекаться в одной или двух точках. В этом разделе мы расскажем вам, как найти точку или точки пересечения квадратичных кривых.
- Если уравнение включает выражение в скобках, раскройте их, чтобы удостовериться, что функция является квадратичной. Например, функция
является квадратичной, так как, раскрыв скобки, вы получите
- Функция, описывающая окружность, включает как
, так и
.[2]
[3]
Если у вас возникли проблемы при решении задач с такой функцией, перейдите в раздел «Советы».
- Если уравнение включает выражение в скобках, раскройте их, чтобы удостовериться, что функция является квадратичной. Например, функция
-
2
Перепишите каждое уравнение, обособив переменную «у» на левой стороне уравнения. Другие члены уравнения должны размещаться на правой стороне уравнения.
-
3
Приравняйте выражения, расположенные с правой стороны каждого уравнения. Так как на левой стороне каждого уравнения находится переменная «у», то выражения, расположенные с правой стороны каждого уравнения, можно приравнять.
-
4
Перенесите все члены полученного уравнения на его левую сторону, а на правой стороне запишите 0. Для этого выполните базовые математические операции. Это позволит вам решить полученное уравнение.
-
5
-
6
Не забудьте про вторую точку пересечения двух графиков. В спешке можно забыть про вторую точку пересечения. Вот как найти координаты «х» двух точек пересечения:
-
7
Графики пересекаются в одной точке или вообще не пересекаются. Такие ситуации имеют место при соблюдении следующих условий:
-
8
Подставьте найденное значение переменной «х» в уравнение (любое) кривой. Так вы найдете значение переменной «у». Если у вас есть два значения переменной «х», проделайте описанный процесс с обоими значениями «х».
-
9
Запишите координаты точки пересечения в виде (х,у). Вычислив значения «х» и «у», вы нашли координаты точки пересечения двух графиков. Если вы определили по два значения «х» и «у», запишите две пары координат, не перепутав соответствующие значения «х» и «у».
Реклама
Советы
- Функция, описывающая окружность, включает как
, так и
. Для нахождения точки (точек) пересечения окружности и прямой вычислите «х», используя линейное уравнение.[4]
Затем подставьте найденное значение «х» в функцию, описывающую окружность, и вы получите простое квадратное уравнение, которое может не иметь решения или иметь одно или два решения. - Окружность и кривая (квадратичная или иная) могут не пересекаться или пересекаться в одной, двух, трех, четырех точках. В этом случае необходимо найти значение x2 (а не «х»), а затем подставить его во вторую функцию. Вычислив «у», вы получите одно или два решения или вообще не получите решений. Теперь подставьте найденное значение «у» в одну из двух функций и найдите значение «х». В этом случае вы получите одно или два решения или вообще не получите решений.
Реклама
Об этой статье
Эту страницу просматривали 94 840 раз.
Была ли эта статья полезной?
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
-
Общее уравнение
прямой
Если на плоскости
введена ПДСК, то всякое уравнение первой
степени относительно текущих координат
и
, (5)
где
и
одновременно не равны нулю, определяет
прямую.
Верно и обратное
утверждение: в ПДСК любая прямая может
быть задана уравнением первой степени
вида (5).
Уравнение вида
(5) называется общим
уравнением прямой.
Частные случаи
уравнения (5) приведены в следующей
таблице.
|
Значении |
Уравнение прямой |
Положение прямой |
|
|
1 |
|
|
Прямая |
|
2 |
|
|
Прямая |
|
3 |
|
|
Прямая |
|
4 |
|
|
Прямая |
|
5 |
|
|
Прямая |
-
Уравнение прямой
с угловым коэффициентом и начальной
ординатой.
У
наклона прямой к оси
называется наименьший угол
,
на который нужно повернуть против
часовой стрелки ось абсцисс до её
совпадения с данной прямой (Рис.6).
Направление любой прямой характеризуется
еёугловым
коэффициентом
,
который определяется как тангенс угла
наклонаэтой прямой, т. е.
.
Исключение
составляет только прямая, перпендикулярная
оси
,
которая не имеет углового коэффициента.
Уравнение
прямой, имеющей угловой коэффициент
и пересекающей ось
в точке, ордината которой равна
(начальная ордината),
записывается в виде
.
-
Уравнение прямой
в отрезках
Уравнением
прямой в отрезках
называется уравнение вида
, (6)
где
и
соответственно
длины отрезков, отсекаемых прямой на
координатных осях, взятые с определёнными
знаками.
-
Уравнение прямой,
проходящей через данную точку в данном
направлении. Пучок прямых
Уравнение
прямой, проходящей через данную точку
и имеющей угловой коэффициент
записывается в виде
. (7)
Пучком прямых
называется совокупность прямых плоскости,
проходящих через одну и точку
центр
пучка. Если известны координаты центра
пучка, то уравнение (8) можно рассматривать
как уравнение пучка, поскольку любая
прямая пучка может быть получена из
уравнения (8) при соответствующем значении
углового коэффициента(исключение составляет прямая, которая
параллельна осиеё
уравнение).
Если известны
общие уравнения двух прямых, принадлежащих
пучку
и
(образующих пучка), то уравнении любой
прямой из этого пучка можно записать в
виде
. (8)
-
Уравнение прямой,
проходящей через две точки
Уравнение
прямой, проходящей через две данные
точки
и
,
имеет вид
.
Если точки
и
определяют прямую, параллельную оси
или оси
,
то уравнение такой прямой записывается
соответственно в виде
или
.
-
Взаимное
расположение двух прямых. Угол между
прямыми. Условие параллельности. Условие
перпендикулярности
Взаимное расположение
двух прямых, заданных общими уравнениями
и
,
представлено в
следующей таблице.
-
Взаимное
расположение прямыхУсловие
Пересечение
Параллельность
Совпадение
Под углом
между двумя прямыми
понимается один из смежных углов,
образованных при их пересечении. Острый
угол между прямыми
м
,
определяется формулой
.
Заметим, что если
хотя бы одна из данных прямых параллельна
оси
,
то формула (11) не имеет смысла, поэтому
будем использовать общие уравнения
прямых
и
.
формула (11) примет
вид
.
Условие параллельности:
или
.
Условие
перпендикулярности:
или
.
-
Нормальное
уравнение прямой. Расстояние точки от
прямой. Уравнения биссектрис
Нормальное
уравнение прямой
имеет вид
,
где
длина
перпендикуляра (нормали), опущенного
из начала координат на прямую,угол
наклона этого перпендикуляра к оси.
Чтобы привести общее уравнение прямойк нормальному виду, нужно обе части
равенства (12) умножить нанормирующий
множитель
,
взятый со знаком противоположным знаку
свободного члена.
Расстояние
точки
от прямой
найдём по формулам
или
.
(9)
Уравнение
биссектрис углов между прямыми
и
:

Задача 16.
Дана прямая
.
Составить уравнение прямой, проходящей
через точкупараллельно данной прямой.
Решение.
По условию параллельности прямых
.
Для решения задачи будем использовать
уравнение прямой, проходящей через
данную точкув данном направлении (8):
.
Найдём угловой
коэффициент данной прямой. Для этого
от общего уравнения прямой (5) перейдём
к уравнению с угловым коэффициентом
(6) (выразим
через
):
.
Следовательно,
.
Тогда
.
Задача 17.
Найти точку
,
симметричную точке,
относительно прямой.
Решение.
Для того, чтобы найти точку симметричную
точке
относительно прямой
(Рис.7) необходимо:
1) опустить из точки
на прямую
перпендикуляр,
2) найти основание
этого перпендикуляраточку
,
3) на продолжении
перпендикуляра отложить отрезок
.
Итак, запишем
уравнение прямой, проходящей через
точку
перпендикулярно данной прямой. Для
этого воспользуемся уравнением прямой,
проходящей через данную точку в данном
направлении (8):
.
Подставим координаты
точки
:
. (11)
Угловой коэффициент
найдём из условия перпендикулярности
прямых:
.
Угловой коэффициент
данной прямой
,
следовательно,
угловой коэффициент перпендикулярной
прямой
.
Подставим его в
уравнение (11):
.
Далее, найдём точку
точку
пересечения данной прямой и ей
перпендикулярной прямой. Так как точкапринадлежит обеим прямым, то её координаты
удовлетворяют их уравнениям. Значит,
для отыскания координат точки пересечения
требуется решить систему уравнений,
составленную из уравнений этих прямых:
Решение системы
,
,
т. е..
Точка
является серединой отрезка
,
тогда из формул (4):
,
,
найдём координаты
точки
:
,
.
Таким образом,
искомая точка
.
Задача 18.Составить
уравнение прямой, которая проходит
через точку
и отсекает от координатного угла
треугольник с площадью, равной 150 кв.ед.
(Рис.8).
Решение.
Для решения задачи будем использовать
уравнение прямой «в отрезках» (7):
.
(12)
Так как точка
лежит на искомой прямой, то её координаты
должны удовлетворять уравнению этой
прямой:
.
Площадь треугольника,
отсекаемого прямой от координатного
угла вычисляется по формуле:
(записан модуль,
так как
и
могут быть отрицательными).
Таким образом,
получили систему для отыскания параметров
и
:
Эта система
равносильна двум системам:
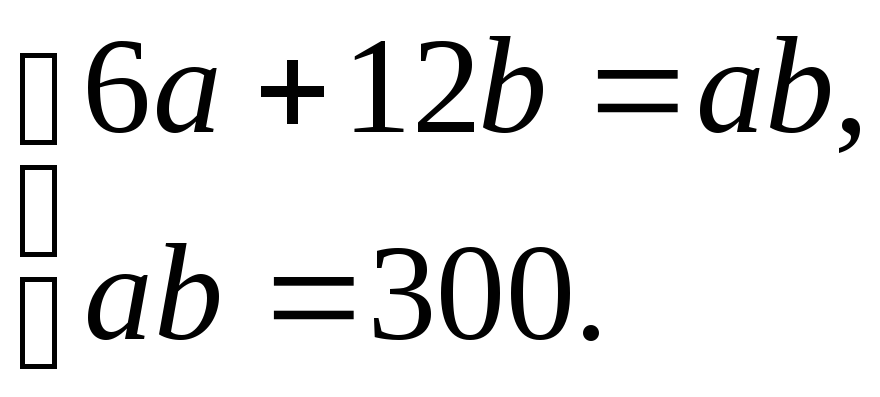
Решение первой
системы
,
и
,
.
Решение второй
системы
,
и
,
.
Подставим найденные
значения в уравнение (12):
,
,
,
.
Запишем общие
уравнения этих прямых:
,
,
,
.
Задача 19.
Вычислить расстояние между параллельными
прямыми
и
.
Решение.
Расстояние между параллельными прямыми
равно расстоянию произвольной точки
одной прямой до второй прямой.
Выберем на прямой
точку
произвольно, следовательно, можно задать
одну координату, т. е. например,
тогда.
Теперь найдём
расстояние точки
до прямой
по формуле (10):

Т
Рис. 1.8.
аким образом, расстояние между
данными параллельными прямыми равно.
Задача 20.
Найти уравнение прямой, проходящей
через точку пересечения прямых
и
(не находя точки пересечения) и
-
проходящей через
точку
;
-
параллельной
прямой
.
Решение.
1) Запишем уравнение пучка прямых с
известными образующими (9):
.
Тогда искомая
прямая имеет уравнение
. (13)
Требуется найти
такие значения
и
,
при которых прямая пучка пройдёт через
точку,
т. е. её координаты должны удовлетворять
уравнению (13):
.
Отсюда
.
Подставим найденное
в уравнение (13) и после упрощении получим
искомую прямую:
.
-
По условию задачи
искомая прямая
параллельна прямой
.
Воспользуемся
условием параллельности прямых:
.
Найдём угловые коэффициенты прямыхи
.
Имеем, что,
.
Следовательно,
.
Подставим найденное
значение
в уравнение (13) и упростим, получим
уравнение искомой прямой.
Задачи для
самостоятельного решения.
Задача 21.
Составить уравнение прямой, проходящей
через точки
и
:
1) с угловым коэффициентом; 2) общее;
3)
«в отрезках».
Задача 22.
Составить уравнение прямой, которая
проходит через точку
и образует с осью
угол
,
если 1),
;
2),
.
Задача 23.
Написать уравнения сторон ромба с
диагоналями 10 см и 6 см, приняв большую
диагональ за ось
,
а меньшуюза ось
.
Задача 24.
Равносторонний треугольник
со стороной, равной 2 единицам, расположен
так, как показано на рисунке 9. составить
уравнения его сторон.
Задача 25.
Через точку
провести прямую, отсекающую на
положительных полуосях координат равные
отрезки.
Задача 26.
Найти площадь треугольника, который
отсекает от координатного угла прямая:
1)
;
2).
Задача 27.Написать
уравнение прямой, проходящей через
точку
и отсекающей от координатного угла
треугольник площадью, равной,
если
1)
,
кв. ед.; 2)
,
кв. ед.
Задача 28. Даны
вершины треугольника
.
Найти уравнение средней линии, параллельной
стороне,
если
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #