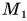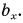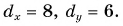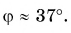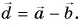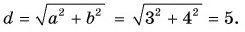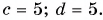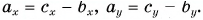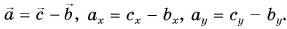В математике существуют два определения:
1) геометрическая проекция вектора — вектор;
2) проекция вектора на ось — число.
Геометрическая проекция вектора — это вектор, который можно получить, если провести перпендикуляры от концов вектора до выбранной оси. Проекция начала вектора соответствует началу геометрической проекции, а проекция конца вектора соответствует концу геометрической проекции.
Ваш браузер не поддерживает HTML5 видео
Для вектора
v→
геометрическая проекция на оси (t) — это вектор
vt→
.
Для вектора
n→
геометрическая проекция на оси (y) — это вектор
ny→
.
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
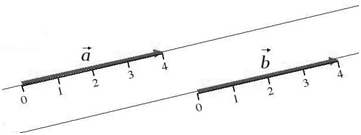
ax=4bx=−3
Если длина вектора
a→
равна
a→
и
α
— это острый угол, созданный вектором и осью (x), то скалярная проекция вектора вычисляется по формуле:
ax=a→⋅cosα
.
Знак проекции вектора выбирается в зависимости от направления оси.
На рисунке видно, что эту формулу можно получить из соотношения в прямоугольном треугольнике:
.
Обрати внимание!
Если вектор и ось проекций параллельны, то скалярная проекция на этой оси — число, которое равно длине вектора, если направления вектора и оси совпадают, или число, противоположное длине вектора, если направления вектора и оси — противоположные.
Если вектор и ось проекций перпендикулярны, то проекция вектора на этой оси равна (0).
at=3bt=−5ct=0dt=0
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Для понятия проекции вектора на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
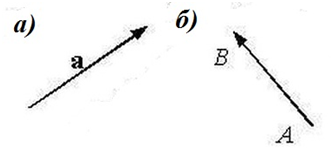
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
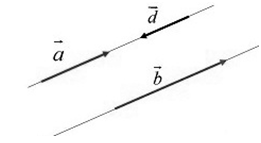
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
«Проекция вектора на ось. Как найти проекцию вектора» 👇
Определение 4
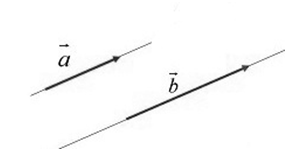
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
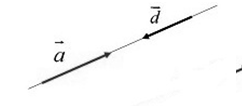
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A’$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B’$ — конец искомого вектора. Вектор $overline{A’B’}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
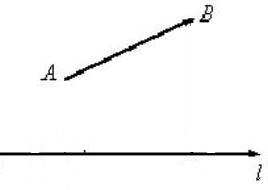
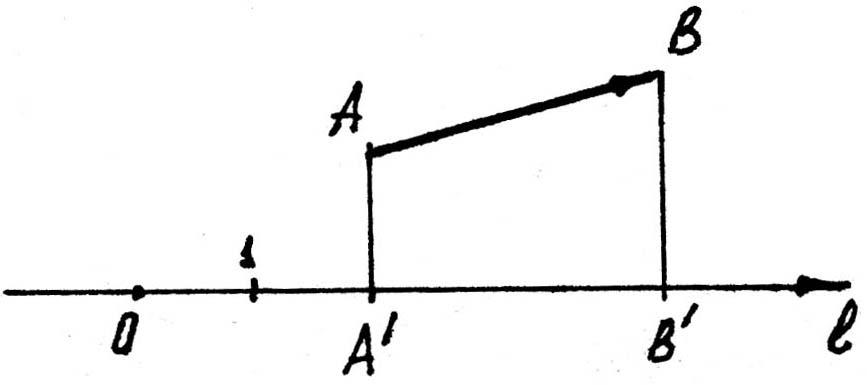
Постройте геометрическую проекцию $overline{AB}$ на ось $l$, изображенные на рисунке 6.
Решение.
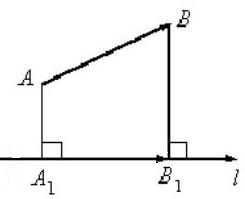
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A’$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B’$ (рис. 7).
Полученный на оси $l$ вектор $overline{A’B’}$ и будет искомой геометрической проекцией.
Замечание 1
Заметим, что если угол между вектором и осью острый, то проекция сонаправлена с осью, а если тупой, то проекция противоположно направлена с осью.
Числовая проекция
Как мы уже знаем, результатом алгебраической проекции будет неотрицательное действительное число.
Определение 9
Числовой (алгебраической) проекцией на ось будем называть неотрицательное число, равное длине вектора геометрической проекции.
Рассмотрим это понятие на примере задачи:
Пример 2
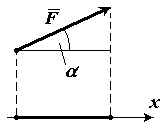
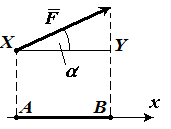
Найти числовую проекцию вектора $overline{F} на сонаправленную ему ось $x$, если угол между ними равняется $α$ (рис. 8). (рис. 8).
Решение.
Введем на рисунке следующие обозначения:
Видим, что длина вектора геометрической проекции, равняется длине $XY$. Из определения косинуса получим, что
$XY=|overline{F}|cosα$
где $|overline{F}|$ — длина вектора $overline{F}$. Это и будет искомая алгебраическая проекция на ось.
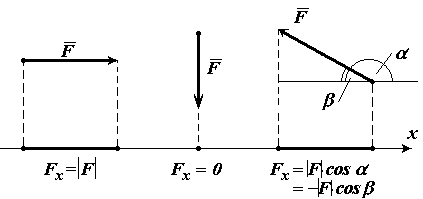
Другие случаи можете видеть на рисунке 9.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Преподаватель который помогает студентам и школьникам в учёбе.
Проекция вектора на ось в физике — формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 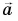
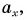
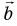
Проекция 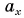
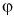
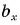
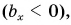
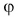
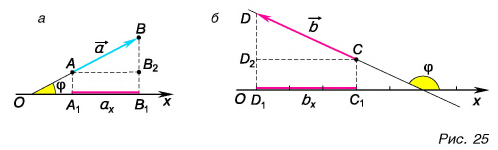
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 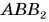
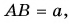
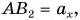
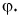
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
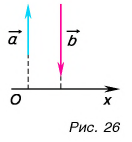
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 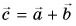
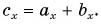
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 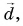
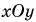
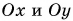
Модуль вектора 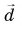
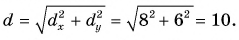
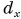
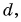
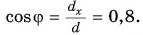
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 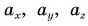
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
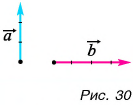
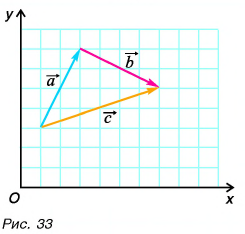
1. Определите сумму и разность взаимно перпендикулярных векторов 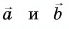
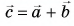
Решение
Сумму векторов 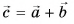
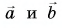
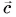
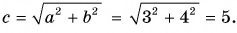
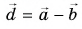
Модуль вектора 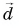
Ответ:
- Заказать решение задач по физике
Пример №2
Выразите вектор 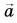
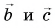
Решение
По правилу треугольника находим: 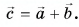
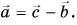
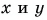
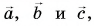
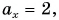
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
Проекция вектора на ось
Ориентированной
осью
называется
прямая, на которой закреплена точка —
начало отсчета, выбрана единица длины
и направление отсчета.
Рис. 6
Проекцией
вектора
на ось
называется величина, численно равная
длине отрезка
между основаниями перпендикуляров,
опущенных из точек А
и В
на l.
Эта длина берется со знаком плюс,
если направление от
к
совпадает с направлением оси l
и минус
в противном
случае (рис. 6). Аналогично определяется
проекция одного вектора на другой.
Углом
между осью и вектором
называется угол,
на который
нужно повернуть ось до совмещения с
вектором кратчайшим образом (так чтобы
их стрелки совпали). Из такого определения
следует, что
.
Свойства
проекции вектора на ось.
1.
Проекция
равна нулю тогда и только тогда, когда
вектор перпендикулярен оси (говорят,
вектор ортогонален
оси).
2.
При параллельном переносе вектора его
проекция не меняется.
3.
Проекция вектора на ось равна произведению
длины вектора на
косинус
угла между вектором и осью.

Рис.
7 Рис. 8
В
этой формуле знак проекции регулируется
знаком косинуса:
—
если
острый угол (рис. 7), то
и
;
—
если
тупой угол (рис. 8), то
и
.
4. Скалярный
множитель можно выносить за знак проекции
.
5.
Проекция суммы векторов равна сумме
проекций слагаемых
.
Декартова прямоугольная система координат
Базис
называется ортонормированным,
если его векторы попарно ортогональны
и по длине равны единицам.
Система
координат, базис которой ортонормирован,
называется декартовой
прямоугольной системой координат.
Рис.
9
Б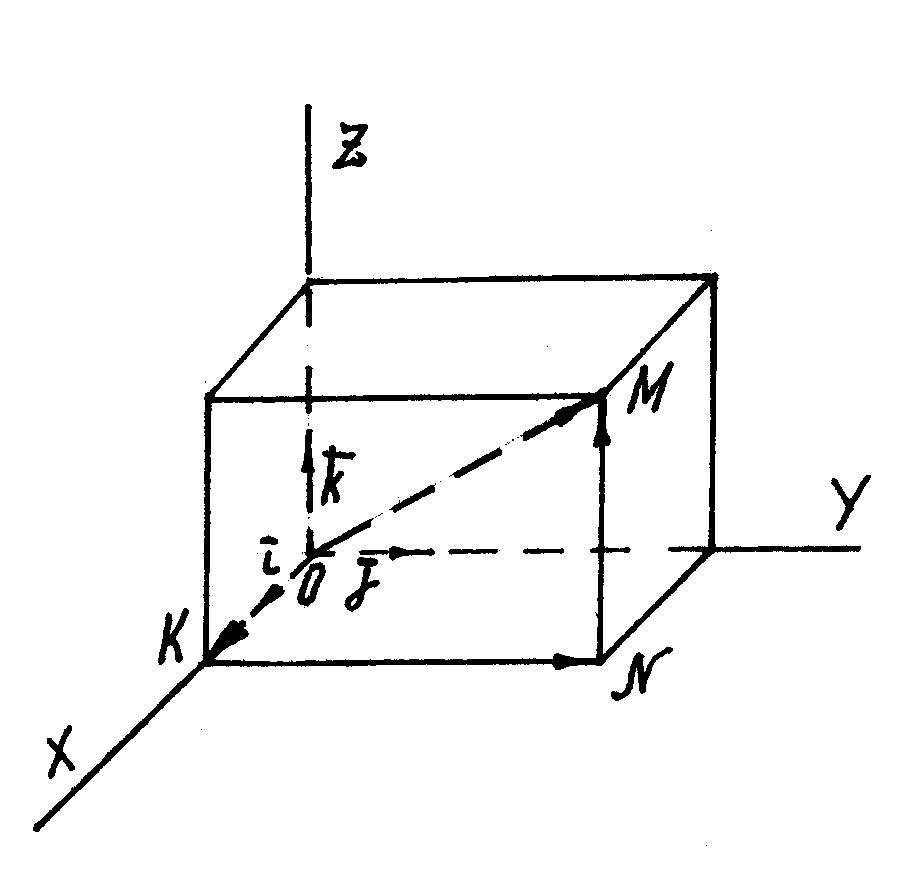
векторы такой системы называются ортами
и обозначаются соответственно
,
,
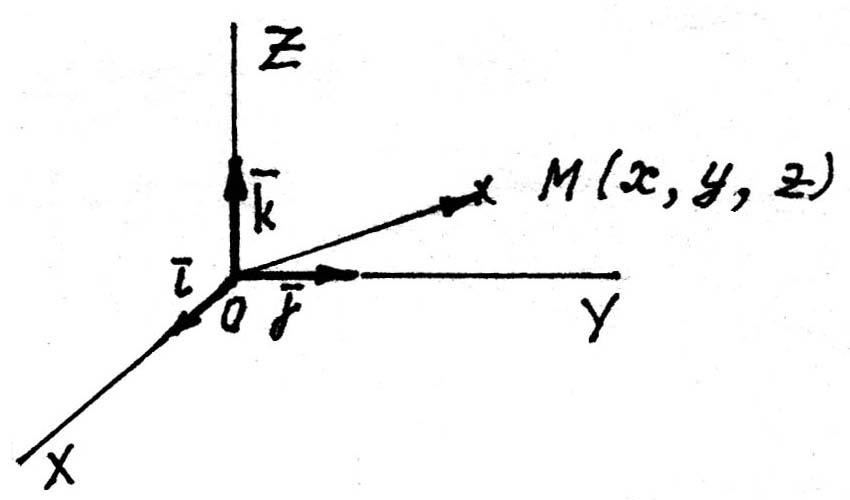
(рис. 9). Оси идущие в направлении базисных
векторов соответственно OX
– ось абсцисс,
OY
– ось ординат,
OZ
– ось
аппликат. Система координат называется
правой,
если кратчайший поворот первого базисного
вектора
до совмещения со вторым базисным вектором
смотрится с конца третьего базисного
вектора
происходящим против хода часовой
стрелки. В противном случае имеем левую
систему координат. Нетрудно видеть
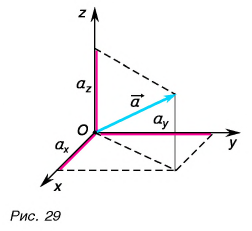
(рис. 10), что координатами вектора
,
равно как и точки М,
являются проекции
на координатные оси.
Рис.
10
Тогда
,
аналогично
,
.
Теперь радиус-вектор
или
,
где
–
координаты
радиус-вектора
,
а
,
,
— составляющие или компоненты
этого вектора.
.
Поскольку,
например,
,
а
.
Теперь
.
,
где
— угол между вектором
и осью OX.
Теперь
,
аналогично
,
,
где
и
— углы между
и осями OY
и OZ
соответственно.
Приведенные косинусы называются
направляющими
косинусами
радиуса вектора
.
Если
—
произвольный вектор и X,
Y,
Z
– его проекции
на оси, то перенося начало
в точку О,
будем иметь
,
,
,
,
.
Если
вектор задан координатами начала
и конца
,
то
и расстояние
между точками А
и В будет
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§ 3.
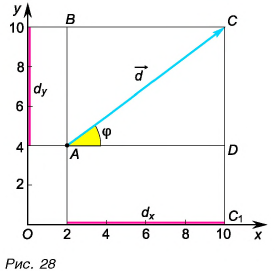
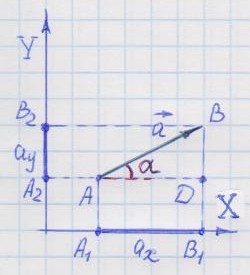
Проекции вектора на оси координат
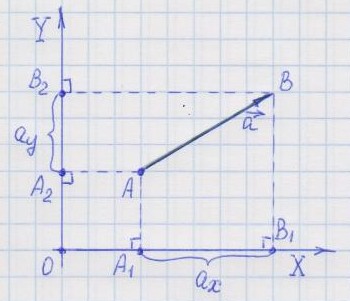
1.
Нахождение проекций геометрически.
— вектор
— проекция вектора
на ось OX
— проекция вектора
на ось OY
Определение
1.
Проекцией вектора на какую-либо ось
координат называется взятое со
знаком «плюс» или «минус»
число, соответствующее длине отрезка,
расположенного между основаниями
перпендикуляров, опущенных из начала
и конца вектора на ось координат.
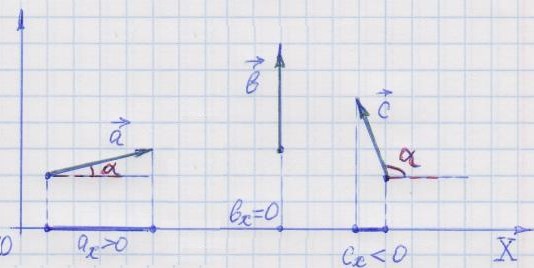
Знак
проекции определяется так. Если при
движении вдоль оси координат
происходит перемещение от точки
проекции начала вектора к точке
проекции конца вектора в положительном
направлении оси, то проекция вектора
считается положительной. Если же —
противоположно оси, то проекция
считается отрицательной.
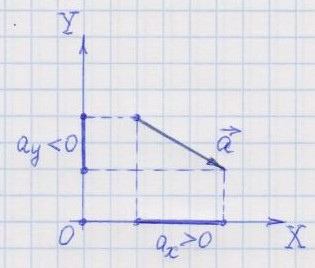
По
рисунку видно, что если вектор
ориентирован как-то противоположно оси
координат, то его проекция на эту ось
отрицательна. Если вектор ориентирован
как-то в положительном направлении оси
координат, то его проекция на эту ось
положительна.
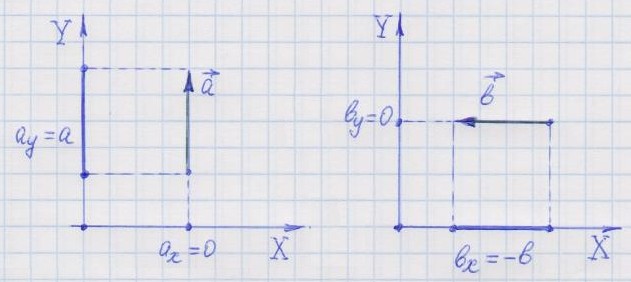
Если
вектор перпендикулярен оси координат,
то его проекция на эту ось равна нулю.
Если вектор сонаправлен с осью,
то его проекция на эту ось равна модулю
вектора.
Если вектор противоположно
направлен оси координат, то его
проекция на эту ось по абсолютной
величине равна модулю вектора, взятому
со знаком минус.
2. Наиболее
общее определение проекции.
Из прямоугольного
треугольника ABD:.
Определение
2. Проекцией вектора на какую-либо
ось координат называется число,
равное произведению модуля вектора и
косинуса угла, образованного
вектором с положительным
направлением оси координат.
Знак
проекции определяется знаком косинуса
угла, образованного вектором с
положительным направлением оси.
Если угол острый, то косинус
имеет положительный знак, и проекции —
положительны. Для тупых углов косинус
имеет отрицательный знак, поэтому в
таких случаях проекции на ось
отрицательны.
—
поэтому для векторов, перпендикулярных
к оси, проекция равна нулю.