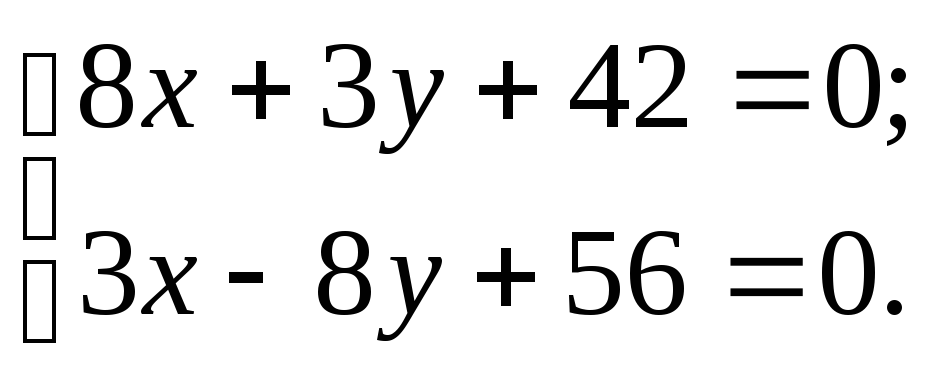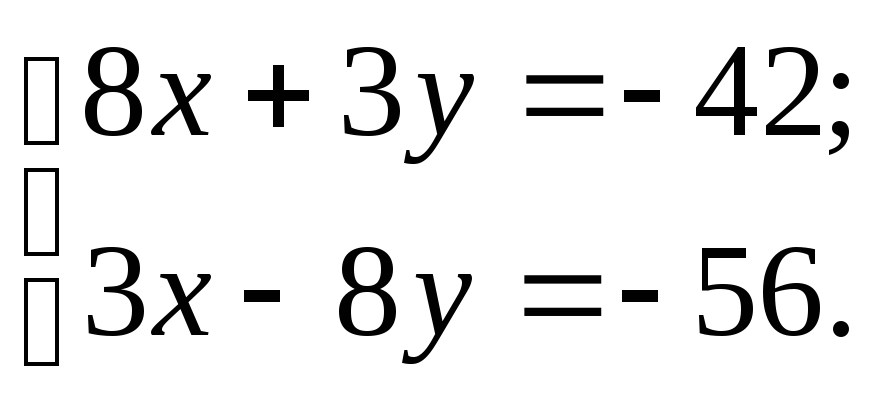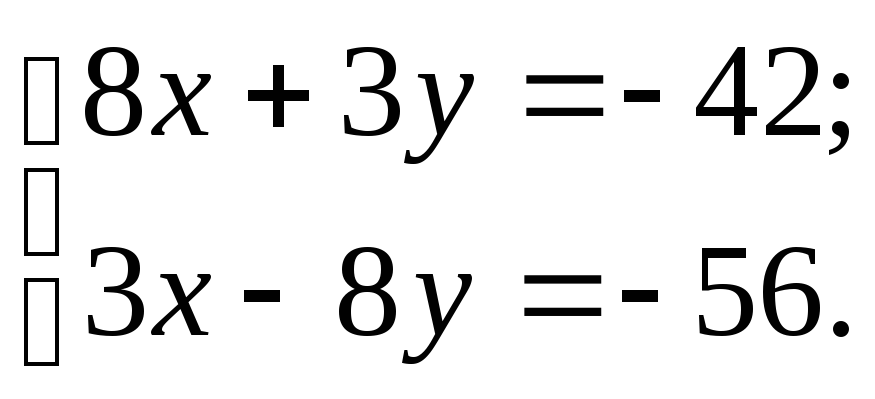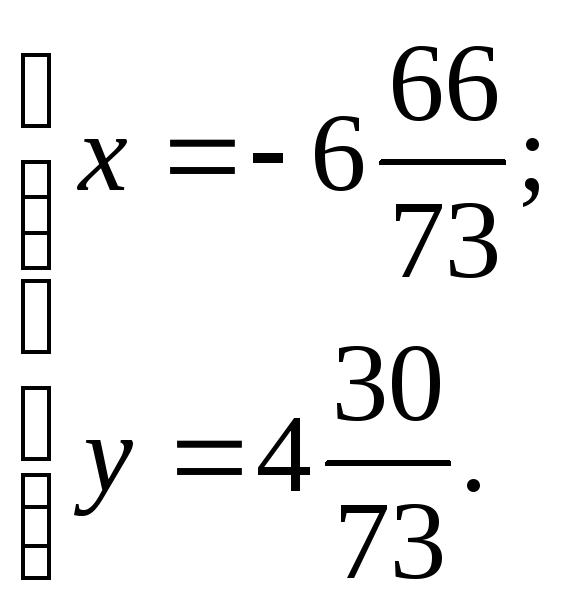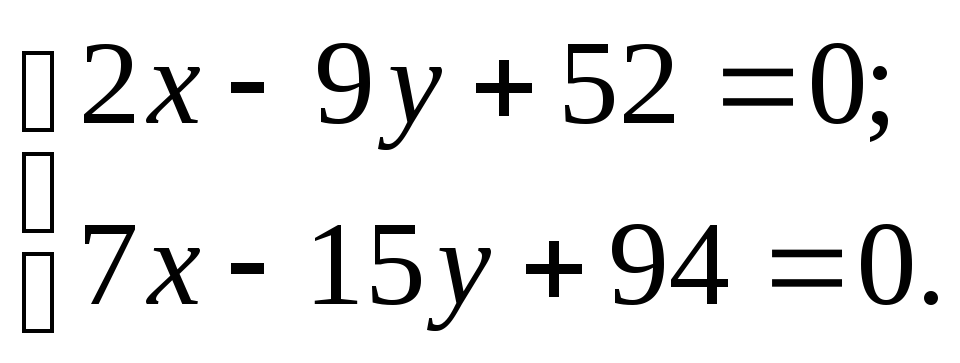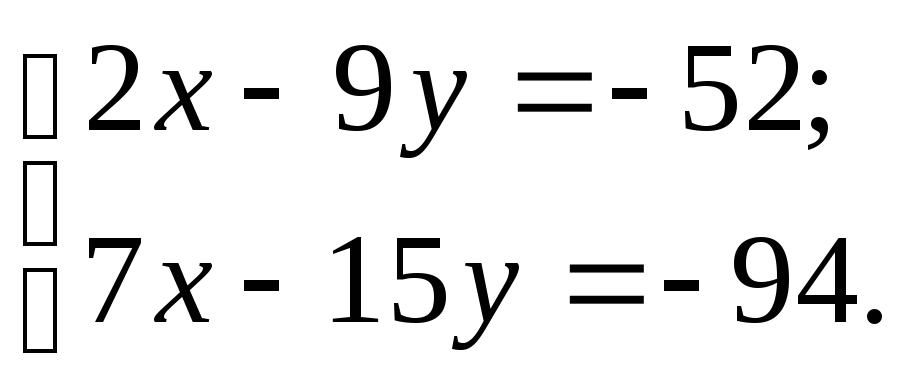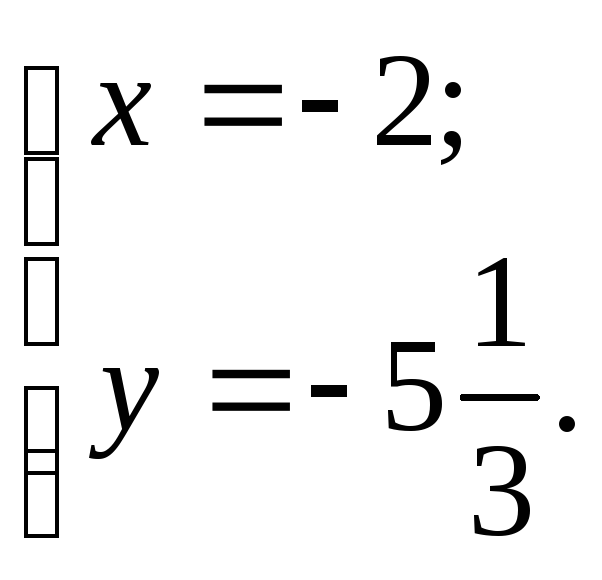Как найти проекцию данной точки на прямую - Исправление недочетов и поиск решений вместе с Examum.ru

Проекция точки на прямую онлайн

С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Проекция точки на прямую − теория, примеры и решения

Рассмотрим эту задачу в двухмерном и трехмерном пространствах.

1. Пусть в двухмерном пространстве задана точка M₀(x₀, y₀) и прямая L:

где q=(m,p) направляющий вектор прямой L.

Найдем проекцию точки M₀ на прямую (1)(Рис.1).

Алгоритм нахождения проекции точки на прямую L содержит следующие шаги:

построить прямую L₁, проходящую через точку M₀ и перпендикулярную прямой L,
найти пересечение прямых L и L₁(точка M₁)

Уравнение прямой, проходящей через точку M₀(x₀, y₀) имеет следующий вид:

где n=(A,B) нормальный вектор прямой L₁.

Как видно из рисунка Рис.1, для того, чтобы прямая L₁ была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L₁, поэтому в качестве нормального вектора прямой L₁ достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L₁, представленной уравнением (2) можно записать так:

Откроем скобки

Для нахождения точки пересечения прямых L и L₁, которая и будет проекцией точки M₀ на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M₁(x₁, y₁).

Найдем точку пересечения прямых L и L₁ другим методом.

Выведем параметрическое уравнение прямой (1):

Подставим значения x и y в (4):

Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L₁(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M₀ на прямую L:

где x₁=mt’+x’, y₁=pt’+y’.

Пример 1. Найти проекцию точки M₀(1, 3) на прямую

Решение.

Направляющий вектор прямой (6) имеет вид:

Т.е. m=4, p=5. Из уравнения прямой (6) видно, что она проходит через точку M’ (x’, y’)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x’=2, y’=-3. Подставим значения m, p, x₀, y₀, x’, y’ в (5′):

Подставляя значение t в (5), получим:

Ответ:

Проекцией точки M₀(1, 3) на прямую (6) является точка:

2. Пусть в трехмерном пространстве задана точка M₀(x₀, y₀, z₀) и прямая L:

где q=(m, p, l) направляющий вектор прямой L.

Найдем проекцию точки M₀ на прямую (7)(Рис.2).

Нахождение проекцию точки на прямую L содержит следующие шаги:

построить плоскость α, проходящую через точку M₀ и перпендикулярную прямой L,
найти пересечение плоскости α и прямой L(точка M₁)

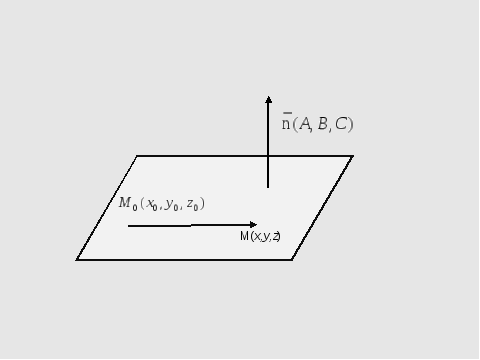
Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) имеет следующий вид:

где n=(A,B,C) нормальный вектор плоскости α.

Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (8) можно записать так:

Откроем скобки

Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M₀ на прямую L, выведем параметрическое уравнение прямой (7):

Подставим значения x и y в (9):

Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (9). Следовательно, подставляя значение t’ в (10) получим координаты проекции точки M₀ на прямую L:

где x₁=mt’+x’, y₁=pt’+y’, z₁=lt’+z’.

Пример 2. Найти проекцию точки M₀(3, −1, −2) на прямую

Решение.

Направляющий вектор прямой (11) имеет вид:

Т.е. m=2, p=3, l=−4. Из уравнения прямой (11) видно, что она проходит через точку M’ (x’, y’, z’)=(2, 1, 1)(в этом легко убедится − подставляя эти значения в (11) получим тождество 0=0=0), т.е. x’=2, y’=1, z’=1. Подставим значения m, p, l x₀, y₀, z₀ x’, y’, z’ в (10′):

Подставляя значение t=t’ в (10), получим:

Ответ:

Проекцией точки M₀(3, −1, −2) на прямую (11) является точка:

Источник

Проекция точки на прямую

Пусть
необходимо спроектировать точку

на прямую

Ах+Ву+С=0. проекцией точки на прямую
является основание перпендикуляра,
опущенного из точки на прямую. Нормалью
к данной прямой является вектор
.
Составим уравнение проецирующей прямой.
Она проходит через точку

и параллельна вектору
.
Подставив координаты точки и вектора
в каноническое уравнение прямой
,
получим:.
Теперь необходимо найти координаты
точки пересечения данной прямой и
проектирующей, для чего объединим их в
систему: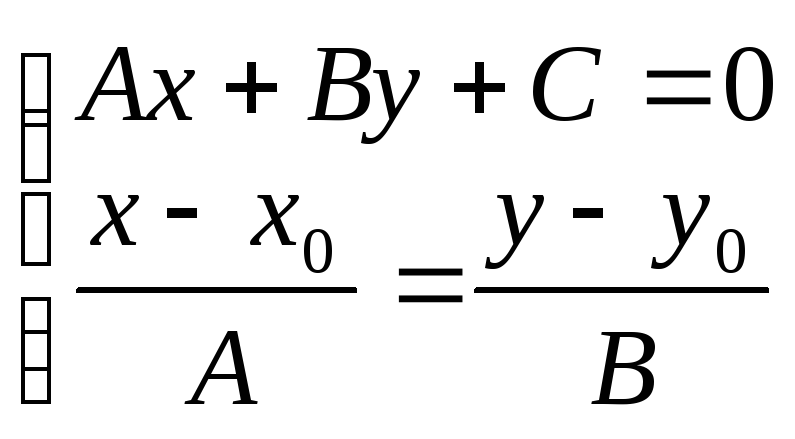решение
этой системы есть координаты точки,
являющейся проекцией точки

на прямую

Пример:
Даны вершины треугольника
:
;
;.
Найти:

1)
уравнение высоты, опущенной из вершины
;

2)
точку пересечения высоты

и стороны
;

3)
точку пересечения медиан треугольника
.

Решение:
1) Составим уравнение высоты
,
проходящей через точку
перпендикулярно вектору
:

;

Ответ:
.

2)
Составим уравнение стороны
:

Найдем
точку пересечения высоты

и стороны
.Обозначим
эту точку N,
она является проекцией точки А на
сторону ВС. Для нахождения точки N,
решим следующую систему уравнений:

Ответ:
N.

3)
Найдем середину стороны
:

Составим
уравнение прямой проходящей через точку

и точку М:

Найдем
середину стороны
:

Составим
уравнение прямой проходящей через точку

и точку N:

Найдем точку
О пересечения найденных медиан:

Ответ:
О.

Плоскость Общее уравнение плоскости

Алгебраическое
уравнение первой степени в пространстве
определяет плоскость. Общее уравнение
плоскости можно записать в виде:

Ax+
By+
Cz+
D=0

Любую плоскость
можно представить в виде такого уравнение
единственным способом. с точностью до
коэффициента (т. е. при умножении уравнения
на число, полученное уравнение задает
ту же плоскость ) Плоскость в пространстве
можно задать различными способами,
рассмотрим некоторые из них:

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Опр.:
Нормалью к плоскости называется вектор,
перпендикулярный к данной плоскости.

Пусть
необходимо составить уравнение плоскости,
проходящей через заданную точку
и
перпендикулярной вектору
.

Предположим,
что такая плоскость построена, возьмем
на ней произвольную точку М(x,y,z)
. Составим вектор
.
Вектор

перпендикулярен вектору
,
следовательно, их скалярное произведение
равно нулю:
,
это условие имеет вид::

Данный
способ задания плоскости называется
плоскость по точке М(
и нормали
.
Имея уравнение плоскости в общем виде:
Ax+
By+
Cz+
D=0,
можно выписать нормаль к плоскости
.

Пример:
Составить уравнение плоскости, проходящей
через точку А(1,2,-3), параллельно плоскости
3x-4y+5z-2=0

Решение:
Выпишем нормаль к плоскости, т.е. вектор
перпендикулярный плоскости:
.
Так как необходимо построить плоскость
параллельную данной, то можно использовать
вектор

в качестве нормали к искомой плоскости.
Составляем уравнение плоскости по точке
А и нормали
:

после преобразования получим:
3x-4y+5z+20=0

Ответ:
3x-4y+5z+20=0.

Соседние файлы в предмете Высшая математика

Источник

Содержание

— Что такое ортогональная проекция точки на прямую?
— Что такое проекция точки на ось?
— Что такое ортогональная проекция точки на плоскость?
— Как найти точку на прямой?
— Как строится центральная проекция точки?
— Какие виды проекции существуют?
— Как найти проекцию в геометрии?
— Как найти наклонную и ее проекцию?
— Как обозначить проекцию точки?

Что такое ортогональная проекция точки на прямую?

Ортогональная проекция точки P на прямую (или плоскость) – это основание P’ перпендикуляра, опущенного из точки P на эту прямую (плоскость). Отображение, сопоставляющее точке P точку P’, также называется ортогональной проекцией.

Что такое проекция точки на ось?

Проекция точки на ось — это основание перпендикуляра, опущенного из этой точки на данную ось (рис. … 8). То есть, проекцией точки на ось является точка.

Что такое ортогональная проекция точки на плоскость?

Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.

Как найти точку на прямой?

Для поиска точки на прямой достаточно взять одну из координат, и подставить в уравнение, а затем выразить из полученного уравнение вторую. Таким образом найдется точка с заданной одной из координат.

Как строится центральная проекция точки?

Для получения центральных проекций надо задаться плоскостью проекций и центром проекций – точкой, не лежащей в этой плоскости (плоскость п₀ и точка S). Взяв некоторую точку А и проведя через S и А прямую линию до пересечения ее с пл. … п₀: они получаются в пересечении проецирующих прямых SA, SB, SC с плоскостью проекций.

Какие виды проекции существуют?

По характеру искажений проекции разделяются на равноугольные (или конформные), равновеликие (или эквивалентные) и произвольные.

Равноугольные проекции. …
Равновеликие проекции. …
Произвольные проекции. …
Конические проекции. …
Цилиндрические проекции. …
Азимутальные проекции. …
Перспективные проекции. …
Условные проекции.

Как найти проекцию в геометрии?

Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой О (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета.

Как найти наклонную и ее проекцию?

Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.

Как обозначить проекцию точки?

Точки обозначают прописными буквами латинского алфавита или арабскими цифрами: A, B, C, D, …. 1, 2, 3, 4, …. 2. Линии, произвольно расположенные по отношению к плоскости проекций, обозначают строчными буквами латинского алфавита: a, b, c, d, ….

Интересные материалы:

Nfc в фитнес браслете что это?
Nfc в наушниках что это?
Ниссан кашкай сборка где?
Ниссан кашкай СЕ где производство?
Ниссан х трейл где собирают для России?
Ниссан х трейл сборка где?
Ниссан мурано где производят?
Ниссан террано что это?
Ниссан террано где производится сборка авто?
Ночной паралич что это такое?

Источник

Как найти проекцию точки на прямую

Для решения сложных геометрических задач часто оказывается достаточно знания алгоритмов простых операций. Так иногда оказывается достаточно просто найти проекцию точки на прямую и сделать несколько дополнительных построений, чтобы нерешаемая на первый взгляд задача превратилась в доступную.

Инструкция

Научитесь пользовать координатной плоскостью. Основные затруднения могут возникнуть с отрицательными числами. Запомните, что всего имеется четыре квадранта: в первом расположены положительные значения, во втором – положительные только по оси абсцисс, в третьем – отрицательные по обеим осям, а в четвертом отрицательные сохраняются только на оси абсцисс. Вы можете произвольно задавать направления координатных осей, но в математике по традиции принято, чтобы ось ординат была направлена вверх (соответственно, внизу расположены отрицательные числа), а ось абсцисс шла слева направо (равно как и смена отрицательных чисел через ноль на положительные).

Зафиксируйте данные задачи. Вам нужно знать координаты точки, а также уравнение прямой, проекцию точки на которую необходимо найти. Нарисуйте чертеж. Начинайте с изображения координатной плоскости, обозначения центра координат, осей и их направления, а также единичных отрезков. Выполнив это действие, нанесите на полученную плоскость данную вам точку, исходя из знания о ее координатах, и проведите заданную прямую. Если вы хотите быть математически грамотным, ваша прямая должна занимать всю координатную плоскость, не выходя за ее пределы, но и не завершаться до их достижения.

Опустите перпендикуляр из данной точки на прямую. Найти проекцию точки означает найти координаты точки пересечения. Для этого проведите через исходную точку и точку пересечения прямую. Вы получите две перпендикулярных прямых. Воспользуйтесь теоремой о том, что у двух перпендикулярных прямых отношение угловых коэффициентов есть минус единица.

Исходя из этого, составьте систему уравнений. Координаты искомой точки – (А, В), данной – (А1, В1), уравнение прямой – Сх+Е, уравнение проведенной прямой – (-С)х+К, где К пока неизвестно. Первое уравнение: АС+Е=В. Оно верно, так как искомая точка лежит на данной прямой. Второе уравнение: А1(-С)+К=В1. И третье уравнение: А(-С)+К=В. Имея три линейных уравнения с тремя неизвестными (– А, В, К), вы легко решите поставленную задачу.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Проекция точки на прямую — это точка пересечения перпендикуляра из точки к прямой и прямой.

Содержание

1 Обозначения
2 Формулы:
- 2.1 Пример
3 Другие формулы:
4 Ссылки

Обозначения[править]

Введём обозначения:

${displaystyle {bar {r}}_{2}=(x_{2},y_{2},z_{2})}$ — радиус-вектор проекции точки;

${displaystyle {bar {r}}_{0}=(x_{0},y_{0},z_{0})}$ — радиус-вектор точки;

${displaystyle {bar {r}}_{1}=(x_{1},y_{1},z_{1})}$ — радиус-вектор точки прямой;

${displaystyle {bar {s}}_{1}=(l_{1},m_{1},n_{1})}$ — направляющий вектор прямой;

${displaystyle {frac {x-x_{1}}{l_{1}}}={frac {y-y_{1}}{m_{1}}}={frac {z-z_{1}}{n_{1}}}}$ — уравнение прямой;

${displaystyle p_{01}}$ — отклонение точки прямой от перпендикулярной к прямой плоскости, проходящей через точку.

Формулы:[править]

Векторная форма:

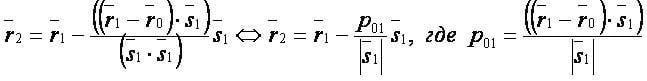
Координатная форма:

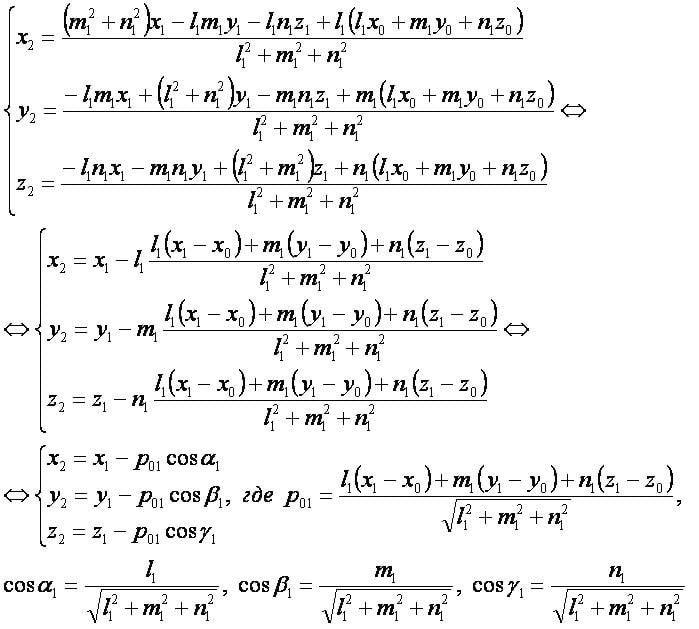
Заметим, что формулы проекции точки на прямую аналогичны формулам основания перпендикуляра из точки к прямой.

Пример[править]

Даны точка и прямая:
и ${displaystyle {frac {x-1}{-2}}={frac {y+5}{3}}={frac {z+1}{4}}}$ .

Найти проекцию точки на прямую.

Решение.

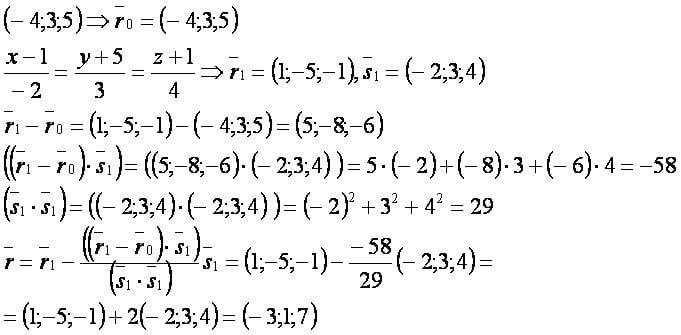
Другие формулы:[править]

Проекция вектора на вектор;
Проекция точки на прямую;
Проекция точки на плоскость.

Ссылки[править]

Участник:Logic-samara

Источник