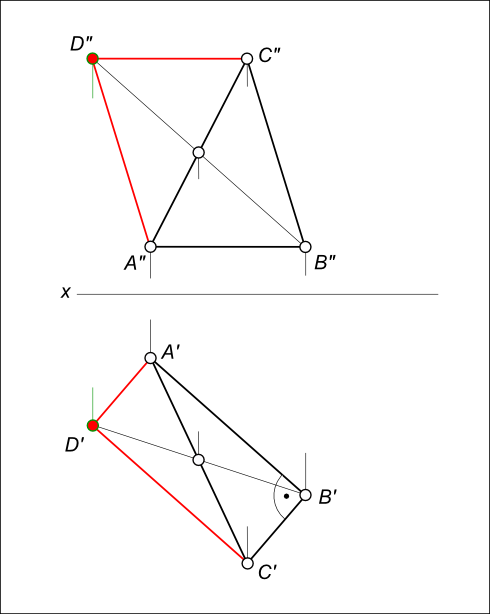
Проекции треугольника
Проекции треугольника,одного и того же, представлены в трех вариантах:
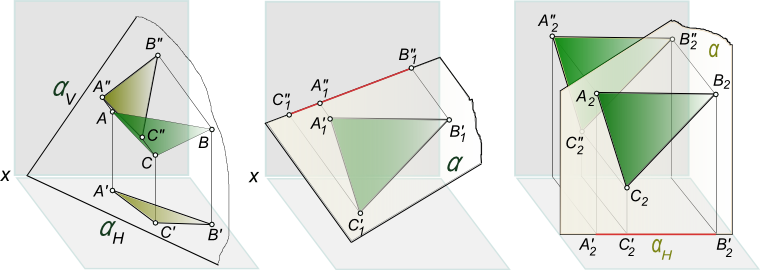
1. вариант — ΔABC, занимает общее положение; 2. вариант — ΔA1B1C1 ⊥ V, занимает положение перпендикулярное к фронталной плоскости проекций; 2. вариант — ΔA2B2C2 ║ V, занимает положение параллельное относительно фронталной плоскости проекций; ΔABC≅ΔA1B1C1≅ΔA2B2C2
Данные проекции треугольника показывают, что вид проекции (ее форма и размеры) определяются не только формой и размерами проецируемой фигуры, но и в значительной степени зависит от взаимного расположения объекта проецирования и плоскости проекций.
Действительно, три конгруентных прямоугольных треугольника ΔABC≅ΔA1B1C1≅ΔA2B2C2 (рисунок) в зависимости от взаимного расположения плоскости треугольника и плоскости проекции V могут проецироваться на эту плоскость в виде: а) ΔA»B»C» соответствует ΔABC, плоскость треугольника занимает произвольное положение относительно плоскости V. ΔA»B»C» в метрическом отношении не имеет ничего общего с оригиналом — ΔABC (рисунок слева); б) отрезка прямой [C»1B»1], в случае, когда плоскость ΔA1B1C1⊥V (рисунок в центре) перпендикулярна к фронталной плоскости проекций; в) либо в виде ΔA»2B»2C»2 ≅ ΔA2B2C2, когда плоскость ΔA2B2C2 ║ V (рисунок справа) параллельна относительно фронталной плоскости проекций.
Сопоставляя между собой оригинал — треугольник ABC и проекции треугольника в различных положениях, мы видим, что только в случае параллельности проецируемой фигуры плоскости проекции возможно получить проекцию на эту плоскость, конгруентную самой фигуре, и, следовательно, полностью сохраняющую ее метрику. Форма и размеры фронтальной проекции ΔA»2B»2C»2 (рисунок справа) позволяют, без каких либо построений, ответить на вопросы: какова длина сторон треугольника, величина углов при вершинах, чему равна его площадь и другие метрические характеристики ΔA2B2C2.
Решение задачи по определению натуральной величины треугольника ΔABC показано в статьях: Графическая работа 3; Натуральная величина треугольника.
Построить натуральную величину треугольника авс
Натуральная величина треугольника на эпюре Монжа может быть определена: – способом прямоугольного треугольника;
Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.
Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:
– Способ вращения вокруг осей перпендикулярных плоскостям проекций;
– Вращение вокруг горизонтали представляющих собой линии уровня;
представляющих собой линии уровня;
– Вращение вокруг следа или способ совмещения с плоскостью проекций;
Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.
Ниже приведены решения одной и той же задачи вышеописанными методами.
9.6.1. Задание:определить натуральную величину треугольника ABC(рис. 9.8), а также угол наклона плоскости треугольника к плоскости П1.
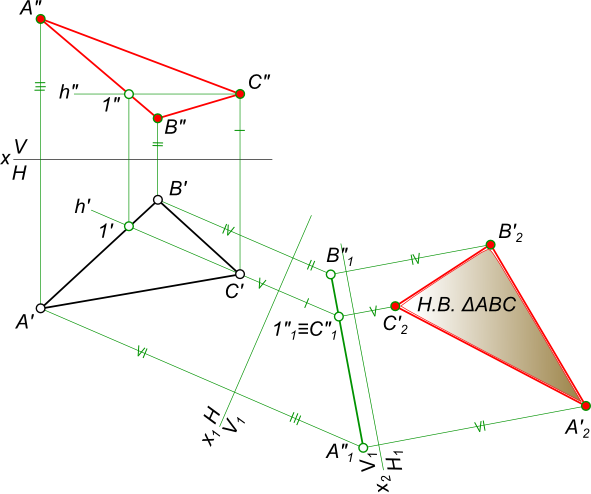
1) Решение методом замены плоскостей проекций (рис. 9.9).

Первый этап. Одним из условий перпендикулярности двух плоскостей является наличие прямой, принадлежащей одной из плоскостей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). Затем на произвольном расстоянии от горизонтальной проекции треугольника A1B1C1 проводят ось x1,4новой системы плоскостей проекций П1/П4перпендикулярно к горизонтальной проекции горизонтали h1.В новой системе треугольник ABC стал перпендикулярен к новой плоскости проекций П4.
На линиях проекционной связи в новой системе откладывают координатыzточек А, В, С с фронтальной проекции исходной системы плоскостей П1/П2.
При соединении новых проекций А4,B4, С4получают прямую линию, в которую спроецировался треугольник ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П1 – угол α. На чертеже это угол между осью x1,4и проекцией С4А4В4.
Второй этап. Выбираем новую плоскость проекции П5,параллельную плоскости треугольника, т.е. новую ось x4,5проводят параллельно С4А4В4на произвольном расстоянии. Получают новую систему П4/П5.Полученный треугольник А5В5С5и есть искомая натуральная величина треугольника ABC.
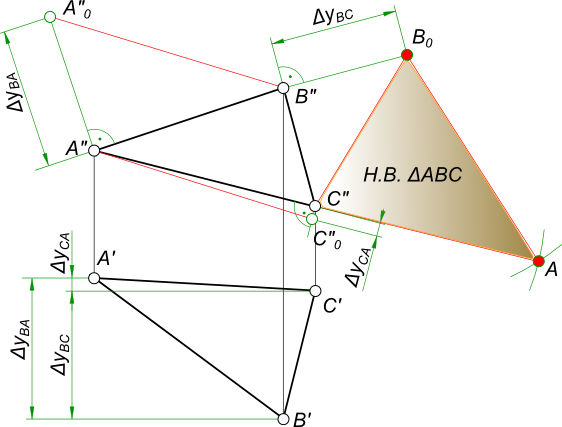
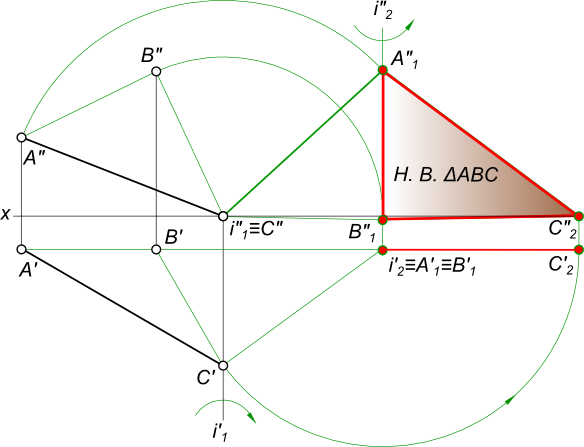
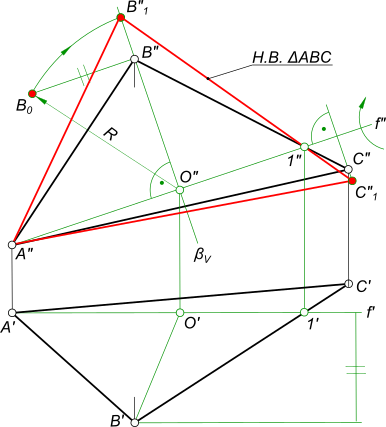
2) Решение методом вращения вокруг проецирующей оси(рис. 9.10).
Задача решается в два этапа. На первом этапе выполняют вращение так, чтобы плоскость треугольника ABCпреобразовалась в проецирующую плоскость, т.е. стала перпендикулярна к одной из плоскостей проекций. Для этого проводят горизонталь h (h1,h2) через точку А. (построение начинают с фронтальной проекции h2,она проходит через проекцию точки A2и проекцию точки 12 при этомh2 параллельна оси х).Далее находят горизонтальную проекцию h1 горизонтали h (через проекции A1 и 11). Через точку А проводят ось i – ось вращения треугольника так, чтобы она была перпендикулярна к П1. На фронтальной проекции через вершины А2 и В2 проводят следы горизонтальных плоскостей уровня Δ и Σв которых при вращении будут перемещаться точки АиВ. Вершина С принадлежит плоскости П1поэтому ее плоскостью вращения будет плоскость проекций П1.На горизонтальной проекции, взяв за центр вращения проекцию i1 поворачивают горизонталь А так, чтобы на плоскость П2 она спроецировалась в точку. На чертеже это выразится 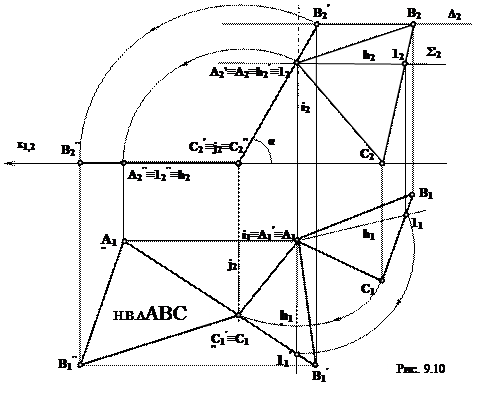
При этом на фронтальной проекции А2 остается неизменной, находясь на следе плоскости Σ2 и ее обозначим a2‘.
На горизонтальной проекции поворачиваем оставшиеся вершины В и С вокруг оси i так, чтобы 

На втором этапе проводят ось jчерез вершинуС так, чтобы ось была фронтально проецирующая. При этом С’2 ≡ j’2, а горизонтальная проекция j’1 пройдет через проекцию С’1. Вокруг оси поворачивают треугольник так, чтобы он стал параллелен горизонтальной плоскости проекций. В данной задаче вращают точки А’2 и В’1, вокруг j2 до совмещения с осью х,при этом проекции B’1 и A’1 будут перемещаться параллельно оси хи займут новое положение В»1, и А»1 вершина С останется на месте. Соединив точки между собой, получают новое положение плоскости (оно соответствует натуральной величине треугольника ABC).
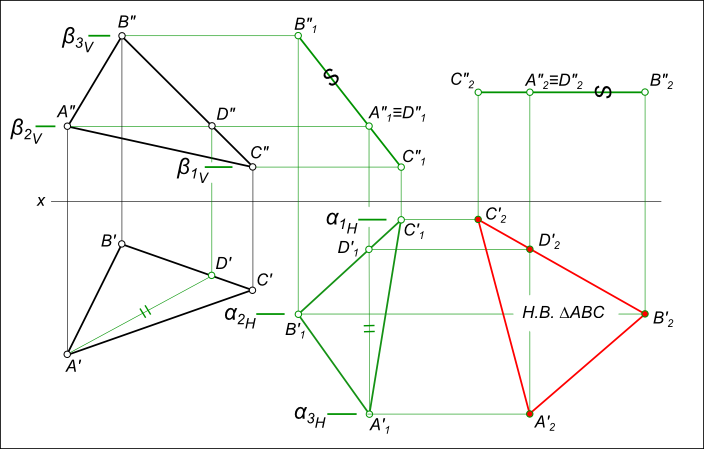
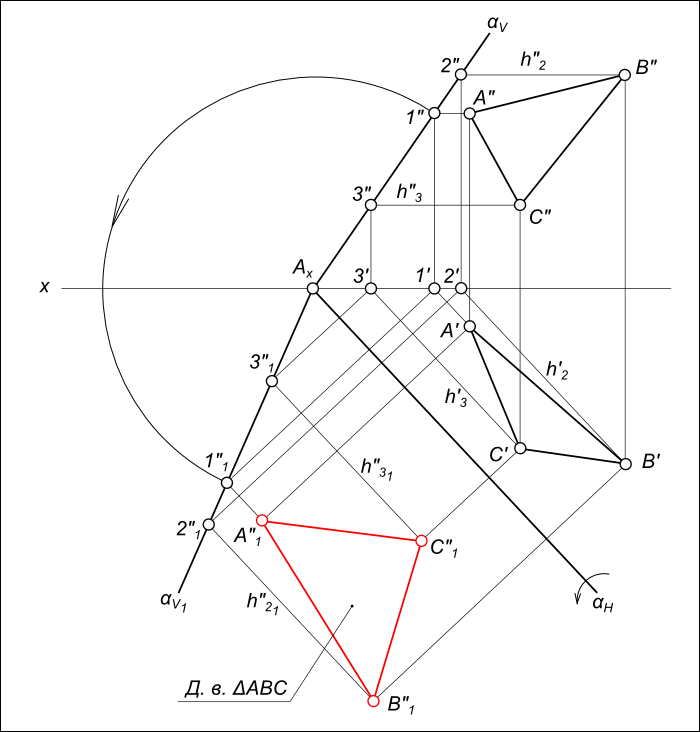
3) Решение методом плоскопараллельного перемещения (рис. 9.11).
Задача решается в два этапа. На первом этапе преобразуют чертеж так, чтобы плоскость треугольника ABC стала перпендикулярна к одной из плоскостей проекций. Для этого проводят в плоскости треугольника горизонталь h (фронтальная проекция А212║х,). Каждую вершину треугольника заключают в свою плоскость уровня, параллельную плоскости П1. В рассматриваемом примере вершина С принадлежит плоскости проекций П1, А принадлежит плоскости Σ, В — плоскости Δ.
Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h1 треугольника не станет перпендикулярна к фронтальной плоскости проекций П2.
Для этого на свободном поле чертежа вычерчивают горизонтальную проекцию треугольника A1 ′ B1 ′ C1 ′ с условием, чтобы А111
На втором этапе, чтобы получить натуральную величину треугольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А2‘В2‘С2‘располагают на произвольном расстоянии от оси хпараллельно плоскости П1. При этом вершины А, Ви С треугольника заключают в горизонтально проецирующие плоскости θ, Т, Р. По следам этих плоскостей будут перемещаться горизонтальные проекции вершин А1‘В1‘С1‘. От нового положения фронтальной проекции А2«В2«С2« проводят линии проекционной связи до пресечения с соответствующими следами плоскостей, в которых они перемещаются (θ1,T1,P1), и получая проекции точек А1» В1» C1«. Соединив эти проекции, получают треугольник ABC в натуральную величину.
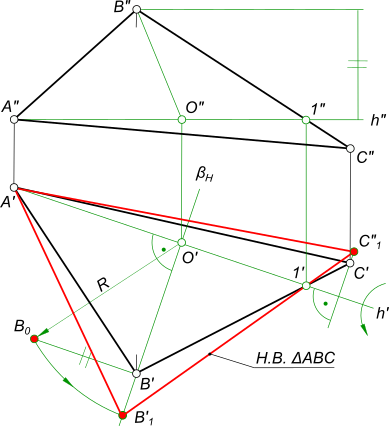
4) Решение методом вращения вокруг линии уровня(рис.9.12)
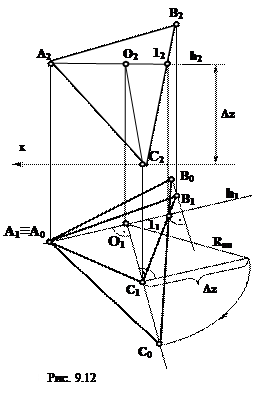
Для определения натуральной величины радиуса вращения используют любой метод (в данном случае способ прямоугольного треугольника) строят прямоугольный треугольник, в котором O1C1 – один из катетов. Второй катет – разность координат Δzотрезка О2С2, взятого с фронтальной проекции. В построенном треугольнике гипотенуза O1C – натуральная величина радиуса вращения.
На продолжении перпендикуляра O1C1 откладывают |RBp.| и получают новое положение вершины С после вращения — С . Проекция вершины В получается пересечением луча C 11 и перпендикуляра к горизонтальной проекции h1 проведенного через проекцию точки В1.
Треугольник A B C есть искомая натуральная величина треугольника ABC.
5) Решение методом совмещения(рис. 9.13).
Для решения задачи методом совмещения необходимо построить следы плоскости Σ, которой принадлежит треугольник ABC. Для этого проводят в плоскости треугольника ABC фронталь f и находят горизонтальный след этой фронтали – N1. По условию задачи вершина С треугольника принадлежит горизонтальной плоскости проекций П1. Тогда горизонтальный след Σ1 плоскости Σпроводят через проекции N1 и C1. Соединив эти две точки и продлив отрезок до пересечения с осью х, находят точку схода следов Σх. Учитывая, что все фронтали плоскости параллельны ее фронтальному следу, фронтальный след Σ2 плоскости Σпроводят через точку Σхпараллельно проекции фронтали f2.
Для нахождения натуральной величины треугольника ABCнеобходимо построить совмещенное положение плоскости Σ с горизонтальной плоскостью проекций П1. Для этого через вершину Апроводят горизонталь h1. На фронтальном следе Σ2 фиксируют точку 22. Ее горизонтальная проекция – точка 21. Точка 2 вращается в плоскости, перпендикулярной к горизонтальному следу плоскости Σ. Поэтому, чтобы построить точку 2 в совмещенном положении 2 , проводят из 21перпендикуляр к горизонтальному следу Σ, а из центра Σх дугу окружности радиусом Σх22 до пересечения с направлением перпендикуляра. Соединив Σх с 2 , получают совмещенное положение фронтального следа Σ – Далее через точку 2 проводят горизонталь h всовмещенном положении. На этой горизонтали находят точку А , проведя перпендикуляр из точки A1 к горизонтальному следу Σ1.
По такой же схеме строят совмещенное положение точки В . Совмещенное положение точки С совпадает с ее горизонтальной проекцией С1 т.е. С1≡С . Соединив построенные точки, получают треугольник А В С – это и есть натуральная величина треугольника ABC.
Не нашли то, что искали? Воспользуйтесь поиском:
Метки
Натуральная величина треугольника с описанием.
Натуральная величина треугольника определяется 2 методами:
- замена плоскостей проекции;
- плоскопараллельное перемещение.
Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».
Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.
Алгоритм определения натуральной величины плоскости:
Замена плоскостей проекции
1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.
2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.
3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:
- от С2 до оси Х;
- от В2 до оси Х;
- от А0 до оси Х.
Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.
4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.
5.) Отмеряются расстояния:
- от В1 до Х1;
- от С1 до Х1;
- от А1 до Х1.
Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

Плоскопараллельное перемещение
7.) Откладывается отрезок на оси Х (обозначен синим цветом).
8.) Переносятся точки на текущее построение.
9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 


Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).




Как определить проекцию треугольника
Плоскостью называется поверхность, образуемая движением прямой линии, которая движется параллельно самой себе по неподвижной направляющей прямой .
Проекции плоскости на комплексном чертеже будут различны в зависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана: а) тремя точками, не лежащими на одной прямой; б) прямой линией и точкой, лежащей вне этой прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми.
На комплексном чертеже (рис. 99) проекции плоскости также задаются проекциями этих элементов, например, на рис 99, а — проекциями трех точек А, , и С, не лежащих на одной прямой; на рис. 99, б — проекциями прямой ВС и точки А у не лежащей на этой прямой; на рис. 99, в — проекциями двух пересекающихся прямых; на рис. 99, г проекциями двух параллельных прямых линий АВ и CD.
На рис. 100 плоскость задана прямыми линиями, по которым эта плоскость пересекает плоскости проекций. Такие линии называются следами плоскости.
Линия пересечения данной плоскости Р с горизонтальной плоскостью проекций Н называется горизонтальным следом плоскости Р и обозначается Рн.
Линия пересечения плоскости Р с фронтальной плоскостью проекций V называется фронтальным следом этой плоскости и обозначается Рv.
Линия пересечения плоскости Р с профильной плоскостью проекций W называется профильным следом этой плоскости и обозначается Pw.
Следы плоскости пересекаются на осях проекций. Точки пересечения следов плоскости с осями проекций называются точками схода следов. Эти точки обозначаются Рx, Рy и Рz.
Расположение следов плоскости Р на комплексном чертеже по отношению к осям проекций определяет положение самой плоскости по отношению к плоскостям проекций. Например, если плоскость Р имеет фронтальный и профильный следы Pv и Pw, параллельные осям Ох и Оу то такая плоскость параллельна плоскости Н и называется горизонтальной (рис. 101, и). Плоскость Р со следами Рн и Pw , параллельными осям проекций Ох и Oz (рис. 101, называется фронтальной, а плоскость Р со следами Pv и Pн параллельными осям проекций Оу и Oz, — профильной (рис. 101, в).
Горизонтальная, фронтальная и профильная плоскости, перпендикулярные к двум плоскостям проекций, называются плоскостями уровня. Если на комплексном чертеже плоскость уровня задана не следами, а какой-нибудь плоской фигурой, например, треугольником или параллелограммом (рис. 101, г, д, е), то на одну из плоскостей проекций эта фигура проецируется без искажения, а на две другие плоскости проекций — в виде отрезков прямых.
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
Плоскость, перпендикулярная к плоскости Н (рис. 102, а),называется горизонтально-проецирующей плоскостью. Фронтальный след Pv этой плоскости перпендикулярен оси Ох, а горизонтальный след Рн расположен под углом к оси Ох (комплексный чертеж на рис. 102, а)
Если горизонтально-проецирующая плоскость задана не следами, а какой-либо фигурой, например треугольником АВС (рис. 102, 6), то горизонтальная проекция этой плоскости представляет собой прямую линию, а фронтальная и профильная проекции — искаженный вид треугольника АВС.
Фронтально-проецирующей плоскостью называется плоскость, перпендикулярная к фронтальной плоскости проекций (рис. 102, в).
Горизонтальный след этой плоскости перпендикулярен оси Ох, а фронтальный след расположен под некоторым углом к оси Ох (комплексный чертеж на рис. 102, в).
При задании фронтально-проецирующей плоскости не следами, а, например, параллелограммом ABCD фронтальная проекция такой плоскости представляет собой прямую линию (рис. 102, г), а на горизонтальную и профильную плоскости проекций параллелограмм проецируется с искажением.
Профильно-проецирующей плоскостью называется плоскость, перпендикулярная к плоскости W (рис. 102, д). Следы Pv и Рн этой плоскости параллельны оси Ох.
При задании профильно-проецирующей плоскости не следами, а, например, треугольником АВС (рис. 102, е) профильная проекция такой плоскости представляет собой прямую линию. Плоскости, перпендикулярные двум плоскостям проекций, как было сказано, называются плоскостями уровня.
Если плоскость Р не перпендикулярна ни одной из плоскостей проекций (рис. 102, ж), то такая плоскость называется плоскостью общего положения. Все три
следа Pv, Рн и Pw плоскости Р наклонены к осям проекций.
Если плоскость общего положения задана не следами, а, например, треугольником АВС (рис. 102, з), то этот треугольник проецируется на плоскости H, V и W в искаженном виде.
ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ
Если прямая расположена на плоскости, то она должна проходить через две какие-либо точки, принадлежащие этой плоскости. Такие две точки могут быть взяты на следах плоскости — одна на горизонтальном, а другая на фронтальном. Так как следы прямой и плоскости находятся на плоскостях проекций и то следы прямой, принадлежащей плоскости, должны быть расположены на одноименных следах этой плоскости (рис. 103, а);например, горизонтальный след Н прямой — на горизонтальном следе плоскости, фронтальный след V прямой — на фронтальном следе Рv плоскости (рис. 103, б).
Для того чтобы на комплексном чертеже плоскости Р, заданной следами, провести какую-либо прямую общего положения, необходимо наметить на следах плоскости точки v’ или считать их следами искомой прямой (точнее, v’ — фронтальной проекцией горизонтального следа прямой).
Опустив перпендикуляры из v’ и на ось проекций х, находим на ней вторые проекции следов прямой: v — горизонтальную проекцию фронтального следа прямой и h’ — фронтальную проекцию горизонтального следа прямой. Соединив одноименные проекции следов, т. е. v’c h и v c h прямыми, получим две проекции прямой линии, расположенной в плоскости общего положения Р.
Очень часто требуется провести на плоскости горизонталь и фронталь, которые называются главными линиями плоскости или линиями уровня. Главные линии помогают решать многие задачи проекционного черчения.
Горизонталь и фронталь имеют в системе двух плоскостей V и Н только по одному следу (например, горизонталь имеет только фронтальный след). Поэтому, зная один след главной линии, проекцию главной линии проводят по заранее известному направлению. Это направление для горизонтали видно из рис. 104, а, где показана плоскость общего положения и горизонталь, лежащая на ней. Из рисунка видно, что горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.
Таким образом, чтобы на комплексном чертеже плоскости Р провести в этой плоскости какую-либо горизонталь, нужно наметить на следе Рv плоскости точку v’ (рис. 104, б) и считать ее фронтальной проекцией фронтального следа горизонтали. Затем через точку v’ параллельно оси х проводят прямую, которая будет фронтальной проекцией горизонтали.
Опустив перпендикуляр из точки v’ на ось x , получают точку v, которая будет горизонтальной проекцией фронтального следа горизонтали. Прямая, проведенная из точки v параллельно следу PH плоскости, представляет собой горизонтальную проекцию искомой горизонтали. Построение проекции фронтали показано на рис. 104, в и г.
11 с редко требуется провести горизонталь и фронталь на проецирующих плоскостях. Рассмотрим, например, построение горизонтали на фронтально-проецирующей плоскости (рис. 105). На следе плоскости Рv намечаем фронтальную проекцию фронтального следа горизонтали и на оси находим его горизонтальную проекцию v (рис. 105, а). Затем через точку проводим параллельно Рн горизонтальную проекцию горизонтали; фронтальная проекция горизонтали совпадает с точкой v’.
Если плоскость задана не следами, а пересекающимися или параллельными прямыми, то построение проекций горизонтали или фронтали, расположенных в этой плоскости, выполняется следующим образом.
Пусть плоскость задана двумя параллельными прямыми AВ и СD (рис. 105, 6). Для построения горизонтали, лежащей в этой плоскости, проводим параллельно оси х фронтальную проекцию горизонтали и отмечаем точки е’и f’ пересечения фронтальной проекции горизонтали с фронтальными проекциями параллельных прямых, которыми задана плоскость. Через точки е’и f’ проводим вертикальные линии связи до пересечения с ab и cd в точках е и f. Точки е и f соединяем прямой линией, которая и будет горизонтальной проекцией горизонтали.
Если требуется найти следы плоскости, заданной пересекающимися или параллельными прямыми, надо найти следы этих прямых и через полученные точки провести искомые следы плоскости.
Рассмотрим комплексный чертеж параллелограмма ABCD (рис. 106, a),который задает некоторую плоскость X. Отрезок DC расположен в плоскости H, следовательно, его горизонтальная проекция dc является горизонтальным следом плоскости (точнее — горизонтальной проекцией горизонтального следа плоскости).
Чтобы найти фронтальный след этой плоскости, необходимо продолжить горизонтальную проекцию dc прямой DC до пересечения с осью х в точке Рх, через которую должен пройти искомый фронтальный след плоскости.
Второй точкой v’, через которую пройдет искомый фронтальный след плоскости, является фронтальный след прямой АВ (фронтальная проекция фронтального следа). Фронтальную проекцию фронтального следа прямой АВ находим, продолжая горизонтальную проекцию ab прямой АВ до пересечения с осью х в точке v, которая будет горизонтальной проекцией искомого фронтального следа прямой АВ. Фронтальная проекция фронтального следа этой прямой находится на перпендикуляре, восставленном из точки v к оси х, в точке v’ его пересечения с продолжением фронтальной проекции а’в’ прямой АB. Соединив точки Px с v’, находим фронтальный след Pv плоскости.
Пример решения подобной задачи приведен на рис 106, б.
Часто на комплексных чертежах приходится решать такую задачу: по одной из заданных проекций точки, расположенной на заданной плоскости, определить две другие проекции точки. Ход решения задачи следующий.
Через заданную проекцию точки, например фронтальную проекцию n’ точки N, расположенной на плоскости треугольника АВС (рис. 107), проводим одноименную проекцию вспомогательной прямой любого направления, например m’к’.
Горизонталью плоскости называется прямая, принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций Н.
Строим другую проекцию mк вспомогательной прямой. Для этого проводим вертикальные линии связи через точки m’ и к’ до пересечения с линиями ас и вс. Из точки n’ проводим линию связи до пересечения с проекцией mк в искомой точке n.
Профильную проекцию n» находим по общим правилам проецирования.
В качестве вспомогательной прямой для упрощения построения чаще используются горизонталь или фронталь.
Чтобы найти какую-либо точку на плоскости Р, например точку А (рис. 108, а и б) надо найти ее проекции а’и а, которые располагаются на одноименных проекциях горизонтали, проходящей через эту точку. Через точку А проведена горизонталь Av’ .
Проводим проекции горизонтали: фронтальную — через v’ параллельно оси х, горизонтальную — через v параллельно следу Рн плоскости Р. На фронтальной проекции горизонтали намечаем фронтальную проекцию а’ искомой точки и, проводя вертикальную линию связи, определяем горизонтальную проекцию а точки А.
Если точка лежит на проецирующей плоскости, то построение ее проекций упрощается. В этом случае одна из проекций точки всегда расположена на следу плоскости (точнее, на его проекции). Например, горизонтальная проекция а точки А, расположенной на горизонтально-проецирующей плоскости Р, находится на горизонтальной проекции горизонтального следа плоскости (рис. 108, в и г)
При заданной фронтальной проекции a’ точки А, лежащей на горизонтально-проецирующей плоскости , найти вторую проекцию этой точки (горизонтальную) можно без вспомогательной прямой, посредством проведения линии связи через а’ до пересечения со следом РН.
Если точка расположена на фронтально-проецирующей плоскости Р (рис. 108, д и е), то ее фронтальная проекция а’ находится на фронтальном следе Хv плоскости Р.
ПРОЕКЦИИ ПЛОСКИХ ФИГУР
Зная построение проекций прямых и точек, расположенных на плоскости, можно построить проекции любой плоской фигуры, например, прямоугольника, треугольника, круга.
Как известно, каждая плоская фигура ограничена отрезками прямых или кривых линий, которые могут быть построены по точкам.
Проекции фигуры, ограниченной прямыми линиями (треугольника и многоугольника), строят по точкам (вершинам). Затем одноименные проекции вершин соединяют прямыми линиями и получают проекции фигур.
Проекции круга или другой криволинейной фигуры строят при помощи нескольких точек, которые берут равномерно по контуру фигуры. Одноименные проекции точек соединяют плавной кривой по лекалу.
Проекции плоской фигуры строят различными способами в зависимости от положения фигуры относительно плоскостей проекций и Наиболее просто построить проекции фигуры, расположенной параллельно плоскостям Н и V; сложнее — при расположении фигуры на проецирующей плоскости или на плоскости общего положения.
Рассмотрим несколько примеров.
Если треугольник АВС расположен на плоскости, параллельной плоскости H (рис. 109, a), то горизонтальная проекция этого треугольника будет его действительным видом, а фронтальная проекция — отрезком прямой, параллельным оси х. Комплексный чертеж треугольника АВС показан на рис. 109, 6. Такой треугольник можно видеть на изображении резьбового резца (рис. 109, в),передняя грань которого треугольная.
Трапеция ABCD расположена на фронтально-проецирующей плоскости (рис. 110, а). Фронтальная проекция трапеции представляет собой отрезок прямой линии, а горизонтальная — трапецию (рис. 110, б)
Задняя грань отрезного резца (рис. 110, в) имеет форму трапеции.
Рассматривая плоскость, параллельную горизонтальной, фронтальной или профильной плоскости проекций (плоскость уровня), можно заметить, что любая фигура, лежащая в этой плоскости, имеет одну из проекций, представляющую собой действительный вид этой фигуры; вторая и третья проекции фигуры совпадают со следами этой плоскости.
Рассматривая проецирующую плоскость, заметим, что любая точка, отрезок прямой или кривой линии, а также фигуры, расположенные на проецирующей плоскости, имеют одну проекцию, расположенную на следе этой плоскости. Например, если круг лежит на фронтально-проецирующей плоскости Р (рис. 111), то фронтальная проекция круга совпадает с фронтальным следом Pv плоскости Р. Две другие проекции круга искажены и представляют собой эллипсы. Большие оси эллипсов равны проекциям диаметра круга 37. Малые оси эллипсов равны проекциям диаметра круга 15, перпендикулярного диаметру 37.
На рис. 111,6 показано колено трубы с двумя фланцами. Горизонтальная проекция контура нижнего фланца, который расположен в горизонтальной плоскости, будет действительным видом окружности. Горизонтальная проекция контура верхнего фланца изобразится в виде эллипса.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Две плоскости могут быть взаимно параллельными или пересекающимися.
Из стереометрии известно, что если две параллельные плоскости пересекают какую-либо третью плоскость, то линии пересечения этих плоскостей параллельны между собой. Исходя из этого положения, можно сделать вывод, что одноименные следы двух параллельных плоскостей Р и Q также параллельны между собой.
Если даны две профильно-проецирующие плоскости Р и К (рис. 112, а), то параллельность их фронтальных и горизонтальных следов на комплексном чертеже в системе V и Н недостаточна для того, чтобы определить, параллельны эти плоскости или нет. Для этого необходимо построить их профильные следы в системе V, Н и W (рис. 112, б). Плоскости Р и K будут параллельны только в том случае, если параллельны их профильные следы Pw и Kw.
Одноименные следы пересекающихся плоскостей Р и Q (рис. 112, в) пересекаются в точках V и H, которые принадлежат обеим плоскостям, т. е. линии их пересечения. Так как эти точки расположены на плоскостях проекций, то, следовательно, они являются также следами линии пересечения плоскостей. Чтобы на комплексном чертеже построить проекции линии пересечения двух плоскостей Р и Q, заданных следами Pv, Рн и Qv,Qh, необходимо отметить точки пересечения одноименных следов плоскостей, т. е. точки v’ и h (рис. 112, г); точка v’ — фронтальная проекция фронтального следа искомой линии пересечения плоскостей Р и Q, h — горизонтальная проекция горизонтального следа этой же прямой. Опуская перпендикуляры из точек v’ и h на ось х, находим точки v и h’. Соединив прямыми одноименные проекции следов, т. е. точки v’ и h’, v и h’ получим проекции линии пересечения плоскостей Р и Q.
ПРЯМАЯ, ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ
Для этого фронтальную проекцию отрезка m’n’ продолжаем до пересечения с отрезками a’b’ и c’d’ (проекциями сторон треугольника АВС), получаем точки (рис. 113, б).
Из точек е’к’ проводим линии связи на горизонтальную проекцию до пересечения с отрезками ab и ca , получаем точки еk. Продолжим горизонтальную проекцию mn отрезка прямой MN до пересечения с проекциями сторон bа и са, если точки пересечения совпадут с ранее полученными точками e и k то прямая MN принадлежит плоскости треугольника.
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ
Если прямая АВ пересекается с плоскостью Р, то на комплексном чертеже точка их пересечения определяется следующим образом.
Через прямую А В проводят любую вспомогательную плоскость Q. Для упрощения построений плоскость Q обычно берется проецирующей (рис. 114, a). В данном случае проведена вспомогательная горизонтально-проецирующая плоскость Q. Через горизонтальную проекцию аb прямой АВ проводят горизонтальный след QH плоскости Q и продолжают его до пересечения с осью x в точке Qx . Из точки Qx к оси х восставляют перпендикуляр QxQy , который будет фронтальным следом Qv вспомогательной плоскости Q.
Вспомогательная плоскость Q пересекает данную плоскость Р по прямой VH, следы которой лежат на пересечении следов плоскостей Р и Q. Заметив точки пересечения следов Pv и Qv — точку v’ и следов Qн и PH — точку h,опускают из этих точек на ось х перпендикуляры, основания которых — точки v’ и h’ — будут вторыми проекциями следов прямой VH. Соединяя точки v’и h’, v и h, получают фронтальную и горизонтальную проекции линии пересечения плоскостей.
Точка пересечения М заданной прямой AB и найденной прямой VH и будет искомой точкой пересечения прямой АВ с плоскостью Р. Фронтальная проекция m’ этой точки расположена на пересечении проекций a’b’ и v’h’. Горизонтальную проекцию m точки М находят, проводя вертикальную линию связи из точки m’ до пересечения с ab.
Если плоскость задана не следами, а плоской фигурой, например, треугольником (рис. 114, 6), то точку пересечения прямой MN с плоскостью треугольника АВС находят следующим образом.
Через прямую МN проводят вспомогательную фронтально-проецирующую плоскость . Для этого через точки m’ и n’ проводят фронтальный след плоскости Ру продолжают его до оси x и из точки пересечения следа плоскости Ру с осью х опускают перпендикуляр Рн, который будет горизонтальным следом плоскости Р.
Затем находят линию ED пересечения плоскости Р с плоскостью данного треугольника ABC. Фронтальная проекция e’d’ линии ED совпадает с m’n’. Горизонтальную проекцию ed находят, проводя вертикальные линии связи из точек е’и d’ до встречи с проекциями ab и ас сторон треугольника АВС. Точки e и d соединяют прямой. На пересечении горизонтальной проекции ed линии ED с горизонтальной проекцией прямой MN находят горизонтальную проекцию k искомой точки К. Проведя из точки k вертикальную линяю связи, на ходят фронтальную проекцию k’ Точка К — искомая точка пересечения прямой МК с плоскостью треугольника АВС.
В частном случае прямая может быть перпендикулярна плоскости Р.Из условия перпендикулярности прямой к плоскости следует, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим на этой плоскости (в частности, этими прямыми могут быть следы плоскости). Тогда проекции прямой АВ будут перпендикулярны одноименным следам этой плоскости (рис 115, а) Фронтальная проекция а’b’ перпендикулярна фронтальному следу Ру, а горизонтальная проекция ab перпендикулярна горизонтальному следу Рн плоскости Р.
Если плоскость задана параллельными или пересекающимися прямыми, то проекции прямой, перпендикулярной этой плоскости, будут перпендикулярны горизонтальной проекции горизонтали и фронтальной проекции фронтали, лежащих на плоскости.
Таким образом, если, например, на плоскость, заданную треугольником АВС необходимо опустить перпендикуляр, то построение выполняется следующим образом (рис. 115, б).
На плоскости проводят горизонталь СЕ и фронталь FA. Затем из заданных проекций d и d’ точки D опускают перпендикуляры соответственно на ce и f’a’. Прямая, проведенная из точки D будет перпендикулярна плоскости треугольника АВС.
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Задачи на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение плоскости с прямыми линиями. На рис. 116 показано построение линии пересечения плоскостей, заданных треугольниками АВС и DEF. Прямая MN построена по найденным точкам пересечения сторон DE и EF треугольника DEF с плоскостью треугольника АВС.
Например, чтобы найти точку M, через прямую DF проводят фронтально-проецирующую плоскость Р, которая пересекается с плоскостью треугольника АВС по прямой 12. Через полученные точки 1′ и 2′ проводят вертикальные линии связи до пересечения их с горизонтальными проекциями ав и ас сторон треугольника АВС в точках 1 и 2. На пересечении горизонтальных проекций df и 12 получают горизонтальную проекцию m искомой точки М, которая будет точкой пересечения прямой DF с плоскостью АВС. Затем находят фронтальную проекцию m’ точки M. Точку N пересечения прямой EF с плоскостью АВС находят так же, как и точку М.
Соединив попарно точки m’ и n’, m и n, получают проекции линий пересечения MN плоскостей АВС и DEF.
http://planshet-info.ru/kompjutery/postroit-naturalnuju-velichinu-treugolnika-avs
http://forkettle.ru/vidioteka/tekhnicheskie-nauki/cherchenie/780-osnovy-nachertatelnoj-geometrii/8631-proetsirovanie-ploskikh-figur
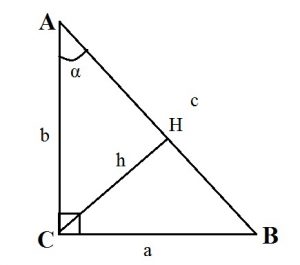
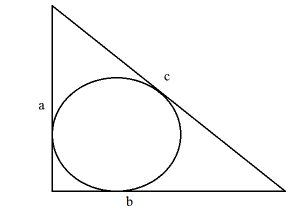
Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.
1) Свойство высоты, проведенной к гипотенузе.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.
или
2) Свойства катетов прямоугольного треугольника.
Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
или
Как найти проекцию
В прямоугольном треугольнике существует два вида сторон – короткая сторона «катет» и длинная сторона «гипотенуза». Если провести проекцию катета на гипотенузу, та разделится на два отрезка. Чтобы определить величину одного из них, нужно прописать набор исходных данных.

Инструкция
В исходных данных задачи может быть прописана длина гипотенузы D и длина катета N, чью проекцию требуется найти. Чтобы определить величину проекции Nd, воспользуйтесь свойствами прямоугольного треугольника. Определите длину катета A, используя тот факт, что среднее геометрическое, взятое от длины гипотенузы и проекции катета, равняется искомой величине катета. То есть N = √(D*Nd).
Учитывая, что корень из произведения означает то же самое, что и среднее геометрическое, возведите в квадрат значение N (длину искомого катета), и разделите на длину гипотенузы. То есть Nd = (N/√D)² = N²/D.В исходных данных задачи длина могут быть даны значения только катетов N и T. В этом случае длину проекции Nd находите с помощью теоремы Пифагора.
Определите длину гипотенузы D, используя значения катетов √(N²+T²) и подставьте полученное значение в формулу для нахождения проекции. Для чего Nd = N²/√(N²+T²).
Если в исходных данных содержится информация о длине проекции катета Rd и величине гипотенузы D, то длину проекции второго катета Nd вычислите с помощью простейшей формулы вычитания – Nd = D – Rd.
В ситуации, когда известно лишь значение длины гипотенузы D и дано простое соотношение длин катетов (m/h) обратитесь за помощью к формулам из первого шага и третьего шага.
Согласно формуле из первого шага примите как факт, что соотношение проекций Nd и Rd приравнивается к соотношению квадратных значений их длин. То есть Nd/Rd = m²/h². Также сумма проекций катетов Nd и Rd равняется длине гипотенузы.
Выразите значение проекции катета Rd через искомый катет Nd и подставьте в формулу суммирования. В результате вы получите Nd + Nd*m²/h² = Nd*(1 + m²/h²) = D, после чего выведите формулу нахождения Nd = D/(1 + m²/h²). Значение Nd и укажет величину искомого катета.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
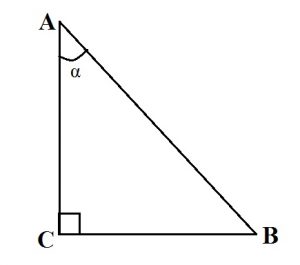
Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.
Прямоугольный треугольник: основные формулы
- Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
- Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
- Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. AB2 = AC2 + CB2
Прямоугольный треугольник: формулы площади и проекции
- Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
- Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH2 = AH·BH.
- Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу: CA2 = AB·AH; CB2 = AB·BH.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
- Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
- Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты. S = (hc):2.
Прямоугольный треугольник: формулы тригонометрия
- Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. cosα = AC: AB.
- Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. sinα = BC:AB.
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. tgα = BC:AC.
- Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему. ctgα = AC:BC.
- Основное тригонометрическое тождество: cos2α + sin2α = 1.
- Теорема косинусов: b2 = a2 + c2 – 2ac·cosα.
- Теорема синусов: CB :sinA = AC : sinB = AB.
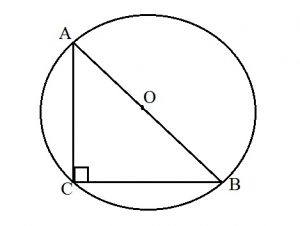
Прямоугольный треугольник: формулы для описанной окружности
- Радиус описанной окружности равен половине гипотенузы : R=AB:2.
- Центр описанной окружности лежит на середине гипотенузы.
Прямоугольный треугольник: формулы для вписанной окружности
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b -c):2.
Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из сборника для подготовки к ЕГЭ по математике профиль автора Ященко.
В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.
Решение:
- Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
- По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.
Ответ: AB = 28.
ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)
Проекции прямоугольного треугольника
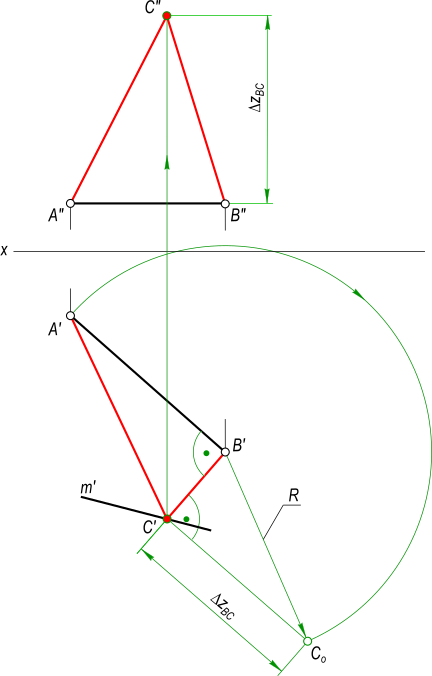
Построить Проекции прямоугольного треугольника ABC, если его катет AB(A`B`, …) принадежит горизонтальной прямой h(h`, h»), катеты равны между собой, а вершина C принадлежит прямой m(m`, …) и zC больше zB
Проекции прямоугольного треугольника
AB — один из катетов прямоугольного треугольника, представляет собой прямую уровня — горизонтальную прямую так как A»B» || Ox. На горизонтальную плоскость
проекции он проецируется в натуральную величину.
Выполняем построение BC:
— прямой угол при вершине B проецируется без искажения на горизонтальную плоскость проекции, следовательно здесь можно провести направление для катета BC;
— в пересечении направления катета BC с m` получим C`.
По способу прямоугольного треугольника определяем Δz = zC-zB:
— из центра O описываем дугу радиусом R=|AB|=A`B` до пересечения с направлением перпендикуляра в точке C0;
— определяем разницу аппликат катета BC — Δz.
Откладываем Δz на фронтальной плоскости проекций от точки B» и по линии проекционной связи находим точку C».
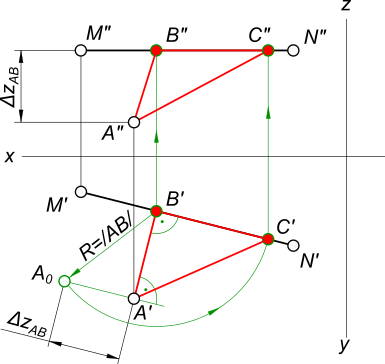
Построить проекции прямоугольного равнобедренного треугольника ABC, катет которого BC лежит на
прямой MN. A(60,40,10), M(75,10,30); N(15,25,30).
Проекции прямоугольного треугольника
Так как zM=zN делаем вывод, что отрезок MN — горизонтальная прямая и мы можем опустить из точки A перпендикуляр на него. В пересечении которого с M`N` находим B` и затем по линии проекционной связи B».
Находим натуральную величину катета AB способом прямоугольного треугольника:
— через точку A проводим перпендикуляр к AB и на нем откладываем ΔzAB и находим A0 и BA0;
— откладываем на отрезке MN катет BC, описывая дугу радиуса R=/AB/ и отмечая точку C` и по линии проекционной связи C»;
— вершины A`B`C` и A»B»C» соединяем прямыми линиями, получая проекции искомого треугольника.
Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
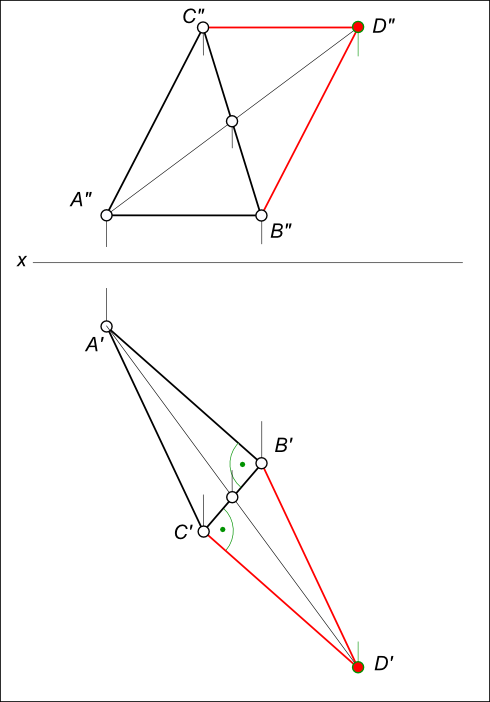
Построить фронтальную и горизонтальную проекции параллелограмма ABCD
Проекции прямоугольного треугольника
Построение параллелограмма заключается:
— в проведении BD // AC;
— в проведении CD // AB.
Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
Построить фронтальную и горизонтальную проекции квадрата ABCD
Проекции прямоугольного треугольника
Построение квадрата заключается:
— в проведении AD // BC;
— в проведении CD // AB.
+