Как найти проекцию катета в прямоугольном треугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

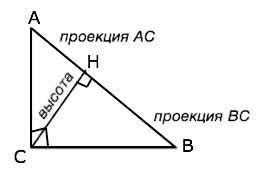
Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.

1) Свойство высоты, проведенной к гипотенузе.

Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.

или

$[C{D^2} = AD cdot BD.]$

2) Свойства катетов прямоугольного треугольника.

Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.

или

$[A{C^2} = AB cdot AD]$

$[B{C^2} = AB cdot BD.]$

Источник

Как найти проекцию катета на гипотенузу

Две короткие стороны прямоугольного треугольника называют катетами, а длинную — гипотенузой. Проекции коротких сторон на длинную делят гипотенузу на два отрезка разной длины. Если возникает необходимость в вычислении величины одного из этих отрезков, то способы решения задачи целиком зависят от предлагаемого в условиях набора исходных данных.

Инструкция

Если в исходных условиях задачи приведены длины гипотенузы (С) и того катета (А), проекцию которого (Ас) требуется вычислить, то используйте одно из свойств треугольника. Воспользуйтесь тем, что среднее геометрическое длин гипотенузы и искомой проекции равно длине катета: А = √(С*Ас). Так как понятие «среднее геометрическое» эквивалентно «корню из произведения», то для нахождения проекции катета возводите в квадрат длину катета и делите полученное значение на длину гипотенузы: Ас = (А/√С)² = А²/С.

Если длина гипотенузы неизвестна, а даны лишь длины обоих катетов (А и В), то в вычислении длины нужной проекции (Ас) можно задействовать теорему Пифагора. Выразите в соответствии с ней длину гипотенузы через длины катетов √(А²+В²) и подставьте полученное выражение в формулу из предыдущего шага: Ас = А²/√(А²+В²).

Если известна длина проекции одного из катетов (Вс) и длина гипотенузы (С), то способ нахождения длины проекции другого катета (Ас) очевиден — просто отнимите от второй известной величины первую: Ас = С-Вс.

Если длины катетов неизвестны, но дано их соотношение (x/y), а также длина гипотенузы (C), то воспользуйтесь парой формул из первого и третьего шагов. Согласно выражению из первого шага, соотношение проекций катетов (Ас и Вс) будет равно соотношению квадратов их длин: Ас/Вс = x²/y². С другой стороны, согласно формуле из предыдущего шага, Ас+Вс = С. В первом равенстве выразите длину ненужной проекции через нужную и подставьте полученное значение во вторую формулу: Ас + Ас*x²/y² = Ас*(1 + x²/y²) = С. Из этого равенства выведите формулу нахождения нужной проекции катета: Ас = С/(1 + x²/y²).

Если известна длина проекции на гипотенузу одного катета (Вс), а длина самой гипотенузы не приведена в условиях, но дана высота (Н), проведенная из прямого угла треугольника, то этого тоже будет достаточно для вычисления длины проекции другого катета (Ас). Возведите высоту в квадрат и разделите на длину известной проекции: Ас = Н²/Вс.

Источники:

формула катета

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Если провести из прямого угла к гипотенузе высоту, то гипотенуза основанием высоты разделится на два отрезка. Каждый такой отрезок называется проекцией соседнего катета. (См. рисунок).
Гипотенуза АВ=25, катет СВ=20.
Так как высота прямоугольного треугольника делит его на подобные, проекцию катета можно вычислить по т.Пифагора из подобия треугольников.
Для этого сначала находят второй катет.
Но из того же подобия выведено, что:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. ⇒
ВС²=АВ•ВН
400=25•ВН, откуда проекция катета ВС на гипотенузу
ВН+400:25=16.

Источник

Пусть треугольник ABC — прямоугольный с прямым углом при вершине B; AB = 30 [см], AC = 60 [см]. Опустим из вершины B высоту на AC в точку D. Требуется найти AD:

Т.к., DB — высота, то треугольники ADB и CDB — прямоугольные. Теорема Пифагора для всех трёх имеющихся треугольников позволяет записать такую систему уравнений:

30^2 + BC^2 = 60^2, (1)

CD^2 + DB^2 = BC^2, (2)

AD^2 + DB^2 = 30^2, (3)

AD + CD = 60. (4)

Из (1), BC^2 = 60^2 — 30^2. Приравниваем к (2) и получаем CD^2 + DB^2 = 60^2 — 30^2. Подставляем сюда CD из (4):

(60-AD)^2 + DB^2 = 60^2 — 30^2 =>

=> 60^2 — 2*60*AD + AD^2 + DB^2 = 60^2 — 30^2 =>

=> AD^2 — 2*60*AD + DB^2 + 30^2 = 0.

В полученное уравнение подставляем DB^2 из (3):

AD^2 — 2*60*AD + 30^2 — AD^2 + 30^2 = 0 =>

=> -2*60*AD = -2*30^2 => 60*AD = 30^2 =>

=> AD = 30^2/(2*30) = 30/2 = 15 [см].

Источник

Как вычислить проекции катетов на гипотенузу.

Если известна гипотенуза 25 и катет 20, пожалуйста помогите, а то понять не могу.

Вы зашли на страницу вопроса Как вычислить проекции катетов на гипотенузу?, который относится к
категории Геометрия. По уровню сложности вопрос соответствует учебной
программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.

Источник