Как найти проэкцию наклонной

Стереометрия

Глава 9. Прямые и плоскости в пространстве

9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью

Определение 1

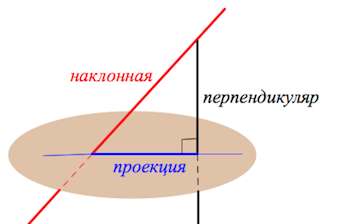
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.

Определение 2

Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).

Определение 3

Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.

Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.

Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.

Следствие

Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).

Определение 4

Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.

Определение 5

Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.

Теорема 5

Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.

Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

AB – перпендикуляр к плоскости α. AC – наклонная, CB – проекция. С – основание наклонной, B – основание перпендикуляра.

У равных наклонных, проведенных к плоскости из одной точки, проекции равны.

Из двух наклонных, проведенных к плоскости из одной точки, больше та, у которой проекция больше.

Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.

Обратная теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

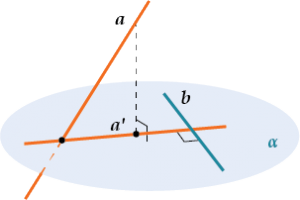
Прямая a, не лежащая в плоскости α, перпендикулярна прямой b, лежащей в плоскости α, тогда и только тогда, когда проекция a‘​​ прямой a перпендикулярна прямой b.

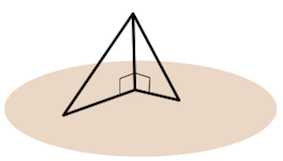
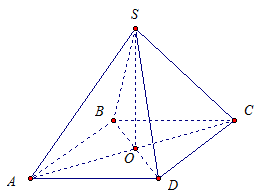
Пример. От­ре­зок SО – пер­пен­ди­ку­ляр к плос­ко­сти квад­ра­та АВСD, где точка О – центр квад­ра­та. До­ка­зать: (BD perp SC).

До­ка­за­тель­ство:

Пер­вый спо­соб.

Имеем квад­рат, центр квад­ра­та точка – О, SО – пер­пен­ди­ку­ляр. Зна­чит, для на­клон­ной SC от­ре­зок ОС есть про­ек­ция.

Пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой ОС, ко­то­рая яв­ля­ет­ся про­ек­ци­ей на­клон­ной SC, зна­чит, по тео­ре­ме о трех пер­пен­ди­ку­ля­рах, пря­мая ВD пер­пен­ди­ку­ляр­на на­клон­ной SC.

Вто­рой спо­соб.

Пря­мая SО пер­пен­ди­ку­ляр­на плос­ко­сти АВС, а зна­чит – и пря­мой ВD, ле­жа­щей в ней.

Пря­мая ВD пер­пен­ди­ку­ляр­на SО и пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой АС по свой­ству квад­ра­та.

По­лу­ча­ем, что пря­мая ВD пер­пен­ди­ку­ляр­на двум пе­ре­се­ка­ю­щим­ся пря­мым плос­ко­сти SОС, зна­чит, она пер­пен­ди­ку­ляр­на ко всей плос­ко­сти SОС, а зна­чит – и к пря­мой SC, ле­жа­щей в этой плос­ко­сти.

Расстояние от точки до плоскости есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ.

1. Если прямая параллельна плоскости, то расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
2. Если две плоскости параллельны, то расстояние от произвольной точки одной из плоскостей до другой называется расстоянием между данными плоскостями.
3. Если две прямые скрещиваются, то расстояние между одной из этих прямых и плоскостью, проведенной через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

План урока:

Понятие перпендикуляра

Расстояния между плоскостями и прямыми

Теорема о трех перпендикулярах

Угол между прямой и плоскостью

Задачи на перпендикуляры, наклонные, расстояния

Понятие перпендикуляра

Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.

Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:

Запомним некоторые геометрические термины. В таком построении:

• отрезок МН – это наклонная;
• отрезок НК – это проекция наклонной, или просто проекция;
• К – основание перпендикуляра;
• Н – основание наклонной.

Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).

Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.

Расстояния между плоскостями и прямыми

Докажем довольно очевидный факт:

Действительно, пусть α и β – параллельные плоскости. Выберем на α произвольные точки М и Р, а далее опустим перпендикуляры из точек М и Р на β, которые пересекут β в точках Н и К соответственно:

Так как МН и РК перпендикулярны плоскости α, то они параллельны. Но также и α||β. Тогда, по теореме 12 из этого урока, отрезки МН и РК одинаковы, ч. т. д.

Этот факт позволяет ввести понятия расстояния между параллельными плоскостями.

Уточним, что если плоскости пересекаются, то расстояние между ними не может быть определено.

Далее рассмотрим случай с плоскостью α и параллельной ей прямой m. Оказывается, и в этом случае точки прямой равноудалены от плоскости.

Действительно, отметим на m произвольную точку К. Далее через K проведем такую плоскость β, что α||β. Так как точки β равноудалены от α, то нам достаточно показать, что m будет полностью принадлежать β:

Так как m и β уже имеют общую точку K, то они m либо пересекает β, либо лежит в ней. Будем рассуждать от противного и предположим, что m и β пересекаются. Так как m||α, то в α можно построить прямую n, параллельную m. Если m пересекает β, то и nтакже должна ее пересекать (по теореме 3 из этого урока). Но если n пересекает β, то точка их пересечения будет одновременно принадлежать и β, и α. То есть у этих плоскостей будет общая точка. Но α и β параллельны и потому не могут иметь общих точек. Значит, на самом деле m и β НЕ пересекаются. Остается один вариант – m принадлежит β, ч. т. д.

Из этой теоремы вытекает понятие расстояния между прямой и плоскостью.

Уточним, что если плоскость и прямая не параллельны, то расстояние между ними определить нельзя.

Осталось понять, как определять расстояние между прямыми в пространстве. Для параллельных прямых определение расстояния известно ещё из курса планиметрии. Естественно, что для пересекающихся прямых расстояние определить невозможно. Остается только случай скрещивающихся прямых.

Пусть прямые m и n скрещиваются. Тогда через n можно построить плоскость α, параллельную m. И наоборот, через m возможно провести плоскость β, параллельную n:

Далее опустим из какой-нибудь точки m перпендикуляр на α. Обозначим этот перпендикуляр как р. Тогда через пересекающиеся прямые m и р можно провести единственную плоскость γ:

Заметим, что плоскости α и γ обязательно пересекутся по некоторой прямой m’, причем m’||m. Действительно, m’ и m не могут скрещиваться, ведь они находятся в одной плоскости γ. Не могут они и пересекаться, ведь в противном случае точка их пересечения была бы общей для m и α, а они параллельны и общих точек не имеют.

Также заметим, что прямые n и m’ пересекаются, ведь они располагаются в одной плоскости α. Параллельными они быть не могут, ведь тогда по свойству транзитивности параллельности получилось бы, что и n||m, а это не так. Обозначим точку пересечения n и m’ буквой K.

Далее через K в плоскости γ проведем прямую р’, параллельную р:

Теперь начнем рассуждения. Если р⊥α, то также р⊥m’. Так как р’||р, то и р’⊥m’, ведь прямая, перпендикулярная одной из параллельных прямых, будет перпендикулярна и второй прямой. По этому же правилу из того факта, что m’||m и р’⊥m’ вытекает, что и m⊥р’. Наконец, если р⊥α, то р⊥n. Для ясности отметим все найденные нами прямые углы на рисунке:

В итоге получилось, что отрезок HK перпендикулярен и n, и m. По этой причине его называют общим перпендикуляром к прямым n и m. Именно он и считается расстоянием между скрещивающимися прямыми m и n.

Отдельно отметим, что HK – это ещё и общий перпендикуляр к α и β. Понятно, что так как р⊥α и р’||р, то и р’⊥α, то есть HK – перпендикуляр к α.

Теперь через точку H проведем прямую n’, параллельную n. Так как β||n, то n’ будет находиться в β (по теор. 6 в этом уроке).

Раз n||n’ и р’⊥n, то и р’⊥n’. Тогда получается, что в β есть сразу две пересекающихся прямых (это m и n’), которые перпендикулярны р’. Поэтому можно утверждать, что р’⊥β, то есть HK– перпендикуляр к β.

Отсюда сразу вытекает ещё один важный вывод – плоскости α и β параллельны, так как имеют общий перпендикуляр.

Итак, мы показали, что общий перпендикуляр можно построить для любых двух скрещивающихся прямых. Но можно построить ещё один такой перпендикуляр? Нельзя, и это можно показать.

Сначала заметим, что второй перпендикуляр нельзя провести через точку К, ведь в таком случае получалось бы, что к m проведены два различных перпендикуляра из одной и той же точки, что невозможно. Аналогично перпендикуляр не может проходить и через Н.

Предположим тогда, что второй перпендикуляр проходит через точки С и D, причем С находится на m, а D находится на n. То есть CD⊥m и СD⊥n:

Проведем через С прямую n’’, параллельную n. Раз СD⊥n и n||n’’, то и СD⊥n’’. При этом n’’ находится в β (это доказывается также, как и в случае с n’). Тогда получается, что в β есть две прямые, n’’ и m, каждая из которых перпендикулярна СD, и при этом n’’ и m пересекаются. Тогда CD⊥β. Из этого вытекает, что СD и HK параллельны, а потому через них можно провести плоскость δ. Этой плоскости будут принадлежать точки С, H, К и D. Но тогда в этой плоскости должны находиться прямые m и n, ведь они имеют с ней по две общих точки. Но m и n – скрещивающиеся прямые, то есть они никак не могут находиться в одной плоскости. Это противоречие означает, что второй общий перпендикуляр CD не существует.

Итак, из всех наших рассуждений мы можем сделать следующие выводы:

Теорема о трех перпендикулярах

Сформулируем важное утверждение, которое называют теоремой о трех перпендикулярах.

Проиллюстрируем теорему с помощью картинки:

Доказательство этой теоремы очень простое. Так как МК⊥α, то также МК⊥m. Теперь рассмотрим расположение плоскости МНК и прямой m. МК⊥m и HK⊥m. Тогда по признаку перпендикулярности можно утверждать, что m перпендикулярна всей плоскости HM, то есть каждой находящейся в ней прямой. В частности, m⊥HK, ч. т. д.

Оказывается, верно и обратное утверждение (так называемая обратная теорема о трех перпендикулярах):

Доказательство аналогично предыдущему. Так как m⊥MH и m⊥MK, то m⊥HMK. Отсюда вытекает, что и m⊥HK.

Угол между прямой и плоскостью

Проекция наклонной позволяет ввести такое понятие, как угол между прямой и плоскостью.

Пусть надо определить угол между прямой HM и плоскостью α:

Здесь надо просто построить перпендикуляр МК. В результате появится отрезок HK– проекция HM на α. Тогда угол между HM и HK, то есть ∠MHK, как раз и будет углом между HM и α.

Однако не всегда таким образом можно построить проекцию прямой. Проблемы возникнут, если прямая либо параллельна, либо перпендикулярна плоскости. В таких случаях используются такие правила:

Задачи на перпендикуляры, наклонные, расстояния

Рассмотрим несколько задач, в каждой из которых рассматривается куб АВСDEFGH. При этом предполагается, что ребро такого куба имеет длину, равную единице.

Задание. В кубе АВСDEFGH найдите расстояние между точкой А и гранью CDHG:

Решение. Ребро AD перпендикулярно грани DH (так как AD⊥DH и AD⊥CD). Поэтому как раз АD и является расстоянием между А и СDHG. Значит, оно равно единице.

Ответ: 1.

Примечание. Для решения следующих задач запомним, что ребро DH перпендикулярно грани АВСD. Вообще в кубе все ребра, пересекающиеся с гранями, перпендикулярны таким граням.

Задание. Найдите в кубе расстояние между вершиной А и плоскостью BDH:

Решение. Проведем на грани АВСD перпендикуляр АК из А к прямой BD:

Докажем, что АК – перпендикуляр в BDH. Для этого надо найти две прямые в BDH, перпендикулярные АК. Первая такая прямая – это BD (мы специально провели АК⊥BD). Вторая такая прямая – это DH. Действительно, DH перпендикулярна всей грани АВСD, а значит, и прямой АК.

Теперь найдем длину АК. Ее можно вычислить из прямоугольного ∆АКD. В нём ∠ADB =45°, ведь это угол между стороной квадрата АВСD и его диагональю.

Найти АК можно с помощью тригонометрии в ∆АКD:

Задание. Найдите расстояние от H до плоскости EDG:

Решение. Обозначим середину отрезка ЕD буквой М.Далее в ∆МНG опустим высоту из НК на сторону MG:

Попытаемся доказать, что HK – это перпендикуляр к EDG. Заметим, что ∆HDG и ∆EHG равны, ведь у них одинаковую длину имеют ребра DH, EH, ребро GH – общее, а ∠DHG и ∠EHG прямые. Тогда одинаковы отрезки EG и DG. Это означает, что ∆EGD – равнобедренный.

В ∆EGDMG– это медиана. Так как ∆EGD – равнобедренный, то MG одновременно ещё и высота, поэтому MD⊥MG.

Аналогично ∆EHD– равнобедренный (EH = HD), а потому MH в нем – и медиана, и высота. Поэтому MD⊥MH.

Получили, что MD перпендикулярен и MH, и MG, то есть двум прямым в плоскости MHG. Тогда MD перпендикулярен всей плоскости MHG, и, в частности, отрезку HK: HK⊥MD.

Но также MD⊥MG. Получается, KH перпендикулярен двум прямым в плоскости EDG, и потому он является перпендикуляром к плоскости EDG. Значит, именно его длину нам и надо найти.

Рассмотрим ∆MDH. Он прямоугольный, а ∠MDH = 45° (угол между стороной и диагональю квадрата). Тогда длину MH можно найти так:

Так как ребро GH перпендикулярно грани АЕНD, то ∆MHG – прямоугольный. Тогда по теореме Пифагора можно найти MG:

Далее можно найти HK разными способами, но проще воспользоваться подобием ∆MHG и ∆MKH. Они оба – прямоугольные, и у них есть общий угол ∠KMH, этого достаточно для подобия треугольников. Записываем пропорцию:

Здесь слева записано отношение сторон, лежащих против ∠KMH, а справа – отношение сторон, лежащих против прямых углов (то есть отношение гипотенуз). Используем пропорцию дальше:

Задание. Найдите расстояние между прямыми ВС и DH:

Решение. ВС и DH – скрещивающиеся. Надо найти общий перпендикуляр к ним. В данном случае он очевиден – это отрезок CD. Действительно, CD⊥ВС как стороны квадрата АВСD, но и DH⊥CD как стороны в другом квадрате, СDHG.. Длина же ребра CD равна единице, ведь у куба все ребра одинаковы.

Ответ: 1.

Задание. Каково расстояние между прямыми ВС и DG:

Решение.На грани СDHG опустим из С перпендикуляр СК на диагональ GD:

Будет ли СК являться расстоянием между ВС и DG? Ясно, что СК⊥DG. При этом ребро ВС перпендикулярно грани СGHD, так как ВС⊥СG и ВС⊥СD. Значит, также ВС⊥СК. То есть СК – общий перпендикуляр к ВС и DG, и по определению как раз и является искомым расстоянием.

Длину СК найдем из прямоугольного ∆СKG. ∠СGK составляет 45°, ведь это угол между диагональю DG и стороной квадрата СG. Тогда можно записать:

Задание. Найдите расстояние между ребрами АВ и HG:

Решение. Здесь ребра АВ и HG параллельны, так как каждая их них параллельна ребру CD. Проведем отрезок АН. Так как и АВ, и HG перпендикулярны грани АЕНD, то эти ребра одновременно перпендикулярны и АН. То есть АН – общий перпендикуляр к АВ и HG, и поэтому именно его длину и надо найти.

Сделать это можно из прямоугольного ∆АНD, в котором ∠НАD составляет 45°:

Задание. Чему равно расстояние между ребром AB и диагональю FD:

Решение. Пусть А₁, D₁, H₁ и Е₁ – середины ребер АВ, DC, HG, и EF соответственно. Проведем через А₁, D₁, H₁ плоскость. Диагональ FD пересечет ее в какой-нибудь точке К:

Сначала покажем, что плоскости α и ADH (то есть нижняя грань) параллельны.

Заметим, что в четырехугольнике АА₁D₁D стороны АА₁ и DD₁ параллельны (ведь они лежат на сторонах квадрата АВСD) и одинаковы (ведь они составляют половину от длины ребер АВ и CD, то есть имеют длину 0,5). Тогда АА₁D₁D – параллелограмм. Более того, раз у него есть прямые углы ∠А₁АDи ∠АDD₁, то можно утверждать, что АА₁D₁D – прямоугольник. Тогда АD||A₁D₁. Аналогично можно показать, что DHH₁D₁ – прямоугольник, и DH||D₁H₁.

Далее можно действовать разными способами. Первый способ – это использование признака параллельности плоскостей (теорема 9 из этого урока). Так как в α есть пересекающиеся прямые А₁D₁и D₁H₁, а в плоскости ADH находятся прямые AD и DH, и АD||A₁D₁, и DH||D₁H₁, то по этому признаку α||ADH.

Однако, если этот признак вдруг оказался «забыт», то можно использовать отрезок DD₁. Он перпендикулярен и грани ADHE, и плоскости α, ведь в каждой из них есть по две прямых, перпендикулярных ему. Это AD и DH на грани ADHE и A₁D₁и D₁H₁ в α. Тогда α и ADH перпендикулярны одной и той же прямой, а потому они параллельны. Так или иначе, мы выяснили, что α||ADH.

Отсюда вытекает, что α должна проходить через середину Е₁. Действительно, расстояние между параллельными плоскостями не зависит от выбора точек измерения. В данном случае оно равно отрезку АА₁, то есть 0,5. Но FE– это также общий перпендикуляр к α и ADH. Значит, α пересекает FE в точке, находящейся на расстоянии 0,5 от Е. А это как раз и есть середина FE, то есть точка Е₁.

Далее докажем, что точка К, в которой прямая FD пересекает α – это середина отрезка Е₁D₁. Для этого удобно отдельно показать плоскость, проходящую через параллельные ребра FE и CD, то есть четырехугольник FEDC:

Заметим, так как ребра FE и CD перпендикулярны верхней и нижней грани, то они перпендикулярны и отрезкам FC и ED, то есть FEDC прямоугольник. Тогда FC||ED, и ∠Е₁FD = ∠D₁DF (накрест лежащие углы при секущей FD). ∠FKE₁ и ∠DKD₁ одинаковы уже как вертикальные углы. Тогда ∆FKE₁ и ∆DKD₁ подобны по 2 углам. Но отрезки FE₁ и DD₁ одинаковы как половины равных ребер FE и CD. Получается, что ∆FKE₁ и ∆DKD₁ равны, и поэтому Е₁К = KD₁. Это и значит, что К – середина Е₁D₁.

Также отметим, что Е₁D₁ – диагональ в четырехугольнике А₁Е₁Н₁D₁. Докажем, что А₁Е₁Н₁D – это квадрат. Ранее мы уже показали, что АА₁D₁D и DHH₁D₁ – прямоугольники. Аналогично можно продемонстрировать, что прямоугольниками являются также АА₁Е₁Е и ЕЕ₁Н₁Н. Из этого вытекает равенство сторон:

То есть в А₁Е₁Н₁D₁ все стороны одинаковы, и эта фигура – ромб. Теперь надо показать, что и углы в этом четырехугольнике составляют 90°. Продемонстрируем это на примере ∠А₁D₁H₁. AD⊥CDHG и AD||A₁D₁, поэтому А₁D₁⊥CDHG. Значит, также А₁D перпендикулярна любой прямой на грани CDHG, в том числе и D₁H₁. То есть ∠А₁D₁H₁ = 90°. Но если в ромбе хотя бы один угол прямой, то он является квадратом.

Итак, мы выяснили, что А₁Е₁Н₁D₁ – квадрат, а К – середина его диагонали Е₁D₁. Получается, что К – точка пересечения диагоналей квадрата А₁Е₁Н₁D₁, ведь эта точка пересечения как раз делит диагонали пополам.

Теперь мы можем наконец доказать, что А₁К – это и есть искомое расстояние. Действительно, так как АВ – перпендикуляр к α, та А₁К принадлежит α, то А₁К⊥АВ. Но как же доказать, что А₁К⊥FD. Здесь поможет теорема о трех перпендикулярах. Е₁К – это проекция FK на α, и Е₁К⊥А₁К, ведь диагонали квадрата пересекаются под прямым углом. Раз отрезок А₁К перпендикулярен проекции, то он перпендикулярен и самой наклонной, то есть А₁К⊥FK.

Осталось лишь вычислить длину А₁К. Для этого по аналогии с предыдущими задачами используем прямоугольный∆А₁Е₁К, в котором ∠А₁Е₁К = 45°:

Отвлечемся от куба и рассмотрим другую задачу.

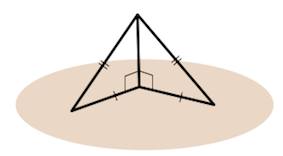
Задание. В ∆АВС вписана окружность. Через центр этой окружности (точку О) проведена прямая ОН, причем она перпендикулярна плоскости АВС. Верно ли, что точка Н находится на одинаковом расстоянии от прямых АВ, АС и ВС?

Решение. Пусть N, K и M – точки касания окружности и сторон АВ, АС и ВС соответственно. Тогда ОN, OK и OM– радиусы, а они должны быть перпендикулярны касательным, то есть

Заметим, что ОN, OK и OM – это также проекции прямых HN, HK и HM соответственно. Раз отрезки АВ, АС и ВС перпендикулярны этим проекциям, то они должны быть перпендикулярны и наклонным:

Это значит, что HN, HK и HM– это расстояния от H до сторон ∆АВС. Осталось показать, что они одинаковы. Это можно сделать с помощью ∆HON, ∆HOK и ∆HOM. Они все прямоугольные, причем катет OH– общий, а катеты ON, OM и OK одинаковы как радиусы одной окружности. Отсюда вытекает вывод, что эти треугольники равны, то есть одинаковы и их гипотенузы HN, HKи HM, ч. т. д.

Теперь снова вернемся к кубу, чтобы на практике научиться определять угол между прямой и плоскостью.

Задание. Найдите угол между ребром куба BD и гранью СDHG:

Решение. ВС – это перпендикуляр к грани СDHG, поэтому CD– проекция BD на грань СDHG. Тогда нам надо найти ∠BDC. Он составляет 45°, так как это угол между стороной и диагональю квадрата АВСD:

Ответ: 45°.

Задание. Вычислите угол между ребром CD и плоскостью BDHF:

Решение. Нам надо из С опустить перпендикуляр на BDHF. Несложно догадаться, что для этого надо на грани ABCD опустить перпендикуляр СК на диагональ BD:

Действительно, СK⊥BD. Надо найти ещё одну прямую в BDHF, перпендикулярную СК. И такой прямой может быть BF. Так как BF перпендикулярна всей грани АВСD, то она обязательно перпендикулярна и СК. Получаем, что СК⊥BF и CK⊥BD, и тогда СK⊥BDHF.

Если СK– перпендикуляр, то KD – это проекция СD. Тогда искомый нами угол – это ∠СDK. Он равен 45°, ведь BD – диагональ квадрата АВСD, а CD – его сторона.

Ответ: 45°

Задание. Чему равен угол между прямой BD и плоскостью ABGH:

Решение. На нижней грани АЕНD опустим на АН перпендикуляр DK:

Заметим, что ребро АВ перпендикулярно грани АЕНD, поэтому KD⊥АВ. Но также KD⊥AH (мы специально построили так KD). Тогда можно утверждать, что KD – это перпендикуляр ко всей плоскости АВGH.

В таком случае BK – это проекция BD на AB. Значит, нам необходимо вычислить ∠DBK. Его можно найти из прямоугольного ∆DBK, но сперва надо вычислить длины сторон KD и BD.

ВD найдем из прямоугольного ∆ABD:

Теперь мы можем найти ∠DBK, а точнее его синус, из ∆DBK:

По таблице синусов легко определить, что ∠DBK = 30°.

Ответ: 30°.

В ходе сегодняшнего урока мы узнали о перпендикуляре к плоскости. Перпендикуляры используются для определения расстояний в стереометрии, а также угла между прямой и плоскостью.

Государственное
бюджетное образовательное учреждение

профессиональная
образовательная организация

«Магнитогорский
технологический колледж имени В.П.Омельченко»

 

Методическая разработка

урока по математике

Тема: «Наклонная и ее проекция»

Разработчик: преподаватель   Шаранова Т.Б.

Магнитогорск

2017г

Введение.

Методическая
разработка урока усвоения новых знаний по математике   по теме «Наклонная и ее проекция» предназначена для текущего урока  по
разделу: « Геометрия»  

Методическая идея проведения урока усвоения новых знаний с использованием интерактивных технологий , воплощенная в
данной разработке и реализованная преподавателем, способствует воспитанию чувств коллективизма,;
развитию сотрудничества педагога и учащихся; развитию познавательного интереса
к математике, навыков  вычислительной культуры
при решении задач, внимательности,  аккуратности и трудолюбия;
реализации внутрипредметных и межпредметных связей, формирует у учащихся
целостную научную картину мира.

 

Методическая разработка включает в себя:

·       
Технологическую карту урока
усвоения новых знаний;

·       
Описание хода урока;

·       
Отражение собственного опыта проведения урока.

 

Проведение урока
усвоения новых знаний по данному
разделу подразумевает не только взаимосвязь знаний по разным темам на одном
занятии, но и интегрирование педагогических технологий, методов и форм обучения
в пределах занятия.

Данная
методическая разработка может быть рекомендована к использованию в средних
профессиональных учебных заведениях.

План урока

теоретического обучения

1. Тема урока: «Наклонная и ее проекция».

2. Тип урока: урока усвоения новых знаний

3. Форма проведения урока: Комбинированный.

 

 

Параметры качества обучения

4. Цели урока

Воспитательная:  Воспитание положительной мотивации и
интереса к изучению математики, ориентации на успех, корпоративной культуры,
коммуникативных навыков. умения
рационально использовать рабочее время, организованности, дисциплинированности, навыков  вычислительной культуры при решении задач,
внимательности,  аккуратности и трудолюбия.

Развивающая: Развитие профессионально-значимых
психофизиологических свойств личности: мыслительных опера­ций (анализ, синтез,  обобщение);
произвольного внимания; смысловой памяти; интеллектуальных
чувств любознательности, стремления к новому, прогрессивному,
удовлетворения от правильно выполненного задания.

Обучающая: сформировать  знания о понятиях перпендикуляра и наклонной, умения
решать  простейшие стереометрические задачи на вычисление расстояния от точки
до плоскости, длин наклонной и её проекции.

Знать:

•                  
определения и теоремы о
перпендикулярности в пространстве;

•                  
определения понятий
«перпендикуляр», «наклонная»;

Уметь:

•                  
распознавать на чертежах и
моделях пространственные формы; соотносить трехмерные объекты с их описаниями,
изображениями;

 5. Методическая характеристика урока

Метод	Методический прием	Средства обучения
Методы стимулирования и мотивации интереса к учению.	Создание   ситуаций   познавательной новизны. Поощрение в учении.	Постановка проблемы Примеры использования стереометрический понятий применения в жизни, в профессиональной деятельности. Психологическое поглаживание.
Словесный.	Проблемная беседа.	1)                  Вопросник; 2)                  Атанасян, Л. С.  и др.  «Геометрия,  10-11: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др. – 11-е изд. —  М.: Просвещение, 2002. – 206с.
Наглядно-демонстрационный.	— Использование ИКТ. — Использование доски, цветных мелков	-Презентация. -Доска, цветные мелки, -примеры на доске.
Практический.	Решение задач. -Алгоритмическая запись на доске и в тетрадях решения типовых задач; -Разбор разных способов решения задач на наклонную и ее проекцию; -Оформление конспекта.	— Атанасян, Л. С.  и др.  «Геометрия,  10-11», стр. 40 – 42, 44-46, §2, п. 19-20 — Доска, мел, тетради, ручки
Методы контроля.	— Входной контроль. — Текущий контроль. — Самоконтроль. — Взаимоконтроль.	Вопросник. Задания на доске Раздаточный материал: дидактические карточки по вариантам Критерий оценок.

6. Ход урока

№ и название этапа	Дидактические задачи этапа	Деятельность преподавателя	ЦОР	Рефлексивная деятельность учащихся
1	2	3	4	5
I. Организационный этап.	Подготовка учащихся к работе на уроке.	Предъявление единых педагогических требований: —          приветствие; —          выявление отсутствующих на уроке; —          проверка внешнего вида (соответствие требованиям внутреннего распорядка лицея).		Отвечают на приветствие. Староста докладывает о явке учащихся на занятие. Приводят в соответствие с требованиями внешний вид, рабочее место.
	Психологическая установка на восприятие материала урока.	Организация внимания и готовности учащихся к уроку (устранение отвлекающих факторов: посторонний шум, лишние предметы на рабочем месте).		Готовятся к восприятию урока.
II. Вводный этап урока.	Подготовка к основному этапу урока.
Проверка домашнего задания.	Установление правильности и полноты выполнения домашнего задания.	Организация контроля знаний и умений учащихся и коррекция		Самоосмысление учебного материала.
Мотивация.	Обеспечение возникновения у учащихся мотива – внутреннего побудителя деятельности, придающего ей личностный смысл и соответствующего требованиям учения и будущей профессии.	-Знаете ли вы как называется процесс получения неразъёмных соединений посредством установления межатомных связей между свариваемыми частями при их местном или общем нагреве, пластическом деформировании или совместном действии того и другого? — Правильно, сва́рка  — А как называется неразъёмное соединение, выполненное с помощью сварки? — сварным соединением; — А какими основными умениями должен обладать сварщик? —производить сварку конструкций во всех пространственных положениях сварного шва и уметь читать рабочие чертежи и схемы; Рассмотрим сварку закладных деталей.    Закладные детали – это специальные металлические элементы, которые состоят из полосовой, круглой, уголковой стали.  Бывают открытые закладные конструкции и закрытые, закладные детали с перпендикулярными, параллельным, наклонным или же смешанным размещением анкерных стержней (последние могут быть с резьбой).  Т.о., простейшие приемы сварки вполне доступы, нужно иметь богатую фантазию и хорошо владеть сварочными аппаратами. От того как вы привариваете детали, можно получить нужную конструкцию. Скажите, как с точки зрения геометрии можно  расположить деталь относительно плоскости (поверхности)? (Предполагаемый ответ: параллельно, перпендикулярно и под углом). Совершенно верно, причем в геометрии для каждого такого положения детали– «прямо» и « под углом» есть свое название: перпендикуляр и наклонная, а для их стыковки на плоскости  —  «проекция наклонной». Сегодня на уроке мы  и познакомимся с этими геометрическими понятиями.		Осмысливают значимость материала данного урока в формировании профессионального опыта.
Сообщение темы		Тема сегодняшнего урока: «Наклонная и ее проекция». Запишите тему в тетради.		Слушают название темы. Записывают в тетрадь.
Постановка цели.	Обеспечение самоосмысления через постановку цели.	Перед вами стоит следующая цель: Знать: •определения и теоремы о перпендикулярности в пространстве; •определения понятий «перпендикуляр», «наклонная»; уметь: •распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями; •описывать взаимное расположение прямых и плоскостей в пространстве; анализировать в простейших случаях взаимное расположение объектов в пространстве.		Учащиеся осмысливают и записывают цель в терминалах «иметь представление», «знать», «уметь».
Входной контроль.	Актуализация опорных знаний. Реализация связей: —    межпредметных (производственное обучение – спецпредметы – общеобразовательные предметы); —    внутрепредметных (материал предыдущих и данного уроков).	Входной контроль. Входной тест  проводить в виде фронтального опроса все задачи решаются устно (См. приложение №1). Вопросы базовых дисциплин или предыдущих уроков: 1) Сформулируйте теорему Пифагора. 2)       Продолжить фразу: «Прямая d перпендикулярна плоскости β, если …» Ответ: 1) называют определение перпендикулярности прямой и плоскости;  2)называют  признак перпендикулярности прямой и плоскости		Отвечают на вопросы. Сравнивают свои ответы с эталонами (прилагаются).  Определяют Ку – коэф. усвоения Ку = РпрР, где Р – общее число существенных операций (ответов), Рпр. – число правильно выполненных существенных операций (ответов).
Коррекция опорных знаний.	Выявление пробелов и внесение исправлений, поправок в опорных знаниях учащихся.	Разбор вопросов, вызвавших затруднения. Доведение до Ку=0,7 опорных знаний.		Определяют и восполняют пробелы в знаниях.
Организация взаимопомощи	Сильные помогают более слабым.
II. Формирование  ориен-тировчной основы учебной деятельности. Получение новой информации.	Обеспечение восприятия и осмысления способов действий.	Разберём  возможное применение понятия перпендикулярности прямой. Изобразите рисунок у себя в тетради. Возьмём на данной прямой некоторую точку А. Назовите понятие, которое определяет прямая по отношению точки А и плоскости.		С помощью перпендикулярной прямой можно определить расстояние от точки А до данной плоскости.
Отрезок АО называют расстоянием от точки А до данной плоскости, под которым понимают длину перпендикуляра опущенного на данную плоскость из данной точки.		Осмысливают . Записывают в тетради.
АО – перпендикуляр. Можно вместе с учащимися сформулировать определение данного понятия и затем записать в тетради.		С помощью преподавателя формулируют определение перпендикуляра
		Через точку А можно провести различные прямые, назовите прямую проходящую под прямым углом. Назовите прямые, проходящие через точку А  под углом к плоскости меньше  900.		Прямая проходящая под прямым углом к плоскости является перпендикулярной прямой к плоскости. Такие прямые можно назвать наклонные.
		Сформулируем определение наклонной прямой, и записывают его в тетради.		С помощью преподавателя формулируют определение наклонной.
		Проведя различные прямые, мы получили множество точек в пересечении этих прямых и плоскости. Назовём их: О – основание перпендикуляра. С — основание наклонной.		Записывают новые понятия.
		Мы назвали два отрезка: АО-перпендикуляр, АС – наклонная. Остался ещё один отрезок СО, соединяющий основания перпендикуляра и наклонной. Этот отрезок называют проекцией наклонной. Запишите это определение (можно пояснить, что СО состоит из совокупности точек, являющихся проекциями точек прямой АС).		Записывают новые понятия.
Первичное закрепление базисного уровня	Обеспечение репродуктивного воспроизведения материала на основе алгоритма действий.	Итак, перечислите понятия, с которыми мы познакомились.		АО – перпендикуляр, АС – наклонная, СО – проекция наклонной.
Проверка понимания алгоритма действий.	Определение возможности допуска студентов к самостоятельной работе.	Рассмотрим задачи на закрепление данных понятий.  (см. Приложение № 2) Задача 1. Из точки А на плоскость опущен перпендикуляр длиной 4 см и проведена наклонная длиной 5 см. найдите длину проекции наклонной.		Отвечают на вопросы. Воспроизведение знаний ориентировочной основы действий. С помощью преподавателя решают данную задачу (метод решения: Th Пифагора).
Организация самоконтроля.	Сравнение своих ответов с эталонами Ответ: 3 см
Закрепление базисного уровня.	Обеспечение репродуктивного воспроизведения материала.	Задача 2. Из точки к плоскости проведены перпендикуляр и наклонная. Длина наклонной равна 8 см., а угол между ею  и перпендикуляром равен 600. Найти длины перпендикуляра и проекции наклонной.		Метод решения: 1 способ: можно воспользоваться соотношениями Sin, Cos, Tg. 2 способ: угол между наклонной и её проекцией равен 300. Следовательно, перпендикуляр равен 4см. Длину проекции можно найти с помощью Th Пифагора.
Организация самоконтроля.	Сравнение своих ответов с эталонами Ответ: 4 см, 4√3 см.
Проверка понимания алгоритма действий.	Определение возможности допуска учащихся к итоговому тесту.	Задача 3. Из точки А к плоскости проведены две наклонные равные 10 см и 12 см. разность проекций этих наклонных равна 9 см. найдите проекции наклонных.		С помощью преподавателя решают данную задачу (Метод решения: рассматривается два прямоугольных треугольника, для которых по теореме Пифагора записываются формулы для вычисления длины перпендикуляра. Из этих формул приравниваются правые части, не содержащие отрезок-перпендикуляр и решается квадратное уравнение).
Организация самоконтроля.	Сравнение своих ответов с эталонами Ответ: 6см и 15 см.
Коррекция знаний ориентировочной основы действий	Выявление пробелов и исправление ошибок в понимании ориентировочной основы действий.	Организация взаимопомощи.		Определяют и восполняют пробелы в знаниях. Задают вопросы. Сильные помогают более слабым.
III. Основной этап работы. Самостоятельная работа студентов по применению полученных знаний.	Обеспечение самореализации через саморегуляцию и  самоосмысление. Обеспечение усвоения новых знаний и способов действий на уровне применения в знакомой и измененной ситуации.	Предлагается выполнить итоговый контроль  по индивидуальным карточкам  (см. Приложение № 3)		Самостоятельное выполнение заданий с применением знаний в знакомой и измененной ситуациях.
IV. Заключительный этап урока	Анализ и оценка успешности достижения цели урока.	Подвести итоги за урок Анализ работы каждого учащегося. Сообщить оценку качества работы каждого учащегося. Отметить, кто достиг отличного качества работы. Разобрать наиболее характерные недочёты  в работе учащихся и рекомендации по их устранению.	Слайд текст с целями проведённого мероприятия.	Самоанализ выполненной работы. Самокоррекция. Самооценка. Развитие творческих способностей. Саморегуляция.
Мотивация.	Формирование у учащихся ориентации на успех.	Поощрение учащихся в процессе достижения ими поставленной цели (в т.ч. слабых).		Самоактуализация Саморегуляция через достижения цели
Домашнее задание.	Обеспечение понимания цели домашнего задания. Обеспечение понимания содержания и способов выполнения домашнего задания.	1) Выучить определения перпендикуляра, наклонной и проекции наклонной, признак перпендикулярности прямой и плоскости 2) Домашнее задание. Атанасян, Л. С.  и др.  «Геометрия,  10-11», с 40-42, №139.		Самоосмысливают способов выполнения домашнего задания.
Постановка новой цели к следующему уроку.	Создание мотивации через анализ результатов  достигнутого, развивает аналитико – синтетическую деятельность учащихся.	— Тема следующего урока: «Плоскости в пространстве.».  На следующем уроке мы рассмотрим: Двугранный угол Перпендикулярные плоскости.  Параллельные плоскости.		Самоосмысление информации о задачах на ближайший урок.

Приложение № 1.

1)     
Решить квадратное
уравнение: х² + 3х – 4 = 0

2)     
Вычислить длину гипотенузы
прямоугольного треугольника, если длины его катетов равны 2см и 3
см.

3)     
Длина одного из катетов
прямоугольного треугольника равен 4см, острый угол 30⁰. Вычислите длины
гипотенузы и второго катета.

(Можно предложить учащимся
данные задания в 2 вариантах)

Приложение №2

Тема: «Перпендикуляр и наклонная»
	АС – перпендикуляр – отрезок, соединяющий данную точку с точкой плоскости и лежащий  на прямой, перпендикулярной плоскости. АВ – наклонная – любой отрезок, соединяющий данную точку с точкой плоскости и не являющийся перпендикуляром. ВС – проекция наклонной  —  отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки. Точка С — основание перпендикуляра — конец перпендикуляра, лежащий в плоскости. Точка В — основание наклонной  — конец наклонной, лежащий в плоскости.
Примеры решения задач
Задача 1. Из точки на плоскость проведены перпендикуляр и наклонная длиной 10 см. Найдите длину перпендикуляра, если длина проекции наклонной равна 6см.	Задача 2. Из точки  к плоскости проведены две наклонные, длины проекций которой  которых равны 9см и 5см. Найдите длины наклонных, если разность их длин равна 2 см.
	Дано: АС – перпендикуляр, АВ – наклонная, ВС – проекция наклонной, ВС = 6см. АВ = 10см, Найти: АС.		Дано: АС – перпендикуляр, АВ и АД – наклонные, ВС и СД – проекции наклонных АВ и АД, ВС = 10см, СД = 6см, АВ – АД = 2см → АВ =  АД + 2 (см). Найти: АД,  АВ
Решение: Рассмотрим  Δ АВС – прямоугольный (АС – перпендикуляр).  По теореме Пифагора:  АС2 = АВ2 — ВС2 , АС2 = 102 — 62 = 100 — 36 = 64, АС = 8см. Ответ: 8см.	Решение:  Рассмотрим Δ АСВ и  Δ АСД – прямоугольные  (АС – перпендикуляр).    АС – общая сторона. По теореме Пифагора: Из Δ АСВ: АС2 = АВ2 — ВС2, Из Δ АСД: АС2 = АД2 — СД2, Т.к. левые части уравнений равны, то должны равняться и правые части, поэтому справедливо следующее равенство: АВ2 — ВС2 = АД2 — СД2.  Пусть АД = х см,   тогда  АВ = х + 2 (см). Получаем  (х+2)2 — 102 = 62 -х2; х2 + 2х + 4  —  100 = 36 -х2; х2 + 2х + х2 = 36  + 96;  2х = 132;                     х = 66 см – длина наклонной АД. АВ = 66 + 2 = 68 см.                                                    Ответ: 66 см, 68 см.