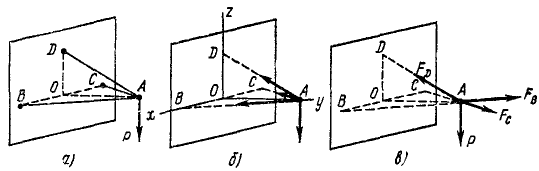
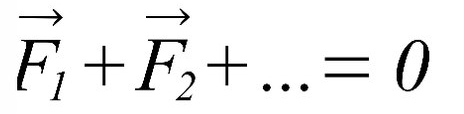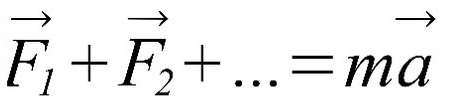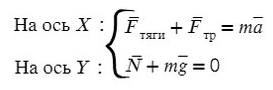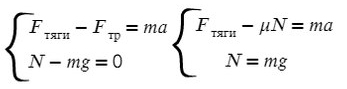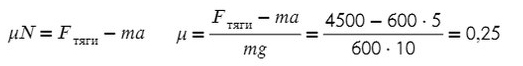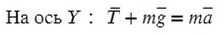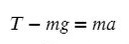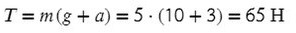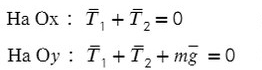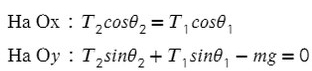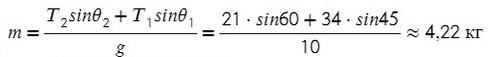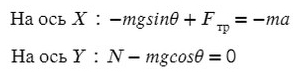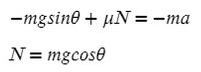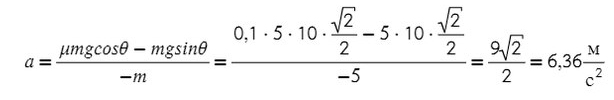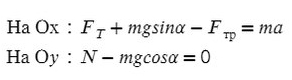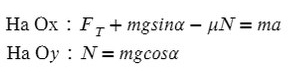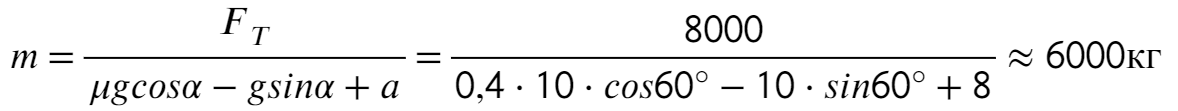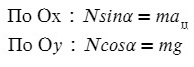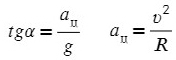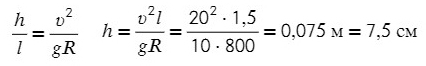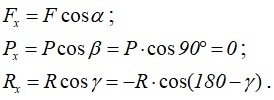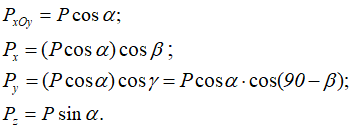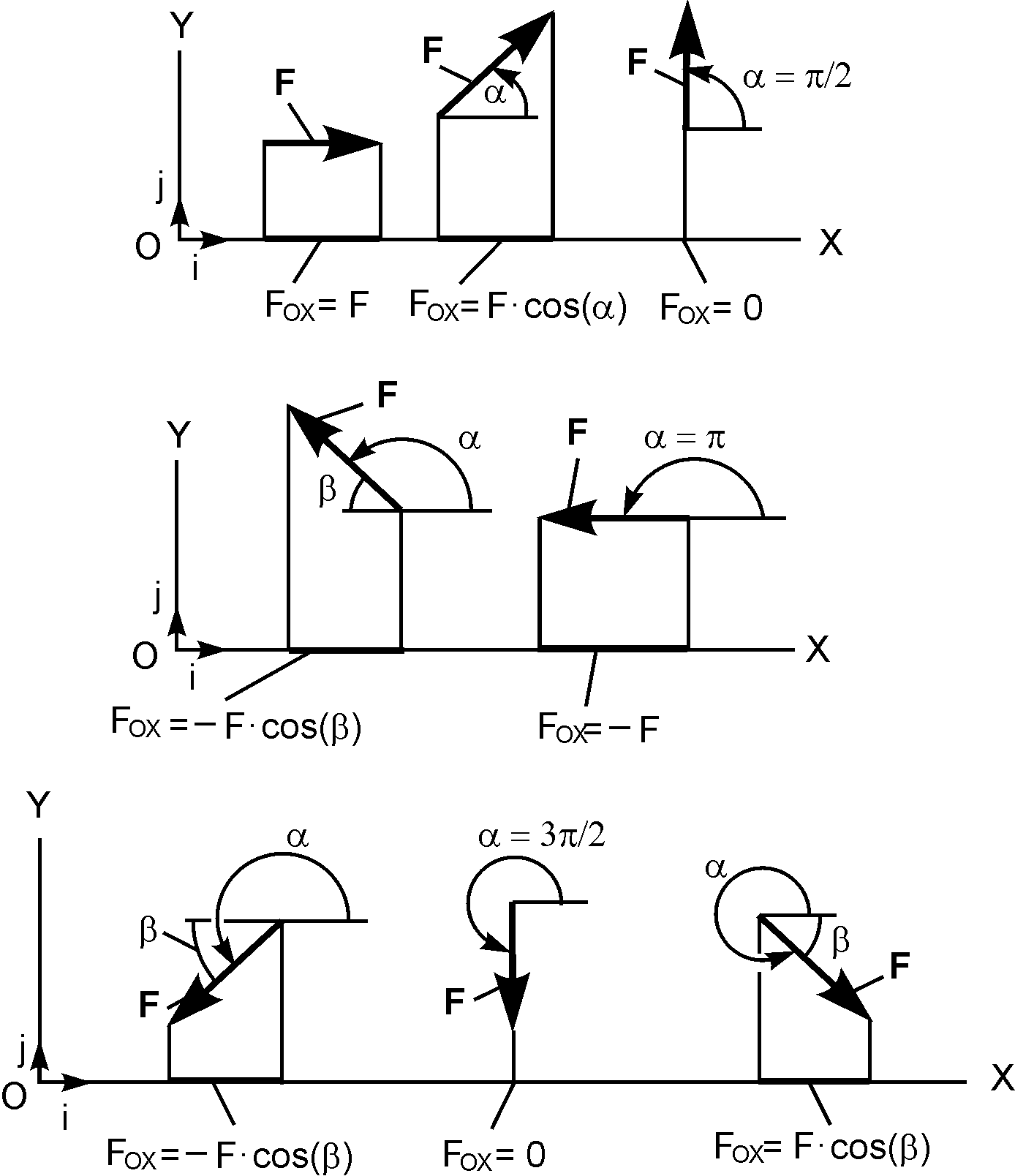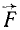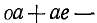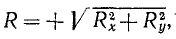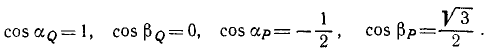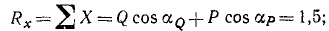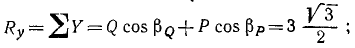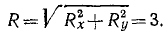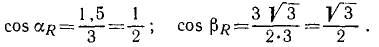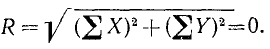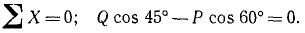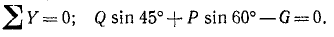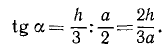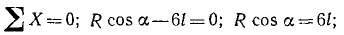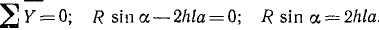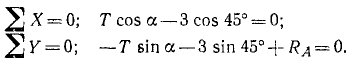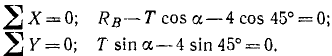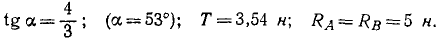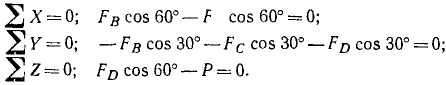Проецирование сил. Движение по наклонной плоскости
Задачи по динамике.
I и II закон Ньютона.
Ввод и направление осей.
Неколлинеарные силы.
Проецирование сил на оси.
Решение систем уравнений.
Самые типовые задачи по динамике
Начнем с I и II законов Ньютона.
Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.
I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.
II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.
При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².
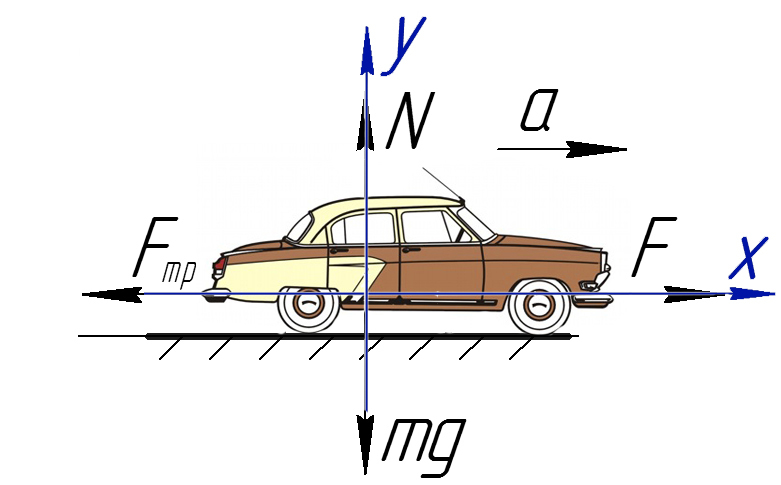
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:
На Ось Х: движение с ускорением
На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.
По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.
Получаем, что:
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.
Ответ: 0,25
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.
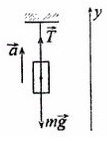
Сделаем рисунок, покажем силы, которые дествуют на груз
T — сила натяжения нити
На ось X: нет сил
Разберемся с направлением сил на ось Y:
Выразим T (силу натяжения) и подставим числительные значения:
Ответ: 65 Н
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.
Далеко не всегда все силы, действующие на тело, направлены вдоль осей.
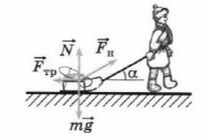
Простой пример: мальчик тянет санки
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.
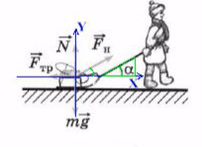
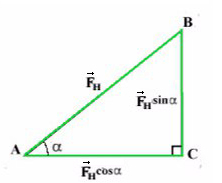
Отношение противолежащего катета к гипотенузе — это синус.
Отношение прилежащего катета к гипотенузе — это косинус.
Сила тяги на ось Y — отрезок (вектор) BC.
Сила тяги на ось X — отрезок (вектор) AC.
Если это непонятно, посмотрите задачу №4.
Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.
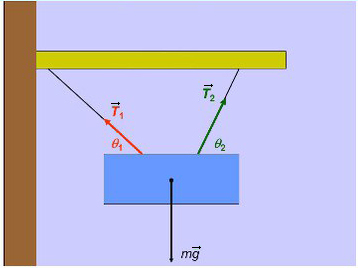
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.
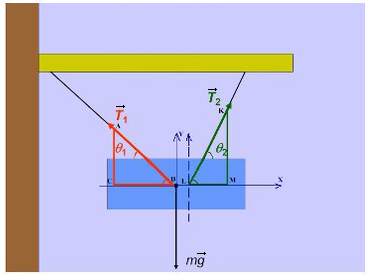
Введем оси и спроецируем силы:
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.
Ответ: 4,22 кг
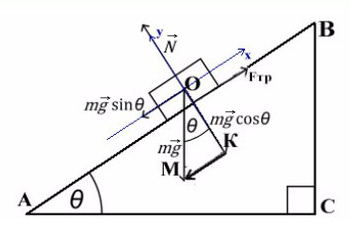
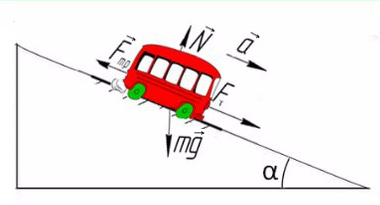
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
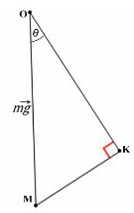
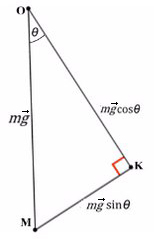
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).
Рассмотрим поподробнее ΔKOM:
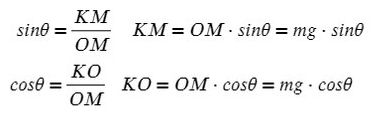
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!
Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:
Ответ: 6,36 м/с²
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.
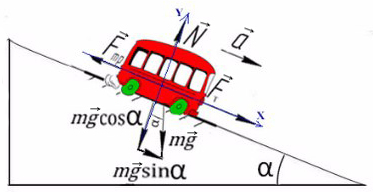
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.
Сделаем рисунок с силами:
Введем оси X и Y. Спроецируем mg на оси:
Запишем второй закон Ньютона на X и Y:
Ответ: 6000 кг
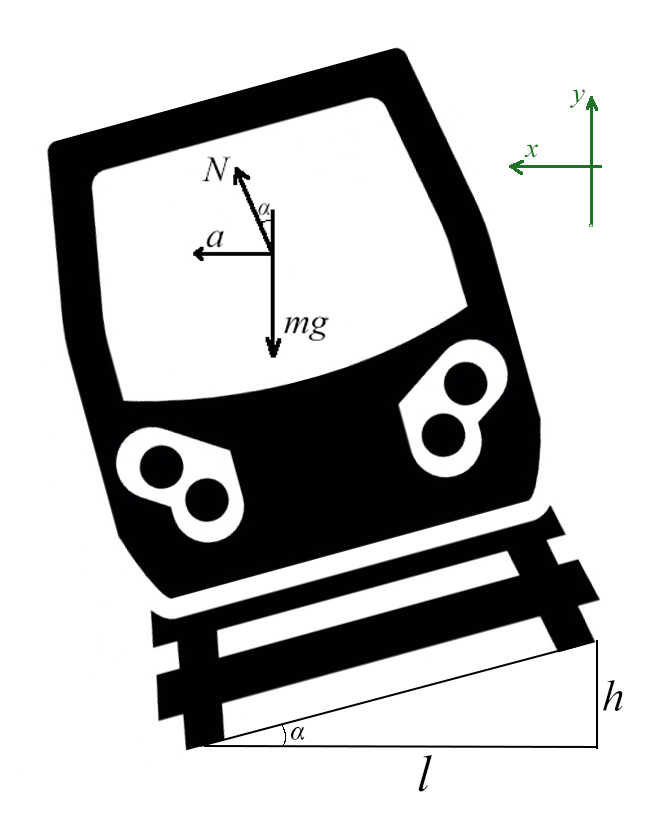
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.
Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!
Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)
Запишем какие силы действуют на оси:
Ускорение в данной задачи центростремительное!
Поделим одно уравнение на другое:
Тангенс — это отношение противолежащего катета к прилежащему:
Ответ: 7,5 см
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.
В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
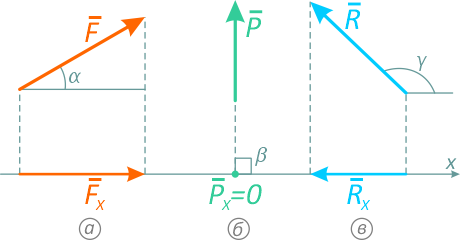
Проекция силы на ось – это алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на соответствующие оси. Рисунок 1.13):
Рисунок 1.13
Проекция силы на ось может быть положительной, рис. 1.13а (0 ≤ α < π/2), равной нулю, рис. 1.13б (β = π/2) и отрицательной, рис. 1.13в (π/2 < γ ≤ π).
Проекцию силы на ось можно представить себе как тень, отбрасываемую вектором силы на соответствующую ось от бесконечно далекого источника света.
Как определяются знаки проекций сил на оси показано в нашем видео:
Другие видео
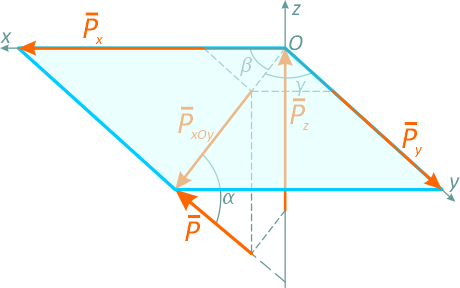
В случае пространственных (трехмерных) систем для нахождения проекции силы на ось сначала бывает удобнее найти ее проекцию на плоскость, которую потом надо спроецировать на ось (рисунок 1.14):
Рисунок 1.14
Примеры решения задач >
Момент силы >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Вектор силы под углом
1. Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.
2. Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.
3. Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.
Краткая теория:
Ввиду того, что сила — вектор, вычитание сил проводится по правилам, принятым для векторов. Пусть надо вычесть силу F2 из силы F1.
Параллельным переносом начало силы F2 совмещаем с началом силы F1.
Из конца вектора F2 проводим вектор в конец вектора F1. Направление — от F2 к F1. Это и есть разность.
Разложение силы на составляющие по направлениям — операция, обратная нахождению равнодействующей. Технически она выполняется переносом направлений. Сумма составляющих должна давать исходный вектор.
Пусть задан вектор силы F. Надо разложить его на составляющие по заданным направлениям A и B.
Перенесем линии направлений A и B так, чтобы они прошли через конец вектора F. В полученной фигуре мы легко узнаем параллелограмм сил, построенный на составляющих FA и FB.
Проекции сил на оси координат можно считать частным случаем разложения на заданные направления. Оси координат, как правило, мы выбираем прямоугольными, что облегчает задачу. Проекции получают опусканием перпендикуляров на заданные оси координат. Проекции — скалярные величины, то есть они не имеют направления. Но каждой проекции приписывается знак «+» или «-«, в зависимости от направления исходного вектора относительно выбранных направлений осей.
Задан вектор силы F. Надо найти его проекции на выбранные оси прямоугольной системы координат.
Опускаем перпендикуляры на оси. Получаем проекции.
Формулы для решения:
где «альфа» — угол между вектором F и осью X.
Где «альфа» — угол между векторами
Алгоритм решения типовой задачи:
1. Кратко записываем условие задачи.
2. Изображаем условие графически.
3. Проводим графическое построение.
4. Проводим аналитический расчет.
5. Подставляем величины в общее решение, вычисляем.
6. Записываем ответ.
Примеры решения:
Задача 1.
Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.
1. Кратко записываем условие задачи. Отметим, что в условии не сказано, какой вектор — уменьшаемое, а какой — вычитаемое. Поэтому разберем оба случая
а) Из первого вектора вычитается второй.
2. Изображаем условие графически.
3. Проводим графическое построение.
4. Проводим аналитический расчет.
5. Подставляем величины в общее решение, вычисляем.
Направление — от второго вектора к первому.
б) Из второго вектора вычитается первый
2. Изображаем условие графически.
3. Проводим графическое построение.
4,5. Проведение аналитического расчета и вычислений такое же, как и выше, но направление вектора разности — противоположное.
6. Ответ: Вектор разности в обоих случаях имеет величину 9,45 Н, направление в первом случае от второго вектора к первому, во втором случае — наоборот.
Задача 2.
Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.
1. Кратко записываем условие задачи.
2. Изображаем условие графически.
3. Проводим графическое построение. Равнодействующая двух сил «T» должна уравновешивать силу «F».
4. Проводим аналитический расчет. Треугольники, на которые разделился параллелограмм сил — равносторонние, так как они равнобедренные по построению, а вектор «F» делит угол пополам, то есть угол при основании равен 60 градусам. Таким образом, каждая из сил «T» равна силе «F».
5. Подставляем величины в общее решение, вычисляем.
T=60 кг. Переводим в систему СИ. В одном килограмме 9,8 ньютона. Поэтому:
6. Ответ: Сила натяжения троса 60 кг или 591 ньютон.
Задача 3.
Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.
1. Кратко записываем условие задачи.
2. Изображаем условие графически.
3. Проводим графическое построение.
4. Проводим аналитический расчет.
5. Подставляем величины в общее решение, вычисляем.
6. Ответ: Проекция на ось абсцисс равна 129,5 ньютона, проекция на ось ординат равна 75 ньютонов.
Вращательный момент, примеры расчетов
Рассмотрим несколько задач на тему «вращательный момент» с пояснениями. Будем осуществлять расчет перпендикулярных частей сил и плеч сил в случаях, когда углы между силой и рычагом отличаются от прямого.
Это вторая часть статьи о моменте силы. Первая часть находится тут (откроется в новой вкладке).
Угол между силой и рычагом отличается от прямого
Рассмотрим рисунок 1. На рисунке 1а сила приложена к рукоятке ключа под прямым углом. На рисунках 1б и 1в углы между силой и рукояткой (рычагом) отличаются от прямого.
Длина рычага является расстоянием между точкой приложения силы и осью вращения. Когда угол отличается от прямого, для вычисления момента силы нужно раскладывать на проекции либо силу, либо длину рычага (рукоятки).
Раскладываем силу
Разложим приложенную силу ( F ) на части. Одна часть будет располагаться перпендикулярно рукоятке, а другая – параллельно (см. рис. 2).
Рукоятку вращает только перпендикулярная часть силы. На рисунке 2 она обозначена, как ( F_ <1>).
Параллельная рукоятке часть обозначена ( F_ <2>). Она не вращает рукоятку, а сдвигает ключ либо от гайки (рис. 2а), либо в сторону гайки (рис 2б).
Рукоятка ключа – это плечо для перпендикулярной части силы.
Момент силы для рисунка 2 считаем по формуле:
Наиболее выгодно прикладывать силу перпендикулярно рукоятке (см. рис 1а). В этом случае вращательный момент силы будет наибольшим.
В остальных случаях вращать рукоятку будет не вся сила целиком, а только лишь ее перпендикулярная часть.
Помним! Между силой и ее плечом угол прямой.
Задача 1
Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить часть вектора силы, вращающего гаечный ключ. С помощью этой части вектора силы рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.
Решение:
- Проведем перпендикулярную ( F_ <1>) часть и параллельную рычагу ( F_ <2>) часть силы (рис. 3).
Примечание:
Чтобы разложить вектор силы на части, нужно нарисовать прямоугольник. Так, чтобы вектор, который мы раскладываем, оказался диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны рукоятке, а другие две – перпендикулярны ей.
Тогда стороны прямоугольника обозначат проекции – перпендикулярную и продольную (параллельную).
- Вычислим перпендикулярную ( F_ <1>) часть силы:
[ F_ <1>= F cdot sin(alpha)]
( F_ <1>= 10 left(Hright))
- Рассчитаем теперь вращательный момент M этой силы:
( M = 2 left( H cdot text <м>right) )
Ответ: Вращательный момент равен ( 2 left( H cdot text <м>right) )
Раскладываем расстояние
Для подсчета вращательного момента, на проекции можно раскладывать не только силу.
На части можно разложить длину рукоятки, так, чтобы одна часть оказалась продольной силе, а другая – параллельной (рис. 4).
После выбираем часть длины, перпендикулярную силе. Эта сторона является плечом силы.
На рисунке 4а перпендикулярно силе располагается ( d_ <1>), для этого случая момент силы считаем так:
Из рисунка 4б выбираем перпендикулярную силе величину ( d_ <2>). Момент силы вычисляем, пользуясь формулой:
Задача 2
Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить плечо вектора приложенной силы. С помощью этого плеча рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.
Решение:
- Проведем параллельную ( d_ <1>) и перпендикулярную силе ( d_ <2>) часть рычага (рис. 5).
Примечание:
Снова рисуем прямоугольник. Но теперь не сила, а рукоятка должна оказаться диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны силе, а другие две – перпендикулярны ей.
В прямоугольнике выбираем сторону, перпендикулярную силе. Эта сторона является плечом силы.
О формулах разложения векторов на проекции подробно написано тут (откроется в новой вкладке).
- Вычислим перпендикулярную силе F часть длины ( d_ <2>) рычага – плечо силы F:
[ d_ <2>= d cdot sin(alpha)]
( d_ <2>= 0,1 left( text <м>right))
- Рассчитаем теперь с помощью найденного плеча ( d_ <2>) силы F вращательный момент M:
( M = 2 left( H cdot text <м>right) )
Ответ: Вращательный момент равен ( 2 left( H cdot text <м>right) )
Расчет момента силы с помощью формулы, содержащей угол между силой и рычагом
Вращательный момент можно рассчитать без прямого указания плеча силы, зная угол между силой и рычагом. Подробнее в первой части статьи (откроется в новом окне)
Задача 3
Угол между приложенной силой и рукояткой ключа равен 30 градусам. Не рассчитывая плеча силы найти вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.
Решение:
- Воспользуемся формулой для вычисления вращательного момента:
[ M = F cdot d cdot sin(alpha)]
( M = 20 cdot 0,2 cdot 0,5)
( M = 2 left( H cdot text <м>right) )
Ответ: Вращательный момент равен ( 2 left( H cdot text <м>right) )
Как видно из задач 1 — 3, все три способа вычисления вращательного момента дают аналогичные результаты.
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
http://zaochnik.com/spravochnik/fizika/elementy-statiki/zakony-slozhenija-sil-v-mehanike/
П
Рис. 1.25
усть линия действия силыF
лежит в плоскости OXY
(рис. 1.25).
По
правилу параллелограмма разложим эту
силу на составляющие силы FОХ,
FOY
по координатным осям OX
и OY.
Силы FOX,
FOY
называют компонентами
силы F
по координатным
осям OX
и OY.
Очевидно векторное равенство
F
= FOX
+ FOY.
Спроецируем
компоненты FOX,
FOY
силы F
на координатные оси и получим скалярные
величины FOX,
FOY,
которые называют проекциями
силы на оси OX
и OY.
Компоненты
силы и её проекции на координатные оси
связаны равенствами: FOX
= iFOX;
FOY
= jFOY.
Проекция
силы на ось –
скалярная величина, равная взятой со
знаком плюс или минус длине отрезка,
заключённого между проекциями на ось
начала и конца силы.
Из
определения следует, что проекции данной
силы на любые параллельные оси равны
друг другу: FOX
= FO1X1,
FOY
= FO1Y1,
где FO1X1,
FO1Y1
– проекции силы F
на координатные оси системы отсчёта
O1X1Y1.
П
Рис. 1.26
усть в пространстве в
системе отсчёта OXYZ задана силаF,
(рис. 1.26).
Используя
правило параллелепипеда, разложим силу
F
на компоненты FOX,
FOY,
FOZ.
По правилу сложения векторов справедливо
равенство
F
= FOX
+ FOY
+ FOZ.
Компоненты
FOX,
FOY,
FOZ
силы F
связаны с их проекциями FOX,
FOY,
FOZ
на координатные оси соотношениями: FOX
= iFOX;
FOY
= jFOY;
FOZ
= kFOZ.
Следовательно, справедливо равенство
F
= i·FOX
+ j·FOY
+ k·FOZ.
Последнее
равенство представляет собой формулу
разложения силы на составляющие силы
по координатным осям.
Проекция
силы на координатную ось
равна произведению модуля силы на
косинус угла, составленного направлениями
силы и оси.
FOX
= Fcos(F,
i);
FOY
= Fcos(F,
j);
FOZ
= Fcos(F,
k).
Модуль
силы через её проекции определяют по
формуле
.
Направляющие
косинусы,
используемые для определения направления
силы, находят по формулам:
cos(F,
i)
= FOX/F;
cos(F,
j)
= FOY/F;
cos(F,
k)
= FOZ/F.
Если
рассматривается сила, лежащая в плоскости
OXY, то применяются формулы:
F
= FOX
+ FOY;
;
cos(F,
i)
= FOX/F;
cos(F,
j)
= FOY/F.
П
Рис. 1.27
ри определении проекции
силы на ось возможны следующие частные
случаи (рис. 1.27).
Анализ
частных случаев определения проекции
силы на ось позволяет сделать следующие
выводы: 1) если сила и ось направлены в
одну полуплоскость, то проекция силы
на ось положительна; 2) если сила и ось
направлены в разные полуплоскости, то
проекция силы на ось отрицательна; 3)
если сила и ось взаимно перпендикулярны,
то проекция силы на ось равна нулю; 4)
если сила и ось параллельны, то сила
проецируется на ось в натуральную
величину с соответствующим знаком.
При
решении задач статики рекомендуется
вычислять абсолютное значение проекции
как произведение модуля силы на косинус
острого угла между линией действия силы
и осью, определяя знак проекции
непосредственно по чертежу.
В
Рис. 1.28
инженерной практике
принято использовать заданный угол и
выражать через него проекции силы на
оси (рис. 1.28).
Проекцией
силы на плоскость OXY
называется вектор
FOXY,
заключенный между проекциями начала и
конца силы F
на эту плоскость (рис.
1.29).
Таким
образом, в отличие от проекции силы на
ось, проекция
силы на плоскость есть величина векторная,
так как она характеризуется не только
модулем, но и направлением по плоскости
OXY. По модулю FОXY
= F·cos(),
где
– угол между направлением силы F
и её проекцией FOXY,
Рис. 1.29
В
некоторых случаях для нахождения
проекции силы на ось бывает удобнее
найти сначала её проекцию на плоскость,
в которой эта ось лежит, а затем найденную
проекцию силы на плоскость спроецировать
на данную ось. Тогда:
FOX
= FOXY·sinα
= F·cos·sinα;
FOY
= FOXY·cosα
= F·cos·cosα;
FOZ
= F·sin(.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Условия равновесия системы сходящихся сил в аналитической форме:
Проекцией силы на ось называют скалярную величину, равную произведению модуля силы на косинус угла между положительным направлением оси и направлением силы
Проекция силы на ось
C только что рассмотренным понятием «составляющая силы по оси» тесно соприкасается другое важное понятие—«проекция силы на ось».
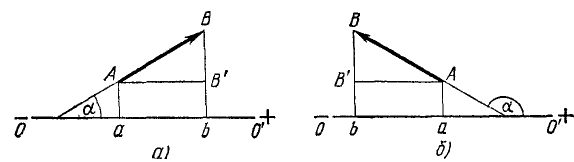
Изобразим силу
ab = AB’ = AB cos а.
Для получения проекции мы умножали на cos а не вектор, а его модуль, его абсолютную величину. Проекция силы на ось не является вектором, поскольку она не имеет собственного направления, а вполне определяется направлением оси, величиной проекции (длиной ab) и знаком « + » или «—». Проекция ab силы AB положительна (+ab), если направление вектора силы составляет с положительным направлением оси острый угол (рис. 14, а), и отрицательна (—ab), если—тупой (рис. 14, б). Мы подчеркиваем, что проекция вектора на ось не имеет своего направления, тем не менее условимся, что положительная проекция «направлена» в сторону положительного направления оси, а отрицательная — в противоположную сторону, и иногда на чертежах будем изображать стрелками проекции вектора на ось.
Рис. 14
Напомним, что всякую величину, определяемую числом и только числом, называют скаляром. Например, плотность, температура, масса являются скалярами. Скалярами первого рода называют величины, не зависящие от направления осей координат. Если же число, определяющее рассматриваемую величину, меняет знак при перемене направления осей координат на обратные, то скаляр является скаляром второго рода (см., например, Аппель. Теоретическая механика). Следовательно, проекция силы на ось есть скаляр второго рода.
Направляющим косинусом называют косинус угла между положительным направлением оси и направлением вектора; он выражается отношением проекции вектора на эту ось к модулю вектора и по знаку совпадает со знаком проекции
Направляющий косинус
Знак проекции определяется знаком косинуса угла между направлением вектора и положительным направлением оси, этот косинус называют направляющим косинусом. Если этот угол острый, то направляющий косинус положителен и проекция вектора на ось положительна, если же угол тупой, то направляющий косинус отрицателен и проекция вектора на ось тоже отрицательна.
Часто требуется по заданным проекциям вектора на координатные оси определять величины и знаки направляющих косинусов. Как видно из предыдущего равенства, выражения является существенно положительной величиной. В дальнейшем мы не всегда будем ставить эти вертикальные черточки, помня, что знаменатель в выражении направляющего косинуса является положительным.
По этой формуле можно определять не только направляющие косинусы вектора силы, но и направляющие косинусы всякого другого вектора (скорости, ускорения и πp.). Во всех отделах нашего курса направляющим косинусам отведена значительная роль.
Углы, составляемые каким-либо вектором с осями х, y и z, мы будем обозначать соответственно буквами α, β и γ с индексом вектора. Например, углы, составляемые вектором F с осями координат, будем обозначать αF, βF, γF∙. Если проекции силы 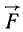
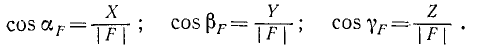
Практически при решении задач для определения проекции силы на ось обычно умножают модуль силы на косинус острого угла между осью (ее положительным или отрицательным направлением) и линией действия силы и приписывают проекции знак «+» или «—» в зависимости от того, «направлена» ли проекция в сторону положительного или в сторону отрицательного направления оси.
Проекция вектора на плоскость является вектором
Проекция силы на плоскость
В отличие от проекции силы на ось проекция силы на плоскость является вектором и имеет собственное направление на плоскости.
Чтобы спроецировать силу 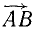
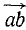
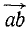
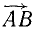
Модуль проекции равен произведению модуля силы на косинус угла наклона вектора силы к плоскости:
αb = AB cos a.
Проекция равнодействующей равна сумме проекций составляющих сил
Теорема о проекции равнодействующей
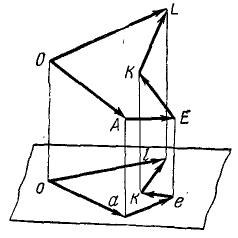
Покажем, что проекция равнодействующей на плоскость равна геометрической сумме проекций составляющих.
Дан пучок сил, представленный силовым многоугольником OAEKL, и дана некоторая плоскость (рис. 16). Опуская перпендикуляры Oo, Aa, Ее, Kk и Ll на плоскость из вершин силового многоугольника, найдем проекции составляющих сил на плоскость: проекция 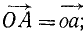
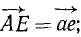
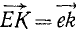
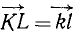
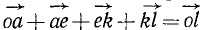
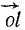
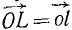
Сопоставляя между собой два последних равенства, найдем, что проекция равнодействующей на плоскость равна сумме проекций составляющих на ту же плоскость. Проекция сил на плоскость — вектор, поэтому сумма геометрическая.
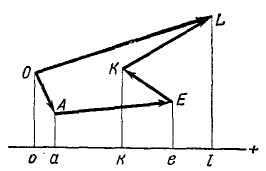
Напротив, проекции силы на ось—скалярные величины, а потому проекция равнодействующей на ось равна алгебраической сумме проекций составляющих на ту же ось. Пусть дан пучок сил, представленный силовым многоугольником OAEKL, и дана ось (рис. 17). Опуская перпендикуляры Oo, Aa, Ее, Kk и Ll на ось из вершин силового многоугольника, найдем проекции составляющих сил на ось: проекция 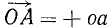
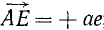
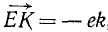
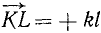
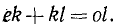
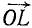
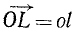
Рис. 16
Рис. 17
Величину и направление равнодействующей пучка сил можно определить по суммам проекций составляющих на взаимно перпендикулярные оси.
Если угол, составляемый равнодействующей с данной осью, известен, то, поделив сумму проекций составляющих на косинус этого угла, можно определить численную величину равнодействующей. Если же, как это обычно и бывает, направление равнодействующей неизвестно, то для определения равнодействующей составляют суммы проекций всех составляющих на пересекающиеся (обычно взаимно перпендикулярные) оси.
Пусть дана система сил, сходящихся в одной точке. Для простоты рассуждений предположим, что все эти силы лежат в одной плоскости. Проведем в этой плоскости декартову систему координат хОу и спроецируем все силы на оси Ox и Оу.
Обозначим проекцию силы 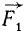
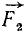
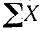
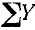
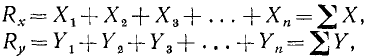
где Rx и Ry означают проекции равнодействующей на оси координат. Теперь мы можем найти величину равнодействующей:
или
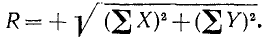
Направление равнодействующей можно определить по направляющим косинусам:
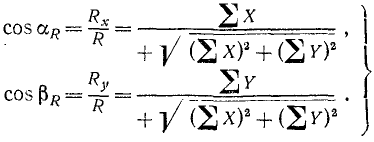
Если силы системы не лежат в одной плоскости, то, спррецировав силы на три координатные оси, получим
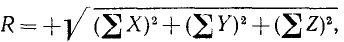
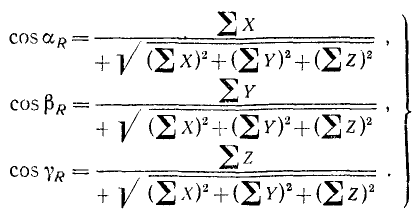
Знак направляющего косинуса определяется знаком числителя. Возведя равенства (6) или (6′) в квадрат и сложив, убедимся, что сумма квадратов направляющих косинусов равна единице:
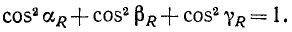
Задача №1
Найти равнодействующую 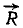
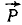
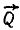
Решение. Примем точку приложения сил за начало координат, направим ось Ox по силе Q, а ось Oy к ней —перпендикулярно. Как видно из чертежа, направляющие косинусы складываемых сил таковы:
Найдем проекции равнодействующей по формулам (4) и модуль равнодействующей по (5′):
Ее направление определим по направляющим косинусам (6′):
Ответ.R = 3н и направлена под углом 60° к силам.
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат
Условия равновесия пучка сил в аналитической форме. Как было показано в § 3, при равновесии системы сходящихся сил ее равнодействующая равна нулю. Если пучок сил является плоским, то из (5′) следует
Сумма квадратов двух величин может равняться нулю только в случае, если равна нулю каждая из этих величин, а потому
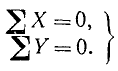
Эти равенства называют условиями равновесия плоской системы сходящихся сил в аналитической форме. Они являются необходимыми и достаточными условиями.
Если же пучок сил не лежит в одной плоскости, но является уравновешенной системой, то путем аналогичных рассуждений мы выведем условия равновесия пространственной системы сходящихся сил в аналитической форме:
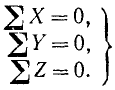
Если условия равновесия (8) и (9) содержат неизвестные величины, то их называют уравнениями равновесия сходящихся сил.
- Заказать решение задач по теоретической механике
Задача №2
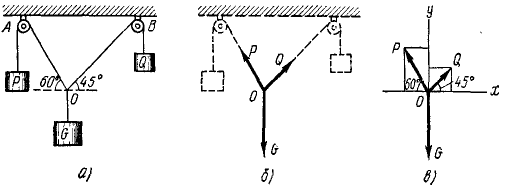
Нить с грузами P и Q на концах перекинута через блоки А и В, находящиеся на одной горизонтали (рис. 18, α). В точке О нити, находящейся между блоками, привязан груз G = 27,3 н. При равновесии системы ветвь OA образует с горизонталью угол 60°, а ветвь OB— угол 45°. Пренебрегая трением в блоках, определить величину грузов P и Q.
Решение. Равновесие какого объекта надо рассмотреть для решения задачи? Ответим на этот вопрос. Требуется определить веса грузов P и Q. Веса грузов приложены к этим грузам и направлены вертикально вниз. Каждый груз натягивает нить силой, равной своему весу. Блок меняет направление нити, а следовательно, и направление силы натяжения нити, не меняя ее величины. Силы, по модулю равные P и Q и направленные по OA и OB, пересекаются в точке 0, где приложена и заданная сила G (рис. 18, б). Поэтому для решения задачи надо рассмотреть равновесие точки О.
Какие же силы действуют на точку О? На нее действуют сила G; натяжение P ветви OA-, натяжение Q ветви OB. Веса грузов PhQ, приложенные к этим грузам, учитывать не надо, потому что они не приложены к точке О.
Рис. 18
Для изучения равновесия сил, приложенных к точке О, можно построить силовой многоугольник или составить уравнения равновесия. Выберем второй путь. Построим систему координат с началом в точке О (рис. 18, в), спроецируем силы на оси и составим уравнения равновесия.
Для проекций на ось Ox имеем
Знак проекции Q положительный, потому что она направлена в положительном направлении оси Ox (вправо). Знак у проекции P отрицательный, так как она направлена в отрицательном направлении оси Ох. Проекция силы G на ось Ox равна нулю.
Аналогично получаем
Проекции P и Q на ось Oy положительны, так как направлены в положительном направлении оси. Проекция G отрицательна, так как направлена вниз. Подставляя числовые значения и решая уравнения, получаем ответ.
Ответ. P = 20 н, Q = 14,1 н.
Задача №3
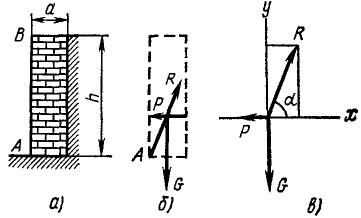
Земляная насыпь подпирается вертикальной каменной стеной АВ. Найти необходимую толщину стены а, предполагая, что давление земли на стену направлено горизонтально, приложено на 1/3 ее высоты и равно 6 тонн на метр длины стены; удельный вес кладки 2 Г/см3. Стена должна быть рассчитана на опрокидывание вокруг ребра А (рис. 19, а).
Решение. Первый вопрос: равновесие какого тела надо рассмотреть?
Нужно рассмотреть равновесие каменной стены АВ.
Второй вопрос: какие силы действуют на рассматриваемое тело?
На стену действуют следующие силы (рис. 19, б):
а) вес G стены, приложенный в ее центре тяжести, направленный по вертикали вниз и равный произведению объема стены на удельный вес кладки. Обозначим высоту, длину и ширину стены в метрах соответственно h,l и а. Удельный вес кладки 2 Г/см3, или, что то же, 2 Т/м3, следовательно,
G = 2hla Т;
б) давление P земляной насыпи, приложенное на 1/3 высоты стены, направленное горизонтально от насыпи к стенке и равное (в Т)
P =6l;
в) реакция R опоры. При решении подобных задач, называемых задачами на опрокидывание, нужно иметь в виду, что реакция связи бывает только в той опоре, вокруг которой опрокидывается тело, реакции же связей в опорах, в которых связь нарушится при опрокидывании тела, равны нулю.
Определив точку приложения реакции опоры, найдем направление реакции. Стена находится в равновесии под действием трех сил, а следовательно, линии действия всех трех сил должны пересекаться в одной точке, поэтому реакция опоры направлена под углом а к горизонтальной оси, причем
Рис. 19
Проецируя все приложенные к стене силы на горизонтальную и на вертикальную оси (рис. 19, в) и приравнивая нулю суммы проекций, найдем
Легко находим, что наименьшая толщина стены a= 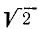
В условии задачи использованы различные единицы измерений (тонна, грамм, метр, сантиметр). При решении мы выразили все величины в тоннах и метрах. Решим эту же задачу в СИ или MKC (м, кг, сек), для чего выразим в этих единицах все величины, заданные в условии задачи.
Давление земли на один метр длины стены
6 Т∕м = 6000 кГ/л = 6000 . 9,81 н/м.
Если длина стены I м, то давление на всю стену
P = 6000 . 9,81 . 1н.
Удельный вес кладки
2 Г∕cм3 = 2000 кГ/л» = 2000 . 9,81 н/м3.
Тогда вес стены
G = 2000 . 9,81 . hla н.
Составляя и решая уравнения равновесия всех сил, приложенных к стене, получим тот же ответ.
Ответ: a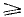
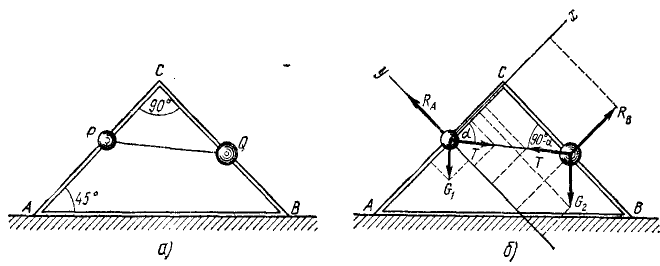
Задача №4
На катеты равнобедренного прямоугольного треугольника АВС, сделанного из проволоки и установленного в вертикальной плоскости так, что гипотенуза AB горизонтальна (рис. 20, а), нанизаны два шарика: P весом Gl = 3 н и Q весом G2 = 4 н, связанные нерастяжимой нитью. Найти положение равновесия (Угол 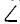
Решение. Равновесие какого объекта надо рассмотреть, чтобы определить угол а натяжение нити T и две реакции катетов? Если рассматривать равновесие шарика Р, получим два уравнения равновесия (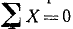
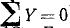
Для решения задачи надо: 1) рассмотреть равновесие шарика P и составить уравнения равновесия; 2) рассмотреть равновесие шарика Q и составить уравнения равновесия; 3) решить совместно все четыре уравнения и найти из них четыре неизвестных α, Т, RА и RВ.
1) Равновесие шарика P. На шарик P действуют силы: его вес 3 н, направленный вниз, натяжение T нити, направленное к Q, и реакция RА катета АС.
Рис. 20
Катет (проволока АС) осуществляет связь шарика Р. Эта связь допускает перемещение шарика лишь по АС. Реакция направлена перпендикулярно виртуальным перемещениям, т. е. перпендикулярно АС.
Построим систему координат с началом в центре шарика Р, направив ось Ox по катету к точке C (рис. 20, б).
Заметим, что мы вправе выбирать направления осей так, как это представляется целесообразным для упрощения выкладок. Мы свободны также в выборе начала координат.
Составляем уравнения равновесия системы сил, приложенных к шарику Р:
2) Равновесие шарика Q. На шарик Q действуют вес 4 н, направленный вниз, сила T натяжения нити, направленная к шарику P (по принципу равенства действия и противодействия), и реакция RВ катета ВС, направленная перпендикулярно виртуальному перемещению шарика Q.
Нет необходимости строить новую систему координат, и мы можем проецировать силы, приложенные к шарику Q, на уже имеющиеся координатные оси. Получаем два новых уравнения:
3) Решая совместно четыре уравнения, находим четыре неизвестных.
Ответ.
Задача №5
К шарниру кронштейна ABCD (рис. 21, а) приложена сила p= 6000 н. Кронштейн состоит из трех стержней АВ, AC и AD равной длины; крепления А, В, C и D шарнирные, плоскость ABC горизонтальна и BC=4D= =2 OD. Найти усилия в стержнях.
Решение. Рассматриваем равновесие точки А, в которой сходятся все неизвестные силы.
На точку А действует пространственный пучок сил: вес P = 6000 н, направленный вниз, усилия в стержнях АВ, AC и AD. Усилием в стержне называют силу, действующую вдоль стержня и растягивающую или сжимающую его; если стержень растянут, то на шарнир действует сила, направленная к стержню, если сжат, то от стержня. Не всегда бывает просто без предварительных расчетов определить, сжат данный стержень или растянут. Иногда этому помогает следующий прием: если от замены стержня нитью равновесие не нарушается, то стержень растянут, а если нарушается, то сжат. В данной задаче стержень AD, очевидно, можно заменить нитью, следовательно, он растянут и сила FD, приложенная к шарниру А, направлена так, как тянула бы его нить, т. е. к D. Стержни AB и AC нитями заменить нельзя, так как кронштейн потеряет жесткость, следовательно, силы, приложенные к шарниру А, направлены от В и от С. Существует и другой способ, требующий предварительных расчетов: силы, действующие на шарнир со стороны стержней, при предварительном расчете считать растягивающими и всегда направлять от шарнира к стержням, составлять и решать уравнения равновесия, и если в результате решения этих уравнений для сил получаются положительные значения, то стержни растянуты, а если отрицательные, то сжаты. Этот способ мы применим в данной задаче и будем считать, что, кроме вертикальной нагрузки Р, на шарнир А действуют усилия в стержнях АВ, AC и AD, направленные условно от А к В, C и D.
Рис. 21
Построим пространственную систему координат с началом в точке О (рис. 21,6), направив оси, как показано на чертеже. Из условия задачи следует, что ,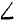
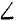
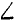
Решая эти уравнения, находим ответ.
Ответ. Стержень AB сжат, FВ=-6000 н; стержень AC сжат, Fc=—6000 н; стержень AD растянут, FD=12000 н (рис. 21,в).
Для отличия сжимающую силу условимся писать (в некоторых задачах) c отрицательным знаком. Этот знак сжимающим силам приписывают условно.
- Приведение двух параллельных сил к равнодействующей
- Пара сил в теоретической механике
- Приведение системы сил к данной точке
- Система сил на плоскости
- Теорема количества движения
- Теорема моментов количества движения
- Теорема кинетической энергии
- Условие равновесия системы сходящихся сил в геометрической форме