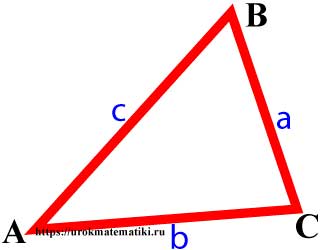
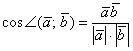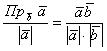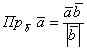Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
— все углы треугольника острые.
— один из углов треугольника тупой (больше 90°).
— один из углов треугольника прямой (равен 90°).
— все три стороны не равны.
— две стороны равны.
— все три стороны равны.
Стороны треугольника пропорциональны синусам противолежащих углов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 b c · cos α
b 2 = a 2 + c 2 — 2 a c · cos β
c 2 = a 2 + b 2 — 2 a b · cos γ
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AO OD = BO OE = CO OF = 2 1
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AE AB = EC BC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°
где p = a + b + c 2 — полупериметр треугольника.
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
∆MBN
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон.
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S = 1 2 a · h a ,
S = 1 2 b · h b ,
S = 1 2 c · h c ,
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
S = 1 2 b · c · sin α ,
S = 1 2 a · c · sin β ,
где a, b, c — стороны треугольника,
γ — угол между сторонами a и b ,
α — угол между сторонами b и c ,
β — угол между сторонами a и c .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
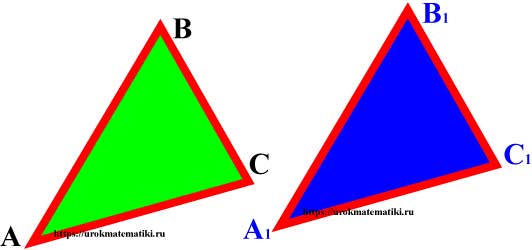
Равенство треугольников
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
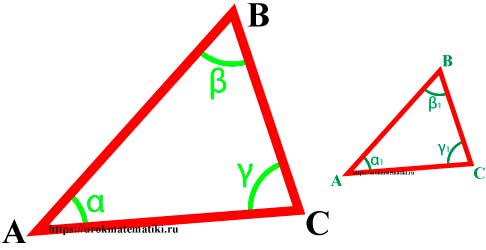
Подобие треугольников
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
∆MNK => α = α 1 , β = β 1 , γ = γ 1 и AB MN = BC NK = AC MK = k
где k — коэффициент подобия.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S ∆АВС S ∆MNK = k 2
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.
Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.
Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Проекция на сторону треугольника
Плоскостью называется поверхность, образуемая движением прямой линии, которая движется параллельно самой себе по неподвижной направляющей прямой .
Проекции плоскости на комплексном чертеже будут различны в зависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана: а) тремя точками, не лежащими на одной прямой; б) прямой линией и точкой, лежащей вне этой прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми.
На комплексном чертеже (рис. 99) проекции плоскости также задаются проекциями этих элементов, например, на рис 99, а — проекциями трех точек А, , и С, не лежащих на одной прямой; на рис. 99, б — проекциями прямой ВС и точки А у не лежащей на этой прямой; на рис. 99, в — проекциями двух пересекающихся прямых; на рис. 99, г проекциями двух параллельных прямых линий АВ и CD.
На рис. 100 плоскость задана прямыми линиями, по которым эта плоскость пересекает плоскости проекций. Такие линии называются следами плоскости.
Линия пересечения данной плоскости Р с горизонтальной плоскостью проекций Н называется горизонтальным следом плоскости Р и обозначается Рн.
Линия пересечения плоскости Р с фронтальной плоскостью проекций V называется фронтальным следом этой плоскости и обозначается Рv.
Линия пересечения плоскости Р с профильной плоскостью проекций W называется профильным следом этой плоскости и обозначается Pw.
Следы плоскости пересекаются на осях проекций. Точки пересечения следов плоскости с осями проекций называются точками схода следов. Эти точки обозначаются Рx, Рy и Рz.
Расположение следов плоскости Р на комплексном чертеже по отношению к осям проекций определяет положение самой плоскости по отношению к плоскостям проекций. Например, если плоскость Р имеет фронтальный и профильный следы Pv и Pw, параллельные осям Ох и Оу то такая плоскость параллельна плоскости Н и называется горизонтальной (рис. 101, и). Плоскость Р со следами Рн и Pw , параллельными осям проекций Ох и Oz (рис. 101, называется фронтальной, а плоскость Р со следами Pv и Pн параллельными осям проекций Оу и Oz, — профильной (рис. 101, в).
Горизонтальная, фронтальная и профильная плоскости, перпендикулярные к двум плоскостям проекций, называются плоскостями уровня. Если на комплексном чертеже плоскость уровня задана не следами, а какой-нибудь плоской фигурой, например, треугольником или параллелограммом (рис. 101, г, д, е), то на одну из плоскостей проекций эта фигура проецируется без искажения, а на две другие плоскости проекций — в виде отрезков прямых.
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
Плоскость, перпендикулярная к плоскости Н (рис. 102, а),называется горизонтально-проецирующей плоскостью. Фронтальный след Pv этой плоскости перпендикулярен оси Ох, а горизонтальный след Рн расположен под углом к оси Ох (комплексный чертеж на рис. 102, а)
Если горизонтально-проецирующая плоскость задана не следами, а какой-либо фигурой, например треугольником АВС (рис. 102, 6), то горизонтальная проекция этой плоскости представляет собой прямую линию, а фронтальная и профильная проекции — искаженный вид треугольника АВС.
Фронтально-проецирующей плоскостью называется плоскость, перпендикулярная к фронтальной плоскости проекций (рис. 102, в).
Горизонтальный след этой плоскости перпендикулярен оси Ох, а фронтальный след расположен под некоторым углом к оси Ох (комплексный чертеж на рис. 102, в).
При задании фронтально-проецирующей плоскости не следами, а, например, параллелограммом ABCD фронтальная проекция такой плоскости представляет собой прямую линию (рис. 102, г), а на горизонтальную и профильную плоскости проекций параллелограмм проецируется с искажением.
Профильно-проецирующей плоскостью называется плоскость, перпендикулярная к плоскости W (рис. 102, д). Следы Pv и Рн этой плоскости параллельны оси Ох.
При задании профильно-проецирующей плоскости не следами, а, например, треугольником АВС (рис. 102, е) профильная проекция такой плоскости представляет собой прямую линию. Плоскости, перпендикулярные двум плоскостям проекций, как было сказано, называются плоскостями уровня.
Если плоскость Р не перпендикулярна ни одной из плоскостей проекций (рис. 102, ж), то такая плоскость называется плоскостью общего положения. Все три
следа Pv, Рн и Pw плоскости Р наклонены к осям проекций.
Если плоскость общего положения задана не следами, а, например, треугольником АВС (рис. 102, з), то этот треугольник проецируется на плоскости H, V и W в искаженном виде.
ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ
Если прямая расположена на плоскости, то она должна проходить через две какие-либо точки, принадлежащие этой плоскости. Такие две точки могут быть взяты на следах плоскости — одна на горизонтальном, а другая на фронтальном. Так как следы прямой и плоскости находятся на плоскостях проекций и то следы прямой, принадлежащей плоскости, должны быть расположены на одноименных следах этой плоскости (рис. 103, а);например, горизонтальный след Н прямой — на горизонтальном следе плоскости, фронтальный след V прямой — на фронтальном следе Рv плоскости (рис. 103, б).
Для того чтобы на комплексном чертеже плоскости Р, заданной следами, провести какую-либо прямую общего положения, необходимо наметить на следах плоскости точки v’ или считать их следами искомой прямой (точнее, v’ — фронтальной проекцией горизонтального следа прямой).
Опустив перпендикуляры из v’ и на ось проекций х, находим на ней вторые проекции следов прямой: v — горизонтальную проекцию фронтального следа прямой и h’ — фронтальную проекцию горизонтального следа прямой. Соединив одноименные проекции следов, т. е. v’c h и v c h прямыми, получим две проекции прямой линии, расположенной в плоскости общего положения Р.
Очень часто требуется провести на плоскости горизонталь и фронталь, которые называются главными линиями плоскости или линиями уровня. Главные линии помогают решать многие задачи проекционного черчения.
Горизонталь и фронталь имеют в системе двух плоскостей V и Н только по одному следу (например, горизонталь имеет только фронтальный след). Поэтому, зная один след главной линии, проекцию главной линии проводят по заранее известному направлению. Это направление для горизонтали видно из рис. 104, а, где показана плоскость общего положения и горизонталь, лежащая на ней. Из рисунка видно, что горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.
Таким образом, чтобы на комплексном чертеже плоскости Р провести в этой плоскости какую-либо горизонталь, нужно наметить на следе Рv плоскости точку v’ (рис. 104, б) и считать ее фронтальной проекцией фронтального следа горизонтали. Затем через точку v’ параллельно оси х проводят прямую, которая будет фронтальной проекцией горизонтали.
Опустив перпендикуляр из точки v’ на ось x , получают точку v, которая будет горизонтальной проекцией фронтального следа горизонтали. Прямая, проведенная из точки v параллельно следу PH плоскости, представляет собой горизонтальную проекцию искомой горизонтали. Построение проекции фронтали показано на рис. 104, в и г.
11 с редко требуется провести горизонталь и фронталь на проецирующих плоскостях. Рассмотрим, например, построение горизонтали на фронтально-проецирующей плоскости (рис. 105). На следе плоскости Рv намечаем фронтальную проекцию фронтального следа горизонтали и на оси находим его горизонтальную проекцию v (рис. 105, а). Затем через точку проводим параллельно Рн горизонтальную проекцию горизонтали; фронтальная проекция горизонтали совпадает с точкой v’.
Если плоскость задана не следами, а пересекающимися или параллельными прямыми, то построение проекций горизонтали или фронтали, расположенных в этой плоскости, выполняется следующим образом.
Пусть плоскость задана двумя параллельными прямыми AВ и СD (рис. 105, 6). Для построения горизонтали, лежащей в этой плоскости, проводим параллельно оси х фронтальную проекцию горизонтали и отмечаем точки е’и f’ пересечения фронтальной проекции горизонтали с фронтальными проекциями параллельных прямых, которыми задана плоскость. Через точки е’и f’ проводим вертикальные линии связи до пересечения с ab и cd в точках е и f. Точки е и f соединяем прямой линией, которая и будет горизонтальной проекцией горизонтали.
Если требуется найти следы плоскости, заданной пересекающимися или параллельными прямыми, надо найти следы этих прямых и через полученные точки провести искомые следы плоскости.
Рассмотрим комплексный чертеж параллелограмма ABCD (рис. 106, a),который задает некоторую плоскость X. Отрезок DC расположен в плоскости H, следовательно, его горизонтальная проекция dc является горизонтальным следом плоскости (точнее — горизонтальной проекцией горизонтального следа плоскости).
Чтобы найти фронтальный след этой плоскости, необходимо продолжить горизонтальную проекцию dc прямой DC до пересечения с осью х в точке Рх, через которую должен пройти искомый фронтальный след плоскости.
Второй точкой v’, через которую пройдет искомый фронтальный след плоскости, является фронтальный след прямой АВ (фронтальная проекция фронтального следа). Фронтальную проекцию фронтального следа прямой АВ находим, продолжая горизонтальную проекцию ab прямой АВ до пересечения с осью х в точке v, которая будет горизонтальной проекцией искомого фронтального следа прямой АВ. Фронтальная проекция фронтального следа этой прямой находится на перпендикуляре, восставленном из точки v к оси х, в точке v’ его пересечения с продолжением фронтальной проекции а’в’ прямой АB. Соединив точки Px с v’, находим фронтальный след Pv плоскости.
Пример решения подобной задачи приведен на рис 106, б.
Часто на комплексных чертежах приходится решать такую задачу: по одной из заданных проекций точки, расположенной на заданной плоскости, определить две другие проекции точки. Ход решения задачи следующий.
Через заданную проекцию точки, например фронтальную проекцию n’ точки N, расположенной на плоскости треугольника АВС (рис. 107), проводим одноименную проекцию вспомогательной прямой любого направления, например m’к’.
Горизонталью плоскости называется прямая, принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций Н.
Строим другую проекцию mк вспомогательной прямой. Для этого проводим вертикальные линии связи через точки m’ и к’ до пересечения с линиями ас и вс. Из точки n’ проводим линию связи до пересечения с проекцией mк в искомой точке n.
Профильную проекцию n» находим по общим правилам проецирования.
В качестве вспомогательной прямой для упрощения построения чаще используются горизонталь или фронталь.
Чтобы найти какую-либо точку на плоскости Р, например точку А (рис. 108, а и б) надо найти ее проекции а’и а, которые располагаются на одноименных проекциях горизонтали, проходящей через эту точку. Через точку А проведена горизонталь Av’ .
Проводим проекции горизонтали: фронтальную — через v’ параллельно оси х, горизонтальную — через v параллельно следу Рн плоскости Р. На фронтальной проекции горизонтали намечаем фронтальную проекцию а’ искомой точки и, проводя вертикальную линию связи, определяем горизонтальную проекцию а точки А.
Если точка лежит на проецирующей плоскости, то построение ее проекций упрощается. В этом случае одна из проекций точки всегда расположена на следу плоскости (точнее, на его проекции). Например, горизонтальная проекция а точки А, расположенной на горизонтально-проецирующей плоскости Р, находится на горизонтальной проекции горизонтального следа плоскости (рис. 108, в и г)
При заданной фронтальной проекции a’ точки А, лежащей на горизонтально-проецирующей плоскости , найти вторую проекцию этой точки (горизонтальную) можно без вспомогательной прямой, посредством проведения линии связи через а’ до пересечения со следом РН.
Если точка расположена на фронтально-проецирующей плоскости Р (рис. 108, д и е), то ее фронтальная проекция а’ находится на фронтальном следе Хv плоскости Р.
ПРОЕКЦИИ ПЛОСКИХ ФИГУР
Зная построение проекций прямых и точек, расположенных на плоскости, можно построить проекции любой плоской фигуры, например, прямоугольника, треугольника, круга.
Как известно, каждая плоская фигура ограничена отрезками прямых или кривых линий, которые могут быть построены по точкам.
Проекции фигуры, ограниченной прямыми линиями (треугольника и многоугольника), строят по точкам (вершинам). Затем одноименные проекции вершин соединяют прямыми линиями и получают проекции фигур.
Проекции круга или другой криволинейной фигуры строят при помощи нескольких точек, которые берут равномерно по контуру фигуры. Одноименные проекции точек соединяют плавной кривой по лекалу.
Проекции плоской фигуры строят различными способами в зависимости от положения фигуры относительно плоскостей проекций и Наиболее просто построить проекции фигуры, расположенной параллельно плоскостям Н и V; сложнее — при расположении фигуры на проецирующей плоскости или на плоскости общего положения.
Рассмотрим несколько примеров.
Если треугольник АВС расположен на плоскости, параллельной плоскости H (рис. 109, a), то горизонтальная проекция этого треугольника будет его действительным видом, а фронтальная проекция — отрезком прямой, параллельным оси х. Комплексный чертеж треугольника АВС показан на рис. 109, 6. Такой треугольник можно видеть на изображении резьбового резца (рис. 109, в),передняя грань которого треугольная.
Трапеция ABCD расположена на фронтально-проецирующей плоскости (рис. 110, а). Фронтальная проекция трапеции представляет собой отрезок прямой линии, а горизонтальная — трапецию (рис. 110, б)
Задняя грань отрезного резца (рис. 110, в) имеет форму трапеции.
Рассматривая плоскость, параллельную горизонтальной, фронтальной или профильной плоскости проекций (плоскость уровня), можно заметить, что любая фигура, лежащая в этой плоскости, имеет одну из проекций, представляющую собой действительный вид этой фигуры; вторая и третья проекции фигуры совпадают со следами этой плоскости.
Рассматривая проецирующую плоскость, заметим, что любая точка, отрезок прямой или кривой линии, а также фигуры, расположенные на проецирующей плоскости, имеют одну проекцию, расположенную на следе этой плоскости. Например, если круг лежит на фронтально-проецирующей плоскости Р (рис. 111), то фронтальная проекция круга совпадает с фронтальным следом Pv плоскости Р. Две другие проекции круга искажены и представляют собой эллипсы. Большие оси эллипсов равны проекциям диаметра круга 37. Малые оси эллипсов равны проекциям диаметра круга 15, перпендикулярного диаметру 37.
На рис. 111,6 показано колено трубы с двумя фланцами. Горизонтальная проекция контура нижнего фланца, который расположен в горизонтальной плоскости, будет действительным видом окружности. Горизонтальная проекция контура верхнего фланца изобразится в виде эллипса.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Две плоскости могут быть взаимно параллельными или пересекающимися.
Из стереометрии известно, что если две параллельные плоскости пересекают какую-либо третью плоскость, то линии пересечения этих плоскостей параллельны между собой. Исходя из этого положения, можно сделать вывод, что одноименные следы двух параллельных плоскостей Р и Q также параллельны между собой.
Если даны две профильно-проецирующие плоскости Р и К (рис. 112, а), то параллельность их фронтальных и горизонтальных следов на комплексном чертеже в системе V и Н недостаточна для того, чтобы определить, параллельны эти плоскости или нет. Для этого необходимо построить их профильные следы в системе V, Н и W (рис. 112, б). Плоскости Р и K будут параллельны только в том случае, если параллельны их профильные следы Pw и Kw.
Одноименные следы пересекающихся плоскостей Р и Q (рис. 112, в) пересекаются в точках V и H, которые принадлежат обеим плоскостям, т. е. линии их пересечения. Так как эти точки расположены на плоскостях проекций, то, следовательно, они являются также следами линии пересечения плоскостей. Чтобы на комплексном чертеже построить проекции линии пересечения двух плоскостей Р и Q, заданных следами Pv, Рн и Qv,Qh, необходимо отметить точки пересечения одноименных следов плоскостей, т. е. точки v’ и h (рис. 112, г); точка v’ — фронтальная проекция фронтального следа искомой линии пересечения плоскостей Р и Q, h — горизонтальная проекция горизонтального следа этой же прямой. Опуская перпендикуляры из точек v’ и h на ось х, находим точки v и h’. Соединив прямыми одноименные проекции следов, т. е. точки v’ и h’, v и h’ получим проекции линии пересечения плоскостей Р и Q.
ПРЯМАЯ, ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ
Для этого фронтальную проекцию отрезка m’n’ продолжаем до пересечения с отрезками a’b’ и c’d’ (проекциями сторон треугольника АВС), получаем точки (рис. 113, б).
Из точек е’к’ проводим линии связи на горизонтальную проекцию до пересечения с отрезками ab и ca , получаем точки еk. Продолжим горизонтальную проекцию mn отрезка прямой MN до пересечения с проекциями сторон bа и са, если точки пересечения совпадут с ранее полученными точками e и k то прямая MN принадлежит плоскости треугольника.
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ
Если прямая АВ пересекается с плоскостью Р, то на комплексном чертеже точка их пересечения определяется следующим образом.
Через прямую А В проводят любую вспомогательную плоскость Q. Для упрощения построений плоскость Q обычно берется проецирующей (рис. 114, a). В данном случае проведена вспомогательная горизонтально-проецирующая плоскость Q. Через горизонтальную проекцию аb прямой АВ проводят горизонтальный след QH плоскости Q и продолжают его до пересечения с осью x в точке Qx . Из точки Qx к оси х восставляют перпендикуляр QxQy , который будет фронтальным следом Qv вспомогательной плоскости Q.
Вспомогательная плоскость Q пересекает данную плоскость Р по прямой VH, следы которой лежат на пересечении следов плоскостей Р и Q. Заметив точки пересечения следов Pv и Qv — точку v’ и следов Qн и PH — точку h,опускают из этих точек на ось х перпендикуляры, основания которых — точки v’ и h’ — будут вторыми проекциями следов прямой VH. Соединяя точки v’и h’, v и h, получают фронтальную и горизонтальную проекции линии пересечения плоскостей.
Точка пересечения М заданной прямой AB и найденной прямой VH и будет искомой точкой пересечения прямой АВ с плоскостью Р. Фронтальная проекция m’ этой точки расположена на пересечении проекций a’b’ и v’h’. Горизонтальную проекцию m точки М находят, проводя вертикальную линию связи из точки m’ до пересечения с ab.
Если плоскость задана не следами, а плоской фигурой, например, треугольником (рис. 114, 6), то точку пересечения прямой MN с плоскостью треугольника АВС находят следующим образом.
Через прямую МN проводят вспомогательную фронтально-проецирующую плоскость . Для этого через точки m’ и n’ проводят фронтальный след плоскости Ру продолжают его до оси x и из точки пересечения следа плоскости Ру с осью х опускают перпендикуляр Рн, который будет горизонтальным следом плоскости Р.
Затем находят линию ED пересечения плоскости Р с плоскостью данного треугольника ABC. Фронтальная проекция e’d’ линии ED совпадает с m’n’. Горизонтальную проекцию ed находят, проводя вертикальные линии связи из точек е’и d’ до встречи с проекциями ab и ас сторон треугольника АВС. Точки e и d соединяют прямой. На пересечении горизонтальной проекции ed линии ED с горизонтальной проекцией прямой MN находят горизонтальную проекцию k искомой точки К. Проведя из точки k вертикальную линяю связи, на ходят фронтальную проекцию k’ Точка К — искомая точка пересечения прямой МК с плоскостью треугольника АВС.
В частном случае прямая может быть перпендикулярна плоскости Р.Из условия перпендикулярности прямой к плоскости следует, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим на этой плоскости (в частности, этими прямыми могут быть следы плоскости). Тогда проекции прямой АВ будут перпендикулярны одноименным следам этой плоскости (рис 115, а) Фронтальная проекция а’b’ перпендикулярна фронтальному следу Ру, а горизонтальная проекция ab перпендикулярна горизонтальному следу Рн плоскости Р.
Если плоскость задана параллельными или пересекающимися прямыми, то проекции прямой, перпендикулярной этой плоскости, будут перпендикулярны горизонтальной проекции горизонтали и фронтальной проекции фронтали, лежащих на плоскости.
Таким образом, если, например, на плоскость, заданную треугольником АВС необходимо опустить перпендикуляр, то построение выполняется следующим образом (рис. 115, б).
На плоскости проводят горизонталь СЕ и фронталь FA. Затем из заданных проекций d и d’ точки D опускают перпендикуляры соответственно на ce и f’a’. Прямая, проведенная из точки D будет перпендикулярна плоскости треугольника АВС.
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Задачи на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение плоскости с прямыми линиями. На рис. 116 показано построение линии пересечения плоскостей, заданных треугольниками АВС и DEF. Прямая MN построена по найденным точкам пересечения сторон DE и EF треугольника DEF с плоскостью треугольника АВС.
Например, чтобы найти точку M, через прямую DF проводят фронтально-проецирующую плоскость Р, которая пересекается с плоскостью треугольника АВС по прямой 12. Через полученные точки 1′ и 2′ проводят вертикальные линии связи до пересечения их с горизонтальными проекциями ав и ас сторон треугольника АВС в точках 1 и 2. На пересечении горизонтальных проекций df и 12 получают горизонтальную проекцию m искомой точки М, которая будет точкой пересечения прямой DF с плоскостью АВС. Затем находят фронтальную проекцию m’ точки M. Точку N пересечения прямой EF с плоскостью АВС находят так же, как и точку М.
Соединив попарно точки m’ и n’, m и n, получают проекции линий пересечения MN плоскостей АВС и DEF.
http://ru.onlinemschool.com/math/formula/triangle/
http://forkettle.ru/vidioteka/tekhnicheskie-nauki/cherchenie/780-osnovy-nachertatelnoj-geometrii/8631-proetsirovanie-ploskikh-figur
Как найти проекцию
В прямоугольном треугольнике существует два вида сторон – короткая сторона «катет» и длинная сторона «гипотенуза». Если провести проекцию катета на гипотенузу, та разделится на два отрезка. Чтобы определить величину одного из них, нужно прописать набор исходных данных.

Инструкция
В исходных данных задачи может быть прописана длина гипотенузы D и длина катета N, чью проекцию требуется найти. Чтобы определить величину проекции Nd, воспользуйтесь свойствами прямоугольного треугольника. Определите длину катета A, используя тот факт, что среднее геометрическое, взятое от длины гипотенузы и проекции катета, равняется искомой величине катета. То есть N = √(D*Nd).
Учитывая, что корень из произведения означает то же самое, что и среднее геометрическое, возведите в квадрат значение N (длину искомого катета), и разделите на длину гипотенузы. То есть Nd = (N/√D)² = N²/D.В исходных данных задачи длина могут быть даны значения только катетов N и T. В этом случае длину проекции Nd находите с помощью теоремы Пифагора.
Определите длину гипотенузы D, используя значения катетов √(N²+T²) и подставьте полученное значение в формулу для нахождения проекции. Для чего Nd = N²/√(N²+T²).
Если в исходных данных содержится информация о длине проекции катета Rd и величине гипотенузы D, то длину проекции второго катета Nd вычислите с помощью простейшей формулы вычитания – Nd = D – Rd.
В ситуации, когда известно лишь значение длины гипотенузы D и дано простое соотношение длин катетов (m/h) обратитесь за помощью к формулам из первого шага и третьего шага.
Согласно формуле из первого шага примите как факт, что соотношение проекций Nd и Rd приравнивается к соотношению квадратных значений их длин. То есть Nd/Rd = m²/h². Также сумма проекций катетов Nd и Rd равняется длине гипотенузы.
Выразите значение проекции катета Rd через искомый катет Nd и подставьте в формулу суммирования. В результате вы получите Nd + Nd*m²/h² = Nd*(1 + m²/h²) = D, после чего выведите формулу нахождения Nd = D/(1 + m²/h²). Значение Nd и укажет величину искомого катета.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
1.7.1. Как найти проекцию вектора на вектор?
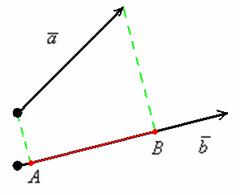
Рассмотрим ненулевые векторы и
:
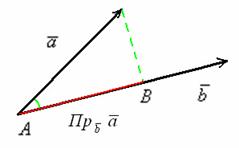
Спроецируем вектор на вектор
, для этого из начала и конца вектора
опустим перпендикуляры на вектор
(зелёные пунктирные линии).
Представьте,
что на вектор перпендикулярно сверху падают
лучи света. Тогда отрезок будет «тенью»
вектора . Проекцией вектора
на вектор
является ДЛИНА отрезка
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами острый (как на рисунке выше), то
Если векторы ортогональны, то
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами тупой (на рисунке мысленно переставьте стрелочку вектора
), то
(та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора на любой ненулевой сонаправленный вектор
будет точно такой же:
– фактически это проекция вектора
на прямую
, которая содержит сонаправленные векторы
(и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно , то
добавится знак «минус»:
Отложим наши подопытные векторы от одной точки:
и рассмотрим прямоугольный треугольник. Косинус угла – есть отношение прилежащего катета к гипотенузе:
, но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
…все ли догадались, что будет дальше?
Приравниваем формулы:
и сокращаем знаменатели обеих частей на ,
получая формулу для вычисления проекции:
Распишем её в координатах:
Если векторы плоскости и
заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Если векторы пространства заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Легко убедиться, что проекция вектора на
коллинеарный вектор может
отличаться лишь знАком, приведу выкладки для «плоского» случая :
, если
, и
, если
Задача 34
Найти проекцию вектора на вектор
Решение в одну строчку:
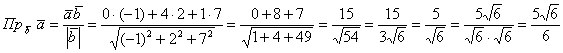
знаменатель на , избавившись тем самым от
иррациональности в знаменателе.
Ответ:
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами .
Найти:
а) проекцию стороны на сторону
;
б) проекцию стороны на сторону
.
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора на отрезок с известными концами
? (как вариант, на продолжение этого отрезка). Находим вектор
и используем формулу
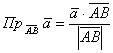
и формулу
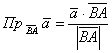
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Отрезок, соединяющий основание перпендикуляра и наклонной, проведённых из одной и той же точки, является проекцией этой наклонной. (см. рисунок в приложении).
В треугольнике боковая сторона — наклонная, его высота — перпендикуляр к прямой, содержащей другую сторону.
Высота равностороннего треугольника еще и медиана и биссектриса. Все углы равностороннего треугольника =60°. Поэтому проекция стороны — катет прямоугольного треугольника, который противолежит углу 30°. По свойству такого катета он равен половине гипотенузы. ⇒
Проекция стороны данного треугольника на прямую, содержащую другую сторону – 1:2=0,5
Ортогональная проекция стороны треугольника и формула Герона.
Канал видеоролика: Red Pen
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #матан #репетиторпоматематике #огэпоматематике
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

Ортогональная проекция фигуры | Нестандартные задачи — 18
Элементарная математика

Найти медиану треугольника, если даны три стороны. Геометрия 9 класс. Диагонали параллелограмма.
Math

Найти высоту треугольника, если известны три стороны. Метод нахождения высоты. Геометрия 8. 9 класс.
Math

Найдите стороны треугольника
GetAClass — Просто математика
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
08.02.2023
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…