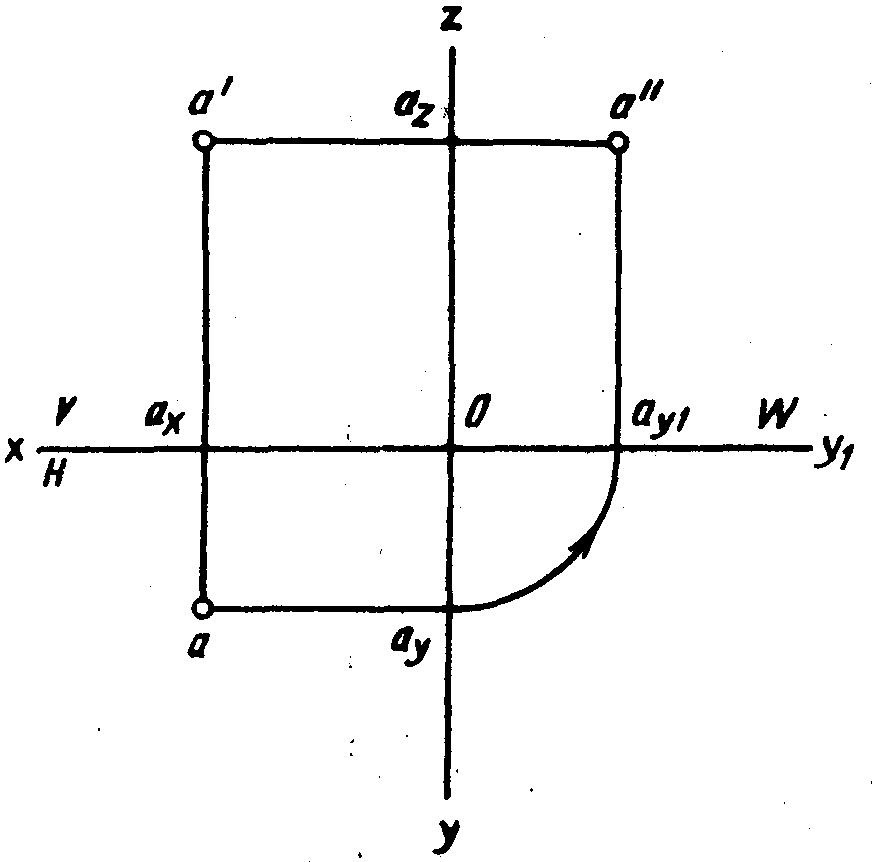Как найти проекцию точек на ось - Исправление недочетов и поиск решений вместе с Examum.ru

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

На рис. 1.1:

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

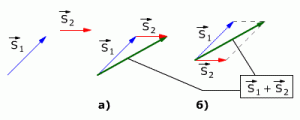
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

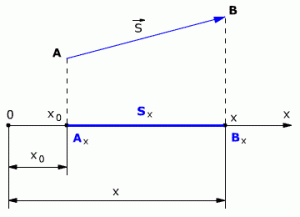
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения (см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

S_x = A_xB_x

ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, S_x). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

S_x = x – x₀

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

S_y = y – y₀
S_z = z – z₀

Здесь x₀, y₀, z₀ — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

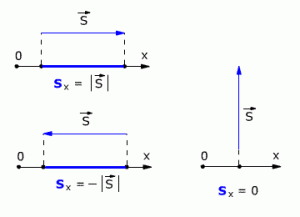
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

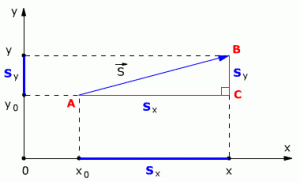
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

S_x = x – x₀
S_y = y – y₀

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

АС = s_x
CB = s_y

По теореме Пифагора

S² = S_x² + S_y²

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Источник

Проекция вектора. Координатные оси. Проекция точки. Координаты точки на ось

Вначале вспомним, что такое координатная ось, проекция точки на ось и координаты точки на оси.

Координатная ось – это прямая, которой придается какое–то направление. Можете считать, что это вектор с бесконечно большим модулем.

Координатная ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.

Проекция точки на ось — это основание перпендикуляра, опущенного из этой точки на данную ось (рис. 8). То есть, проекцией точки на ось является точка.

Рис. 8

Координата точки на ось — это число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.

Скалярная проекция вектора на ось — это число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Важно! Обычно вместо выражения скалярная проекция вектора на ось говорят просто – проекция вектора на ось, то есть слово скалярная опускают. Проекция вектора обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектор а, то его проекция обозначается а_x. При проектировании этого же вектора на другую ось, скажем, ось Y , его проекция будет обозначаться а_y (рис. 9).

Рис. 9

Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть

а_x = х_к − x_н.

Надо помнить: скалярная проекция вектора на ось (или, просто, проекция вектора на ось) — это число (не вектор)! Причем, проекция может быть положительной, если величина х_к больше величины х_н, отрицательной, если величина х_к меньше величины х_н и равной нулю, если х_к равно х_н (рис. 10).

Рис. 10

Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.

Из рисунка 11 видно, что а_x = а Cos α

то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то Cos α > 0 и а_x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.

Рис. 11

Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу — отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.

При решении задач часто будут использоваться следующие свойства проекций: если

а = b + c +…+ d , то а_x = b_x + c_x +…+ d_x (аналогично на другие оси),

если

a = mb, то а_x = mb_x (аналогично на другие оси).

Формула а_x = а Cos α будет очень часто встречаться при решении задач, поэтому ее обязательно надо знать. Правило определения проекции надо знать наизусть!

Запомните!

Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.

Еще раз — НАИЗУСТЬ!

Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

Источник

Вы здесь

Проецирование точки

СОДЕРЖАНИЕ

Проецирование точки
Пример проецирования точки
Литература

Проецирование точки

Точка относится к основным, неопределяемым понятиям геометрии. Она не может быть определена другими более элементарными понятиями. Точка не имеет размеров.

Положение точки А в пространстве определяется тремя координатами (x, y, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций.

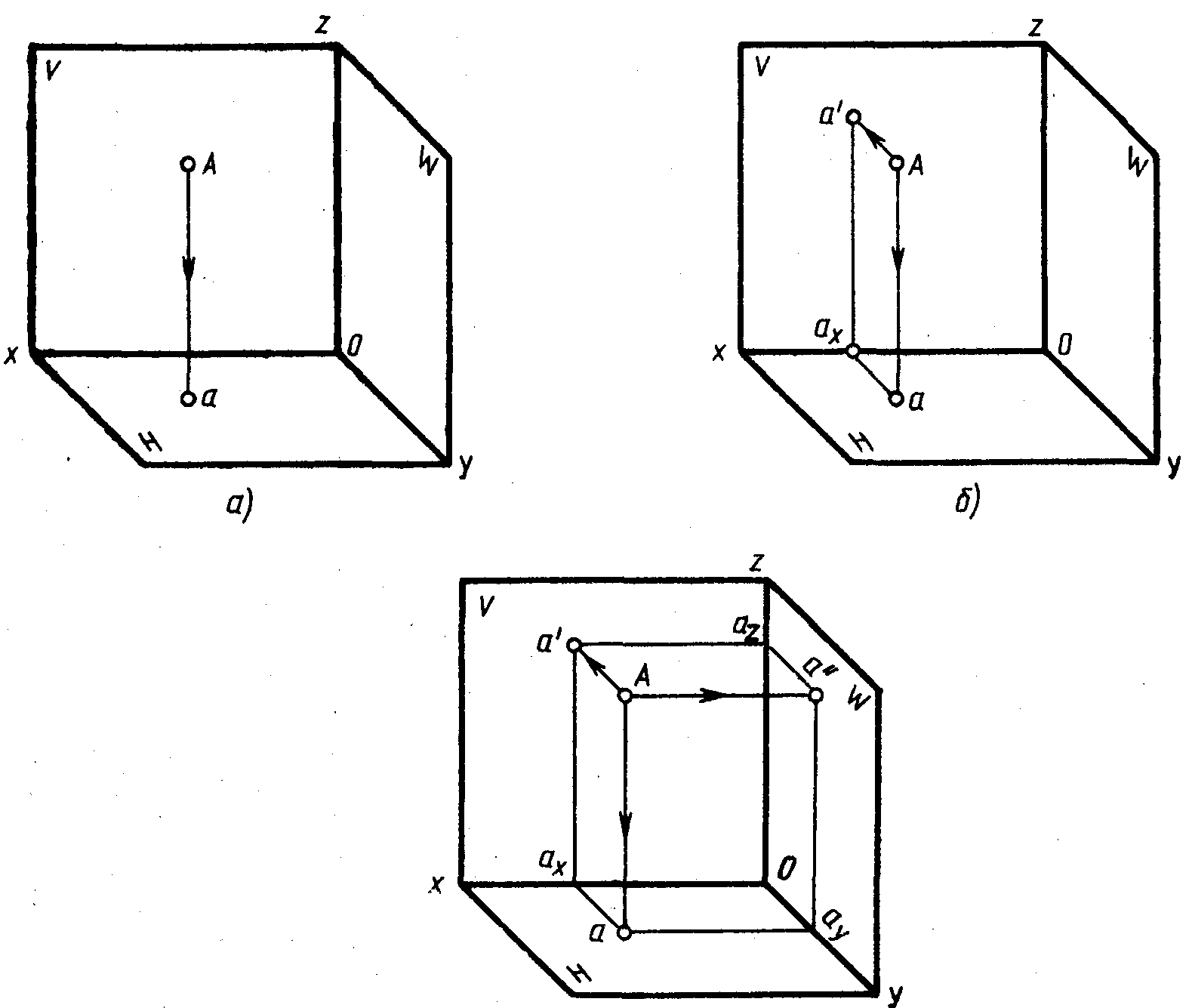
Чтобы определить эти расстояния достаточно через точку А провести прямые, перпендикулярные к плоскостям, определить точки А′, А″, А′″ пересечения этих прямых с плоскостями проекций и измерить величины отрезков [АA′], [АA″], [АA′″], которые равны значениям аппликаты z, ординаты y и абсциссы x точки А (рис.1).

Рис.1. Проецирование точки

Точки А′, А″, А′″ называют ортогональными проекциями точки А:

Принятые обозначения:

А₁ или А′	—	горизонтальная проекция точки А;
А₂ или А″	—	фронтальная проекция точки А;
А₃ или А′″	—	профильная проекция точки А.

Отрезки:

[АA′]=[ОА_x]	—	абсцисса точки А (определяет расстояние точки от плоскости П₃);
[АA″]=[ОА_y]	—	ордината точки А (определяет расстояние точки от плоскости П₂);
[АA′″]=[ОА_z]	—	аппликата точки А (определяет расстояние точки от плоскости П₁).

Прямые АA′, АA″, АA′″ называют проецирующими прямыми или проецирующими лучами.

АA′	—	горизонтально проецирующая прямая;
АA″	—	фронтально проецирующая прямая;
АA′″	—	профильно проецирующая прямая.

При построении проекций точки А необходимо знать, что горизонтальная проекция определяется абсциссой x и ординатой y, фронтальная проекция – абсциссой x и аппликатой z, а профильная – ординатой y и аппликатой z, т.е.

А′ (x, y)

А″ (x, z)

А′″ (y, z)

Если даны две проекции точки, то по ним можно найти третью проекцию, так как все проекции связаны между собой линиями связи.

Пример проецирования точки

Пример: Даны две проекции точки А (рис.2), необходимо найти третью проекцию точки.

Рис.2. Проецирование точки

Для начала найдем проекции точки А на оси координат, т.е. А_x, А_yП1 и А_z (рис.3).

Рис.3. Проецирование точки

При помощи циркуля получаем проекцию точки А_yП3 (рис.4).

Рис.4. Проецирование точки

Зная, что проекция точки А′″ имеет координаты (y, z), проводим проецирующие лучи из точки А_yП3 и А_z. Точкой пересечения этих лучей будет точка А′″ (рис.5).

Рис.5. Проецирование точки

ЛИТЕРАТУРА

Начертательная геометрия / С.А. Фролов. – М.: Машиностроение, 1987 – 240 с.
Черчение / Н.С. Брилинг. – М.: Стройиздат, 1989. – 420 с.
Краткий справочник по начертательной геометрии и машиностроительному черчению / Н.П. Сберегаев, М.А. Герб. М. – Л., Машиностроение, 1965, 264 с.

12495 просмотров

Источник

Проекции точки

Проецирование
точки на три плоскости проекций
координатного угла начинают с получения
ее изображения на плоскости H
— горизонтальной плоскости проекций.
Для этого через точку А (рис. 4.12, а)
проводят проецирующий луч перпендикулярно
плоскости H.

На
рисунке перпендикуляр к плоскости Н
параллелен оси Oz. Точку пересечения
луча с плоскостью Н (точку а) выбирают
произвольно. Отрезок Аа определяет,
на каком расстоянии находится точка А
от плоскости Н, указывая тем самым
однозначно положение точки А на рисунке
по отношению к плоскостям проекций.
Точка а является прямоугольной проекцией
точки А на плоскость Н и называется
горизонтальной проекцией точки А (рис.
4.12, а).

в)

Рис.
4.12.

Для
получения изображения точки А на
плоскости V (рис. 4.12,б) через точку А
проводят проецирующий луч перпендикулярно
фронтальной плоскости проекций V. На
рисунке перпендикуляр к плоскости V
параллелен оси Оу. На плоскости Н
расстояние от точки А до плоскости V
изобразится отрезком аа_х,
параллельным оси Оу и перпендикулярным
оси Ох. Если представить себе, что
проецирующий луч и его изображение
проводят одновременно в направлении
плоскости V, то когда изображение луча
пересечет ось Ох в точке а_х,
луч пересечет плоскость V в точке а’.
Проведя из точки а_х
в плоскости V перпендикуляр к оси Ох,
который является изображением
проецирующего луча Аа на плоскости V, в
пересечении с проецирующим лучом
получают точку а’. Точка а’ является
фронтальной проекцией точки А, т. е. ее
изображением на плоскости V.

Изображение
точки А на профильной плоскости проекций
(рис. 4.12, в) строят с помощью проецирующего
луча, перпендикулярного плоскости W. На
рисунке перпендикуляр к плоскости W
параллелен оси Ох. Проецирующий луч от
точки А до плоскости W на плоскости Н
изобразится отрезком аа_у,
параллельным оси Ох и перпендикулярным
оси Оу. Из точки Оу параллельно оси Oz и
перпендикулярно оси Оу строят изображение
проецирующего луча аА и в пересечении
с проецирующим лучом получают точку
а». Точка а» является профильной
проекцией точки А, т. е. изображением
точки А на плоскости W.

Точку
а» можно построить, проведя от точки
а’ отрезок а’а_z
(изображение проецирующего луча Аа»
на плоскости V) параллельно оси Ох, а от
точки а_z
— отрезок а»а_z
параллельно оси Оу до пересечения с
проецирующим лучом.

Получив
три проекции точки А на плоскостях
проекций, координатный угол развертывают
в одну плоскость, как показано на рис.
4.11,б, вместе с проекциями точки А и
проецирующих лучей, а точку А и проецирующие
лучи Аа, Аа’ и Аа» убирают. Края
совмещенных плоскостей проекций не
проводят, а проводят только оси проекций
Oz, Оу и Ох, Оу₁
(рис. 4.13).

Анализ
ортогонального чертежа точки показывает,
что три расстояния — Аа’, Аа и Аа»
(рис. 4.12, в), характеризующие положение
точки А в пространстве, можно определить,
отбросив сам объект проецирования —
точку А, на развернутом в одну плоскость
координатном угле (рис. 4.13). Отрезки
а’а_z,
аа_y
и Оа_х
равны Аа» как противоположные стороны
соответствующих прямоугольников (рис.
4.12,в и 4.13). Они определяют расстояние,
на котором находится точка А от профильной
плоскости проекций. Отрезки а’а_х,
а»а_у1
и Оа_у
равны отрезку Аа, определяют расстояние
от точки А до горизонтальной плоскости
проекций, отрезки аа_х,
а»а_z
и Оа_y₁
равны отрезку Аа’, определяющему
расстояние от точки А до фронтальной
плоскости проекций.

Рис.
4.13.

Отрезки
Оа_х,
Оа_у
и Оа_z,
расположенные на осях проекций, являются
графическим выражением размеров
координат X, Y и Z точки А. Координаты
точки обозначают с индексом соответствующей
буквы. Измерив величину этих отрезков,
можно определить положение точки в
пространстве, т. е. задать координаты
точки.

На
эпюре отрезки а’а_х
и аа_х
располагаются как одна линия,
перпендикулярная к оси Ох а отрезки
а’а_z
и a»a_z
— к оси Оz.
Эти лини называются линиями проекционной
связи. Они пересекают оси проекций в
точках а_х
и а_z
соответственно. Линия проекционной
связи, соединяющая горизонтальную
проекцию точки А с профильной, оказалась
«разрезанной» в точке а_у.

Две
проекции одной и той же точки всегда
располагаются на одной линии проекционной
связи, перпендикулярной к оси проекций.

Для
представления положения точки в
пространстве достаточно двух ее проекций
и заданного начала координат (точка О)
На рис. 4.14, б две проекции точки полностью
определяют ее положение в пространстве
По этим двум проекциям можно построит
профильную проекцию точки А. Поэтому в
дальнейшем, если не будет необходимости
в профильной проекции, эпюры будут
построены на двух плоскостях проекций:
V и Н.

Рис.
4.14. Рис. 4.15.

Рассмотрим
несколько примеров построения и чтения
чертежа точки.

Пример
1.
Определение координат точки J заданной
на эпюре двумя проекциях (рис. 4.14).
Измеряются три отрезка: отрезок Ов_Х
(координата X), отрезок b_Хb
(координата Y) и отрезок b_Хb’
(координата Z). Координаты записывают в
следующем п рядке: X, Y и Z, после буквенного
обозначения точки, например, В20; 30; 15.

Пример
2.
Построение точки по заданным координатам.
Точка С задана координатами С30; 10; 40. На
оси Ох (рис. 4.15) находят точку с_х,
в которой линия проекционной связи
пересекает ось проекций. Для этого по
оси Ох от начала координат (точка О)
откладывают координату X (размер 30) и
получают точку с_х.
Через эту точку перпендикулярно оси Ох
проводят линию проекционной связи и от
точки вниз откладывают координату У
(размер 10), получают точку с — горизонтальную
проекцию точки С. Вверх от точки с_х
по линии проекционной связи откладывают
координату Z (размер 40), получают точку
с’ — фронтальную проекцию точки С.

Рис.
4.16.

Пример
3.
Построение профильной проекции точки
по заданным проекциям. Заданы проекции
точки D — d и d’. Через точку О проводят
оси проекций Oz, Oy и Оу₁
(рис. 4.16, а). Для построения профильной
проекции точки D отточки d’ проводят
линию проекционной связи, перпендикулярную
оси Oz, и продолжают ее вправо за ось Oz.
На этой линии будет располагаться
профильная проекция точки D. Она будет
находиться на таком расстоянии от оси
Oz, на каком горизонтальная проекция
точки d располагается: от оси Ох, т. е. на
расстоянии dd_x.
Отрезки d_zd»
и dd_x
одинаковы, так как определяют одно и то
же расстояние — расстояние от точки D
до фронтальной плоскости проекций. Это
расстояние является координатой У точки
D.

Графически
отрезок d_zd»
строят перенесением отрезка dd_x
с горизонтальной плоскости проекций
на профильную. Для этого проводят линию
проекционной связи параллельно оси Ох,
получают на оси Оу точку d_y
(рис. 4.16,б). Затем переносят размер отрезка
Od_y
на ось Оу₁,
проведя из точки О дугу радиусом, равным
отрезку Od_y,
до пересечения с осью Оу₁
(рис. 4.16,б), получают точку dy₁.
Эту точку можно построить и как показано
на рис. 4.16, в, проведя прямую под углом
45° к оси Оу из точки d_y.
Из точки d_y1
проводят линию проекционной связи
параллельно оси Oz и на ней откладывают
отрезок, равный отрезку d’d_x,
получают точку d».

Перенос
величины отрезка d_xd
на профильную плоскость проекций можно
осуществить с помощью постоянной прямой
чертежа (рис. 4.16, г). В этом случае линию
проекционной связи dd_y
проводят через горизонтальную проекцию
точки параллельно оси Оу₁
до пересечения с постоянной прямой, а
затем параллельно оси Оу до пересечения
с продолжением линии проекционной связи
d’d_z.

Частные
случаи расположения точек относительно
плоскостей проекций

Положение
точки относительно плоскости проекций
определяется соответствующей координатой,
т. е. величиной отрезка линии проекционной
связи от оси Ох до соответствующей
проекции. На рис. 4.17 координата У точки
А определяется отрезком аа_х
— расстояние от точки А до плоскости
V. Координата Z точки А определяется
отрезком а’а_х
— расстояние от точки А до плоскости
Н. Если одна из координат равна нулю, то
точка расположена на плоскости проекций.
На рис. 4.17 приведены примеры различного
расположения точек относительно
плоскостей проекций. Координата Z точки
В равна нулю, точка находится в плоскости
Н. Ее фронтальная проекция находится
на оси Ох и совпадает с точкой b_х.
Координата У точки С равна нулю, точка
располагается на плоскости V, ее
горизонтальная проекция с находится
на оси Ох и совпадает с точкой с_х.

Следовательно,
если точка находится на плоскости
проекций, то одна из проекций этой точки
лежит на оси проекций.

Рис.
4.17.

На
рис. 4.17 координаты Z и Y точки D равны
нулю, следовательно, точка D находится
на оси проекций Ох и две ее проекции
совпадают.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

matematicus.ru

matematicus включает разделы – высшая математика, аналитическая геометрия в пространстве и на плоскости, теория вероятностей, Arduino, Android Studio, Excel, программирование, программы, Windows, ошибки, таблицы, формулы, примеры, физика, химия

Проекция точки на ось (прямую)

Осью называется всякая прямая, на которой выделено одно из двух её направлений.

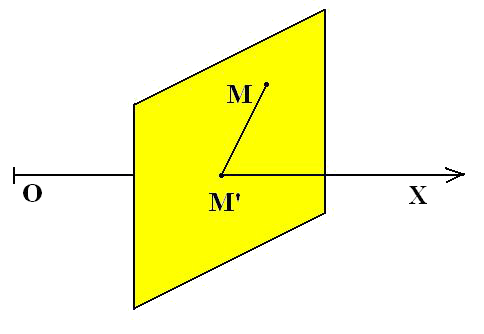
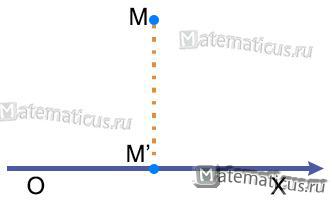
Пусть дана прямая (ось) OX и некоторая точка M (вне оси или на ней). Проведём через точку M плоскость, перпендикулярную к прямой (оси); она пересечёт прямую (ось) в некоторой точки M’. Точка M’ называется проекцией точки M на прямую (ось) OX (если точка M лежит на оси, то она сама является своей проекцией.)