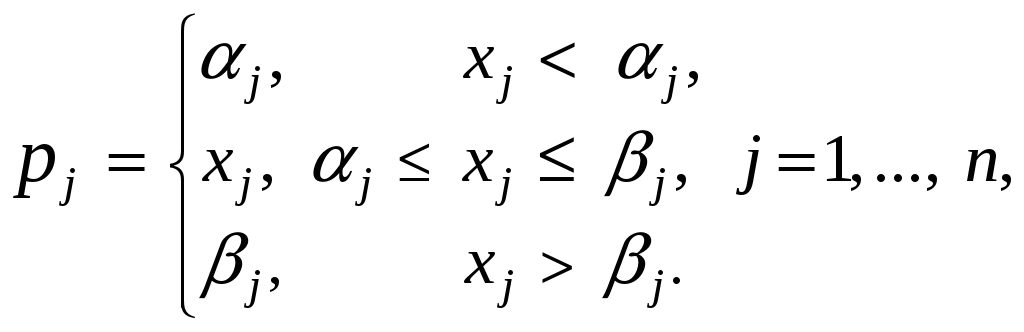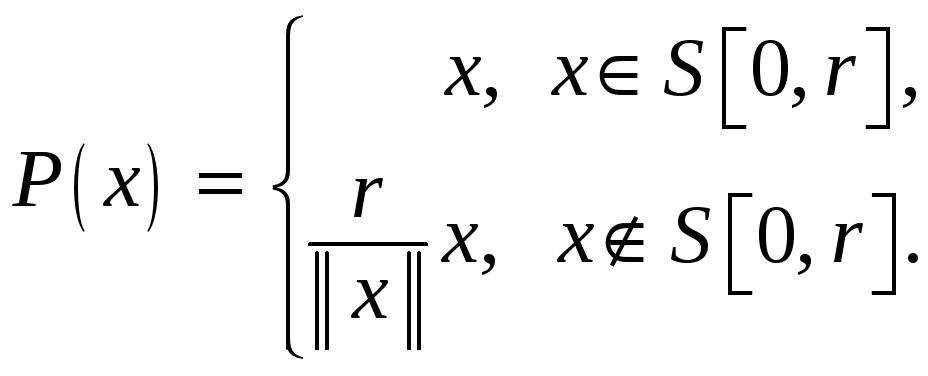Как найти проекцию точки на множество

Методы Оптимизации. Даниил Меркулов. Отделимость. Проекция. Опорная гиперплоскость

Interior

Внутренность множества

Внутренностью множества $S$ называется следующее множество:
$$mathbf{int} (S) = {mathbf{x} in S mid exists varepsilon > 0, B(mathbf{x}, varepsilon) subset S}$$
где $B(mathbf{x}, varepsilon) = mathbf{x} + varepsilon B$ — шар с центром в т.$mathbf{x}$ и радиусом $varepsilon$

Относительная внутренность множества

Относительной внутренностью множества $S$ называется следующее множество:
$$mathbf{relint} (S) = {mathbf{x} in S mid exists varepsilon > 0, B(mathbf{x}, varepsilon) cap mathbf{aff} (S) subseteq S}$$

• Любое непустое выпуклое множество $S subseteq mathbb{R}^n$ имеет непустую относительную внутренность $mathbf{relint}(S)$

Projection

Расстояние между точкой и множеством

Расстоянием $d$ от точки $mathbf{y} in mathbb{R}^n$ до замкнутого множества $S subset mathbb{R}^n$ является:
$$d(mathbf{y}, S, | cdot |) = inf{|x — y| mid x in S }$$

Проекция точки на множество

Проекцией точки $mathbf{y} in mathbb{R}^n$ на множество $S subseteq mathbb{R}^n$ называется точка $pi_S(mathbf{y}) in S$: $$| pi_S(mathbf{y}) — mathbf{y}| le |mathbf{x} — mathbf{y}|, forall mathbf{x} in S$$

• Если множество — открыто, и точка в нем не лежит, то её проекции на это множество не существует
• Если точка лежит в множестве, то её проекция — это сама точка
• $$pi_S(mathbf{y}) = underset{mathbf{y}}{operatorname{argmin}} |mathbf{x}-mathbf{y}|$$
• Пусть $S subseteq mathbb{R}^n$ — выпуклое замкнутое множество. Пусть так же имеются точки $mathbf{y} in mathbb{R}^n$ и $mathbf{pi} in S$. Тогда если для всех $mathbf{x} in S$ справедливо неравенство: $$langle pi -mathbf{y}, mathbf{x} — pirangle ge 0, $$ то $pi$ является проекцией точки $mathbf{y}$ на $S$, т.е. $pi_S (mathbf{y}) = pi$
• Пусть $S subseteq mathbb{R}^n$ — афинное множество. Пусть так же имеются точки $mathbf{y} in mathbb{R}^n$ и $mathbf{pi} in S$. Тогда $pi$ является проекцией точки $mathbf{y}$ на $S$, т.е. $pi_S (mathbf{y}) = pi$ тогда и только тогда, когда для всех $mathbf{x} in S$ справедливо равенство: $$langle pi -mathbf{y}, mathbf{x} — pirangle = 0 $$

Пример 1

Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid |x — x_c| le R }$, $y notin S$

Решение:

• Из рисунка строим гипотезу: $pi = x_0 + R cdot frac{y — x_0}{|y — x_0|}$

• Проверяем неравенство для выпуклого замкнутого множества: $(pi — y)^T(x — pi) ge 0$

$$left( x_0 — y + R frac{y — x_0}{|y — x_0|} right)^Tleft( x — x_0 — R frac{y — x_0}{|y — x_0|} right) =$$
$$left( frac{(y — x_0)(R — |y — x_0|)}{|y — x_0|} right)^Tleft( frac{(x-x_0)|y-x_0|-R(y — x_0)}{|y — x_0|} right) =$$
$$frac{R — |y — x_0|}{|y — x_0|^2} left(y — x_0 right)^Tleft( left(x-x_0right)|y-x_0|-Rleft(y — x_0right) right) = $$

$$frac{R — |y — x_0|}{|y — x_0|} left( left(y — x_0 right)^Tleft( x-x_0right)-R|y — x_0| right) =$$

$$left(R — |y — x_0| right) left( frac{(y — x_0 )^T( x-x_0)}{|y — x_0|}-R right)$$

Первый сомножитель отрицателен по выбору точки $y$. Второй сомножитель так же отрицателен, если применить к его записи теорему Коши — Буняковского: $$(y — x_0 )^T( x-x_0) le |y — x_0||x-x_0|$$
$$frac{(y — x_0 )^T( x-x_0)}{|y — x_0|} — R le frac{|y — x_0||x-x_0|}{|y — x_0|} — R = |x — x_0| — R le 0$$

Пример 2

Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid c^T x = b }$, $y notin S$

Решение:

• Из рисунка строим гипотезу: $pi = y + alpha c$. Коэффициент $alpha$ подбирается так, чтобы $pi in S$: $c^T pi = b$, т.е.: $$c^T (y + alpha c) = b$$
  $$c^Ty + alpha c^T c = b$$
  $$c^Ty = b — alpha c^T c$$

• Проверяем неравенство для выпуклого замкнутого множества: $(pi — y)^T(x — pi) ge 0$
  $$(y + alpha c — y)^T(x — y — alpha c) = $$
  $$ alpha c^T(x — y — alpha c) = $$
  $$ alpha (c^Tx) — alpha (c^T y) — alpha^2 c^Tc) = $$
  $$ alpha b — alpha (b — alpha c^T c) — alpha^2 c^Tc = $$
  $$ alpha b — alpha b + alpha^2 c^T c — alpha^2 c^Tc = 0 ge 0$$

Пример 3

Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid Ax = b, A in mathbb{R}^{m times n}, b in mathbb{R}^{m} }$, $y notin S$

Решение:

• Из рисунка строим гипотезу: $pi = y + sumlimits_{i=1}^malpha_i A_i = y + A^T alpha$. Коэффициент $alpha$ подбирается так, чтобы $pi in S$: $A pi = b$, т.е.: $$c^T (y + A^T alpha) = b$$
  $$A(y + A^Talpha) = b$$
  $$Ay = b — A A^Talpha$$

• Проверяем неравенство для выпуклого замкнутого множества: $(pi — y)^T(x — pi) ge 0$
  $$(y + A^Talpha — y)^T(x — y — A^Talpha) = $$
  $$ alpha^T A(x — y — A^Talpha) = $$
  $$ alpha^T (Ax) — alpha^T (A y) — alpha^T AA^T alpha) = $$
  $$ alpha^T b — alpha^T (b — A A^Talpha) — alpha^T AA^T alpha = $$
  $$ alpha^T b — alpha^T b + alpha^T AA^T alpha — alpha^T AA^T alpha = 0 ge 0$$

Separation

Отделимые множества

Множества $S_1$ и $S_2$ называются отделимыми, если существуют $mathbf{p} neq mathbf{0} in mathbb{R}^n$ и $beta in mathbb{R}$, что:
$$langle mathbf{p}, mathbf{x_1}rangle le beta le langle mathbf{p}, mathbf{x_2}rangle, ;; forall mathbf{x_1} in S_1, ;; forall mathbf{x_2} in S_2$$

Собственно отделимые множества

Множества $S_1$ и $S_2$ называются собственно отделимыми, если они отделимы и дополнительно можно указать такие $mathbf{x_1} in S_1, mathbf{x_2} in S_2$
$$langle mathbf{p}, mathbf{x_1}rangle < langle mathbf{p}, mathbf{x_2}rangle$$

Строго отделимые множества

Множества $S_1$ и $S_2$ называются строго отделимыми, если существует $mathbf{p} neq mathbf{0} in mathbb{R}^n$, что:
$$langle mathbf{p}, mathbf{x_1}rangle < langle mathbf{p}, mathbf{x_2}rangle, ;; forall mathbf{x_1} in S_1, ;; forall mathbf{x_2} in S_2$$

Сильно отделимые множества

Множества $S_1$ и $S_2$ называются сильно отделимыми, если существуют $mathbf{p} neq mathbf{0} in mathbb{R}^n$ и $beta in mathbb{R}$, что:
$$ underset{mathbf{x_1} in S_1}{operatorname{sup}} langle mathbf{p}, mathbf{x_1}rangle < beta < underset{mathbf{x_2} in S_2}{operatorname{inf}}langle mathbf{p}, mathbf{x_2}rangle, ;; forall mathbf{x_1} in S_1, ;; forall mathbf{x_2} in S_2$$

Расстояние между множествами

Расстоянием между множествами $S_1$ и $S_2$ называется число:
$$d(S_1, S_2,| cdot |) = underset{mathbf{x_1} in S_1, mathbf{x_2} in S_2}{operatorname{inf}} |mathbf{x_1} — mathbf{x_2}|$$

• Если $X$ и $Y$ — непустые выпуклые множества в $mathbb{R}^n$ и $X cap Y = emptyset$, тогда $X$ и $Y$ — отделимы.
• Если $X$ — непустое выпуклое замкнутое множество в $mathbb{R}^n$ и $mathbf{y} notin X$, тогда точку $mathbf{y}$ можно строго отделить от множества $X$.

Supporting hyperplane

Опорная гиперплоскость

Гиперплоскость $Gamma_{p,beta} = left{mathbf{x} in mathbb{R}^n : langle p, mathbf{x} rangle &gt; beta right}$ называется опорной к множеству $S$ в граничной точке $mathbf{a} in partial S$, если $$langle p, mathbf{x} rangle ge beta = langle p, mathbf{a} rangle ;; forall mathbf{x} in S$$

Опорная гиперплоскость называется собственно опорной, если, кроме того, можно указать $mathbf{x_0} in S: langle p, mathbf{x_0} rangle &gt; beta$

• В любой граничной (относительно граничной) точке выпуклого множества существует опорная (собственно опорная) гиперплоскость.
• Касательная плоскость к поверхности $F(x) = 0,$ где $F: mathbb{R}^n rightarrow mathbb{R}^1$ в точке $x_0$ определяется уравнением: $$nabla F(x_0)^T(x-x_0) = 0$$
• Касательная плоскость к графику функции $f(x),$ где $f: mathbb{R}^n rightarrow mathbb{R}^1$ в точке $x_0$ определяется уравнением: $$phi(x) = f(x_0) + nabla f(x_0)^T(x-x_0) = 0$$

Пример 4

Построить гиперплоскость, разделяющую $S_1$ и $S_2$:
$$S_1 = left{ x in mathbb{R}^2 mid x_1 x_2 ge 1, x_1 &gt; 0right}, ;;; S_2 = left{ x in mathbb{R}^2 mid x_2 le frac{4}{x_1 — 1} +9right}$$

Решение:

• Найдем $partial S_1 cap partial S_2$:
  $$
  begin{cases}
  x_1 x_2 = 1
  x_2 = frac{4}{x_1 — 1} +9
  end{cases}
  $$

$$
begin{cases}
x_1 = frac{1}{3}
x_2 = 3
end{cases}
$$
т.е. множества пересекаются в точке $x_0 = (frac{1}{3}, 3)$

• Построим касательные плоскости к обеим поверхностям в точке пересечения:
  $$
  begin{cases}
  nabla F_1(x_0)^T(x-x_0) = 0
  nabla F_2(x_0)^T(x-x_0) = 0
  end{cases}
  $$

$$
begin{cases}
3 x_1 + frac{1}{3}x_2 — 2 = 0 \
-6 x_1 — frac{2}{3}x_2 + 4 = 0
end{cases}
$$

Итого, получаем: $9x_1 + x_2 = 6$, т.е. $p = (9,1), beta = 6$

Пример 5

Построить опорную гиперплоскость для множества $S = left{ x in mathbb{R}^2 mid e^{x_1} le x_2right}$ в граничной точке $x_0 = (0,1)$

Решение:

• Имеем поверхность $F(x_1, x_2) = e^{x_1} — x_2, ;;; nabla F = (e^{x_1}, -1), ;;; nabla F(x_0) = (1,-1)$
• Тогда $$nabla F(x_0)^T(x-x_0) = 0$$
  $$(1,-1)^T (x_1, x_2 — 1) = 0$$
• Искомая опорная гиперплоскость: $x_1 — x_2 + 1 = 0$

Пример 6

Построить опорную гиперплоскость для множества $S = left{ x in mathbb{R}^3 mid x_3 ge x_1^2 + x_2^2right}$ так, чтобы она отделяла его от точки $x_0 = left(-frac{5}{4}, frac{5}{16}, frac{15}{16}right)$

Решение:

• Заметим, что здесь $x_0 notin partial S$. А значит, таких гиперплоскостей много. Возможный вариант: искать опорную гиперплоскость в точке $pi_S(x_0) = pi in S$. Значит, $Gamma_{p, beta} = left{ x in mathbb{R}^3 mid p^Tx = beta, p^T pi = beta right}$

• Будем искать $pi$, решая задачу минимизации:

$$underset{x in partial S}{operatorname{min}}|x — x_0|^2$$
$$underset{x in partial S}{operatorname{min}}(x — x_0)^T(x — x_0)$$

Учитывая структуру множества $partial S = {x in mathbb{R}^3 mid x_3 = x_1^2 + x_2^2}$, можем перейти к задаче безусловной минимизации.

$$ left( x_1 + frac{5}{4} right)^2 + left( x_2 — frac{5}{16} right)^2 + left( x_1^2 + x_2^2 — frac{15}{16} right)^2 rightarrow operatorname{min}$$

Единственным решением которой является точка $pi = left( -1, frac{1}{4}, frac{17}{16}right)$.

• Тогда $p = x_0 — pi = left( -frac{1}{4}, frac{1}{16}, -frac{1}{8}right), ;; beta = p^T pi = frac{17}{128}$

Домашнее задание 3

1. Найти $pi_S (y) = pi​$, если $S = {x in mathbb{R}^n mid c^T x ge b }​$

2. Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid x = x_0 + X alpha, X in mathbb{R}^{n times m}, alpha in mathbb{R}^{m}}$, $y notin S$

3. Построить гиперплоскость, разделяющую $S_1$ и $S_2$:
   $$S_1 = left{ x in mathbb{R}^n mid x_1^2 + x_2^2 + ldots + x_n^2 le 1right}, ;;; S_2 = left{ x in mathbb{R}^n mid x_1^2 + x_2^2 + ldots + x_{n-1}^2 + 1 le x_n right}$$

4. Построить опорную гиперплоскость для множества $S = left{ x in mathbb{R}^3 mid frac{x_1^2}{4}+frac{x_2^2}{8}+frac{x_3^2}{25} le 1 right}$ в граничной точке $x_0 = left(-1, frac{12}{5}, frac{sqrt{3}}{2}right)$

5. Пусть $S subset mathbb{R}^n$ — замкнутое выпуклое множество, $mathbf{x} in S$. Найти множество $Y subset mathbb{R}^n$ такое, что $forall mathbf{y} in Y$ выполнено $mathbf{x} = pi_S(mathbf{y})$

6. Пусть даны $mathbf{x} in mathbb{R}^n$ и выпуклый конус $K subseteq mathbb{R}^n$. Пусть $Y = mathbf{x} + K$, $mathbf{y} in Y$. Найти множество $X subset mathbb{R}^n,$ такое, что $mathbf{x} in X, forall mathbf{y} in Y: x = pi_X(mathbf{y})$

В качестве решения необходимо предоставить либо:

• .pdf файл, сверстанный с помощью $ LaTeX ​$ с решениями задач
• .ipynb с оформленным решением