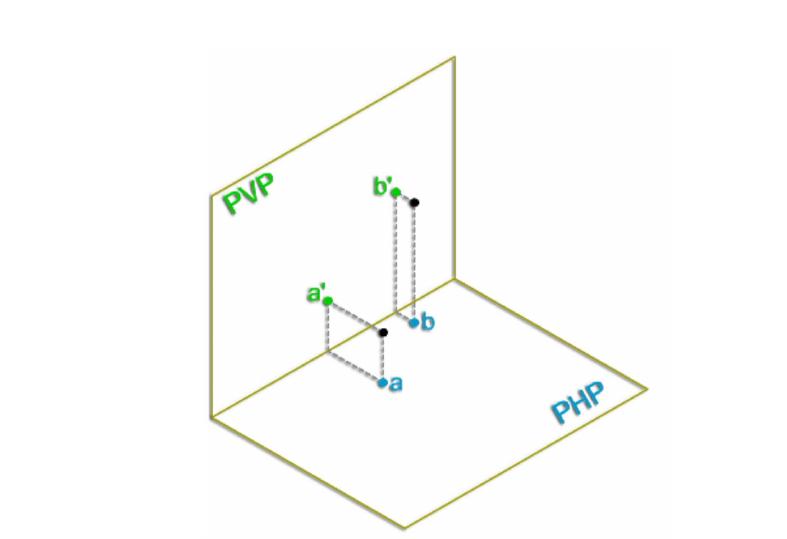
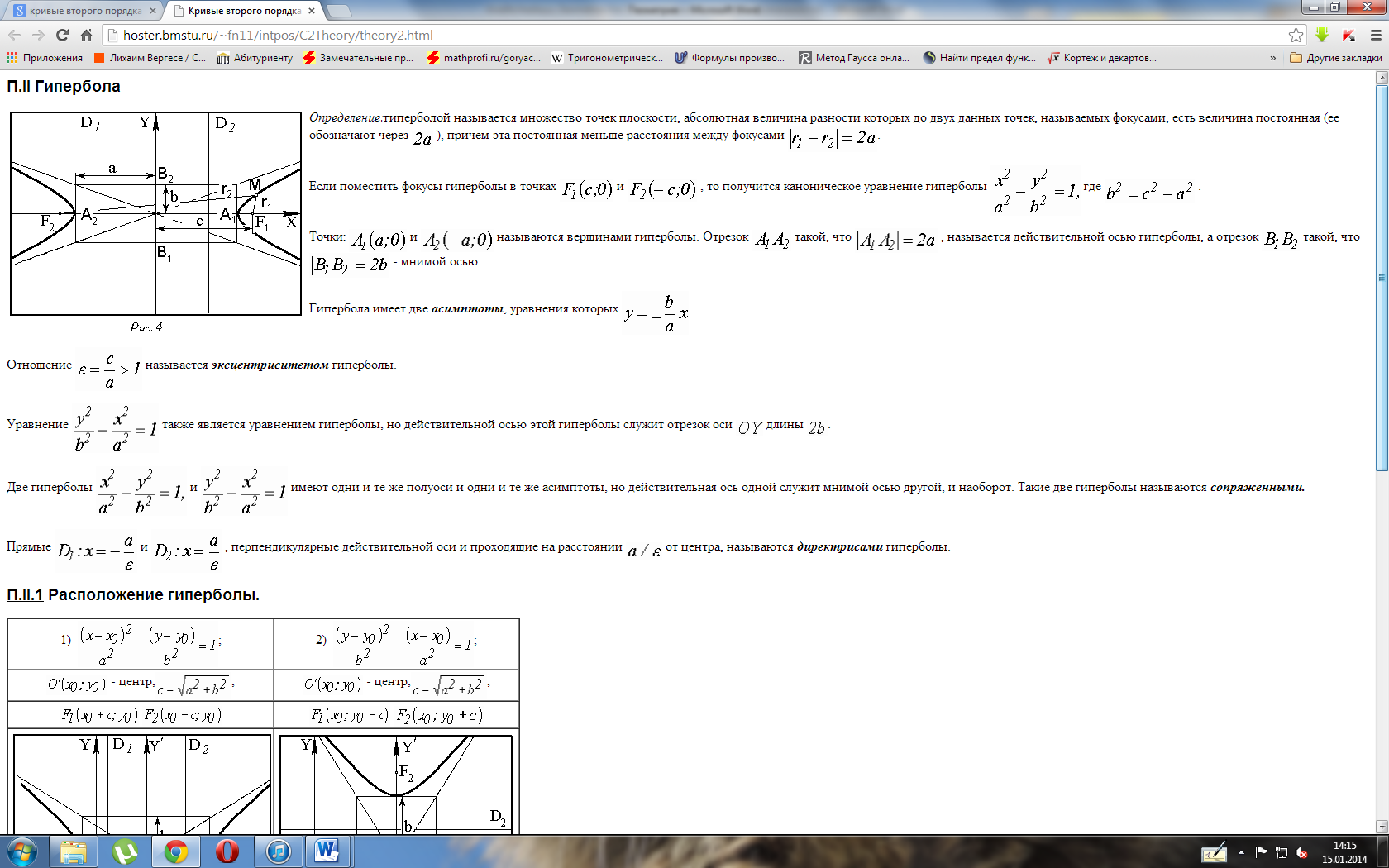
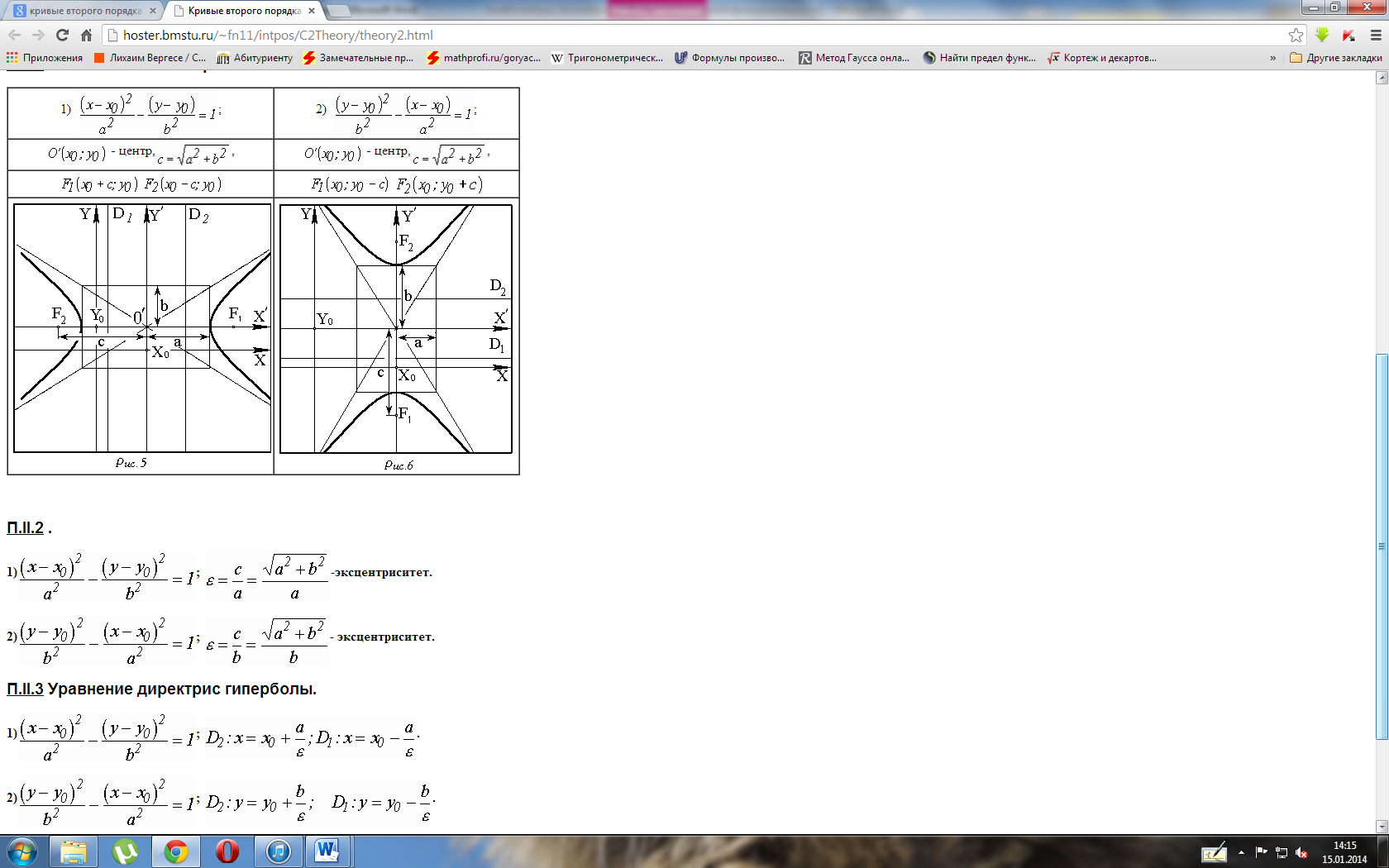
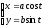Как найти проекцию точки на плоскость формула - Исправление недочетов и поиск решений вместе с Examum.ru

Проекция точки на плоскость онлайн

С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Проекция точки на плоскость − теория, примеры и решения

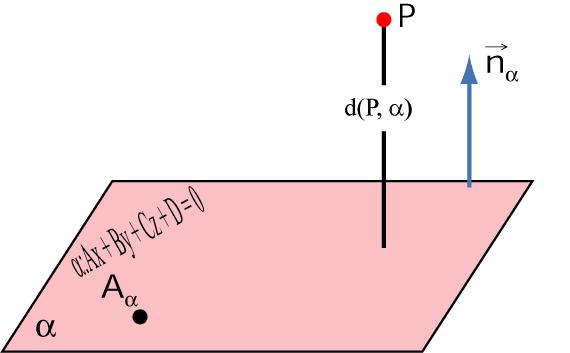
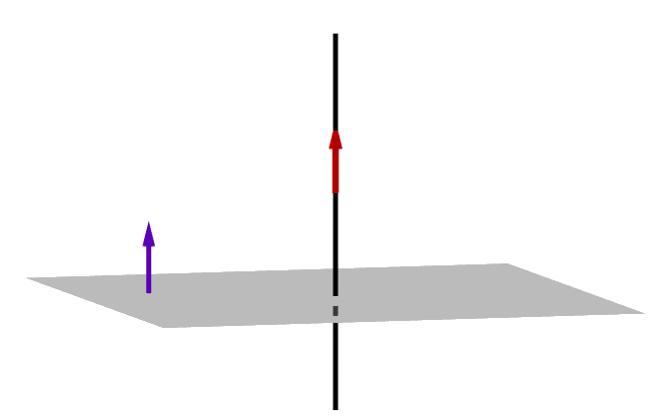
Для нахождения проекции точки M₀ на плоскость α, необходимо:

построить прямую L, проходящую через точку M₀ и ортогональной плоскости α.
найти пересечение данной плоскости α с прямой L(Рис.1).

Общее уравнение плоскости имеет вид:

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональной плоскости (1) имеет следующий вид:

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр t.

Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

Подставляя значение параметра t в выражения (4), находим проекцию M₁ точки M₀ на плоскость (1).

Пример 1.Найти проекцию M₁ точки M₀(4, -3, 2) на плоскость

Решение.

Нормальный вектор плоскости имеет вид:

т.е. A=5, B=1, C=−8.

Координаты точки M₀: x₀=4, y₀=−3, z₀=2.

Подставляя координаты точки M₀ и нормального вектора плоскости в (5), получим:

Из выражений (7) находим:

Ответ:

Проекцией точки M₀(4, -3, 2) на плоскость (6) является точка:

Источник

При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.

Уравнение для описания плоскости

Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее — ниже.

Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:

A*x + B*y + C*z + D = 0.

Первые три коэффициента — это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.

Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.

Понятие о проекции точки и ее вычисление

Предположим, что задана некоторая точка P(x₁; y₁; z₁) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x₂; y₂; z₂). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.

Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:

(x; y; z) = (x₁; y₁; z₁) + λ*(A; B; C).

Где λ — действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.

После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.

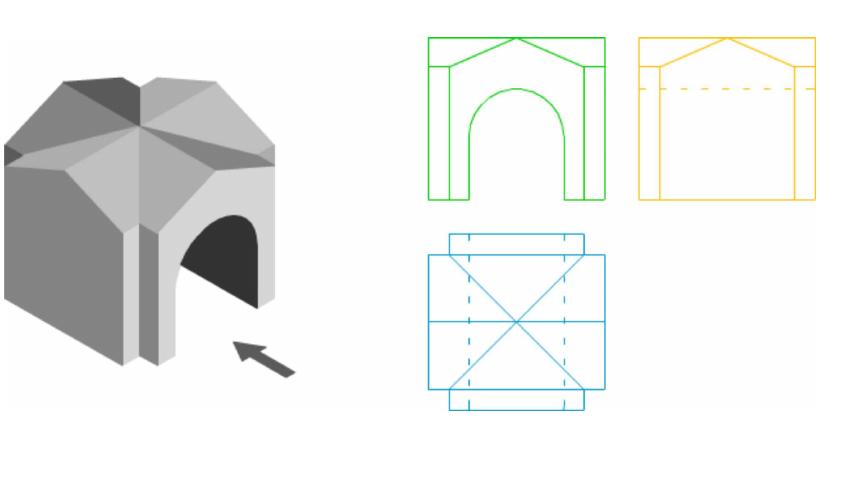
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.

Вычисление расстояния от плоскости до точки

Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:

d = |PQ¯| = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²).

Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.

Пример задачи

Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:

2*x — y + z + 4 = 0.

Следует найти точки проекцию на плоскость и вычислить между ними расстояние.

В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90^o. Имеем:

(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).

Записывая это равенство в явном виде, приходим к следующей системе уравнений:

x = 2*λ;

y = -2 — λ;

z = λ + 3;

2*x — y + z + 4 = 0.

Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:

2*(2*λ) — (-2 — λ) + λ + 3 + 4 = 0 =>

6*λ + 9 = 0 =>

λ = 9/6 = 3/2 = 1,5.

Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:

(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).

Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:

d = √((3 — 0 )² + (-3,5 + 2 )² + (4,5 — 3 )²) = 3,674.

В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.

Источник

Проекция точки на плоскость

Определите
координаты проекции точки М1(-1,-2.5) на
плоскость

x-2y+2z-4=0

Нормальный
вектор плоскости x-2y+2z-4=0

имеет
координаты (1.-2.2), следовательно,
вектор является направляющим вектором
прямой a. Теперь мы можем написать
параметрические
уравнения прямой в пространстве, так
как знаем координаты точки прямой
М1(-1,-2.5) и координаты ее направляющего
вектора (1.-):

X=1t-1

Y=-2t-2

Z=2t+5

Осталось
определить координаты точки пересечения
прямой и плоскости.
Для этого в уравнение плоскости подставим :
.

Теперь
по параметрическим уравнениям 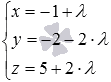вычислим
значения переменныхx, y и z при :
.

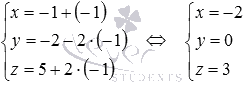
Таким
образом, проекция точки М₁ на
плоскость АВС имеет
координаты .

Проекция
прямой на плоскость

Эллипс

Эллипсом
называется множество точек плоскости,
сумма расстояний которых до двух данных
точек, называемых фокусами и есть
величина постоянная (ее обозначают
через 2*а ). Причем эта постоянная больше
расстояния между фокусами.

Для
вывода уравнения эллипса выберем систему
координат так,
чтобы фокусыF₁ и F₂
лежали на оси ,
а начало координат совпадало с серединой
отрезкаF₁F₂.
Тогда фокусы будут иметь следующие
координаты: и.

Пусть —
произвольная точка эллипса. Тогда,
согласно определению эллипса,,
т. е.

(11.5)

Это,
по сути, и есть уравнение эллипса.

Преобразуем
уравнение (11.5) к более простому
виду следующим образом:

Так
как a>с,
то .
Положим

(11.6)

Тогда
последнее уравнение примет вид или

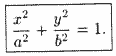
(11.7)

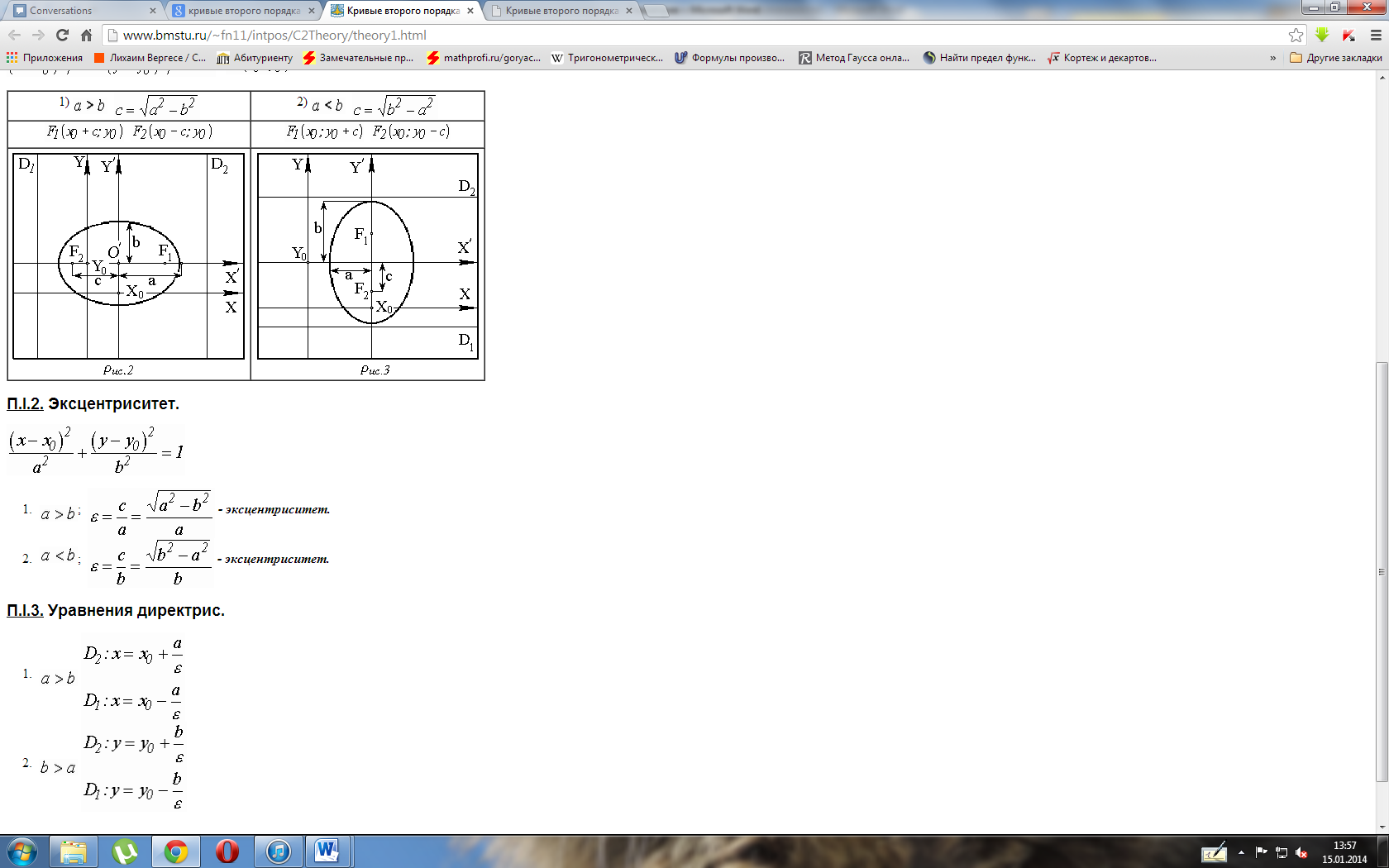
Эксцентрисите́т —
числовая характеристика конического
сечения,
показывающая степень его отклонения
от окружности.
Обычно обозначается “”
или “”.

Форма
эллипса (мера его «сжатия»)
характеризуется его эксцентриситетом.

(так
как ,
то)

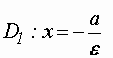
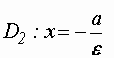
Прямые: иперпендикулярные
главной оси и проходящие на расстоянииот
центра, называютсядиректрисами эллипса.

Параметрические уравнения эллипса

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Проекция точки на плоскость — это точка пересечения перпендикуляра из точки на плоскость и плоскости.

Содержание

1 Обозначения
2 Формулы:
- 2.1 Пример
3 Другие формулы:
4 Ссылки

Обозначения[править]

Введём обозначения:

${displaystyle {bar {r}}_{1}=(x_{1},y_{1},z_{1})}$ — радиус-вектор проекции точки;

${displaystyle {bar {r}}_{0}=(x_{0},y_{0},z_{0})}$ — радиус-вектор точки;

${displaystyle {bar {n}}_{1}=(A_{1},B_{1},C_{1})}$ — нормаль к плоскости;

${displaystyle A_{1}x+B_{1}y+C_{1}z+D_{1}=0}$ — уравнение плоскости;

${displaystyle p_{01}}$ — отклонение точки от плоскости.

Формулы:[править]

Векторная форма:

${displaystyle {overline {r}}_{1}={overline {r}}_{0}-{frac {left({overline {r}}_{0}cdot {overline {n}}_{1}right)+D_{1}}{left({overline {n}}_{1}cdot {overline {n}}_{1}right)}}{overline {n}}_{1}Leftrightarrow {overline {r}}_{1}={overline {r}}_{0}-{frac {p_{01}}{left|{overline {n}}_{1}right|}}{overline {n}}_{1},}$

где

${displaystyle p_{01}={frac {left({overline {r}}_{0}cdot {overline {n}}_{1}right)+D_{1}}{left|{overline {n}}_{1}right|}}}$

Координатная форма:

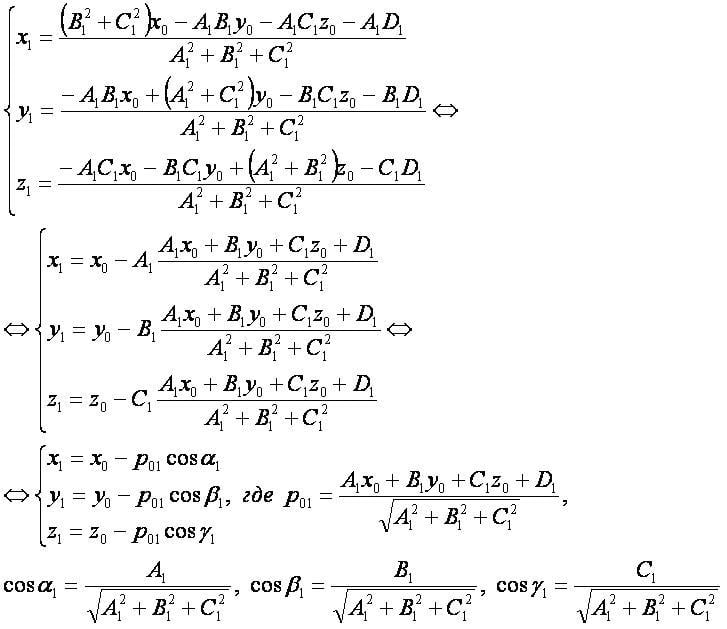
Заметим, что формулы проекции точки на плоскость аналогичны формулам основания перпендикуляра из точки к плоскости.

Пример[править]

Даны точка и плоскость:
и
.

Найти проекцию точки на плоскость.

Решение.

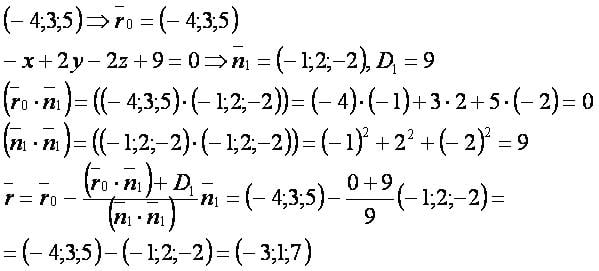
Другие формулы:[править]

Проекция вектора на вектор;
Проекция точки на прямую;
Проекция точки на плоскость.

Ссылки[править]

Участник:Logic-samara

Источник

Изучение свойств фигур в пространстве и на плоскости невозможно без знания расстояний между точкой и такими геометрическими объектами, как прямая и плоскость. В данной статье покажем, как находить эти расстояния, рассматривая проекцию точки на плоскость и на прямую.

Уравнение прямой для двумерного и трехмерного пространств

Расчет расстояний точки до прямой и плоскости осуществляется с использованием ее проекции на эти объекты. Чтобы уметь находить эти проекции, следует знать, в каком виде задаются уравнения для прямых и плоскостей. Начнем с первых.

Прямая представляет собой совокупность точек, каждую из которых можно получить из предыдущей с помощью переноса на параллельные друг другу вектора. Например, имеется точка M и N. Соединяющий их вектор MN¯ переводит M в N. Имеется также третья точка P. Если вектор MP¯ или NP¯ параллелен MN¯, тогда все три точки на одной прямой лежат и образуют ее.

В зависимости от размерности пространства уравнение, задающее прямую, может изменять свою форму. Так, всем известная линейная зависимость координаты y от x в пространстве описывает плоскость, которая параллельна третьей оси z. В связи с этим в данной статье будем рассматривать только векторное уравнение для прямой. Оно имеет одинаковый вид для плоскости и трехмерного пространства.

В пространстве прямую можно задать следующим выражением:

(x; y; z) = (x₀; y₀; z₀) + α*(a; b; c)

Здесь значения координат с нулевыми индексами соответствуют принадлежащей прямой некоторой точки, u¯(a; b; c) — координаты направляющего вектора, который лежит на данной прямой, α — произвольное действительное число, изменяя которое можно получить все точки прямой. Это уравнение называется векторным.

Часто приведенное уравнение записывают в раскрытом виде:

x= x₀ + α*a;

y= y₀ + α*b;

z= z₀ + α*c

Аналогичным образом можно записать уравнение для прямой, находящейся в плоскости, то есть в двумерном пространстве:

(x; y) = (x₀; y₀ ) + α*(a; b);

x= x₀ + α*a;

y= y₀ + α*b

Уравнение плоскости

Чтобы уметь находить расстояние от точки до плоскостей проекций, необходимо знать, как задается плоскость. Так же, как и прямую, ее можно представить несколькими способами. Здесь рассмотрим один единственный: общее уравнение.

Предположим, что точка M(x₀; y₀; z₀) плоскости принадлежит, а вектор n¯(A; B; C) ей перпендикулярен, тогда для всех точек (x; y; z) плоскости справедливым будет равенство:

A*x + B*y + C*z + D = 0, где D = -1*(A*x₀ + B*y₀ + C*z₀)

Следует запомнить, что в этом общем уравнении плоскости коэффициенты A, B и C являются координатами нормального к плоскости вектора.

Расчет расстояний по координатам

Перед тем как переходить к рассмотрению проекций на плоскость точки и на прямую, следует напомнить, как следует рассчитывать расстояние между двумя известными точками.

Пусть имеются две пространственные точки:

A₁(x₁; y₁; z₁) и A₂(x₂; y₂; z₂)

Тогда дистанция между ними вычисляется по формуле:

A₁A₂ = √( (x₂-x₁)²+(y₂-y₁)²+(z₂-z₁)²)

С помощью этого выражения также определяют длину вектора A₁A₂¯.

Для случая на плоскости, когда две точки заданы всего парой координат, можно записать аналогичное равенство без присутствия в нем члена с z:

A₁A₂ = √( (x₂-x₁)²+(y₂-y₁)²)

Теперь рассмотрим различные случаи проекции на плоскости точки на прямую и на плоскость в пространстве.

Точка, прямая и расстояние между ними

Предположим, что имеется некоторая точка и прямая:

P₂(x₁; y₁);

(x; y) = (x₀; y₀) + α*(a; b)

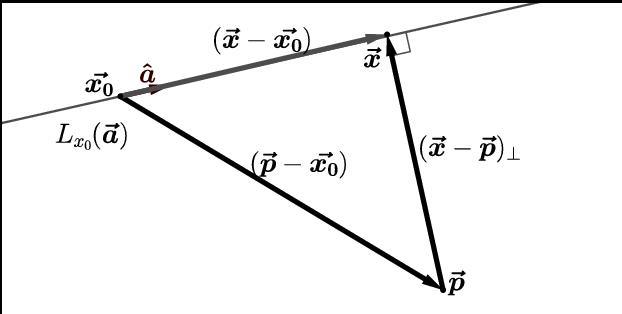
Расстояние между этими геометрическими объектами будет соответствовать длине вектора, начало которого лежит в точке P₂, а конец находится в такой точке P на указанной прямой, для которой вектор P₂P ¯ этой прямой перпендикулярен. Точка P называется проекцией точки P₂ на рассматриваемую прямую.

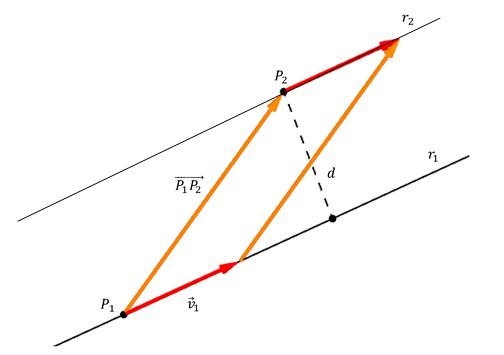
Ниже приведен рисунок, на котором изображена точка P₂, ее расстояние d до прямой, а также вектор направляющий v₁¯. Также на прямой выбрана произвольная точка P₁ и от нее до P₂ проведен вектор. Точка P здесь совпадает с местом, где перпендикуляр пересекает прямую.

Видно, что оранжевые и красные стрелки образуют параллелограмм, сторонами которого являются вектора P₁P₂¯ и v₁¯, а высотой — d. Из геометрии известно, что для нахождения высоты параллелограмма следует разделить его площадь на длину основания, на которое опущен перпендикуляр. Поскольку площадь параллелограмма вычисляется как векторное произведение его сторон, то получаем формулу для расчета d:

d = |[P₁P₂¯*v₁¯]|/|v₁¯|

Все вектора и координаты точек в этом выражении известны, поэтому можно им пользоваться без выполнения каких-либо преобразований.

Решить эту задачу можно было бы иначе. Для этого следует записать два уравнения:

скалярное произведение P₂P ¯ на v₁¯ должно равняться нулю, поскольку эти вектора взаимно перпендикулярны;
координаты точки P должны удовлетворять уравнению прямой.

Этих уравнений достаточно, чтобы найти координаты P, а затем и длину d по формуле, приведенной в предыдущем пункте.

Задача на нахождение дистанции между прямой и точкой

Покажем, как использовать данные теоретические сведения для решения конкретной задачи. Допустим, известны следующая точка и прямая:

M(5; -3);

(x; y) = (3; 1) — α*(0; 2)

Необходимо найти точки проекции на прямую на плоскости, а также расстояние от M до прямой.

Обозначим проекцию, которую следует найти, точкой M₁(x₁; y₁). Решим эту задачу двумя способами, описанными в предыдущем пункте.

Способ 1. Направляющий вектор v₁¯ координаты имеет (0; 2). Чтобы построить параллелограмм, выберем принадлежащую прямой какую-нибудь точку. Например, точку с координатами (3; 1). Тогда вектор второй стороны параллелограмма будет иметь координаты:

(5; -3) — (3; 1) = (2; -4)

Теперь следует вычислить произведение векторов, задающих стороны параллелограмма:

[(2; -4)*(0; 2)] = 4

Подставляем это значение в формулу, получаем расстояние d от M до прямой:

d = 4/√4 = 2

Способ 2. Теперь найдем другим способом не только расстояние, но и координаты проекции M на прямую, как это требует условие задачи. Как было сказано выше, для решения задачи необходимо составить систему уравнений. Она примет вид:

(x₁-5)*0+(y₁+3)*2 = 0;

(x₁; y₁) = (3; 1)-α*(0; 2)

Решаем эту систему:

y₁ = -3;

x₁ = 3

Проекция исходной точки координаты имеет M₁(3; -3 ). Тогда искомое расстояние равно:

d = |MM₁¯| = √(4+0) = 2

Как видим, оба способа решения дали одинаковый результат, что говорит о правильности выполненных математических операций.

Проекция точки на плоскость

Теперь рассмотрим, что представляет собой проекция точки, заданной в пространстве, на некоторую плоскость. Несложно догадаться, что этой проекцией также является точка, которая вместе с исходной образует перпендикулярный плоскости вектор.

Предположим, что проекция на плоскость точки М координаты имеет следующие:

M₁(x₁; y₁; z₁)

Сама плоскость описывается уравнением:

A*x + B*y + C*z + D = 0

Исходя из этих данных, мы можем составить уравнение прямой, пересекающей плоскость под прямым углом и проходящей через M и M₁:

(x; y; z) = (x₀; y₀; z₀) + α*(A; B; C)

Здесь переменные с нулевыми индексами — координаты точки M. Рассчитать положение на плоскости точки M₁ можно исходя из того, что ее координаты должны удовлетворять обоим записанным уравнениям. Если этих уравнений при решении задачи будет недостаточно, то можно использовать условие параллельности MM₁¯ и вектора направляющего для заданной плоскости.

Очевидно, что проекция точки, принадлежащей плоскости, совпадает сама с собой, а соответствующее расстояние равно нулю.

Задача с точкой и плоскостью

Пусть дана точка M(1; -1; 3) и плоскость, которая описывается следующим общим уравнением:

-x + 3*y -2*z + 4 = 0

Следует вычислить координаты проекции на плоскость точки и рассчитать расстояние между этими геометрическими объектами.

Для начала построим уравнение прямой, проходящей через М и перпендикулярной указанной плоскости. Оно имеет вид:

(x; y; z) = (1; -1; 3) + α*(-1; 3; -2)

Обозначим точку, где эта прямая пересекает плоскость, M₁. Равенства для плоскости и прямой должны выполняться, если в них подставить координаты M₁. Записывая в явном виде уравнение прямой, получаем следующие четыре равенства:

-x₁ + 3*y₁ -2*z₁ + 4 = 0;

x₁ = 1 — α;

y₁ = -1 + 3*α;

z₁ = 3 — 2*α

Из последнего равенства получим параметр α, затем подставим его в предпоследнее и во второе выражение, получаем:

α = (3-z₁)/2;

y₁ = -1 + 3*(3-z₁)/2 = -3/2*z₁ + 3,5;

x₁ = 1 — (3-z₁)/2 = 1/2*z₁ — 1/2

Выражение для y₁ и x₁ подставим в уравнение для плоскости, имеем:

-1*(1/2*z₁ — 1/2) + 3*(-3/2*z₁ + 3,5) -2*z₁ + 4 = 0

Откуда получаем:

z₁ = 15/7

Тогда:

y₁ = -3/2*15/7 + 3,5 = 2/7;

x₁ = 1/2*15/7 — 1/2 = 4/7

Мы определили, что проекция точки M на заданную плоскость соответствует координатам (4/7; 2/7; 15/7).

Теперь рассчитаем расстояние |MM₁¯|. Координаты соответствующего вектора равны:

MM₁¯(-3/7; 9/7; -6/7)

Искомое расстояние равно:

d = |MM₁¯| = √126/7 ≈ 1,6

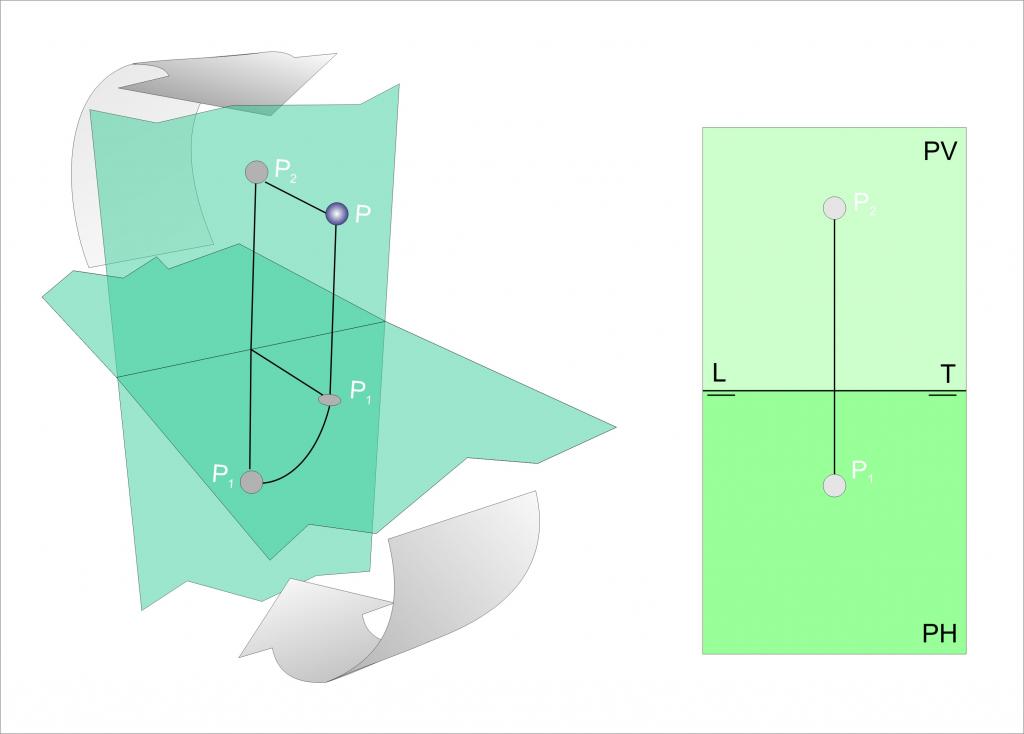
Три точки проекции

Во время изготовления чертежей часто приходится получать проекции сечений на взаимно перпендикулярные три плоскости. Поэтому полезно рассмотреть, чему будут равны проекции некоторой точки M с координатами (x₀; y₀; z₀) на три координатные плоскости.

Не сложно показать, что плоскость xy описывается уравнением z = 0, плоскость xz соответствует выражению y = 0, а оставшаяся плоскость yz обозначается равенством x = 0. Нетрудно догадаться, что проекции точки на 3 плоскости будут равны:

для x = 0: (0; y₀; z₀);

для y = 0: (x₀; 0 ; z₀);

для z = 0: (x₀; y₀; 0 )

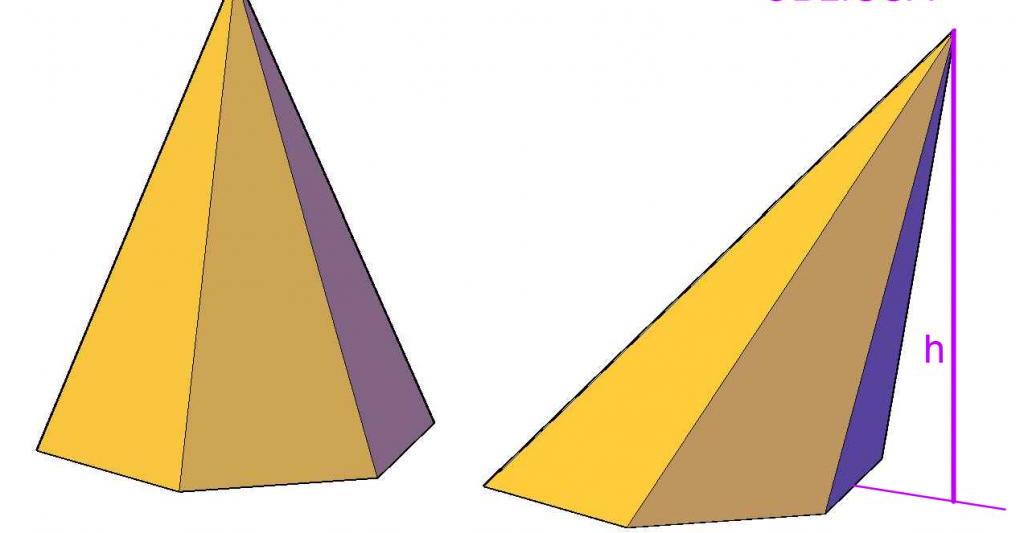
Где важно знать проекции точки и ее расстояния до плоскостей?

Определение положения проекции точек на заданную плоскость важно при нахождении таких величин, как площадь поверхности и объем для наклонных призм и пирамид. Например, расстояние от вершины пирамиды до плоскости основания является высотой. Последняя входит в формулу для объема этой фигуры.

Рассмотренные формулы и методики определения проекций и расстояний от точки до прямой и плоскости являются достаточно простыми. Важно лишь запомнить соответствующие формы уравнений плоскости и прямой, а также иметь хорошее пространственное воображение, чтобы успешно их применять.

Источник