Проекция точки на плоскость онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
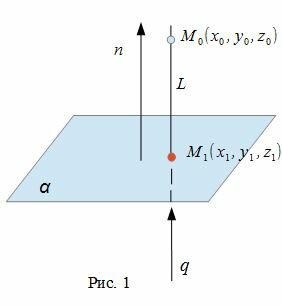
Для нахождения проекции точки M0 на плоскость α, необходимо:
- построить прямую L, проходящую через точку M0 и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M0 на плоскость (1).
Пример 1.Найти проекцию M1 точки M0(4, -3, 2) на плоскость
Решение.
Нормальный вектор плоскости имеет вид:
т.е. A=5, B=1, C=−8.
Координаты точки M0: x0=4, y0=−3, z0=2.
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (7) находим:
Ответ:
Проекцией точки M0(4, -3, 2) на плоскость (6) является точка:
Проекция точки на плоскость онлайн
| Координаты проекции точки |
В данном материале мы рассмотрим решение задачи нахождения координат проекции точки на какую либо плоскость в пространстве.
Теории практически не будет и думаю для тех кто интересуется могут понять это все из ниже разобранного примера
Найти проекцию точки M(1,-3,2) на плоскость 2x+5y-3z-19=0
Проекция точки М на данную поверхность — есть точка пересечения с данной плоскостью прямой, проходящей через точку М перпендикулярно к данной плоскости.
Уравнение прямой, проходящей через точку M(1,-3,2) перпедикулярно к плоскости 2x+5y-3z-19=0 имеет вид
или в виде системы
Добавив сюда исходное уравнение плоскости получим полноценную систему линейных уравнений которая легко решается
В данном примере проекция точки имеет координаты (3,2,-1)
Удачных расчетов!!
Проекция точки на плоскость онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
Для нахождения проекции точки M0 на плоскость α, необходимо:
- построить прямую L, проходящую через точку M0 и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
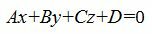 |
(1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
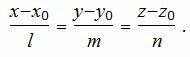 |
(2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
 |
(3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
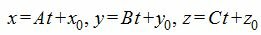 |
(4) |
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
A(At+x0)+B(Bt+y0)+C(At+z0)+D=0,
A 2 t+Ax0+B 2 t+By0+C 2 t+Cz0+D=0,
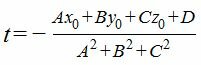 |
(5) |
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M0 на плоскость (1).
Пример 1. Найти проекцию M1 точки M0(4, -3, 2) на плоскость
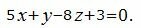 |
(6) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
 |
(7) |
Из выражений (7) находим:
Проекцией точки M0(4, -3, 2) на плоскость (6) является точка:
Проекция точки на плоскость, координаты проекции точки на плоскость
В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров.
Проецирование, виды проецирования
Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур.
Проекция фигуры на плоскость – чертеж пространственной фигуры.
Очевидно, что для построения проекции существует ряд используемых правил.
Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения.
Плоскость проекции — это плоскость, в которой строится изображение.
Использование тех или иных правил определяет тип проецирования: центральное или параллельное.
Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное.
Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже.
Проекция точки на плоскость
Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции.
Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость.
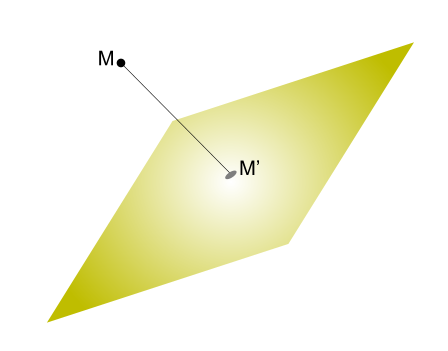
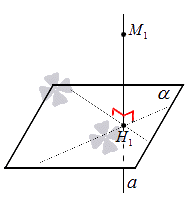
Допустим, задано трехмерное пространство, а в нем — плоскость α и точка М 1 , не принадлежащая плоскости α . Начертим через заданную точку М 1 прямую а перпендикулярно заданной плоскости α . Точку пересечения прямой a и плоскости α обозначим как H 1 , она по построению будет служить основанием перпендикуляра, опущенного из точки М 1 на плоскость α .
В случае, если задана точка М 2 , принадлежащая заданной плоскости α , то М 2 будет служить проекцией самой себя на плоскость α .
Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость.
Нахождение координат проекции точки на плоскость, примеры
Пускай в трехмерном пространстве заданы: прямоугольная система координат O x y z , плоскость α , точка М 1 ( x 1 , y 1 , z 1 ) . Необходимо найти координаты проекции точки М 1 на заданную плоскость.
Решение очевидным образом следует из данного выше определения проекции точки на плоскость.
Обозначим проекцию точки М 1 на плоскость α как Н 1 . Согласно определению, H 1 является точкой пересечения данной плоскости α и прямой a , проведенной через точку М 1 (перпендикулярной плоскости). Т.е. необходимые нам координаты проекции точки М 1 – это координаты точки пересечения прямой a и плоскости α .
Таким образом, для нахождения координат проекции точки на плоскость необходимо:
— получить уравнение плоскости α (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости;
— определить уравнение прямой a , проходящей через точку М 1 и перпендикулярной плоскости α (изучите тему об уравнении прямой, проходящей через заданную точку перпендикулярно к заданной плоскости);
— найти координаты точки пересечения прямой a и плоскости α (статья – нахождение координат точки пересечения плоскости и прямой). Полученные данные и будут являться нужными нам координатами проекции точки М 1 на плоскость α .
Рассмотрим теорию на практических примерах.
Определите координаты проекции точки М 1 ( — 2 , 4 , 4 ) на плоскость 2 х – 3 y + z — 2 = 0 .
Решение
Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет.
Запишем канонические уравнения прямой a , проходящей через точку М 1 и перпендикулярной заданной плоскости. В этих целях определим координаты направляющего вектора прямой a . Поскольку прямая а перпендикулярна заданной плоскости, то направляющий вектор прямой a – это нормальный вектор плоскости 2 х – 3 y + z — 2 = 0 . Таким образом, a → = ( 2 , — 3 , 1 ) – направляющий вектор прямой a .
Теперь составим канонические уравнения прямой в пространстве, проходящей через точку М 1 ( — 2 , 4 , 4 ) и имеющей направляющий вектор a → = ( 2 , — 3 , 1 ) :
x + 2 2 = y — 4 — 3 = z — 4 1
Для нахождения искомых координат следующим шагом определим координаты точки пересечения прямой x + 2 2 = y — 4 — 3 = z — 4 1 и плоскости 2 х — 3 y + z — 2 = 0 . В этих целях переходим от канонических уравнений к уравнениям двух пересекающихся плоскостей:
x + 2 2 = y — 4 — 3 = z — 4 1 ⇔ — 3 · ( x + 2 ) = 2 · ( y — 4 ) 1 · ( x + 2 ) = 2 · ( z — 4 ) 1 · ( y — 4 ) = — 3 · ( z + 4 ) ⇔ 3 x + 2 y — 2 = 0 x — 2 z + 10 = 0
Составим систему уравнений:
3 x + 2 y — 2 = 0 x — 2 z + 10 = 0 2 x — 3 y + z — 2 = 0 ⇔ 3 x + 2 y = 2 x — 2 z = — 10 2 x — 3 y + z = 2
И решим ее, используя метод Крамера:
∆ = 3 2 0 1 0 — 2 2 — 3 1 = — 28 ∆ x = 2 2 0 — 10 0 — 2 2 — 3 1 = 0 ⇒ x = ∆ x ∆ = 0 — 28 = 0 ∆ y = 3 2 0 1 — 10 — 2 2 2 1 = — 28 ⇒ y = ∆ y ∆ = — 28 — 28 = 1 ∆ z = 3 2 2 1 0 — 10 2 — 3 2 = — 140 ⇒ z = ∆ z ∆ = — 140 — 28 = 5
Таким образом, искомые координаты заданной точки М 1 на заданную плоскость α будут: ( 0 , 1 , 5 ) .
Ответ: ( 0 , 1 , 5 ) .
В прямоугольной системе координат O x y z трехмерного пространства даны точки А ( 0 , 0 , 2 ) ; В ( 2 , — 1 , 0 ) ; С ( 4 , 1 , 1 ) и М1(-1, -2, 5). Необходимо найти координаты проекции М 1 на плоскость А В С
Решение
В первую очередь запишем уравнение плоскости, проходящей через три заданные точки:
x — 0 y — 0 z — 0 2 — 0 — 1 — 0 0 — 2 4 — 0 1 — 0 1 — 2 = 0 ⇔ x y z — 2 2 — 1 — 2 4 1 — 1 = 0 ⇔ ⇔ 3 x — 6 y + 6 z — 12 = 0 ⇔ x — 2 y + 2 z — 4 = 0
Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере.
Запишем параметрические уравнения прямой a , которая будет проходить через точку М 1 перпендикулярно плоскости А В С . Плоскость х – 2 y + 2 z – 4 = 0 имеет нормальный вектор с координатами ( 1 , — 2 , 2 ) , т.е. вектор a → = ( 1 , — 2 , 2 ) – направляющий вектор прямой a .
Теперь, имея координаты точки прямой М 1 и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве:
x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ
Затем определим координаты точки пересечения плоскости х – 2 y + 2 z – 4 = 0 и прямой
x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ
Для этого в уравнение плоскости подставим:
x = — 1 + λ , y = — 2 — 2 · λ , z = 5 + 2 · λ
Теперь по параметрическим уравнениям x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ найдем значения переменных x , y и z при λ = — 1 : x = — 1 + ( — 1 ) y = — 2 — 2 · ( — 1 ) z = 5 + 2 · ( — 1 ) ⇔ x = — 2 y = 0 z = 3
Таким образом, проекция точки М 1 на плоскость А В С будет иметь координаты ( — 2 , 0 , 3 ) .
Ответ: ( — 2 , 0 , 3 ) .
Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям.
Пусть задана точки М 1 ( x 1 , y 1 , z 1 ) и координатные плоскости O x y , О x z и O y z . Координатами проекции этой точки на данные плоскости будут соответственно: ( x 1 , y 1 , 0 ) , ( x 1 , 0 , z 1 ) и ( 0 , y 1 , z 1 ) . Рассмотрим также плоскости, параллельные заданным координатным плоскостям:
C z + D = 0 ⇔ z = — D C , B y + D = 0 ⇔ y = — D B
И проекциями заданной точки М 1 на эти плоскости будут точки с координатами x 1 , y 1 , — D C , x 1 , — D B , z 1 и — D A , y 1 , z 1 .
Продемонстрируем, как был получен этот результат.
В качестве примера определим проекцию точки М 1 ( x 1 , y 1 , z 1 ) на плоскость A x + D = 0 . Остальные случаи – по аналогии.
Заданная плоскость параллельна координатной плоскости O y z и i → = ( 1 , 0 , 0 ) является ее нормальным вектором. Этот же вектор служит направляющим вектором прямой, перпендикулярной к плоскости O y z . Тогда параметрические уравнения прямой, проведенной через точку M 1 и перпендикулярной заданной плоскости, будут иметь вид:
x = x 1 + λ y = y 1 z = z 1
Найдем координаты точки пересечения этой прямой и заданной плоскости. Подставим сначала в уравнение А x + D = 0 равенства: x = x 1 + λ , y = y 1 , z = z 1 и получим: A · ( x 1 + λ ) + D = 0 ⇒ λ = — D A — x 1
Затем вычислим искомые координаты, используя параметрические уравнения прямой при λ = — D A — x 1 :
x = x 1 + — D A — x 1 y = y 1 z = z 1 ⇔ x = — D A y = y 1 z = z 1
Т.е., проекцией точки М 1 ( x 1 , y 1 , z 1 ) на плоскость будет являться точка с координатами — D A , y 1 , z 1 .
Необходимо определить координаты проекции точки М 1 ( — 6 , 0 , 1 2 ) на координатную плоскость O x y и на плоскость 2 y — 3 = 0 .
Решение
Координатной плоскости O x y будет соответствовать неполное общее уравнение плоскости z = 0 . Проекция точки М 1 на плоскость z = 0 будет иметь координаты ( — 6 , 0 , 0 ) .
Уравнение плоскости 2 y — 3 = 0 возможно записать как y = 3 2 2 . Теперь просто записать координаты проекции точки M 1 ( — 6 , 0 , 1 2 ) на плоскость y = 3 2 2 :
Ответ: ( — 6 , 0 , 0 ) и — 6 , 3 2 2 , 1 2
Проекция точки на плоскость онлайн
| Коэффициенты плоскости |
| Координаты точки разделенные хотя бы одним пробелом |
Координаты проекции точки
В данном материале мы рассмотрим решение задачи нахождения координат проекции точки на какую либо плоскость в пространстве.
Теории практически не будет и думаю для тех кто интересуется могут понять это все из ниже разобранного примера
Найти проекцию точки M(1,-3,2) на плоскость 2x+5y-3z-19=0
Проекция точки М на данную поверхность — есть точка пересечения с данной плоскостью прямой, проходящей через точку М перпендикулярно к данной плоскости.
Уравнение прямой, проходящей через точку M(1,-3,2) перпедикулярно к плоскости 2x+5y-3z-19=0 имеет вид
или в виде системы
Добавив сюда исходное уравнение плоскости получим полноценную систему линейных уравнений которая легко решается
В данном примере проекция точки имеет координаты (3,2,-1)
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/proektsija-tochki-na-ploskost-koordinaty-proektsii/
http://abakbot.ru/online-2/411-projection
|
|||||||||
|
|||||||||
|
|||||||||
|
Проекция точки на плоскость онлайн
|
|
|
Построение третьего вида по двум заданным.
Похожие презентации:
Основы архитектуры и строительных конструкций. Основы проектирования
Конструктивные схемы многоэтажных зданий
Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)
Правила выполнения архитектурно-строительных чертежей
ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)
задачи на построение (геометрия 7 класс)
Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)
Параллельность в пространстве. (Графическая работа 2)
Строительное черчение. Графическое оформление и чтение строительных чертежей
Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты
ГРАНЕЙ.
ПОСТРОЕНИЕ ТРЕТЬЕГО ВИДА
ПО ДВУМ ЗАДАННЫМ.
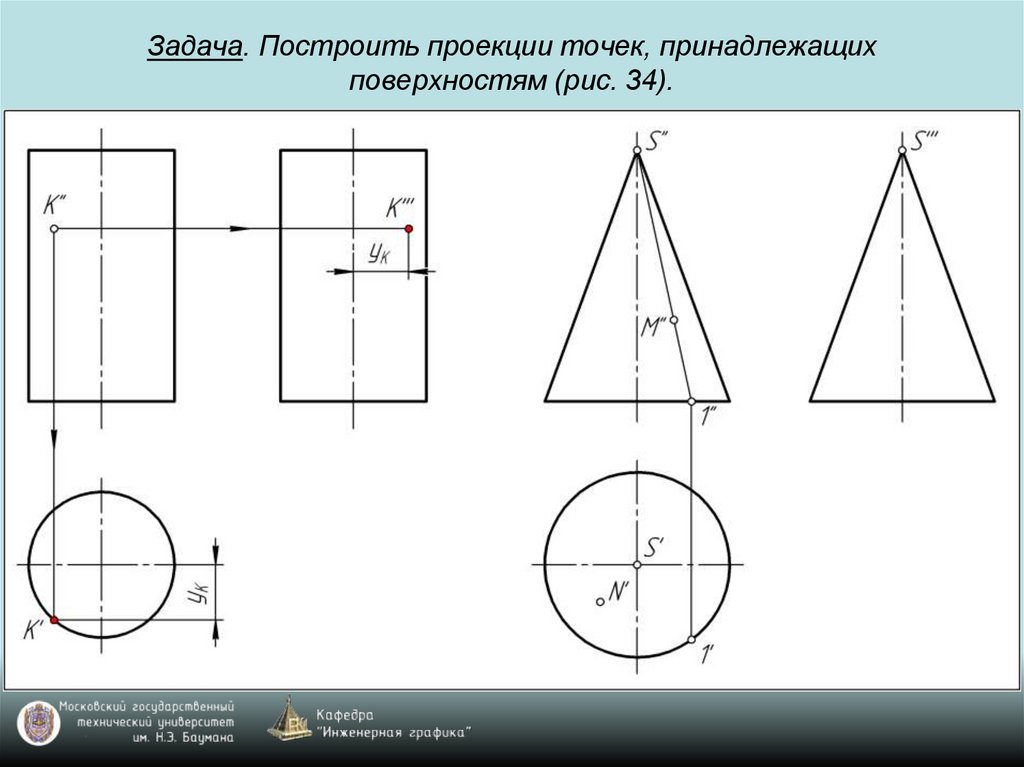
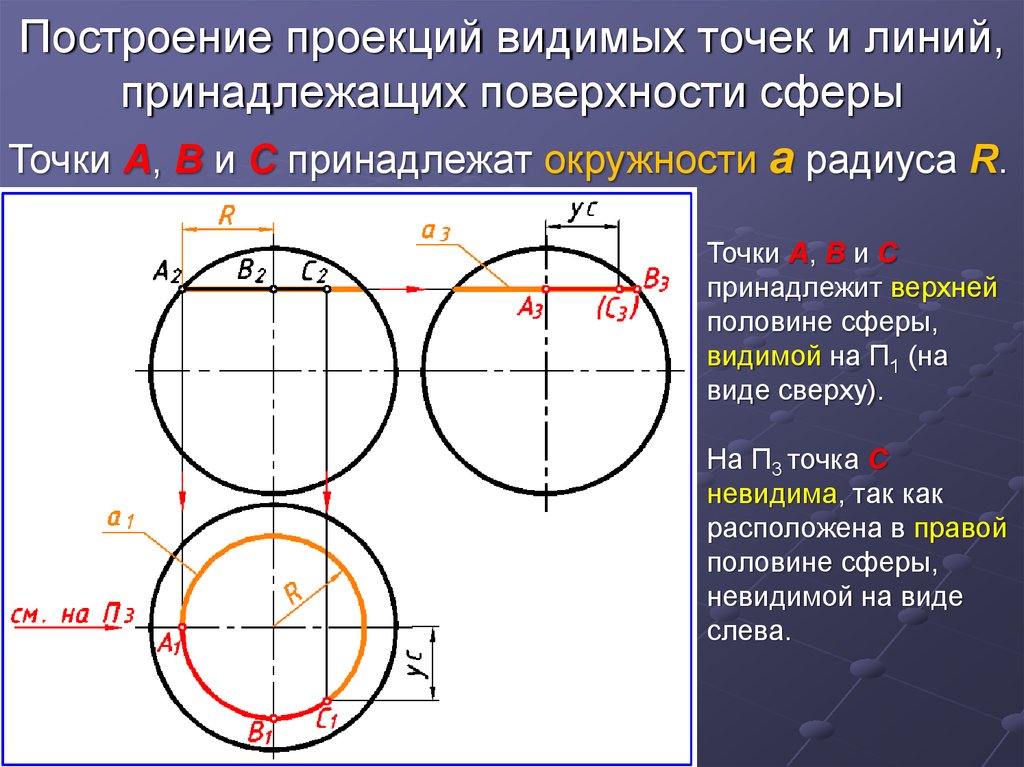
ПОСТРОЕНИЕ ПРОЕКЦИЙ
ТОЧКИ,
ЛЕЖАЩЕЙ НА ГРАНИ
ПРЕДМЕТА.
ПРАВИЛО №1:
Если
плоскость
(грань) параллельна
плоскости проекций,
то она проецируется
на эту плоскость без
искажения в
натуральную
величину.
ПРАВИЛО №2:
Если
плоскость
(грань)
перпендикулярна
плоскости проекций,
то она проецируется
на эту плоскость в
линию (отрезок).
ПРАВИЛО №3:
Если
плоскость
(грань) расположена
под наклоном к
плоскости проекций,
то она проецируется
на эту плоскость с
искажением.
ПРОЕКЦИИ
ПЛОСКОСТИ:
V
W
ПРОЕКЦИИ
ПЛОСКОСТИ:
V
W
ПРОЕКЦИИ
ПЛОСКОСТИ:
V
W
V
W
V
W
РЕБРО — линия пересечения
двух соседних граней
многогранника.
ПРАВИЛО №4:
Если
прямая (ребро)
параллельна
плоскости проекций, то
она проецируется на
эту плоскость без
искажения в
натуральную
величину.
ПРАВИЛО №5:
Если
прямая (ребро)
перпендикулярна
плоскости проекций, то
она проецируется на
эту плоскость в точку.
ПРАВИЛО №6:
Если
прямая (ребро)
расположена под
наклоном к плоскости
проекций, то она
проецируется на эту
плоскость в отрезок с
искажением.
ПРОЕКЦИИ ПРЯМОЙ:
V
W
Проекции прямой:
V
W
Проекции прямой:
V
W
V
W
ВЕРШИНА — точка, элемент
ломаных или кривых
линий, плоских и
многогранных углов,
многогранников и
некоторых других тел.
Правило №7:
ПРАВИЛО №8:
Если
две точки (вершины)
лежат на одном
проецирующем луче, то они
проецируются в одну точку.
Из двух совпадающих на
изображении точек одна
является изображением
видимой точки, другая –
закрытой (невидимой).
АНАЛИЗ ГЕОМЕТРИЧЕСКОЙ
ФОРМЫ ПРЕДМЕТА
Цилиндр
Параллелепипед
Шестигранная
призма
НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ
ПРЕДМЕТА
И ТОЧКИ НА ЕГО ПОВЕРХНОСТИ.
ГРАНЬ, КОТОРОЙ ПРИНАДЛЕЖИТ
ТОЧКА.
ДАНО:
— ФРОНТАЛЬНАЯ
ПРОЕКЦИЯ
ПРЕДМЕТА;
— ГОРИЗОНТАЛЬНАЯ
ПРОЕКЦИЯ
ПРЕДМЕТА;
— А–
ГОРИЗОНТАЛЬНАЯ
ПРОЕКЦИЯ ТОЧКИ А.
ПОСТРОИТЬ:
— А` — ФРОНТАЛЬНУЮ
ПРОЕКЦИЮ ТОЧКИ
А;
— А« — ПРОФИЛЬНУЮ
ПРОЕКЦИЮ ТОЧКИ
А.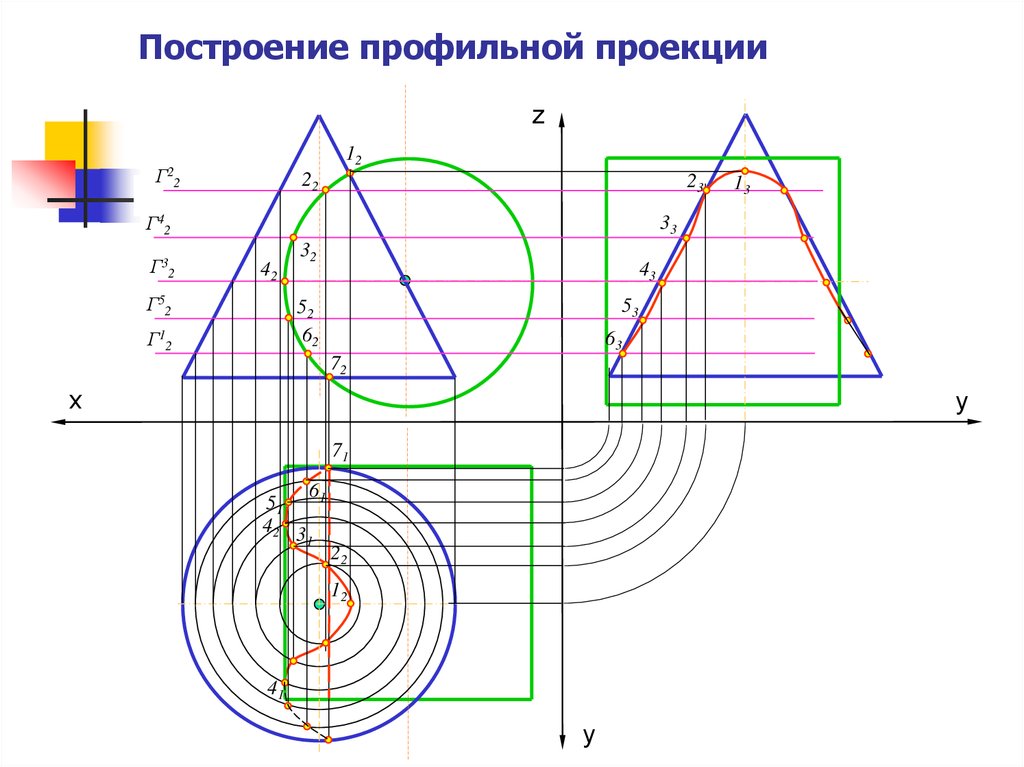
ПОСТРОЕНИЕ ПРОФИЛЬНОЙ ПРОЕКЦИИ
ПРЕДМЕТА.
ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧКИ А.
Домашняя работа.
§12 читать, задание по
рис.96
English
Русский
Правила
Проекционное картографирование дома с помощью Lightform — Lightform
Картографирование дома с использованием проектора в сочетании с программным обеспечением для картографирования для освещения дома — популярная тема среди клиентов Lightform. Нашу команду часто спрашивают: «Могу ли я нанести на карту свой дом с помощью Lightform?» и ответ: «Да, можно». Lightform упрощает процесс создания иммерсивных дисплеев для украшения вашего дома и демонстрации ваших дизайнерских навыков.
В этом сообщении блога мы обсудим лучшие практики и рекомендации по картированию домов при использовании Lightform.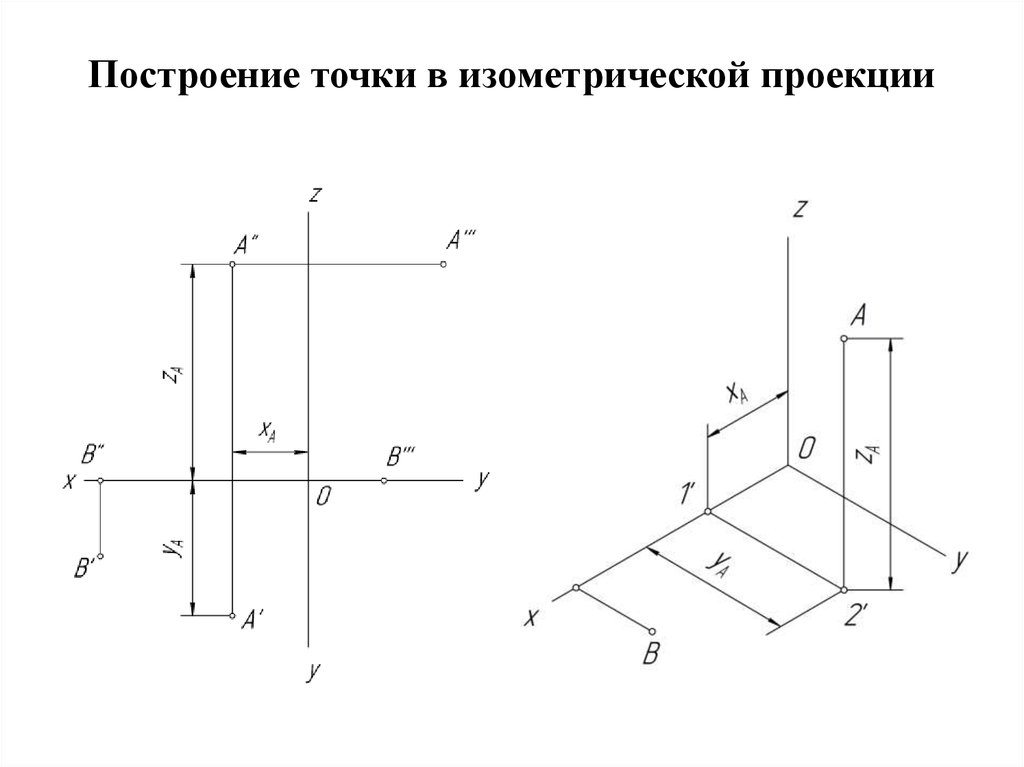
Какой модуль Lightform использовать?
Когда дело доходит до проецирования дома с помощью Lightform, рекомендуется использовать комплект Lightform LFC Kit с мощным проектором . Важно учитывать использование проектора, который будет достаточно ярким для отображения проекций на расстоянии. Это относится ко всем крупномасштабным проекционным картографическим установкам. Если вас интересуют различия между комплектом LFC и проектором LF2 AR, мы рекомендуем прочитать: Комплект Lightform LFC против LF2 — выбор правильного инструмента для правильной работы.
Картографирование домов Советы и рекомендации
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Картографирование домов Джоэла Диттриха.
Яркие проекторы (высокий световой поток) идеально подходят для использования с комплектом LFC для картирования дома. Проектор с яркостью не менее 3000 люмен — хорошая отправная точка для одноэтажного дома. Для проецирования в больших домах рекомендуется более яркий проектор >5000 люмен.
Что такое люмены?
Люмены — это единица измерения общего количества видимого света от лампы или источника света. Яркость проектора измеряется в люменах. Чем выше значение люмена, тем ярче будет казаться источник света. Короче говоря, больше люменов означает больше света. Официальное название люменов проектора — люмены ANSI (ANSI — сокращение от Американского национального института стандартов). Например, проекторы для домашнего кинотеатра обычно излучают от 1500 до 3000 люмен.
Добавление пользовательских анимаций и видеоциклов
- Поддерживаются пользовательские анимации, в том числе созданные с помощью After Effects. Чтобы использовать пользовательские анимации, преобразуйте их в видео и импортируйте в Lightform Creator.
- Пользовательские видеолупы можно загружать и комбинировать с эффектами из встроенной библиотеки Lightform Creator для создания незабываемого шоу. Клиенты сообщают об успешном использовании контента на таких веб-сайтах, как pixabay или MotionLoops , для создания собственных циклов.
Как добавить пользовательский контент с помощью Lightform Creator
Идеальный способ создать уникальные проекции Хэллоуина и праздников.
Условия окружающей среды
Проекции кабины A-Frame от John Meehan. Сделано с комплектом LFC + Panasonic PT-VX500U (5000 люмен)
Weather следует учитывать, чтобы обеспечить положительный опыт при проецировании на открытом воздухе.
Количество света , будь то солнечное или искусственное освещение, может отрицательно сказаться на качестве проекции сцены. Проецирование при ярком дневном свете или прямом солнечном свете не рекомендуется. Чтобы получить наилучшие результаты, дождитесь более низкого уровня освещенности в ранние вечерние часы или в ночное время. Следите за уличными фонарями, так как они могут создавать нежелательные тени в вашей сцене.
Примеры карт Beyond House
В следующих примерах показаны дополнительные возможности помимо картирования домов, включая проекты, охватывающие сады, террасы, домики у бассейна и многое другое.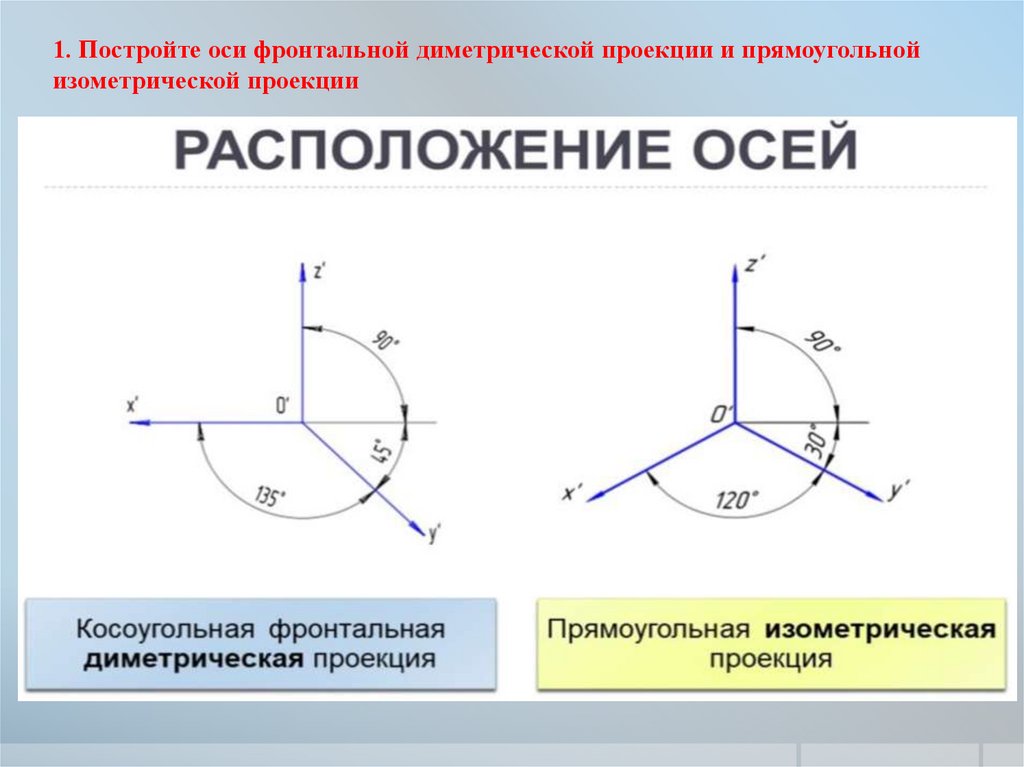
Картографирование деревьев
Даэлен Кори из L’Esperance Design использовала шесть комплектов LFC, чтобы превратить собственность этого клиента в мистическую страну чудес, нанеся на карту деревья и траву вокруг дома.
Карта дома у бассейна
Тейлор Хенсон решил превратить свой дом у бассейна в классный дом с проекцией AR и некоторыми умопомрачительными эффектами.
Картографирование розового сада
Люк Ли — производитель Fusiform Design Workshop LLC.
Что ты создашь?
Благодаря этим передовым методам и рекомендациям вам будет проще составить план дома и создать собственное световое шоу. Мы с нетерпением ждем возможности увидеть, как вы удивите свою аудиторию, и приглашаем вас поделиться опытом картографирования домов в комментариях ниже.
Если вы пользуетесь социальными сетями, не стесняйтесь отмечать свои видео #lightformcreations в Facebook, Instagram и Twitter, чтобы ваша работа была освещена в нашем блоге и социальных сетях.
Есть дополнительные вопросы? Ознакомьтесь с информацией в разделе часто задаваемых вопросов или свяжитесь с нами, и мы сделаем все возможное, чтобы помочь вам.
HeavyM, самая простая в использовании программа для проекционного картографирования в мире
HeavyM


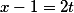
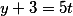
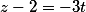
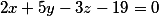
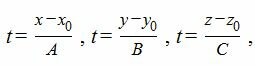
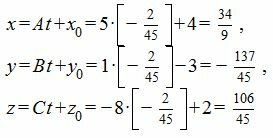
 Угол между ними.
Угол между ними.
 Матрица смежности онлайн
Матрица смежности онлайн