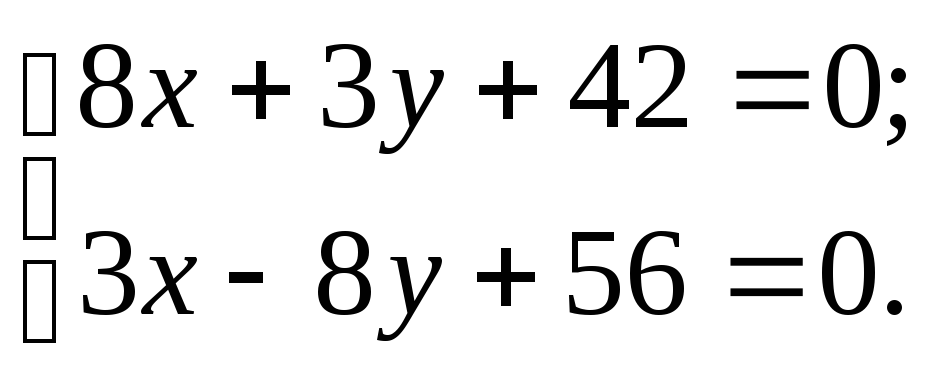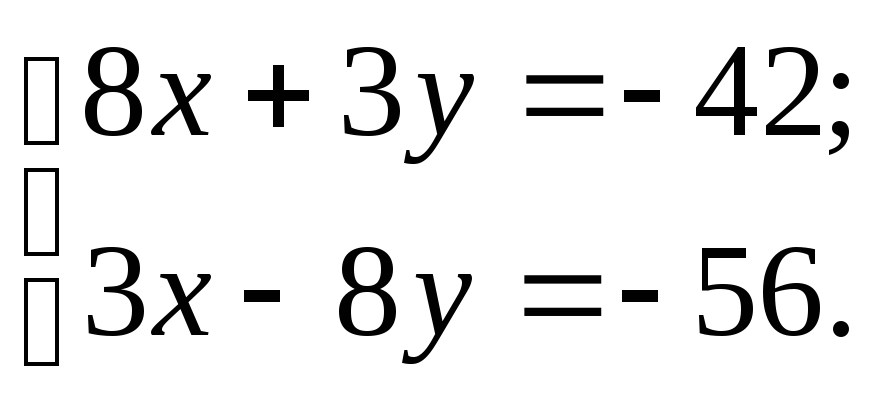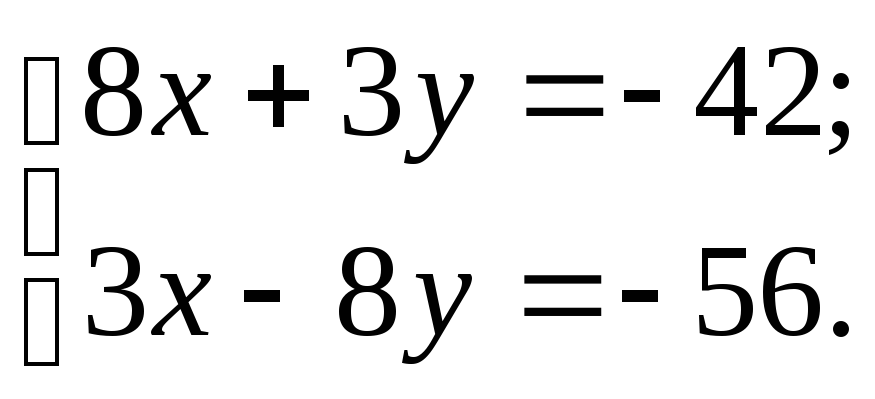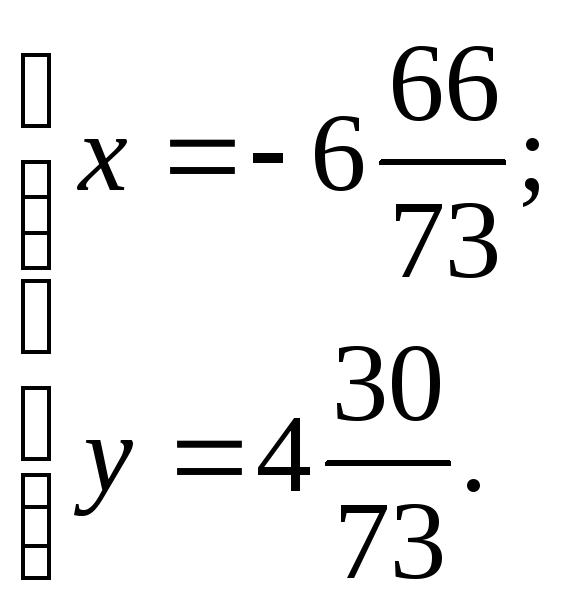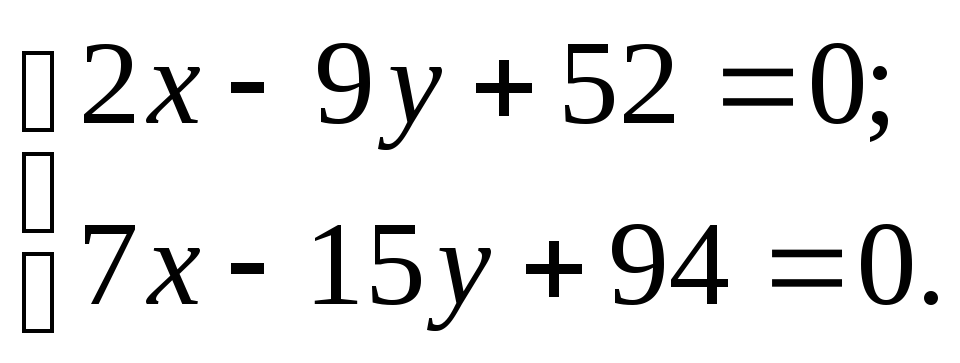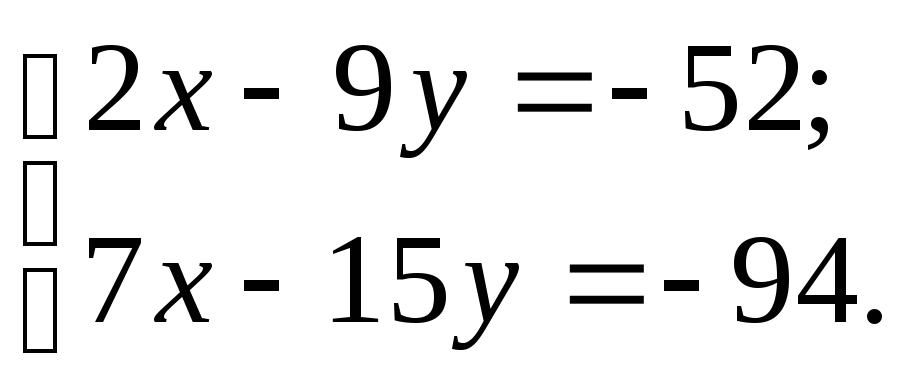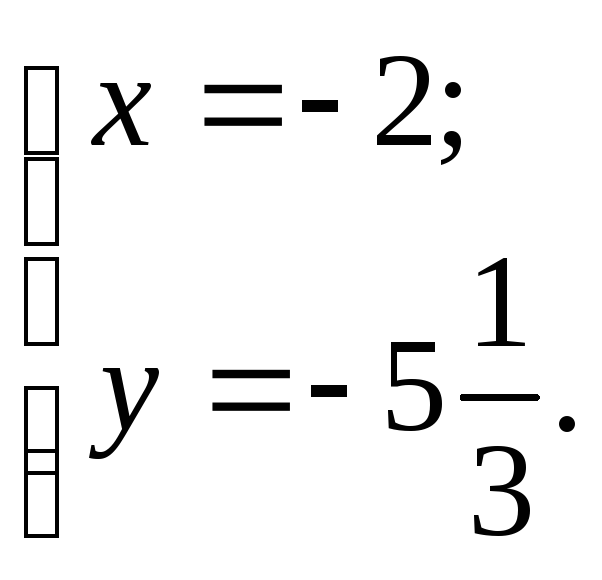Как найти проекцию точки напрямую

Проекция точки на прямую онлайн

С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».

Проекция точки на прямую − теория, примеры и решения

Рассмотрим эту задачу в двухмерном и трехмерном пространствах.

1. Пусть в двухмерном пространстве задана точка M₀(x₀, y₀) и прямая L:

где q=(m,p) направляющий вектор прямой L.

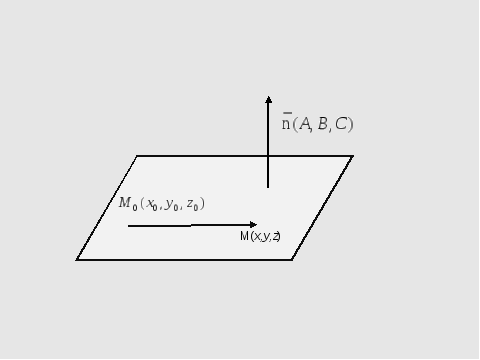
Найдем проекцию точки M₀ на прямую (1)(Рис.1).

Алгоритм нахождения проекции точки на прямую L содержит следующие шаги:

• построить прямую L₁, проходящую через точку M₀ и перпендикулярную прямой L,
• найти пересечение прямых L и L₁(точка M₁)

Уравнение прямой, проходящей через точку M₀(x₀, y₀) имеет следующий вид:

где n=(A,B) нормальный вектор прямой L₁.

Как видно из рисунка Рис.1, для того, чтобы прямая L₁ была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L₁, поэтому в качестве нормального вектора прямой L₁ достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L₁, представленной уравнением (2) можно записать так:

Откроем скобки

Для нахождения точки пересечения прямых L и L₁, которая и будет проекцией точки M₀ на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M₁(x₁, y₁).

Найдем точку пересечения прямых L и L₁ другим методом.

Выведем параметрическое уравнение прямой (1):

Подставим значения x и y в (4):

Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L₁(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M₀ на прямую L:

где x₁=mt’+x’, y₁=pt’+y’.

Пример 1. Найти проекцию точки M₀(1, 3) на прямую

Решение.

Направляющий вектор прямой (6) имеет вид:

Т.е. m=4, p=5. Из уравнения прямой (6) видно, что она проходит через точку M’ (x’, y’)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x’=2, y’=-3. Подставим значения m, p, x₀, y₀, x’, y’ в (5′):

Подставляя значение t в (5), получим:

Ответ:

Проекцией точки M₀(1, 3) на прямую (6) является точка:

2. Пусть в трехмерном пространстве задана точка M₀(x₀, y₀, z₀) и прямая L:

где q=(m, p, l) направляющий вектор прямой L.

Найдем проекцию точки M₀ на прямую (7)(Рис.2).

Нахождение проекцию точки на прямую L содержит следующие шаги:

• построить плоскость α, проходящую через точку M₀ и перпендикулярную прямой L,
• найти пересечение плоскости α и прямой L(точка M₁)

Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) имеет следующий вид:

где n=(A,B,C) нормальный вектор плоскости α.

Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (8) можно записать так:

Откроем скобки

Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M₀ на прямую L, выведем параметрическое уравнение прямой (7):

Подставим значения x и y в (9):

Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (9). Следовательно, подставляя значение t’ в (10) получим координаты проекции точки M₀ на прямую L:

где x₁=mt’+x’, y₁=pt’+y’, z₁=lt’+z’.

Пример 2. Найти проекцию точки M₀(3, −1, −2) на прямую

Решение.

Направляющий вектор прямой (11) имеет вид:

Т.е. m=2, p=3, l=−4. Из уравнения прямой (11) видно, что она проходит через точку M’ (x’, y’, z’)=(2, 1, 1)(в этом легко убедится − подставляя эти значения в (11) получим тождество 0=0=0), т.е. x’=2, y’=1, z’=1. Подставим значения m, p, l x₀, y₀, z₀ x’, y’, z’ в (10′):

Подставляя значение t=t’ в (10), получим:

Ответ:

Проекцией точки M₀(3, −1, −2) на прямую (11) является точка:

Проекция точки на прямую

Пусть
необходимо спроектировать точку

на прямую

Ах+Ву+С=0. проекцией точки на прямую
является основание перпендикуляра,
опущенного из точки на прямую. Нормалью
к данной прямой является вектор
.
Составим уравнение проецирующей прямой.
Она проходит через точку

и параллельна вектору
.
Подставив координаты точки и вектора
в каноническое уравнение прямой
,
получим:.
Теперь необходимо найти координаты
точки пересечения данной прямой и
проектирующей, для чего объединим их в
систему: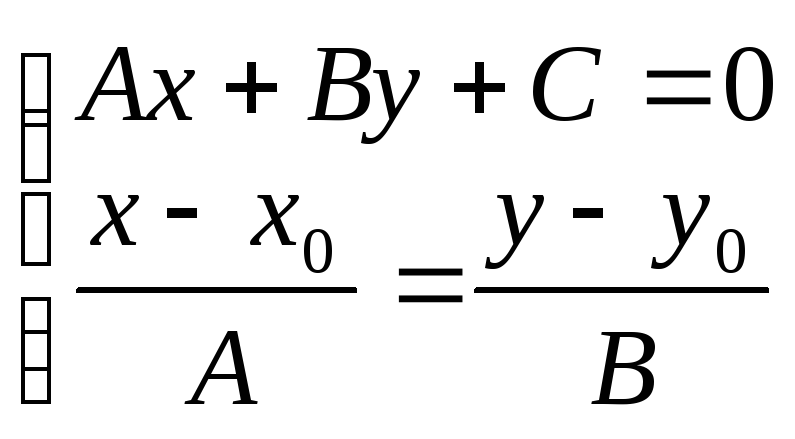решение
этой системы есть координаты точки,
являющейся проекцией точки

на прямую

Пример:
Даны вершины треугольника
:
;
;.
Найти:

1)
уравнение высоты, опущенной из вершины
;

2)
точку пересечения высоты

и стороны
;

3)
точку пересечения медиан треугольника
.

Решение:
1) Составим уравнение высоты
,
проходящей через точку
перпендикулярно вектору
:

;

,

.

Ответ:
.

2)
Составим уравнение стороны
:

,

,

,

.

Найдем
точку пересечения высоты

и стороны
.Обозначим
эту точку N,
она является проекцией точки А на
сторону ВС. Для нахождения точки N,
решим следующую систему уравнений:

Ответ:
N.

3)
Найдем середину стороны
:

,

,

,

.

Составим
уравнение прямой проходящей через точку

и точку М:

,

,

,

.

Найдем
середину стороны
:

,

.

,

.

Составим
уравнение прямой проходящей через точку

и точку N:

,

,

,

.

Найдем точку
О пересечения найденных медиан:

Ответ:
О.

Плоскость Общее уравнение плоскости

Алгебраическое
уравнение первой степени в пространстве
определяет плоскость. Общее уравнение
плоскости можно записать в виде:

Ax+
By+
Cz+
D=0

Любую плоскость
можно представить в виде такого уравнение
единственным способом. с точностью до
коэффициента (т. е. при умножении уравнения
на число, полученное уравнение задает
ту же плоскость ) Плоскость в пространстве
можно задать различными способами,
рассмотрим некоторые из них:

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Опр.:
Нормалью к плоскости называется вектор,
перпендикулярный к данной плоскости.

Пусть
необходимо составить уравнение плоскости,
проходящей через заданную точку
и
перпендикулярной вектору
.

Предположим,
что такая плоскость построена, возьмем
на ней произвольную точку М(x,y,z)
. Составим вектор
.
Вектор

перпендикулярен вектору
,
следовательно, их скалярное произведение
равно нулю:
,
это условие имеет вид::

Данный
способ задания плоскости называется
плоскость по точке М(
и нормали
.
Имея уравнение плоскости в общем виде:
Ax+
By+
Cz+
D=0,
можно выписать нормаль к плоскости
.

Пример:
Составить уравнение плоскости, проходящей
через точку А(1,2,-3), параллельно плоскости
3x-4y+5z-2=0

Решение:
Выпишем нормаль к плоскости, т.е. вектор
перпендикулярный плоскости:
.
Так как необходимо построить плоскость
параллельную данной, то можно использовать
вектор

в качестве нормали к искомой плоскости.
Составляем уравнение плоскости по точке
А и нормали
:

после преобразования получим:
3x-4y+5z+20=0

Ответ:
3x-4y+5z+20=0.

Соседние файлы в предмете Высшая математика

• #
• #
• #
• #
• #
• #

Проекция точки на прямую

Условие:

Найти проекцию точки М
 на
прямую  

Решение:

Составим уравнение плоскости,
проходящей через точку М и перпендикулярной данной прямой.
Направляющий вектор прямой
 может
служить вектором нормали к плоскости.

Общий вид уравнения плоскости:

Подставляем вместо
 координаты
вектора нормали, вместо
  —
координаты  точки .
Получим:

 Отсюда

Искомая плоскость:

Точка пересечения данной прямой и
полученной плоскости  будет проекцией точки М на данную прямую.

 отсюда
.

Координаты проекции:

Ответ: