Проекции скорости и ускорения
Для выполнения
расчетов скоростей и ускорений необходимо
переходить от записи уравнений в
векторной форме к записи уравнений в
алгебраической форме.
Векторы начальной
скорости
и ускорения
могут иметь различные направления,
поэтому переход от векторной записи
уравнений к алгебраической может
оказаться весьма трудоемким.
Известно, что
проекция суммы двух векторов на какую-либо
координатную ось равна сумме проекций
слагаемых векторов на ту же ось.
|
|
Поэтому для Проекцию |
|
|
График скорости
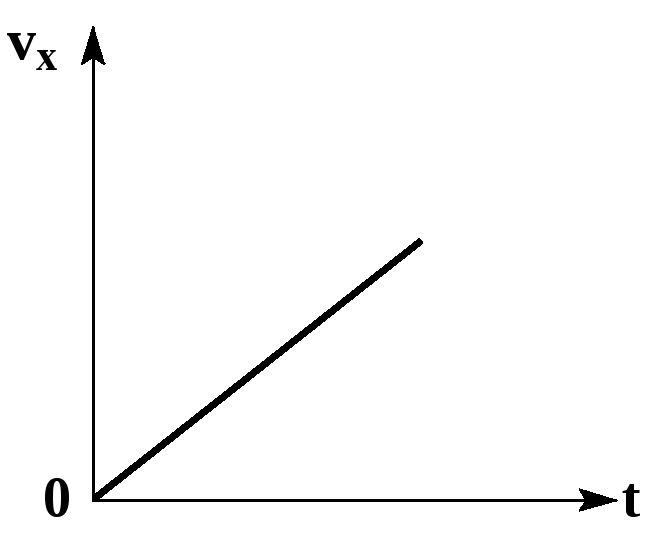
Из уравнения
следует, что графиком зависимости
проекции скорости равноускоренного
движения от времени является прямая.
Если проекция начальной скорости на
ось OX равна нулю, то прямая проходит
через начало координат.
|
|
|
Основные
виды движения
-
аn
= 0, a
= 0 –
прямолинейное равномерное движение; -
аn
= 0, a
= const
– прямолинейное равнопеременное
движение; -
аn
= 0, a
0 – прямолинейное
с переменным ускорением; -
аn
= const,
a
= 0 – равномерное
по окружности -
аn
= const,
a
= const
– равнопеременное по окружности -
аn
const,
a
const
– криволинейное с переменным ускорением.
Вращательное движение твердого тела.
Вращательное
движение твердого тела относительно
неподвижной оси
– движение, при котором все точки
твердого тела описывают окружности,
центры которых лежат на одной прямой,
называемой осью
вращения.
Равномерное движение по окружности
Рассмотрим наиболее
простой вид вращательного движения, и
уделим особое внимание центростремительному
ускорению.
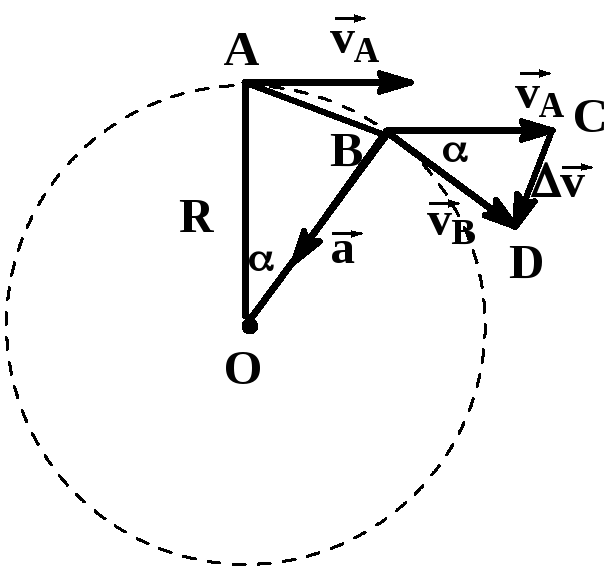
При равномерном
движении по окружности значение скорости
остается постоянным, а направление
вектора скорости
изменяется в процессе движения.
|
|
За |
Из подобия
треугольников OAB и BCD следует
Если интервал
времени ∆t
мал, то мал и угол .
При малых значениях угла
длина хорды AB примерно равна длине дуги
AB, т.е.
.
Т.к.,
,
то получаем
.
Поскольку
,
то получаем
Период и частота
Промежуток времени,
за который тело совершает полный оборот
при движении по окружности, называется
периодам
обращения
(Т).
Т.к. длина окружности равна 2R,
период обращения при равномерном
движении тела со скоростью v
по окружности радиусом R
равняется:
Величина, обратная
периоду обращения, называется частотой.
Частота показывает, сколько оборотов
по окружности совершает тело в единицу
времени:
(с-1)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
01.06.2015304.13 Кб31KP.doc
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Координатный способ определения движения точки:
При координатном способе определения движения точки должны быть даны уравнения движения, т. е. заданы координаты точки как функции времени:
Задание движения точки в прямоугольных координатах
Как известно из курса аналитической геометрии, положение точки M в пространстве может быть определено положением ее проекций P, Q и R на три взаимно перпендикулярные оси (рис. 84), называемые осями координат.
Рис. 84
Положение точки P на оси Ox вполне определяют абсциссой х. Совершенно так же положение точек Q и R определяют ординатой у и аппликатой z.
Если точка M движется относительно осей xOyz, то проекции Р, Q и R перемещаются по осям и координаты точки M изменяются.
Для определения движения точки M нужно знать ее координаты для каждого мгновения, выразить их в функциях времени.
x = x(t), (58′)
y = y(t), (58″)
z = z(t), (58″‘)
Эти функции непрерывны, так как точка не может из одного положения перейти в другое, минуя промежуточные. Они должны быть однозначны, так как точка занимает в пространстве в каждое мгновение только одно положение.
Соотношения (58) называют кинематическими уравнениями движения точки в прямоугольных координатах, а способ определения движения точки посредством соотношений (58) называют координатным способом определения движения точки. Это название неточно, потому что, кроме прямолинейных прямоугольных координат, существует множество других координатных систем.
Если траектория точки лежит в одной плоскости, то движение точки определяют двумя уравнениями в системе координат xОy: x=x(t), y=y(t).
Следовательно, при координатном способе задания движения точки в пространстве нужно задать ее три координаты, а на плоскости—две координаты как функции времени. Если точка движется прямолинейно, то, приняв прямую, по которой она движется, за ось абсцисс, мы определим движение точки одним уравнением
x = x(t).
Если движение точки задано в координатной форме, то для определения ее траектории надо из уравнений движения исключить время
Уравнение траектории
Можно определить траекторию точки, если в уравнениях движения (58) давать аргументу t различные значения и, вычислив соответствующие значения функций, отмечать положения точки по ее координатам. Следовательно. кинематические уравнения движения точки (58) можно
рассматривать как уравнения ее траектории в параметрической форме, а время — как независимый переменный параметр.
Однако более удобно получить уравнение траектории, исключив время из уравнений (58). В самом деле, траекторией называют геометрическое место всех положений движущейся точки, но в геометрии нет понятия времени, а поэтому для получения уравнения траектории нужно из кинематических уравнений движения (58) исключить время t. Если точка движется в плоскости, то, исключив время из уравнений (58′) и (58″), мы получим соотношение, связывающее х и у:
f(x, у) = 0. (59)
Это уравнение плоской кривой—траектории точки. Если же движение задано тремя уравнениями (58), то, исключив время, получим два уравнения между тремя координатами:
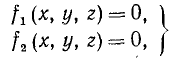
выражающие, как известно из аналитической геометрии, кривую (траекторию) в пространстве. Точнее говоря, уравнения (59) или (59′) выражают кривую, которая полностью или в некоторой своей части является геометрическим местом всех положений движущейся точки.
Иногда бывает нужно выразить в естественной форме движение точки, заданное в прямоугольных координатах уравнениями (58), и, кроме уравнения траектории, дать также уравнение (51) движения точки по траектории. Чтобы его получить, надо продифференцировать уравнения (58) и полученные дифференциалы координат точки подставить в известную из курса высшей математики формулу, выражающую абсолютную величину элемента дуги:
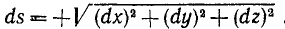
Проинтегрировав (60), мы получим уравнение (51), выражающее длину дуги s как функцию времени, или, что то же, закон движения точки по траектории.
Задача №1
По заданным уравнениям движения точки в координатной форме найти уравнение траектории и уравнение движения по траектории:
1) х = 5 cos 2t, y = 3+5sin 2t;
2) x=21,2 sin2 t, у = 21,2 cos 2t.
В обоих примерах за единицу длины принят сантиметр, за единицу времени — секунда.
Решение. Чтобы определить уравнение траектории по уравнениям движения, перенесем во втором из заданных уравнений 3 влево, возведем оба уравнения в квадрат и, сложив, получим
x2 + (y-3)2 = 25.
Это уравнение окружности с центром в точке: x = 0, y = +3.
Чтобы получить закон движения, продифференцируем заданные уравнения: dx=—10 sin 2t dt, dy = 10 cos 2t dt.
Возводя в квадрат, складывая, извлекая квадратный корень и интегрируя, находим закон движения по траектории:
s=10t + C, где C = s0.
2) Исключим время из уравнений движения во втором примере:
x+y = 21,2.
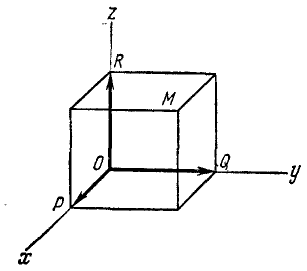
Это уравнение первого порядка относительно х и у, следовательно, траектория-прямая линия. Прямая отсекает на положительных направлениях осей координат отрезки по 21,2 см. Однако не вся прямая служит траекторией точки: из заданных уравнений видно, что х и у должны быть всегда положительны и не могут быть больше 21,2 см каждый, поэтому траекторией точки является лишь отрезок прямой x+y = 21,2, лежащей в первом квадранте (рис. 85).
Рис. 85
На этом примере мы видим, что траекторией точки иногда является лишь часть линии, выражаемой уравнением траектории.
Продифференцируем уравнения движения:
dx = 21,2 ∙ 2 sin t cos t dt,
dy = 21,2 ∙ 2 sin t cos t dt.
Теперь no формуле (60) нетрудно найти элемент дуги траектории:
ля получения уравнения (51) движения точки по траектории остается лишь проинтегрировать найденное выражение. Интегрируем и подставляем начальные условия (при t= 0, s0 = 0):
Ответ. Уравнения траекторий x2+(y-3)2= 25 и x+y=21,2; уравнения движения по траектории s=10t+s0 и s = 30 sin 2t.
Задача №2
Движение точки задано уравнениями:
х = x’ cos φ (t)—y’ sin φ (t),
y = x’ sin φ (t) + y’ cos φ (t),
где х’ и у’ — некоторые постоянные величины, a φ(t)— любая функция времени. Определить траекторию точки.
Решение. Возведем каждое из уравнений в квадрат, а затем сложим их:
x2 + y2 = χ‘2 + y‘2.
По условию, х’ и у’ — постоянные. Обозначая сумму их квадратов через r2, получим
x2 + y2 = r2.
Ответ. Окружность с центром в начале координат радиуса 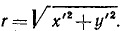
Задача №3
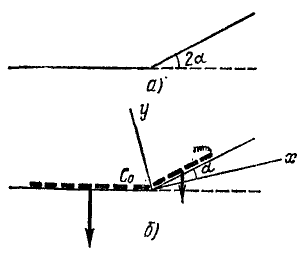
Поезд длиной l м сначала идет по горизонтальному пути (рис. 86, а), а потом поднимается в гору под углом 2α к горизонту. Считая поезд однородной лентой, найти траекторию его центра тяжести.
Рис. 86
Решение. Для решения задачи нужно определить координаты центра тяжести поезда, найти уравнения движения центра тяжести и исключить из них время.
Направим оси координат по внутренней и внешней равиоделяшнм угла 2α (рис. 86, б). Траектория центра тяжести поезда не зависит от скорости поезда. Для простоты подсчетов предположим, что он идет равномерно со скоростью υ м/сек и в начальное мгновение t=0 подошел к горе.
Тогда за время t сек на гору поднимется υt м состава поезда и останется на горизонтальном пути l — υt м. Будем считать, что единица длины поезда весит γ.
Применяя формулы (48), найдем координаты центра тяжести поезда:
Координаты центра тяжести представлены здесь как функции времени, следовательно, полученные соотношения являются уравнениями движения центра тяжести поезда. Определяя t (или υt) из первого уравнения и подставляя во второе, найдем уравнение траектории:
Ответ. Парабола.
Задача №4
Мостовой кран движется вдоль цеха согласно уравнению х = t; по крану катится в поперечном направлении тележка согласно уравнению у = 1,5t (х и у—в м, t — в сек). Цепь укорачивается со скоростью t>=0,5. Определить траекторию центра тяжести груза (в начальном положении центр тяжести груза находился в горизонтальной плоскости хОу, ось Oz направлена вертикально вверх).
Решение. В условии задачи даны лишь два уравнения движения и вертикальная скорость груза:
откуда dz = 0,5dt, и легко получаем третье уравнение:
z = 0,5t
Определив t из первого уравнения, подставим во второе и в третье:
y= 1,5x, z = 0,5x
Координаты груза должны удовлетворять одновременно обоим уравнениям, т. е. траектория лежит одновременно в обеих плоскостях и является линией их пересечения.
Ответ. Прямая.
Алгебраическая величина скорости проекции точки на координатную ось равна первой производной от текущей координаты по времени:
Алгебраическая величина скорости проекции точки на ось
Пусть движение точки M определяется тремя уравнениями:
x =x(t), (58′)
y = y(t), (58″)
z = z(t). (58″‘)
По мере движения точки M в пространстве ее проекции P, Q и R движутся по своим прямолинейным траекториям, т. е. по осям координат, и их движения вполне соответствуют движению точки М.
Так, координата (абсцисса) точки P всегда равна абсциссе точки М, а координаты точек QnR всегда равны ординате и аппликате точки М. Следовательно, при движении точки M в пространстве согласно уравнениям (58) точка P движется по оси Ox согласно уравнению (58′), а точки Q и R— соответственно по осям Oy и Oz согласно уравнениям (58″) и (58″‘).
Таким образом, движение точки M в пространстве можно разложить на три прямолинейных движения ее проекций P, Q и R.
Определим скорость υp точки P при движении этой точки по ее прямолинейной траектории Ох, иными словами, определим скорость проекции точки M на ось Ох.
Алгебраическая величина скорости выражается по формуле (53), причем дифференциалом расстояния точки P является дифференциал абсциссы х, а поэтому
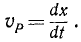
Следовательно, алгебраическая величина скорости проекции P точки M на координатную ось равна первой производной от текущей координаты х по времени t. Она положительна, если точка P движется в положительном направлении оси Ох, и отрицательна, если точка P движется в отрицательном направлении.
Аналогично получаем алгебраические скорости проекций Q и R на ось Oy и на ось Oz:
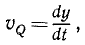
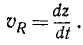
Чтобы получить векторы скоростей проекций, надо умножить величины (61) на единичные векторы:
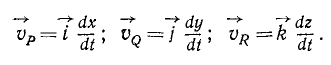
Алгебраическая величина скорости проекции точки на ось равна проекции скорости той же точки на туже ось:
Скорость проекции и проекция скорости
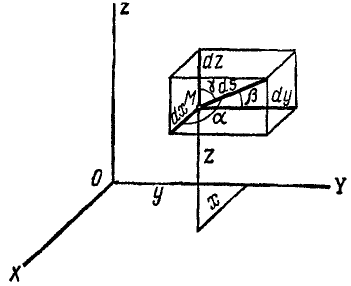
Пусть точка М за бесконечно малый отрезок времени dt передвинулась по своей траектории на элемент дуги ds, абсолютную величину которого выразим формулой (60):
где dx, dy и dz — проекции элемента дуги на оси координат, или, Что то же, элементарные приращения координат точки М.
На рис. 87 эти элементы условно изображены конечными отрезками. Как видно из чертежа, косинусы углов, составляемых элементарным перемещением (а следовательно, и скоростью точки), с осями х, у и z соответственно равны
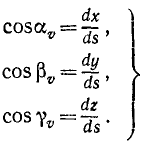
Величина скорости точки M может быть определена по (53):
Чтобы определить проекцию скорости 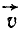
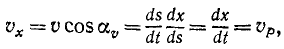
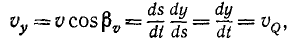
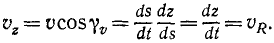
Рис. 87
Равенства (63) словами нужно читать так: проекция скорости точки на ось равна алгебраической скорости проекции точки на ту же ось.
Задача №5
Доказать, что проекция 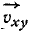
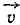
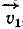
Решение. Скорость 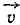
Подводя 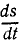
Направления векторов 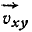
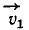
Модуль скорости точки равен квадратному корню из суммы квадратов проекций скорости на оси координат:
Модуль скорости. Возведем в квадрат каждое из равенств:
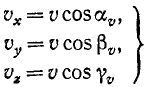
и сложим их:
Сумма квадратов направляющих косинусов равна единице и
или
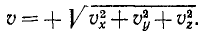
Перед радикалом взят положительный знак, так как величина скорости (ее модуль) всегда положительна. В этом ее существенное отличие от алгебраической величины скорости (53), характеризующей скорость точки при движении по заданной траектории и имеющей знак « + » или «—» в зависимости от направления движения. Величину (64) иногда называют полной скоростью.
Направление скорости можно определить по направляющим косинусам скорости:
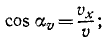
Направляющие косинусы скорости
Равенство (64) позволяет определить модуль скорости точки, движение которой задано уравнениями (58). Направление скорости определяется по косинусам углов, составляемых положительными направлениями осей координат с направлением скорости. Значения этих косинусов, называемых направляющими косинусами скорости, мы получим из уравнений (63):
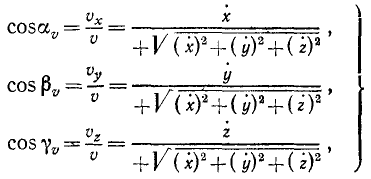
где 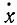
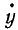
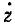
Если точка движется в плоскости хОу, то γυ = 90o, cosγυ = 0 и cos αυ = sin βυ.
Задача №6
Уравнения движения суть
Определить траекторию и скорость.
Решение. Из уравнений движения следует, что х и у всегда больше нуля.
Для определения уравнения траектории возведем каждое из уравнений движения в квадрат и составим разность
x2 — у2 = a2
Для определения скорости найдем сначала ее проекции:
а затем уже и полную скорость.
Ответ. Траектория — ветвь гиперболы x2 — у2 = a2 — расположена в области положительных значений х; скорость 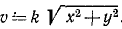
Задача №7
Движение точки задано уравнениями
причем ось Ox горизонтальна, ось Oy направлена по вертикали вверх, υ0, g и 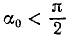
Решение. Уравнения описывают движение тела, брошенного со скоростью υ0 под углом α0 к горизонту (к оси Ох).
Чтобы найти уравнение траектории, определим время из первого уравнения и подставим найденное значение во второе; получим
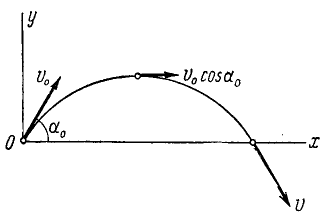
уравнение параболы, проходящей через начало координат (рис. 88).
Рис. 88
Чтобы определить координаты наивысшего положения, мы можем применить известные из дифференциального исчисления правила нахождения максимума функции, т. е. взять производную 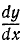
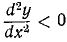
Первое из этих уравнений показывает, что проекция скорости на горизонтальную ось постоянна и равна проекции начальной скорости.
Исследование второго уравнения убеждает, что проекция скорости на вертикальную ось в начальное мгновение положительна и равна υ0 sin α0; затем, по мере увеличения t, проекция υy уменьшается, оставаясь положительной до мгновения 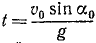
Таким образом, точка движется вправо, сначала поднимаясь, затем опускаясь. Мгновение 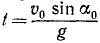
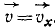
Определим проекции скорости в мгновение, когда точка находится на оси Ох. В это мгновение ордината точки равна нулю. Приравняем пулю второе из уравнений движения:
Точка находится на оси Ox два раза: при t=0 при
Первое значение t соответствует началу движения, второе —падению точки на ось Ох. Второе значение равно времени всего полета, и оно вдвое больше полученного нами ранее времени наивысшего подъема: время падения равно времени подъема.
Подставляя значение t=0 в уравнения, определяющие проекции скорости, найдем проекции скорости в начальное мгновение:
υx = + υ0 cos α0, υy = + υ0 sin α0.
Подставляя второе из найденных значений t, найдем скорости в момент падения:
υx = + υ0 cos α0, υy = — υ0 sin α0.
Ответ: 1) Парабола
2)
3) υx = υ0 cos α0, υy = 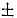
причем верхний знак соответствует началу движения, а нижний—концу.
Задача №8
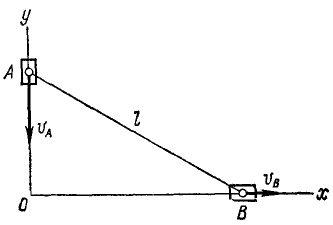
По осям координат (рис. 89) скользят две муфты A и B, соединенные стержнем AB длиной l. Скорость В равна υB.
При каком положении муфт скорость муфты А вдвое больше υB?
Рис. 89
Решение. Координата точки А связана с координатой точки В соотношением
Считая х и у функциями времени и продифференцировав это равенство по времени, найдем зависимость между скоростями обеих точек:
Но 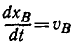
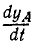
откуда после алгебраических преобразований получаем ответ.
Ответ: 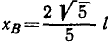
Проекция ускорения точки на координатную ось равна первой производной по времени от проекции скорости на ту же ось или второй производной от текущей координаты по времени:
Ускорение проекции и проекция ускорения
Ускорение характеризует изменение скорости точки в данное мгновение. Оно выражается пределом отношения изменения вектора скорости к соответствующему промежутку времени при стремлении этого промежутка времени к нулю.
Для того чтобы определить ускорение точки M при ее движении в пространстве, рассмотрим сначала движение по оси Ox точки Р, являющейся проекцией точки M на эту ось.
Пусть в некоторое мгновение t алгебраическая величина скорости точки P была υх, а в мгновение tl = t + Δt стала υx+∆υx. Тогда ускорение точки P по величине и по знаку выразится пределом
Если знаки υx и ap одинаковы, то движение точки P ускоренное, а если различны, то замедленное.
Аналогично выразятся ускорения проекций Q и R точки M на другие координатные оси:
Проекции υx, υy и υz сами являются производными по времени от координат точки, поэтому ускорения проекций можно выразить вторыми производными по времени от координат точки. Эти равенства характеризуют не только величины, но и знаки ускорений проекций. Иными словами, они выражают изменение алгебраических скоростей проекций P, Q и R в мгновение t.
Только что доказанная теорема о равенстве алгебраической скорости проекции точки на ось и проекции скорости той же точки на ту же ось справедлива для любого момента времени. Следовательно, эта теорема относится не только к скорости, но и к ее изменению в любое мгновение, т. е. к ускорению. Это значит, что написанные выше равенства выражают также проекции ax, ау и аz ускорения а точки M на оси координат Ox, Oy и Oz:
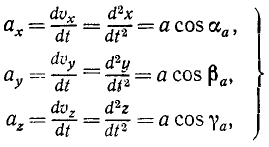
где cosαa, cosβa и cosγa—направляющие косинусы ускорения.
Можно рассматривать эти величины (65) как векторы, направленные по осям координат:
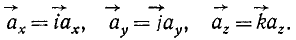
Модуль ускорения точки равен квадратному корню из суммы квадратов проекций ускорения на оси координат:
Величина ускорения при координатном способе задания движения точки
Возведем в квадрат каждое из равенств:
и затем сложим их:
откуда
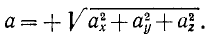
Перед радикалом взят знак плюс, так как модуль вектора—величина положительная. Ускорение точки в отличие от проекций ускорения на оси координат или на другие направления обычно называют полным ускорением. Поэтому равенство (66) можно прочитать так: величина полного ускорения точки равна квадратному корню из суммы квадратов его проекций на оси координат.
Направление ускорения можно определить по направляющим косинусам ускорения:
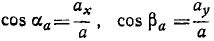
Направляющие косинусы ускорения
Направление ускорения определяют по косинусам углов, составляемых положительными направлениями осей координат с вектором ускорения. Формулы направляющих косинусов получаем из уравнений (65):
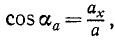
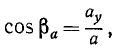
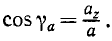
Для определения направления ускорения в каждом конкретном случае надо сначала найти ускорение проекций по (65), для чего необходимо дважды продифференцировать уравнения движения (58), затем найти величину ускорения по (66), а потом определить направляющие косинусы ускорения по (67).
Направление ускорения обычно не совпадает с направлением скорости, и направляющие косинусы (67) ускорения только при прямолинейном ускоренном движении точки постоянно равны направляющим косинусам (62) скорости.
Если точка движется в плоскости хОу, то γa = 90o, cosγa = 0, cosα0 = sin βa.
Задача №9
Точка M движется в системе координат хОу согласно уравнениям х= r cos πt, y=r sinπt, где х и у—в см, a t — в сек. Найти уравнение траектории точки М, ее скорость, направляющие косинусы скорости, ускорение, направляющие косинусы ускорения. Для значений времени t=0; 0,25; 0,5; 0,75, …. 2 сек дать чертежи положений точки M, вектора скорости и вектора ускорения.
Решение. Из уравнения движения видно, что координаты точки M являются проекциями на соответствующие оси радиуса-вектора r, составляющего с осью абсцисс угол πt:
Для определения траектории точки исключаем время из уравнений движения. Получаем уравнение окружности
x2 + y2 = r2
Найдем теперь проекции скорости на оси координат, для чего продифференцируем по времени уравнения движения:
откуда по (64) получаем модуль скорости
Величина скорости точки M постоянна.
Направляющие косинусы скорости определим по формуле (62′):
Эти соотношения показывают, что направление скорости непрерывно меняется и что скорость перпендикулярна радиусу-вектору, проведенному из центра О в точку М.
Ускорение точки M найдем по его проекциям, для чего продифференцируем выражения, полученные для проекций скорости:
откуда по (66) получаем величину ускорения
Ускорение характеризует быстроту изменения вектора скорости не только по величине, но и по направлению, поэтому, несмотря на постоянство модуля скорости точки М, ускорение этой точки не равно нулю. Как видно из полученного
Рис. 90
равенства, величина полного ускорения постоянна. Направление ускорения определим по направляющим косинусам согласно (67):
Направление ускорения точки M противоположно направлению радиуса-вектора.
Положения точки M в различные мгновения показаны на рис. 90, а, векторы скорости — на рис. 90,6 и векторы ускорения — на рис. 90, в.
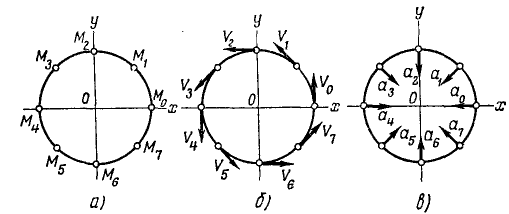
Ответ. Точка M движется по окружности радиуса r против часовой стрелки с постоянной по величине скоростью υ = rπ и с постоянным по величине ускорением a = rπ2.
Задача №10
Снаряд выбрасывается из орудия с начальной скоростью υ=1600 м/сек под утлом α0 = 55o к горизонту. Определить теоретическую дальность и высоту обстрела, учитывая, что ускорение свободно падающих тел g = 9,81 м/сек2.
Решение. Сначала составим уравнения движения снаряда в координатной форме, направив оси, как показано на чертеже (см. рис. 88), для этого определим проекции ускорения:
Разделив переменные, интегрируем:
υх= С1, υy = — gt + С2
Подставляя вместо переменных величин их начальные значения, увидим, что C1 и C2 равны проекциям начальной скорости:
1600 cos 55o = C1, 1600 sin 55o = — gt + C2.
Подставим их в уравнения, полученные для проекций скорости:
Разделяя переменные и интегрируя, найдем
При t = 0 координаты снаряда были: х =0, у = 0. Подставляя эти данные, найдем, что C3 = O и C4 = O. Значения cos 55° и sin 55° найдем в тригонометрических таблицах. Уравнения движения снаряда примут вид:
Далее поступим, как при решении задачи № 42: приравняв вертикальную скорость нулю, найдем время подъема снаряда (t= 133,7 сек); подставляя это значение t в уравнение движения по оси Оу, найдем теоретическую высоту обстрела (h = 87 636 м); удваивая время /, найдем время полета снаряда (t = 267,4 сек); подставляя это значение- в уравнение движения по оси Ох, найдем теоретическую дальность обстрела (l = 245 393 м).
Ответ. l = 245 км; h = 87,5κм.
- Касательное и нормальное ускорения точки
- Основные законы динамики
- Колебания материальной точки
- Количество движения
- Пара сил в теоретической механике
- Приведение системы сил к данной точке
- Система сил на плоскости
- Естественный и векторный способы определения движения точки
Решение задачи (РГР) К1 «Определение скорости и ускорения точки по заданным уравнениям ее движения» по разделу «кинематика» теоретической механики.
Пример определения для заданного момента времени положения точки на траектории, скорости, полного, касательного и нормального ускорения, радиуса кривизны траектории и вида траектории движения точки, если движение точки задано уравнениями.
Задача
Движение точки M задано уравнениями:
Требуется:
Установить вид траектории движения точки M, и для момента времени t = t1 = 0,5 с найти:
- положение точки на траектории,
- скорость, полное, касательное и нормальное ускорения,
- радиус кривизны траектории.
Другие примеры решений >
Помощь с решением задач >
Решение
Расчет траектории движения точки
Уравнения движения можно рассматривать как параметрические уравнения траектории точки.
Другие видео
Чтобы узнать вид траектории в координатной форме, надо получить прямую зависимость между переменными x и y, для этого избавимся от параметра времени t, выразив его, например, из первого уравнения и подставив во второе.
Получилось квадратное уравнение. То есть точка движется по параболе.
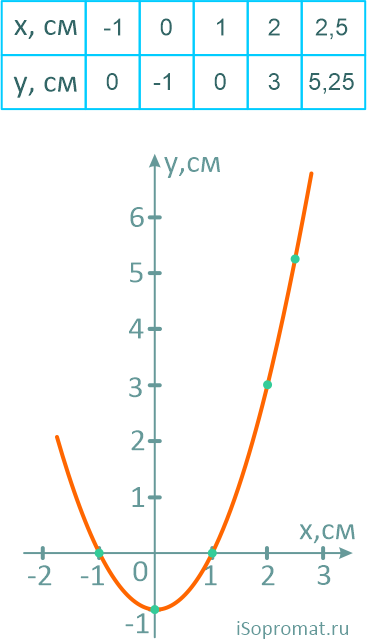
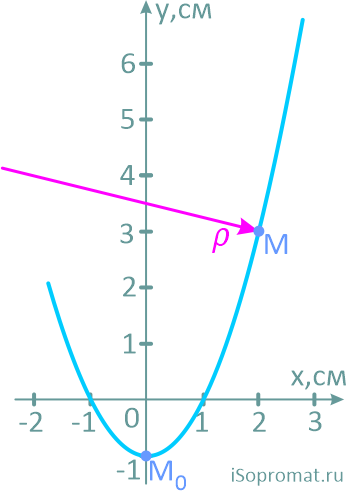
Построим траекторию движения, рассчитав несколько её точек.
Положение точки на траектории
Определим положения точки в начале движения и в заданный момент времени.
Для этого в исходные уравнения подставляем соответственно сначала 0
а затем, половину секунды.
Положение точки на ее траектории в заданный момент обозначим буквой M, и все остальные параметры будем рассчитывать для неё.
Расчет скорости точки
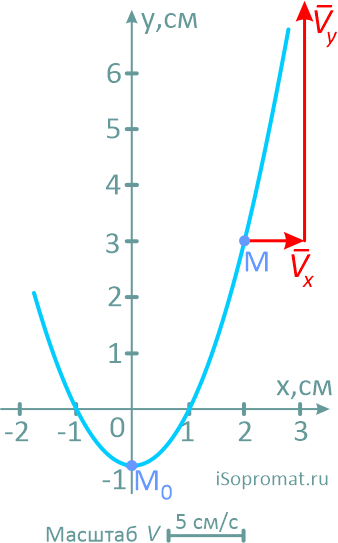
Направление и величину скорости точки определим как векторную сумму её проекций на оси координат.
Здесь i, j — орты осей x и y.
vx, vy — проекции вектора скорости на оси координат.
Проекции вектора скорости получим, взяв первые производные по времени t от соответствующих заданных уравнений движения точки.
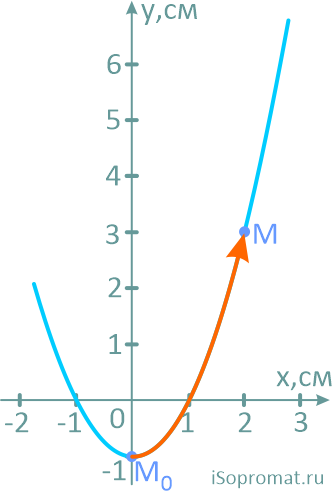
Далее выбрав масштаб, из точки M последовательно и с учетом знака, откладываем оба вектора.
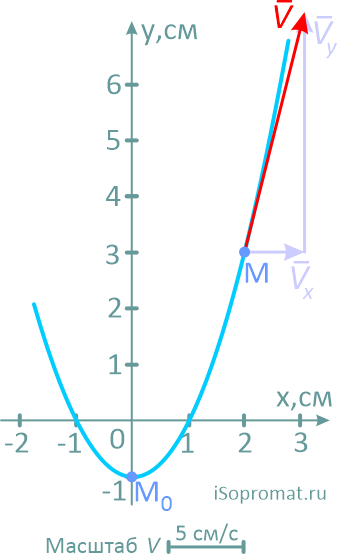
Сам вектор скорости получим, соединив точку M с концом второго вектора и направив его по ходу движения точки.
Здесь надо отметить, что вектор скорости всегда должен располагаться по касательной к траектории. Любое другое положение будет указывать на ошибки в расчетах.
Рассчитаем модуль вектора скорости
Расчет ускорений точки
Проекции полного ускорения точки на оси координат определяются как вторая производная от исходных уравнений движения точки.
Здесь, ax, ay – проекции ускорения точки на оси координат.
В этом примере, горизонтальная проекция ускорения оказалась равной нулю, поэтому его модуль и направление будут совпадать с вертикальной.
Касательная составляющая полного ускорения это производная скорости точки по времени.
Ее можно рассчитать по этой формуле.
Вектор касательного ускорения всегда направлен по линии вектора скорости.
Положительная величина говорит об ускоренном движении точки и тогда направления скорости и касательного ускорения совпадают.
В противном случае они разнонаправлены, и движение точки замедляется.
Модуль нормального ускорения определим по формуле Пифагора, так как векторы касательного и центростремительного ускорений всегда взаимно перпендикулярны.
Расчет радиуса кривизны траектории
Осталось найти только радиус кривизны траектории в точке M, который равен отношению квадрата скорости к модулю нормального ускорения.
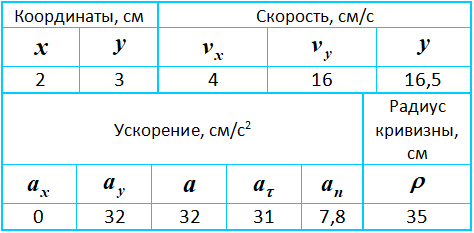
Результаты расчетов
Результаты вычислений для заданного момента времени t1=0,5c приведены в таблице:
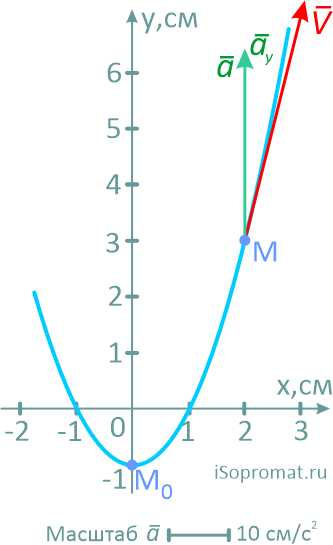
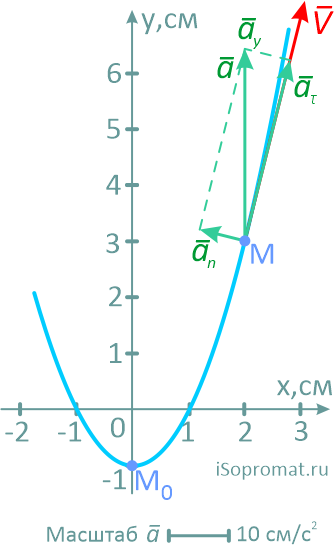
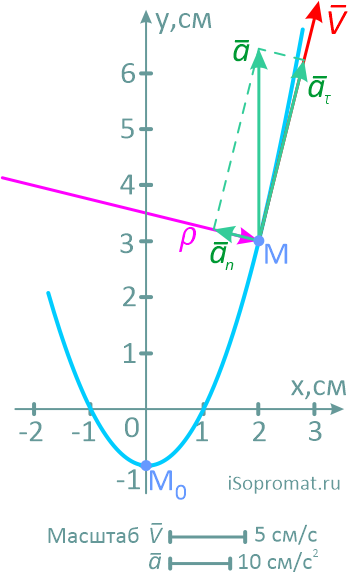
На рисунке показано положение точки M в заданный момент времени и векторы скорости и ускорений в выбранном масштабе.
Вектор v строим по составляющим vx и vy, причем этот вектор должен по направлению совпадать с касательной к траектории.
Вектор a строим по составляющим ax и ay и затем раскладываем на составляющие векторы aτ и an. Совпадение величин aτ и an, найденных из чертежа, с их значениями, полученными аналитически, служит критерием правильности решения.
Другие примеры решения задач >
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
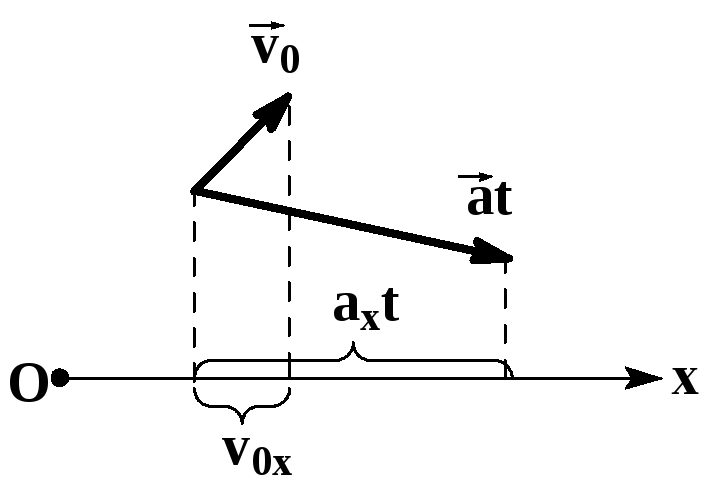
Проекция ускорения
Проекция ускорения на ось ОХ
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
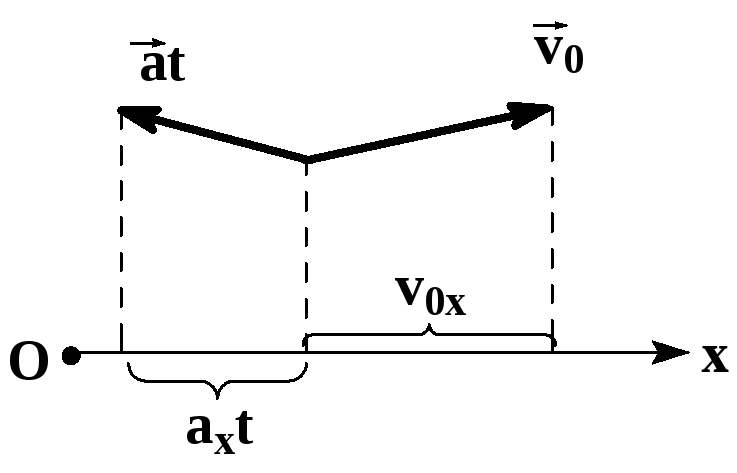
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
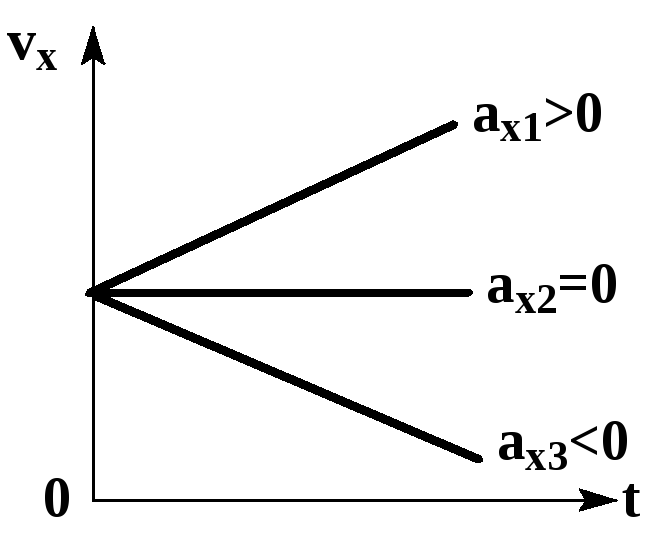
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
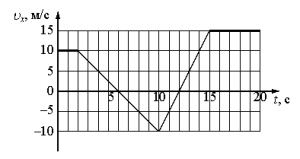
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.9k
Кинематика точки.
- Определение скорости и ускорения точки при координатном способе задания ее движения.
- Определение скорости точки при естественном способе задания ее движения.
- Естественные координатные оси.
- Вектор кривизны.
- Определение ускорения точки при естественном способе задания ее движения.
1. Определение скорости и ускорения точки при координатном способе задания движения
ТЕОРЕМА: Проекция производной от вектора на какую-нибудь неподвижную ось равна производной от проекции вектора на ту же ось.



Если
то 
Определение скорости точки
Так как, 
но
На основании (1.13), получим

или 
Таким образом, проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени.
|
|
|
Система (1.15) определяет модуль и направление вектора скорости точки в пространстве. 
Определение ускорения точки

Следовательно

или

Таким образом, проекции ускорения на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени.
Модуль и направление ускорения

Где 
Движение точки в плоскости
Движение точки по прямой
2. Определение скорости точки при естественном способе задания движения

Единичный орт

3. Естественные координатные оси
Особенностью данной системы отсчета является то, что начало отсчета всегда находится в точке М и вся система движется вместе с точкой
4. Вектор кривизны кривой в данной точке
|
|
|
Таким образом, вектор кривизны кривой в данной точке всегда направлен по нормали и модуль вектора обратно пропорционален радиусу кривизны.
5. Определение ускорения точки при естественном способе задания движения
Так как, 





Частные случаи движения точки
Прямолинейное движение
Касательное ускорение характеризует изменение скорости по численной величине
Равномерное криволинейное движение
Нормальное ускорение характеризует изменение скорости по направлению
Равнопеременное криволинейное движение
v= vo + at t

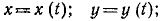
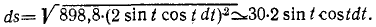
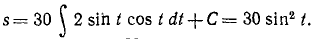
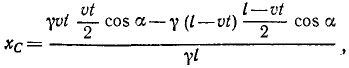
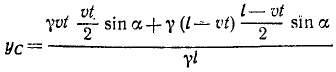
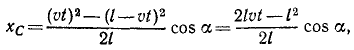
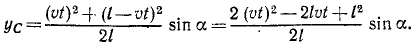
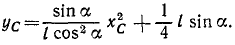
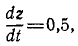
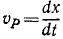
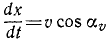
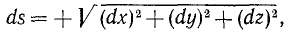
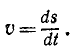
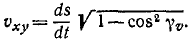
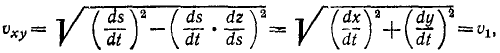
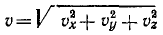
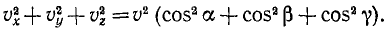
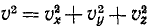
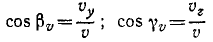
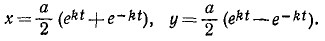
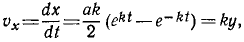
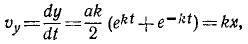
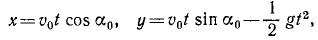
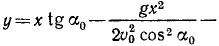
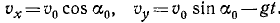
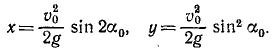
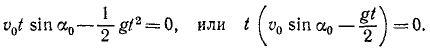
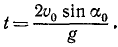
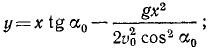
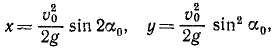
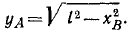
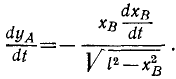
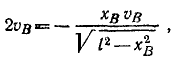
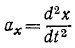
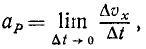
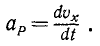
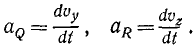
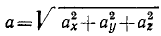
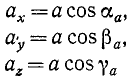
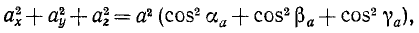
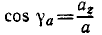
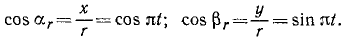
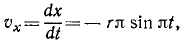
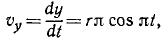
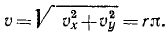
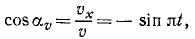
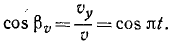
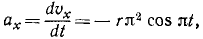
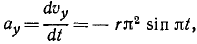
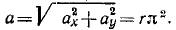
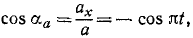
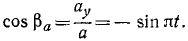
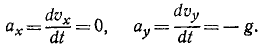
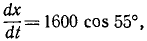
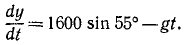
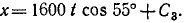
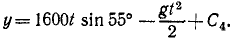
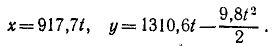
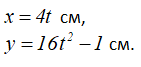
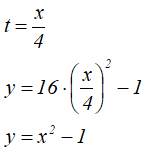
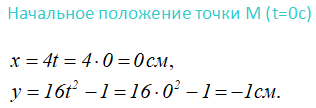

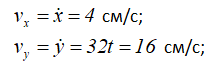
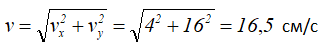

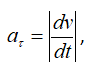
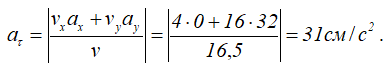
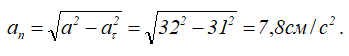
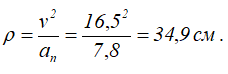















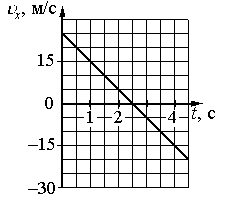







 (2.5)
(2.5)









 модуль вектора кривизны
модуль вектора кривизны










