Свойства равнобедренной трапеции
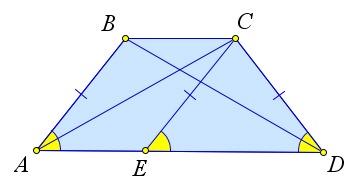
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
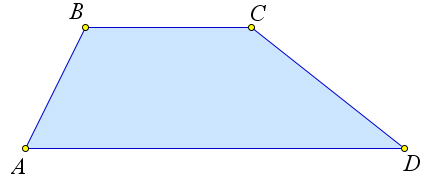
Трапеция АВСD на рисунке – равнобедренная, АВ = CD, ВН и СК – перпендикуляры к АD. Тогда АН и КD – проекция боковых сторон на основание .
АК – проекция диагонали АС на основание АD, .
Задача ЕГЭ по теме «Средняя линия равнобедренной трапеции»
Перпендикуляр, опущенный из вершины тупого угла С на большее основание АD равнобедренной трапеции ABCD, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
По условию, АК = 10. При этом АК – проекция диагонали АС трапеции ABCD на основание AD, и длина АК равна средней линии трапеции.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Свойства равнобедренной трапеции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
math-public:trapeciya
Содержание
Трапеция
Определение
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
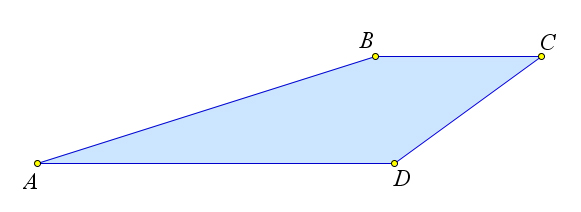
Замечание
Сумма углов при боковой стороне трапеции равна $180^circ$.
Доказательство
Действительно, так как основания трапеции параллельны, а боковая
сторона является секущей, то углы при боковой стороне являются
внутренними односторонними углами при параллельных прямых, и,
следовательно, их сумма равна $180^circ$.
Определение
-
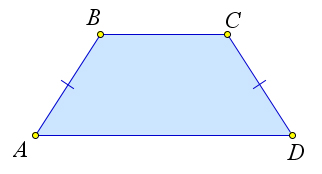
Трапеция называется равнобедренной, если ее боковые стороны равны.
-
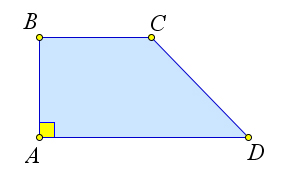
Трапеция называется прямоугольной, если один из ее углов равен $90^circ$.
Свойства равнобедренной трапеции
-
Углы при основании равнобедренной трапеции равны.
-
Диагонали равнобедренной трапеции равны.
-
Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
-
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.
Докажем, что $angle A=angle D$.
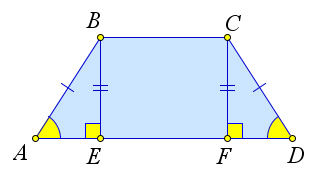
Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.
Треугольники $triangle ABE$ и $triangle CFD$ равны по катету и гипотенузе ($AB=CD,
BE=CF$).
Следовательно, $angle A=angle D$.
Докажем второй пункт теоремы.
В равнобедренной трапеции $ABCD$ рассмотрим треугольники $triangle ABD$ и $triangle ACD$.
Они равны по первому признаку ($AB=CD$, $AD$ – общая, $angle A=angle D$ по
первому пункту).
Следовательно, $AC=BD$.
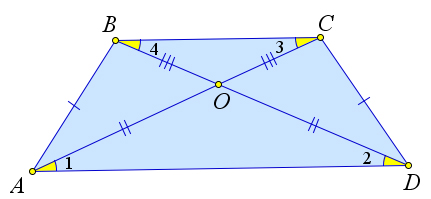
Докажем третий пункт теоремы.
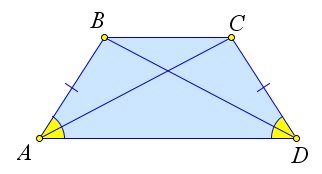
Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные, а треугольники $triangle AOB$ и $triangle COD$ равны.
Действительно, во втором пункте уже было доказано, что $triangle ABD=triangle ACD$.
Следовательно, $angle 1=angle 2$, а так как они накрест лежащие с углами $angle 3$ и $angle 4$ соответственно, то $angle 3=angle 4$, что
и означает, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные.
Тогда $AO=OD$ и $BO=OC$, и как следствие, $triangle AOB=triangle COD$ по
третьему признаку равенства треугольников.
Докажем четвертый пункт теоремы.
Так как $triangle AEB=triangle CFD$ (по катету и
гипотенузе), то $AE=FD$.
Кроме того, $EF=BC$, следовательно, $AE=dfrac{AD-BC}{2}$ и
$AF=dfrac{AD-BC}{2}+BC=dfrac{AD+BC}{2}$.
Признаки равнобедренной трапеции
-
Если углы при основании трапеции равны, то она равнобедренная.
-
Если диагонали трапеции равны, то она равнобедренная.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим трапецию $ABCD$, в которой $angle A=angle D$.
Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.
Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.
Тогда $angle A=angle CED$, как соответственные углы.
Следовательно, $angle CED=angle D$, а тогда $triangle CED$ – равнобедренный.
А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.
Докажем второй пункт теоремы.
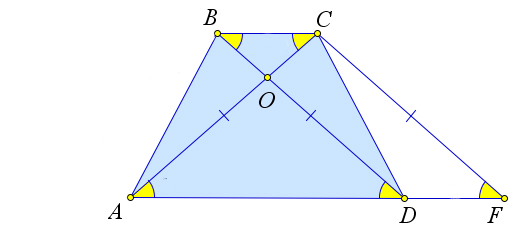
Рассмотрим трапецию $ABCD$, у которой $AC=BD$.
Докажем, что тогда $AB=CD$.
Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.
Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.
Тогда $triangle ACF$ – равнобедренный, так как $AC=CF$.
Следовательно $angle OAD=angle ODA$, и $triangle AOD$ – равнобедренный.
Тогда $AO=OD$ и $BO=OC$.
Следовательно, $triangle BOA=triangle COD$ по первому признаку ($angle BOA=angle COD$ — как вертикальные).
Следовательно, $AB=CD$.
Теорема (о равнобедренной трапеции с перпендикулярными диагоналями)
В равнобедренной трапеции со взаимно перпендикулярными диагоналями
высота равна средней линии.
Доказательство
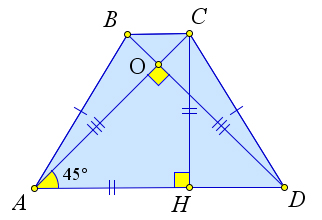
Рассмотрим равнобедренную трапецию $ABCD$, в которой $ACperp BD$.
Докажем, что в такой трапеции высота $CH$ равна средней линии то есть полусумме оснований.
Действительно, $triangle AOD$ – равнобедренный и прямоугольный, следовательно, $angle OAD = 45^circ$. Тогда $triangle AHC$ – равнобедренный, то есть $AH=CH$.
Но отрезок $AH$ равен полусумме оснований.
· Последнее изменение: 2016/04/13 23:56 —
labreslav
Kазак
5 лет назад
Светило науки — 2751 ответ — 13554 помощи
проекция стороны? интересно 
обозначим её l
l=(36-15)/2=10.5 см
теперь с высотой.
проекция и высота — катеты прямоугольного треугольника, а боковая сторона — гипотенуза.
и по Пифагору
h^2+10.5^2=37.5^2
h^2=37.5^2-10.5^2=(37.5-10.5)*(37.5+10.5)=27*48
h=√(27*48)=√(9*3*3*16)=9*4=36 см
Дана параллельная проекция равнобедренной трапеции АВСD на плоскости р. Из основных инвариантных свойств параллельного проецирования имеем: «Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций». Отсюда ясно, что проекцией отрезка, соединяющего середины параллельных оснований исходной трапеции будет отрезок, соединяющий середины проекций этих оснований. Делим отрезки АD и ВС пополам и соединяем полученные середины М и N.
Мы знаем, что в равнобедренной трапеции отрезок, соединяющий середины оснований перпендикулярен этим основаниям. А высота из вершины тупого угла трапеции параллельна этому отрезку. Таким образом, проведя прямую из точки В (проекция вершины тупого угла трапеции) параллельно прямой MN, получим искомое изображение высоты из тупого угла на большее основание.
25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы