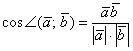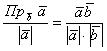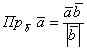Как найти проекцию вектора на вектор?
Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$
| Пример 1 |
| Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$ |
| Решение |
|
Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$ Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$ Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ |
| Пример 2 |
| Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$ |
| Решение |
|
Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 — 3 = 1$$ Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$ По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
Проекция вектора на ось. Проекция вектора на вектор
Навигация по странице:
- Определение проекции вектора на ось
- Определение проекции вектора на вектор
- Формула вычисления проекции вектора на вектор
- Примеры задач на проекцию вектора
- плоские задачи
- пространственные задачи
Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются проекциями точек A и B на ось l. (рис. 1).
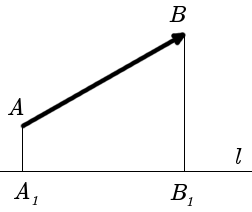 |
| рис. 1 |
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
|b| = √32 + 42 = √9 + 16 = √25 = 5
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 11 | = 2.2 |
| |b| | 5 |
Ответ: Пр ba = 2.2.
Примеры вычисления проекции вектора для пространственных задачи
Пример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 12 | = 2 |
| |b| | 6 |
Ответ: Пр ba = 2.
Содержание:
- Формула
- Примеры нахождения проекции вектора на вектор
Формула
Чтобы найти проекцию вектора $bar{a}$ на вектор
$bar{b}$, надо
скалярное произведение указанных векторов поделить на
длину (модуль) вектора
$bar{b}$, то есть
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}$$
В случае если векторы заданы на плоскости и имеют координаты
$bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Если векторы заданы в пространстве, то есть имеют координаты bar{a}=left(a_{x} ; a_{y} ; a_{z}right) text { и } bar{b}=left(b_{x} ; b_{y} ; b_{z}right), то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
Примеры нахождения проекции вектора на вектор
Пример
Задание. Найти проекцию вектора
$bar{a}$ на вектор
$bar{b}$, если
$bar{a}=(-1 ; 0)$ и $bar{b}=(3 ;-4)$
Решение. Для нахождения проекции вектора
$bar{a}$ на вектор
$bar{b}$, будем использовать формулу
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Подставляя в неё координаты заданных векторов, получим:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{-1 cdot 3+0 cdot(-4)}{sqrt{3^{2}+(-4)^{2}}}=frac{-3+0}{sqrt{9+16}}=frac{-3}{sqrt{25}}=-frac{3}{5}$$
Ответ. $Пр_{bar{b}} bar{a}=-frac{3}{5}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти проекцию вектора
$bar{a}=(-2 ; 3 ; 0)$ на вектор
$bar{b}=(-2 ; -1 ; 5)$
Решение. Подставляя координаты заданных векторов в формулу
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
получим:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|b|} =frac{-2 cdot(-2)+3 cdot(-1)+0 cdot 5}{sqrt{(-2)^{2}+(-1)^{2}+5^{2}}}=$$
$$=frac{4-3+0}{sqrt{4+1+25}}=frac{1}{sqrt{30}}$$
Ответ. $Пр_{bar{b}} bar{a}=frac{1}{sqrt{30}}$
Читать дальше: как найти длину вектора.
Проекция вектора на вектор
Рассмотрим
векторы
и
:
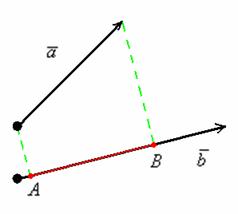
Спроецируем
вектор
на
вектор
,
для этого из начала и конца вектора
опустим
перпендикуляры на
вектор
(пунктирные
линии). В данном случае проекцией
вектора
на
вектор
является
ДЛИНА отрезка
.
То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Данное
ЧИСЛО обозначается следующим образом:
,
«большим вектором» обозначают
вектор, КОТОРЫЙ проецируют,
«маленьким подстрочным вектором»
обозначают вектор НА
который проецируют.
Сама
запись
читается
так: «проекция вектора «а» на вектор
«бэ»».
Что
произойдёт, если вектор «бэ» будет
«слишком коротким»? Проводим прямую
линию, содержащую вектор «бэ». И вектор
«а» будет проецироваться уже на
направление вектора «бэ»,
попросту – на прямую, содержащую вектор
«бэ». То же самое произойдёт, если вектор
«а» отложить в тридесятом царстве – он
всё равно легко спроецируется на прямую,
содержащую вектор «бэ».
Если
угол между
векторами
острый (как
на рисунке), то
Если
векторы
ортогональны,
то
(проекцией
является точка, размеры которой считаются
нулевыми).
Если
угол между
векторами
тупой (на
рисунке мысленно переставьте стрелочку
вектора
),
то
(та
же длина, но взятая со знаком минус).
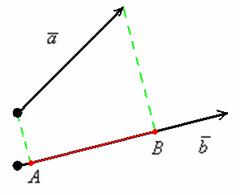
Отложим
данные векторы от одной точки:
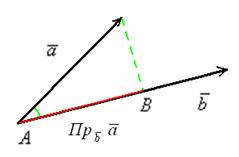
Очевидно,
что при перемещении вектора его проекция
не меняется
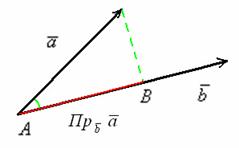
Рассмотрим
прямоугольный треугольник. Косинусом
острого угла называется отношение
прилежащего катета к гипотенузе. В
данном случае:
С
другой стороны, у нас уже получена
формула косинуса угла между векторами:
Таким
образом:

Сокращаем
знаменатели обеих частей на
и
получаем формулу для вычисления
проекции:

Формула
выведена, распишем её в координатах:
Если
векторы плоскости
и
,
заданы в ортонормированном базисе
,
то проекция вектора
на
вектор
выражается
формулой:
.
Если
векторы пространства
,
заданы в ортонормированном базисе
,
то проекция вектора
на
вектор
выражается
формулой:
Пример
Найти
проекцию вектора
на
вектор
Решение:
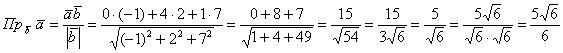
Ответ:
Проекция вектора на координатные оси. Направляющие косинусы вектора
Рассмотрим
вектор плоскости
,
заданный своими координатами в
ортонормированном базисе
.
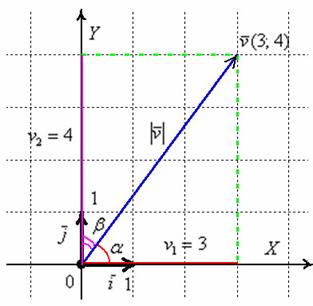
Проекцией
вектора
на
координатную ось
является
в точности его первая координата:
.
Обозначим через
угол
между вектором
и
координатным вектором
:
.
Тогда:
(определение
косинуса в прямоугольном треугольнике
недавно упоминалось).
Аналогично
со второй координатой: проекцией
вектора
на
координатную ось
является
его вторая координата:
.
Обозначим через
угол
между вектором
и
координатным вектором
:
.
Тогда:
Косинусы
называются направляющими
косинусами вектора.
Причём, для любого ненулевого вектора
справедливо равенство
.
Проверим его справедливость для
рассматриваемого вектора:
,
что и требовалось проверить.
Заметьте,
что приведённые выше выкладки не
изменятся, если вектор
отложить
от любой другой точки плоскости.
Координаты
вектора в ортонормированном базисе –
это его проекции на направления
соответствующих координатных векторов
(координатные оси).
Направляющие
косинусы ненулевого
вектора
,
заданного в ортонормированном
базисе
, выражаются
формулами
,
а сами координаты вектора можно выразить
через его длину и данные косинусы:
,
то есть:
.
С
пространственными векторами, заданными
в ортонормированном базисе
,
разборки точно такие же. Рассмотрим
произвольный ненулевой вектор
.
Его координаты представляют собой
проекции вектора на оси
соответственно.
Обозначим углы данного вектора с ортами
через:
.
Тогда направляющие
косинусы вектора выражаются формулами:
,
и справедливым является равенство
.
Пример
Найти
направляющие косинусы векторов:
а)
,
проверить, что
;
б)
,
проверить, что
.
Решение:
а)
Найдём длину вектора:
.
Направляющие
косинусы:
.
Проверка:
,
что и требовалось проверить.
б)
Найдём длину вектора:
.
Направляющие
косинусы:
.
Проверка:
,
что и требовалось проверить.
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1.7.1. Как найти проекцию вектора на вектор?
Рассмотрим ненулевые векторы и
:
Спроецируем вектор на вектор
, для этого из начала и конца вектора
опустим перпендикуляры на вектор
(зелёные пунктирные линии).
Представьте,
что на вектор перпендикулярно сверху падают
лучи света. Тогда отрезок будет «тенью»
вектора . Проекцией вектора
на вектор
является ДЛИНА отрезка
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами острый (как на рисунке выше), то
Если векторы ортогональны, то
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами тупой (на рисунке мысленно переставьте стрелочку вектора
), то
(та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора на любой ненулевой сонаправленный вектор
будет точно такой же:
– фактически это проекция вектора
на прямую
, которая содержит сонаправленные векторы
(и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно , то
добавится знак «минус»:
Отложим наши подопытные векторы от одной точки:
и рассмотрим прямоугольный треугольник. Косинус угла – есть отношение прилежащего катета к гипотенузе:
, но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
…все ли догадались, что будет дальше?
Приравниваем формулы:
и сокращаем знаменатели обеих частей на ,
получая формулу для вычисления проекции:
Распишем её в координатах:
Если векторы плоскости и
заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Если векторы пространства заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Легко убедиться, что проекция вектора на
коллинеарный вектор может
отличаться лишь знАком, приведу выкладки для «плоского» случая :
, если
, и
, если
Задача 34
Найти проекцию вектора на вектор
Решение в одну строчку:
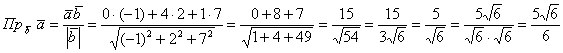
знаменатель на , избавившись тем самым от
иррациональности в знаменателе.
Ответ:
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами .
Найти:
а) проекцию стороны на сторону
;
б) проекцию стороны на сторону
.
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора на отрезок с известными концами
? (как вариант, на продолжение этого отрезка). Находим вектор
и используем формулу
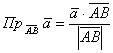
и формулу
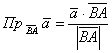
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:


| Оглавление |
Автор: Aлeксaндр Eмeлин