Заказать задачи по любым предметам можно здесь от 10 минут
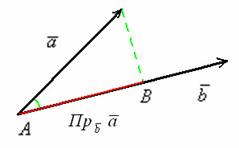
Как найти проекцию вектора на вектор?
Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$
| Пример 1 |
| Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$ |
| Решение |
|
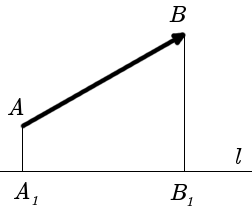
Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$ Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$ Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ |
| Пример 2 |
| Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$ |
| Решение |
|
Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 — 3 = 1$$ Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$ По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
Проекция вектора на ось. Проекция вектора на вектор
Навигация по странице:
- Определение проекции вектора на ось
- Определение проекции вектора на вектор
- Формула вычисления проекции вектора на вектор
- Примеры задач на проекцию вектора
- плоские задачи
- пространственные задачи
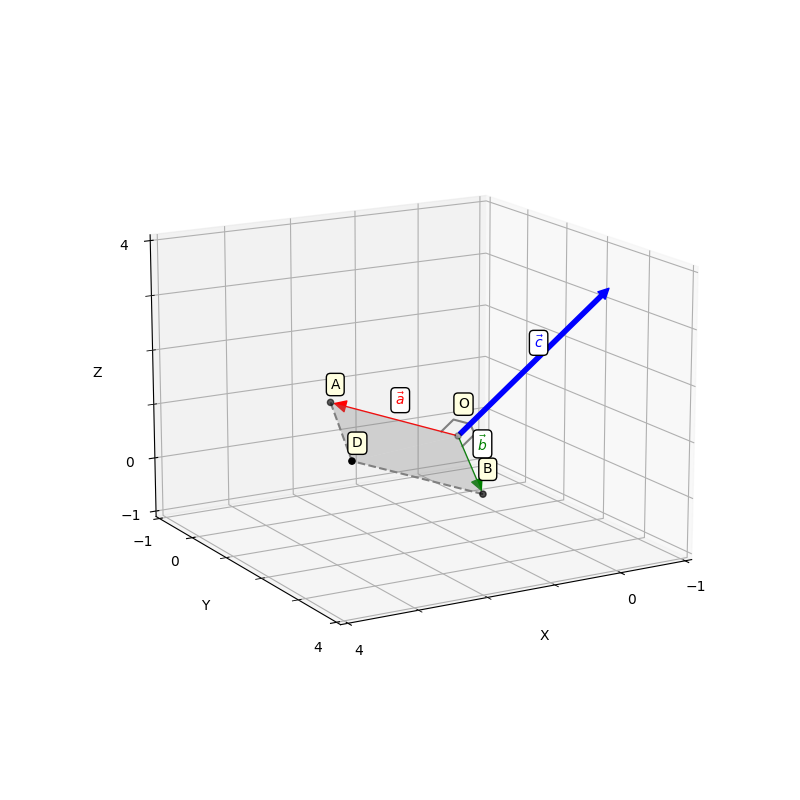
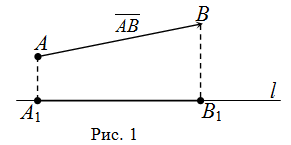
Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются проекциями точек A и B на ось l. (рис. 1).
 |
| рис. 1 |
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
|b| = √32 + 42 = √9 + 16 = √25 = 5
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 11 | = 2.2 |
| |b| | 5 |
Ответ: Пр ba = 2.2.
Примеры вычисления проекции вектора для пространственных задачи
Пример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 12 | = 2 |
| |b| | 6 |
Ответ: Пр ba = 2.
1.7.1. Как найти проекцию вектора на вектор?
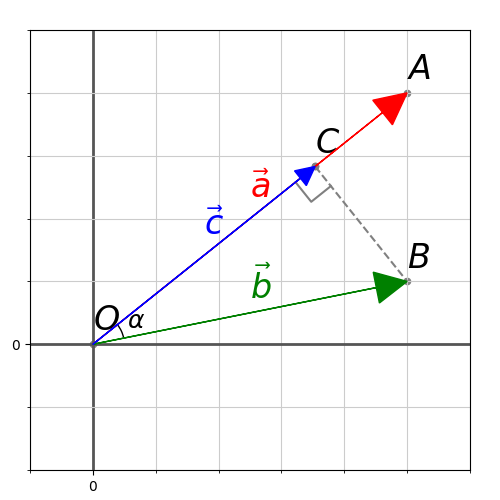
Рассмотрим ненулевые векторы и
:
Спроецируем вектор на вектор
, для этого из начала и конца вектора
опустим перпендикуляры на вектор
(зелёные пунктирные линии).
Представьте,
что на вектор перпендикулярно сверху падают
лучи света. Тогда отрезок будет «тенью»
вектора . Проекцией вектора
на вектор
является ДЛИНА отрезка
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами острый (как на рисунке выше), то
Если векторы ортогональны, то
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами тупой (на рисунке мысленно переставьте стрелочку вектора
), то
(та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора на любой ненулевой сонаправленный вектор
будет точно такой же:
– фактически это проекция вектора
на прямую
, которая содержит сонаправленные векторы
(и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно , то
добавится знак «минус»:
Отложим наши подопытные векторы от одной точки:
и рассмотрим прямоугольный треугольник. Косинус угла – есть отношение прилежащего катета к гипотенузе:
, но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
…все ли догадались, что будет дальше?
Приравниваем формулы:
и сокращаем знаменатели обеих частей на ,
получая формулу для вычисления проекции:
Распишем её в координатах:
Если векторы плоскости и
заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Если векторы пространства заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Легко убедиться, что проекция вектора на
коллинеарный вектор может
отличаться лишь знАком, приведу выкладки для «плоского» случая :
, если
, и
, если
Задача 34
Найти проекцию вектора на вектор
Решение в одну строчку:
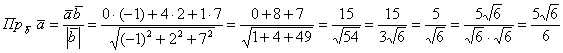
знаменатель на , избавившись тем самым от
иррациональности в знаменателе.
Ответ:
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами .
Найти:
а) проекцию стороны на сторону
;
б) проекцию стороны на сторону
.
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора на отрезок с известными концами
? (как вариант, на продолжение этого отрезка). Находим вектор
и используем формулу
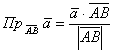
и формулу
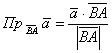
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Время на прочтение
10 мин
Количество просмотров 12K
В настоящий момент появилось достаточно большое количество библиотек дополненной реальности с богатым функционалом (ARCore, ARKit, Vuforia). Тем не менее я решил начать свой открытый проект, попутно описывая как это работает изнутри. Если повезет, то позже получится добавить какой-то особый интересный функционал, которого нет в других библиотеках. В качестве целевых платформ пока возьмем Windows и Android. Библиотека пишется на C++, и сторонние библиотеки будут задействованы по минимуму, т.е. преимущественно не будет использовано ничего готового. Фокус в статьях будет направлен на алгоритмы и математику, которые постараюсь описать максимально доступно и подробно. В этой статье пойдет речь про основы векторной алгебры.
Дополненная реальность — это совмещение виртуального мира и реального. Для этого, нам нужно представить окружающее реальное пространство в виде математической модели, понимая закономерности которой, мы сможем получить данные для совмещения. Начнем с основ векторной алгебры.
Вектора — это частный случай матриц, состоящие либо из одного столбца, либо из одной строки. Когда мы говорим о векторе, обычно имеется вектор-столбец . Но записывать вектор как столбец неудобно, поэтому будем его транспонировать —
.
Длина вектора
Первое, что мы рассмотрим — получение длины вектора — , где
— значение длины,
— наш вектор. Для примера возьмем двумерный вектор:
, где
и
— компоненты вектора, значения проекций вектора на оси двумерных координат. И мы видим прямоугольный треугольник, где
и
— это длины катетов, а
— длина его гипотенузы. По теореме Пифагора получается, что
. Значит
. Вид формулы сохраняется и для векторов большей размерности, например —
.
Скалярное произведение
Скалярное произведение векторов — это сумма произведение их компонентов: . Но так как мы знаем, что вектора — это матрицы, то тогда удобнее записать это в таком виде:
. Это же произведение можно записать в другой форме:
, где
— угол между векторами
и
(для двумерного случая эта формула доказывается через теорему косинусов). По этой формуле можно заключить, что скалярное произведение — это мера сонаправленности векторов. Ведь, если
, то
, и
— это просто произведение длин векторов. Так как
— не может быть больше 1, то это максимальное значение, которые мы можем получить, изменяя только угол
. Минимальное значение
будет равно -1, и получается при
, т.е. когда вектора смотрят в противоположные направления. Также заметим, что при
, а значит какие бы длины не имели вектора
и
, все равно
. Можно в таком случае сказать, что вектора не имеют общего направления, и называются ортогональными.
Также при помощи скалярного произведения, мы можем записать формулу длины вектора красивее: ,
.
Проекция вектора на другой вектор
Возьмем два вектора: и
.
Проекцию вектора на другой вектор можно рассматривать в двух смыслах: геометрическом и алгебраическом. В геометрическом смысле проекция вектора на ось — это вектор, а в алгебраическом – число.
Вектора — это направления, поэтому их начало лежит в начале координат. Обозначим ключевые точки: — начало координат,
— конечная точка вектора
,
— конечная точка вектора
.
В геометрическом смысле мы ищем такой , чтобы конечная точка вектора (обозначим ее как —
) была ближайшей точкой к точке
, лежащей на прямой
.
Иначе говоря, мы хотим найти составляющую в
, т.е. такое значение
, чтобы
и
Расстояние между точками и
будет минимальным, если
. Получаем прямоугольный треугольник —
. Обозначим
. Мы знаем, что
по определению косинуса через соотношение сторон прямоугольного треугольника
( — гипотенуза,
— прилежащий катет).
Также возьмем скалярное произведение . Отсюда следует, что
. А значит
.
Тут вспоминаем, что — это искомый вектор
, а
—
, и получаем
. Умножаем обе части на
и получаем —
. Теперь мы знаем длину
. Вектор
отличается от вектора
длинной, но не направлением, а значит через соотношение длин можно получить:
. И мы можем вывести финальные формулы:
и
Нормализованный вектор
Хороший способ упростить работу над векторами — использовать вектора единичной длины. Возьмем вектор и получим сонаправленный вектор
единичной длины. Для этого вектор разделим на его длину:
. Эта операция называется нормализацией, а вектор — нормализованным.
Зная нормализованный вектор и длину исходного вектора, можно получить исходный вектор: .
Зная нормализованный вектор и исходный вектор, можно получить его длину: .
Хорошим преимуществом нормализованных векторов является то, что сильно упрощается формула проекции (т.к. длина равна 1, то она сокращается). Проекция вектора на
единичной длины:
Матрица поворота двумерного пространства
Предположим у нас есть некая фигура:
Чтобы ее нарисовать, заданы координаты ее вершин, от которых строятся линии. Координаты заданы в виде набора векторов следующим образом . Наша координатная сетка задана двумя осями — единичными ортогональными (перпендикулярными) векторами. В двумерном пространстве можно получить два перпендикулярных вектора к другому вектору такой же длины следующим образом:
— левый и правый перпендикуляры. Берем вектор, задающим ось
—
и ось
— левый к нему перпендикуляр —
.
Выведем новый вектор, получаемый из наших базисный векторов:
Сюрприз — он совпадает с нашим исходным вектором.
Теперь попробуем как-то изменить нашу фигуру — повернем ее на угол . Для этого повернем векторы
и
, задающих оси координат. Поворот вектора
задается косинусом и синусом угла —
. А чтобы получить вектор оси
, возьмем перпендикуляр к
:
. Выполнив эту трансформацию, получаем новую фигуру:
Вектора и
являются ортонормированным базисом, потому как вектора ортогональны между собой (а значит базис ортогонален), и вектора имеют единичную длину, т.е. нормированы.
Теперь мы говорим о нескольких системах координат — базовой системы координат (назовем ее мировой), и локальной для нашего объекта (которую мы поворачивали). Удобно объединить наш набор векторов в матрицу —
Тогда .
В итоге — .
Матрица , составляющая ортонормированный базис и описывающая поворот, называется матрицей поворота.
Также матрица поворота имеет ряд полезных свойств, которые следует иметь ввиду:
- При
, где
— единичная матрица, матрица соответствует нулевому повороту (угол
), и в таком случае локальные оси совпадают с мировыми. Как рассматривали выше, матрица никак не меняет исходный вектор.
— определитель матрицы равен 1, если у нас, как обычно бывает, правая тройка векторов.
, если тройка векторов левая.
.
.
.
, поворот не меняет длины вектора.
- зная
и
, можем получить исходный вектор
—
. Т.е. умножая вектор на матрицу поворота мы выполняем преобразование координат вектора из локальной системы координат объекта в мировую, но также мы можем поступать и наоборот — преобразовывать мировые координаты в локальную систему координат объекта, умножая на обратную матрицу поворота.
Теперь попробуем повернуть наш объект два раза, первый раз на угол , второй раз на угол
. Матрицу, полученную из угла
, обозначим как
, из угла
—
. Распишем наше итоговое преобразование:
.

Обозначим , тогда
. И из двух операций мы получили одну. Так как поворот — это линейное преобразование (описали ее при помощи одной матрицы), множество преобразований можно описать одной матрицей, что сильно упрощает над ними работу.
Масштабирование в двумерном пространстве
Масштабировать объект достаточно просто, нужно только умножить координаты точек на коэффициент масштаба: . Если мы хотим масштабировать объект на разную величину по разным осям, то формула принимает вид:
. Для удобства переведем операцию в матричный вид:
.
Теперь предположим, что нам нужно повернуть и масштабировать наш объект. Нужно отметить, что если сначала масштабировать, а затем повернуть, то результат будет отличаться, от того результата, где мы сначала повернули, а затем масштабировали:
Сначала поворот, а затем масштабирование по осям:
Сначала масштабирование по осям, а затем поворот:
Как мы видим порядок операций играет большое значение, и его нужно обязательно учитывать.
Также здесь мы также можем объединять матрицы преобразования в одну:
Хотя в данном случае, если , то
. Тем не менее, с порядком преобразований нужно быть очень аккуратным. Их нельзя просто так менять местами.
Векторное произведение векторов
Перейдем в трехмерное пространство и рассмотрим определенное на нем векторное произведение.
Векторное произведение двух векторов в трёхмерном пространстве — вектор, ортогональный к обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Для примера возьмем два трехмерных вектора — ,
. И в результате векторного произведения получим
Визуализируем данную операцию:
Здесь наши вектора ,
и
. Вектора начинаются с начала координат, обозначенной точкой
. Конечная точка вектора
— точка
. Конечная точка
— точка
. Параллелограмм из определения формируются точками
,
,
,
. Координаты точки
находим как —
. В итоге имеем следующие соотношения:
Два вектора образуют плоскость, а векторное произведение позволяет получить перпендикуляр к этой плоскости. Получившиеся вектора образуют образуют правую тройку векторов. Если берем обратный вектор, то получаем второй перпендикуляр к плоскости, и тройка векторов будет уже левой.
Для запоминания этой формулы удобно использовать мнемонический определитель. Пусть , и мы раскладываем определить по строке как сумму определителей миноров исходной матрицы
:
Некоторые удобные свойства данного произведения:
- Если два вектора ортогональны и нормализованы, то вектор также будет иметь единичную длину. Параллелограмм, который образуется двумя исходными векторами, станет квадратом с длинной сторон равной единице. Т.е. площадь равна единице, отсюда длина выходного вектора — единица.
Матрица поворота трехмерного пространства.
С тем, как формировать матрицу в двумерном пространстве мы разобрались. В трехмерном она формируется уже не двумя, а тремя ортогональными векторами — . По свойствам, описанным выше, можно вывести следующие отношения между этими векторам:
Вычислить вектора этих осей сложнее, чем в матрице поворота двумерного пространства. Для примера получения этих векторов рассмотрим алгоритм, который в трехмерных движках называется lookAt. Для этого нам понадобятся вектор направления взгляда — и опорный вектор для оси
—
. Сам алгоритм:
- Обычно направление камеры совпадает с осью
. Поэтому нормализуем
и получаем ось
—
.
- Получаем вектор оси
—
. В итоге у нас есть два нормализованных ортогональных вектора
и
, описывающих оси
и
, при этом ось
сонаправлена с входным вектором
, а ось
перпендикулярна к входному опорному вектору
.
- Получаем вектор оси
из полученных
и
—
.
- В итоге
В трехмерных редакторах и движках в интерфейсах часто используются углы Эйлера для задания поворота. Углы Эйлера более интуитивно понятны — это три числа, обозначающие три последовательных поворота вокруг трех основных осей . Однако, работать с ними не очень то просто. Если попробовать выразить итоговый вектор напрямую через эти повороты, то получим довольно объемную формулу, состоящую из синусов и косинусов наших углов. Есть еще пара проблем с этими углами. Первая проблема — это то, что сами по себе углы не задают однозначного поворота, так как результат зависит от того, в какой последовательности происходили повороты —
или
или как-то еще. Углы Эйлера — это последовательность поворотов, а как мы помним, смена порядка трансформаций меняет итоговый результат. Вторая проблема — это gimbal lock.
Внутри же трехмерные движки чаще всего используют кватернионы, которых мы касаться не будем.
Существуют разные способы задания поворота в трехмерном пространстве, и каждый имеет свои плюсы и минусы:
- Матрица поворота. С ней просто работать (т.к. это просто матрицы). Но есть логическая избыточность данных — все элементы матрицы связаны определенными условиями, так как количество элементов больше степеней свободы (12 элементов против трех степеней). Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота.
- Углы Эйлера. Они интуитивно понятны, но работать с ними сложно.
- Вектор оси вращения и угол порота вокруг нее. Любой возможный поворот можно описать таким образом. Поворота вектора вокруг заданной оси рассмотрим ниже.
- Вектор поворота Родрига. Это трехмерный вектор, где нормализованный вектор представляет собой ось вращения, а длина вектора угол поворота. Этот способ задания поворота похож на предыдущий способ, но количество элементов здесь равно числу степеней свободы, и элементы не связаны между собой жесткими ограничениями. И мы можем взять трехмерный вектор с абсолютно случайными числами, и любой полученный вектор будет задавать какое-то возможное вращение.
Поворот вектора вокруг заданной оси
Теперь рассмотрим операцию, позволяющую реализовать поворот вектора вокруг оси.
Возьмем вектор — описывающий ось, вокруг которой нужно повернуть вектор
на угол
. Результирующий вектор обозначим как
. Иллюстрируем процесс:
Вектор мы можем разложить сумму векторов: вектора, параллельный к вектору
—
, и вектора, перпендикулярному к вектору к вектору
—
.
.
Вектор — это проекция вектора
на вектор
. Т.к.
— нормализованный вектор, то:
Та часть , которая принадлежит оси вращения (
) не измениться во время вращения. Повернуть нам нужно только
в плоскости перпендикулярной к
на угол
, Обозначим этот вектор как
. Тогда наш искомый вектор —
.
Вектор можем найти следующим образом:
Для того, чтобы повернуть , выведем оси
и
в плоскости, в которой будем выполнять поворот. Это должны быть два ортогональных нормализованных вектора, ортогональных к
. Один ортогональный вектор у нас уже есть —
, нормализуем его и обозначим как ось
—
.
Теперь получим вектор оси . Это должен быть вектор, ортогональный к
и
(т.е. и к
). Получить его можно через векторное произведение:
. Значит
. По свойству векторного произведения
будет равно площади параллелограмма, образуемого двумя исходными векторами (
и
). Так как вектора ортогональны, то у нас будет не параллелограмм, а прямоугольник, а значит
.
. Значит
.
Поворот двумерного вектора на угол
можно получить через синус и косинус —
. Т.к.
в координатах полученной плоскости сонаправлен с осью
, то он будет равен
. Этот вектор после поворота —
. Отсюда можем вывести:
Теперь мы можем получить наш искомый вектор:
Мы разобрались с тем, как поворачивать вектор вокруг заданной оси на заданный угол, значит теперь мы умеем использовать поворот, заданный таким образом.
Получить вектор оси вращения и угол из вектора Родрига не составляет большого труда, а значит мы теперь умеем работать и с ним тоже.
Напоминаю, что матрица поворота представляет собой три базисных вектора , а углы Эйлера — три последовательных поворота вокруг осей
,
,
. Значит мы можем взять единичную матрицу, как нулевой поворот
, а затем последовательно поворачивать базисные вектора вокруг нужных нам осей. В результате получим матрицу поворота соответствующую углам Эйлера. Например:
Также можно отдельно вывести матрицы вращения по каждой из осей ,
,
(
,
,
соответственно) и получить итоговую матрицу последовательным их умножением:
Таким же образом можно перевести вектор поворота Родрига в матрицу поворота: также поворачиваем оси матрицы поворота, полученные от единичной матрицы.
Итак, с вращением объекта разобрались. Переходим к остальным трансформациям.
Масштабирование в трехмерном пространстве
Все тоже самое что и двумерном пространстве, только матрица масштабирования принимает вид:
Перемещение объекта
До этого момента точка начала локальных координат не смещалась в мировом пространстве. Так как точка начала координат нашего объекта — это его центр, то центр объект никуда не смещался. Реализовать это смещение просто: , где
— вектор, задающий смещение.
Теперь мы умеем масштабировать объект по осям, поворачивать его и перемещать.
Объединим все одной формулой: :
Чтобы упростить формулу, мы можем, как уже делали ранее, объединить матрицы . В итоге наше преобразование описывает матрица
и вектор
. Объединение вектора
с матрицей
еще более бы упростило формулу, однако сделать в данном случае не получится, потому как сложение здесь — это не линейная операция. Тем не менее сделать это возможно, и рассмотрим этот момент уже в следующей статье.
Заключение
Для какого-то покажется, что статья описывает очевидные вещи, кому-то может показаться наоборот немного запутанной. Тем не менее это базовый фундамент, на котором будет строиться все остальное. Векторная алгебра — является фундаментом для многих областей, так что статья может вам оказаться полезной не только в дополненной реальности. Следующая статья будет уже более узконаправленной.
Проекция вектора на вектор
Определение и формула проекции вектора на вектор
Проекцией вектора на ось
называется число, которое равно величине отрезка
, принадлежащего указанной оси, где точки
и
– проекции точек
и
на рассматриваемую ось
соответственно (рис. 1).
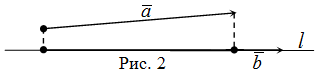
Проекция вектора на направление вектора
равна скалярному произведению этих векторов, деленному на длину вектора
:
Примеры нахождения проекции вектора на вектор
ПРИМЕР
| Задание | Найти проекцию вектора |
| Решение |
Вычислим скалярное произведение заданных векторов. Оно равно сумме произведений соответствующих координат векторов-сомножителей
Модуль вектора Тогда искомая проекция |
| Ответ | |
ПРИМЕР
| Задание | Найти модуль вектора |
| Решение |
Согласно формуле имеем, что
Тогда |
| Ответ | |
| Понравился сайт? Расскажи друзьям! | |

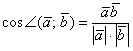
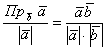
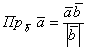








![Rendered by QuickLaTeX.com [{Pi text{p}}_{bar{b}} bar{a}=frac{left(bar{a},; bar{b}right)}{left|bar{b}right|} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-86442d66cfafef044cc11e06dcf15f5f_l3.png)
![Rendered by QuickLaTeX.com [{Pi text{p}}_{bar{b}} bar{a}=frac{left(bar{a},; bar{b}right)}{left|bar{b}right|} Leftrightarrow 2=frac{4}{left|bar{b}right|} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4b180d797414af935e6af87b73db117b_l3.png)
