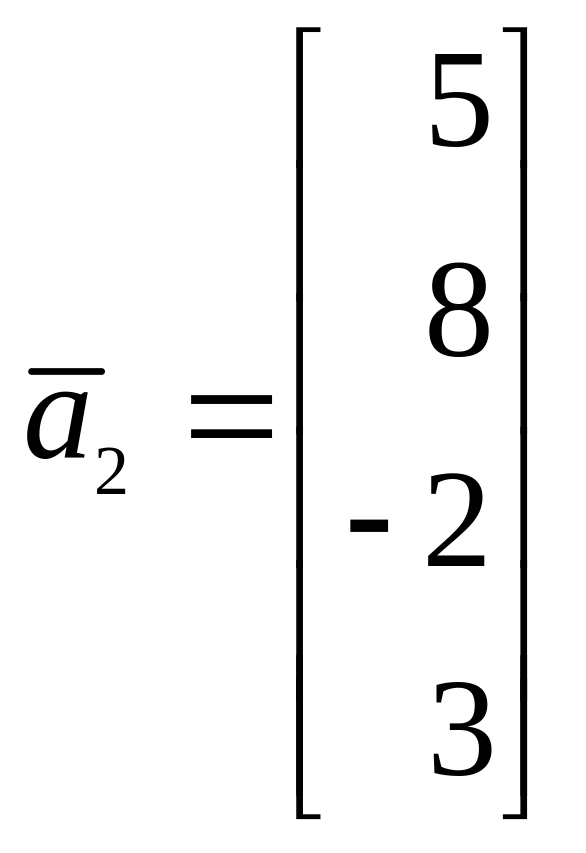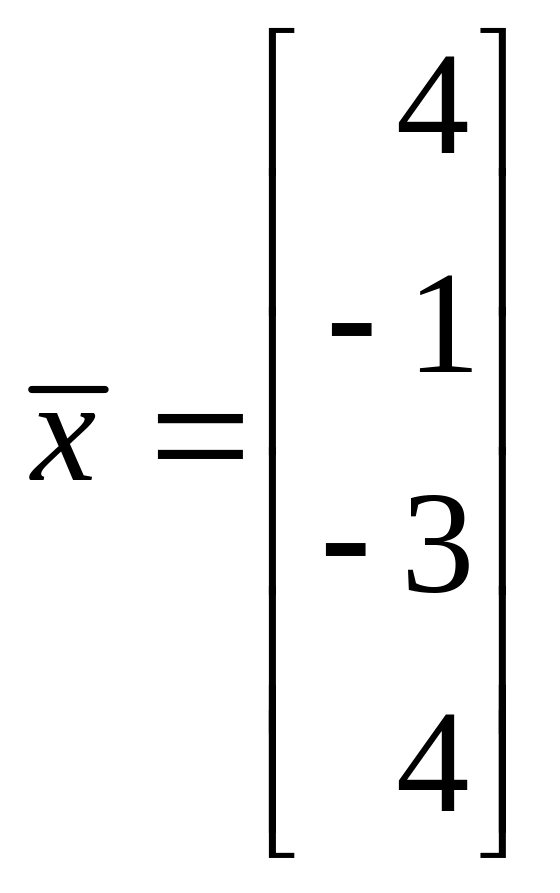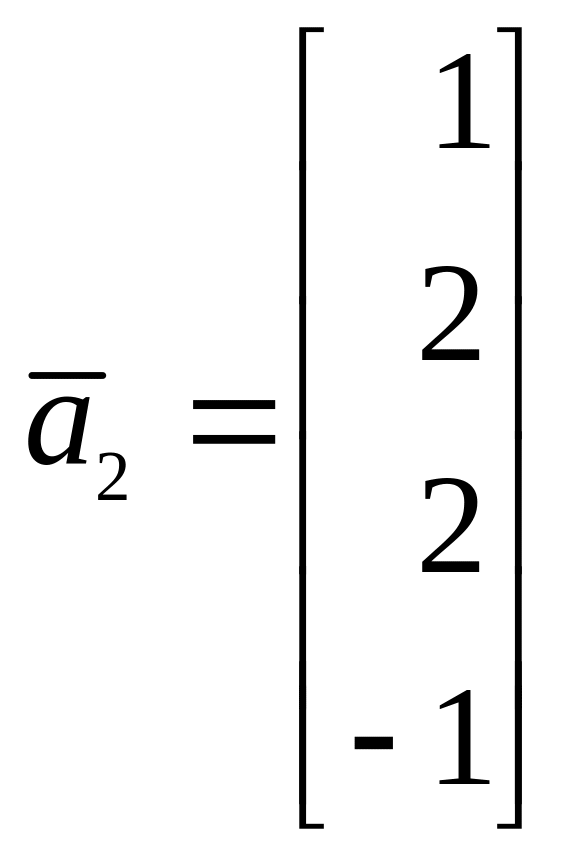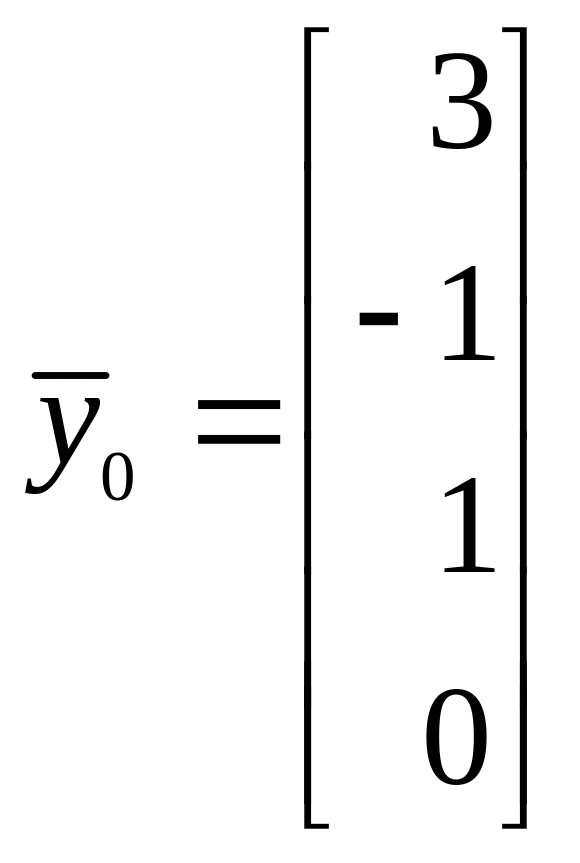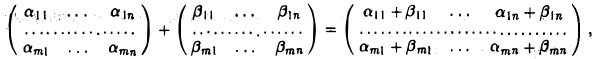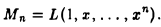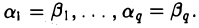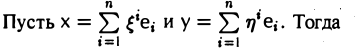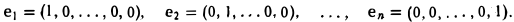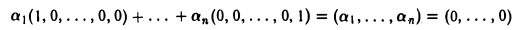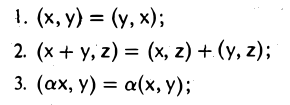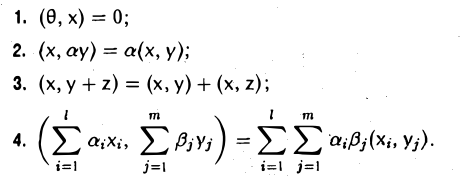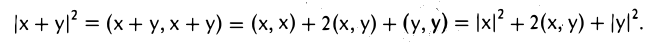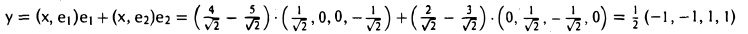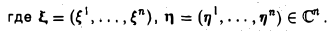Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Линейное пространство, проекция вектора на подпространство
|
|
13/01/10 |
|
|
|
|
|
AKM |
Re: Линейное пространство
|
||
18/05/09 |
|||
|
|
|||
|
ewert |
Re: Линейное пространство
|
||
11/05/08 |
|||
|
|
|||
|
swact |
Re: Линейное пространство
|
|
13/01/10 |
|
|
|
|
|
voipp |
Re: Линейное пространство
|
|
13/12/09 |
Чтобы задача была корректной, требуется, чтобы векторы А почему задача будет некорректной, если векторы не образуют базис всего пространства?
|
|
|
|
|
Massaget |
Re: Линейное пространство
|
|
11/03/13 |
Потому что тогда не каждый вектор будет однозначно раскладываться в сумму векторов из
|
|
|
|
|
Alexey Rodionov |
Re: Линейное пространство, проекция вектора на подпространство
|
|
07/05/13 |
Цитата: Чтобы задача была корректной, требуется, чтобы векторы Не совсем так. Даже линейная независимость систем не является необходимой. А если почувствовать себя вектором, который не любой, а ДАННЫЙ, чиста конкретный, то еще найдется, где покувыркаться.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Определение. Два множества F
и G векторов евклидова
пространства E
называются ортогональными, если каждый
вектор из F ортогонален
каждому вектору из G.
Определение. Пусть F
– подпространство E.
Совокупность всех векторов подпространства
E, ортогональных
подпространству F,
называется ортогональным дополнением
подпространства F.
Всякое ортогональное дополнение
является, в свою очередь, линейным
подпространством.
Всякое произвольное евклидово пространство
E разлагается в прямую
сумму своего произвольного подпространства
F и его ортогонального
дополнения
Примеры
1. Требуется найти базис ортогонального
дополнения
подпространства L,
натянутого на векторы
,
,

Будем считать, что базис, относительно
которого заданы векторы, ортонормированный.
По определению, если
,
то
.
Далее, каждый вектор
из
должен быть ортогонален к
.
Для этого достаточно, чтобы
.
Расписывая скалярные произведения,
получим три уравнения относительно
координат
вектора
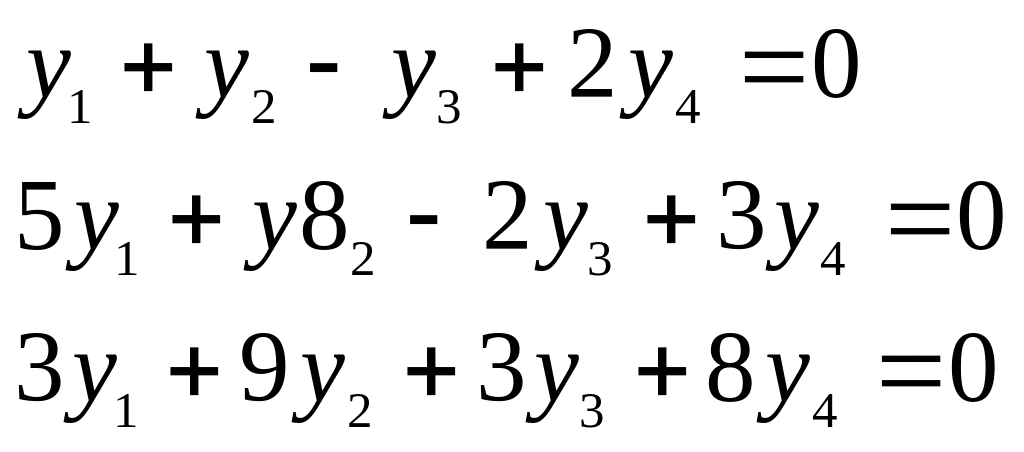
Совокупность решений этой системы и
образует ортогональное дополнение. За
базис в
можно принять любую фундаментальную
систему решений. Например, вектор
.
2. Линейное подпространство
задано уравнениями
Требуется найти уравнения, которые
задают ортогональное дополнение
.
Пусть
,
.
Тогда
.
Этому условию удовлетворяют два линейно
независимых вектора
и
,
которые образуют коэффициенты системы
уравнений, задающей F.
Далее,
.
Ранг системы равен 2. Значит
и, так как
,
то
.
Поэтому найденные векторы можно принять
за базис в
,
и
есть линейная оболочка данных векторов.
Далее задача решается так же как в
примере из § 3. Дословно повторяя решение,
получим следующую систему уравнений
которая и задает
.
5.3. Проектирование вектора на подпространства
Пусть
.
Тогда всякий вектор
можно представить в виде
,
где
и
.
Вектор
называется ортогональной проекцией
вектора x на
подпространство L, а
вектор
называется ортогональной составляющей
вектора
.
Пусть
и
— расстояние между векторами
,
тогда
Таким образом, ортогональная проекция
есть ближайший к
вектору подпространства L.
Часто используются следующие обозначения
,
.
Укажем в заключение как вычисляются
координаты вектора
.
Пусть
— базис в L. Так как
,
то
.
Поэтому
Отсюда имеем, что в случае ортонормированного
базиса
Примеры
1. Найти ортогональную проекцию
и ортогональную составляющую
вектора
на линейное подпространство L,
натянутое на векторы
.
Все векторы заданы координатами
относительно ортонормированного базиса.
,
,
,

Нетрудно убедиться, что
и что за базис можно принять векторы
и
.
Нам будет удобно перейти к ортонормированному
базису в L. Применяя
процедуру ортогонализации к векторам
и
,
получим ортонормированный базис в L:
,
Заметьте, что векторы
и
линейно выражаются через
и
и, значит, также принадлежат L.
Имеем теперь

2. Требуется найти расстояние от точки,
заданной вектором
до плоскости (линейного многообразия),
заданной системой уравнений
Расстояние между точкой
и множеством L
определится следующим образом
Для вычисления расстояния удобно перейти
к параметрическому уравнению плоскости.
Имеем
и поэтому всякий вектор
представляется в виде
где
— фиксированный радиус-вектор точки
плоскости;
и
— базис направляющего линейного
подпространства, которое задается
соответствующей однородной системой.
Решая уравнение, получим, например,
,
,

Затем
Векторы
и
принадлежат направляющему подпространству
M плоскости L.
Вектор
.
Так как
,
а
,
то
Правая часть этого неравенства и есть
искомое расстояние. Осталось вычислить
вектор
и найти его норму. Проделав для этого
аналогичные вычисления и вычислив длину
вектора, получим, что
.
3. Пусть
— ортонормированная система векторов
евклидова пространства En.
Нужно доказать, что для любого вектора
имеет место неравенство Бесселя
с равенством тогда и только тогда, когда
,
т.е. векторы
образуют ортонормированный базис в En.
Так как
— ортонормированная система, то ее
всегда можно векторами
достроить до ортонормированного базиса
в En.
Разложим вектор
по этому базису. Имеем
Далее,
или
С равенством тогда и только тогда, когда
.
Исключение составляют случаи, когда
или когда
принадлежит линейной оболочке векторов
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
I am trying to understand how — exactly — I go about projecting a vector onto a subspace.
Now, I know enough about linear algebra to know about projections, dot products, spans, etc etc, so I am not sure if I am reading too much into this, or if this is something that I have missed.
For a class I am taking, the proff is saying that we take a vector, and ‘simply project it onto a subspace’, (where that subspace is formed from a set of orthogonal basis vectors).
Now, I know that a subspace is really, at the end of the day, just a set of vectors. (That satisfy properties here). I get that part — that its this set of vectors. So, how do I «project a vector on this subspace»?
Am I projecting my one vector, (lets call it a[n]) onto ALL the vectors in this subspace? (What if there is an infinite number of them?)
For further context, the proff was saying that lets say we found a set of basis vectors for a signal, (lets call them b[n] and c[n]) then we would project a[n] onto its signal subspace. We project a[n] onto the signal-subspace formed by b[n] and c[n]. Well, how is this done exactly?..
Thanks in advance, let me know if I can clarify anything!
P.S. I appreciate your help, and I would really like for the clarification to this problem to be somewhat ‘concrete’ — for example, something that I can show for myself over MATLAB. Analogues using 2-D or 3-D space so that I can visualize what is going on would be very much appreciated as well.
Thanks again.
asked Feb 24, 2012 at 2:47
$endgroup$
2
$begingroup$
I will talk about orthogonal projection here.
When one projects a vector, say $v$, onto a subspace, you find the vector in the subspace which is «closest» to $v$. The simplest case is of course if $v$ is already in the subspace, then the projection of $v$ onto the subspace is $v$ itself.
Now, the simplest kind of subspace is a one dimensional subspace, say the subspace is $U = operatorname{span}(u)$. Given an arbitrary vector $v$ not in $U$, we can project it onto $U$ by
$$v_{| U} = frac{langle v , u rangle}{langle u , u rangle} u$$
which will be a vector in $U$. There will be more vectors than $v$ that have the same projection onto $U$.
Now, let’s assume $U = operatorname{span}(u_1, u_2, dots, u_k)$ and, since you said so in your question, assume that the $u_i$ are orthogonal. For a vector $v$, you can project $v$ onto $U$ by
$$v_{| U} = sum_{i =1}^k frac{langle v, u_irangle}{langle u_i, u_i rangle} u_i = frac{langle v , u_1 rangle}{langle u_1 , u_1 rangle} u_1 + dots + frac{langle v , u_k rangle}{langle u_k , u_k rangle} u_k.$$
answered Feb 24, 2012 at 3:16
CalleCalle
7,5411 gold badge34 silver badges47 bronze badges
$endgroup$
7
$begingroup$
Take a basis ${v_1, dots, v_n}$ for the «signal subspace» $V$. Let’s assume $V$ is finite dimensional for simplicity and practical purposes, but you can generalize to infinite dimensions. Let’s also assume the basis is orthonormal.
The projection of your signal $f$ onto the subspace $V$ is just
$$mathrm{proj}_V(f) = sum_{i=1}^n langle f, v_i rangle v_i$$
and $f = mathrm{proj}_V(f) + R(f)$, where $R(f)$ is the remainder, or orthogonal complement, which will be 0 if $f$ lies in the subspace $V$.
The $i$-th term of the sum, $langle f, v_irangle$, is the projection of $f$ onto the subspace spanned by the $i$-th basis vector. (Note, if the $v_i$ are orthogonal, but not necessarily orthonormal, you must divide the $i$-th term by $|v_i|^2$.)
answered Feb 24, 2012 at 3:17
$endgroup$
1
$begingroup$
The projection of the vector is the vector belonging to the subspace that best approximates the former, i.e. such that the (squared) norm of the difference is the smallest.
WLOG take a subspace spanned by three vectors. We minimize for the coordinates $u,v,w$
$$epsilon=(vec d-uvec a-vvec b-wvec c)^2.$$
This is achieved by canceling the gradient (factor $2$ omitted),
$$begin{cases}
dfrac{depsilon}{du}=vec acdot(vec d-uvec a-vvec b-wvec c)=0,\
dfrac{depsilon}{dv}=vec bcdot(vec d-uvec a-vvec b-wvec c)=0,\
dfrac{depsilon}{dw}=vec ccdot(vec d-uvec a-vvec b-wvec c)=0.\
end{cases}$$ giving a linear system of three equations in three unknonws.
In the special case that $vec a,vec b,vec c$ form an orthonormal basis, we simply have
$$u=vec dcdotvec a,v=vec dcdotvec b,w=vec dcdotvec c,$$ and the projection is
$$vec u^*=(vec dcdotvec a)vec a+(vec dcdotvec b)vec b+(vec dcdotvec c)vec c.$$
answered Jul 6, 2016 at 12:48
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Евклидово пространство — это вещественное линейное пространство, в котором зафиксирована симметричная положительно определенная билинейная форма. Значение билинейной формы на паре элементов называется скалярным произведением этих векторов.
Линейные и евклидовы пространства
Определение линейного пространства
Определение:
Множество V элементов х, у, z,… называется линейным пространством (действительным или комплексным), если по некоторому правилу
I. любым двум элементам х и у из V поставлен в соответствие элемент из V, обозначаемый х + у и называемый суммой элементов х и у;
II. любому элементу х из V и каждому числу а (вещественному или комплексному) поставлен в соответствие элемент из V, обозначаемый ах и называемый произведением элемента х на число а, и эти правила сложения и умножения на число удовлетворяют следующим аксиомам:
- (х + у) + z = х + (у + z) (ассоциативность);
- х + у = у + х (коммутативность)-,
- во множестве V существует элемент θ такой, что для любого элемента х из V выполняется равенство х + θ = х;
- для любого элемента х из V во множестве V существует элемент (-х) такой, что х + (-х) = θ;
- а(х + у) = ах + ау;
- (а + β)х = ах + βх;
- а( β х) = (а β )х;
- 1х = х.
Элемент θ называется нулевым элементом, а элемент (-х) — противоположным элементу х.
Элементы х, у, z,… линейного пространства часто называют векторами. Поэтому линейное пространство называют также векторным пространством.
Примеры линейных пространств
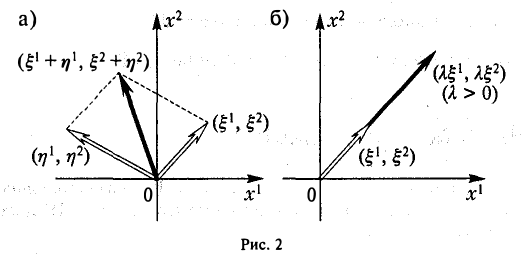
- Совокупность свободных геометрических векторов V3 в пространстве с введенными операциями сложения векторов и умножения вектора на число (рис. 1).
Этим же свойством обладают: совокупность V1 векторов на прямой и совокупность V2 векторов на плоскости.
2, Совокупность упорядоченных наборов (
Операции — сложение и умножение на действительное число — вводятся так:
а) сложение —
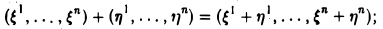
б) умножение на число —
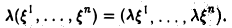
Обозначение: Rn (n -мерное вещественное координатное пространство).
3. Совокупность всевозможных матриц Rmxn размера m х n с введенными правилами сложения матриц,
и умножения матрицы на число,
В частности, совокупность n-строк, R1xn и совокупность столбцов высоты m, Rmx1, являются линейными пространствами.
4. Множество С(-1, 1) вещественных функций, непрерывных на интервале (-1, I), с естественными операциями сложения функций и умножения функции на число.
Во всех приведенных примерах требования 1-8 проверяются непосредственно.
Простейшие свойства линейных пространств
- Нулевой элемент θ определен однозначно.
Пусть θ1 и θ2 — нулевые элементы пространства V. Рассмотрим их сумму θ1 + θ2. Вследствие того, что θ2 — нулевой элемент, из аксиомы 3 получаем, что θ1+ θ2 = θ1, а так как элемент θ1 — также нулевой, то θ1 + θ2 = θ2 + θ1 = θ2 , т. е. θ1 = θ2 .
2. Для любого элемента х противоположный ему элемент (—х) определен однозначно.
Пусть x— и х_ — элементы, противоположные элементу х. Покажем, что они равны.
Рассмотрим сумму х_ + х + x— . Пользуясь аксиомой 1 и тем, что элемент x— противоположен элементу х, получаем:
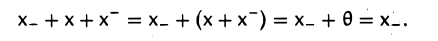
Аналогично убеждаемся в том, что
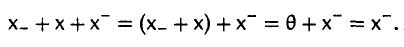
Нетрудно убедится также в справедливости следующих свойств:
- Для любого элемента х выполняется равенство 0х = θ.
- Для любого элемента х выполняется равенство —х = (- 1)х.
- Для любого числа а выполняется равенство аθ = θ.
- Из того, что ах = θ, следует, что либо а = 0, либо х = θ.
Линейные подпространства
Непустое подмножество W линейного пространства V называется линейным подпространством пространства V, если для любых элементов х и у из W и любого числа а выполняются следующие условия:
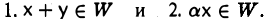
Иногда говорят: «множество W замкнуто относительно указанных операций».
Примеры линейных подпространств
1.Множество векторов на плоскости V2 является линейным подпространством линейного пространства V3.
2. Совокупность решений однородной системы m линейных уравнений с n неизвестными
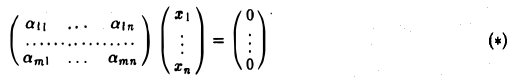
образует линейное подпространство линейного пространства Rnx1. В самом деле, сумма решений однородной системы () является решением этой же системы и произведение решения системы (*) на число также является ее решением.
3. Совокупность всех вещественнозначных функций, непрерывных на интервале (-1, 1) и обращающихся в нуль при t = 0, образует линейное подпространство линейного пространства С(— 1,1).
Сумма f(t) + g(t) функций f(t) и g(t), обращающихся в нуль при t = 0, t(0) = f(0) = 0, и произведение af(t) функции f(t), обращающейся в нуль при t = 0, f(0) = 0, на число а равны нулю при t = 0.
Свойства линейного подпространства
- Если x1, …, хq — элементы линейного подпространства W, то любая их линейная комбинация
также лежит в W.
- Линейное подпространство W само является линейным пространством.
Достаточно убедиться лишь в том, что нулевой элемент 0 и элемент, противоположный произвольному элементу из W, лежат в W. Указанные векторы получаются умножением произвольного элемента х ∈ W на 0 и на -1: θ = 0х, -х = (- 1)х.
Сумма и пересечение линейных подпространств
Пусть V — линейное пространство, W1 w W2 — его линейные подпространства. Суммой W1 + W2 линейных подпространств W1 и W2 называется совокупность всевозможных элементов х пространства V, которые можно представить в следующем виде

где x1 лежит в W1, а х2 — в W2. Коротко это можно записать так:
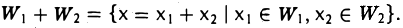
Сумма линейных подпространств W1 и W2 нaзывается прямой, если для каждого элемента х этой суммы разложение (1) единственно (рис. 3).
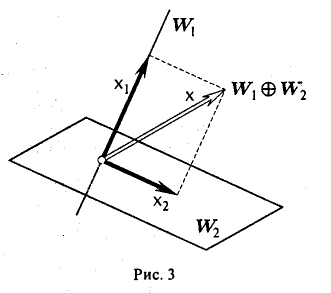
Обозначение: W1⊕W2
Пересечением W1 ∩ W2 линейных подпространств W1 и W2 линейного пространства V называется совокупность элементов, которые принадлежат одновременно и линейному подпространству W1, и линейному подпространству W2.
Свойства пересечения и суммы линейных подпространств
- Сумма W1 + W2 является линейным подпространством пространства V.
Возьмем в W1 + W2 два произвольных элемента х и у. По определению суммы подпространств найдутся элементы х1, у1, из W1 и х2, у2, из W2 такие, что
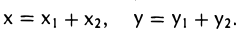
Это позволяет записать сумму х + у в следующем виде
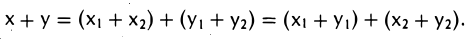
Так как 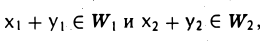
Аналогично доказывается включение ах ∈ W1 + W2.
2. Пересечение W1 ∩ W2 является линейным подпространством пространства V.
3. Если нулевой элемент является единственным общим вектором подпространств W1 й W2 линейного пространства V, то их сумма является прямой — W1 ⊕ W2.
Линейная оболочка
Линейной оболочкой L(X) подмножества X линейного пространства V называется совокупность всевозможных линейных комбинаций элементов из X,
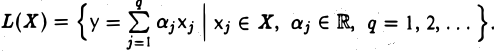
Последнее читается так: «линейная оболочка L(X) состоит из всевозможных элементов у, представимых в виде линейных комбинаций элементов множества X».
Основные свойства линейной оболочки
- Линейная оболочка L(X) содержит само множество X.
- L(X) — линейное подпространство пространства V.
Сумма линейных комбинаций элементов множества X и произведение линейной комбинации элементов на любое число снова являются линейными комбинациями элементов множества X.
3. L(X) — наименьшее линейное подпространство, содержащее множество X.
Это свойство следует понимать так: если линейное подпространство W содержит множество X , то W содержит и его линейную оболочку L(X).
Пусть W — линейное подпространство, содержащее заданное множество X. Тогда произвольная линейная комбинация 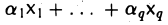
Пример:
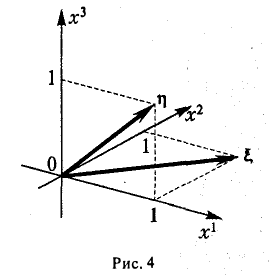
Рассмотрим в линейном пространстве R3 две тройки ξ = (1,1,0) и η = (1,0, I) (рис.4). Множество решений уравнения

является линейной оболочкой L(ξ , η) троек ξ и η.
Действительно, тройки (I, 1, 0) и (1, 0, I) образуют фундаментальную систему решений однородного уравнения (2), и значит, любое решение этого уравнения является их линейной комбинацией.
Пример:
Рассмотрим в линейном пространстве С(- ∞, ∞) вещественнозначных функций, непрерывных на всей числовой оси, набор X одночленов 1, х,…, хn:
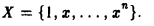
Линейная оболочка L(X) представляет собой совокупность многочленов с вещественными коэффициентами, степени которых не превосходят n.
Обозначение:
Линейная зависимость
Определение. Система элементов х1 . .. , хq линейного пространства V называется линейно зависимой, если найдутся числа a1,… , аq, не все равные нулю и такие, что
(1)
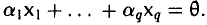
Если равенство (1) выполняется только при а1 = … = аq = 0, то система элементов x1,…, хq называется линейно независимой.
Справедливы следующие утверждения.
Теорема:
Система элементов x1,…, хq (q ≥ 2) линейно зависима в том и только в том случае, если хотя бы один из ее элементов можно представить в виде линейной комбинации остальных.
Предположим сначала, что система элементов x1,…, xq линейно зависима. Будем Считать для определенности, что в равенстве (1) отличен от нуля коэффициент аq. Перенося все слагаемые, кроме последнего, в правую часть, после деления на аq ≠ 0 получим, что элемент хq является линейной комбинацией элементов х1 …, хq:
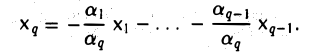
Обратно, если один из элементов равен линейной комбинации остальных,
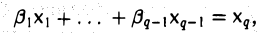
то, перенося его в левую часть, получим линейную комбинацию
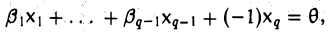
в которой есть отличные от нуля коэффициенты (-1 ≠ 0). Значит, система элементов x1,…., хq линейно зависима.
Теорема:
Пусть система элементов х1,…,хq линейно независима и y=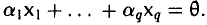
Пусть
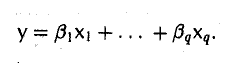
Тогда
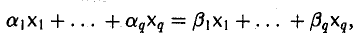
откуда
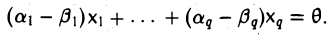
Из линейной независимости элементов x1…, xq вытекает, что a1 — β1 = … = аq — βq = 0 и, значит,
Теорема:
Система элементов, содержащая линейно зависимую подсистему, линейно зависима.
Пусть первые q элементов системы х1 … , хq, xq+1… , xm линейно зависимы. Тогда найдется линейная комбинация этих элементов такая, что
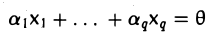
и не все коэффициенты а1 … ,аq равны нулю. Добавляя элементы xq+1… , xm с нулевыми множителями, получаем, что и в линейной комбинации
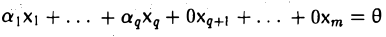
равны нулю не все коэффициенты.
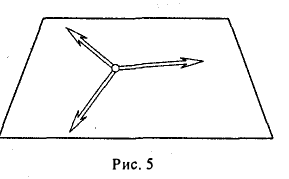
Пример. Векторы из V2 линейно зависимы тогда и только тогда, когда они компланарны (рис.5).
Базис. Размерность
Упорядоченная система элементов e1,…, еn линейного пространства V называется базисом этого линейного пространства, если элементы e1,…, еn линейно независимы и каждый элемент из V можно представить в виде их линейной комбинации. Упорядоченность означает здесь, что каждому элементу приписан определенный (порядковый) номер. Из одной системы п элементов можно построить n! упорядоченных систем.
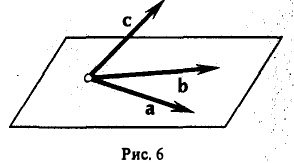
Пример:
Пусть a, b, с — тройка некомпланарных векторов из Vз (рис.6). Тогда упорядоченные тройки а, b, с; b, с, а; с, а, b; b, а, с; а, с, b и с, b, а — различные базисы V3.
Пусть с = (e1 … еn) — базис пространства V.
Тогда для любого элемента х из V найдется набор чисел 
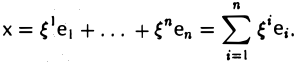
В силу теоремы 2 числа 
Посмотрим, что происходит с координатами элементов при простейших действиях с ними.
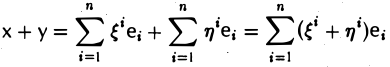
и для любого числа а
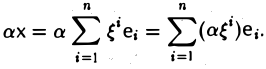
Таким образом, при сложении элементов их соответствующие координаты складываются, а при умножении элемента на число все его координаты умножаются на это число.
Координаты элемента часто удобно записывать в виде столбца. Например,
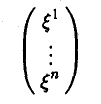
— координатный столбец элемента 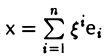
Разложим произвольную систему элементов x1,…, хq по базису e,
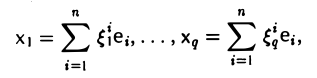
ли рассмотрим координатные столбцы элементов ч1,…, хq в этом базисе:
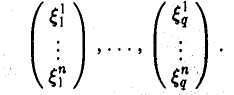
Теорема:
Система элементов х1,… ,хq линейно зависима тогда и только тогда, когда линейно зависима система их координатных столбцов в каком-нибудь базисе.
Пусть
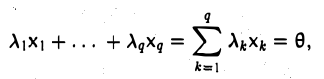
причем хотя бы один из коэффициентов λk отличен от нуля. Запишем это подробнее
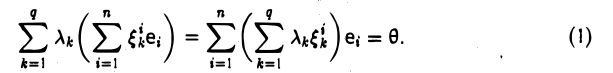
Отсюда в силу единственности разложения элемента по базису вытекает, что
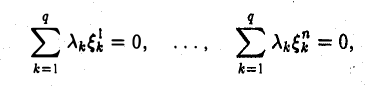
или, что тоже,
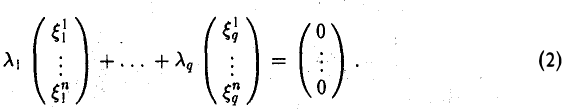
Таким образом, линейная комбинация координатных столбцов элементов x1,…, xq равна нулевому столбцу (с теми же коэффициентами λ1,…, λg). Это и означает, что система координатных столбцов линейно зависима.
Если же выполняется равенство (2), то, проводя рассуждения в обратном порядке, получаем формулу (1).
Тем самым, обращение в нуль некоторой нетривиальной (хотя бы один из коэффициентов отличен от нуля) линейной комбинации элементов линейного пространства равносильно тому, что нетривиальная линейная комбинация их координатных столбцов (с теми же коэффициентами) равна нулевому столбцу.
Теорема:
Пусть базис с линейного пространства V состоит из п элементов. Тогда всякая система из то элементов, где т > п, линейно зависима.
4 В силу теоремы 3 достаточно рассмотреть случай m = п + 1.
Пусть x1,.. . ,хп+1 — произвольные элементы пространства V. Разложим каждый элемент по базису e = (е1 …, еп):
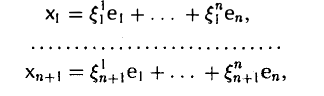
и запишем координаты элементов х1 …, xn+1 в виде матрицы, отводя j-й столбец координатам элемента xj, j = 1,…, п + 1. Получим матрицу из п строк и п + 1 столбцов —
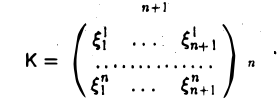
Ввиду того, что ранг матрицы К не превосходит числа п ее строк, столбцы матрицы К (их п + 1) линейно зависимы. А так как это координатные столбцы элементов x1…..хп+1, то согласно теореме 4 система элементов x1…..хп+1 также линейно зависима.
Следствие:
Все базисы линейного пространства V состоят из одинакового числа элементов.
Пусть базис e состоит из п элементов, а базис e’ из п‘ элементов. В силу только что доказанной теоремы из линейной независимости системы е’1,…, е’n заключаем, что п’ ≤ п. Меняя базисы e и e’ местами, в силу этой же теоремы получаем, что п ≤ п’.
Тем самым, п = п’.
Размерностью линейного пространства V называется число элементов базиса этого пространства.
Пример:
Базис координатного пространства R» образуют элементы
Система элементов e1,e2, …,еп линейно независима: из равенства
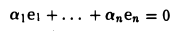
получаем, что
и значит, a1 = … = an = 0.
Кроме того, любой элемент 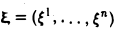
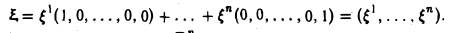
Тем самым, размерность пространства R» равна п.
Пример:
Однородная линейная система
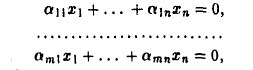
имеющая ненулевые решения, обладает фундаментальной системой решений (ФСР). ФСР является базисом линейного пространства решений однородной системы. Размерность этого линейного пространства равна числу элементов ФСР, т.е. п — r, где r — ранг матрицы коэффициентов однородной системы, an — число неизвестных.
Пример:
Размерность линейного пространства Мп многочленов степени не выше п равна п + I.
Так как всякий многочлен P(t) степени не выше п имеет вид
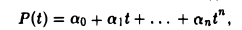
то достаточно показать линейную независимость элементов
Рассмотрим равенство
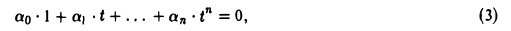
где t произвольно. Полагая t = 0, получаем, что ао = 0.
Продифференцируем равенство (3) по t:
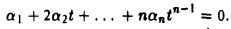
Вновь положив t = 0, получим, что a1 = 0.
Продолжая этот процесс, последовательно убеждаемся в том, что a0 = a1 = … = ап = 0. Это означает, что система элементов e1 = I,… ,en+1 = t» линейно независима. Следовательно, искомая размерность равна n + 1.
Линейное пространство, размерность которого равна п, называется п-мерным.
Обозначение: dim V = п.
Соглашение. Далее в этой главе всюду считается, если не оговорено противное, что размерность линейного пространства V равна п.
Ясно, что если W — подпространство n-мерного линейного пространства V, то dim W ≤ п.
Покажем, что в п-мерном линейном пространстве V есть линейные подпространства любой размерности k ≤ п.
Пусть e = (е1 … еn) — базис пространства V. Легко убедиться в том, что линейная оболочка
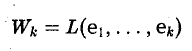
имеет размерность k.
По определению dim{ θ } = 0.
Теорема:
О пополнении базиса. Пусть система элементов а1.. , аk линейного пространства V размерности п линейно независима и к < п. Тогда в пространстве V найдутся элементы 

Пусть b — произвольный элемент линейного пространства V. Если система а1…. , аk, b линейно зависима, то

так как в нетривиальной линейной комбинации
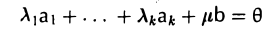
коэффициент μ ≠ 0 вследствие линейной независимости системы а1…., аk.
Если бы разложение вида (4) можно было бы написать для любого элемента b пространства V, то исходная система a1…, аk была бы базисом согласно определению. Но в силу условия k < п это невозможно. Поэтому должен существовать элемент 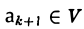
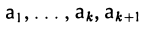
Если k + 1 = п, то эта система — базис пространства V.
Если k + 1 < п, то для системы 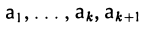
Таким способом любую заданную линейно независимую систему элементов можно достроить до базиса всего пространства V.
Пример:
Дополнить систему из двух векторов а1 = (1,2,0,1), а2 = (-1,1.1,0) пространства R4 до базиса этого пространства.
Возьмем в пространстве R4 векторы a3 = (1,0,0,0) и а4 = (0, 1,0,0) и покажем, что система векторов a1,а2,а3,а4 — базис R4.
Ранг матрицы

строками которой являются координаты векторов а1, а2, а3, а4, равен четырем. Это означает, что строки матрицы А, а, значит, и векторы а1, а2, а3, а4 линейно независимы.
Подобный подход используется и в общем случае: чтобы дополнить систему k линейно независимых элементов
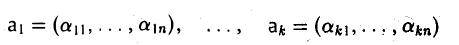
до базиса пространства R» , матрица
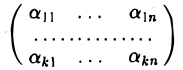
элементарными преобразованиями строк приводится к трапециевидной форме, а затем дополняется п — k строками вида
(0 … 1 … 0)
так, чтобы ранг получаемой матрицы был равен п. Справедливо следующее утверждение.
Теорема:
Пусть W1 и W2 — линейные подпространства линейного пространства V. Тогда
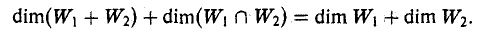
Замена базиса
Пусть e = (e1 … еn) и e’ = (е’1, … е’n) — базисы линейного пространства V. Разложим элементы базиса e’ по базису с. Имеем
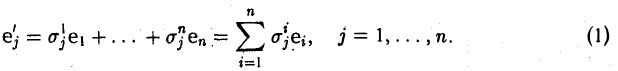
Эти соотношения удобно записать в матричной форме
(2)
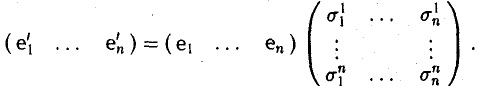
Матрица
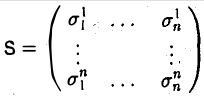
называется матрицей перехода от базиса e к базису e’.
Свойства матрицы перехода
- det S ≠ 0.
Доказательство этого свойства проводится от противного.
Из равенства detS = 0 вытекает линейная зависимость столбцов матрицы S. Эти столбцы являются координатными столбцами элементов е’1,…, е’n в базисе e. Поэтому (и вследствие теоремы 4) элементы е’1…..с’n должны быть линейно зависимыми.
Последнее противоречит тому, что e’ — базис. Значит, допущение, что det S = 0, неверно.
2. Если и 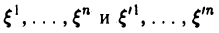
(3)
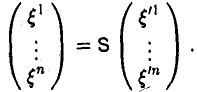
Заменяя в формуле
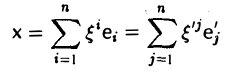
e’j их выражениями (1), получаем, что
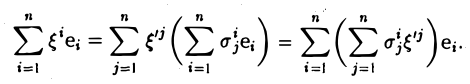
Отсюда в силу единственности разложения элемента по базису имеем
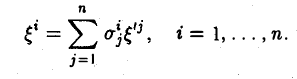
Переходя к матричной записи найденных равенств, убеждаемся в справедливости свойства 2.
3. S -1 — матрица перехода от базиса e’ к базису e.
Свойство 3 доказывается умножением обеих частей матричного равенства (2) на матрицу S-1 справа.
Евклидовы пространства
Вещественное линейное пространство V называется (вещественным) евклидовым пространством, если любым двум элементам х и у из V ставится в соответствие число, обозначаемое через (х,у), такое, что для любых элементов х, y,z и произвольного вещественного числа а выполняются следующие условия:
4. (х, х) ≥ 0; причем равенство нулю возможно в том и только в том случае, если х = θ.
Число (х, у) называется скалярным произведением элементов х и у. Примеры евклидовых пространств.
- В пространстве свободных векторов К] скалярное произведение векторов а и b определяется так:
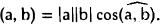
2. Скалярное произведение произвольных элементов 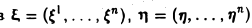
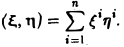
3, Линейное подпространство евклидова пространства само является евклидовым пространством.
Пользуясь определением евклидова пространства, нетрудно доказать следующие свойства:
Теорема:
Неравенство Коши—Буняковского. Для любых двух элементов х и у евклидова пространства V справедливо неравенство
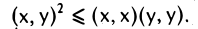
Если (х, х) = θ , то х = θ и неравенство выполняется вследствие того, что ( θ , у) = 0.
Обратимся к случаю (х, х) ≠ 0. Тогда (х, х) > 0. По определению скалярного произведения неравенство

справедливо для любых элементов х и у из пространства V и любого вещественного числа t. Запишем неравенство (1) подробнее:
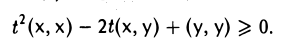
Левую часть последнего неравенства можно рассматривать как квадратный трехчлен относительно t. Из того, что знак этого квадратного трехчлена не изменяется при любых t, заключаем, что его дискриминант неположителен,
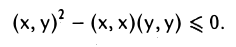
Перенося вычитаемое в правую часть, получаем требуемое неравенство.
Замечание:
Часто доказанное неравенство записывают в равносильной форме,
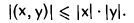
Следует подчеркнуть, что слева в этом неравенстве стоит абсолютная величина (модуль) скалярного произведения, а в правой части — нормы векторов х и у.
Определение:
Длиной (нормой) элемента х называется число |х|, вычисляемое по правилу
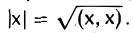
Ясно, что |х| ≥ 0 для любого х, причем равенство |х| = 0 возможно лишь в случае, если х = θ.
Рассмотрим цепочку равенств:
Заменяя второе слагаемое на 2|(х, у)| ≥ 2(х, у) и применяя неравенство Коши—Буняковского |(х,у)| ≤ |х| • |у|, получаем, что
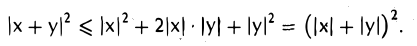
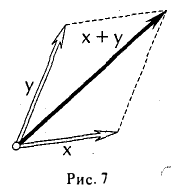
После извлечения квадратного корня приходим к неравенству треугольника:
|х + у| ≤ |х| + |у|
(рис.7).
Углом между ненулевыми элементами х и у евклидова пространства называется число φ, подчиненное следующим двум условиям:
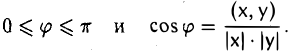
Определение угла корректно, так как согласно теореме 8 имеем
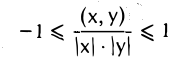
для любых ненулевых элементов х и у.
Элементы х и у называются ортогональными, если (х, у) = 0. Для ортогональных элементов из соотношения (2) вытекает равенство
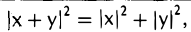
являющееся обобщением известной теоремы Пифагора’, квадрат длины суммы ортогональных элементов равен сумме квадратов их длин (рис. 8).
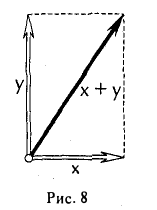
Система элементов f1…..f k называется ортогональной, если (fi, fj) =0′ при i ≠ j, и ортонормированной, если
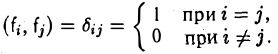
Определение:
Символ
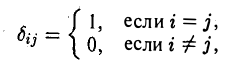
называют символом Кронекера.
Теорема:
Ортонормированная система элементов линейно независима.
Умножая обе части равенства
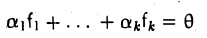
скалярно на элемент fj, j = 1 ,… ,k, получаем, что
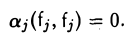
И так как (fj, fj) = 1,то aj = 0, j = 1,…, k.
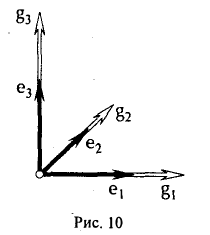
Метод ортогонализации
Покажем, как, пользуясь заданной системой линейно независимых элементов f1,… ,fk евклидова пространства Е, построить в нем ортонормированную систему из к элементов.
Положим g1 = f1.
Для того, чтобы элемент
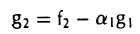
был ортогонален элементу g1, необходимо выполнение следующего равенства:
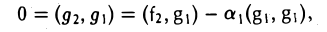
откуда
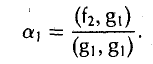
Тем самым, элемент
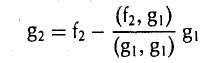
ортогонален элементу g1 (рис. 9 а).
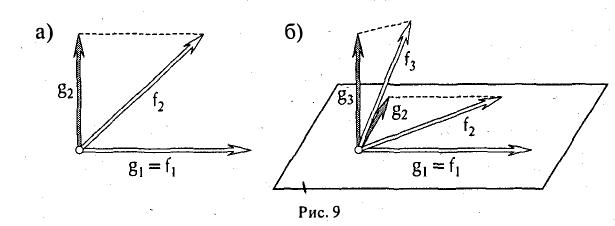
Пользуясь построенными элементами g1, g2 и заданным элементом fз, построим элемент
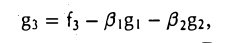
ортогональный как элементу g1, так и элементу g2. Для этого коэффициенты β1 и β2 должны удовлетворять следующим условиям:
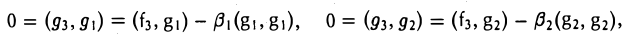
откуда
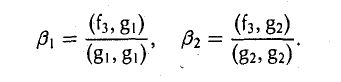
Таким образом, элемент
, (f3,g|) (f3,g2)
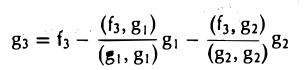
ортогонален элементам g1 и g2 (рис. 9 6).
Аналогичными рассуждениями можно показать, что элемент
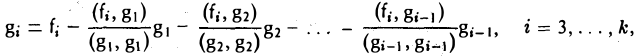
ортогонален элементам
Делением каждого элемента gi (i = 1…..k) на его длину |g<|, получаем ортонормированную систему
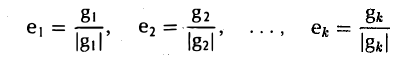
(рис. 10).
Базис e = (e1 … еn) евклидова пространства называется ортонормированным, или ортобазисом, если
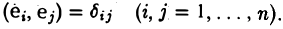
Суммируя вышеизложенное, получаем следующий результат.
Теорема:
В любом евклидовом пространстве существует о ртонормированный базис.
Пример:
Методом ортогонализации построить ортоиормированный базис евклидова пространства Е по его базису
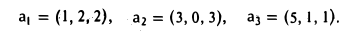
Полагаем b1 = a1 и b2 = а2 — ab1. Для того, чтобы вектор
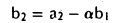
был ортогонален вектору b1, необходимо выполнение неравенства
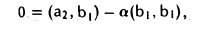
откуда
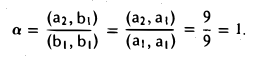
Тем самым,
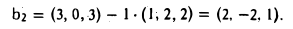
Для того, чтобы вектор
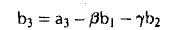
был ортогонален векторам b1 и b2, необходимо выполнение равенств
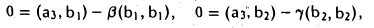
откуда
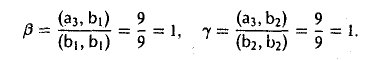
Тем самым, вектор
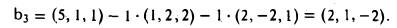
Система векторов b1, b2, b3 ортогональна. Поделив каждый вектор на его длину, получим
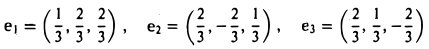
— ортонормированный базис пространства Е.
При помощи ортонормированного базиса скалярное произведение элементов вычисляется особенно просто. Пусть e = (e1 … еn) — ортонормированный базис пространства Е. Вычислим скалярное произведение элементов х и у, предварительно разложив их по базису e
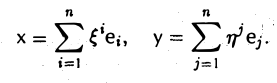
Имеем
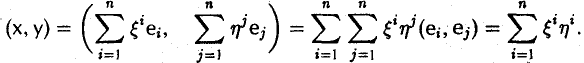
В частности,
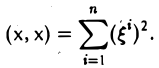
Откуда
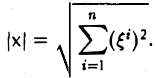
Ортогональное дополнение
Пусть W — линейное подпространство евклидова пространства V. Совокупность W⊥ элементов у пространства V, обладающих свойством
(y. х) = 0,
где х — произвольный элемент из W, называется ортогональным дополнением подпространства W. Другими словами, ортогональное дополнение W⊥ состоит из всех элементов у, ортогональных всем элементам подпространства W.
Свойства ортогонального дополнения
- W⊥ — линейное подпространство пространства V. Пусть элементы y1, у2 лежат в W⊥ , т. е.
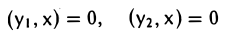
для любого элемента х из W. Складывая эти равенства и пользуясь свойствами скалярного произведения, получаем,что
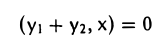
для любого элемента х из W. Это означает, что
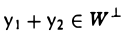
Из того, что (у, х) = 0 для любого элемента х из W, вытекает равенство (ау, х) = а(у, х) и, значит, включение ay ∈ W⊥ .
- V = W ⊕ W⊥ .
Свойство 2 означает, что любой элемент х пространства V можно представить, причем единственным образом, в виде суммы элементов из W и W⊥ :
x = y+z. ‘ (*)
Элемент у ∈ W называется ортогональной проекцией элемента х на линейное подпространство W, а элемент z ∈ W⊥ — его ортогональной составляющей (рис. 11).
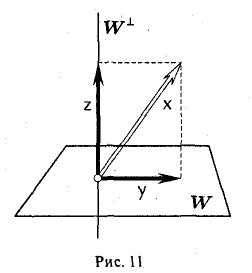
Покажем, как по заданным элементу х и линейному подпространству W найти его ортогональную проекцию у и ортогональную составляющую г.
Можно считать, что в линейном подпространстве W задан ортонормированный базис e1…..еk. Запишем искомый элемент у в виде линейной комбинации
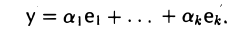
Подставляя это выражение в формулу (*):

и умножая обе части полученного равенства последовательно на элементы e1,…, еk, в предположении z ⊥ W приходим к соотношениям
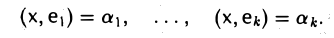
Элементы
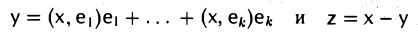
обладают требуемыми свойствами. *
Пример:
Найти ортогональную проекцию вектора х = (4, 2, 3, 5) на линейное подпространство W ⊂ R4, заданное системой уравнений
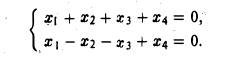
Векторы a1 = (1,0,0,-1) и а2 = (0,1,-1,0) образуют фундаментальную систему решений и, следовательно, базис подпространства W. Кроме того, векторы a1 и а2 ортогональны. Для того, чтобы построить ортонормированный базис подпространства W, достаточно разделить эти векторы на иx длины. В результате получим
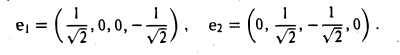
Вектор
является ортогональной проекцией вектора х = (4,2, 3, 5), на подпространство W, а вектор
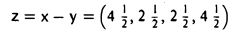
— его ортогональной составляющей.
Унитарные пространства
Унитарным пространством называется линейное комплексное пространство U, в котором каждой упорядоченной паре элементов х и у из U ставится в соответствие число — скалярное произведение (х, у) так, что для любых элементов х, у и z из U и любого комплексного числа а выполняются следующие соотношения:
- (у, х) = (х, у) (черта в правой части указывает на операцию комплексного сопряжения);
- (x + y,z) = (x,z) + (y,z);
- (ах, у) = а(х, у);
- (х, х) ≥ 0, причем равенство (х, х) = 0 возможно лишь в случае, если х = θ.
Пример:
В координатном пространстве Сn, элементами которого являются всевозможные упорядоченные наборы п комплексных чисел, скалярное произведение можно ввести так
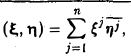
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат


 в совокупности образовывали базис во всём пространстве. Тогда нужно просто разложить вектор
в совокупности образовывали базис во всём пространстве. Тогда нужно просто разложить вектор  по этому базису. Та часть разложения, которая складывается из векторов
по этому базису. Та часть разложения, которая складывается из векторов  и из
и из  , и проекция не будет определена.
, и проекция не будет определена.