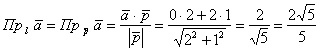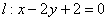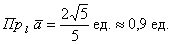Как найти проекцию вектора на прямую если - Исправление недочетов и поиск решений вместе с Examum.ru

2.5.8. Как найти проекцию вектора на прямую?

Об ортогональной проекции вектора на вектор мы говорили ранее, и фактически было установлено

следующее:

Чтобы найти ортогональную проекцию вектора на прямую, нужно найти его проекцию на любой направляющий вектор этой прямой.

…возможно, не всем понятен термин «ортогональная» – это такая проекция, при которой на вектор «падают лучи света» строго

перпендикулярно по отношению к прямой (см. рис. ниже). Существует куча иных («косых») проекций, когда проецирование осуществляется под

другими углами, но для данной книги этот материал не столь актуален.

Решим символическую задачку:

Задача 85

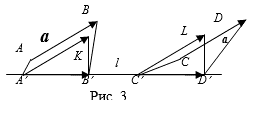
Найти проекцию вектора на прямую

Решение: найдём какой-нибудь направляющий вектор прямой, проще и быстрее

взять стандартный вариант: .
Проекция вектора на прямую – есть его проекция на любой направляющий вектор этой прямой, по

соответствующей формуле:

Ответ:

Напоминаю, что проекция – это длина «тени» вектора (красный цвет):

Желающие могут взять любые точки прямой, найти направляющий вектор и убедиться в том, что проекция будет такой же, как вариант, со знАком «минус».

Ну вот и подошло к концу наше путешествие по основным задачам с «плоской» прямой, и никакого Кащея Бессмертного тут нет…. – Здесь есть я, с

новыми знаниями и задачами J Потому что Бабу-Ягу никто не отменял =)

2.6. Линейные неравенства

2.5.7. Как найти угол между прямыми?

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

2.5.8. Как найти проекцию вектора на прямую?

Об ортогональной проекции вектора на вектор мы говорили ранее, и фактически было установлено следующее:

…возможно, не всем понятен термин «ортогональная» – это такая проекция, при которой на вектор «падают лучи света» строго перпендикулярно по отношению к прямой (см. рис. ниже). Существует куча иных («косых») проекций, когда проецирование осуществляется под другими углами, но для данной книги этот материал не столь актуален.

Решим символическую задачку:

Задача 85

Найти проекцию вектора 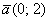на прямую

Решение: найдём какой-нибудь направляющий вектор прямой, проще и быстрее взять стандартный вариант: .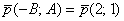
Проекция вектора на прямую – есть его проекция на любой направляющий вектор этой прямой, по соответствующей формуле:

Ответ:

Напоминаю, что проекция – это длина «тени» вектора (красный цвет):

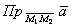
Ну вот и подошло к концу наше путешествие по основным задачам с «плоской» прямой, и никакого Кащея Бессмертного тут нет…. – Здесь есть я, с новыми знаниями и задачами J Потому что Бабу-Ягу никто не отменял =)

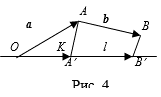
Проекции векторов на прямую и на плоскость

Проекция вектора на прямую

Пусть на плоскости задана прямая и пересекающая ее прямая . Проекцией вектора на прямую параллельно прямой (вдоль прямой ) называется вектор , началом которого служит проекция , начала , а концом — проекция конца вектора (рис.1.13,а). Если прямая перпендикулярна прямой , то проекция называется ортогональной.

Пусть в пространстве дана прямая и пересекающая ее плоскость . Проекцией вектора на прямую параллельно плоскости (вдоль плоскости ) называется вектор , началом которого служит проекция , начала , а концом — проекция конца вектора (рис. 1.13,6). Если плоскость перпендикулярна прямой , то проекция называется ортогональной.

Проекция вектора на плоскость

Пусть в пространстве задана плоскость я и пересекающая ее прямая . Проекцией вектора на плоскость параллельно прямой (вдоль прямой ) называется вектор , началом которого служит проекция начала , а концом — проекция конца вектора (рис. 1.14). Если прямая перпендикулярна плоскости , то проекция называется ортогональной.

Свойства проекций векторов

1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.

2. Проекции равных векторов равны.

3. Проекция суммы векторов равна сумме их проекций.

4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, другими словами, отношение коллинеарных векторов равно отношению их проекций (если оно определено).

5. Проекция линейной комбинации векторов равна линейной комбинации проекций.

Рассмотрим эти свойства для проекций векторов на прямую параллельно прямой . Для проекций векторов на плоскость или на прямую параллельно плоскости доказательства аналогичные.

Докажем первое свойство. Пусть — проекция вектора на прямую вдоль прямой , а — проекция вектора на прямую вдоль той же прямой , причем прямые и параллельные (рис. 1.15). Четырехугольник, образованный пересечением пары параллельных прямых и штриховыми линиями, параллельными прямой , является параллелограммом. Следовательно, , т.е. проекции одного и того же вектора на параллельные прямые равны.

Докажем второе свойство. Пусть на плоскости даны равные векторы и , не параллельные прямой (см. рис. 1.16). Построим равные им векторы и . Из равенства следует, что четырехугольник — параллелограмм, а треугольники и равны по стороне и двум прилежащим углам

как углы с соответственно параллельными сторонами). Следовательно, , т.е. равные векторы, не параллельные прямой , имеют равные проекции. Если же векторы параллельны прямой , то их проекции также равны, как нулевые векторы. Второе свойство доказано.

Доказательство третьего свойства очевидно для векторов и (рис. 1.17): проекция вектора равна сумме проекций и , векторов и , т.е. . Для произвольных векторов и (у которых конец вектора не совпадает с началом вектора ) доказательство сводится к рассмотренному случаю для равных им векторов и , так как равные векторы имеют равные проекции (по второму свойству).

Доказательство четвертого свойства следует из теоремы Фалеса (см. разд. В.2). На рис.1.18 изображены векторы и 0)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEAAAAAWBAMAAACCkIcHAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAvWZBmjHwIdCB4BFRAWKYcvQAAAFOSURBVCjPY2AgDHgm4JK5EgCmAjcwcAphSPIaX2DgXgpicS8G8vwU0BWEuQDFLUAsTgEgUSeAJs+exHCugOEWSN+1A0CC4zVYOKQApoDlLQObAwPTWiDz3AYgwfQILMwsEgBVwNHLcHEtA+tTIHPGBSBx+8UFiApBW4iCe7IMF98y8CYBmYJgATmo4eyOtjAFjE8ZeIGSvCJgAT0HqO+ue+mCaDsBBsbHYN28K0F8pmVrYc67PQPk6n1QBRcYeDtBomohj2EKuMEKQFYAfeZ4AWIF02OeJ7AAmAG24lYvA2MuxIEgrKfAuwziDXYPSJheecBwTQDsSJA3mYDa/UAGM7BCPcHA+obBzoCBNxPk3g0M9xyggQ0PBqCrlIBhwA5y2a0DDKwgsw1QgpqBXQnIZsqFRRYOcAOUVLhTcSuwgiQYnPLcrQSSHIsBESkWAKi0S8GJu/2KAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, а также их проекции и . По теореме Фалеса , следовательно, , что и требовалось доказать. В случае доказательство аналогичное.

Пятое свойство проекций следует из третьего и четвертого.

Теорема 1.1 (о проекциях вектора на пересекающиеся прямые).

1. Если на плоскости заданы две пересекающиеся прямые и , то любой вектор на плоскости можно однозначно представить в виде суммы своих проекций и на эти прямые (проекции на каждую прямую берутся вдоль другой прямой), т.е. .

2. Если в пространстве заданы три прямые и , пересекающиеся в одной точке и не лежащие в одной плоскости, то любой вектор в пространстве можно однозначно представить в виде суммы своих проекций на эти прямые (проекции на каждую прямую берутся вдоль плоскости, содержащей две другие прямые), т.е. .

В самом деле, пусть прямые и пересекаются в точке (рис.1.19,а). Приложим вектор к точке , т.е. рассмотрим вектор . По правилу параллелограмма сложения векторов (см. разд. 1.2) получаем равенство , которое равносильно доказываемому равенству , так как равные векторы имеют равные проекции (см. свойство 2 проекций). Единственность представления следует из однозначности нахождения проекций вектора.

Если же вектор коллинеарен одной из прямых, например , то соответствующие проекции имеют вид: и равенство , очевидно, выполняется.

Аналогично доказывается второе утверждение.

Справедливы утверждения, обратные к указанным в теореме 1.1.

Если вектор на плоскости равен сумме двух неколлинеарных векторов, т.е. , то слагаемые и являются проекциями вектора на прямые, содержащие векторы и соответственно.

Если вектор в пространстве равен сумме трех некомпланарных векторов, т.е. , то слагаемые и являются проекциями вектора на прямые, содержащие векторы соответственно.

В самом деле, отложим от произвольной точки векторы (рис.1.19,6). Тогда из равенства следует, что , т.е. вектор — является диагональю параллелепипеда, построенного на векторах (отсюда следует правило параллелепипеда сложения трех некомпланарных векторов). Поэтому — проекции вектора на прямые (проекция на каждую прямую берется вдоль плоскости, проходящей через две другие прямые). Так как равные векторы и имеют равные проекции (свойство 2), заключаем, что проекции вектора на прямые равны соответственно. Наконец, проекции на прямые равны проекциям на параллельные им прямые, содержащие векторы соответственно.

Пример 1.5. Если прямая пересекает стороны треугольника (или их продолжения) в точках соответственно, то

Решение. Найдем отношения проекций векторов на прямую вдоль прямой (рис. 1.20). Для этого через точку проведем прямую , параллельную прямой . По свойству 4 проекций имеем:

Перемножая эти пропорции, получаем , что равносильно доказываемому равенству.

Заметим, что доказанное утверждение является частью теоремы Менелая.

Пример 1.6. Если на сторонах треугольника взяты соответственно точки так, что прямые пересекаются в одной точке, то

Решение. Пусть прямые пересекаются в точке (рис.1.21). Через точку проведем прямые и параллельно и соответственно. По свойству проекций (свойство 4):

Учитывая эти равенства и свойства отношений коллинеарных векторов (см, разд.1.2.1), преобразуем левую и правую части последнего равенства:

Запишем произведение правых частей этих равенств, учитывая, что произведение левых частей равно единице:

Найдем обратное отношение , что и требовалось доказать.

Заметим, что доказанное утверждение является частью теоремы Чевы.

Проекция точки на прямую, координаты проекции точки на прямую

Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.

Проекция точки на прямую, определение

В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.

Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.

Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.

Рассмотрим рисунок ниже: точка H 1 служит проекцией точки М 1 на прямую a , а точка М 2 , принадлежащая прямой, является проекцией сама себя.

Данное определение верно для случая на плоскости и в трехмерном пространстве.

Чтобы на плоскости получить проекцию точки М 1 на прямую a , проводится прямая b , проходящая через заданную точку M 1 и перпендикулярная прямой a . Таким образом, точка пересечения прямых a и b будет проекцией точки М 1 на прямую a .

В трехмерном пространстве проекцией точки на прямую будет служить точка пересечения прямой a и плоскости α , проходящей через точку М 1 и перпендикулярной прямой a .

Нахождение координат проекции точки на прямую

Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.

Пусть нам заданы прямоугольная система координат O x y , точка М 1 ( x 1 , y 1 ) и прямая a . Необходимо найти координаты проекции точки М 1 на прямую a .

Проложим через заданную точку М 1 ( x 1 , y 1 ) прямую b перпендикулярно прямой a . Точку пересечения маркируем как H 1 . Точка Н 1 будет являться точкой проекции точки М 1 на прямую a .

Из описанного построения можно сформулировать алгоритм, который позволяет находить координаты проекции точки М 1 ( x 1 , y 1 ) на прямую a :

— составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;

— записываем уравнение прямой b (проходящей через точку М 1 и перпендикулярной прямой a ). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;

— определяем искомые координаты проекции как координаты точки пересечения прямых a и b . Для этого решаем систему уравнений, составляющие которой – уравнения прямых a и b .

На плоскости O x y заданы точки М 1 ( 1 , 0 ) и прямая a (общее уравнение – 3 x + y + 7 = 0 ). Необходимо определить координаты проекции точки М 1 на прямую a .

Решение

Уравнение заданной прямой известно, поэтому, согласно алгоритму, переходим к шагу записи уравнения прямой b . Прямая b перпендикулярна прямой a , а значит нормальный вектор прямой a служит направляющим вектором прямой b . Тогда направляющий вектор прямой b запишем как b → = ( 3 , 1 ) . Запишем и каноническое уравнение прямой b , поскольку нам также заданы координаты точки М 1 , через которую проходит прямая b :

Заключительным шагом определяем координаты точки пересечения прямых a и b . Перейдем от канонических уравнений прямой b к общему ее уравнению:

x — 1 3 = y 1 ⇔ 1 · ( x — 1 ) = 3 · y ⇔ x — 3 y — 1 = 0

Составим систему уравнений из общих уравнений прямых a и b и решим ее:

3 x + y + 7 = 0 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 · ( — 3 x — 7 ) — 1 = 0 ⇔ ⇔ y = — 3 x — 7 x = — 2 ⇔ y = — 3 · ( — 2 ) — 7 x = — 2 ⇔ y = — 1 x = — 2

В конечном итоге мы получили координаты проекции точки М 1 ( 1 , 0 ) на прямую 3 x + y + 7 = 0 : ( — 2 , — 1 ) .

Ответ: ( — 2 , — 1 ) .

Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.

Пусть заданы координатные прямые O x и O y , а также точка М 1 ( x 1 , y 1 ) . Понятно, что проекцией заданной точки на координатную прямую O x вида y = 0 будет точка с координатами ( x 1 , 0 ) . Так и проекция заданной точки на координатную прямую O y будет иметь координаты 0 , y 1 .

Любую произвольную прямую, параллельную оси абсцисс, возможно задать неполным общим уравнением B y + C = 0 ⇔ y = — C B , а прямую, параллельную оси ординат — A x + C = 0 ⇔ x = — C A.

Тогда проекциями точки М 1 ( x 1 , y 1 ) на прямые y = — C B и x = — C A станут точки с координатами x 1 , — C B и — C A , y 1 .

Определите координаты проекции точки М 1 ( 7 , — 5 ) на координатную прямую O y , а также на прямую, параллельную прямой O y 2 y — 3 = 0 .

Решение

Запишем координаты проекции заданной точки на прямую O y : ( 0 , — 5 ) .

Запишем уравнение прямой 2 y — 3 = 0 в виде y = 3 2 . Становится видно, что проекция заданной точки на прямую y = 3 2 будет иметь координаты 7 , 3 2 .

Ответ: ( 0 , — 5 ) и 7 , 3 2 .

Пусть в трехмерном пространстве заданы прямоугольная система координат O x y z , точка М 1 ( x 1 , y 1 , z 1 ) и прямая a . Найдем координаты проекции точки М 1 на прямую a .

Построим плоскость α , проходящую через точку М 1 и перпендикулярную прямой a . Проекцией заданной точки на прямую a станет точка пересечения прямой a и плоскости α . Исходя из этого, приведем алгоритм для нахождения координат проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a :

— запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;

— составим уравнение плоскости α , проходящей через точку М 1 и перпендикулярной прямой a (см. статью «Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой»);

— найдем искомые координаты проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a – это будут координаты точки пересечения прямой α и плоскости α (в помощь – статья «Координаты точки пересечения прямой и плоскости»).

Задана прямоугольная система координат O x y z , и в ней – точка М 1 ( 0 , 1 , — 1 ) и прямая a . Прямой a соответствуют канонические уравнения вида: x + 2 3 = y — 6 — 4 = z + 1 1 . Определите координаты проекции точки М 1 на прямую a .

Решение

Используем указанный выше алгоритм. Уравнения прямой a известны, поэтому первый шаг алгоритма пропускаем. Запишем уравнение плоскости α . Для этого определим координаты нормального вектора плоскости α . Из заданных канонических уравнений прямой a выделим координаты направляющего вектора этой прямой: ( 3 , — 4 , 1 ) , который будет являться нормальным вектором плоскости α , перпендикулярной прямой a . Тогда n → = ( 3 , — 4 , 1 ) – нормальный вектор плоскости α . Таким образом, уравнение плоскости α будет иметь вид:

3 · ( x — 0 ) — 4 · ( y — 1 ) + 1 · ( z — ( — 1 ) ) = 0 ⇔ 3 x — 4 y + z + 5 = 0

Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:

Заданные канонические уравнения позволяют получить уравнения двух пересекающихся плоскостей, определяющих прямую a :

x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ — 4 · ( x + 2 ) = 3 · ( y — 6 ) 1 · ( x + 2 ) = 3 · ( z + 1 ) 1 · ( y — 6 ) = — 4 · ( z + 1 ) ⇔ 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0

Чтобы найти точки пересечения прямой 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 и плоскости 3 x — 4 y + z + 5 = 0 , решим систему уравнений:

4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 3 x — 4 y + z + 5 = 0 ⇔ 4 x + 3 y = 10 x — 3 z = 1 3 x — 4 y + z = — 5

В данном случае используем метод Крамера, но возможно применить любой удобный:

∆ = 4 3 0 1 0 — 3 3 — 4 1 = — 78 ∆ x = 10 3 0 1 0 — 3 — 5 — 4 1 = — 78 ⇒ x = ∆ x ∆ = — 78 — 78 = 1 ∆ y = 4 10 0 1 1 — 3 3 — 5 1 = — 156 ⇒ y = ∆ y ∆ = — 156 — 78 = 2 ∆ z = 4 3 10 1 0 1 3 — 4 — 5 = 0 ⇒ z = ∆ z ∆ = 0 — 78 = 0

Таким образом, проекцией заданной точки на прямую a является точка c координатами ( 1 , 2 , 0 )

На основе заданных канонических уравнений легко записать параметрические уравнения прямой в пространстве:

x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ x = — 2 + 3 · λ y = 6 — 4 · λ z = — 1 + λ

Подставим в уравнение плоскости, имеющее вид 3 x — 4 y + z + 5 = 0 , вместо x , y и z их выражения через параметр:

3 · ( — 2 + 3 · λ ) — 4 · ( 6 — 4 · λ ) + ( — 1 + λ ) + 5 = 0 ⇔ 26 · λ = 0 ⇔ λ = 1

Вычислим искомые координаты точки пересечения прямой a и плоскости α по параметрическим уравнениям прямой a при λ = 1 :

x = — 2 + 3 · 1 y = 6 — 4 · 1 z = — 1 + 1 ⇔ x = 1 y = 2 z = 0

Таким образом, проекция заданной точки на прямую a имеет координаты ( 1 , 2 , 0 )

Ответ: ( 1 , 2 , 0 )

Напоследок отметим, что проекциями точки М 1 ( x 1 , y 1 , z 1 ) на координатные прямые O x , O y и O z буду являться точки с координатами ( x 1 , 0 , 0 ) , ( 0 , y 1 , 0 ) и ( 0 , 0 , z 1 ) соответственно.

источники:

http://mathhelpplanet.com/static.php?p=proektsii-vektorov-na-pryamuyu-i-na-ploskost

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/proektsija-tochki-na-prjamuju-koordinaty-proektsii/

Источник

Проекции векторов на прямую и на плоскость

Проекция вектора на прямую

Пусть на плоскости задана прямая и пересекающая ее прямая . Проекцией вектора vec{a}=overrightarrow{AB} на прямую параллельно прямой (вдоль прямой ) называется вектор $vec{a}_l=overrightarrow{AB}_l$ , началом которого служит проекция A_l , начала , а концом — проекция B_l конца вектора (рис.1.13,а). Если прямая перпендикулярна прямой , то проекция называется ортогональной.

Пусть в пространстве дана прямая и пересекающая ее плоскость rho . Проекцией вектора vec{a}=overrightarrow{AB} на прямую параллельно плоскости rho (вдоль плоскости rho ) называется вектор $vec{a}_l=overrightarrow{AB}_l$ , началом которого служит проекция A_l , начала , а концом — проекция B_l конца вектора (рис. 1.13,6). Если плоскость rho перпендикулярна прямой , то проекция называется ортогональной.

Проекция вектора на прямую

Проекция вектора на плоскость

Пусть в пространстве задана плоскость я и пересекающая ее прямая rho . Проекцией вектора vec{a}=overrightarrow{AB} на плоскость rho параллельно прямой (вдоль прямой ) называется вектор $vec{a}_{rho}=overrightarrow{AB}_{rho}$ , началом которого служит проекция $A_{rho}$ начала , а концом — проекция $B_{rho}$ конца вектора (рис. 1.14). Если прямая перпендикулярна плоскости rho , то проекция называется ортогональной.

Свойства проекций векторов

1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.

2. Проекции равных векторов равны.

3. Проекция суммы векторов равна сумме их проекций.

5. Проекция линейной комбинации векторов равна линейной комбинации проекций.

Докажем первое свойство. Пусть $vec{a}_l$ — проекция вектора vec{a} на прямую вдоль прямой , а $vec{a}_l$ — проекция вектора vec{a} на прямую вдоль той же прямой , причем прямые и параллельные (рис. 1.15). Четырехугольник, образованный пересечением пары параллельных прямых и штриховыми линиями, параллельными прямой , является параллелограммом. Следовательно, $vec{a}_{l'}=vec{a}_l$ , т.е. проекции одного и того же вектора vec{a} на параллельные прямые равны.

Проекции векторов на параллельные прямые

Докажем второе свойство. Пусть на плоскости даны равные векторы overrightarrow{AB} и overrightarrow{CD} , не параллельные прямой (см. рис. 1.16). Построим равные им векторы $mathop{overrightarrow{A_lB'}= overrightarrow{AB}}limits_{.}$ и $mathop{overrightarrow{C_lD'}= overrightarrow{CD}}limits_{.}$ . Из равенства $mathop{overrightarrow{A_lB'}= overrightarrow{C_lD'}}limits_{.}$ следует, что четырехугольник A_lB'D'C_l — параллелограмм, а треугольники A_lB'B_l и C_lD'D_l равны по стороне и двум прилежащим углам

big(A_lB'=C_lD',qquad angle B'A_lB_l=angle D'C_lD_l,qquad angle A_lB'B_l=angle C_lD'D_l

как углы с соответственно параллельными сторонами). Следовательно, $mathop{overrightarrow{A_lB_l}= overrightarrow{C_lD_l}}limits_{.}$ , т.е. равные векторы, не параллельные прямой , имеют равные проекции. Если же векторы параллельны прямой , то их проекции также равны, как нулевые векторы. Второе свойство доказано.

Доказательство третьего свойства очевидно для векторов overrightarrow{AB} и overrightarrow{BC} (рис. 1.17): проекция $overrightarrow{A_lC_l}$ вектора overrightarrow{AC}=overrightarrow{AB}+overrightarrow{BC} равна сумме проекций $overrightarrow{A_lB_l}$ и $overrightarrow{B_lC_l}$ , векторов и , т.е. $overrightarrow{A_lC_l}= overrightarrow{A_lB_l}+ overrightarrow{B_lC_l}$ . Для произвольных векторов vec{a} и vec{b} (у которых конец вектора vec{a} не совпадает с началом вектора vec{b} ) доказательство сводится к рассмотренному случаю для равных им векторов overrightarrow{AB}=vec{a} и overrightarrow{BC}=vec{b} , так как равные векторы имеют равные проекции (по второму свойству).

Доказательство четвертого свойства следует из теоремы Фалеса (см. разд. В.2). На рис.1.18 изображены векторы overrightarrow{AB} и overrightarrow{AC}=lambdaoverrightarrow{AB} (lambda>0) , а также их проекции $overrightarrow{A_lB_l}$ и $overrightarrow{A_lC_l}$ . По теореме Фалеса $frac{AC}{AB}=frac{A_lC_l}{A_lB_l}=lambda$ , следовательно, $overrightarrow{A_lC_l}= lambdaoverrightarrow{A_lB_l}$ , что и требовалось доказать. В случае lambda<0 доказательство аналогичное.

Пятое свойство проекций следует из третьего и четвертого.

Векторы и их проекции

Теорема 1.1 (о проекциях вектора на пересекающиеся прямые).

1. Если на плоскости заданы две пересекающиеся прямые l_1 и l_2 , то любой вектор vec{a} на плоскости можно однозначно представить в виде суммы своих проекций $vec{a}_1$ и $vec{a}_2$ на эти прямые (проекции на каждую прямую берутся вдоль другой прямой), т.е. $vec{a}=vec{a}_1+vec{a}_2$ .

2. Если в пространстве заданы три прямые l_1,l_2 и l_3 , пересекающиеся в одной точке и не лежащие в одной плоскости, то любой вектор vec{a} в пространстве можно однозначно представить в виде суммы своих проекций $vec{a}_1,vec{a}_2,vec{a}_3$ на эти прямые (проекции на каждую прямую берутся вдоль плоскости, содержащей две другие прямые), т.е. $vec{a}=vec{a}_1+vec{a}_2+vec{a}_3$ .

В самом деле, пусть прямые l_1 и l_2 пересекаются в точке (рис.1.19,а). Приложим вектор vec{a} к точке , т.е. рассмотрим вектор overrightarrow{OA}=vec{a} . По правилу параллелограмма сложения векторов (см. разд. 1.2) получаем равенство $overrightarrow{OA}=vec{a}_1+vec{a}_2$ , которое равносильно доказываемому равенству $vec{a}=vec{a}_1+vec{a}_2$ , так как равные векторы имеют равные проекции (см. свойство 2 проекций). Единственность представления следует из однозначности нахождения проекций вектора.

Если же вектор vec{a} коллинеарен одной из прямых, например l_1 , то соответствующие проекции имеют вид: $vec{a}_1=vec{a},~vec{a}_2=vec{o}$ и равенство $vec{a}=vec{a}_1+vec{a}_2=vec{a}+vec{o}$ , очевидно, выполняется.

Аналогично доказывается второе утверждение.

Проекции вектора на пересекающиеся прямые

Замечание 1.3.

Справедливы утверждения, обратные к указанным в теореме 1.1.

Если вектор на плоскости равен сумме двух неколлинеарных векторов, т.е. $vec{a}=vec{a}_1+vec{a}_2$ , то слагаемые $vec{a}_1$ и $vec{a}_2$ являются проекциями вектора vec{a} на прямые, содержащие векторы $vec{a}_1$ и $vec{a}_2$ соответственно.

Если вектор в пространстве равен сумме трех некомпланарных векторов, т.е. $vec{a}=vec{a}_1+vec{a}_2+vec{a}_3$ , то слагаемые $vec{a}_,vec{a}_2$ и $vec{a}_3$ являются проекциями вектора vec{a} на прямые, содержащие векторы $vec{a}_,vec{a}_2,vec{a}_3$ соответственно.

В самом деле, отложим от произвольной точки векторы $overrightarrow{OA}=vec{a},,overrightarrow{OA_1}=vec{a}_1,,overrightarrow{OA_2}=vec{a}_2,,overrightarrow{OA_3}=vec{a}_3$ (рис.1.19,6). Тогда из равенства $vec{a}=vec{a}_1+vec{a}_2+vec{a}_3$ следует, что $overrightarrow{OA}=overrightarrow{OA_1}+overrightarrow{OA_2}+overrightarrow{OA_3}$ , т.е. вектор — является диагональю параллелепипеда, построенного на векторах $overrightarrow{OA_1},,overrightarrow{OA_2},,overrightarrow{OA_3}$ (отсюда следует правило параллелепипеда сложения трех некомпланарных векторов). Поэтому $overrightarrow{OA_1},,overrightarrow{OA_2},,overrightarrow{OA_3}$ — проекции вектора overrightarrow{OA} на прямые l_1,,l_2,,l_3 (проекция на каждую прямую берется вдоль плоскости, проходящей через две другие прямые). Так как равные векторы vec{a} и имеют равные проекции (свойство 2), заключаем, что проекции вектора vec{a} на прямые l_1,,l_2,,l_3 равны $vec{a}_1,,vec{a}_2,,vec{a}_3$ соответственно. Наконец, проекции на прямые равны проекциям на параллельные им прямые, содержащие векторы $vec{a}_1,,vec{a}_2,,vec{a}_3$ соответственно.

Пример 1.5. Если прямая пересекает стороны AB,~BC,~CA треугольника ABC (или их продолжения) в точках C_1,~B_1,~C_1 соответственно, то

Отношения проекций векторов на прямую вдоль прямой

$frac{overrightarrow{AC_1}}{overrightarrow{BC_1}}cdotfrac{overrightarrow{BA_1}}{overrightarrow{CA_1}}cdotfrac{overrightarrow{CB_1}}{overrightarrow{AB_1}}=1.$

Решение. Найдем отношения проекций векторов на прямую вдоль прямой A_1C_1 (рис. 1.20). Для этого через точку проведем прямую BB_2 , параллельную прямой A_1C_1 . По свойству 4 проекций имеем:

$frac{overrightarrow{AC_1}}{overrightarrow{BC_1}}=frac{overrightarrow{AB_1}}{overrightarrow{B_2B_1}};~~~~frac{overrightarrow{BA_1}}{overrightarrow{CA_1}}=frac{overrightarrow{B_2B_1}}{overrightarrow{CB_1}}.$

Перемножая эти пропорции, получаем $frac{overrightarrow{AC_1}}{overrightarrow{BC_1}}cdotfrac{overrightarrow{BA_1}}{overrightarrow{CA_1}}=frac{overrightarrow{AB_1}}{overrightarrow{CB_1}}$ , что равносильно доказываемому равенству.

Заметим, что доказанное утверждение является частью теоремы Менелая.

Пример 1.6. Если на сторонах AB,~BC,~CA треугольника ABC взяты соответственно точки A_1,~B_1,~C_1 так, что прямые AA_1,~BB_1,~CC_1 пересекаются в одной точке, то

$frac{overrightarrow{AC_1}}{overrightarrow{BC_1}}cdotfrac{overrightarrow{BA_1}}{overrightarrow{CA_1}}cdotfrac{overrightarrow{CB_1}}{overrightarrow{AB_1}}=-1.$

Решение. Пусть прямые пересекаются в точке (рис.1.21). Через точку C_1 проведем прямые C_1B_2 и C_1A_2 параллельно BB_1 и AA_1 соответственно. По свойству проекций (свойство 4):

Пересечение прямых в точке

$frac{overrightarrow{AB_1}}{overrightarrow{B_2B_1}}=-frac{overrightarrow{AB}}{overrightarrow{BC_1}};~~~frac{overrightarrow{BA_1}}{overrightarrow{A_2A_1}}=frac{overrightarrow{AB}}{overrightarrow{AC_1}};~~~frac{overrightarrow{CA_1}}{overrightarrow{A_2A_1}}=frac{overrightarrow{CQ}}{overrightarrow{C_1Q}}=frac{overrightarrow{CB_1}}{overrightarrow{B_2B_1}}$

$begin{gathered}frac{overrightarrow{CQ}}{overrightarrow{C_1Q}}=frac{overrightarrow{CA_1}}{overrightarrow{A_2A_1}}=frac{overrightarrow{CA_1}}{overrightarrow{BA_1}}cdotfrac{overrightarrow{BA_1}}{overrightarrow{A_2A_1}}=frac{overrightarrow{CA_1}}{overrightarrow{BA_1}}cdotfrac{overrightarrow{AB}}{overrightarrow{AC_1}}\[2pt]frac{overrightarrow{C_1Q}}{overrightarrow{CQ}}=frac{overrightarrow{B_2B_1}}{overrightarrow{CB_1}}=frac{overrightarrow{AB_1}}{overrightarrow{CB_1}}cdotfrac{overrightarrow{B_2B_1}}{overrightarrow{AB_1}}=frac{overrightarrow{AB_1}}{overrightarrow{CB_1}}cdotleft(-frac{overrightarrow{BC_1}}{overrightarrow{AB}}right)end{gathered}$

Запишем произведение правых частей этих равенств, учитывая, что произведение левых частей равно единице:

$frac{overrightarrow{CA_1}}{overrightarrow{BA_1}}cdotfrac{overrightarrow{AB}}{overrightarrow{AC_1}}cdotfrac{overrightarrow{AB_1}}{overrightarrow{CB_1}}cdotleft(-frac{overrightarrow{BC_1}}{overrightarrow{AB}}right)=-frac{overrightarrow{BC_1}}{overrightarrow{AC_1}}cdotfrac{overrightarrow{CA_1}}{overrightarrow{BA_1}}cdotfrac{overrightarrow{AB_1}}{overrightarrow{CB_1}}cdotfrac{overrightarrow{AB}}{overrightarrow{AB}}=-frac{overrightarrow{BC_1}}{overrightarrow{AC_1}}cdotfrac{overrightarrow{CA_1}}{overrightarrow{BA_1}}cdotfrac{overrightarrow{AB_1}}{overrightarrow{CB_1}}=1$

Найдем обратное отношение $frac{overrightarrow{AC_1}}{overrightarrow{BC_1}}cdotfrac{overrightarrow{BA_1}}{overrightarrow{CA_1}}cdotfrac{overrightarrow{CB_1}}{overrightarrow{AB_1}}=-1$ , что и требовалось доказать.

Заметим, что доказанное утверждение является частью теоремы Чевы.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Определение 2. Проекцией точки A на прямую L Называется основание A¢ перпендикуляра AA¢, опущенного из точки A на прямую L.

Определение 3. Проекцией направленного отрезка На прямую L Называется направленный отрезок , где A¢ и B¢ Соответственно проекции точек A и B На прямую L.

Определение 4. Проекцией (Векторной проекцией) Вектора A на прямую L Называется вектор, изображаемый проекцией направленного отрезок, который изображает данный вектор a.

Векторная проекция вектора A на прямую L изображается символом ПрL A.

Теорема 1. Векторная проекция ПрL A не зависит от направленного отрезка, которым изображается данный вектор a.

Доказательство. Пусть вектор A изображается направленным отрезком , Проекция на прямую L (см. рис. 21).

Точки A¢ и B¢ можно получить, проведя через точки A и B плоскости перпендикулярные прямой L. От точки A¢ отложим вектор A: a =. Четырехугольник A¢ABK — прямоугольник. Так как A¢A ^ L, То BK ^ L и плоскость B¢BK ^ L. Тогда BK ^ L и точка B¢ — Проекция точки K. Таким образом, направленные отрезки и имеют одну и туже проекцию.

Пусть вектор A изображается также направленным отрезком , проекция на прямую L. От точки С¢ отложим вектор A: a =. Направленные отрезки и имеют одну и туже проекцию . Докажем, что =.

Так как треугольники A¢B¢K И C¢D¢L равны, то A¢B¢ = C¢D¢. Так как лучи A¢ B¢ И C¢ D¢ Сонаправлены, то =.

Теорема 2. Для любой прямой L, Для Любых векторов A, B и для любого числа L справедливы следующие свойства:

1) ПрL (A + B) = ПрL A + ПрL B;

2) ПрL (l A) = l ПрL A.

Доказательство. Возьмем точку O на прямой L И построим сумму векторов a, B: A + B == (см. рис. 22). Пусть A¢ И B¢ проекции точек A И B на прямую L. Тогда

ПрL (A + B) ==

= ПрL A + ПрL B.

Свойство 2 докажите самостоятельно ( рассмотрите три случая l =0, l > 0, l < 0).

< Предыдущая		Следующая >

Источник

Вектор можно рассматривать как упорядоченную пару точек в пространстве или направленный отрезок. В школьном курсе аналитической геометрии часто рассматриваются разные задачи на определение его проекций — на координатные оси, на прямую, на плоскость или на другой вектор. Обычно речь идет о двух- и трехмерных прямоугольных системах координат и перпендикулярных проекциях вектора.

Если вектор ā задан координатами начальной A(X₁,Y₁,Z₁) и конечной B(X₂,Y₂,Z₂) точек, а найти требуется его проекцию (P) на оси прямоугольной координатной системы, сделать это очень просто. Посчитайте разность соответствующих координат двух точек — т.е. проекция вектора AB на ось абсцисс будет равна Px = X₂-X₁, на ось ординат Py = Y₂-Y₁, аппликат — Pz = Z₂-Z₁.

Для вектора, заданного парой или тройкой (в зависимости от размерности пространства) своих координат ā{X,Y} или ā{X,Y,Z} упростите формулы предыдущего шага. В этом случае его проекции на координатные оси (āx, āy, āz) равны соответствующим координатам: āx = X, āy = Y и āz = Z.

Если в условиях задачи координаты направленного отрезка не указаны, но дана его длина |ā| и направляющие косинусы cos(x), cos(y), cos(z), определить проекции на координатные оси (āx, āy, āz) можно как в обычном прямоугольном треугольнике. Просто перемножьте длину на соответствующий косинус: āx = |ā|*cos(x), āy = |ā|*cos(y) и āz = |ā|*cos(z).

По аналогии с предыдущим шагом, проекцией вектора ā(X₁,Y₁) на другой вектор ō(X₂,Y₂) можно считать его проекцию на произвольно взятую ось, параллельную вектору ō и имеющую совпадающее с ним направление. Для вычисления этой величины (ā₀) умножайте модуль вектора ā на косинус угла (α) между направленными отрезками ā и ō: ā₀ = |ā|*cos(α).

Если угол между векторами ā(X₁,Y₁) и ō(X₂,Y₂) неизвестен, для вычисления проекции (ā₀) ā на ō разделите их скалярное произведение на модуль ō: ā₀ = ā*ō/|ō|.

Ортогональной проекцией вектора AB на прямую L называют отрезок этой прямой, образованный перпендикулярными проекциями начальной и конечной точек исходного вектора. Для определения координат точек проекции используйте формулу, описывающую прямую (в общем виде a*X+b*Y+c=0), и координаты начальной A(X₁,Y₁) и конечной B(X₂,Y₂) точек вектора.

Аналогичным способом находите и ортогональную проекцию вектора ā на плоскость, заданную уравнением — это должен быть направленный отрезок между двумя точками плоскости. Координаты его начальной точки рассчитайте из формулы плоскости и координат начальной точки исходного вектора. Это же относится и к конечной точке проекции.

Источник