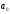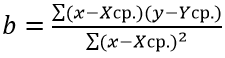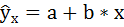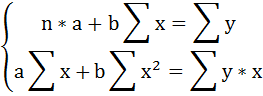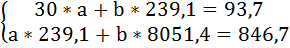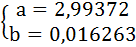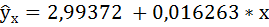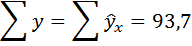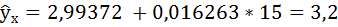Имеются
данные о деятельности предприятия за
ретроспективный период (таблица 2.2).
Требуется:
-
сделать
прогноз на следующие три года с
использованием метода среднегодовых
темпов роста и регрессионного анализа; -
сравнить результаты
прогнозов и обосновать выбор стратегии
развития предприятия.
Таблица 2.2–Значение грузооборота
железной дороги
|
Грузооборот |
Значения |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
Местный |
8811 |
8458 |
9755 |
10170 |
10307 |
10800 |
10898 |
|
Ввоз |
2550 |
2847 |
3255 |
2660 |
2802 |
2823 |
3069 |
|
Вывоз |
4458 |
4922 |
5571 |
5813 |
7423 |
8587 |
8952 |
|
Транзит |
8689 |
9790 |
12054 |
11726 |
10996 |
12014 |
10806 |
|
Общий |
24508 |
26017 |
30635 |
30369 |
31528 |
34224 |
33725 |
1
вариант.
Определим прогнозные значения по
среднегодовым темпам изменения
показателей по формуле 2.1. Для местного
грузооборота среднегодовой темп
изменения значений будет равен
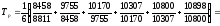
Прогнозные
значения показателей при этом подходе
определяются по формуле (2.2). Тогда для
местного грузооборота значение на
первый плановый год составит
11312,12 млн. т-км.
Остальные значения
определяются аналогично. Результаты
расчетов сведены в таблицу 2.3.
Таблица 2.3–Расчет прогнозных
значений грузооборота
|
Грузооборот, |
Значение |
|
Прогноз |
||
|
8 |
9 |
10 |
|||
|
Местный |
10898 |
1,038 |
11312,1 |
11742 |
12188,2 |
|
Ввоз |
3069 |
1,038 |
3185,6 |
3306,7 |
3432,4 |
|
Вывоз |
8952 |
1,126 |
10080 |
11350,1 |
12780,2 |
|
Транзит |
10806 |
1,043 |
11270,7 |
11755,3 |
12260,8 |
|
Общий |
33725 |
1,057 |
35647,3 |
37679,2 |
39826,9 |
2 вариант.
Определим прогнозные значения для
показателя местного грузооборота с
помощью регрессионного анализа. Анализ
представленных статистических данных
позволяет выбрать линейный вид функции
для описания закономерности изменения
целевых показателей от времени, поэтому
воспользуемся формулами 2.3 и 2.4.
Промежуточные
значения для расчета коэффициентов
уравнения регрессии сведем в таблицу
2.4.
Таблица 2.4
– Значения для расчета
коэффициента регрессии
|
|
|
|
|
|
1 |
8811 |
1 |
8811 |
|
2 |
8458 |
4 |
16916 |
|
3 |
9755 |
9 |
29265 |
|
4 |
10170 |
16 |
40680 |
|
5 |
10307 |
25 |
51535 |
|
6 |
10800 |
36 |
64800 |
|
7 |
10898 |
49 |
76286 |
|
|
|
|
|
Тогда
система уравнений (2.4) примет вид
После решения
данной системы получаем значения
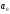
и
регрессии примет вид
Vp=8243,143+410,607·t
где t
—
год, на который делается прогноз: t
= 8,
9 и 10 год.
Расчет
остальных показателей производится
аналогично.
Таблица 2.5–Прогноз значений
грузооборота
|
Грузооборот, |
Коэффициенты |
Прогноз |
|||
|
|
|
8 |
9 |
10 |
|
|
Местный |
8243,143 |
410,6071 |
11528 |
11938,6 |
12349,2 |
|
Ввоз |
2707,143 |
37,71429 |
3008,9 |
3046,6 |
3084,3 |
|
Вывоз |
3294,571 |
809,4286 |
9770 |
10579,4 |
11388,9 |
|
Транзит |
9476,286 |
347,8929 |
12259,4 |
12607,3 |
12955,2 |
|
Общий |
23721,14 |
1605,643 |
36566,3 |
38171,9 |
39777,6 |
Необходимо
учитывать, что общий грузооборот является
комплексным показателем, и определяется
как сумма грузооборота в местном
сообщении, ввоза, вывоза и транзита.
Поэтому при прогнозировании сложных
показателей их необходимо раскладывать
на составляющие (в нашем случае местный,
ввоз, вывоз и транзит), оценивать
прогнозные значения составляющих, а
значение сложного показателя находить
по формулам соответствующих зависимостей.
Проведем анализ прогнозного значения
общего грузооборота, рассчитанного по
двум вариантам, и значений, полученных
при суммировании прогнозов входящих в
грузооборот элементов (таблица 2.6).
Таблица 2.6–Сравнение результатов
прогноза грузооборота
|
Вариант прогноза |
Метод расчета |
Значения |
||
|
8 |
9 |
10 |
||
|
1 |
прогноз |
35647,3 |
37679,2 |
39826,9 |
|
сумма |
35848,4 |
38154,1 |
40661,6 |
|
|
разница значений |
-201,1 |
-474,9 |
-834,7 |
|
|
2 |
прогноз |
36566,3 |
38171,9 |
39777,6 |
|
сумма |
36566,3 |
38171,9 |
39777,6 |
|
|
разница |
0 |
0 |
0 |
Как
видно из таблицы, при первом способе
расчета наблюдается существенное
увеличение расхождения значения общего
грузооборота при увеличении периода
прогноза. При расчете с помощью
корреляционного метода значения
одинаковы.
Для
выбора итоговых значений отобразим
графически значения выполненного общего
грузооборота и прогнозные значения,
рассчитанные по двум вариантам (рисунок
2.1). Второй вариант (регрессионная модель)
более точно отображает дальнейшие темпы
развития объемов производства.
Окончательный выбор варианта прогнозных
значений развития предприятия
осуществляется при наличии прогнозных
значений по всем целевым показателям,
характеризующим стратегию развития
предприятия.
Рисунок 2.1
– Сравнение
результатов прогноза объемов грузооборота
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Любому бизнесу интересно заглянуть в будущее и правильно ответить на вопрос: «А сколько денег мы заработаем за следующий период?» Ответить на такого рода вопросы позволяют различные методики прогнозирования. В данной статье мы с вами рассмотрим несколько таких методик и произведем все необходимые расчеты в Excel. Еще больше про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Постановка задачи
Исходные данные
Для начала, давайте определимся, какие у нас есть исходные данные и что нам нужно получить на выходе. Фактически, все что у нас есть, это некоторые исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут продажи за предыдущие периоды.
Примечание. Собранные в разные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такого временного ряда называется измерением. Например: данные о продажах за последние 5 лет по месяцам — временной ряд; продажи за январь прошлого года — измерение.
Составляющие прогноза
Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:
- Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
- Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.
Эти три пункта в совокупность образуют регулярную составляющую временного ряда.
Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.
Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно – продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.
Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Виды моделей
Следующий вопрос, на который нужно ответить при построении прогноза: “А какие модели временного ряда бывают?”
Обычно выделяют два основных вида:
- Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отклонения
- Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отклонения
Иногда также выделают смешанную модель в отдельную группу:
- Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отклонения
С моделями мы определились, но теперь возникает еще один вопрос: «А когда какую модель лучше использовать?»
Классический вариант такой:
— Аддитивная модель используется, если амплитуда колебаний более-менее постоянная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной компоненты.
Пример:
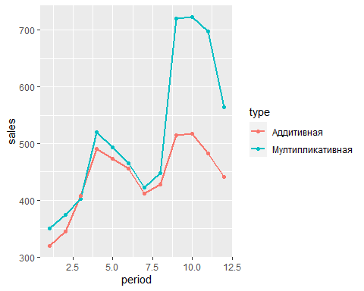
Решение задачи с помощью Excel
Итак, необходимые теоретические знания мы с вами получили, пришло время применить их на практике. Мы будем с вами использовать классическую аддитивную модель для построения прогноза. Однако, мы построим с вами два прогноза:
- с использованием линейного тренда
- с использованием полиномиального тренда
Во всех руководствах, как правило, разбирается только линейный тренд, поэтому полиномиальная модель будет крайне полезна для вас и вашей работы!
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Модель с линейным трендом
Пусть у нас есть исходная информация по продажам за 2 года:
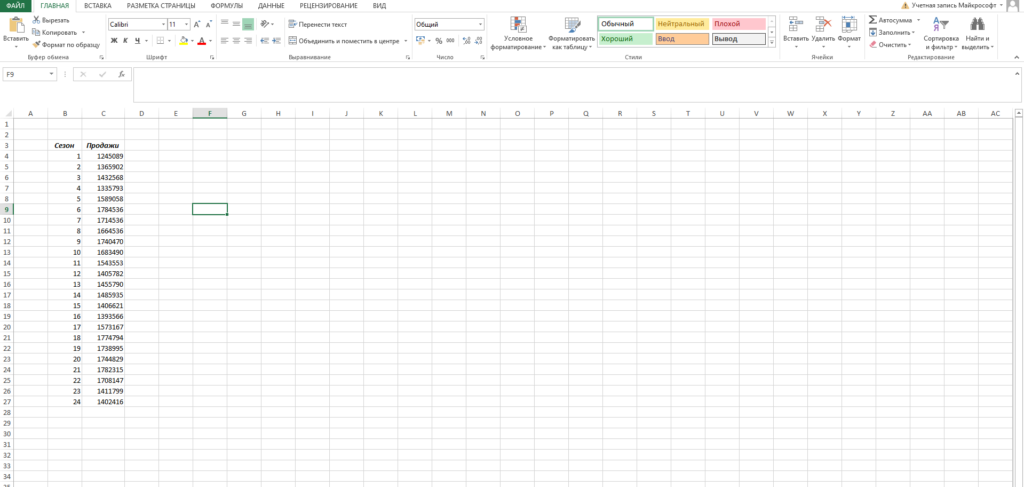
Учитывая, что мы используем линейный тренд, то нам необходимо найти коэффициенты уравнения
y = ax + b
где:
- y – значения продаж
- x – номер периода
- a – коэффициент наклона прямой тренда
- b – свободный член тренда
Рассчитать коэффициенты данного уравнения можно с помощью формулы массива и функции ЛИНЕЙН. Нам необходимо будет сделать следующую последовательность действий:
- Выделяем две ячейки рядом
- Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
- Нажимаем Ctrl+Shift+Enter, чтобы активировать формулу массива
На выходе мы получили 2 числа: первое — коэффициент a, второе – свободный член b.
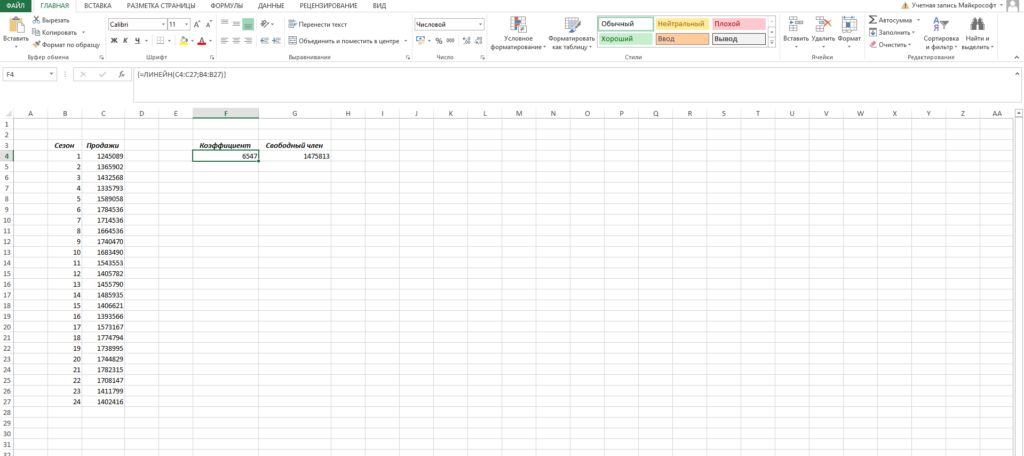
Теперь нам нужно рассчитать для каждого периода значение линейного тренда. Сделать это крайне просто — достаточно в полученное уравнение подставить известные номера периодов. Например, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.
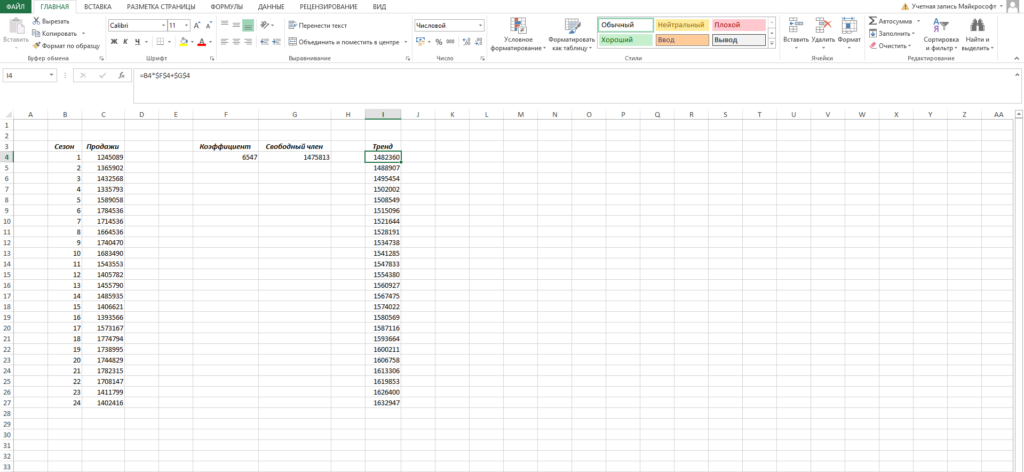
Нам осталось рассчитать коэффициент сезонности для каждого периода. Учитывая, что у нас есть исторические данные за два года, разумно будет учесть это при расчете. Можем сделать следующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).
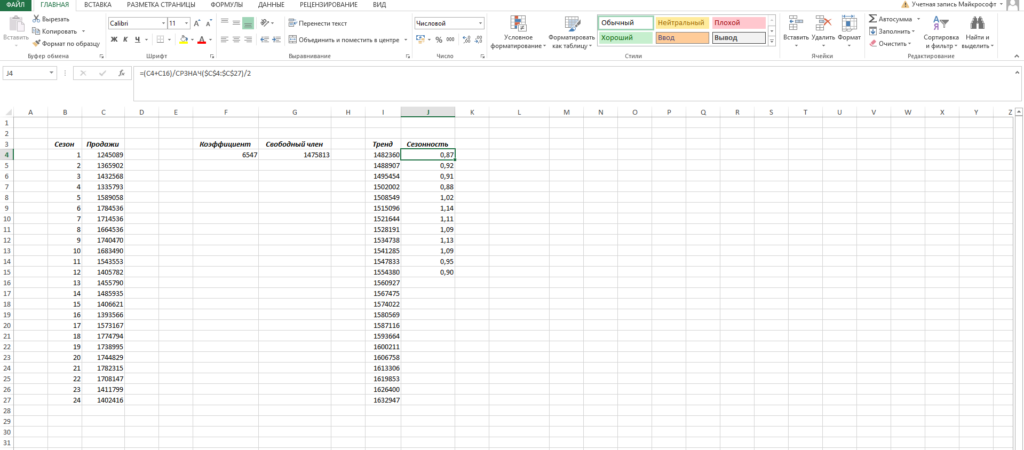
Что нам это дало? Мы посчитали, сколько суммарно продавалось каждый январь/каждый февраль и так далее, а потом разделили это на среднее значение продаж за все два периода.
То есть мы выяснили, как продажи двух январей отклонялись от средних продаж за два года, как продажи двух февралей отклонялись и так далее. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.
Примечание. Рассчитали только 12 коэффициентов, т.к. один коэффициент учитывает продажи сразу за 2 аналогичных периода.
Итак, теперь мы на финишной прямой. Нам осталось рассчитать тренд для будущих периодов и учесть коэффициент сезонности для них. Давайте амбициозно построим прогноз на год вперед.
Сначала создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.
Далее, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 прогнозируемых периодов.
И последний штрих — умножаем полученное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!
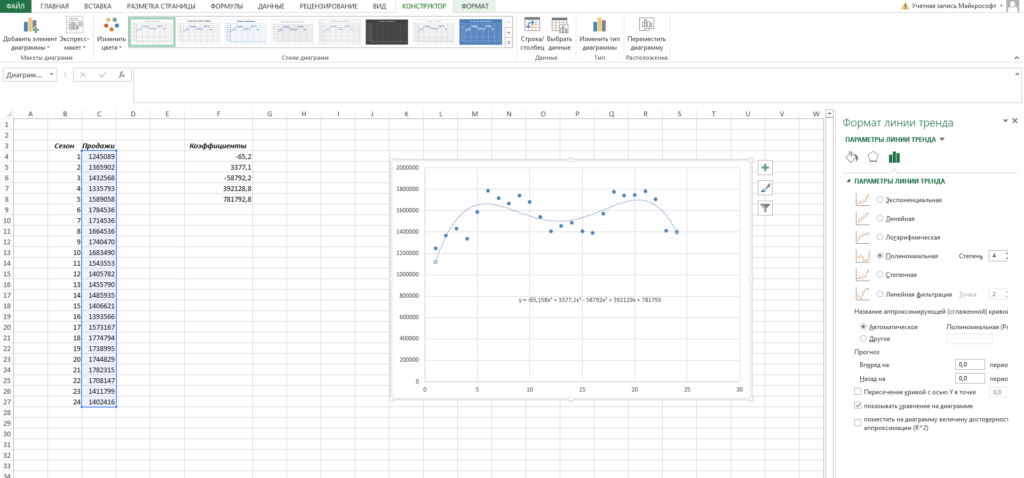
Модель с полиномиальным трендом
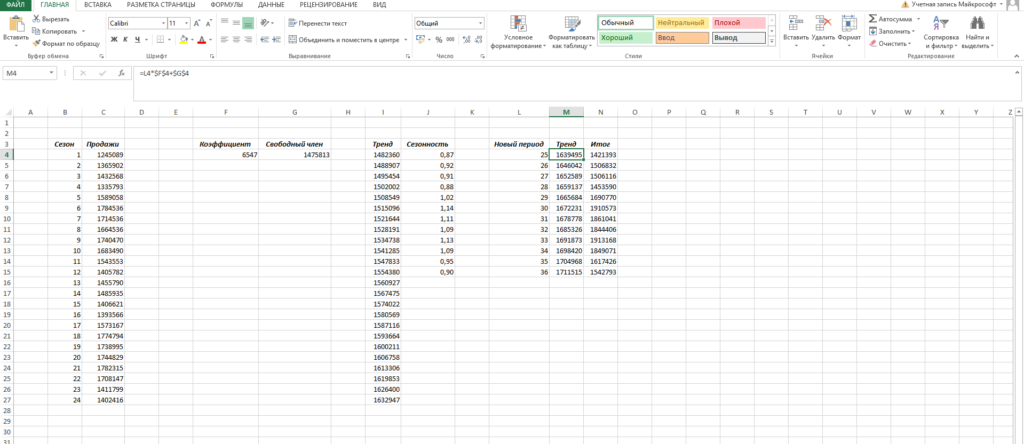
Конструкция, которую мы только что с вами построили, достаточно проста. Но у нее есть один большой минус — далеко не всегда она дает достоверные результаты.
Посмотрите сами, какая модель более точно аппроксимирует наши точки — линейный тренд (прямая зеленая линия) или полиномиальный тренд (красная кривая)? Ответ очевиден. Поэтому сейчас мы с вами и разберем, как построить полиномиальную модель в Excel.
Пусть все исходные данные у нас будут такими же. Для простоты модели будем учитывать только тренд, без сезонной составляющей.
Для начала давайте определимся, чем полиномиальный тренд отличается от обычного линейного. Правильно — формой уравнения. У линейного тренда мы разбирали обычный график прямой:
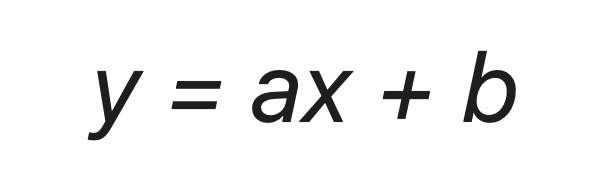
У полиномиального тренда же уравнение выглядит иначе:
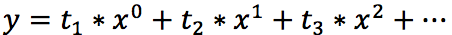
где конечная степень определяется степенью полинома.
Т.е. для полинома 4 степени необходимо найти коэффициенты уравнения:
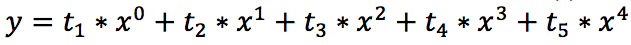
Согласитесь, выглядит немного страшно. Однако, ничего страшного нет, и мы с легкостью можем решить эту задачку с помощью уже известных нам методов.
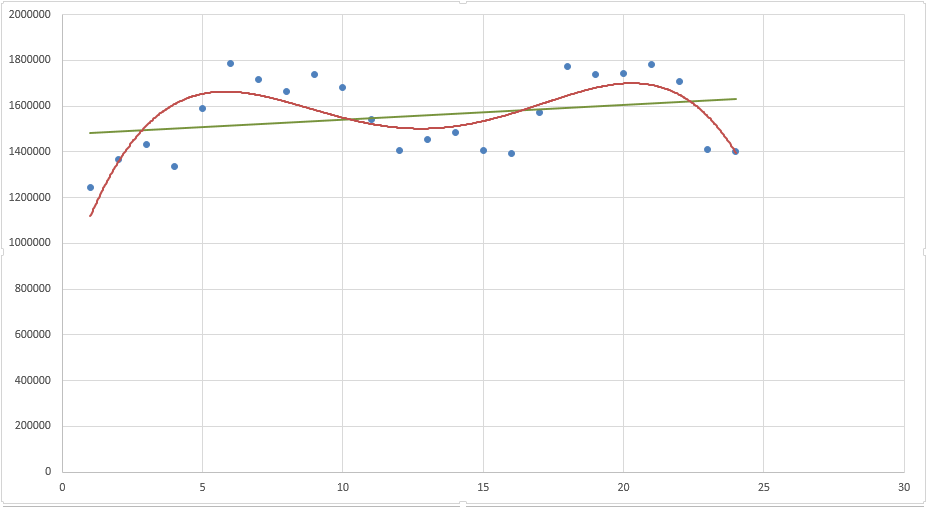
- Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;1). Функция ЛИНЕЙН позволяет произвести расчет коэффициентов, а с помощью функции ИНДЕКС мы вытаскиваем нужный нам коэффициент. В данном случае за выбор коэффициента отвечает самый последний аргумент. У нас стоит 1 — это коэффициент при самой высокой степени (т.е. при 4 степени, коэффициент). Кстати, узнать о самых полезных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
- Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;2) в ячейке ниже.
- Делаем такие же действия, пока не найдем все коэффициенты.
Кстати говоря, мы можем легко сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.
- Выделяем столбец с продажами
- Выбираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
- Нажимаем на любую точку графика правой кнопкой мыши и выбираем «Добавить линию тренда»
- В открывшемся справа меню выбираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Показывать уравнение на диаграмме»
Теперь вы наглядно можете видеть, как рассчитанный тренд аппроксимирует исходные данные и как выглядит само уравнение. Можно сравнить уравнение на графике с вашими коэффициентами. Сходится? Значит сделали все верно!
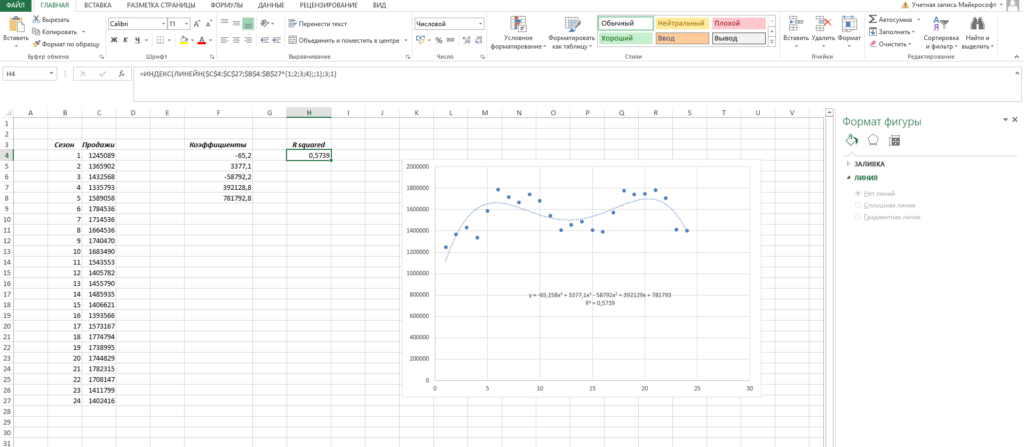
Помимо всего прочего, вы можете сразу оценить точность аппроксимации (не полностью, но хотя бы первично). Это делается с помощью коэффициента R^2. Тут у вас снова есть два пути:
- Вы можете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
- Вы можете рассчитать коэффициент R^2 самостоятельно по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4};;1);3;1)
Заключение
Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.
Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.
Автор: Алексанян Андрон, эксперт SF Education
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Data Science
5 примеров экономии времени в Excel
Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на наш взгляд,…
Функция ПРЕДСКАЗ в Excel позволяет с некоторой степенью точности предсказать будущие значения на основе существующих числовых значений, и возвращает соответствующие величины. Например, некоторый объект характеризуется свойством, значение которого изменяется с течением времени. Такие изменения могут быть зафиксированы опытным путем, в результате чего будет составлена таблица известных значений x и соответствующих им значений y, где x – единица измерения времени, а y – количественная характеристика свойства. С помощью функции ПРЕДСКАЗ можно предположить последующие значения y для новых значений x.
Примеры использования функции ПРЕДСКАЗ в Excel
Функция ПРЕДСКАЗ использует метод линейной регрессии, а ее уравнение имеет вид y=ax+b, где:
- Коэффициент a рассчитывается как Yср.-bXср. (Yср. и Xср. – среднее арифметическое чисел из выборок известных значений y и x соответственно).
- Коэффициент b определяется по формуле:
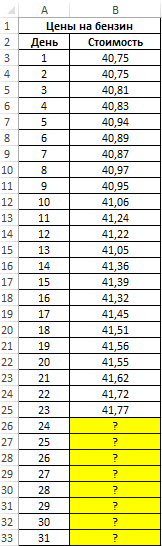
Пример 1. В таблице приведены данные о ценах на бензин за 23 дня текущего месяца. Согласно прогнозам специалистов, средняя стоимость 1 л бензина в текущем месяце не превысит 41,5 рубля. Спрогнозировать стоимость бензина на оставшиеся дни месяца, сравнить рассчитанное среднее значение с предсказанным специалистами.
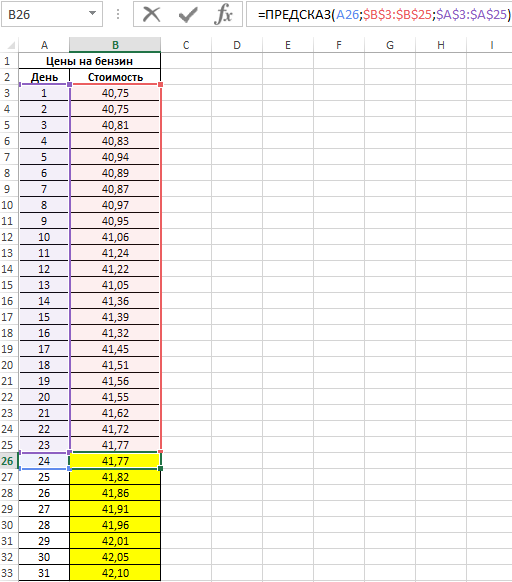
Вид исходной таблицы данных:
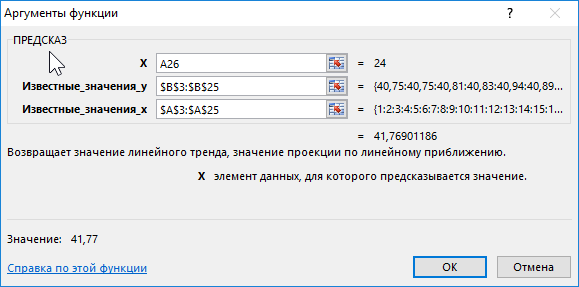
Чтобы определить предполагаемую стоимость бензина на оставшиеся дни используем следующую функцию (как формулу массива):
Описание аргументов:
- A26:A33 – диапазон ячеек с номерами дней месяца, для которых данные о стоимости бензина еще не определены;
- B3:B25 – диапазон ячеек, содержащих данные о стоимости бензина за последние 23 дня;
- A3:A25 – диапазон ячеек с номерами дней, для которых уже известна стоимость бензина.
Результат расчетов:
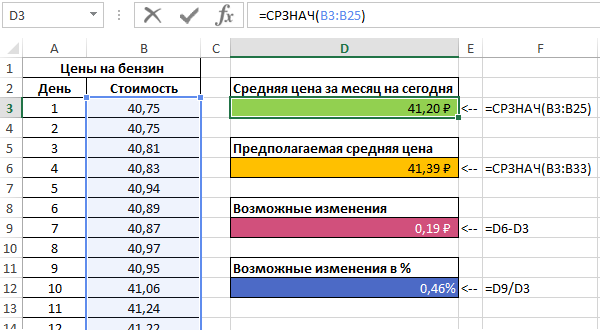
Рассчитаем среднюю стоимость 1 л бензина на основании имеющихся и расчетных данных с помощью функции:
=СРЗНАЧ(B3:B33)
Результат:
Можно сделать вывод о том, что если тенденция изменения цен на бензин сохранится, предсказания специалистов относительно средней стоимости сбудутся.
Анализ прогноза спроса продукции в Excel по функции ПРЕДСКАЗ
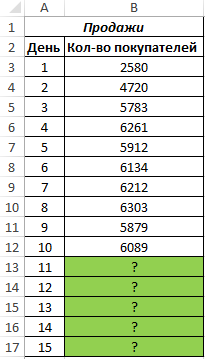
Пример 2. Компания недавно представила новый продукт. С момента вывода на рынок ежедневно ведется учет количества клиентов, купивших этот продукт. Предположить, каким будет спрос на протяжении 5 последующих дней.
Вид исходной таблицы данных:
Как видно, в первые дни спрос был небольшим, затем он рос достаточно большими темпами, а на протяжении последних трех дней изменялся незначительно. Это свидетельствует о том, что основным фактором роста продаж на данный момент является не расширение базы клиентов, а развитие продаж с постоянными клиентами. В таких случаях рекомендуют использовать не линейную регрессию, а логарифмический тренд, чтобы результаты прогнозов были более точными.
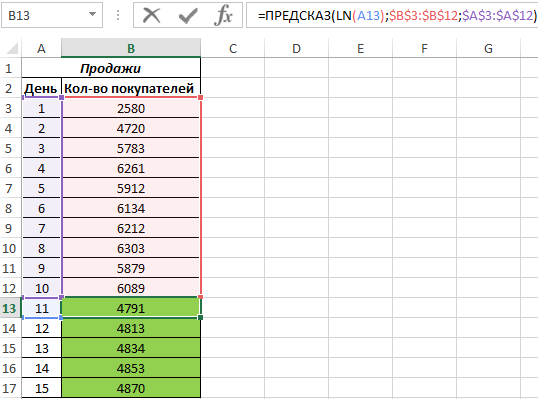
Рассчитаем значения логарифмического тренда с помощью функции ПРЕДСКАЗ следующим способом:
Как видно, в качестве первого аргумента представлен массив натуральных логарифмов последующих номеров дней. Таким образом получаем функцию логарифмического тренда, которая записывается как y=aln(x)+b.
Результат расчетов:
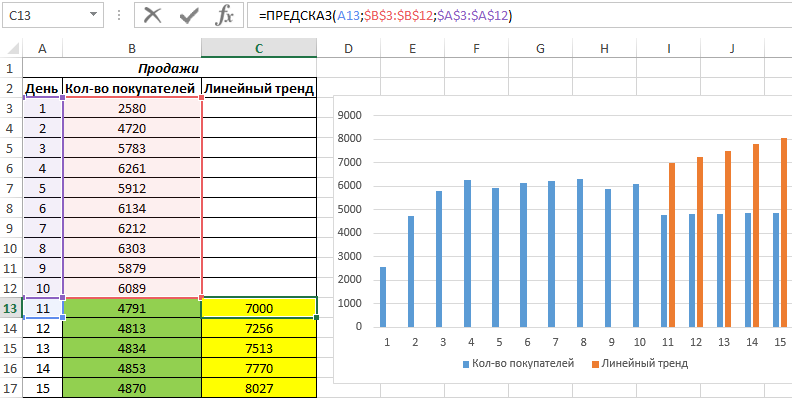
Для сравнения, произведем расчет с использованием функции линейного тренда:
И для визуального сравнительного анализа построим простой график.
Полученные результаты:
Как видно, функцию линейной регрессии следует использовать в тех случаях, когда наблюдается постоянный рост какой-либо величины. В данном случае функция логарифмического тренда позволяет получить более правдоподобные данные (более наглядно при большем количестве данных).
Прогнозирование будущих значений в Excel по условию
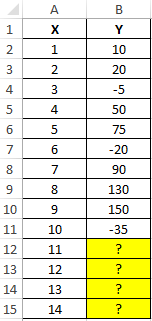
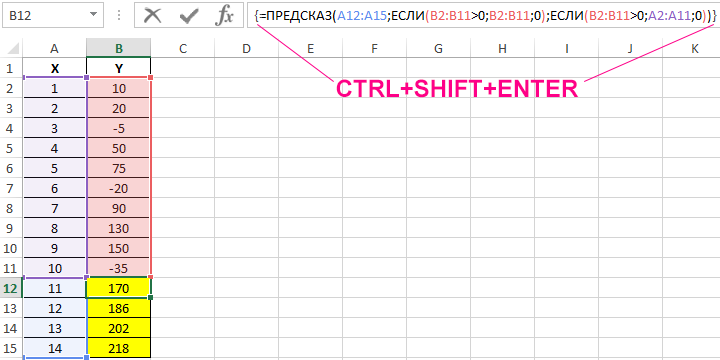
Пример 3. В таблице Excel указаны значения независимой и зависимой переменных. Некоторые значения зависимой переменной указаны в виде отрицательных чисел. Спрогнозировать несколько последующих значений зависимой переменной, исключив из расчетов отрицательные числа.
Вид таблицы данных:
Для расчета будущих значений Y без учета отрицательных значений (-5, -20 и -35) используем формулу:
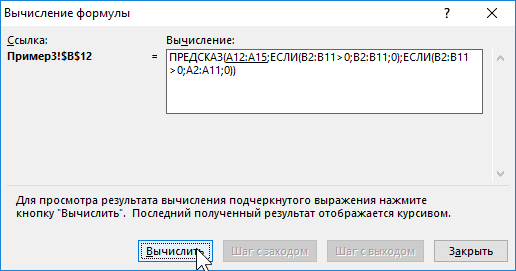
C помощью функций ЕСЛИ выполняется перебор элементов диапазона B2:B11 и отброс отрицательных чисел. Так, получаем прогнозные данные на основании значений в строках с номерами 2,3,5,6,8-10. Для детального анализа формулы выберите инструмент «ФОРМУЛЫ»-«Зависимости формул»-«Вычислить формулу». Один из этапов вычислений формулы:
Полученные результаты:
Особенности использования функции ПРЕДСКАЗ в Excel
Функция имеет следующую синтаксическую запись:
=ПРЕДСКАЗ(x;известные_значения_y;известные_значения_x)
Описание аргументов:
- x – обязательный для заполнения аргумент, характеризующий одно или несколько новых значений независимой переменной, для которых требуется предсказать значения y (зависимой переменной). Может принимать числовое значение, массив чисел, ссылку на одну ячейку или диапазон;
- известные_значения_y – обязательный аргумент, характеризующий уже известные числовые значения зависимой переменной y. Может быть указан в виде массива чисел или ссылки на диапазон ячеек с числами;
- известные_значения_x – обязательный аргумент, который характеризует уже известные значения независимой переменной x, для которой определены значения зависимой переменной y.
Примечания:
- Второй и третий аргументы рассматриваемой функции должны принимать ссылки на непустые диапазоны ячеек или такие диапазоны, в которых число ячеек совпадает. Иначе функция ПРЕДСКАЗ вернет код ошибки #Н/Д.
- Если одна или несколько ячеек из диапазона, ссылка на который передана в качестве аргумента x, содержит нечисловые данные или текстовую строку, которая не может быть преобразована в число, результатом выполнения функции ПРЕДСКАЗ для данных значений x будет код ошибки #ЗНАЧ!.
- Статистическая дисперсия величин (можно рассчитать с помощью формул ДИСП.Г, ДИСП.В и др.), передаваемых в качестве аргумента известные_значения_x, не должна равняться 0 (нулю), иначе функция ПРЕДСКАЗ вернет код ошибки #ДЕЛ/0!.
- Рассматриваемая функция игнорирует ячейки с нечисловыми данными, содержащиеся в диапазонах, которые переданы в качестве второго и третьего аргументов.
- Функция ПРЕДСКАЗ была заменена функцией ПРЕДСКАЗ.ЛИНЕЙН в Excel версии 2016, но была оставлена для обеспечения совместимости с Excel 2013 и более старыми версиями.
- Для предсказания только одного будущего значения на основании известного значения независимой переменной функция ПРЕДСКАЗ используется как обычная формула. Если требуется предсказать сразу несколько значений, в качестве первого аргумента следует передать массив или ссылку на диапазон ячеек со значениями независимой переменной, а функцию ПРЕДСКАЗ использовать в качестве формулы массива.
Имеются данные о рейтинге авиакомпании и ее пассажирообороте. Сделайте точечный прогноз значения рейтинга авиакомпании при пассажирообороте, равном 15 млн. пасс/км (линейная регрессия).
| № п/п | х | y |
|---|---|---|
| 1 | 67,12 | 3,9 |
| 2 | 47,07 | 3,9 |
| 3 | 1,42 | 3,8 |
| 4 | 15,58 | 3,7 |
| 5 | 8,47 | 3,6 |
| 6 | 2,87 | 3,3 |
| 7 | 10,15 | 3,3 |
| 8 | 13,33 | 3,3 |
| 9 | 3,31 | 3,2 |
| 10 | 0,29 | 3,2 |
| 11 | 5,56 | 3,2 |
| 12 | 2,45 | 3,2 |
| 13 | 2,04 | 3,2 |
| 14 | 0,33 | 3,1 |
| 15 | 0,97 | 3,1 |
| 16 | 0,57 | 3,1 |
| 17 | 13,4 | 3,1 |
| 18 | 20,2 | 3,1 |
| 19 | 0,57 | 3,1 |
| 20 | 1,75 | 3 |
| 21 | 0,43 | 3 |
| 22 | 6,06 | 3 |
| 23 | 2,51 | 3 |
| 24 | 0,62 | 2,9 |
| 25 | 2,9 | 2,9 |
| 26 | 3,39 | 2,8 |
| 27 | 0,6 | 2,7 |
| 28 | 0,66 | 2,6 |
| 29 | 4,04 | 2,3 |
| 30 | 0,44 | 2,1 |
Решение:
Для расчёта параметров линейной регрессии
необходимо решить систему нормальных уравнений относительно a и b:
Построим таблицу исходных и расчётных данных.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | y | x2 | x×y | 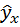 |
|---|---|---|---|---|---|
| 1 | 67,12 | 3,9 | 4505,094 | 261,768 | 4,085272 |
| 2 | 47,07 | 3,9 | 2215,585 | 183,573 | 3,759205 |
| 3 | 1,42 | 3,8 | 2,0164 | 5,396 | 3,016813 |
| 4 | 15,58 | 3,7 | 242,7364 | 57,646 | 3,247093 |
| 5 | 8,47 | 3,6 | 71,7409 | 30,492 | 3,131465 |
| 6 | 2,87 | 3,3 | 8,2369 | 9,471 | 3,040394 |
| 7 | 10,15 | 3,3 | 103,0225 | 33,495 | 3,158786 |
| 8 | 13,33 | 3,3 | 177,6889 | 43,989 | 3,210501 |
| 9 | 3,31 | 3,2 | 10,9561 | 10,592 | 3,047549 |
| 10 | 0,29 | 3,2 | 0,0841 | 0,928 | 2,998436 |
| 11 | 5,56 | 3,2 | 30,9136 | 17,792 | 3,08414 |
| 12 | 2,45 | 3,2 | 6,0025 | 7,84 | 3,033563 |
| 13 | 2,04 | 3,2 | 4,1616 | 6,528 | 3,026896 |
| 14 | 0,33 | 3,1 | 0,1089 | 1,023 | 2,999086 |
| 15 | 0,97 | 3,1 | 0,9409 | 3,007 | 3,009494 |
| 16 | 0,57 | 3,1 | 0,3249 | 1,767 | 3,002989 |
| 17 | 13,4 | 3,1 | 179,56 | 41,54 | 3,21164 |
| 18 | 20,2 | 3,1 | 408,04 | 62,62 | 3,322226 |
| 19 | 0,57 | 3,1 | 0,3249 | 1,767 | 3,002989 |
| 20 | 1,75 | 3 | 3,0625 | 5,25 | 3,022179 |
| 21 | 0,43 | 3 | 0,1849 | 1,29 | 3,000713 |
| 22 | 6,06 | 3 | 36,7236 | 18,18 | 3,092272 |
| 23 | 2,51 | 3 | 6,3001 | 7,53 | 3,034539 |
| 24 | 0,62 | 2,9 | 0,3844 | 1,798 | 3,003802 |
| 25 | 2,9 | 2,9 | 8,41 | 8,41 | 3,040881 |
| 26 | 3,39 | 2,8 | 11,4921 | 9,492 | 3,04885 |
| 27 | 0,6 | 2,7 | 0,36 | 1,62 | 3,003477 |
| 28 | 0,66 | 2,6 | 0,4356 | 1,716 | 3,004453 |
| 29 | 4,04 | 2,3 | 16,3216 | 9,292 | 3,059421 |
| 30 | 0,44 | 2,1 | 0,1936 | 0,924 | 3,000875 |
| Итого | 239,1 | 93,7 | 8051,407 | 846,736 | 93,7 |
Подставив в систему уравнений рассчитанные величины, определим параметры линейного уравнения:
Таким образом, уравнение регрессии имеет вид:
Это значит, что с увеличением пассажирооборота на 1 млн. пасс/км рейтинг авиакомпании увеличится на 0,016263.
Подставим в данное уравнение исходные значения х и найдём сумму расчётных значений у (последняя графа таблицы).
Так как суммы исходных и расчётных значений у совпадают, следовательно, параметры уравнения рассчитаны верно.
Если прогнозное значение пассажирооборота, составит 15 млн. пасс/км, то рейтинг авиакомпании будет равен:
Ответ: значение рейтинга авиакомпании при пассажирообороте, равном 15 млн. пасс/км будет равно 3,2.





 28
28 =69199
=69199 =140
=140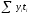 =288293
=288293