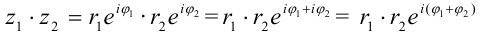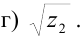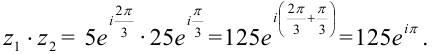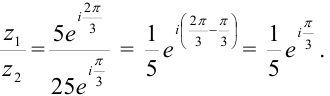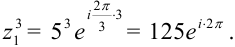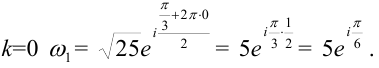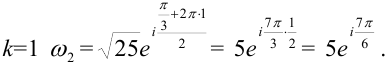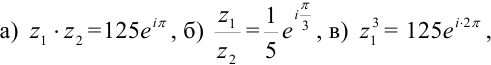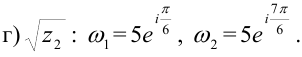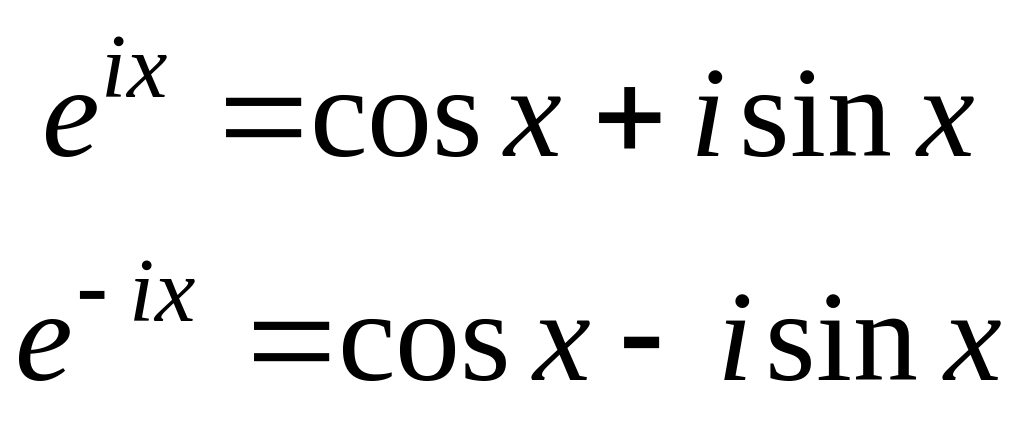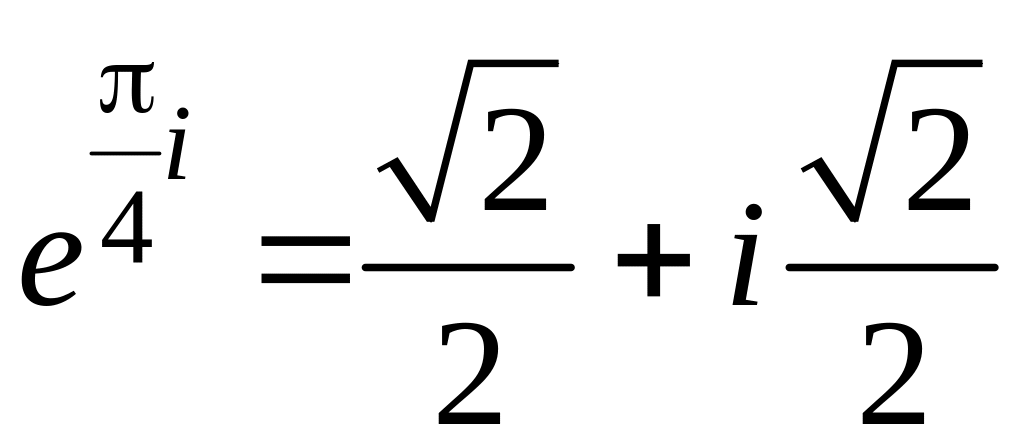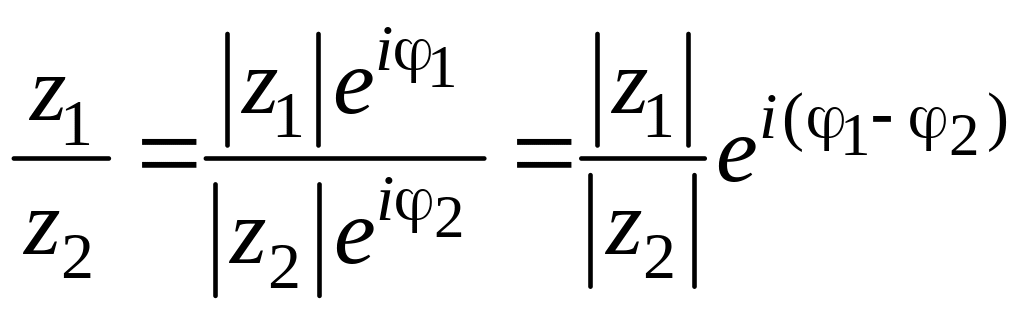Что такое комплексные числа и их умножение
В математических науках часто применяют при решении задач не только натуральные, рациональные и вещественные числа, но и комплексные.
Определение
Комплексное число — это отдельный вид чисел, который представлен множеством, обозначаемым с помощью символа (mathbb{C}).
Рассмотреть комплексное число можно на доказательстве примера. Если записать обычное множество в виде z = a + ib, то под мнимой единицей будет подразумеваться выражение (i = sqrt{-1}). Числа (a,b in mathbb{R}) являются вещественными числами.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда b = 0, комплексное число трансформируется в вещественное число. Исходя из этого, можно сделать вывод, что действительные числа являются частным случаем комплексных чисел. Запись данного заключения будет иметь следующий вид подмножества:
(mathbb{R} subset mathbb{C})
Следует отметить, что также допустимо равенство:
a = 0
Согласно принятым правилам, мнимая часть комплексного числа записывается в виде:
Im(z) = b
Действительная часть комплексного числа представляет собой выражение:
Re(z) = a
Рассмотрев множество на примере, можно представить формулировку комплексно-сопряженных чисел.
Определение
Каждое комплексное число z = a+ib предполагает наличие такого числа, называемого сопряженным, при котором (overline{z} = a-ib).
Разница между записанными числами заключается в неодинаковых знаках перед действительным и мнимым компонентом чисел.
В математической науке для данных чисел предусмотрено несколько форм. Таким образом, одинаковые числа достаточно просто записать разными методами:
- Алгебраическая форма: (z = a+ib).
- Показательная форма: (z = |z|e^{ivarphi}).
- Тригонометрическая форма: (z = |z|cdot(cos(varphi)+isin(varphi))).
С помощью несложных манипуляций одну форму числа можно перевести в другой вариант записи. Алгебраическая запись является более распространенной. Однако допустимо изображать комплексные числа на плоскости. В итоге получим числа (a,b in mathbb{R}) расположенные на соответствующих осях плоскости.
Комплексное число z = a+ib можно представить в качестве вектора (overline{z}). При этом для обозначения аргумента можно использовать запись (varphi). При определении модуля |z| используют длину вектора (overline{z}) и соответствующую формулу:
(|z| = sqrt{a^2+b^2})
С помощью различных уравнений, выбор которых определяется полуплоскостью, в котором расположено само число, определяют аргумент комплексного числа (varphi).
Справедливы следующие закономерности:
- a>0, то (varphi = arctgfrac{b}{a}).
- a<0, b>0, то (varphi = pi + arctgfrac{b}{a}).
- a<0, b<0, то (varphi = -pi + arctgfrac{b}{a}).
Умножить комплексные числа в алгебраической форме можно, таким образом:
(z_1 cdot z_2 = (a_1+ib_1) cdot (a_2+ib_2) = (a_1 a_2 — b_1 b_2)+i(a_1 b_2 + a_2 b_1))
Операция умножения комплексных чисел, записанных в показательном варианте, имеет следующий вид:
(z_1 cdot z_2 = |z_1|e^{ivarphi_1} cdot |z_2|e^{ivarphi_2} = |z_1|cdot|z_2|cdot e^{i(varphi_1 + varphi_2)})
Разновидности формул умножения в зависимости от формы записи
Благодаря наличию специальных формул, можно оперативно выполнять различные операции с комплексными числами, включая примеры из тригонометрии. Теоретический порядок действий при умножении зависит от того, в какой форме записано комплексное число.
Формула умножения в алгебраической форме
В данном случае для того чтобы умножить комплексные числа, необходимо перемножить их компоненты, поочередно раскрывая скобки, согласно формуле. При этом следует учитывать, что (i^2 = -1).
В итоге получим:
(z_1 cdot z_2 = (x_1+y_1i) cdot (x_2 + y_2i) = (x_1 cdot x_2 — y_1 cdot y_2) + (x_1 cdot y_2 + x_2 cdot y_1)i)
Формула умножения в показательной форме
Если требуется найти произведение комплексных чисел, которые записаны в показательной форме, то целесообразно воспользоваться способом прямого перемножения всех элементов:
(z_1 cdot z_2 = r_1e^{varphi_1 i} cdot r_2e^{varphi_2 i} = r_1cdot r_2 cdot e^{(varphi_1+varphi_2)i})
Формула умножения в тригонометрической форме
Найти произведение комплексных чисел, записанных с помощью тригонометрической формы, можно, таким образом:
(z_1 cdot z_2 = r_1 cdot r_2 cdot (cos(varphi_1+varphi_2) + isin(varphi_1+varphi_2)))
Примеры решения задач с комплексными числами
Задача 1
Необходимо представить алгебраическую форму комплексного числа в виде тригонометрической и показательной записи. Комплексное число:
z = 4-4i
Решение
В первую очередь следует определить модуль комплексного числа:
(|z| = sqrt{4^2 + (-4)^2} = sqrt{16 + 16} = sqrt{32} = 4sqrt{2})
Далее целесообразно найти аргумент:
(varphi = arctg frac{b}{a} = arctg frac{-4}{4} = arctg (-1) = -frac{pi}{4})
В результате можно составить тригонометрическую форму комплексного числа, которое дано в условии задачи:
(z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg))
Таким же способом можно представить комплексное число в показательной форме:
(z = 4sqrt{2} e^{-frac{pi}{4}i})
Ответ: (z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg)), (z = 4sqrt{2} e^{-frac{pi}{4}i})
Задача 2
Требуется найти произведение пары комплексных чисел:
(z_1 = 3+i)
(z_2 = 2-3i)
Решение
В первую очередь следует записать выражение:
(z_1 cdot z_2 = (3+i) cdot (2-3i))
Затем целесообразно приступить к раскрытию скобок и перемножить множители поэлементно:
(z_1 cdot z_2 = (3+i) cdot (2-3i)= (3 cdot 2 + 3 cdot (-3i) + i cdot 2 + i cdot (-3i))
Полученное равенство можно упростить. Для этого нужно учитывать, что:
(i^2 = -1)
Запишем готовое выражение:
(6 — 9i + 2i + 3 = 9 — 7i)
Ответ: (z_1 cdot z_2 = 9 — 7i)
Задача 3
Даны комплексные числа:
(z_1 = 3e^{frac{pi}{2}i})
(z_2 = 2e^{frac{pi}{3}i})
Необходимо найти произведение этих комплексных чисел.
Решение
Вначале требуется записать выражение:
(z_1 cdot z_2 = 3e^{frac{pi}{2}i} cdot 2e^{frac{pi}{3}i})
Путем перегруппировки множителей и применения свойства степени:
(e^x cdot e^y = e^{x+y})
Преобразуем выражение:
(3 cdot 2 cdot e^{(frac{pi}{2} + frac{pi}{3})i} = 6e^{frac{5pi}{6}i})
Ответ: (z_1 cdot z_2 = 6e^{frac{5pi}{6}i})
Задача 4
Даны комплексные числа:
(z_1 = 2bigg (cosfrac{pi}{3} + isin frac{pi}{3} bigg ))
(z_2 = 4 bigg (cosfrac{pi}{4} + isin frac{pi}{4} bigg ))
Требуется найти произведение этих комплексных чисел.
Решение
Если необходимо умножить комплексные числа, представленные в тригонометрической форме, то целесообразно сложить их аргументы и перемножить модули:
(z_1 cdot z_2 = 2 cdot 4 cdot bigg ( cos (frac{pi}{3} + frac{pi}{4}) + isin (frac{pi}{3} + frac{pi}{4}) bigg ) = 8 bigg (cos frac{7}{12} + isin frac{7}{12} bigg ))
Ответ: (z_1 cdot z_2 = 8 bigg (cos frac{7}{12} + isin frac{7}{12} bigg ))
Задача 5
Необходимо выполнить несколько действий с комплексными числами:
(z_1 = 3+i)
(z_2 = 5-2i)
Требуется найти их сумму и разность.
Решение
В первую очередь следует сложить комплексные числа. В этом случае нужно найти сумму соответствующих мнимых частей комплексных чисел:
(z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 — i)
Аналогичным способом можно найти разность комплексных чисел:
(z_1 — z_2 = (3+i) — (5-2i) = (3-5)+(i+2i) = -2 + 3i)
Ответ: (z_1 + z_2 = 8 — i; z_1 — z_2 = -2 + 3i)
Задача 6
Даны комплексные числа:
(z_1 = 3+i)
(z_2 = 5-2i)
Необходимо найти их произведение и выполнить деление комплексных чисел.
Решение
Вначале нужно записать выражение:
(z_1 cdot z_2 = (3+i) cdot (5-2i))
Далее требуется раскрыть скобки и выполнить приведение подобных слагаемых с учетом, что:
(i^2 = -1)
Таким образом, получим:
(15 — 6i + 5i -2i^2 = 15 — i — 2cdot(-1) = 15 — i + 2 = 17 — i)
Затем необходимо поделить первое число на второе:
(frac{z_1}{z_2} = frac{3+i}{5-2i})
Принцип деления заключается в исключении комплексного числа, которое расположено в знаменателе. Для того чтобы получить результат, необходимо домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю. По итогу следует раскрыть все скобки:
(=frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = frac{15 + 6i + 5i + 2i^2}{25 + 10i — 10i -4i^2} =)
(= frac{15 + 11i -2}{25 + 4} = frac{13 + 11i}{29})
Поделив числитель на 29, можно записать дробь алгебраическим способом:
(frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i)
Ответ: (z_1 cdot z_2 = 17 — i; frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i)
Задача 7
Дано комплексное число:
z = 3+3i
Данное число требуется возвести в степени:
- n=2
- n=7
Решение
В первом варианте:
(n = 2)
Комплексное число достаточно просто возвести в квадрат, если умножить его само на себя:
(z^2 = (3+3i)^2 = (3+3i)cdot (3+3i) =)
Применяя формулу, справедливую для умножения, следует раскрыть скобки и привести подобные:
(=9 + 9i + 3icdot 3 + 9i^2 = 9 + 18i — 9 = 18i)
В итоге получим:
(z^2 = (3+i)^2 = 18i)
Во втором варианте:
n = 7
Данный пример отличается повышенной сложностью вычислений, по сравнению с первым примером, где потребовалось лишь возвести комплексное число в квадрат. Если пойти стандартным путем и умножать комплексное число само на себя 7 раз, то вычисления могут занять неопределенное время. Упростить задачу легко, если применить к решению формулу Муавра. Данная закономерность справедлива в случае операций с комплексными числами, которые записаны в тригонометрической форме. По условиям задачи число представлено в алгебраическом виде. Поэтому в первую очередь целесообразно перевести его в тригонометрическую форму.
Требуется найти модуль:
(|z| = sqrt{3^2 + 3^2} = sqrt{9 + 9} = sqrt{18} = 3sqrt{2})
Далее следует вычислить аргумент:
(varphi = arctg frac{3}{3} = arctg(1) = frac{pi}{4})
Можно записать комплексное число в тригонометрической форме:
(z = 3sqrt{2}(cos frac{pi}{4} + isin frac{pi}{4}))
Возведение в степень n = 7 будет выглядеть следующим образом:
(z^7 = (3sqrt{2})^7 (cos frac{7pi}{4} + isin frac{7pi}{4}) =)
Представить наглядный ответ лучше в алгебраической форме. Для этого необходимо выполнить ряд манипуляций:
(=(3sqrt{2})^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = 3^7 sqrt{2}^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = 3^7 sqrt{2}^6 (1-i) = 3^7 cdot 8(1-i) =)
(= 2187 cdot 8 (1-i) = 17496(1-i))
Ответ: (z^2 = (3+i)^2 = 18i; ) (z^7 = 17496(1-i)).
Задача 8
Необходимо извлечь корень (sqrt[3]{-1}) над множеством (mathbb{C}.)
Решение
Следует преобразовать комплексное число в тригонометрическую форму. Для этого необходимо найти значение модуля и аргумента:
(|z| = sqrt{(-1)^2 + 0^2} = sqrt{1+0} = sqrt{1}=1)
(varphi = arctg frac{0}{-1} +pi = arctg 0 + pi = pi)
В результате получим выражение:
(z = (cos pi + isin pi))
С помощью формулы Муавра представляется возможным найти значение корней какой-либо степени:
(z^frac{1}{n} = r^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg))
(k=0,1,…,n-1)
По условию степень соответствует n = 3. Таким образом, согласно формуле:
k = 0,1,2
В результате получим:
(z_0 = sqrt[3]{1} (cos frac{pi}{3}+isin frac{pi}{3}) = frac{1}{2}+ifrac{sqrt{3}}{2})
(z_1 = sqrt[3]{1} (cos frac{3pi}{3}+isin frac{3pi}{3}) = -1)
(z_2 = sqrt[3]{1} (cos frac{5pi}{3}+isin frac{5pi}{3}) = frac{1}{2} — ifrac{sqrt{3}}{2})
Ответ: (z_0 = frac{1}{2}+ifrac{sqrt{3}}{2};) (z_1 = -1); (z_2 = frac{1}{2} — ifrac{sqrt{3}}{2})
Задача 9
Необходимо найти решение для квадратного уравнения:
(x^2 + 2x + 2 = 0) над (mathbb{C})
Решение
Найти ответ на данную задачу следует, используя общую формулу. Для начала необходимо вычислить дискриминант:
(D = b^2 — 4ac = 2^2 — 4cdot 1 cdot 2 = 4-8 = -4)
В результате получим:
(D=-4<0)
Однако на этом решение задачи не заканчивается. По условию требуется определить уравнение над комплексным множеством. Получение в итоге отрицательного дискриминанта говорит только о том, что в выражении отсутствуют вещественные корни. Это утверждение не отменяет наличие комплексных корней. Таким образом, следует их найти:
(x_{1,2} = frac{-bpm sqrt{D}}{2a} = frac{-2pm sqrt{-4}}{2} =)
Можно отметить, что:
(sqrt{-4} = 2sqrt{-1} = 2i)
Далее следует продолжить вычисления:
(= frac{-2 pm 2i}{2} = -1 pm i)
В результате получаются комплексно-сопряженные корни:
(x_1 = -1 – i)
(x_2 = -1 — i)
Ответ: (x_1 = -1 – i;) (x_2 = -1 — i)
(схема
43)
Комплексным числом называется выражение вида z=x+iy, (7.1)
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для
мнимой единицы
i2=–1. (7.2)
Если x=0, то число 0+iy=iy
называется чисто мнимым; если y=0, то число x+i∙0=x
отождествляется с действительным числом x, а это означает, что множество R всех действительных чисел является подмножеством
множества C всех
комплексных чисел, то есть 
Число x называется действительной частью комплексного
числа z и обозначается
x=Re z, а y – мнимой частью комплексного числа z и
обозначается y=Im z.
Два комплексных
числа z1=x1+iy1 и z2=x2+iy2
называются равными (z1=z2) тогда, когда равны их действительные и мнимые части: x1=x2, y1=y2. В частности, комплексное число z=x+iy равно
нулю, когда x=y=0.
Понятия «больше» и «меньше» для комплексных чисел не
вводятся.
Числа z=x+iy и 
Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости x0y такой,
что x=Re z, y=Im z.
Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа z=x+iy (рис. 7.1).
Плоскость, на которой изображаются комплексные числа, называется комплексной
плоскостью. Ось абсцисс называется действительной осью, так как на ней
лежат действительные числа z=x+0∙y=x. Ось ординат – мнимой осью, на ней лежат чисто мнимые комплексные числа z=0+iy.
Комплексное
число z=x+iy можно задавать с помощью радиус-вектора 

угла между положительным направлением действительной оси и вектором 
аргументом комплексного
числа, обозначается Arg z или φ.
Для комплексного числа z=0 аргумент не определен. Аргумент комплексного числа 
многозначная и определяется с точностью до слагаемого 2πk (k=0;–1;1;–2;2…): 
заключенное в промежутке (–π;π).
Иногда в качестве главного значения аргумента берут величину, принадлежащую
промежутку [0;2π).
Алгебраической
формой комплексного числа называется запись числа z в виде z=x+iy.
Модуль r и
аргумент φ можно рассматривать как
полярные координаты вектора 

z=x+iy можно
записать в виде 


Равенство
(7.3) есть тригонометрическая форма
комплексного числа. Модуль r=|z| однозначно
определяется по формуле

Аргумент определяется из формул:

При переходе от
алгебраической формы комплексного числа к тригонометрической достаточно
определить главное значение аргумента комплексного числа z, то есть
считать φ=arg z. Знаки полученных значений cos φ и sin φ по
формулам (7.5), дают возможность определить, какой координатной четверти
принадлежит угол φ.
Используя формулу
Эйлера

комплексное число 
называемой показательной (или
экспоненциальной) форме
z=reiφ, (7.7)
где r=|z| — модуль комплексного числа, а угол 
Функция eiφ – периодическая с основным периодом 2π, поэтому для записи комплексного числа в показательной форме по формуле 7.7 достаточно найти главное значение его аргумента, то есть считать φ=arg z.
Пример 7.1. Записать
комплексные числа 
тригонометрической и показательной формах.
Решение. Для z1 имеем 

Для действительного числа 
На множестве комплексных чисел определен ряд операций.
1.
Суммой двух
комплексных чисел z1=x1+iy1 и z2=x2+iy2
называется комплексное число, определяемое равенством

Из (7.8) следует, что геометрически комплексные числа складываются как
векторы, причем сумма комплексных чисел интерпретируется как диагональ
параллелограмма, построенного на векторах, представляющих слагаемые (рис. 7.2).
2.
Вычитание
комплексных чисел определяется
как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2
называется такое комплексное число z, которое, будучи сложенным с z2, дает число z1, то есть
z= z1 – z2, если z+z2=z1. Если z1=x1+iy1, z2=x2+iy2, то из
этого определения получаем:

Из равенства (7.9) следует, что геометрически
комплексные числа вычитаются как векторы. При этом число z= z1 – z2
изображается вектором, соединяющим концы векторов 
вычитаемого

Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости:

3.
Произведением комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется
комплексное число, определяемое равенством

Из (7.11) следует важнейшее соотношение i2= –1.
Действительно,

Найдем произведение комплексных чисел 

получим формулу произведения комплексных чисел, заданных в тригонометрической форме:

Видно, что при умножении комплексных чисел в
тригонометрической форме их модули перемножаются, а аргументы складываются. Это
правило распространяется на любое конечное число множителей. Нетрудно видеть,
что если есть n множителей и все они одинаковые, то частным случаем
равенства (7.12) является формула возведения комплексного числа в
натуральную
степень:

(7.13)
называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

4.
Частным двух
комплексных чисел z1 и 
число z, которое, будучи умноженным на z2, дает число z1, то есть 

Пусть 

На практике при нахождении частного двух комплексных чисел
удобно умножить числитель и знаменатель дроби 
знаменателю, с дальнейшим применением равенства i2= –1 и формулы разности квадратов.
Деление комплексных чисел осуществляется также и в
тригонометрической форме, при этом имеет место формула:

Видно, что при делении
комплексных чисел их модули делятся, а
аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

Пример 7.2. Найти
сумму, разность, произведение и частное комплексных чисел 
Решение. По
формуле (7.8) сумма заданных чисел равна 
Согласно формуле (7.9) разность заданных чисел равна 
Пользуясь формулой (7.11), вычислим их произведение

На основании формулы (7.14) вычислим их частное
Пример 7.3. Найти
произведение и частное комплексных чисел 
Решение.
Используя (7.4) и (7.5), получаем:

(7.3) и (7.7) число z1 имеет
тригонометрическую и показательную форму

Аналогично, для z2 можно
записать:


По формулам (7.12) и (7.16) получим в
тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в
показательной форме:
5.
Извлечение
корня n-ой
степени – операция, обратная возведению
в натуральную степень, определенному ранее формулой (7.13).
Корнем n-ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωn=z, то есть 
Пусть 
определению и формуле (7.13) Муавра можно записать: 


арифметический). Окончательно получаем:

(7.18) называется второй формулой Муавра.
Видно, что для
любого 
из комплексного числа z имеет равно n различных значений.
Пример 7.4. Найти все корни уравнения z4+16=0.
Решение.
Запишем уравнение в виде z4=–16+0∙i. Отсюда по
формуле (7.18) получим:

Рассмотрим различные значения k=0;1;2;3.
Корни z1 и z4, а также
z2 и z3 являются
комплексно сопряженными. Таким образом, корнями заданного уравнения z4+16=0
являются комплексные числа
Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел.
Теорема 7.1 (основная теорема алгебры). Для всякого
многочлена с комплексными коэффициентами

существует точка 
Приведем еще
одну теорему, имеющую место над множеством комплексных чисел.
Теорема 7.2. Если
многочлен Pn(x) с действительными коэффициентами имеет комплексный
корень a+ib, то он
имеет и сопряженный корень a–ib
В разложение
многочлена 
входят сопряженными парами. Пусть корни многочлена x1=a+ib и x2=a–ib. Перемножив линейные множители
разложения 
коэффициентами x2+px+q и
отрицательным дискриминантом. Действительно,
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Вопросы
для самопроверки
Над комплексными числами в показательной форме выполнимы те же операции и по тем же самым правилам, что и для чисел, заданных в тригонометрической форме. Покажем это.
Пусть 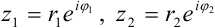
Умножение
Получили что 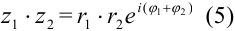
Деление
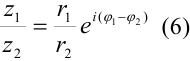
Возведение в степень
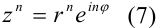


Извлечение корня n-й степени
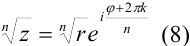
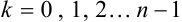

Пример №43.4.
Для комплексных чисел 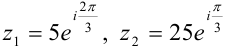
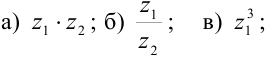
Решение:
а) Согласно формуле (5) получим
б) Используя формулу (6), находим
в) Применяя формулу (7), находим
г) Извлечем квадратный корень из 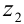
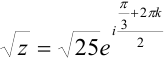
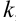
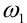
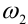
При
При
Ответ:
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
В
математическом анализе в дальнейшем
доказываются формулы, которые впервые
были получены Эйлером. Доказательство
этих формул основано на теории рядов,
поэтому мы приводим их без доказательств.
По
формулам Эйлера показательную функцию
с мнимой единицей в показателе степени
можно выразить через тригонометрические
функции действительного аргумента
следующим образом:
(3.1.1)
Из
формул Эйлера (3.1.1) легко получить другие:
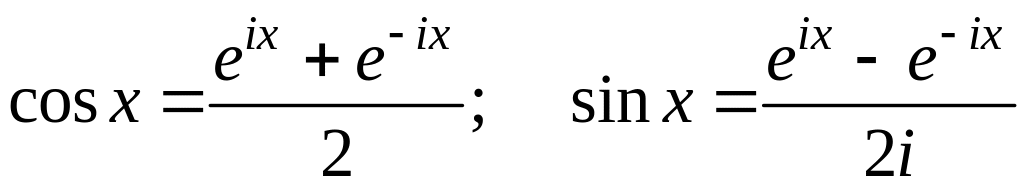
Запишем
комплексное число в тригонометрической
форме:
Выражение
в скобках, согласно формуле Эйлера
(3.1.1) представляет собой показательную
функцию с мнимой единицей в показателе
степени т.е.
Последнюю запись
называют показательной формой комплексного
числа.
Итак, комплексное
число можно представить в трех формах:
– алгебраической
– тригонометрической
– показательной
Пример
1. Представить
в алгебраической форме комплексное
число
.
Решение.
Комплексное число дано в показательной
форме, его модуль
,
аргумент
.
Найдем действительную и мнимую части:
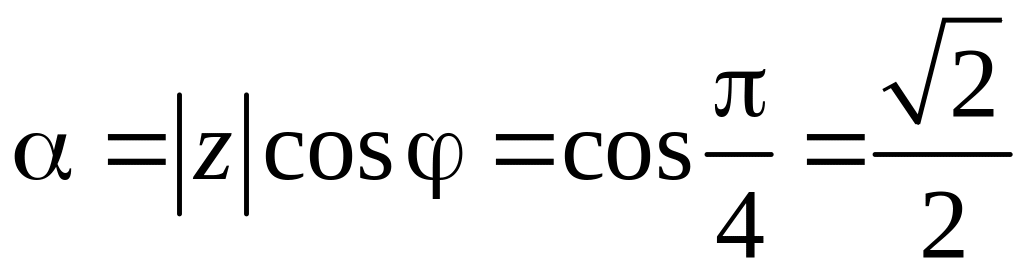
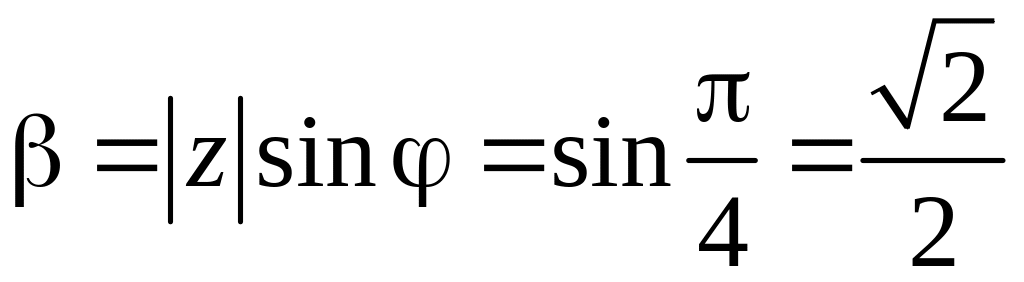
Таким
образом
.
Пример
2. Перейти
от алгебраической к показательной форме
комплексного числа z
= – i.
Р
ешение.
Для данного числа α =0; β = –1, найдем его
модуль и аргумент:
(Рис.3.1.2)
Следовательно
.
3.1.4. Действия над комплексными числами (сложение и вычитание)
О
перацию
сложения и вычитания комплексных чисел
можно рассматривать как операцию
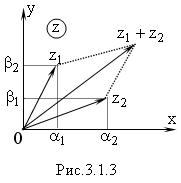
сложения и вычитания векторов (Рис.3.1.3)
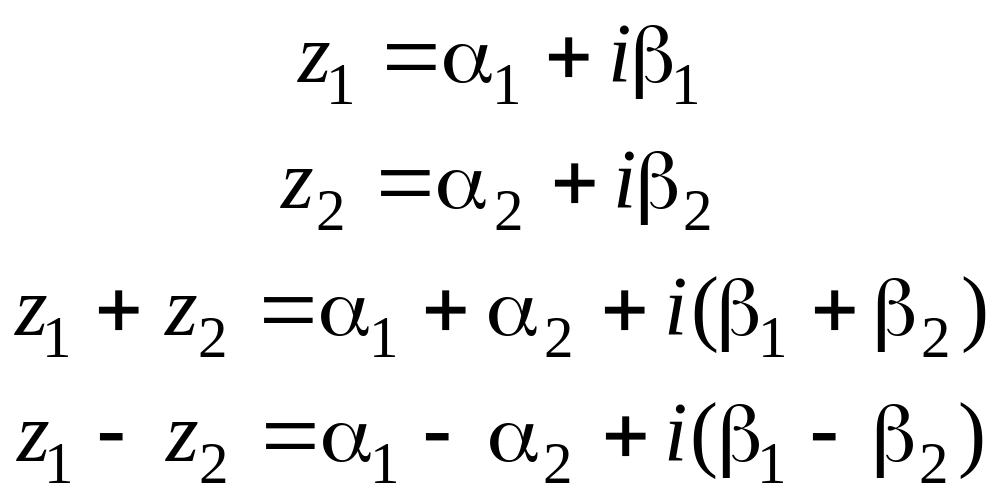
При
сложении и вычитании комплексных чисел,
их действительные и мнимые части
складываются или вычитаются, при этом
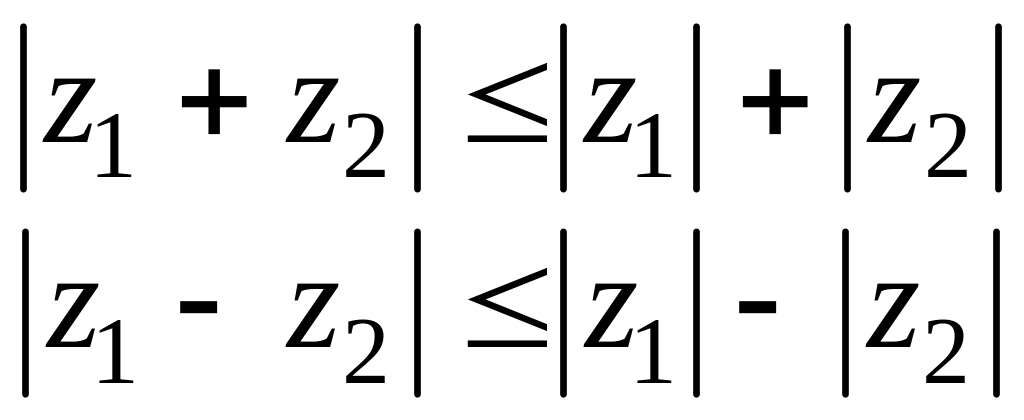
Пример
3. Найти
,
если
Сложение и вычитание
комплексных чисел удобнее проводить,
когда они записаны в алгебраической
форме.
3.1.5. Умножение комплексных чисел
Рассмотрим умножение
комплексных чисел в алгебраической
форме.
Даны два числа:
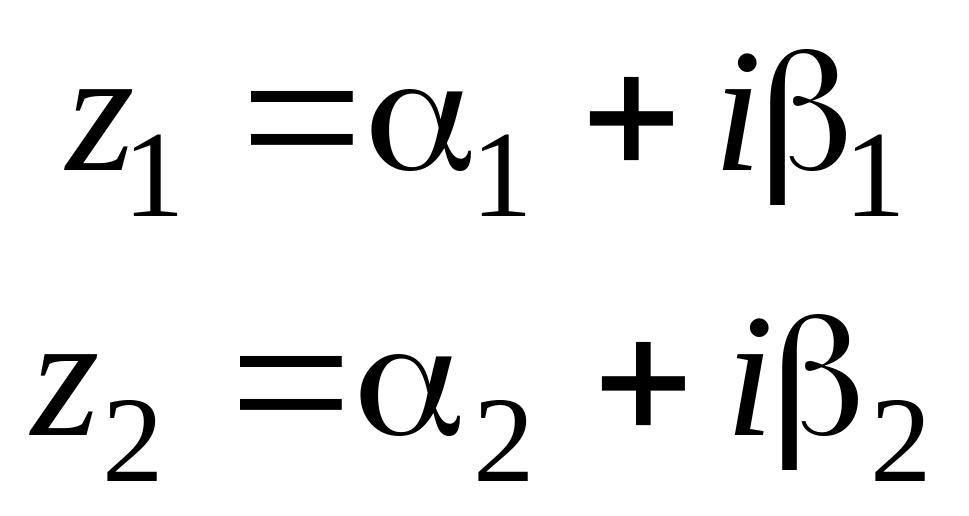
Нужно
найти произведение
.
Перемножим двухчлены
по правилам алгебры:
если
учесть, что
то получим:
Таким
образом, умножение комплексных чисел
в алгебраической форме проводится по
обычным алгебраическим правилам.
Следует отметить,
что произведению сопряженных комплексных
чисел является действительным числом,
в самом деле
Пусть комплексные
числа даны в показательной форме
Найдем их произведение
Складывая
показатели степени у показательных
функций с одинаковым основанием, получим:
По
формулам Эйлера (3.1.1) результат перемножения
двух комплексных чисел можно записать
в тригонометрической форме:
Итак,
при умножении комплексных чисел в
показательной и тригонометрической
формах модули перемножаются, а аргументы
складываются.
3.1.6. Деление комплексных чисел
Деление комплексных
чисел, так же как и умножение, удобнее
вводить, когда они записаны в показательной
или тригонометрической форме.
Найдем частное от
деления двух комплексных чисел:
или
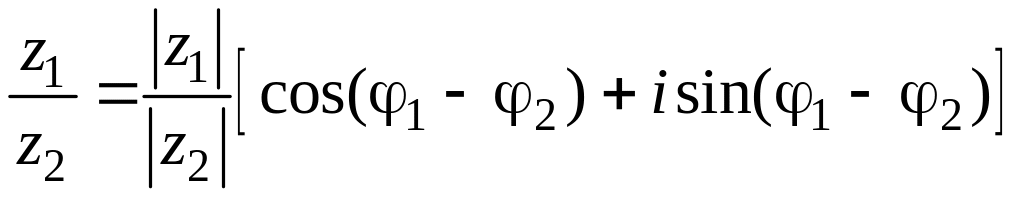
Таким образом, при
делении комплексных чисел их модули
делятся, а аргументы вычитаются.
Деление
комплексных чисел можно проводить и в
алгебраической форме. Найдем частное
от деления:
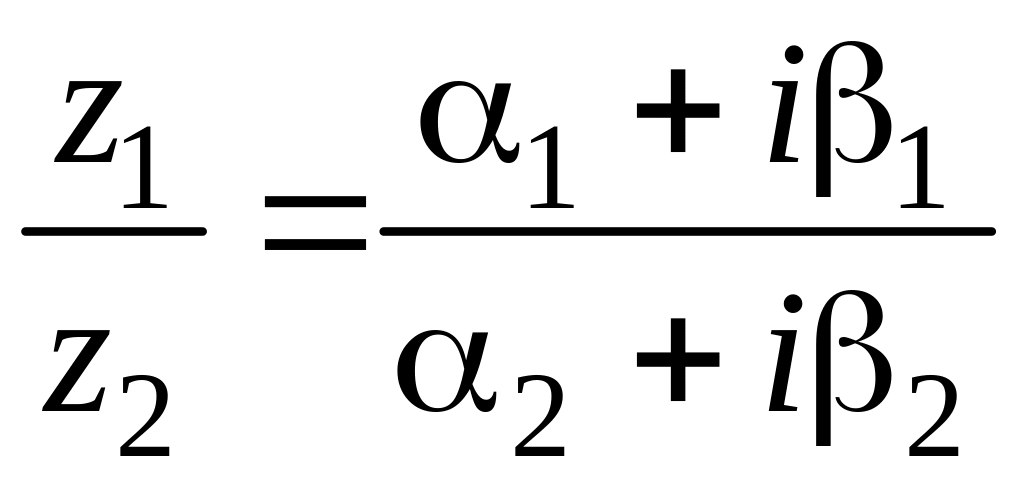
Чтобы
избавится от мнимой единицы в знаменателе,
нужно умножить числитель и знаменатель
на сопряженное число знаменателю:
а затем по обычным
правилам алгебры перемножить двухчлены
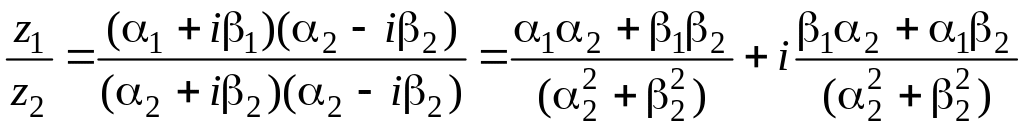
Полученный
результат также является комплексным
числом в алгебраической форме.
Пример
4. Вычислить
Решение.
Умножим числитель и знаменатель на
сопряженное число знаменателю 1
– i:
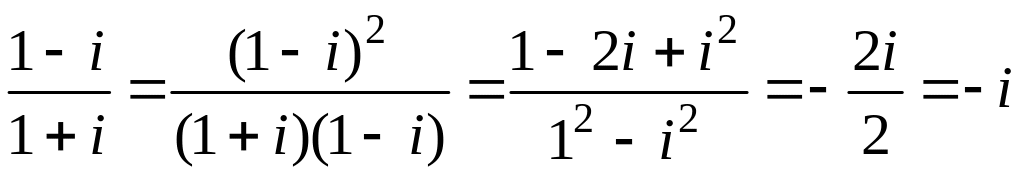
Такой же результат
получается при переходе к показательной
форме
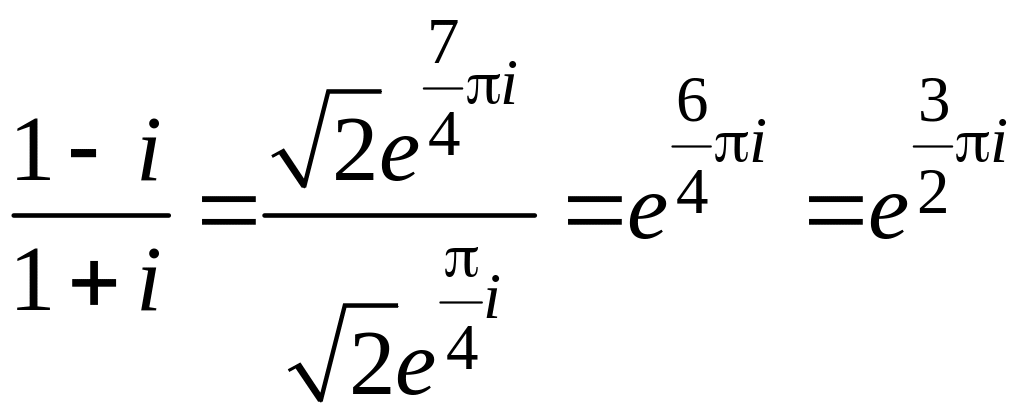
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Формула Эйлера
- Показательная форма записи комплексного числа
- Операции с комплексными числами в показательной форме
Формула Эйлера
Пусть $z=a+b i$ —
некоторое комплексное число. По определению полагают, что
$e^{z}=e^{a+b i}=e^{a} e^{b i}=e^{a}(cos b+i sin b)$
Если число $z$ — действительное, то есть
$z=a=a+0 cdot i$, то
$e^{z}=e^{a+0 cdot i}=e^{a}(cos 0+i sin 0)=e^{a}$
Если число $z$ — чисто мнимое, то есть
$z=b i=0+b i$, то
$e^{z}=e^{0+b i}=e^{b i}=cos b+i sin b$
Таким образом, имеем равенство
$e^{b i}=cos b+i sin b$
которое называется формулой Эйлера.
Показательная форма записи комплексного числа
Рассмотрим произвольное комплексное число,
записанное в тригонометрической форме:
$z=|z|(cos phi+i sin phi)$. По формуле Эйлера
$cos phi+i sin phi=e^{i phi}$
а тогда
$z=|z|(cos phi+i sin phi)=|z| e^{i phi}$
Следовательно, любое комплексное число можно представить в так называемой показательной форме:
Пример
Задание. Записать комплексное число
$z=3-4 i$ в показательной форме.
Решение. Найдем
модуль и аргумент заданного комплексного числа:
$|z|=sqrt{3^{2}+(-4)^{2}}=sqrt{9+16}=sqrt{25}=5$
$phi=operatorname{arctg} frac{-4}{3}=-operatorname{arctg} frac{4}{3}$
Тогда
$z=|z| e^{i phi}=5 e^{-i operatorname{arctg} frac{4}{3}}$
Ответ. $z=5 e^{-i operatorname{arctg} frac{4}{3}}$
Операции с комплексными числами в показательной форме
Такая форма представления позволяет дать наглядную интерпретацию операциям
умножения комплексных чисел, их
деления и
возведения комплексного числа в степень. Например, умножение комплексного числа
$z_{1}=left|z_{1}right| e^{i phi_{1}}$ на комплексное число
$z_{2}=left|z_{2}right| e^{i phi_{2}}$ выглядит следующим образом:
$z_{1} cdot z_{2}=left|z_{1}right| e^{i phi_{1}} cdotleft|z_{2}right| e^{i phi_{2}}=left|z_{1}right| cdotleft|z_{2}right| e^{i phi_{1}+i phi_{2}}=$
$=left|z_{1}right| cdotleft|z_{2}right| e^{ileft(phi_{1}+phi_{2}right)}$
То есть, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.
Аналогично можно довольно легко найти частное от деления комплексного числа
$z_{1}=left|z_{1}right| e^{i phi_{1}}$ на комплексное число
$z_{2}=left|z_{2}right| e^{i phi_{2}}$ :
$frac{z_{1}}{z_{2}}=frac{left|z_{1}right| e^{i phi_{1}}}{left|z_{2}right| e^{i phi_{2}}}=frac{left|z_{1}right|}{left|z_{2}right|} e^{i phi_{1}-i phi_{2}}=frac{left|z_{1}right|}{left|z_{2}right|} e^{ileft(phi_{1}-phi_{2}right)}$
Отсюда получаем правило, что для того чтобы найти частное двух комплексных чисел, надо поделить их модули и отнять аргументы.
Для возведения комплексного числа
$z$ в целую степень
$n$ нужно представить это число в показательной форме
$z=|z| e^{i phi}$, модуль возвести в степень, а аргумент увеличить в
$n$ раз:
$z^{n}=left(|z| e^{i phi}right)^{n}=|z|^{n} e^{i n phi}$
Читать дальше: сложение и вычитание комплексных чисел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!