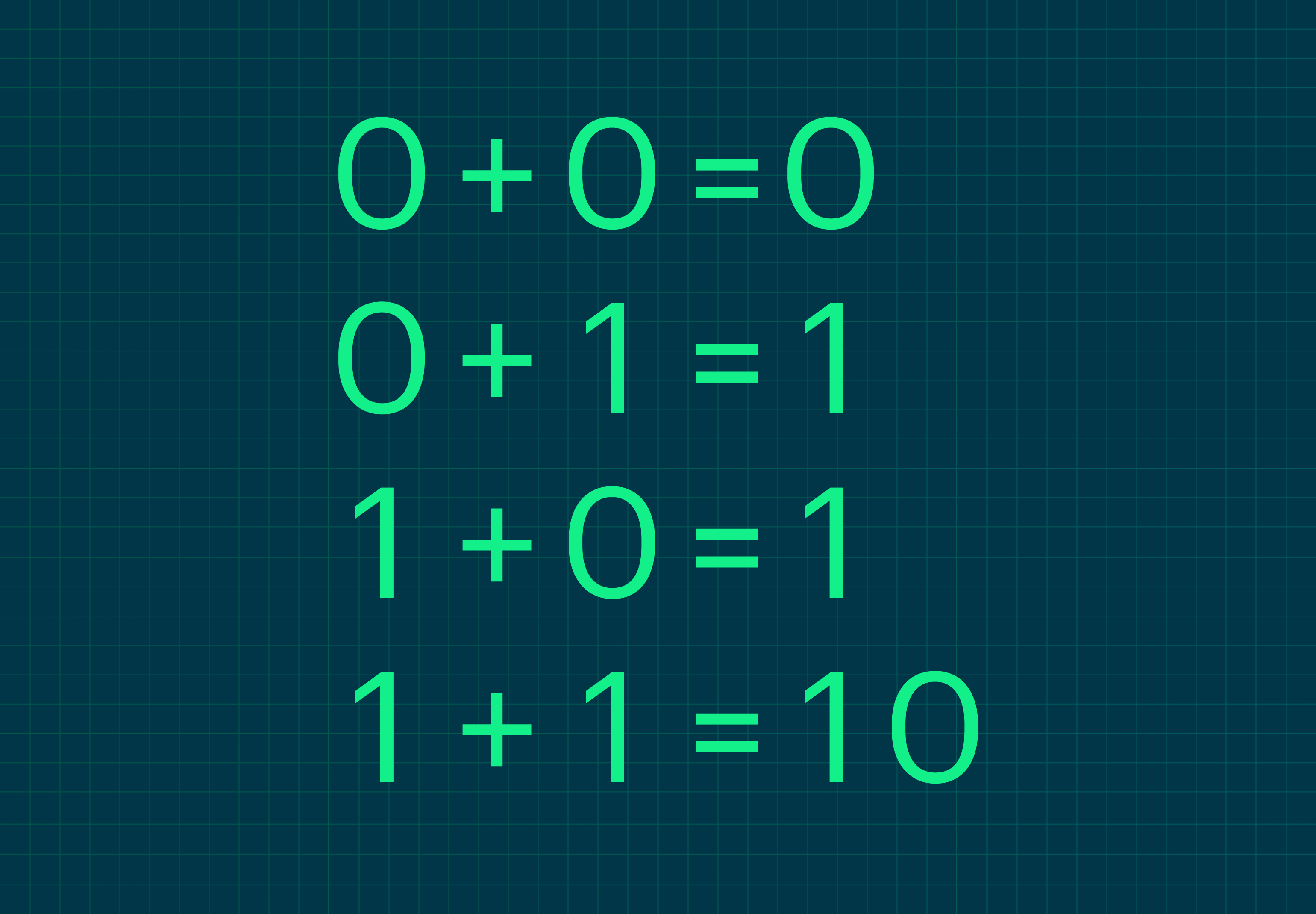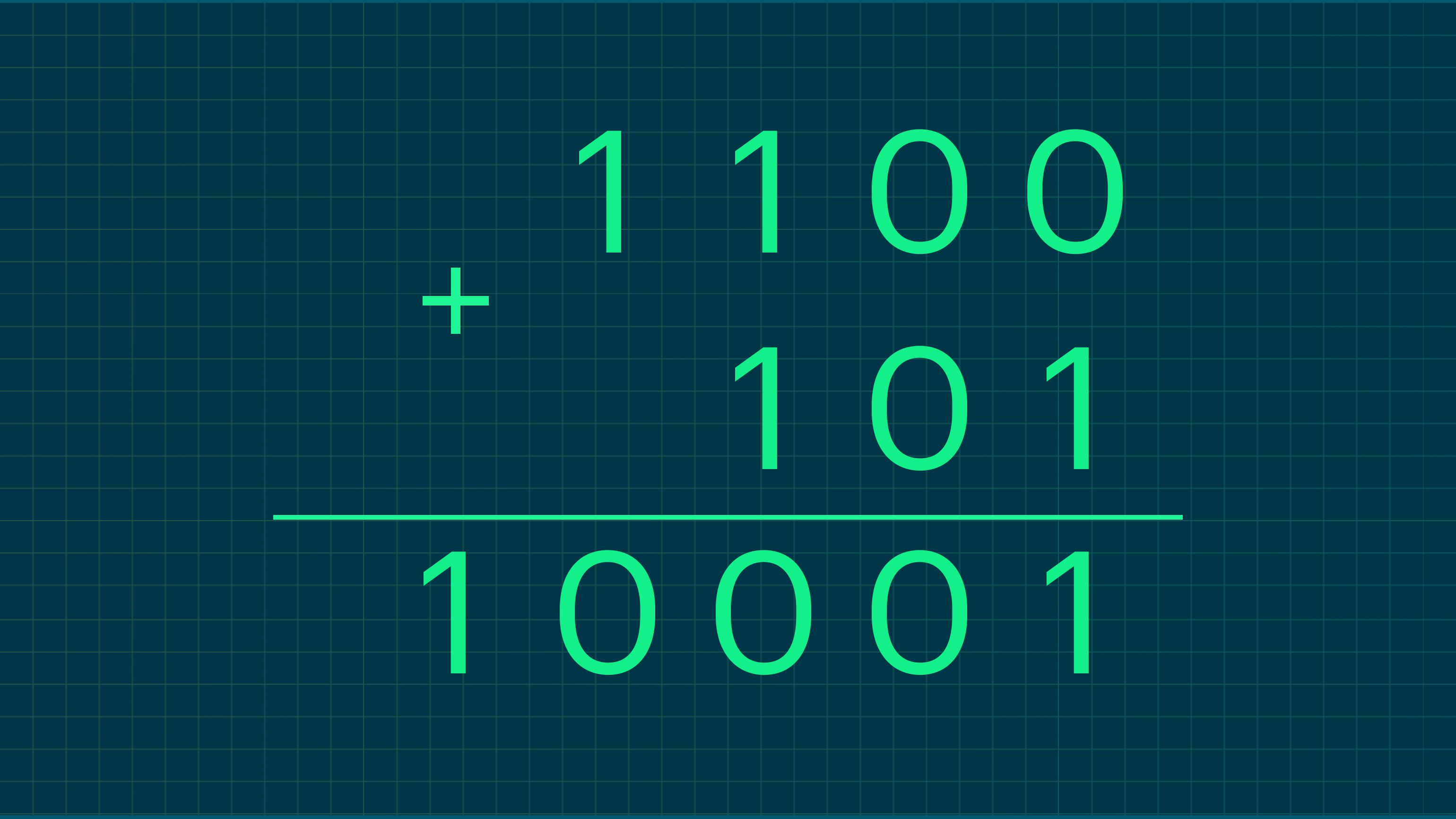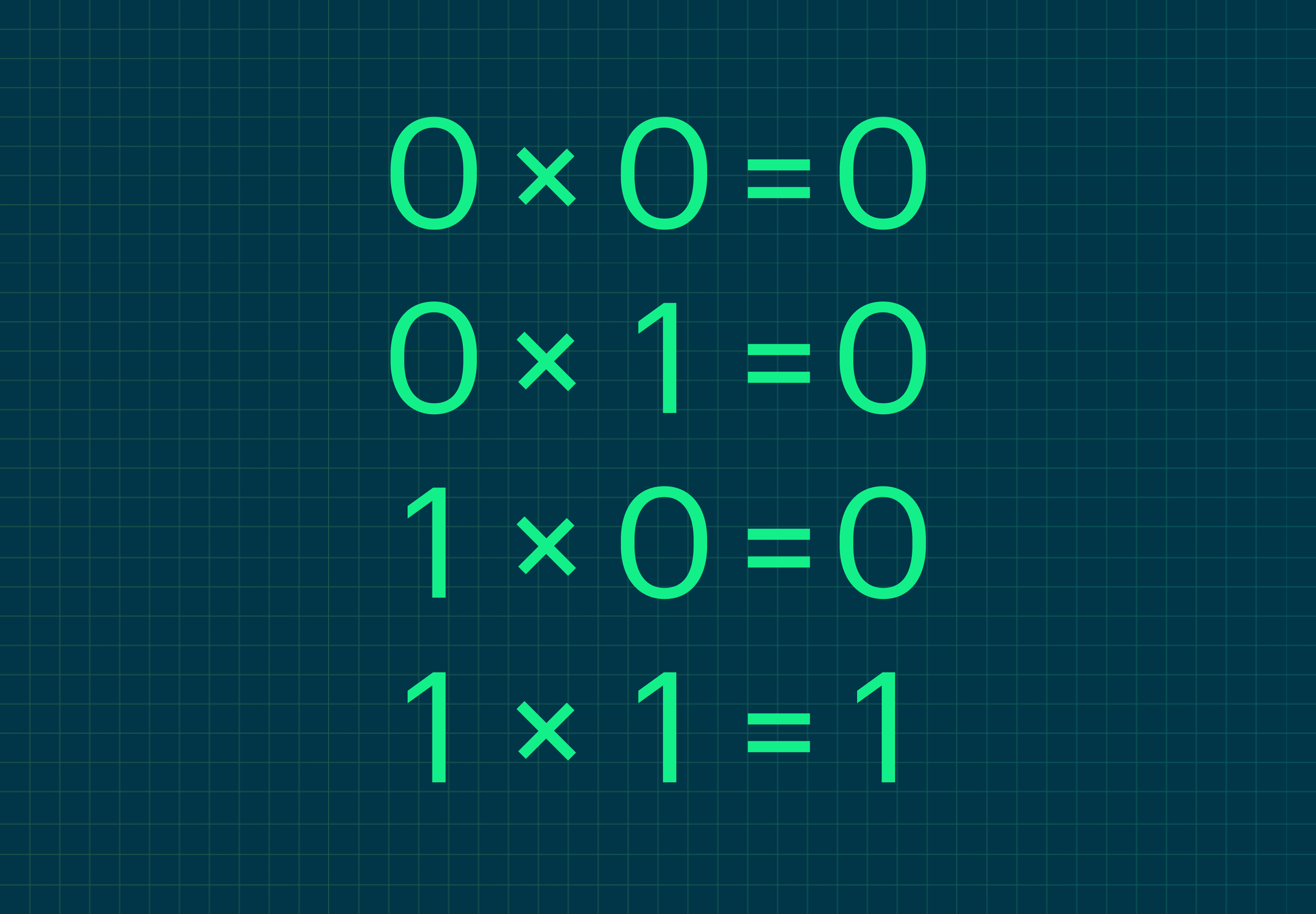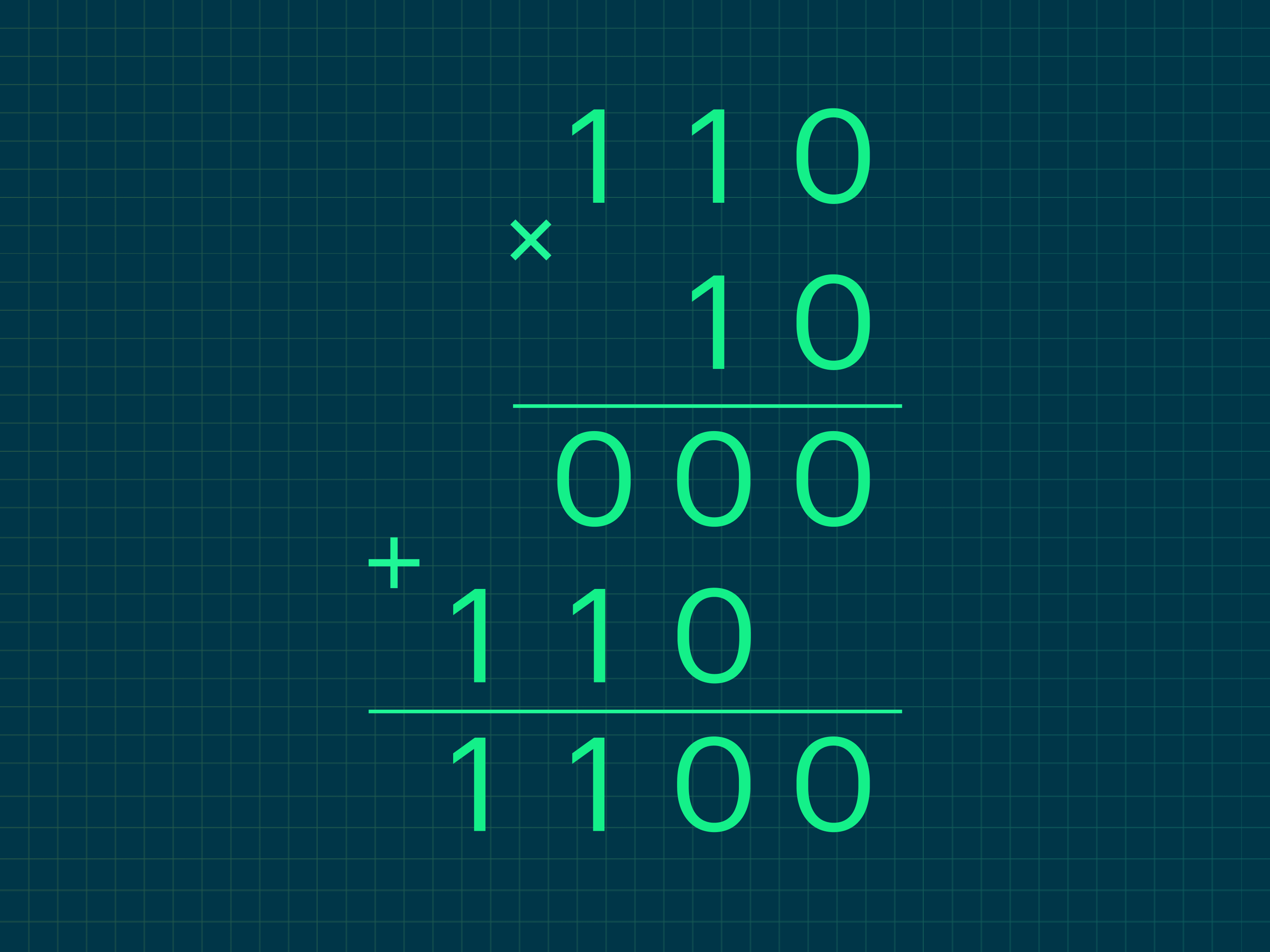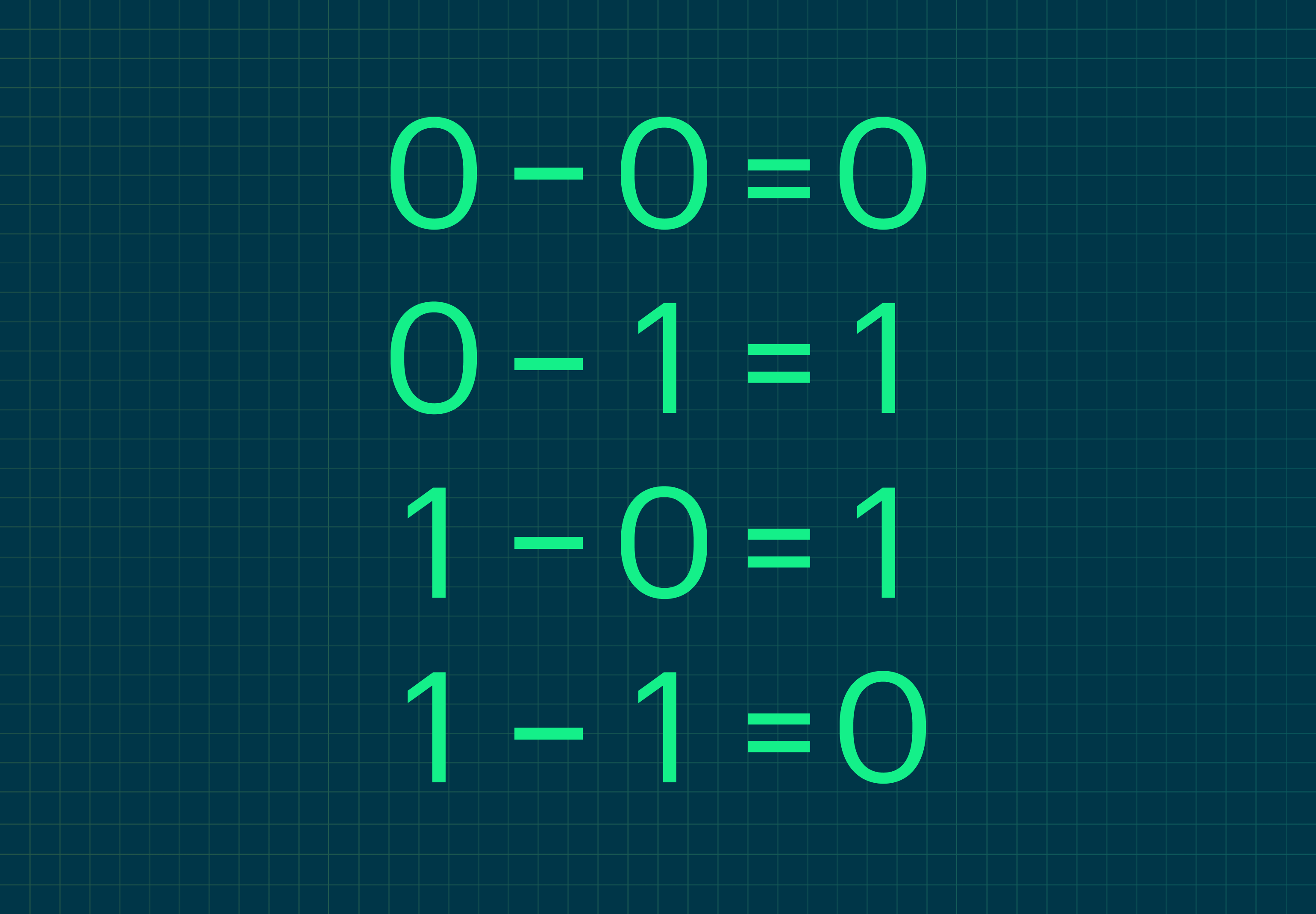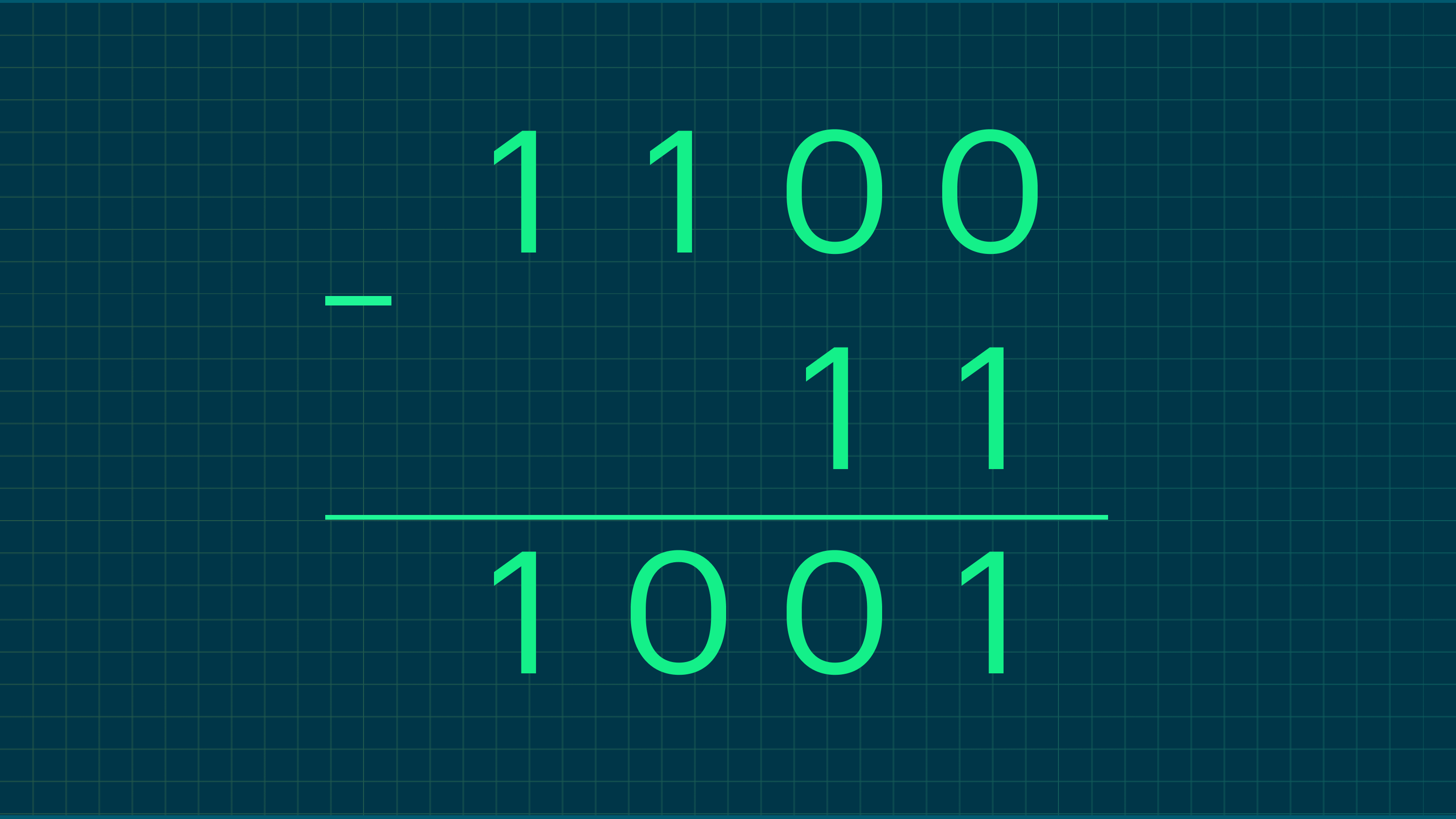#статьи
- 27 фев 2023
-
0
Двоичная арифметика: сложение, умножение, вычитание, деление бинарных чисел
Учимся складывать, вычитать, умножать и делить двоичные числа — работаем с фундаментальными законами современной цифровой электроники.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Мы привыкли считать всё в десятичной системе, потому что у нас 10 пальцев — и это удобно. Но если бы у нас было больше пальцев, например 12, то система могла бы быть двенадцатиричной и мы бы воспринимали её как обычную.
Когда дело доходит до двоичной системы счисления, сложно вот так сразу переключиться на её арифметику — хотя, казалось бы, принципы такие же, как для десятичной. Ведь там есть все привычные операции: сложение, вычитание, умножение, деление. Единственное отличие: в двоичных числах используются всего две цифры — ноль и единица.
Давайте избавимся от страха и наконец узнаем, как проводить знакомые нам математические операции в двоичной системе.
Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд.
В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.
Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).
Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:
Но лучше разобраться на примерах.
Пример 1. Давайте сложим 1100 и 101.
Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:
- Первый: 0 + 1 = 1.
- Второй: 0 + 0 = 0.
- Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.
Пример 2. Сложим 1111 и 111.
Теперь поразрядно:
- Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
- Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1.
Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.
Ответ
1101 + 1011 = 11000.
Умножение в двоичной системе, как в десятичной, основано на сложении — и умении считать в столбик.
Сведём в таблицу правила умножения двоичных чисел:
Давайте теперь посмотрим на реальных примерах, как правильно умножать двоичные числа.
Пример 1. Умножим 110 на 10.
Здесь мы воспользуемся привычным школьным «столбиком»: сначала умножаем верхнее число, 110, на 0, затем на 1, а потом складываем полученные два и получаем результат.
По сути, если мы умножаем число на ноль, то оно превращается в ноль, а если на единицу — остаётся неизменным, но сдвигается на число разрядов, равное номеру разряда этой единицы, как в обычном умножении:
- 110 × 0 = 000;
- 110 × 1 = 110.
Сдвигаем 110 на один разряд влево и складываем результаты промежуточных умножений:
- 000 + 1100 = 1100.
Мы получили 1100, потому что сместили результат умножения 110 × 1 на один разряд влево, а затем добавили один 0 справа — как в обычном умножении.
Пример 2. Давайте теперь умножим 101 на 101.
Не пугайтесь, что у нас получилось три числа, которые нужно сложить: правила остаются теми же. Ещё можно приписывать дополнительные нули туда, где находится пустое пространство — это поможет не запутаться.
Разберём пошагово:
- 101 × 1 = 101;
- 101 × 0 = 000;
- 101 × 1 = 101.
Снова сдвигаем влево промежуточные результаты и складываем:
- 101 + 0000 + 10100 = 11001.
Попробуйте сами умножить 1101 на 111.
Ответ
1011011.
Правила двоичного вычитания тоже ничем не отличаются от десятичного. Мы также вычитаем поразрядно и, если нужно, занимаем единицу из старшего разряда.
Таблица вычитания выглядит так:
Заметьте, что 0 − 1 = 1. Это всё потому, что мы занимаем единицу из старшего разряда и получаем 10, или 2 в десятичной системе, а если вычесть из 10 число 1, получим 1 (ведь 2 − 1 = 1).
Перейдём к примерам, чтобы понять, как вычитать одно число из другого.
Пример 1. Вычтем из 1100 число 11.
Разберём подробнее поразрядно:
- Первый: 0 − 1 = 1 — занимаем единицу из старшего разряда.
- Второй: 1 − 1 = 0 — так как отсюда заняли единицу, но у нас её не было, мы взяли её из следующего разряда и вычли единицу из этого.
- Третий: 0 − 0 = 0 — из этого разряда единица ушла в первый.
- Четвёртый: 1 − 0 = 1 — здесь всё нормально.
Всё то же знакомое нам вычитание.
Пример 2. Вычтем из 1011 число 101.
Тот же алгоритм по разрядам:
- Первый: 1 − 1 = 0.
- Второй: 1 − 0 = 1.
- Третий: 0 − 1 = 1 — заняли единицу из следующего разряда.
- Четвёртый: 0 − 0 = 0 — отдали единицу в предыдущий разряд.
Кажется, что всё несложно. Попробуйте теперь сами вычесть из 11010 число 1111.
Ответ
1011.
Вы удивитесь, но правила деления двоичных чисел похожи на деление десятичных. Рисуем привычный «столбик», умножаем, вычитаем, получаем результат.
Таблицы тут нет, потому что она бессмысленна — давайте сразу на примерах разбирать, как делить двоичные числа.
Пример 1. Поделить 1100 на 10.
У нас есть только два варианта: умножить делитель на 1 или на 0. Поэтому алгоритм будет таким:
- Смотрим на делимое, видим, что первые две его цифры — 11. Умножаем делитель на 1 и вычитаем из 11 число 10.
- Получили 1, дописываем справа следующую по порядку цифру — 0. Теперь 10 равно делителю, значит, тоже умножаем его на 1 и вычитаем.
- Получаем 0. Но у нас ещё остался один 0 у делимого — дописываем его справа от полученного 0.
- Число 0 меньше, чем 10, поэтому умножаем делитель на 0. Получаем конечный ответ — 110.
Пример 2. Поделить 10010 на 110.
Пошаговый алгоритм:
- Первые три числа делимого меньше, чем делитель — значит, умножаем делитель на 0 и вычитаем. Получаем 100.
- Дописываем 1 справа от 100, видим, что 1001 больше, чем 110, поэтому умножаем делитель на 1 и вычитаем его из 1001. Получаем 11.
- Дописываем 0 справа. Полученное 110 равно делителю, поэтому тоже умножаем его на 1, получаем конечный результат.
Попробуйте сами теперь поделить 10100 на 100.
Ответ
101.
Двоичная арифметика во многом похожа на десятичную: мы так же можем складывать, вычитать, делить и умножать числа столбиком. Правда, в двоичной системе всего две цифры: 0 и 1 — поэтому привычные математические операции в ней могут показаться немного странными. К счастью, в основе двоичной арифметики лежат простые принципы, которые нужно запомнить.

Научитесь: Профессия Python-разработчик
Узнать больше
Для того, чтобы
умножить двоичное число на 2 (десятичная
двойка это 10 в двоичной системе) достаточно
к умножаемому числу справа приписать
один ноль.
Пример 3.3.
Выполнить операцию умножения
10101 * 10 =
101010.
Проверка.
10101 = 1*24
+ 0*23
+ 1*22 +
0*21 +1*20
= 16 + 4 + 1 = 21
101010 =1*25
+ 0*24
+ 1*23 +
0*22 +1*21
+0*20
= 32 + 8 + 2 = 42
21 * 2 = 42.
Если вспомнить,
что любое двоичное число разлагается
по степеням двойки, то становится ясно,
что умножение в двоичной системе
счисления сводится к умножению на 10 (то
есть на десятичную 2), а стало быть,
умножение это ряд последовательных
сдвигов. Общее правило таково: как и для
десятичных чисел, умножение двоичных
выполняется поразрядно. И для каждого
разряда второго множителя к первому
множителю добавляется один ноль справа.
Пример 3.4.
Выполнить
операцию умножения 1011 * 101.
Умножение можно
свести к сумме трёх поразрядных умножений:
1011 * 1 + 1011 * 0 + 1011 *
100 = 1011 +101100 = 110111.
В столбик это же
самое можно записать так:
|
1 |
0 |
1 |
1 |
||
|
* |
1 |
0 |
1 |
||
|
1 |
0 |
1 |
1 |
||
|
0 |
0 |
0 |
0 |
||
|
1 |
0 |
1 |
1 |
||
|
1 |
1 |
0 |
1 |
1 |
1 |
Проверка:
101 = 5 (десятичное)
1011 = 11 (десятичное)
110111 = 55 (десятичное)
5*11 = 55 верное
равенство
Умножение
двоичных многоразрядных чисел
производится путём образования частичных
произведений и последующего их
суммирования. В соответствии с таблицей
двоичного умножения каждое частичное
произведение равно нулю, если в
соответствующем разряде множителя
стоит 0, или равно множимому, сдвинутому
на соответствующее число разрядов
влево, если в соответствующем разряде
множителя стоит 1. Таким образом, операция
умножения сводится к операциям сдвига
и сложения. Положение точки определяется
так же, как и при умножении десятичных
чисел.
Пример 3.5.
Выполнить операцию умножения 1010.1 на
101.01.

3.4. Деление двоичных чисел
При делении двоичных
чисел используются таблицы двоичного
умножения и вычитания.
Пример 3.6.
Выполнить деление двоичного числа
1010.101 на двоичное число 10.1:

Деление выполняется
по тем же правилам, что и деление в
десятичной системе счисления.
Выше были рассмотрены
три действия и уже понятно, что, в
общем-то, действия над двоичными числами
мало отличаются от действий над
десятичными числами. Разница появляется
только в том, что цифр две, а не десять,
но это только упрощает арифметические
операции. Так же обстоит дело и с делением,
но для лучшего понимания алгоритм
деления разберём более подробно. Пусть
нам необходимо разделить два десятичных
числа, например 234 разделить на 7.
|
2 |
3 |
4 |
7 |
|
Выделяем справа
(от старшего разряда) такое количество
цифр, чтобы получившееся число было как
можно меньше и в то же время больше
делителя. 2 – меньше делителя, следовательно,
необходимое нам число 23. Затем делим
полученное число на делитель с остатком.
Получаем следующий результат:
|
2 |
3 |
4 |
7 |
||
|
– |
2 |
1 |
3 |
||
|
2 |
4 |
Описанную операцию
повторяем до тех пор, пока полученный
остаток не окажется меньше делителя.
Когда это случится, число, полученное
под чертой, это частное, а последний
остаток – это остаток операции. Операция
деления двоичного числа выполняется
точно также.
Пример 3.7.
Разделить
10010111(2)
на 101(2).
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
Ищем число, от
старшего разряда которое первое было
бы больше чем делитель. Это четырехразрядное
число 1001. Оно выделено жирным шрифтом.
Теперь необходимо подобрать делитель
выделенному числу. И здесь мы опять
выигрываем в сравнении в десятичной
системой. Дело в том, что подбираемый
делитель это обязательно цифра, а цифры
у нас только две. Так как 1001 явно больше
101, то с делителем всё понятно это 1.
Выполним первый
шаг
операции.
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
– |
1 |
0 |
1 |
1 |
|||||||
|
1 |
0 |
0 |
Остаток от
выполненной операции 100. Это меньше чем
101, поэтому чтобы выполнить второй
шаг деления,
необходимо добавить к 100 следующую
цифру, это цифра 0. Теперь имеем следующее
число:
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
– |
1 |
0 |
1 |
1 |
|||||||
|
1 |
0 |
0 |
0 |
1000 больше 101 поэтому
на втором шаге мы опять допишем в частное
цифру 1 и получим следующий результат
(для экономии места сразу опустим
следующую цифру).
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
– |
1 |
0 |
1 |
1 |
1 |
||||||
|
1 |
0 |
0 |
0 |
||||||||
|
– |
1 |
0 |
1 |
||||||||
|
1 |
1 |
0 |
Третий шаг.
Полученное число 110 больше 101, поэтому
и на этом шаге мы запишем в частное 1.
Получиться так:
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
– |
1 |
0 |
1 |
1 |
1 |
1 |
|||||
|
1 |
0 |
0 |
0 |
||||||||
|
– |
1 |
0 |
1 |
||||||||
|
1 |
1 |
0 |
|||||||||
|
– |
1 |
0 |
1 |
||||||||
|
1 |
1 |
Полученное число
11 меньше 101, поэтому записываем в частное
цифру 0 и опускаем вниз следующую цифру.
Получается так:
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
||||
|
– |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|||||||
|
1 |
0 |
0 |
0 |
|||||||||||
|
– |
1 |
0 |
1 |
|||||||||||
|
1 |
1 |
0 |
||||||||||||
|
– |
1 |
0 |
1 |
|||||||||||
|
1 |
1 |
1 |
Полученное число
больше 101, поэтому в частное записываем
цифру 1 и опять выполняем действия.
Получается такая картина:
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|||||
|
– |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
||||||
|
1 |
0 |
0 |
0 |
|||||||||||
|
– |
1 |
0 |
1 |
|||||||||||
|
1 |
1 |
0 |
||||||||||||
|
– |
1 |
0 |
1 |
|||||||||||
|
1 |
1 |
1 |
||||||||||||
|
– |
1 |
0 |
1 |
|||||||||||
|
1 |
0 |
Полученный остаток
10 меньше 101, но у нас закончились цифры
в делимом, поэтому 10 это остаток, а 1110
это искомое частное.
Проверим в десятичных
числах
10010011 = 147
101 = 5
10 = 2
11101 = 29
|
1 |
4 |
7 |
5 |
||
|
– |
1 |
0 |
2 |
9 |
|
|
4 |
7 |
||||
|
– |
4 |
5 |
|||
|
2 |
Запись числа в
двоичной системе существенно упрощает
арифметические операции, но в то же
время сама запись становится значительно
длиннее, что уменьшает ценность
полученного упрощения, поэтому необходимо
найти такие задачи, решение которых
существенно проще в двоичных числах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Двоичная арифметика

4.5
Средняя оценка: 4.5
Всего получено оценок: 285.
4.5
Средняя оценка: 4.5
Всего получено оценок: 285.
Операции сложения, вычитания, умножения и деления в двоичной системе – это двоичная арифметика. Некоторые примеры двоичной арифметики рассмотрены в данной статье.
Двоичная арифметика
Все арифметические действия, которые применимы к двоичным числам, выполняются аналогично как в десятичной системе. Удобнее всего двоичные числа складывать, вычитать, умножать и делить столбиком.
Числа записываются друг под другом с учетом разрядов. При необходимости производится перенос в старший разряд или заем из старшего разряда.
При сложении двоичных чисел следует помнить, что в числовом двоичном ряду после 1 идет 10. Это означает, что 1 + 1 = 10, а 11 + 1= 100.
Изучению двоичной системы много времени посвятил В. Лейбниц. По его просьбе была отчеканена медаль в честь двоичной системы, на которой отображались простейшие арифметические действия с двоичными числами.
Сложение
Вычисление суммы двоичных чисел производится следующим образом: числа записываются в столбик. Затем производится поразрядное суммирование цифр, начиная с младшего разряда, как в десятичной системе. Если сумма цифр текущего разряда превышает его размер, то происходит перенос единицы в старший разряд.
Правила сложения двоичных чисел:
0 + 0 = 0
0 + 1 = 1
1 + 1 =10
Например, сумма двоичных чисел 1000111 + 110011 = 1111010
|
Первое слагаемое |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
Второе слагаемое |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
Сумма |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
На примере видно, как происходит перенос в старший разряд. При сложении единиц самого младшего разряда получается 10. Ноль остается на своем месте, а единица переносится в старший разряд слева, где уже складываются две единицы. Получается 11. И снова, младшую единицу оставляют, а старшую переносят влево.
Вычитание
Действие разности следует также выполнять столбиком. Вычитание производится поразрядно. Если возникает ситуация, что приходится вычитать из нуля единицу, то происходит заем из старшего разряда.
Все как в десятичной системе. Только следует помнить, что в двоичной системе 10 – 1 = 1.
Например, разность чисел: 1000111 – 110011 = 10100
|
Уменьшаемое |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
Вычитаемое |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
Разность |
1 |
0 |
1 |
0 |
0 |
На примере видно, как производится заем в старшем разряде. В пятом справа разряде производится вычитание 0 – 1. Здесь следует занять единицу из ближайшего старшего разряда слева.
Умножение
Умножать следует столбиком с учетом правил умножения:
0 * 0 = 0
0 * 1 = 0
1 * 1 = 1
Произведение выполняется также поразрядно, каждый разряд второго числа умножается на каждую цифру первого числа, результат суммируется
Произведение двоичных чисел 1101 * 11 = 100111
|
Первый множитель |
1 |
1 |
0 |
1 |
||
|
Второй множитель |
1 |
1 |
||||
|
1 |
1 |
0 |
1 |
|||
|
1 |
1 |
0 |
1 |
|||
|
Итог (произведение) |
1 |
0 |
0 |
1 |
1 |
1 |
Деление
Операция деления выполняется столбиком, аналогично как в десятичной системе счисления.
Всегда можно проверить результаты двоичной арифметики с помощью калькулятора. Считать можно и в двоичном формате. Электронный калькулятор в группе стандартных приложений операционной системы MS Windows имеет такой режим работы.
Что мы узнали?
Над двоичными числами можно выполнять арифметические операции сложения, умножения, вычитания, деления. Удобнее всего это делать столбиком. Числа следует располагать с учетом разрядов и помнить об особенностях двоичной системы.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Алексей Беляев
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 285.
А какая ваша оценка?
From Wikipedia, the free encyclopedia
A binary multiplier is an electronic circuit used in digital electronics, such as a computer, to multiply two binary numbers.
A variety of computer arithmetic techniques can be used to implement a digital multiplier. Most techniques involve computing the set of partial products, which are then summed together using binary adders. This process is similar to long multiplication, except that it uses a base-2 (binary) numeral system.
History[edit]
Between 1947 and 1949 Arthur Alec Robinson worked for English Electric Ltd, as a student apprentice, and then as a development engineer. Crucially during this period he studied for a PhD degree at the University of Manchester, where he worked on the design of the hardware multiplier for the early Mark 1 computer.
However, until the late 1970s, most minicomputers did not have a multiply instruction, and so programmers used a «multiply routine»[1][2][3]
which repeatedly shifts and accumulates partial results,
often written using loop unwinding. Mainframe computers had multiply instructions, but they did the same sorts of shifts and adds as a «multiply routine».
Early microprocessors also had no multiply instruction. Though the multiply instruction became common with the 16-bit generation,[4]
at least two 8-bit processors have a multiply instruction: the Motorola 6809, introduced in 1978,[5] and Intel MCS-51 family, developed in 1980, and later the modern Atmel AVR 8-bit microprocessors present in the ATMega, ATTiny and ATXMega microcontrollers.
As more transistors per chip became available due to larger-scale integration, it became possible to put enough adders on a single chip to sum all the partial products at once, rather than reuse a single adder to handle each partial product one at a time.
Because some common digital signal processing algorithms spend most of their time multiplying, digital signal processor designers sacrifice considerable chip area in order to make the multiply as fast as possible; a single-cycle multiply–accumulate unit often used up most of the chip area of early DSPs.
Binary long multiplication[edit]
The method taught in school for multiplying decimal numbers is based on calculating partial products, shifting them to the left and then adding them together. The most difficult part is to obtain the partial products, as that involves multiplying a long number by one digit (from 0 to 9):
123
x 456
=====
738 (this is 123 x 6)
615 (this is 123 x 5, shifted one position to the left)
+ 492 (this is 123 x 4, shifted two positions to the left)
=====
56088
A binary computer does exactly the same multiplication as decimal numbers do, but with binary numbers. In binary encoding each long number is multiplied by one digit (either 0 or 1), and that is much easier than in decimal, as the product by 0 or 1 is just 0 or the same number. Therefore, the multiplication of two binary numbers comes down to calculating partial products (which are 0 or the first number), shifting them left, and then adding them together (a binary addition, of course):
1011 (this is binary for decimal 11)
x 1110 (this is binary for decimal 14)
======
0000 (this is 1011 x 0)
1011 (this is 1011 x 1, shifted one position to the left)
1011 (this is 1011 x 1, shifted two positions to the left)
+ 1011 (this is 1011 x 1, shifted three positions to the left)
=========
10011010 (this is binary for decimal 154)
This is much simpler than in the decimal system, as there is no table of multiplication to remember: just shifts and adds.
This method is mathematically correct and has the advantage that a small CPU may perform the multiplication by using the shift and add features of its arithmetic logic unit rather than a specialized circuit. The method is slow, however, as it involves many intermediate additions. These additions are time-consuming. Faster multipliers may be engineered in order to do fewer additions; a modern processor can multiply two 64-bit numbers with 6 additions (rather than 64), and can do several steps in parallel.[citation needed]
The second problem is that the basic school method handles the sign with a separate rule («+ with + yields +», «+ with − yields −», etc.). Modern computers embed the sign of the number in the number itself, usually in the two’s complement representation. That forces the multiplication process to be adapted to handle two’s complement numbers, and that complicates the process a bit more. Similarly, processors that use ones’ complement, sign-and-magnitude, IEEE-754 or other binary representations require specific adjustments to the multiplication process.
Unsigned integers[edit]
For example, suppose we want to multiply two unsigned eight bit integers together: a[7:0] and b[7:0]. We can produce eight partial products by performing eight one-bit multiplications, one for each bit in multiplicand a:
p0[7:0] = a[0] × b[7:0] = {8{a[0]}} & b[7:0]
p1[7:0] = a[1] × b[7:0] = {8{a[1]}} & b[7:0]
p2[7:0] = a[2] × b[7:0] = {8{a[2]}} & b[7:0]
p3[7:0] = a[3] × b[7:0] = {8{a[3]}} & b[7:0]
p4[7:0] = a[4] × b[7:0] = {8{a[4]}} & b[7:0]
p5[7:0] = a[5] × b[7:0] = {8{a[5]}} & b[7:0]
p6[7:0] = a[6] × b[7:0] = {8{a[6]}} & b[7:0]
p7[7:0] = a[7] × b[7:0] = {8{a[7]}} & b[7:0]
where {8{a[0]}} means repeating a[0] (the 0th bit of a) 8 times (Verilog notation).
In order to obtain our product, we then need to add up all eight of our partial products, as shown here:
p0[7] p0[6] p0[5] p0[4] p0[3] p0[2] p0[1] p0[0]
+ p1[7] p1[6] p1[5] p1[4] p1[3] p1[2] p1[1] p1[0] 0
+ p2[7] p2[6] p2[5] p2[4] p2[3] p2[2] p2[1] p2[0] 0 0
+ p3[7] p3[6] p3[5] p3[4] p3[3] p3[2] p3[1] p3[0] 0 0 0
+ p4[7] p4[6] p4[5] p4[4] p4[3] p4[2] p4[1] p4[0] 0 0 0 0
+ p5[7] p5[6] p5[5] p5[4] p5[3] p5[2] p5[1] p5[0] 0 0 0 0 0
+ p6[7] p6[6] p6[5] p6[4] p6[3] p6[2] p6[1] p6[0] 0 0 0 0 0 0
+ p7[7] p7[6] p7[5] p7[4] p7[3] p7[2] p7[1] p7[0] 0 0 0 0 0 0 0
-------------------------------------------------------------------------------------------
P[15] P[14] P[13] P[12] P[11] P[10] P[9] P[8] P[7] P[6] P[5] P[4] P[3] P[2] P[1] P[0]
In other words, P[15:0] is produced by summing p0, p1 << 1, p2 << 2, and so forth, to produce our final unsigned 16-bit product.
Signed integers[edit]
If b had been a signed integer instead of an unsigned integer, then the partial products would need to have been sign-extended up to the width of the product before summing. If a had been a signed integer, then partial product p7 would need to be subtracted from the final sum, rather than added to it.
The above array multiplier can be modified to support two’s complement notation signed numbers by inverting several of the product terms and inserting a one to the left of the first partial product term:
1 ~p0[7] p0[6] p0[5] p0[4] p0[3] p0[2] p0[1] p0[0]
~p1[7] +p1[6] +p1[5] +p1[4] +p1[3] +p1[2] +p1[1] +p1[0] 0
~p2[7] +p2[6] +p2[5] +p2[4] +p2[3] +p2[2] +p2[1] +p2[0] 0 0
~p3[7] +p3[6] +p3[5] +p3[4] +p3[3] +p3[2] +p3[1] +p3[0] 0 0 0
~p4[7] +p4[6] +p4[5] +p4[4] +p4[3] +p4[2] +p4[1] +p4[0] 0 0 0 0
~p5[7] +p5[6] +p5[5] +p5[4] +p5[3] +p5[2] +p5[1] +p5[0] 0 0 0 0 0
~p6[7] +p6[6] +p6[5] +p6[4] +p6[3] +p6[2] +p6[1] +p6[0] 0 0 0 0 0 0
+p7[7] ~p7[6] ~p7[5] ~p7[4] ~p7[3] ~p7[2] ~p7[1] ~p7[0] 0 0 0 0 0 0 0
------------------------------------------------------------------------------------------------------------
P[15] P[14] P[13] P[12] P[11] P[10] P[9] P[8] P[7] P[6] P[5] P[4] P[3] P[2] P[1] P[0]
Where ~p represents the complement (opposite value) of p.
There are many simplifications in the bit array above that are not shown and are not obvious. The sequences of one complemented bit followed by noncomplemented bits are implementing a two’s complement trick to avoid sign extension. The sequence of p7 (noncomplemented bit followed by all complemented bits) is because we’re subtracting this term so they were all negated to start out with (and a 1 was added in the least significant position). For both types of sequences, the last bit is flipped and an implicit -1 should be added directly below the MSB. When the +1 from the two’s complement negation for p7 in bit position 0 (LSB) and all the -1’s in bit columns 7 through 14 (where each of the MSBs are located) are added together, they can be simplified to the single 1 that «magically» is floating out to the left. For an explanation and proof of why flipping the MSB saves us the sign extension, see a computer arithmetic book.[6]
Floating point numbers[edit]
A binary floating number contains a sign bit, significant bits (known as the significand) and exponent bits (for simplicity, we don’t consider base and combination field). The sign bits of each operand are XOR’d to get the sign of the answer. Then, the two exponents are added to get the exponent of the result. Finally, multiplication of each operand’s significand will return the significand of the result. However, if the result of the binary multiplication is higher than the total number of bits for a specific precision (e.g. 32, 64, 128), rounding is required and the exponent is changed appropriately.
Hardware implementation[edit]
The process of multiplication can be split into 3 steps:[7][8]
- generating partial product
- reducing partial product
- computing final product
Older multiplier architectures employed a shifter and accumulator to sum each partial product, often one partial product per cycle, trading off speed for die area. Modern multiplier architectures use the (Modified) Baugh–Wooley algorithm,[9][10][11][12] Wallace trees, or Dadda multipliers to add the partial products together in a single cycle. The performance of the Wallace tree implementation is sometimes improved by modified Booth encoding one of the two multiplicands, which reduces the number of partial products that must be summed.
For speed, shift-and-add multipliers require a fast adder (something faster than ripple-carry).[13]
A «single cycle» multiplier (or «fast multiplier») is pure combinational logic.
In a fast multiplier,
the partial-product reduction process usually contributes the most to the delay, power, and area of the multiplier.[7]
For speed, the «reduce partial product» stages are typically implemented as a carry-save adder composed of compressors and the «compute final product» step is implemented as a fast adder (something faster than ripple-carry).
Many fast multipliers use full adders as compressors («3:2 compressors») implemented in static CMOS.
To achieve better performance in the same area or the same performance in a smaller area, multiplier designs may use higher order compressors such as 7:3 compressors;[8][7]
implement the compressors in faster logic (such transmission gate logic, pass transistor logic, domino logic);[13]
connect the compressors in a different pattern; or some combination.
Example circuits[edit]
See also[edit]
- Booth’s multiplication algorithm
- Fused multiply–add
- Wallace tree
- BKM algorithm for complex logarithms and exponentials
- Kochanski multiplication for modular multiplication
- Logical shift left
References[edit]
- ^ Rather, Elizabeth D.; Colburn, Donald R.; Moore, Charles H. (1996) [1993]. «The Evolution of Forth». In Bergin, Thomas J.; Gibson, Richard G. (eds.). History of Programming Languages—II. Association for Computing Machinery. pp. 625–670. doi:10.1145/234286.1057832. ISBN 0201895021.
- ^ Davies, A.C.; Fung, Y.T. (1977). «Interfacing a hardware multiplier to a general-purpose microprocessor». Microprocessors. 1 (7): 425–432. doi:10.1016/0308-5953(77)90004-6.
- ^ Rafiquzzaman, M. (2005). «§2.5.1 Binary Arithmetic: Multiplication of Unsigned Binary Numbers». Fundamentals of Digital Logic and Microcomputer Design. Wiley. p. 46. ISBN 978-0-47173349-2.
- ^ Rafiquzzaman 2005, §7.3.3 Addition, Subtraction, Multiplication and Division of Signed and Unsigned Numbers p. 251
- ^ Kant, Krishna (2007). «§2.11.2 16-Bit Microprocessors». Microprocessors and Microcontrollers: Architecture, Programming and System Design 8085, 8086, 8051, 8096. PHI Learning. p. 57. ISBN 9788120331914.
- ^ Parhami, Behrooz (2000). Computer Arithmetic: Algorithms and Hardware Designs. Oxford University Press. ISBN 0-19-512583-5.
- ^ a b c
Rouholamini, Mahnoush; Kavehie, Omid; Mirbaha, Amir-Pasha; Jasbi, Somaye Jafarali; Navi, Keivan. «A New Design for 7:2 Compressors» (PDF). - ^ a b
Leong, Yuhao; Lo, HaiHiung; Drieberg, Michael; Sayuti, Abu Bakar; Sebastian, Patrick. «Performance Comparison Review of 8-3 compressor on FPGA». - ^ Baugh, Charles Richmond; Wooley, Bruce A. (December 1973). «A Two’s Complement Parallel Array Multiplication Algorithm». IEEE Transactions on Computers. C-22 (12): 1045–1047. doi:10.1109/T-C.1973.223648. S2CID 7473784.
- ^ Hatamian, Mehdi; Cash, Glenn (1986). «A 70-MHz 8-bit×8-bit parallel pipelined multiplier in 2.5-μm CMOS». IEEE Journal of Solid-State Circuits. 21 (4): 505–513. Bibcode:1986IJSSC..21..505H. doi:10.1109/jssc.1986.1052564.
- ^ Gebali, Fayez (2003). «Baugh–Wooley Multiplier» (PDF). University of Victoria, CENG 465 Lab 2. Archived (PDF) from the original on 2018-04-14. Retrieved 2018-04-14.
- ^ Reynders, Nele; Dehaene, Wim (2015). Ultra-Low-Voltage Design of Energy-Efficient Digital Circuits. Analog Circuits and Signal Processing Series. Analog Circuits And Signal Processing (ACSP). Springer. doi:10.1007/978-3-319-16136-5. ISBN 978-3-319-16135-8. ISSN 1872-082X. LCCN 2015935431.
- ^ a b
Peng Chang.
«A Reconfigurable Digital Multiplier and 4:2 Compressor Cells Design».
2008.
- Hennessy, John L.; Patterson, David A. (1990). «Section A.2, section A.9». Computer Architecture: A quantitative Approach. Morgan Kaufmann. pp. A–3..A–6, A–39..A–49. ISBN 978-0-12383872-8.
External links[edit]
- Multiplier Designs targeted at FPGAs
- Binary Multiplier circuit using Half -Adders and digital gates.
Двоичный калькулятор онлайн
- Главная
- /
- Информатика
- /
- Двоичный калькулятор онлайн
Если вам необходимо произвести математические операции над двоичными числами воспользуйтесь нашим двоичным онлайн калькулятором:
Просто введите целые двоичные числа, выберите операцию и получите результат.
Данный калькулятор может производить следующие действия над двоичными числами:
- сложение +
- вычитание −
- умножение ×
- деление ÷
- логическое И (AND)
- логическое ИЛИ (OR)
- исключающее ИЛИ (XOR)
Сложение двоичных чисел
Сложение двух двоичных чисел производится столбиком поразрядно. Начиная с младшего разряда (справа на лево), как и при сложении столбиком десятичных чисел. Но так как цифр всего две (0 и 1), их сложение происходит по следующим правилам:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Пример
Для примера сложим 1011 и 101:
| + | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 0 | 0 |
10112 + 1012 = 100002
(1110 + 510 = 1610)
Вычитание двоичных чисел
Вычитание двоичных чисел производится аналогично сложению – столбиком, но по следующим правилам:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1
Пример
Для примера вычтем из числа 1011 число 101:
| − | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 1 | 0 |
10112 − 1012 = 1102
(1110 − 510 = 610)
Умножение двоичных чисел
Умножение двоичных чисел производится в столбик аналогично умножению в десятичной системе, но по следующим правилам:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Пример
Для примера перемножим числа 1011 и 101:
| × | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||||
| + | 1 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | |||
| 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 1 | 1 | 1 |
10112 × 1012 = 1101112
(1110 × 510 = 5510)
Деление двоичных чисел
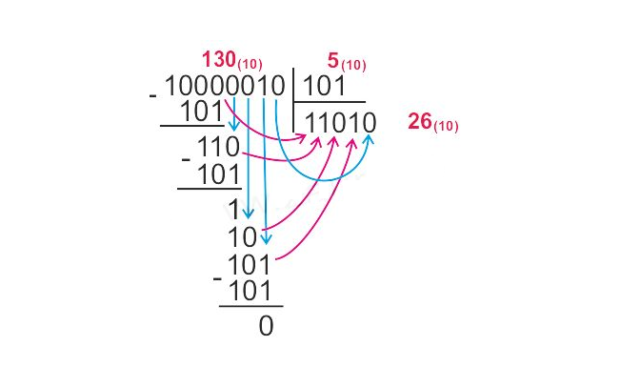
Внешне деление двоичных чисел похоже на деление десятичных чисел, но тут есть свои нюансы: такое деление производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Чтобы понять этот процесс рассмотрим пример:
Пример
Для примера разделим число 11110 на 110:
111102 ÷ 1102 = 1012
(3010 ÷ 610 = 510)