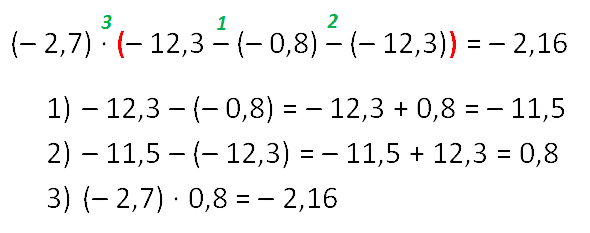Умножение чисел с разными знаками
Чтобы перемножить два числа с разными знаками, надо:
- перемножить модули этих чисел;
- перед полученным числом поставить знак «(-)».
Пример 1.
а) (-25·2=-(25·2)=-50);
б) (25·(-2)=-(25·2)=-50).
Пример 2.
а) (-0,5·1,4=-(0,5·1,4)=-0,7);
б) (0,01·(-7,8)=-(0,01·7,8)=-0,078).
Обрати внимание!
−⋅+=−;+⋅−=−.
Умножение чисел с одинаковыми знаками
Чтобы перемножить два отрицательных числа, надо перемножить их модули.
Пример 3.
Обычно пишут так: (-12·(-3)=12·3=36).
Обрати внимание!
+⋅+=+;−⋅−=+.
В этом уроке мы узнаем, как перемножать два числа с разными знаками, а также разберемся, как перемножить два отрицательных числа.
Научимся возводить в квадрат как положительные, так и отрицательные числа, и предугадывать знаки результата умножения.
Также мы узнаем, как связаны между собой отрицательные числа и умножение на -1 и как это можно использовать.
Задача:
Кондитерская фабрика выпускает шоколадки по 3000 штук в день.
Фабрика изменила вес одной шоколадки на -10 грамм.
Вопрос: на сколько изменилось количество выпускаемого в день?
Для ответа на этот вопрос необходимо перемножить то, насколько меньше стал вес одной шоколадки, на общее количество шоколадок.
Так мы пришли к тому, что нам необходимо уметь перемножать числа с разными знаками.
Эта информация доступна зарегистрированным пользователям
Правило: чтобы перемножить числа с разными знаками, необходимо посчитать произведение модулей этих чисел и к результату приписать “минус”.
Применим это правило к нашей задаче:
1) Считаем модули:
(mathbf{mid3000mid=3000})
(mathbf{mid-10mid=10})
2) Считаем произведение модулей:
(mathbf{3000cdot10=30000})
3) Приписываем “минус” и получаем ответ: на -30000 грамм.
Как видите, все достаточно просто, приведем еще примеры:
(mathbf{3cdot(-5)=-15})
(mathbf{frac{1}{2}cdot(-2)=-1})
(mathbf{-1frac{1}{3}cdot6=-8})
(mathbf{548cdot(-0.5)=-274})
Заметим, что произведение чисел с разными знаками всегда число отрицательное.
Так происходит потому, что сначала считается произведение модулей, поэтому произведение положительных чисел определенно будет положительным.
Далее мы приписываем к нему минус. А если приписать минус к положительному числу, то получится ни что иное, как число отрицательное.
Эта информация доступна зарегистрированным пользователям
Теперь посмотрим, что делать, если надо перемножить два отрицательных числа.
Эта информация доступна зарегистрированным пользователям
Правило: произведение двух отрицательных чисел равняется произведению их модулей.
Пример:
Необходимо перемножить (mathbf{-15}) и (mathbf{-3})
1) Находим их модули:
(mathbf{mid-15mid=15})
(mathbf{mid-3mid=3})
2) Считаем произведение модулей:
(mathbf{15cdot3=45})
Если записать кратко: (mathbf{-15cdot(-3)=45})
Это и будет ответом.
Даже проще, чем с произведением отрицательных чисел, — не надо приписывать минус.
Пример:
Перемножим (mathbf{-frac{1}{6}cdot(-frac{3}{2})})
1) Посчитаем модули:
(mathbf{mid-frac{1}{6}mid=frac{1}{6}})
(mathbf{mid-frac{3}{2}mid=frac{3}{2}})
2) Считаем их произведение:
(mathbf{frac{1}{6}cdotfrac{3}{2}=frac{1cdot3}{6cdot2}=frac{1}{2cdot2}=frac{1}{4}})
Ответ: (mathbf{frac{1}{4}})
И еще несколько примеров:
(mathbf{-54cdot(-2)=108})
(mathbf{-frac{12}{45}cdot(-frac{15}{4})=frac{12cdot15}{45cdot4}=frac{3cdot15}{45}=frac{45}{45}=1})
(mathbf{-0.002cdot(-0.2)=0.0004})
Заметим, что произведение отрицательных чисел всегда получается больше нуля.
Так происходит потому, что, по правилу, это произведение равняется произведению модулей этих чисел.
Сами модули — числа положительные. Значит, и их произведение является числом положительным.
Все наши примеры это только подтверждают, что произведение отрицательных чисел получается положительным.
Эта информация доступна зарегистрированным пользователям
Эта информация доступна зарегистрированным пользователям
Определение: квадратом числа а называется число (mathbf{a^2}) такое, что (mathbf{a^2=acdot a})
Возможно, у вас уже возник вопрос, почему “квадрат”? Сразу ответим на него.
Чтобы найти площадь прямоугольника, необходимо перемножить длины двух его не противоположных сторон.
А у квадрата все стороны одинаковы, поэтому площадь равняется произведению стороны на саму себя, иными словами, площадь квадрата равняется квадрату длины его стороны.
Мы уже немного ушли в геометрию, которую вы будете изучать позже, а сейчас посмотрим на примеры нахождения квадратов.
Пример:
Найдем квадрат числа 3.
Считать будем по определению, перемножим 3 само на себя:
(mathbf{3^2=3cdot3=9})
Еще пример на положительное число, найдем квадрат числа 12 :
Точно также нужно перемножить число само на себя:
(mathbf{12^2=12cdot12=144})
И с нулем все также максимально просто: любое число при умножении на 0 дает 0, и сам 0 при умножении на 0 даст 0 :
(mathbf{0^2=0cdot0=0})
Теперь посмотрим, что будет, если мы будем считать квадрат отрицательного числа:
Посчитаем квадрат (mathbf{-4}):
(mathbf{(-4)^2=(-4)cdot(-4)=16})
Заметим, что мы перемножали отрицательные числа — значит, по сути просто взяли квадрат от модуля данного отрицательного числа.
Правило: квадрат отрицательного числа равен квадрату модуля отрицательных чисел.
Также заметим, что квадрат всегда неотрицателен.
Доказательство:
- Если число в квадрате положительно, то квадрат положительного числа равен произведению положительных чисел и даст результат больший нуля.
- Если число, от которого берется квадрат, равно нулю, то и квадрат равен нулю, что удовлетворяет определению неотрицательности.
- Если же число, от которого берется квадрат, отрицательно, квадрат будет являться произведением двух отрицательных чисел, то есть числом положительным.
Таким образом, мы рассмотрели все возможные случаи, и во всех из них квадрат был числом неотрицательным, то есть положительным.
Эта информация доступна зарегистрированным пользователям
Мы уже знаем, что произведение отрицательного числа на положительное даст нам отрицательное число.
А что, если воспользоваться этим в обратную сторону?
Например, имеется отрицательное число (mathbf{-43})
Заметим, что оно равно (mathbf{-1cdot43})
Также заметим, что квадрат от -1 равен 1.
(mathbf{(-1)^2=(-1)cdot(-1)=-(1cdot1)1})
Используя это в случаях с произведением чисел мы можем ловко менять и переставлять знаки.
Например, было такое произведение:
(mathbf{-636cdot(-452)cdot21cdot(-3)})
Преобразовав его можно оставить только один “минус”, смотрите:
(mathbf{-636cdot(-452)cdot21cdot(-3)=(-1)cdot636cdot(-1)cdot452cdot21cdot(-1)cdot3})
Сейчас для больше наглядности мы переставим все -1 в начало, но этого можно и не делать:
(mathbf{(-1)cdot636cdot(-1)cdot452cdot21cdot(-1)cdot3=(-1)cdot(-1)cdot(-1)cdot636cdot452cdot21cdot3})
Каждая пара минус единиц дает единицу. В данном случае минус единиц три штуки, значит, две из них дадут единицу, а третья останется:
(mathbf{(-1)cdot(-1)cdot(-1)cdot636cdot452cdot21cdot3=(-1)cdot636cdot452cdot21cdot3})
Казалось бы, что нам это дало? А дало это нам то, что теперь знак выражения стал более наглядным: мы видим произведение -1 и произведение положительных чисел, являющегося положительным числом.
Вот теперь можно сказать, что ответом будет отрицательное число.
Правило: произведение нескольких чисел является отрицательным, тогда и только тогда, когда из его множителей нечетное количество является отрицательными и ни один множитель не равен нулю.
Оговорка про нуль важна, так как если один из множителей равен нулю, то и все выражение равно нулю, а значит, не является отрицательным.
Иногда -1 уходят полностью. Так происходят в случаях, когда отрицательных множителей четное число.
Пример:
(mathbf{-7cdot2cdot(-3)cdot(-4)cdot(-2)=(-1)cdot(-1)cdot(-1)cdot(-1)cdot7cdot2cdot3cdot4cdot2=7cdot2cdot3cdot4cdot2})
Правило: произведение нескольких чисел является положительным тогда и только тогда, когда из его множителей их четное количество являются отрицательными и ни один множитель не равен нулю.
Отметим еще один момент: -1 можно выносить и заносить в обе стороны.
Эта информация доступна зарегистрированным пользователям
То есть в данном случае мы можем переписать выражение так:
(mathbf{(-1)cdot636cdot452cdot21cdot3=-(636cdot452cdot21cdot3)})
Это же позволит превращать вычитание отрицательного числа в прибавление положительного. В самом деле:
(mathbf{a-(-b)=a+(-(-b))=a+(-1cdot(-b))=a+(-1cdot(-1)cdot b)=a+b})
Эта информация доступна зарегистрированным пользователям
Интересно посмотреть,как развивалась математика в Древней Руси.
В XVIII веке с приходом к власти Петра Первого (1672- 1725) в России появилась система образования, которая постепенно интегрировалась с общемировой и дала множество открытий.
Однако до этого момента тоже существовали математические познания, о которых мы сейчас и расскажем.
Как и в остальном мире, необходимость в математике была вызвана экономикой.
Поэтому одними из первых денежных знаков были домашние животные и шкуры.
Так, например, были резаны (куски шкур), куны (от слова “куница”) и ногаты.
Позже расчеты свели к гривнам: одна гривна, равная примерно 50-ти граммам серебра, равнялась 50-ти резанам, 25-ти кунам или 20-ти ногатам.
И уже позже, только к XIV веку, начали переходить к рублю, представлявшему из себя на тот момент круглый кусок серебра массой 205 грамм.
Меры длины во многих системах, в том числе и древнерусской, были связаны с параметрами человеческого тела:
- пядь равнялась расстоянию между концами разведенных большого и указательного пальца
- локоть равнялся расстоянию от кончиков пальца до локтя
- сажень была косой и маховой: маховая между разведенными с сторону руками, косая между ногой и отведенной вверх рукой
Эта информация доступна зарегистрированным пользователям
Первый свод математических правил встречается в сборнике “Русская правда” (XI век), там опять же говорилось про экономику: штрафы, долги проценты, что лишний раз показывает, что люди уже умели оперировать целыми и дробными числами.
Далее выходили и другие труды, связанные с математикой, которые постепенно входили и в массы.
Книга “Считание удобное, которым всякий человек купующий или продающий, зело удобно изыскати может, число всякие вещи”, которая вышла в 1682 году, своим названием уже намекает на то, что предназначена была не только для ученых или любителей, но и для купечества.
Ну а дальше при Петре I появлялись школы, приглашались зарубежные специалисты, и наука шагнула далеко вперед.
По сей день российские ученые и студенты-математики выигрывают международные конкурсы и награды, решая нерешенные до этого задачи.
Читайте также
Используя понятие
модуля числа, сформулируем
правила умножения положительных
и отрицательных чисел.
Умножение чисел с одинаковыми знаками
Первый случай, который может вам встретиться — это умножение чисел с
одинаковыми знаками.
Чтобы умножить два числа с одинаковыми знаками надо:
- перемножить модули чисел;
- перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед
первым числом слева можно
опускать).
Примеры умножения отрицательных и положительных чисел.
- (−3) · (−6) = +18 = 18
- 2 · 3 = 6
Умножение чисел с разными знаками
Второй возможный случай — это умножение чисел с разными знаками.
Чтобы умножить два числа с разными знаками, надо:
- перемножить модули чисел;
- перед полученным произведением поставить знак «−».
Примеры умножения отрицательных и положительных чисел.
- (−0,3) · 0,5 = −0,15
- 1,2 · (−7) = −8,4
Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное
правило совпадает с правилом раскрытия скобок.
Запомните!
Минус на минус даёт плюс,
Плюс на минус даёт минус.
| + · (+) = + | + · (−) = − |
| − · (−) = + | − · (+) = − |
В «длинных» примерах, в которых есть только действие умножение, знак произведения можно
определять по количеству отрицательных множителей.
При чётном числе отрицательных множителей результат будет
положительным, а при нечётном количестве — отрицательным.
Пример.
(−6) · (−3) · (−4) · (−2) · 12 · (−1) =
В примере пять отрицательных множителей. Значит, знак результата будет «минус».
Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 · 3 · 4 · 2 · 12 · 1 = 1728
Конечный результат умножения исходных чисел будет:
(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −1728
Умножение на ноль и единицу
Если среди множителей есть число ноль или положительная единица, то умножение
выполняется по известным правилам.
- 0 · a = 0
- a · 0 = 0
- a · 1 = a
Примеры:
- 0 · (−3) = 0
- 0,4 · 1 = 0,4
Особую роль при умножении рациональных чисел играет
отрицательная единица «−1».
Запомните!
При умножении на «−1» число меняется на противоположное.
В буквенном выражении это свойство можно записать:
a · (−1) = (−1) · a = −a
При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется
порядок действий, установленный
для положительных чисел и нуля.
Пример умножения отрицательных и положительных чисел.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Algebra is the branch of mathematics dealing with arithmetic operations and their associated symbols. The symbols are termed as variables that may take different values when subjected to different constraints. The variables are mostly denoted such as x, y, z, p, or q, which can be manipulated through different arithmetic operations of addition, subtraction, multiplication, and division, in order to compute the values.
Negative numbers
A negative number corresponds to an integer value that is less than zero. A negative number is used to denote a loss or deficiency. Negative numbers are prepended with a negative sign. For instance, loans or credit are denoted with negative numbers
Rule: Opposite of an opposite is equivalent to the original value.
For example, −(−3) = 3
Why is the product of negative numbers positive?
Answer:
Upon multiplication of a negative number by another negative number, the resultant operation is positive in nature.
To Prove: The product of two negative numbers or terms is positive:
(−a)(−b) = ab
where, a and b can be:
- Numbers (i.e. a = 5, b = 1/2)
- Constants
- Variables
- Expressions [i.e. a = (y2 + 6), b = (h − w + z)]
Proof
To prove (−a)(−b) = ab, we can consider the equation:
x = ab + (−a)(b) + (−a)(−b)
It can be easily shown that x = ab and x = (−a)(−b).
Factor out −a
First, factoring out −a from the expression (−a)(b) + (−a)(−b):
x = ab +(−a)(b) + (−a)(−b)
Thus, we obtain,
x = ab + (−a)[b + (−b)]
Since, b + (−b) = 0
x = ab + (−a)(0)
Thus,
x = ab
Factor out b
Factoring out b from the expression ab + (−a)(b):
x = ab + (−a)(b) + (−a)(−b)
x = b[a + (−a)] + (−a)(−b)
x = b(0) + (−a)(−b)
Therefore,
x = (−a)(−b)
Result
Since x = ab and x = (−a)(−b):
(−a)(−b) = ab
This can be extended to any even amount of negative numbers by factoring out in steps:
(−a)(−b)(−c)(−d) = ab(−c)(−d) = abcd
Summary
The method easily proves (−a)(−b) = ab.
The fact that the product of two negative numbers, terms, or expressions is positive can be extended to any even number of negative items.
Sample Questions
Question 1. Find the product of -3a × -20b
Solution:
Here we have to find the product of -3a × -20b
As we know that when we multiply two negative numbers the answer will be positive
Now multiplying
-3a × -20b = +60ab
Therefore, the solution is positive.
Question 2. Evaluate 2ab + (−a)(5b) + (−2a)(−3b)?
Solution:
Here we have to find the product of
= 2ab + (−a)(5b) + (−2a)(−3b)
First solving the brackets
= 2ab + (-a × 5b) + (-2a × -3b)
= 2ab + (-5ab) + 6ab
= 2ab – 5ab + 6ab
= 8ab – 5ab
= 3ab
Question 3. Evaluate 10ab + (−21a)[5b + (−10b)]?
Solution:
Here we have to find the product of 10ab + (−21a)[5b + (−10b)]
First solving the brackets
= 10ab + (−21a)× [5b −10b]
= 10ab – 21a × (-5b)
= 10ab + 105ab
= 115ab
Question 4. Find the product of {-(4x + 5x) × (12x – 16x)}?
Solution:
Here we have to find the product of {-(4x + 5x) × (12x – 16x)}
First solving the brackets
= {(-4x – 5x) × (12x – 16x)}
= (-9x) × (-4x)
= 36x2
Last Updated :
29 Nov, 2021
Like Article
Save Article
Как умножить отрицательный числа, теория, на калькуляторе.
Как умножать отрицательные числа!? Сколько вариантво существует умножения отрицательных. Разберем все варианты. и последним — умножим отрицательные на калькуляторе.
Умножить отрицательные в отличии от некоторых других действий с отрицательными, например сложение и вычитание существует только два варианта:
Об умножении отрицательных чисел.
- Правила умножения отрицательных чисел.
- Умножить отрицательные числа.
- Умножить отрицательное и положительное число.
- Умножить отрицательные числа на калькуляторе.
- Умножить отрицательное и положительное число на калькуляторе.
Правила умножения отрицательных чисел.
Для умножения отрицательных чисел существует только два пункта в правилах «умножения отрицательных чисел» :
1.1.) Если два множителя отрицательные .
Первый пункт правил умножения звучит так : «если два множителя отрицательные, то при умножении минус на минус дает плюс, т.е. умножение двух отрицательных чисел равно умножению этих же чисел без минуса.»
(-a) * (-b) = a * b
1.2.) Если у множителей противоположные знаки.
Противоположные знаки у множителей — это означает, что только один множитель отрицательный.
Второй пункт правил умножения звучит так : «если из двух множителей только один отрицательный, то при умножении, минус на плюс, дает минус, т.е. у произведения знак будет отрицательным.»
(-a) * b = -(a * b)
Умножить отрицательные числа.
Далее разберем первый пункт правил умножения отрицательных чисел
(-a) * (-b) = a * b
Пример умножения двух отрицательных чисел
У нас два отрицательных числа и мы их должны умножить :
(-12) * (-15)
У множителей два минуса, а как мы знаем из правил, минус на минус дает плюс. Значит, убираем у наших множителей два минуса.
12 * 15 =
Итого получаем :
(-12) * (-15) = 12 * 15 = 180
Проверить на калькуляторе.
Умножить отрицательное и положительное число.
Рассмотрим пример умножения отрицательных чисел по второму пункту правил.
a * (-b) = -(a * b)
Для этого нам понадобятся цифры :
12 * (-15)
Как мы знаем из правил, в случае, если отрицательное число только одно, то результат умножения будет отрицательным:
12 * (-15) = -(12*15) = -180
Проверить на калькуляторе.
Умножить отрицательные числа на калькуляторе.
Мы уже умножали два отрицательных числа, теперь сделаем умножение отрицательных чисел на калькуляторе!
(-12) * (-15)
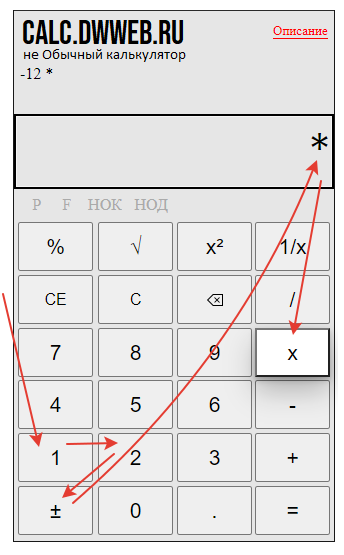
Набираем первый множитель 12.
Меняем знак на отрицательный, кнопкой плюс/минус -«±».
Нажимаем умножить : «*»
Набираем второй множитель : 15.
Меняем знак на отрицательный, кнопкой плюс/минус : «±».
Нажимаем равно «=».
Получаем результат умножения двух отрицательных чисел.

Умножить отрицательное и положительное число на калькуляторе.
Нам осталось разобрать умножение отрицательных на калькуляторе если одно из множителей отрицательное.
(-a) * b = -(a * b)
Набираем первый множитель 12.
Меняем знак на отрицательный, кнопкой плюс/минус -«±».
Нажимаем умножить : «*»
Набираем второй множитель : 15.
Нажимаем равно «=».
Получаем результат умножения двух отрицательных чисел, где лишь один из множителей отрицательный.
Не благодарите, но ссылкой можете поделиться!
COMMENTS+
BBcode