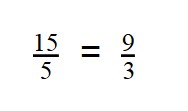Как найти произведение крайних членов

 Равенство двух отношений называют пропорцией.

Тема: «Отношение» рассмотрена на предыдущем занятии («6.1. Отношение»).

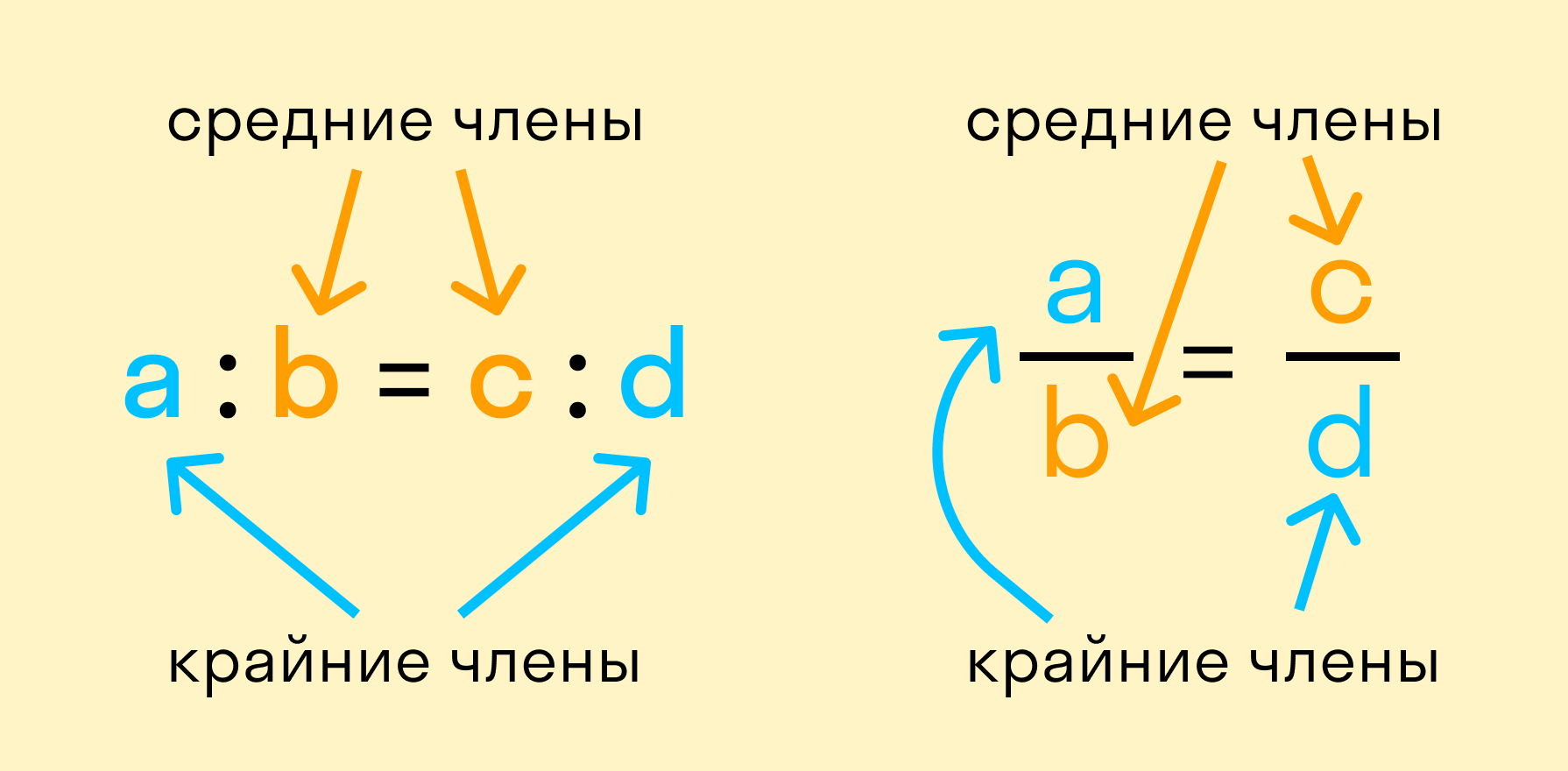
a:b=c:d. Это пропорция. Читают: а так относится к b, как c относится к d. Числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.

Пример пропорции:  12 : 3 = 16 : 4. Это равенство двух отношений: 12:3=4 и 16:4=4. Читают: двенадцать так относится к трем, как шестнадцать относится к четырем. Здесь 12 и 4 -крайние члены пропорции, а 3 и 16 — средние члены пропорции.

Основное свойство пропорции

 Произведение крайних членов пропорции равно произведению ее средних членов.

Для пропорции a:b=c:d или a/b=c/d основное свойство записывается так: a·d=b·c.

Для нашей пропорции 12 : 3 = 16 : 4 основное свойство запишется так: 12·4=3·16. Получается верное равенство: 48=48.  

Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов пропорции разделить на известный крайний член.

Примеры. Найти неизвестный крайний член пропорции.

1) х : 20 = 2 : 5. У нас х и 5 — крайние члены пропорции, а 20 и 2 — средние.

Решение.

х = (20·2):5  — нужно перемножить средние члены (20 и 2) и результат разделить на известный крайний член (число 5);

х = 40 : 5  —  произведение средних членов (40) разделим на известный крайний член (5);

х = 8. Получили искомый крайний член пропорции.

Удобнее записывать нахождение неизвестного члена пропорции с помощью обыкновенной дроби. Вот как тогда запишется рассмотренный нами пример:

Искомый крайний член пропорции (х) будет равен произведению средних членов (20 и 2), деленному на известный крайний член (5).

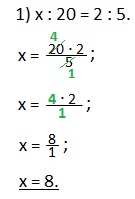
Сокращаем дробь на 5 (делим на 5 и числитель и знаменатель дроби). Находим значение х.

Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»

Еще такие примеры на нахождение неизвестного крайнего члена пропорции.

Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов пропорции разделить на известный средний член.

Примеры. Найти неизвестный средний член пропорции.

5) 9 : х = 3 : 14. Число 3 — известный средний член данной пропорции, числа 9 и 14 — крайние члены пропорции.

Решение. 

х = (9·14):3 —  перемножим крайние члены пропорции и результат разделим на известный средний член пропорции;

х= 136:3;

х=42.

Решение этого примера можно записать иначе:

Искомый средний член пропорции (х) будет равен произведению крайних членов (9 и 14), деленному на известный средний член (3).

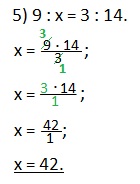
Сокращаем дробь на 3 (делим на 3 и числитель и знаменатель дроби). Находим значение х.

Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»

Еще такие примеры на нахождение неизвестного среднего члена пропорции.

Пропорции

• Члены пропорции: крайние и средние
• Главное свойство пропорции
• Нахождение неизвестного члена пропорции

Равенство двух отношений называется пропорцией.

Пропорцию

a : b = c : d

или

можно прочитать так:  отношение  a  к  b  равно отношению  c  к  d,  или  a  относится к  b,  как  c  относится к  d.

Члены пропорции: крайние и средние

Члены отношений, составляющих пропорцию, называются членами пропорции. Числа  a  и  d  называют крайними членами пропорции, а числа  b  и  c  — средними членами пропорции:

Эти названия условны, так как достаточно написать пропорцию в обратном порядке (переставить отношения местами):

c : d = a : b

или

и крайние члены станут средними, а средние — крайними.

Главное свойство пропорции

Произведение крайних членов пропорции равно произведению средних.

Из главного свойства пропорции следует:

1. Крайний член равен произведению средних, разделённому на другой крайний. То есть для пропорции   :

   

2. Средний член равен произведению крайних, разделённому на другой средний. То есть для пропорции   :

   

Нахождение неизвестного члена пропорции

Свойства пропорции позволяют найти любой из членов пропорции, если он неизвестен. Рассмотрим пропорцию:

x : 8 = 6 : 3.

Тут неизвестен крайний член. Так как крайний член равен произведению средних, разделённому на другой крайний, то

x = (8 · 6) : 3 = 16.

Что такое пропорция

Определение пропорции: 

Пропорция — это равенство двух отношения.

Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.

Пропорция всегда содержит равные коэффициенты. 

Если выразить определение формулой, то выглядеть оно будет так:

• a : b = c : d

Или вот так:

• 

a и d — крайние члены пропорции, b и с — средние члены пропорции.

Читается это выражение так: a так относится к b, как c относится к d

Например:

15 : 5 = 3
 

9 : 3 = 3

Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3. 

15 и 3 — крайние члены пропорции.

5 и 9 — средние члены пропорции.

Наглядный пример для понимания:

У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.

• Запишем эту непростую ситуацию в виде отношения 8 кусочков к 4 голодным друзьям: 8 : 4 
• Далее преобразовываем это отношение в дробь: 8/4
• Выполняем деление: 8/4 = 2

Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!

А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.

• Запишем в виде отношения: 4 : 2
• Преобразовываем получившееся отношение в дробь: 4/2
• Выполняем деление: 4/2 = 2

Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка. 

Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные. 

Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉

Основное свойство пропорции

Запомните основное свойство пропорции:

В виде формулы свойство выглядит так:

a : b = c : d
a * d = b * c

Мы знаем, что a и d — крайние члены пропорции, b и c — средние. 

Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу. 

Давайте проверим несколько пропорций.

Пример 1. Дана пропорция:6/2 = 12/4

• Чтобы проверить, верно ли составлена пропорция, перемножаем ее крайние члены: 6 * 4 = 24.
• Далее перемножаем средние члены пропорции: 2 * 12 = 24
   
• Произведение крайних членов пропорции равно 24, произведение средних членов пропорции также равно 24.
   
• 6 * 4 = 2 * 12
  24 = 24

Делаем вывод, что пропорция 6/2 = 12/4 составлена верно. 

Пример 2. Дана пропорция: 10/2 = 16/4

• Перемножаем крайние члены пропорции: 10 * 4 = 40.
• Перемножаем средние члены: 16 * 2 = 32.
• Произведение крайних членов пропорции равно 40. Произведение средних членов пропорции равно 32. 
• 10 * 4 ≠ 16 * 2
  40 ≠ 32

Отсюда делаем вывод, что  отношения в пропорции 10/2 ≠ 16/4 не являются равными. 

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры решения задач с пропорцией

Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек. 

Задачка 1. Дана математическая пропорция: 15/3 = x/4

Найдите x.

Как решаем:

 

1. По основному свойству пропорции перемножаем множители:
   15 * 4 = 3x
2. Получаем уравнение: 60 = 3x
3. 60/3 = x
   x = 20.

Ответ: в пропорции 15/3 = x/4, x = 20

Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.

Как решаем:

 

1. Записываем чиcла в виде дробей: 18/9 = 24/x
   Где x — четвертый член пропорции.
2. По основному свойству пропорции, перемножаем средние члены: 9 * 24 = 216
3. Выводим уравнение 18x = 216
4. Находим x:
   x = 216 : 18
   x = 12
5. Проверяем: 9 * 24 = 216, 18 * 12 = 216.
   Пропорция составлена верно.

Ответ: четвертый член пропорции — 12.

Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?

Как решаем:

 

1. Записываем числа в виде обратной пропорции: 18/9 = x/8
2. Перемножаем множители по основному свойству пропорции: 18 * 8 = 9x
3. Находим х:
   144 = 9x
   144 : 9 = 16

Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши. 

Задачка 4. Дана пропорция: 20/2 = y/4

Найдите y.

Как решаем:

 

1. По основному свойству пропорции перемножаем множители:
   20 * 4 = 2y
2. Получаем уравнение: 80 = 2y
3. Находим у:
   80/2 = y
   x = 40.
4. Проверяем пропорцию: 20 * 4 = 80, 40 * 2 = 80.

Ответ: в пропорции 20/2 = y/4, y = 40

Пропорции

Пропорции — это сильный инсрумент, который бывает полезен вплоть до 11 класса. Преимущество пропорций в том, что алгоритм нахождения неизвестного члена пропорции хорошо запоминается.

Пропорция

Пропорция — это равенство двух отношений. Пример пропорции:

⁴/₁₂ = ⁹/₂₇. 4 и 27 называются крайние члены пропорции, а 12 и 9 — называются средние члены пропорции.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению ее средних членов. То есть, пропорцию

⁴/₁₂ = ⁹/₂₇

мы можем записать по-другому:

4 × 27 = 12 × 9.

Как найти средний член пропорции?

Средний член пропорции равен произведению крайних членов делённому на другой средний член. То есть, пропорцию

⁴/_? = ⁹/₂₇

мы можем записать по-другому — вот так:

? = ^{4 × 27}/₉

или пропорцию

⁴/₁₂ = ^?/₂₇

мы можем записать по-другому — вот так:

? = ^{4 × 27}/₁₂

Как найти крайний член пропорции?

Крайний член пропорции равен произведению средних членов, делённому на другой крайний член. То есть, пропорцию

^?/₁₂ = ⁹/₂₇

мы можем записать по-другому — вот так:

? = ^{12 × 9}/₂₇

или пропорцию

⁴/₁₂ = ⁹/_?

мы можем записать по-другому — вот так:

? = ^{12 × 9}/₄

Математика

6 класс

Урок № 5

Пропорции

Перечень рассматриваемых вопросов:

• Понятие пропорции.
• Основное свойство пропорции.
• Как правильно составить пропорцию.
• Как найти неизвестный член пропорции.

Тезаурус

Равенство двух отношений называют пропорцией.

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.

Рассмотрим 3 способа нахождения неизвестного члена пропорции.

1 способ.

2 способ.

Способ 3.

Задача.

Решение:

Ответ:

1) можно;

2) можно;

3) нельзя;

4) нельзя.

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

№2. Тип задания: Подстановка элементов в пропуски в тексте.

Найдите неизвестный член пропорции.

Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.

Ответ: 3.
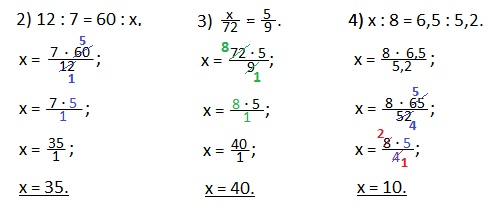
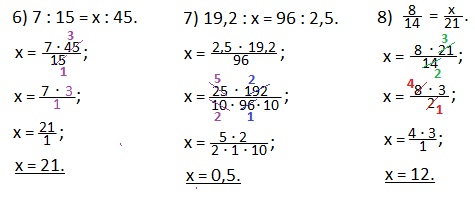