Как найти произведение матрицы на транспонированную матрицу

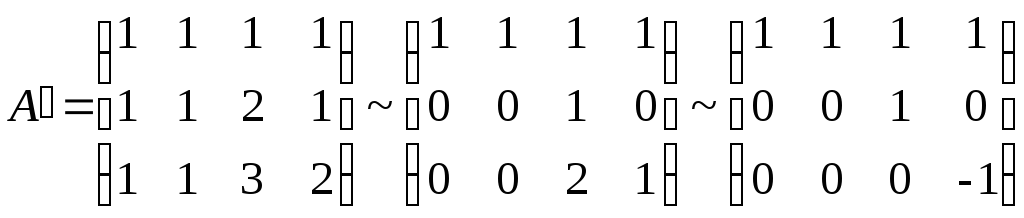
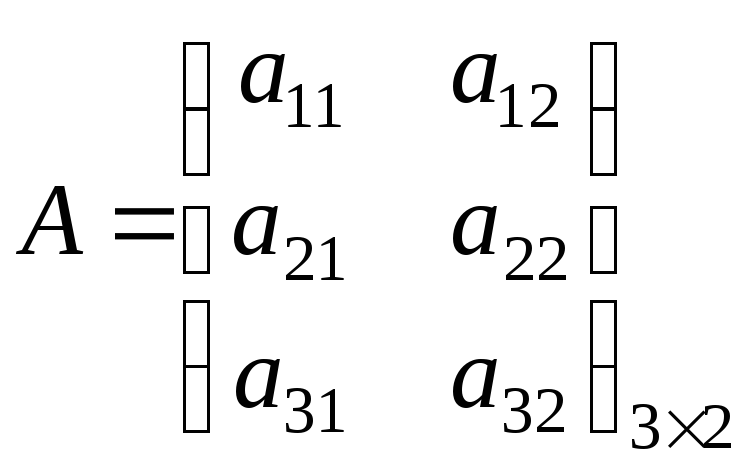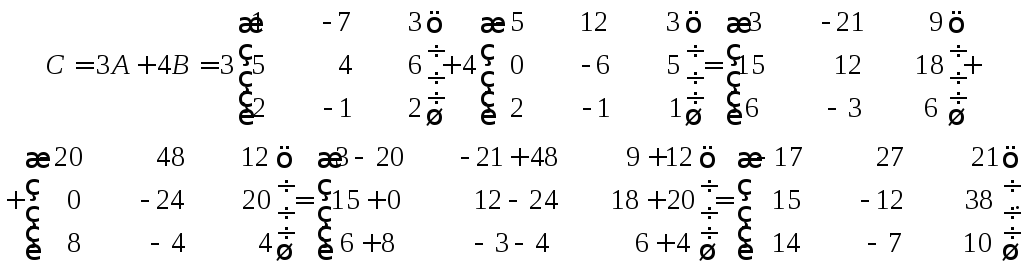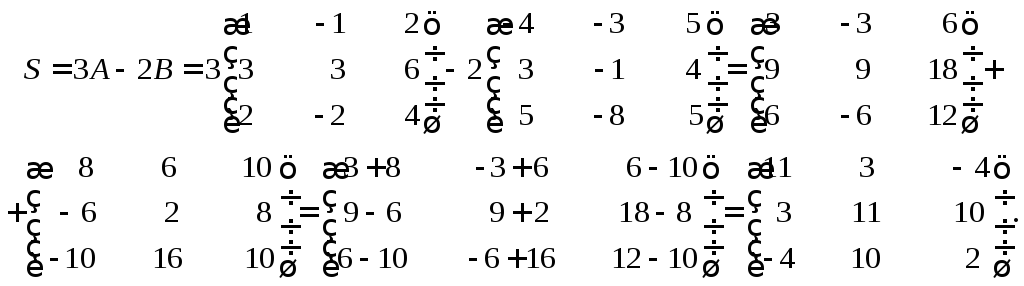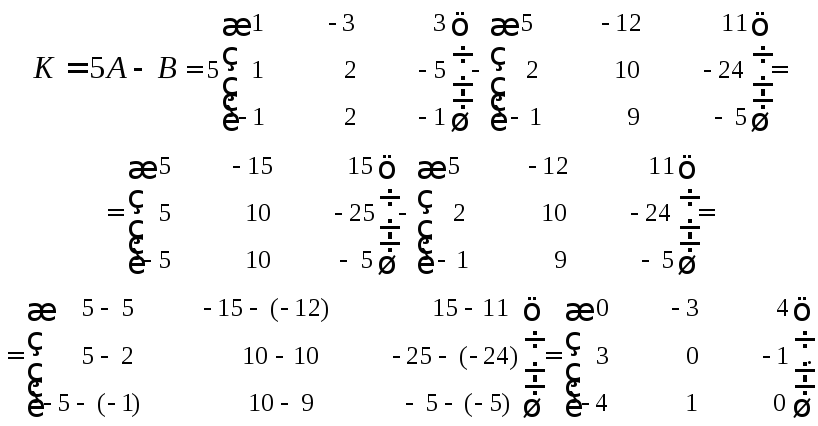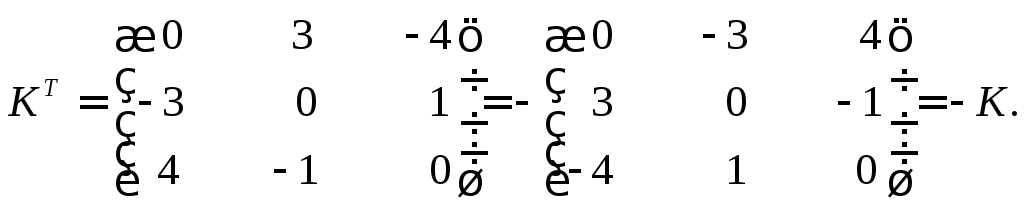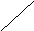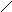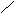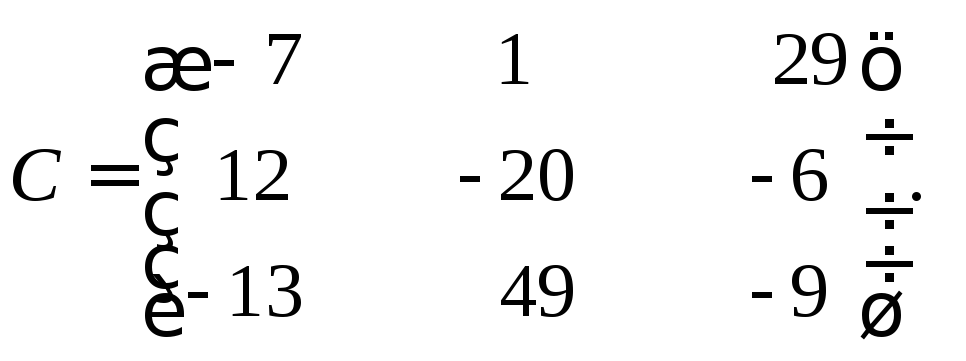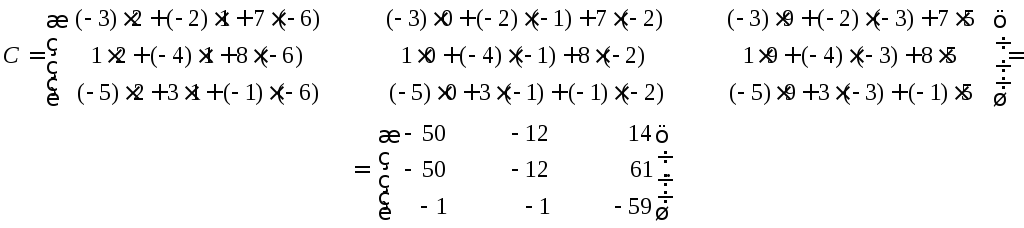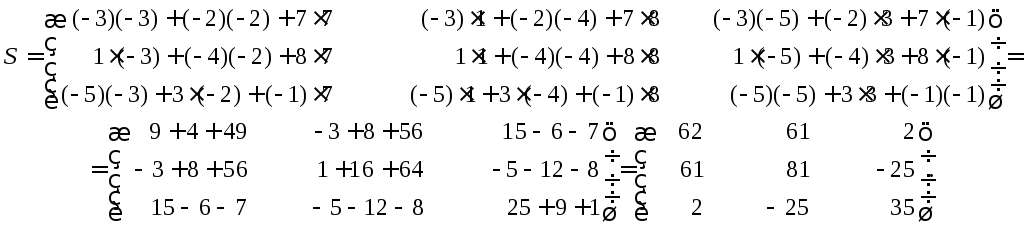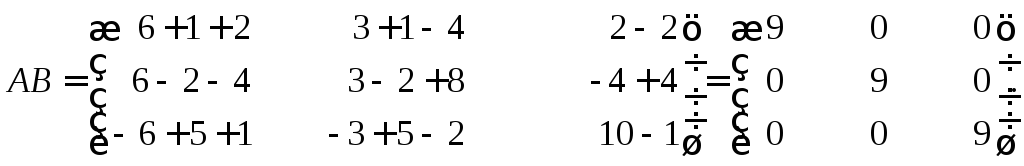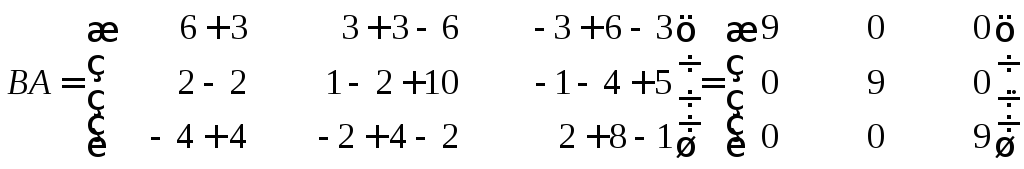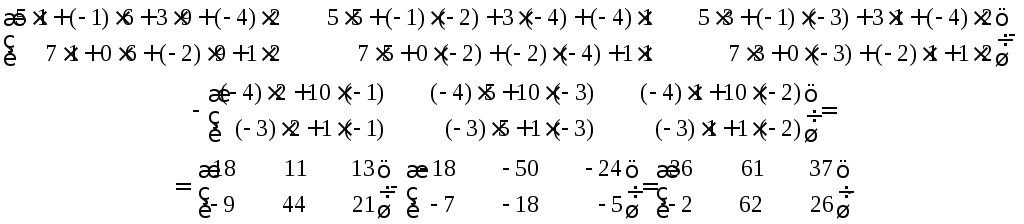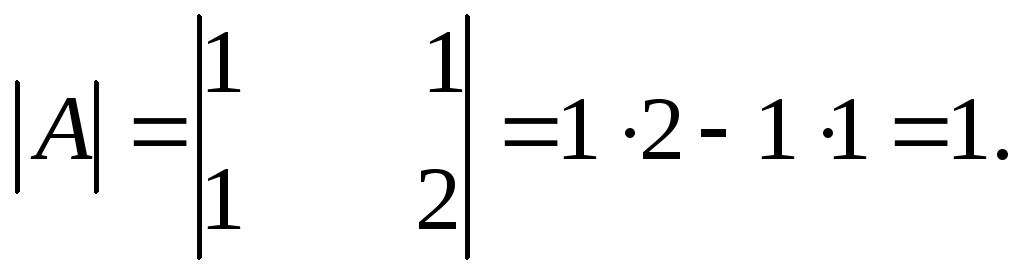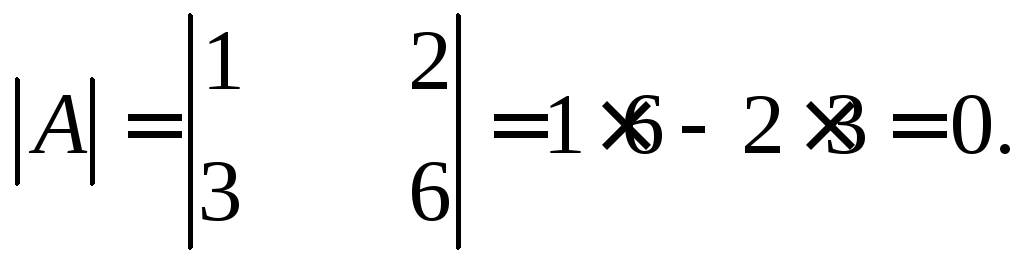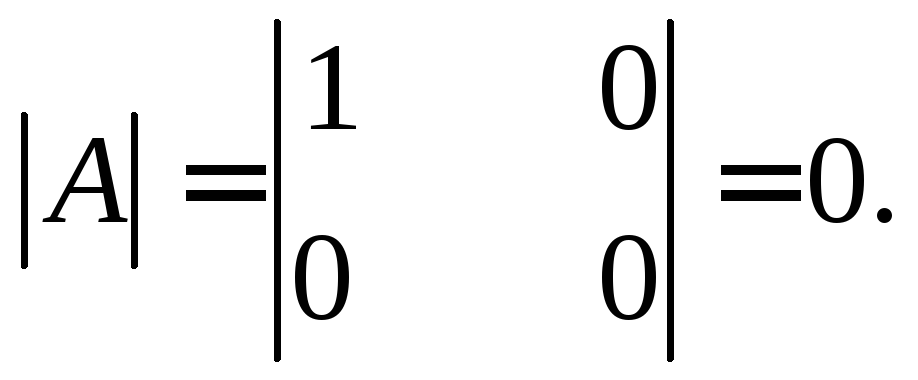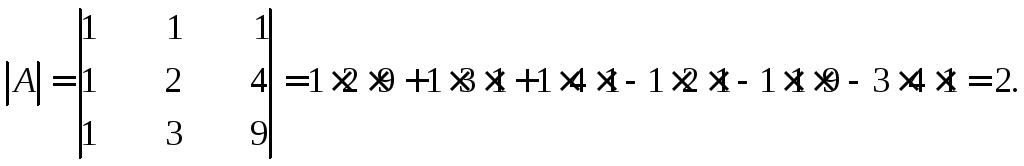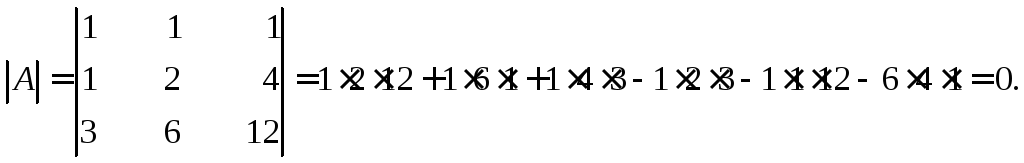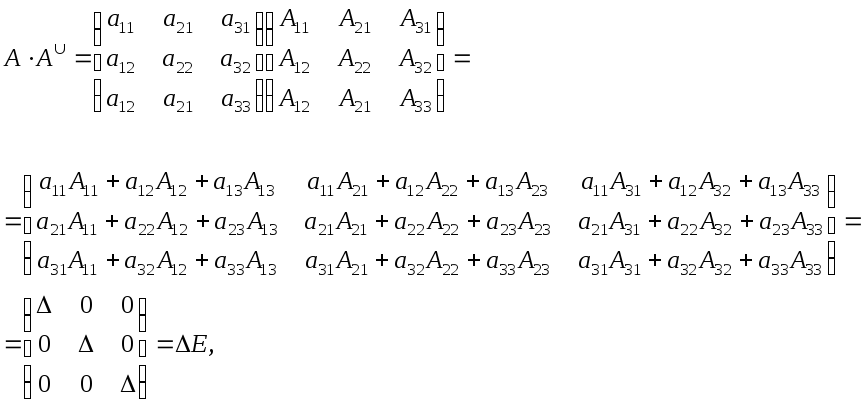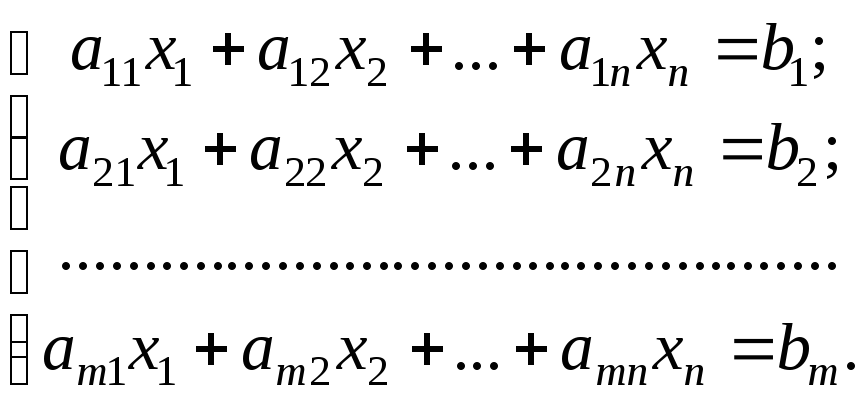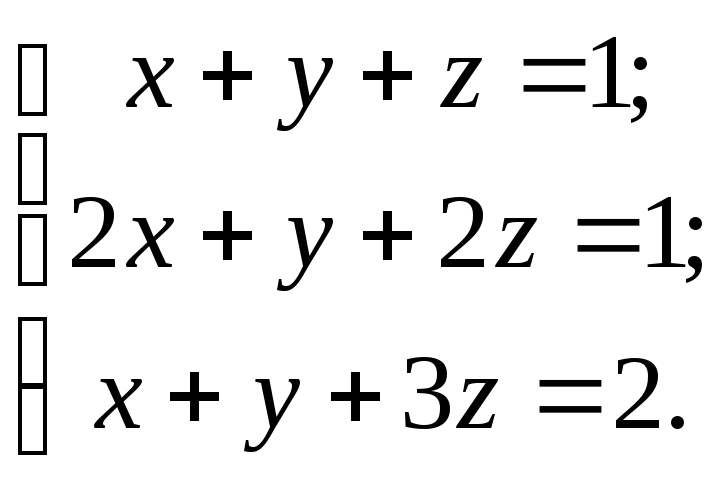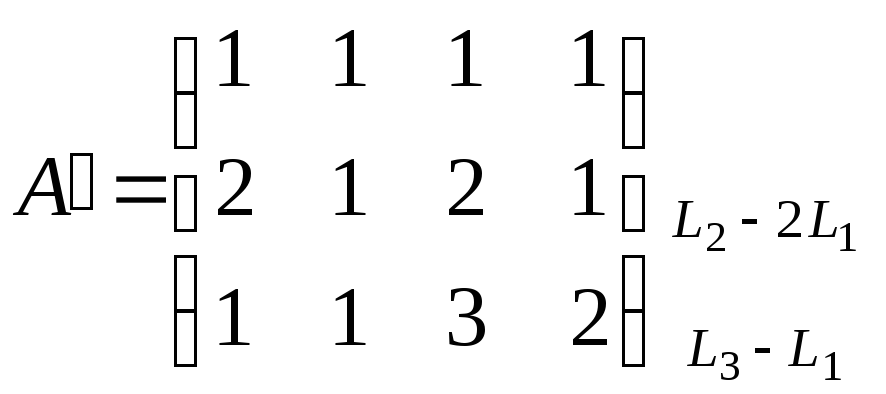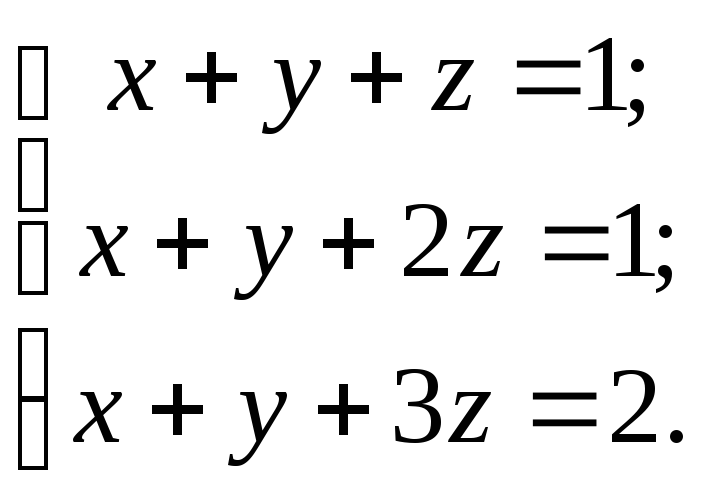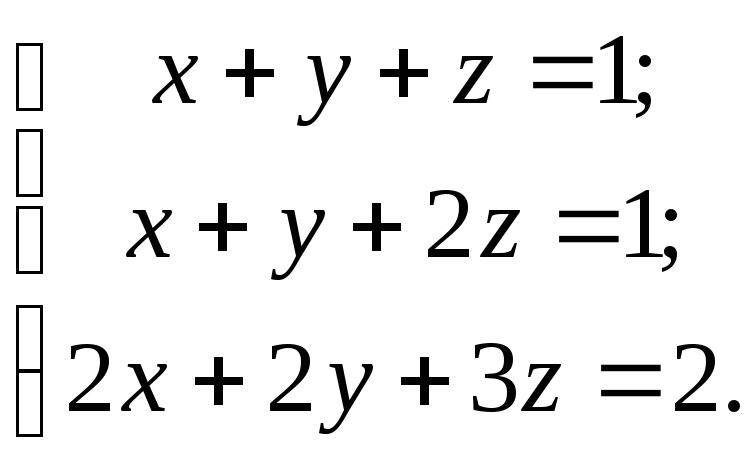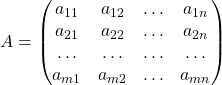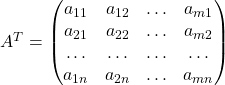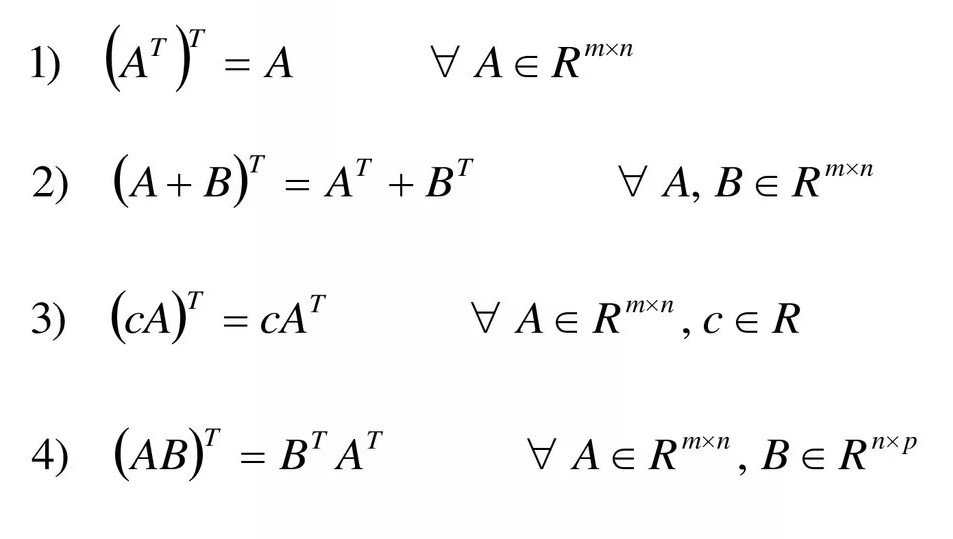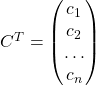Нам уже знакомо понятие матрицы. Этот математический объект имеет прикладное значение: он позволяет структурировать числа и информацию, проводить сложные расчёты. С ним можно проделывать различные операции, и одной из них является транспортирование.

Что такое транспонированная матрица, в чем отличие от обычной

Транспонирование – это алгоритм, при котором m-строки меняются местами с n-столбцами.

Транспонированная матрица, в отличие от обычной, помогает получить одинаковый результат при умножении на вектор-столбец и вектор-строку, что значительно упрощает дальнейшие математические вычисления.

Особенности, определитель и свойства целочисленных

Свойства транспортирования целочисленных матриц:

• (A^T )^T  = A;
• (k · A)^T  = k · AT;
• (A + B)^T  = A^T  + В^T;
• (A · B)^T  = В^T · A^T 

Если матрица А – квадратная (m=n), то определитель исходной и транспортированной матрицы равны: det A^T  = det A.

Напомним, что определитель – это некоторое число, с которым можно сравнить любую квадратную матрицу.

Формула, как обозначается транспонированная матрица

Если исходная матрица обозначается как А, то у транспортированной будет обозначение A^T .    

Тогда формула для транспортировки выглядит следующим образом:

A^T  ij = A ji

Формально, если А = m × n, то A^T = n × m, но математически это записывается через индексы i и j.

Примеры задач на транспонирование матриц

Само транспортирование – довольно лёгкий процесс. Рассмотрим один пример.

Задача: даны А = (m × n) и В = (m × n).

Необходимо выполнить транспортирование.

Решение

Произведение и сумма транспонированных матриц

Теорема: транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.

В математическом виде теорема выглядит так:

С^T = (A · B)^T  = В^T · А^T

Пример:

Сумма вычисляется по аналогичной формуле:

 C^T = (A + B)^T  = A^T  + В^T 

Периодически возникают сложности с учебой? ФениксХэлп может помочь!

Матрицы

1. Матрицы и их типы

Матрица
– это совокупность чисел или объектов
другой природы, расположенных в виде
прямоугольной таблицы.

.

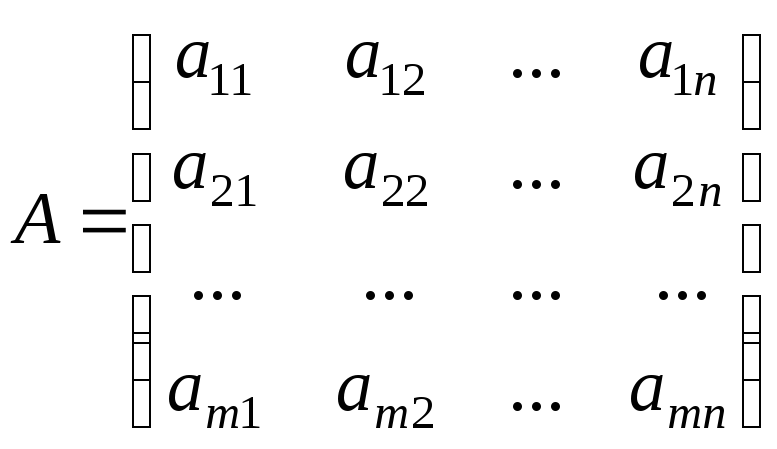
mстрок nстолбцов

Размер матрицы
.

.

Мы
будем рассматривать конечные матрицы
с числовыми элементами.

Классификация по
размеру

1)
– матрица-столбец.

2)
– матрица-строка.

3)
,
т.е.– квадратная матрица.

Элементы
,
где– образуют главную диагональ.

4)
Квадратная матрица, все элементы которой
вне главной диагонали равны нулю,
называется диагональной.

.

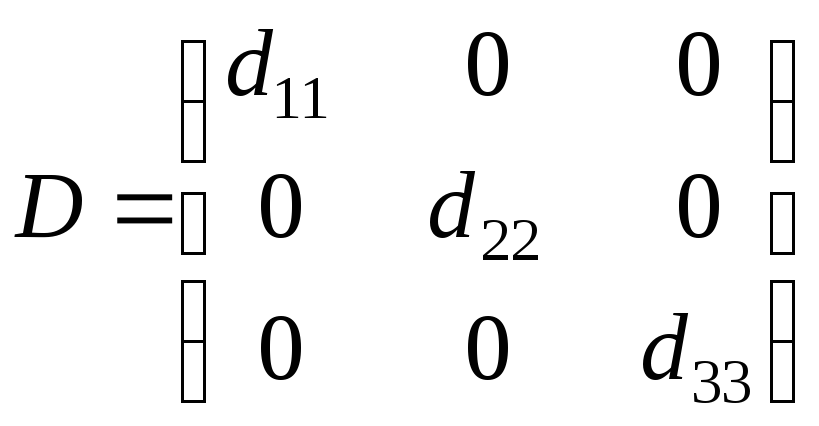
5) Если
в диагональной матрице все
,
то такая матрица называетсяединичной.

.

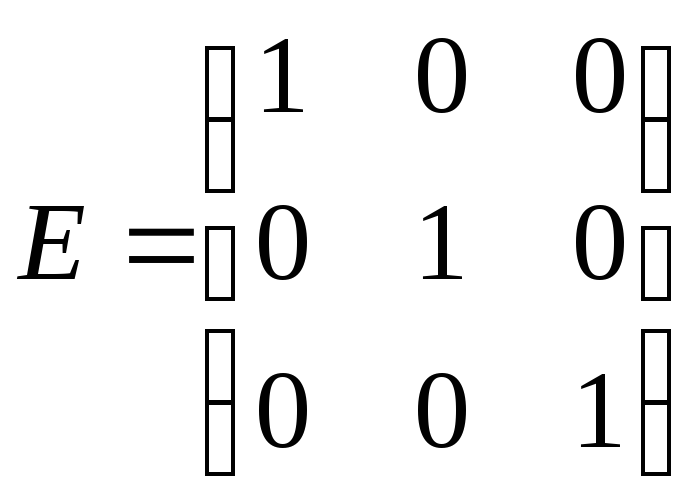
Единичную
матрицу удобно обозначать с помощью
символа Кронекера

.

6)
Нулеваяматрица

.

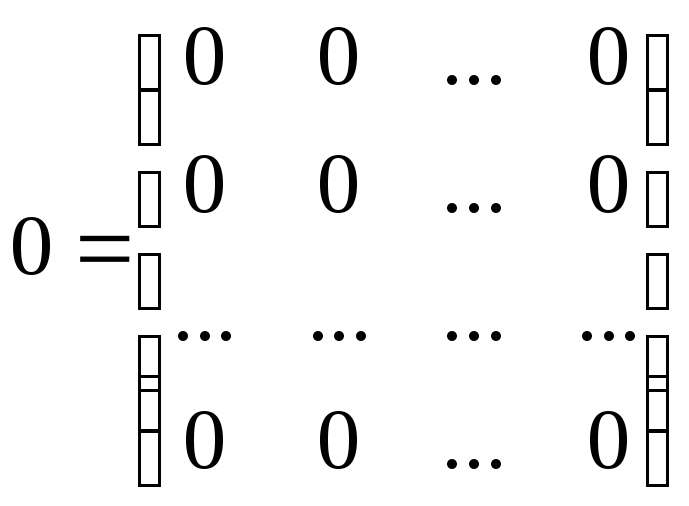
У нее все элементы
равны нулю.

Транспонированиематрицы – это преобразование, состоящее
в замене строк столбцами. Получим
транспонированную матрицу.

Например.

.

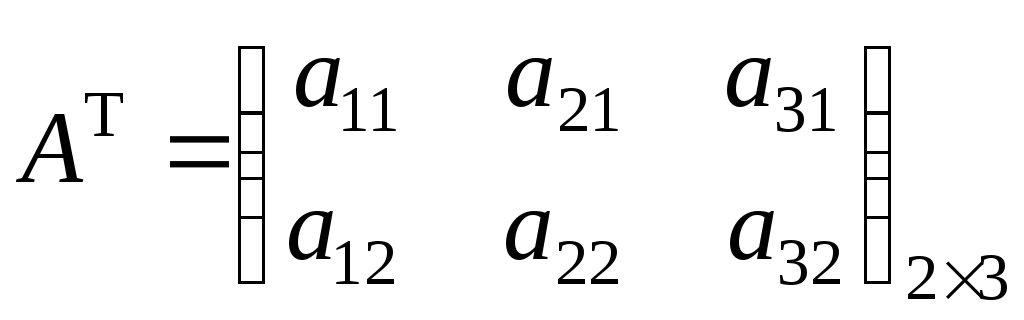
Очевидно
свойство

.

Если
,
то матрица называетсясимметричной.
И у нее

,

т.е. равны элементы,
симметричные относительно главной
диагонали.

Если
,
то матрица называетсякососимметричной.
У нее

.

Очевидно, что у такой
матрицы элементы главной диагонали
равны нулю.

Для
равенстваматриц необходимо и
достаточно, чтобы они были одинакового
размера и чтобы элементы, стоящие на
одинаковых местах были равными.

1. Операции над
   матрицами

1. Сумма матриц.

Матрицы
одинаковых размеров можно складывать,
при этом получаем матрицу того же
размера, что и слагаемые, а элементы ее
образуются сложением элементов, стоящих
на одинаковых местах

.

Пример.

.

Эта
операция обладает свойствами:

1. Коммутативность

.

1. Ассоциативность

.

1. .

2. ,;

,.

1. Произведение
   матрицы на число.

Любую
матрицу можно умножить на число (скаляр),
при этом получаем матрицу того же
размера, а элементы ее получаются
умножением на заданное число всех
элементов данной матрицы.

.

Пример.

.

Свойства
этой операции:

1. Дистрибутивность
   относительно матричной суммы

.

1. Дистрибутивность
   относительно скалярной суммы

.

1. Ассоциативность
   относительно произведения скаляров

.

1. Существование
   элемента нейтрального относительно
   умножения на скаляр

.

1. Умножение матриц.

а) Умножение строки на столбец.

Это
возможно, если число элементов в строке
равно числу элементов в столбце.

.

Пример.

.

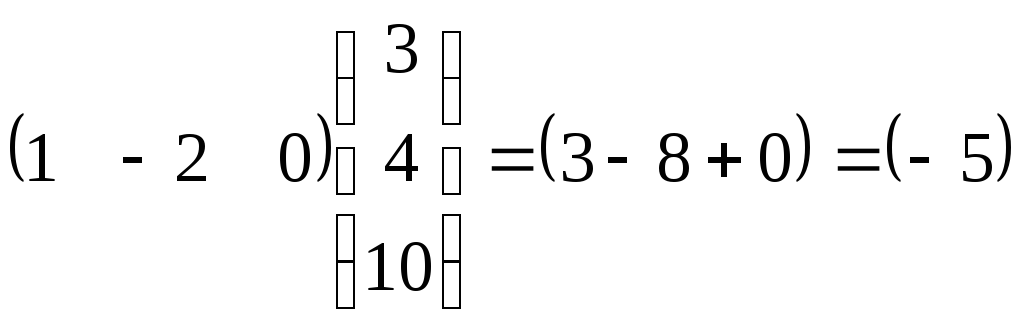
б) Умножение произвольных матриц.

Произведением
матрицы
на матрицуявляется матрицаразмера,
элементкоторой равен результату умноженияi^ойстроки матрицыАнаk^ыйстолбец матрицыВ

.

Пример.

.

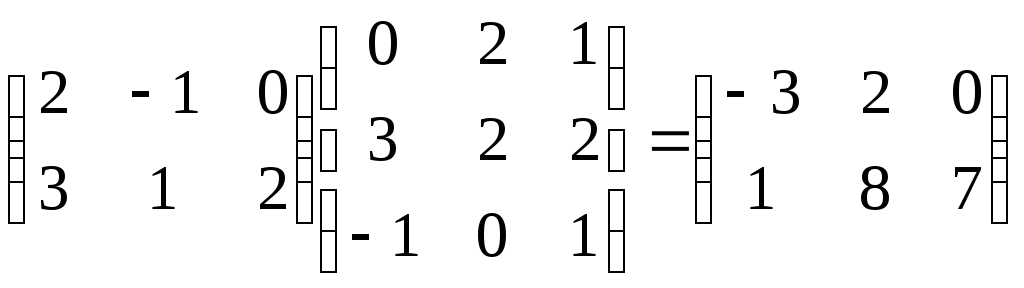
Ясно,
что умножать матрицы можно не всегда,
а с точки зрения их размеров.

Правило
размеров:

.

Поэтому
в общем случае произведение матриц не
коммутативно.

.

Если
же
,
то такие матрицы называютсякоммутирующими.
Однако, если операция произведения
осуществима, то будут справедливы
следующие свойства:

1. Ассоциативность

.

1. Дистрибутивность.

или

.

Рассмотрим выполнение заданий на
действие с матрицами.

Задание 1

Найти матрицу C= 3A+ 4B, если

.

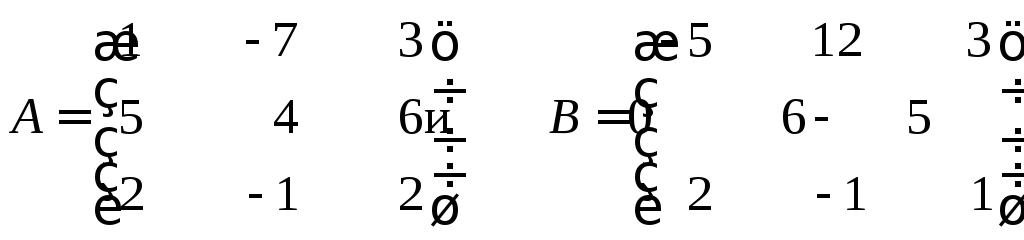
Решение

Используя свойства сложения и умножения
матриц на число, получим

Задание 2

Показать, что матрица S= 3A– 2B
– симметрическая, если

.

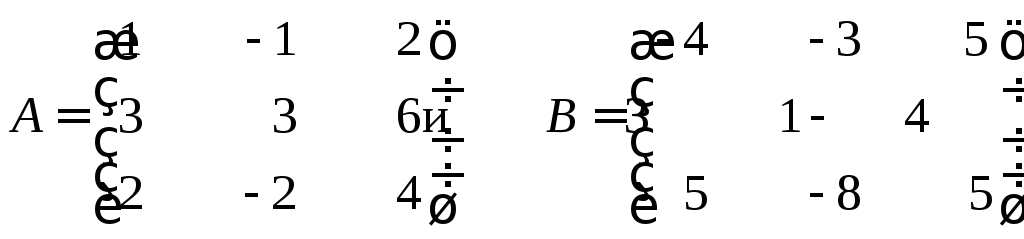
Решение

Используя свойства сложения и умножения
матриц на число, получим

Полученная матрица S–
симметрическая, так как при транспонировании
она не изменяется.

Задание 3

Показать, что матрица K= 5A–B
– кососимметрическая, если

.

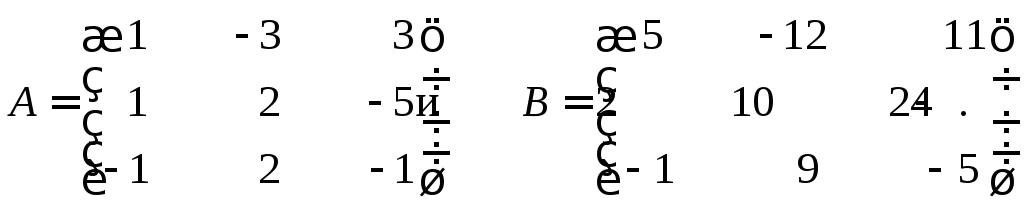
Решение

Используя свойства сложения и умножения
матриц на число, получим

Полученная
матрица K–
кососимметрическая, так как при
транспонировании она меняет знак на
противоположный:

Задание 4

Найти матрицу C=AB,
если

.

Решение

Данные матрицы удовлетворяют правилу
размеров (4), а следовательно, их можно
перемножить. Найдем элементы первой
строки матрицы С, используя формулу
(3) и схему:

===

===

===

Аналогично находим все остальные
элементы матрицы С:

Следовательно,
матрица Симеет вид:

Задание 5

Найти матрицу C=AB,
если

.

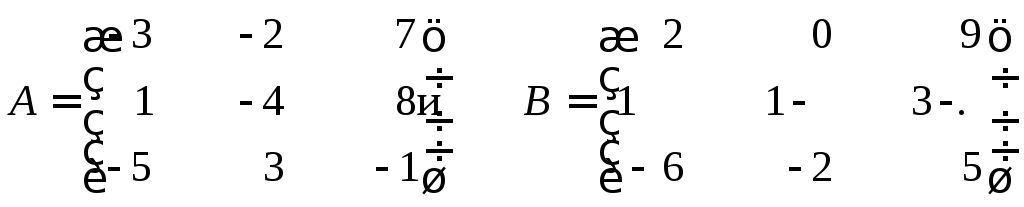
Решение

Данные матрицы удовлетворяют правилу
размеров (4), а следовательно, их можно
перемножить. Умножая по очереди строки
матрицы Ана столбцы матрицыВ,
получим матрицу

Задание 6

Показать, что произведение матрицы
на
транспонированную является симметрической
матрицей.

Решение

Транспонируем матрицу A:

.

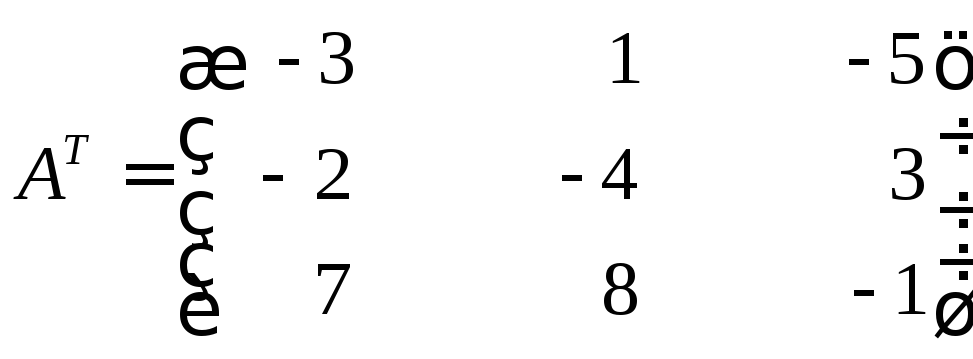
Матрицы AиA^Tудовлетворяют правилу размеров (4), а
следовательно, их можно перемножить.
Умножая по очереди строки матрицыАна столбцы матрицыA^T,
получим матрицу

Матрица S является
симметрической, так как при транспонировании
она не меняется, т.е.S
= S^Т,
что и требовалось доказать.

Задание 7

Показать, что матрицы A
и B перестановочны.

.

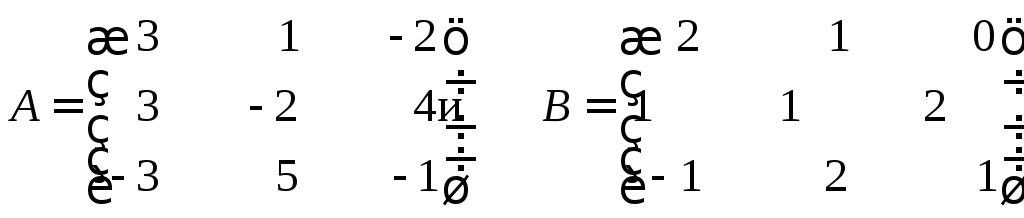
Решение

Данные матрицы удовлетворяют правилу
размеров (4), а, следовательно, их можно
перемножить в любом порядке.

Найдем произведение АВ. Умножая по
очереди строки матрицыАна столбцы
матрицыВ, получим матрицу

Теперь
перемножим эти же матрицы в другом
порядке, т.е. найдем произведение ВА:

Так как
АВ=ВА, то исходные матрицы
перестановочны, что и требовлось
показать.

Задание 8

Выполнить действия:

.

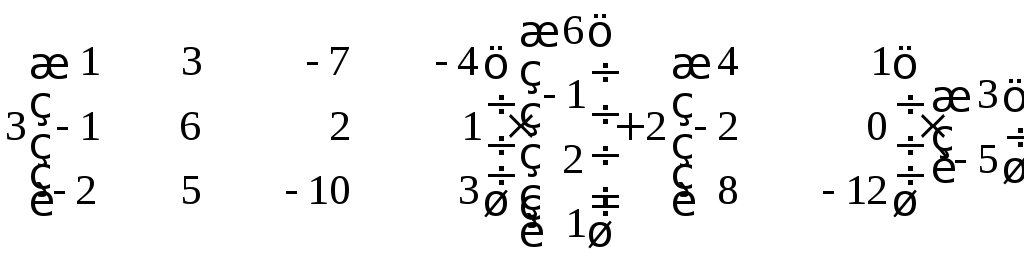
Решение

Данные матрицы удовлетворяют правилу
размеров (4), а следовательно, их можно
перемножить и затем сложить:

Следующее задание выполните самостоятельно:

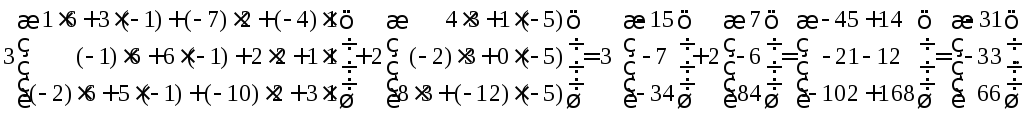
Задание 9

Выполнить действия

.

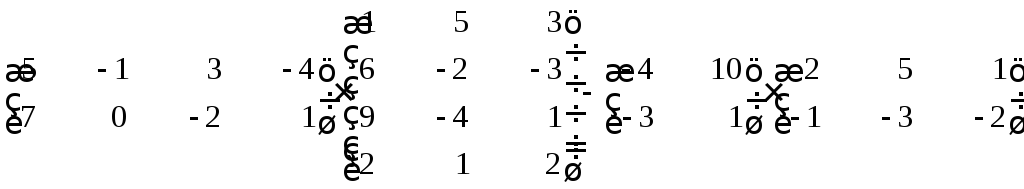
Если у Вас получился результат отличный
от матрицы

, то рассмотрите решение этого
задания.

Решение задания 9.

Данные матрицы удовлетворяют правилу
размеров (4), а, следовательно, их можно
перемножить и затем сложить:

1. Ранг матрицы

Для
квадратной матрицы Аможно записать
определитель, состоящий из тех же
элементов. Обозначается

detA.

Если
,
то матрица называетсянеособенной(вырожденной). Если–вырожденная (особенная).

Пусть
дана прямоугольная матрица размера
.
Образуем минорk^гопорядка этой матрицы. Для этого возьмемkстрок иkстолбцов и выберем элементы, стоящие
на их пересечениях. Из этих элементов
составим определитель. Порядок его
будетk. Это и есть
минорk^гопорядка матрицыА.

Например.

;;

.

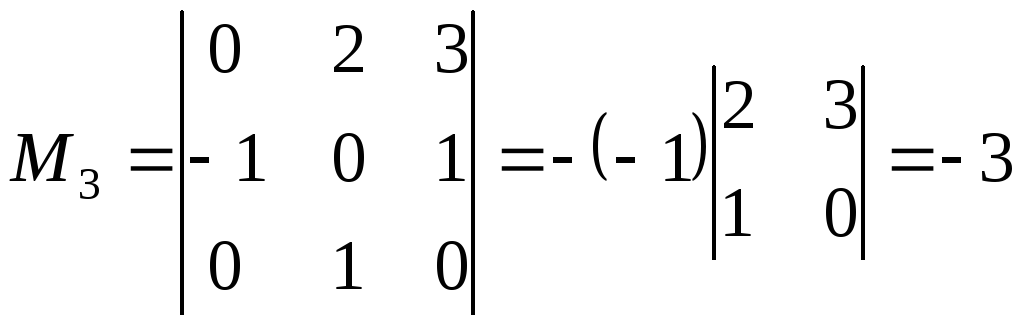
Ясно,
что таких миноров можно образовать
несколько.

Будем
образовывать такие миноры, начиная с
порядка
,
затеми т.д. При некотором порядкехотя бы один из миноров этого порядка
не равен нулю, а при,
т.е. повышении порядка на единицу, уже
все миноры будут равны нулю.

Такое
число rи называется
рангом матрицыА.

или

.

Минор
порядка r, который
отличен от нуля, называетсябазисным
минором, а строки и столбцы, на
пересечении которых стоит базисный
минор, называются базисными строками
или столбцами.

Естественно,
что таких базисных миноров может быть
несколько.

Пример.

.
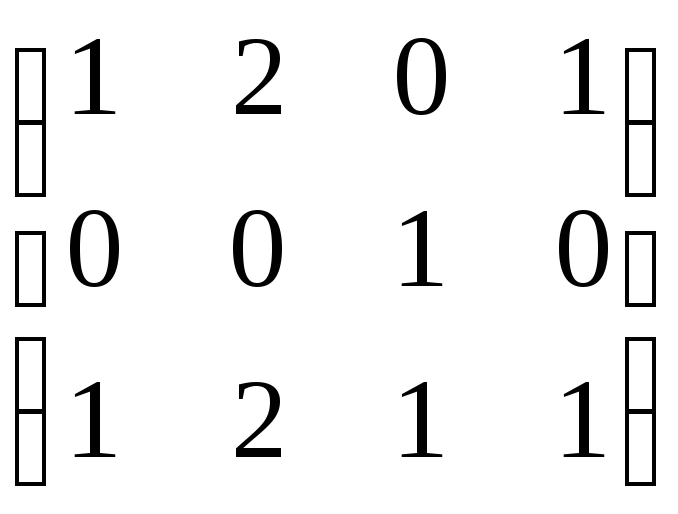
Найти ранг этой матрицы.

Решение.
Среди всех миноров 1^гопорядка
(отдельные элементы) есть ненулевые.
Значит ранг не меньше 1.

Среди
всех миноров 2^гопорядка есть
ненулевые. Например.

Значит ранг не меньше
2.

Переберем
все миноры третьего порядка.

;;;.

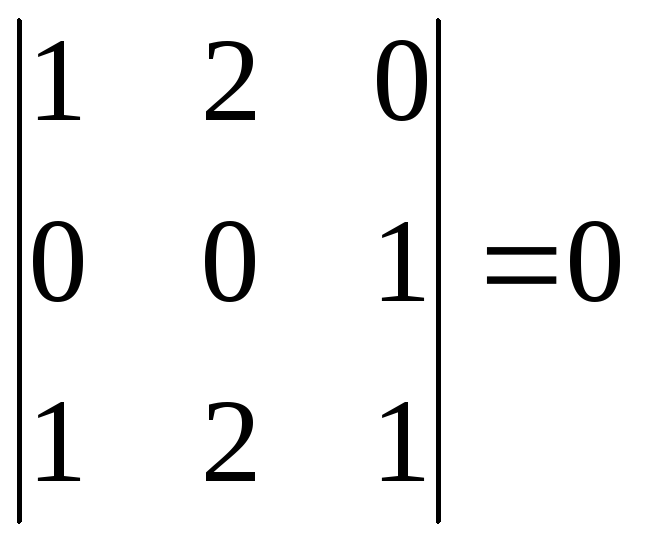
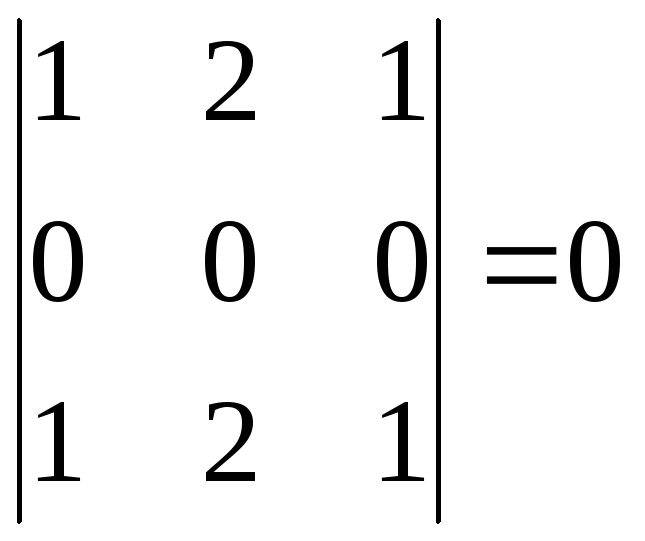
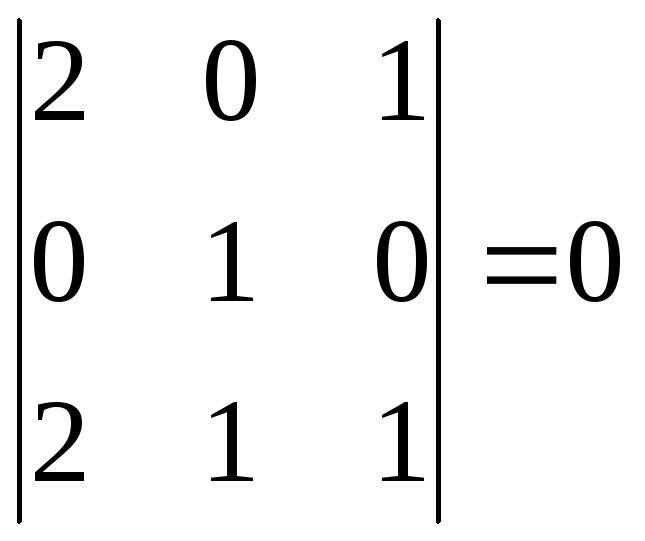
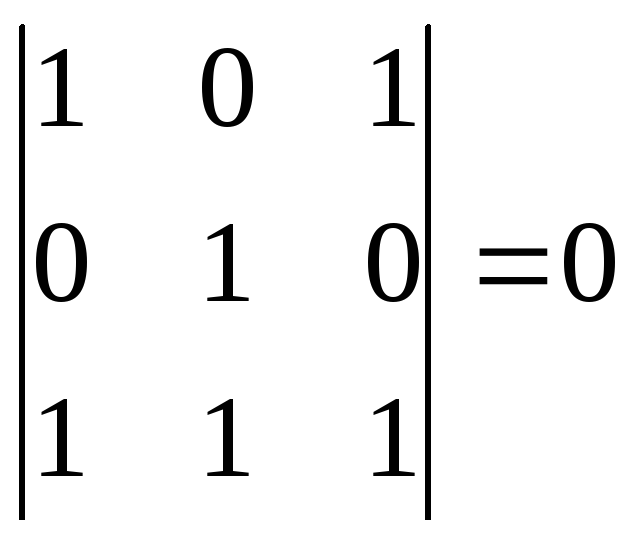
Все миноры третьего
порядка нулевые.

Ранг
равен 2.

Для
вычисления ранга матрицы очень часто
пользуются приемом проведения ее к
виду, позволяющему дать ответ о ранге
исследуемой матрицы. Для этого применяют
операции, не изменяющие ранг матрицы,
но упрощающие ее вид.

Эти
операции называются элементарными, и
они вытекают из свойств определителей:

1. Транспонирование
   матрицы.

2. Перестановка
   строк (столбцов).

3. Умножение всех
   элементов строки (столбца) на какое-либо
   число.

4. Прибавление к
   одному столбцу (строке) другого,
   умноженного на отличное от нуля число.

Пример.
Найти ранг матрицы.

~~

~~

.

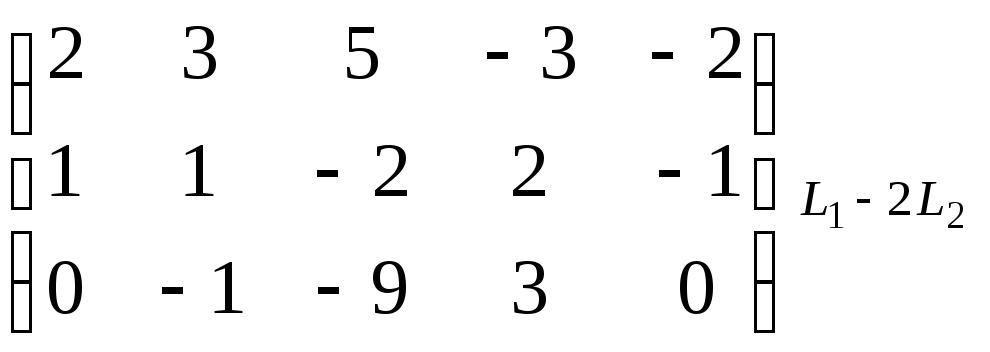
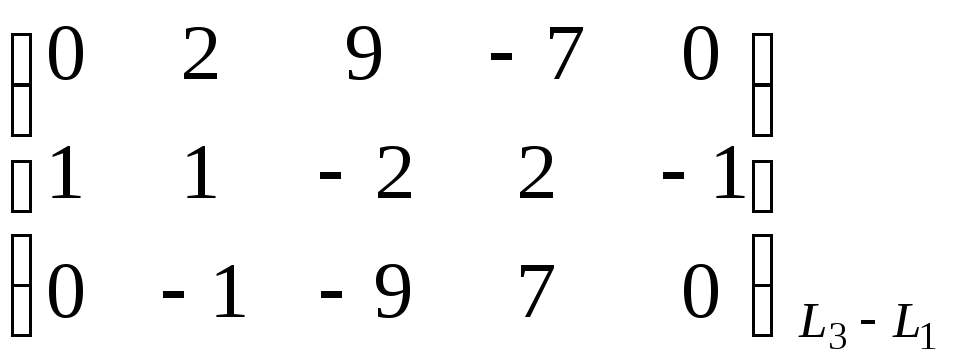
Каноническойназывается матрица, у которой в начале
главной диагонали стоят несколько
единиц, а все остальные равны нулю.

Например

.

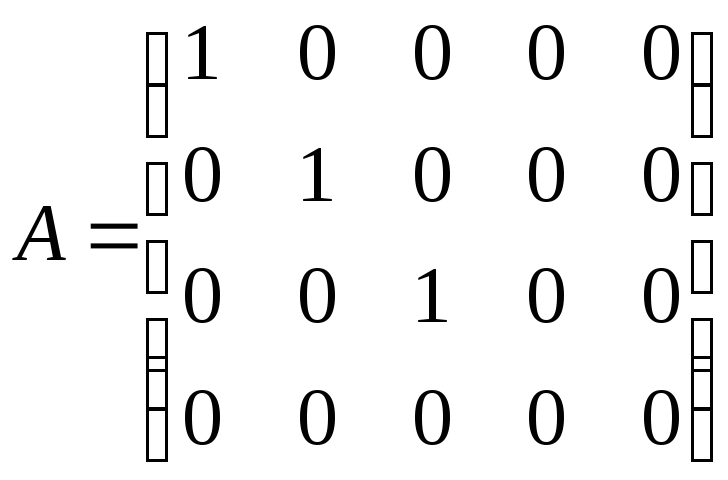
Очевидно
.

При
помощи элементарных преобразований
любую матрицу можно привести к
канонической. Ранг канонической матрицы
равен числу единиц на ее главной
диагонали.

Рассмотрим
выполнение заданий на нахождение ранга
матрицы.

Задание 1

Вычислить ранг матрицы
.

Решение

Все элементы данной матрицы, т.е. миноры
первого порядка, отличны от нуля.
Следовательно, ранг матрицы Ане
меньше 1.

Вычислим определитель данной матрицы
(единственный минор второго порядка):

Так как определитель матрицы А, т.е.
ее минор второго порядка, отличен от
нуля, то ранг данной матрицыr(A)
= 2. Определитель матрицыАбудет ее
единственным базисным минором.

Ответ: r(A)
= 2.

Задание 2

Вычислить ранг матрицы
.

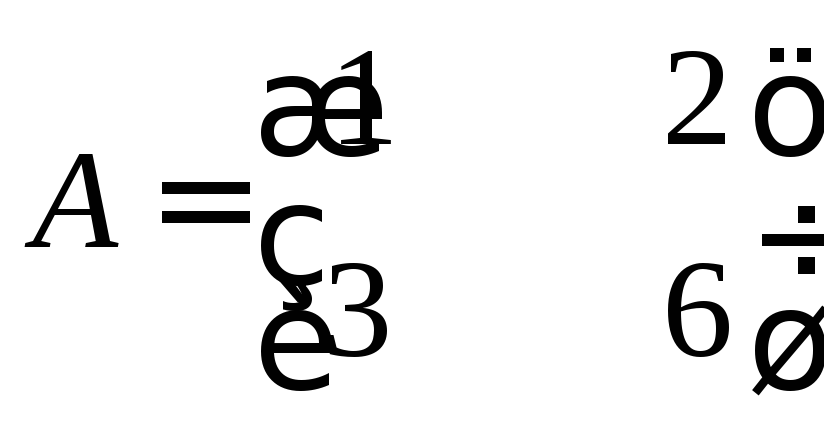
Решение

Все элементы матрицы А, т.е. миноры
первого порядка, отличны от нуля.
Следовательно, ранг матрицыАне
меньше 1. Однако определитель ее, т.е. ее
минор второго порядка, равен нулю:

Следовательно, ранг данной матрицы r(A)
= 1. Данная матрица имеет четыре базисных
минора :

Ответ: r(A)
= 1.

Задание 3

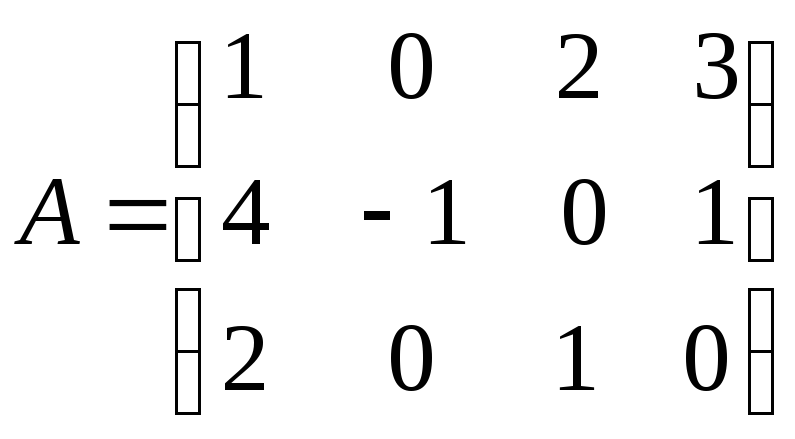
Вычислить ранг матрицы
.

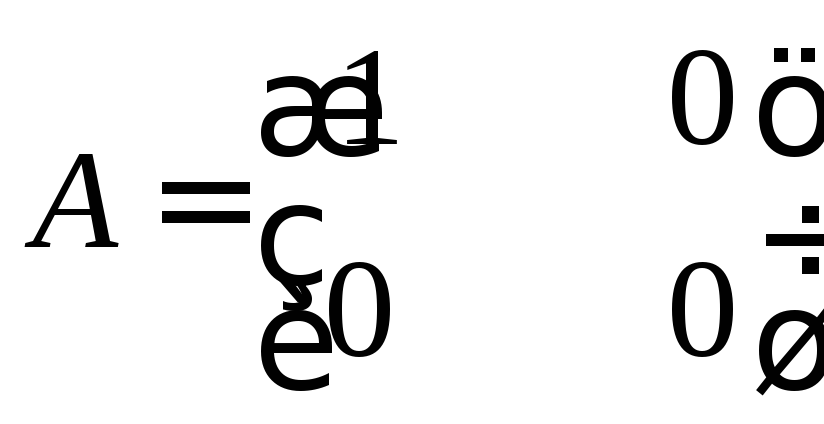
Решение

Один элемент матрицы А, т.е. один
минор первого порядка, отличен от нуля.
Следовательно, ранг матрицыАне
меньше 1. Однако определитель ее, т.е. ее
минор второго порядка, равен нулю:

Следовательно, ранг данной матрицы r(A)
= 1. Данная матрица имеет один базисный
минор

Ответ: r(A)
= 1.

Задание 4

Вычислить
ранг матрицы.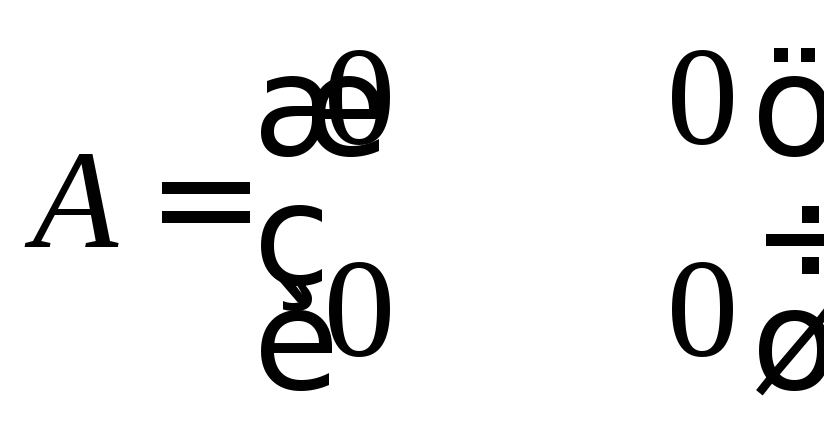

Решение

Так как все элементы матрицы А, т.е.
миноры первого порядка, равны нулю, то
ранг данной матрицыr(A)
= 0.

Ответ: r(A)
= 0.

Задание 5

Вычислить ранг матрицы
.

Решение

Все элементы данной матрицы, т.е. миноры
первого порядка, отличны от нуля.
Следовательно, ранг матрицы Ане
меньше 1.

Среди миноров второго порядка есть
ненулевые. Например,
.

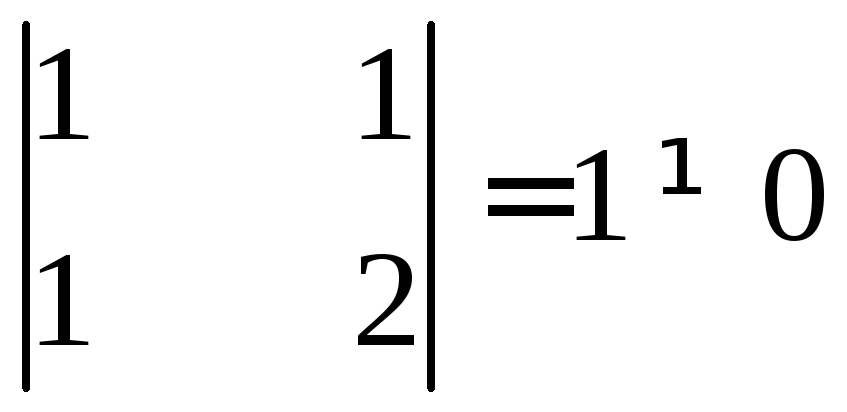
Значит,
ранг не меньше 2.

Вычислим определитель данной матрицы
(единственный минор третьего порядка):

Так как определитель матрицы А, т.е.
ее минор третьего порядка, отличен от
нуля, то ранг данной матрицыr(A)
= 3. Определитель данной матрицыАбудет так же ее единственным базисным
минором.

Ответ: r(A)
= 3.

Задание 6

Вычислить ранг матрицы
.

Решение

Все элементы данной матрицы, т.е. миноры
первого порядка, отличны от нуля.
Следовательно, ранг матрицы Ане
меньше 1.

Среди миноров второго порядка есть
ненулевые. Например,
.

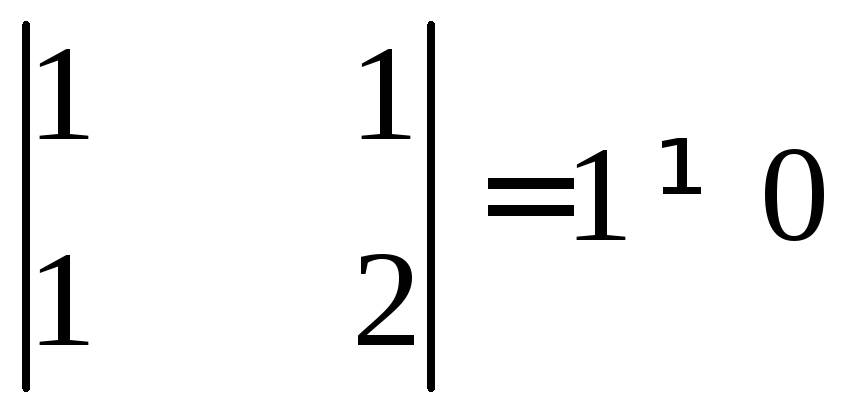
Значит,
ранг не меньше 2.

Вычислим определитель данной матрицы
(единственный минор третьего порядка):

Определитель матрицы А, ее минор
третьего порядка, равен нулю. Значит
ранг данной матрицыr(A)
= 2. Данная матрица имеет шесть базовых
миноров:

Ответ: r(A)
= 2.

Задание 7

Найти ранг матрицы
.

Решение

Посредством последовательных элементарных
преобразований над данной матрицей
получим следующую систему эквивалентных
матриц:

~~~

~
~~~.

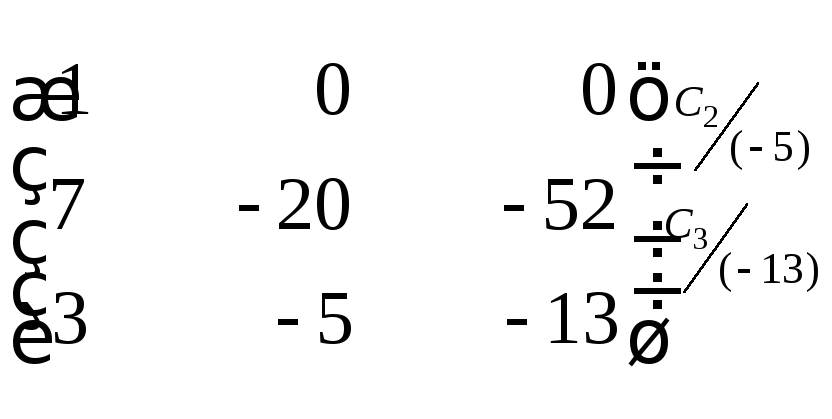
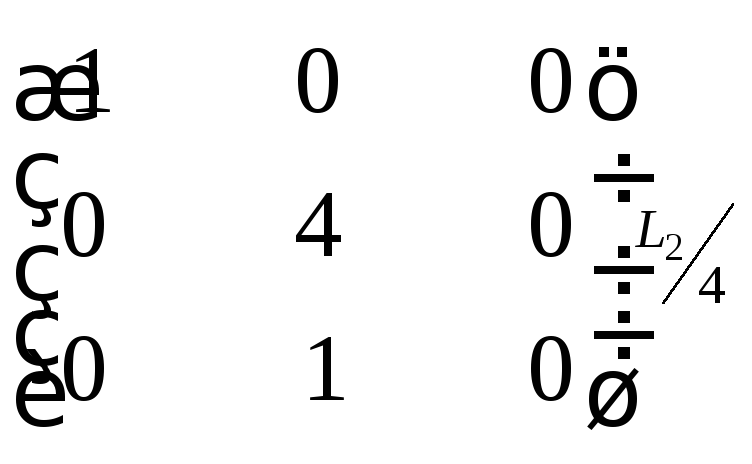
Следовательно, ранг данной матрицы
равен двум.

Ответ:r(A)= 2.

Задание 8

Найти ранг матрицы
.

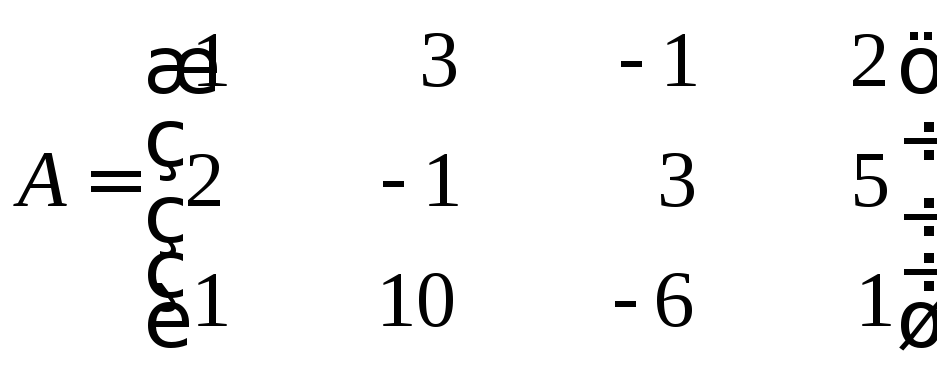
Решение

Посредством
последовательных элементарных
преобразований над данной матрицей
получим следующую систему эквивалентных
матриц:

~~~

~
~~.

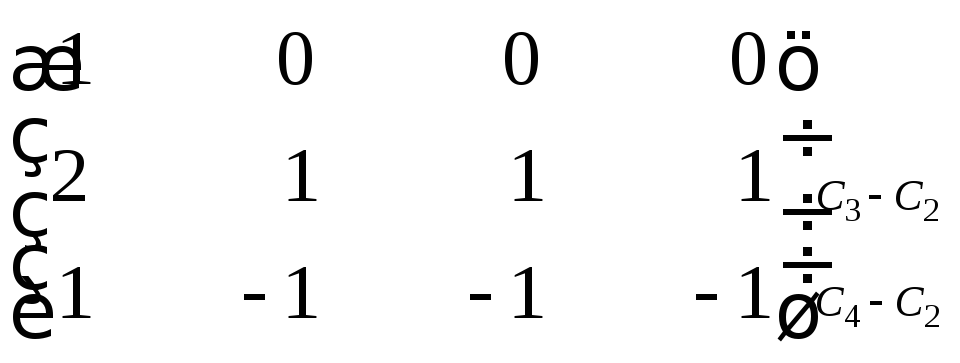
Следовательно, ранг данной матрицы
равен двум.

Ответ:r(A)= 2.

Задание 9

Найти ранг матрицы
.

Решение

Посредством последовательных элементарных
преобразований над данной матрицей
получим следующую систему эквивалентных
матриц:

~~

~~~

~
~~

~
~~

~
~.

Следовательно, ранг данной матрицы
равен двум.

Ответ:r(A)= 2.

Следующее задание выполните самостоятельно

Задание 10

Найти ранг матрицы
.Если
у Вас получился иной результат чем
r(A)= 3, то рассмотрите решение задания 10.

Решение задания 10.

Посредством последовательных элементарных
преобразований над данной матрицей
получим следующую систему эквивалентных
матриц:

~~

~
~~

~
~~

~
~.

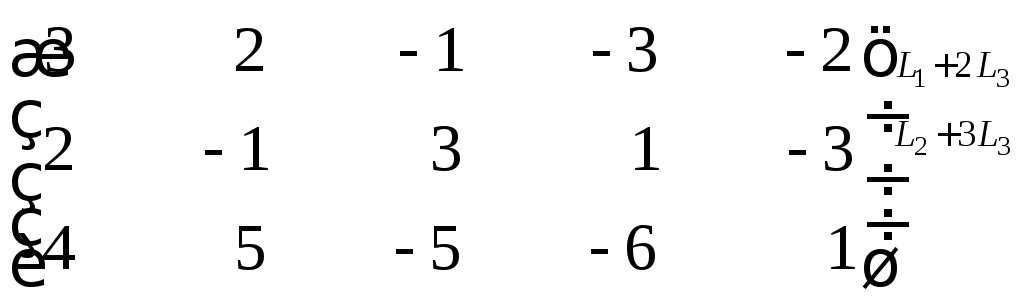
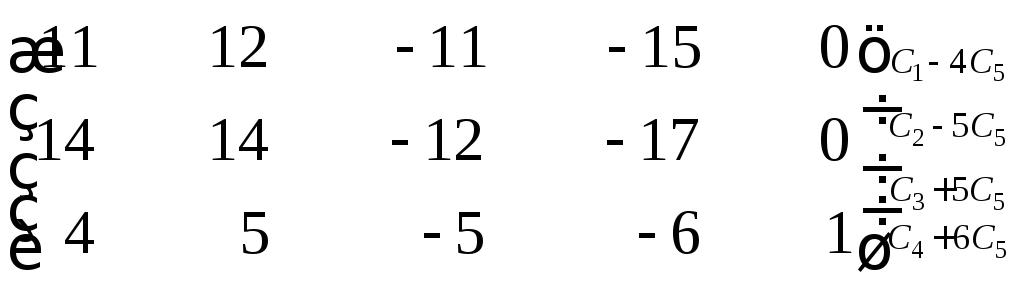
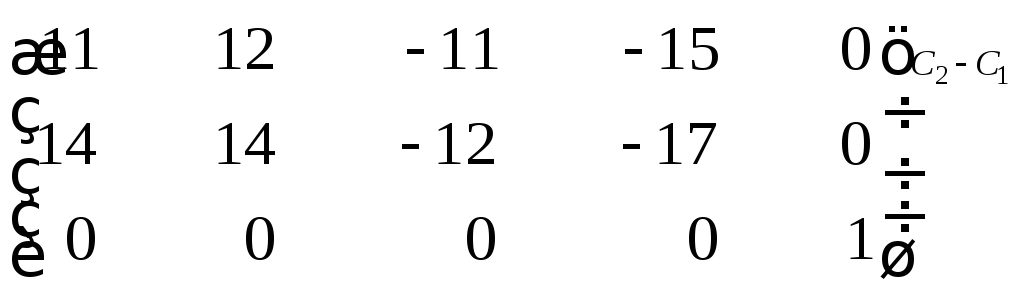
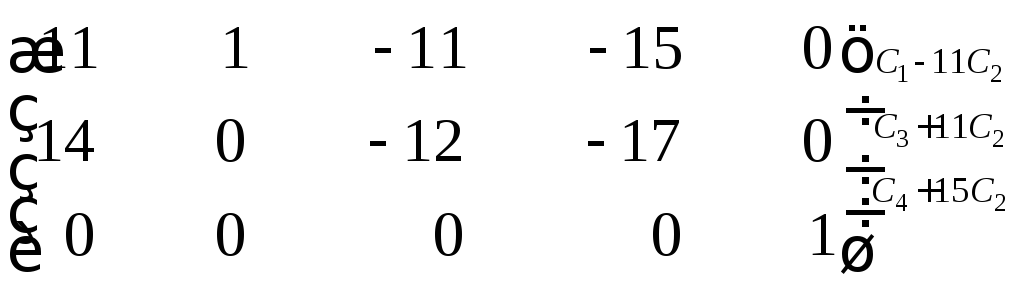
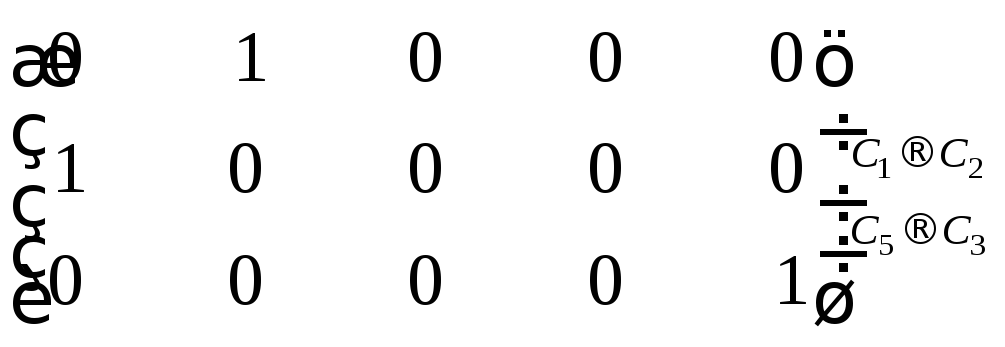
Следовательно, ранг данной матрицы
равен трем.

Ответ:r(A)= 3.

1. Матричная запись
   систем линейных уравнений. Обратная
   матрица

Первоначально
матрицы были введены для упрощения
записи систем линейных уравнений. Это
и обусловило определение основных
матричных операций.

Пусть
дана система тлинейных уравнений
сnнеизвестными.

(1)

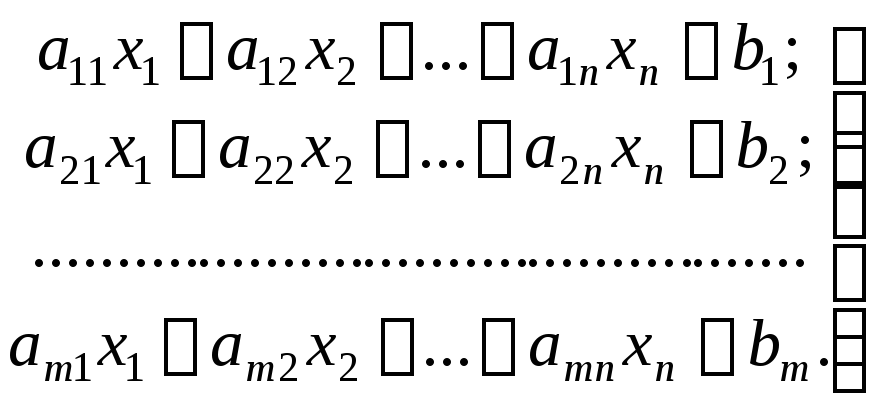
В матричной форме:

(2)

|| || ||

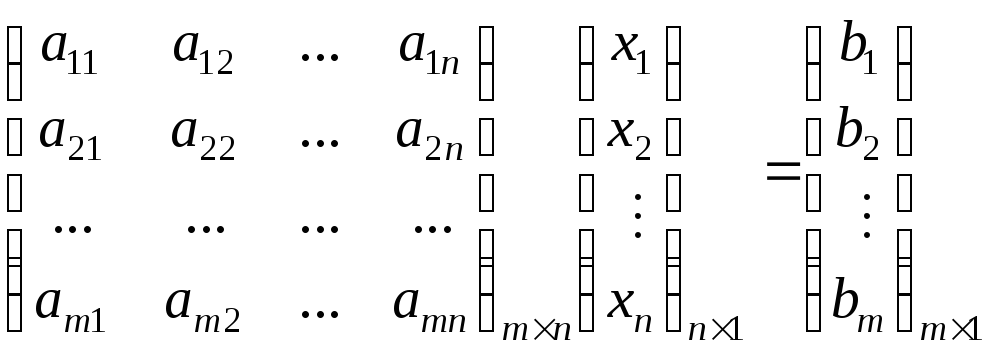
А ∙ Х = В

А– матрица системы;

Х– матрица неизвестных;

В– матрица свободных членов.

Получим
сокращенную запись системы:

(3)

Будем
рассматривать систему n-линейных
уравнений сnнеизвестными. В этом случаеА–
квадратная матрица размера.
Если эта матрица невырожденная, то ее
ранг равенn.

Введем
понятие обратной матрицы.

В
алгебре два числа, произведение которых
равно 1, называются взаимно обратными.

.

Имеет место некоторая
аналогия и для матричной алгебры.

Определение.

Две квадратные матрицы, произведение
которых равно единичной матрице,
называются взаимно обратными.

Обозначение
.

По
определению

.

Теперь,
используя обратную матрицу, решим
матричное уравнение (3). Для этого умножим
обе части (3) на
.

;

;

.
(4)

Это и
есть матричное решение системы уравнений.

Значит
решение системы сводится к отысканию
обратной матрицы и ее умножению на
матрицу свободных членов.

Теорема(существования и единственности обратной
матрицы).

Если
А– квадратная невырожденная
матрица, т.е.,
то для нее существует единственная
обратная матрица.

Доказательство.

Будем
рассматривать для простоты матрицу
.

.

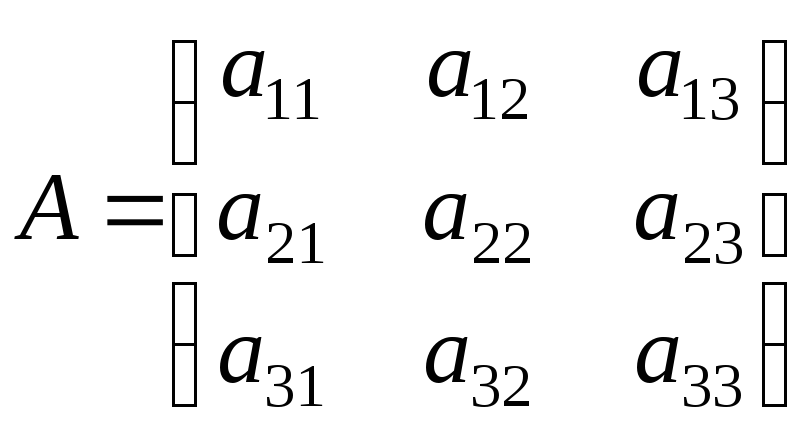
1. Запишем для Атранспонированную матрицу

.

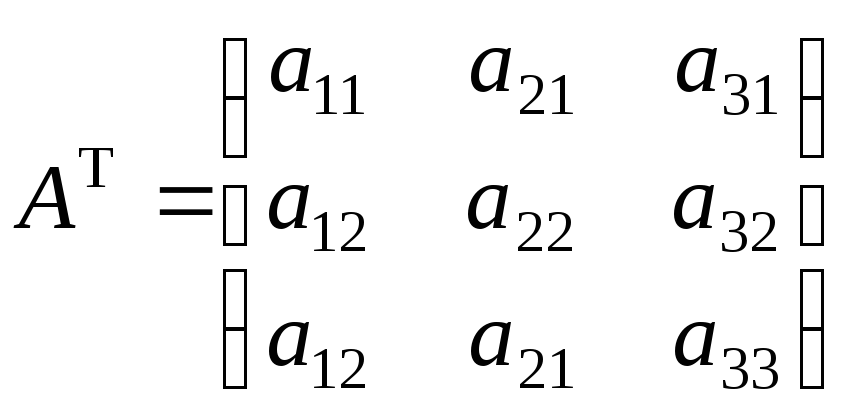
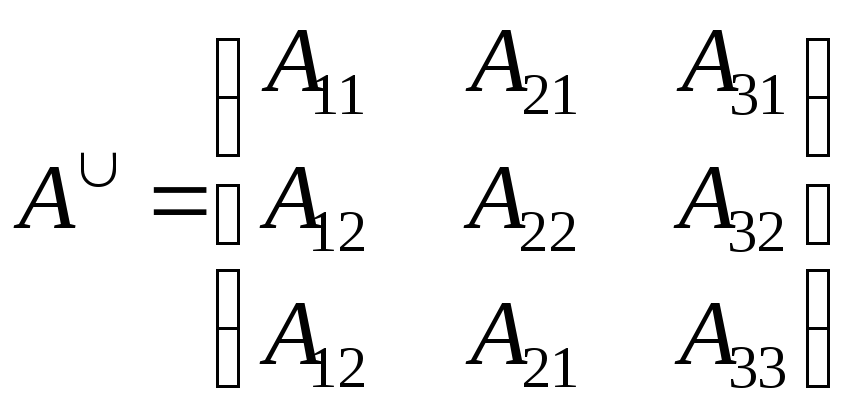
1. Запишем в
   каждый элемент дополнением. Получим
   так называемую союзную (присоединенную)
   матрицу.

.

1. Вычислим произведение
   .

∆

∆

∆

0

0

0

0

0

0

где
.

Аналогично
проверим и другое произведение

.

Итак,
имеем

,

откуда, т.к.
,

.

Сравнивая это равенство
с определением обратной матрицы, можем
сказать, что

.

Мы
доказали существование обратной матрицы
при условии, что
.
Покажем ее единственность.

От
противного:

Предположим,
что существуют две различные обратные
матрицы для матрицы А. Этои.

Тогда

.

Умножаем обе части на

.

Применяя сочетательное
свойство, получим

,

откуда

.

Что противоречит
предположению о том, что имеются две
различные обратные матрицы.

Из
доказанной теоремы следует алгоритм
построения обратной матрицы:

1. Вычисляем
   .
   Если,
   то.

2. Транспонируем
   .

3. Строим
   заменой.

4. .

Пример.
Найти
для.

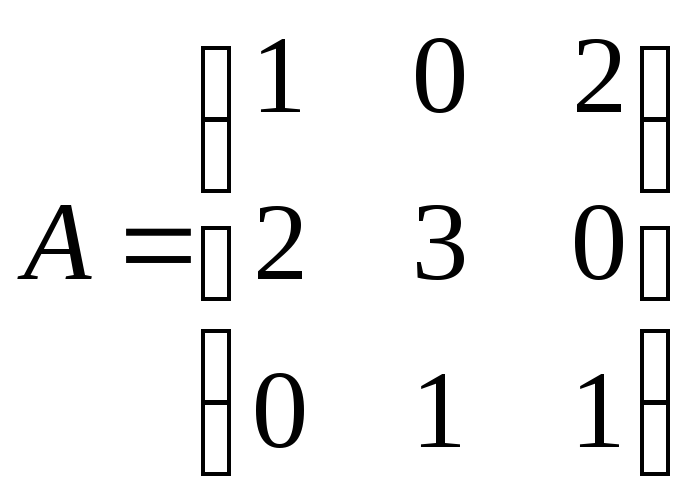
Решение:
1)
.

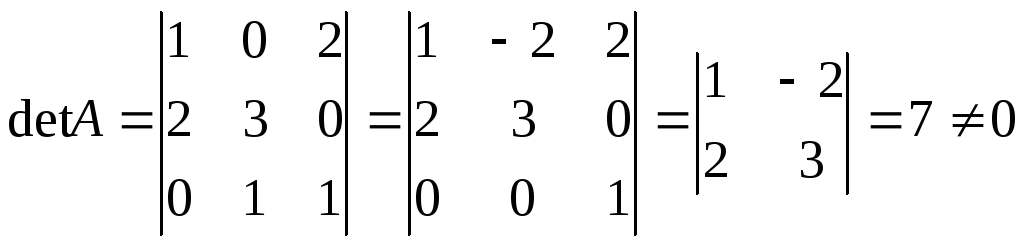
2)
.

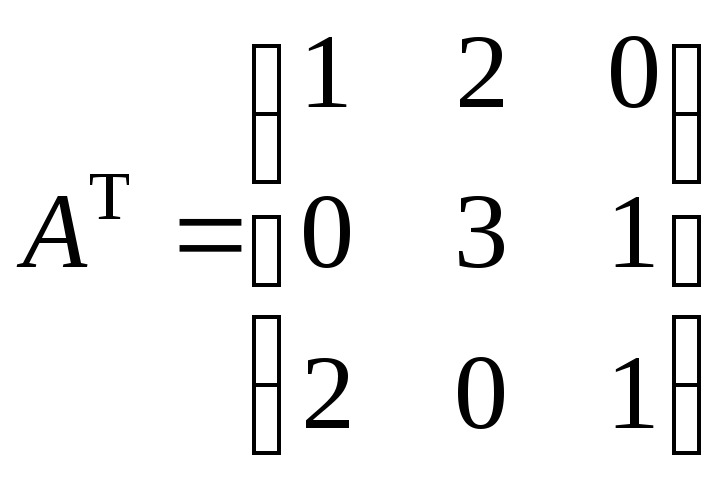
3)
.

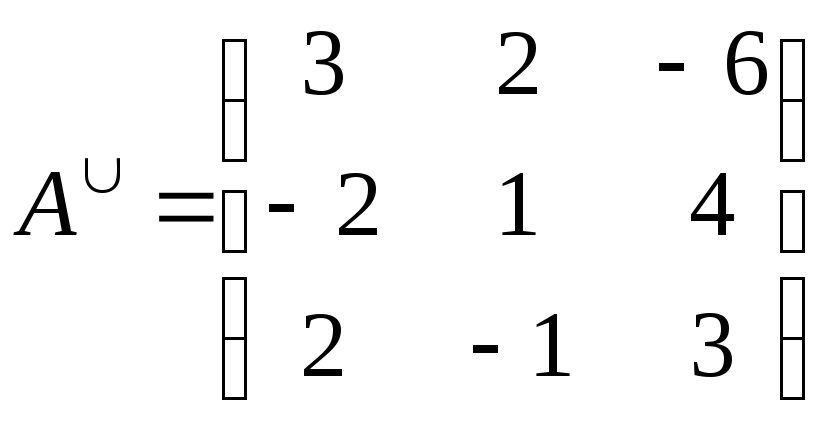
4)
.

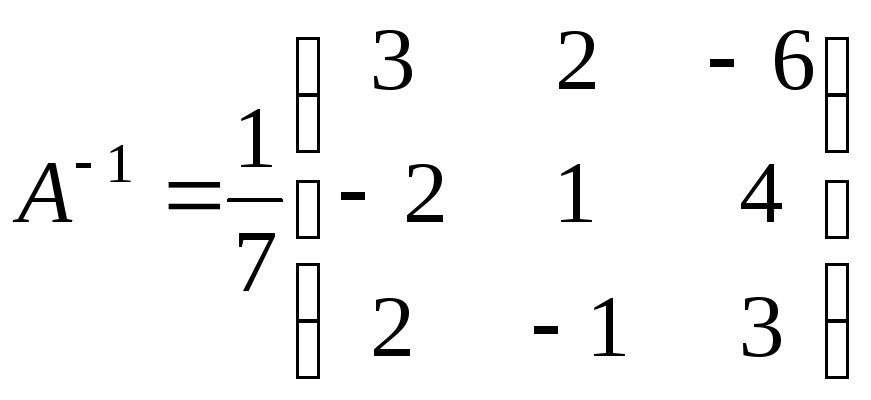
Проверка.

.

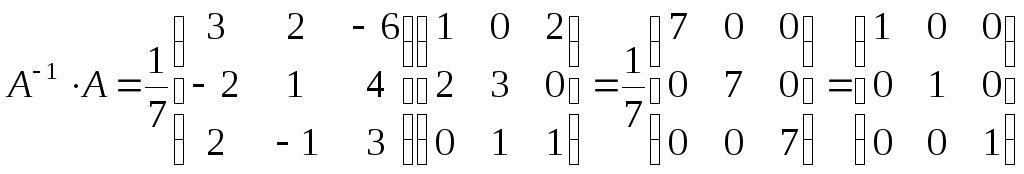
Обратная
матрица обладает свойствами:

1с)
.

Доказательство:

.

2с)
.

3с)
.

4с)
.

Эти
свойства доказываются аналогично
свойству 1с) и путем вычисления.

Существует
и другой способ вычисления обратной
матрицы, основанный на элементарных
преобразованиях вспомогательной
матрицы, которая получается путем
приписывания к данной матрице единичной
матрицы того же размера.

.

Пример.

.

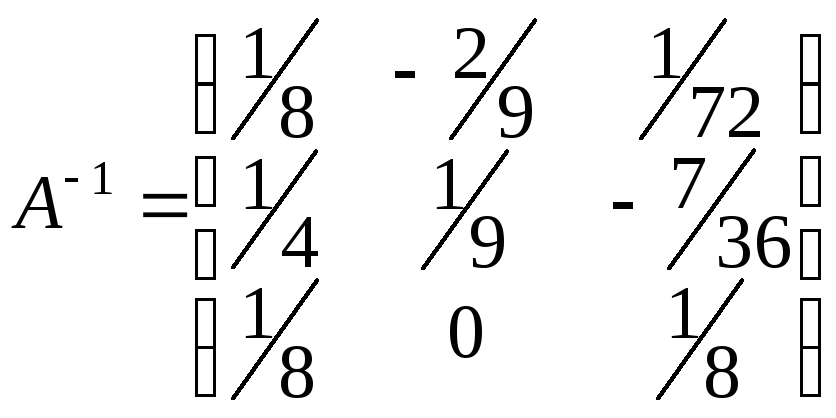
1. Теорема
   Кронекера-Капелли

Рассмотрим
систему mлинейных
уравнений сnнеизвестными:

Матрица системы:

.

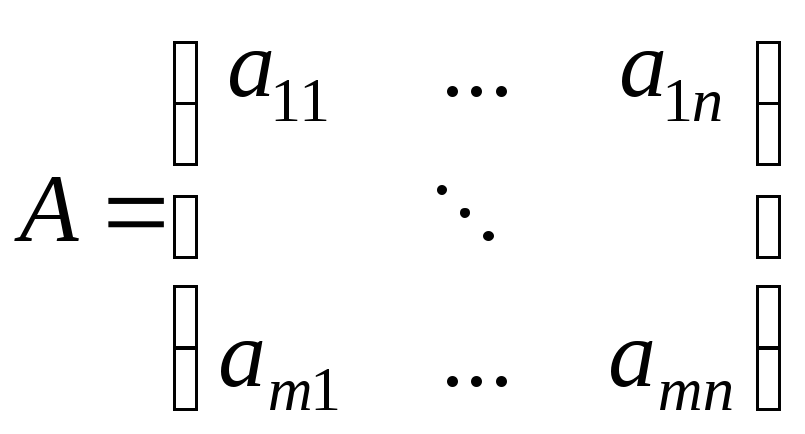
Расширенная матрица
системы:

.

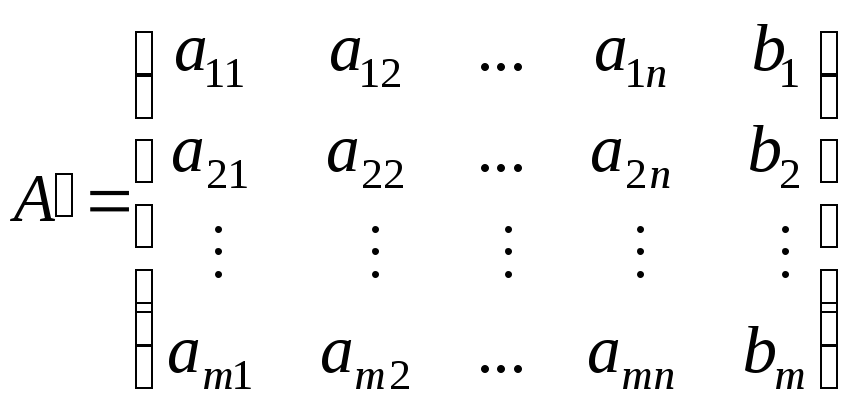
Очевидно
.

Теорема
Кронекера-Капелли утверждает, что

1)система имеет единственное решение
(определенна).

2)система имеет бесконечное множество
решений (неопределенна)

3)система не имеет решений (несовместна)

Примеры.

1)

~.

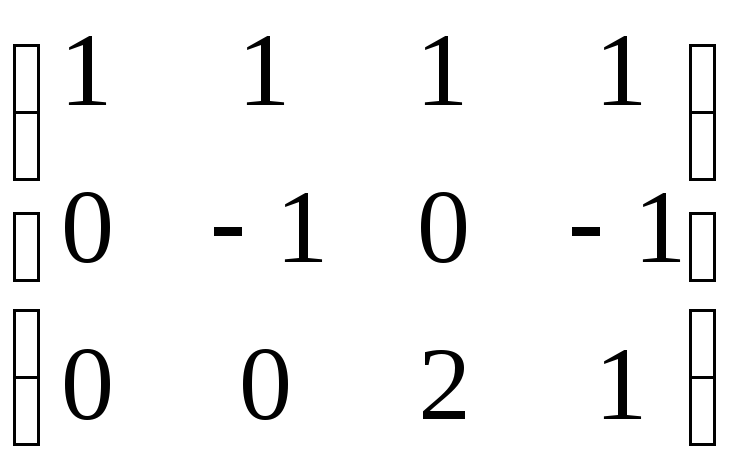
А

определенна.

Решение ,,.

2)

.

,.

.

3)

.

,.

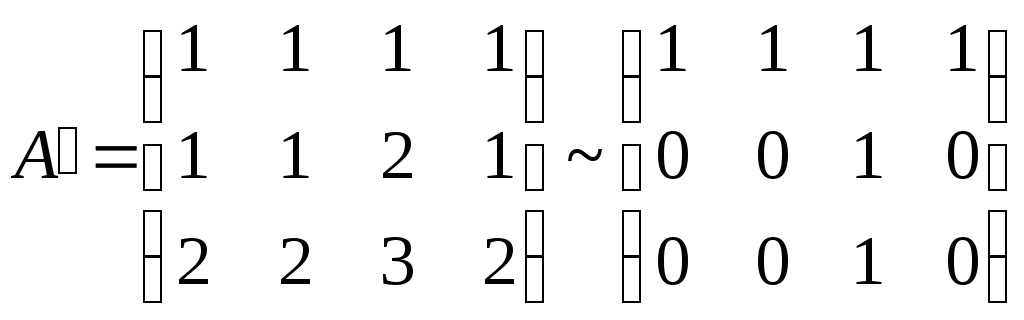
бесконечное множество
решений.

.

,,.

Рассмотрим выполнение
заданий на нахождение обратной матрицы
и решение систем линейных уравнений с
помощью обратной матрицы.

Задание1

Найти
матрицу, обратную матрице
.

Решение

Многие считают, что тема «Транспонированные матрицы» довольно сложная, но это не так. В студенческом курсе математики транспонирование выполняется легко и без каких-либо усилий. Для того чтобы понимать, как именно осуществляется операция, необходимо знать, что такое матрица.

Онлайн-калькулятор

Что такое транспонированная матрица

Матрица, полученная из данной заменой каждой ее строки столбцом с этим же номером, называется матрицей транспонированной данной. Обозначается такая матрица ATA^{T} или A′A’.

При транспонировании матрицы AA размера m×nmtimes n получаем матрицу ATA^{T} размера n×mntimes m.

В общем виде транспонированная матрица для матрицы

Am×n=(a11a12…a1na21a22…a2n…………am1am2…amn)A_{mtimes n}=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix}

выглядит следующим образом:

An×mT=(a11a21…am1a12a22…am2…………a1na2n…amn)A^{T}_{ntimes m}=begin{pmatrix}a_{11}&a_{21}&…&a_{m1}\a_{12}&a_{22}&…&a_{m2}\…&…&…&…\a_{1n}&a_{2n}&…&a_{mn}end{pmatrix}.

Элементы ii строки исходной матрицы становятся элементами ii столбца транспонированной матрицы. Таким образом, транспонирование матрицы заключается в том, что строки исходной матрицы AA записывают в новую матрицу по столбцам.

Пример 1

Транспонировать матрицы K=(15−2314−18)K=begin{pmatrix}15&-23&14&-18end{pmatrix} и L=(25−10118)L=begin{pmatrix}25\-10\11\8end{pmatrix}.

KT=(15−2314−18)K^{T}=begin{pmatrix}15\-23\14\-18end{pmatrix},

LT=(25−10118)L^{T}=begin{pmatrix}25&-10&11&8end{pmatrix}.

Пример 2

Транспонировать матрицу G=(5−311820514−86537−94)G=begin{pmatrix}5&-3&11&8\2&0&5&1\4&-8&6&5\3&7&-9&4end{pmatrix}.

GT=(5243−30−871156−98154)G^{T}=begin{pmatrix}5&2&4&3\-3&0&-8&7\11&5&6&-9\8&1&5&4end{pmatrix}.

Свойства транспонированных матриц

1. Дважды транспонированная матрица равна исходной матрице: ATT=(AT)T=AA^{TT}=(A^{T})^{T}=A.
2. Транспонированная матрица суммы равна сумме транспонированных матриц: (A+B)T=AT+BT(A+B)^{T}=A^{T}+B^{T}.
3. Транспонированная матрица произведения равна произведению транспонированных матриц: (A⋅B)T=AT⋅BT(Acdot B)^{T}=A^{T}cdot B^{T}.
4. При транспонировании можно выносить скаляр (число, на которое можно разделить все элементы матрицы): (k⋅A)T=k⋅AT(kcdot A)^{T}=kcdot A^{T}.
5. Определитель исходной матрицы и определитель транспонированной матрицы равны.

С понятием определителя матрицы мы познакомимся на следующем уроке.

Возникли сложности с матрицей? На нашем сервисе предусмотрена платная помощь с решением задач по алгебре от экспертов!

Тест по теме «Транспонирование матрицы»

Равенство матриц и транспонирование матрицы

На чтение 3 мин. Просмотров 3.1k.

Мы изучили тему «Матрицы», дали определение матриц и рассмотрели основные виды матриц, теперь давайте введем понятие «равенство матриц», то есть определим, когда две матрицы являются равными.

Определение равенства двух матриц

Матрицы называются равными, если они имеют одинаковое число строк и одинаковое число столбцов, а соответствующие элементы матриц равны: .

Таким образом, матрицы

и

равны, если ,   ,  ,  ,  ,   ,  ,  ,  ,   ,  ,  ,  ,   ,  ,  .

Равные матрицы имеют одинаковое строение, так как для неравных по строению матриц невозможно создать равенство .

Транспонирование матриц

Если в матрице типа , имеющей вид

переставить строки со столбцами, получим матрицу, типа , которая является транспонированной матрицей:

Если матрица состоит из одной строки (матрица-строка), то при транспонировании такая матрица становится матрицей-столбцом.

Свойства транспонирования матриц

Перечислим свойства транспонирования матриц, немного забежим вперед:

1. Если матрицу транспонировать дважды, то получится исходная матрица.
2. Транспонирование суммы матриц равно сумме транспонированных матриц.
3. Можно умножить исходную матрицу на число или уже транспонированную матрицу умножить на число, порядок умножения не важен. Таким образом, транспонированное произведение матрицы и числа равно произведению этого же числа на транспонированную матрицу.
4. Транспонированное произведение матриц равно произведению транспонированных матриц в обратном порядке

Транспонирование векторов

При транспонировании векторов матрица-столбец становится матрицей-строкой, а матрица-строка становится матрицей-столбцом. Так, например, матрица-строка

станет матрицей-столбцом:

( 3 оценки, среднее 5 из 5 )

Калькулятор матриц — действия с матрицами онлайн

С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.

Также может быть интересно:

• Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина
• Калькулятор комплексных чисел

Как пользоваться калькулятором матриц

1. Выберите матрицу (или матрицы) с помощью переключателей ()
2. Укажите размер с помощью выпадающих списков под матрицей ( × )
3. Заполните элементы (нулевые элементы можно не заполнять.)
4. Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
5. Нажмите кнопку .
6. Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2), неправильные дроби () и десятичные дроби (2.4) с указанием числа знаков после запятой.

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби (1/2, 29/7, -1/125), десятичные дроби (12, -0.01, 3.14), а также числа в экспоненциальной форме (2.5e3, 1e-2).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (←, ↑, →, ↓) для перемещения по элементам

Что умеет наш калькулятор матриц?

С одной матрицей (только Матрица A или Матрица B)

• Транспонировать;
• Вычислять определитель;
• Находить ранг и след;
• Возводить в степень;
• Умножать на число;
• Вычислять обратную матрицу;
• Приводить к треугольному и ступенчатому вид;
• Находить LU-разложение;
• Выполнять элементарные преобразования;
• Выполнять действия с выражениями, содержащими матрицы.

С двумя матрицами (Матрица A и Матрица B)

• Складывать;
• Вычитать;
• Умножать;
• Решать системы линейных алгебраических уравнений (СЛАУ) вида AX=B;
• Выполнять действия с выражениями, содержащими матрицы.

Вычисление выражений с матрицами

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

• Целые и дробные числа
• Матрицы A, B
• Знаки арифметических действий: + - * /
• Круглые скобки для изменения приоритета операций: ( )
• Транспонирование: ^T
• Возведение в целую степень: ^

Примеры корректных выражений

• Cложение двух матриц: A+B, (A)+(B), ((A) + B)
• Возведение линейной комбинации матриц в степень: (3A - 0.5B)^5
• Произведение транспонированной матрицы на исходную: A^TA
• Обратная матрица в квадрате для B: B^-2

Что такое матрица?

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: An×m.

Примеры матриц

Элементы матрицы

Элементы A обозначаются aij, где i — номер строки, в которой находится элемент, j — номер столбца.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji

Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — aii

Единичная матрица E_n×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: An

Обратная матрица A⁻¹ — матрица, произведение которой на исходную матрицу A равно единичной матрице: A-1×A = A×A-1 = E

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U

Сложение матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij+bij

Разность матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij-bij

Умножение матриц A_n×k и B_k×m — матрица C_n×m, у которой элемент (c_ij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: cij = ai1·b1j + ai2·b2j + ... + aik·bkj