Почему умножение матриц такое
Уровень сложности
Простой
Время на прочтение
3 мин
Количество просмотров 54K
Наверное, каждый задавался вопросом, почему умножение матриц такое. В этой статье мы разберём из каких соображений оно вводится именно так.
Маленькое предисловие
В дальнейшем нам понадобится такая структура, как векторное пространство, а точнее его частный случай — пространство столбцов высоты
над
Кратко напомню, что под этим понимается.
Во-первых, — это следующее множество
где таким образом обозначен вектор-столбец высоты
то есть
Во-вторых, для любых векторовопределено сложение
и для любого вектораопределено умножение на скаляр
В-третьих, каждый векторединственным образом представим в следующем виде
где — скаляры, а
— следующая система векторов
Такая система векторов называется базис, а скаляры, участвующие в разложение вектора, называются координатами этого вектора в данном базисе. Стоит отметить, что в это не единственный базис, но везде далее под «зафиксируем базис» можно понимать именно эту систему векторов.
Умножение матрицы на вектор
Прежде чем переходить к умножению матриц, посмотрим, из каких соображений вводится умножение матрицы на вектор. Для этого рассмотрим линейное отображение
То, что— линейное отображение, означает, что для любых векторов
и любого скаляра
выполняются следующие два условия:
Или их можно объединить в одно
Нас интересует, как линейное отображениедействует на произвольный вектор
Для этого зафиксируем в
базис
а в
базис
Теперь мы можем разложить вектор
по базису
и представитьв следующем виде
Заметим, что а поскольку в
зафиксирован базис, то эти векторы также можно разложить по базису
или тоже самое в векторной записи
Подставляем в равенство выше и получаем
Но правая часть равенства есть не что иное, как формула умножения матрицы на вектор-столбец
где столбцы матрицы есть векторы
Получается, можно ввести умножение матрицы на вектор по следующему правилу
И такое определение умножения будет согласовано с тем, как линейное отображениедействует на вектор
Если теперь обозначить то координаты вектора
выражаются через координаты вектора
следующим образом
Кроме того, мы получили и другой важный результат, вернёмся к выражению для
Из него следует, что линейное отображениеполностью определяется своими значениями на базисных векторах, то есть, если нужно найти
то достаточно знать
Далее, мы поместили эти векторы в матрицу и определили умножение так, чтоесть произведение соответствующей матрицы
на
Получается, что линейному отображению можно поставить в соответствие матрицу, которая полностью его определяет
Такая матрица называется матрицей линейного отображенияв выбранных базисах пространств
и
Если говорить более строго, то существует взаимно однозначное соответствие между линейными отображениями из в
и матрицами размера
Теперь мы можем перейти к умножению матрицы на матрицу.
Умножение матрицы на матрицу
Рассмотрим линейные отображенияи
и их композицию
Легко проверяется, что будет линейным отображением
Поэтому, если зафиксировать в и
базисы, то каждому линейному отображению можно поставить в соответствие его матрицу
Нас теперь интересует, как между собой они связаны. Для этого рассмотрим следующее равенство
и найдём координаты вектора через координаты вектора
Так както
Но из равенстваследует, что
Подставляем в равенство выше и получаем
С другой стороны,то есть
Сравнивая первое и второе равенство для координатполучаем такое соотношение
которое является формулой умножения матрицы на матрицу.
Таким образом, умножение матрицы на матрицу вводится исходя из того, как действует композиция линейных отображений.
Другими словами, если линейным отображениями
поставить в соответствие их матрицы
и
то композиции этих отображений
ставится в соответствие матрица, которая является произведением матриц
Отсюда, кстати, следует, что матрицыи
можно умножить только тогда, когда число столбцов матрицы
равно числу строк матрицы
Пусть — матрица размера
а
— матрица размера
Тогда, если в пространствах
и
зафиксировать базисы, то этим матрицам ставятся в соответствие линейные отображения
и
Но композиция определена только тогда, когда
то есть число столбцов матрицы
равно числу строк матрицы
Заключение
Таким образом, умножение матриц вводится исходя из того, как действуют линейные отображения. И это намекает на некую связь между ними.
Ниже оставлю различные учебники по алгебре, где можно про всё это прочитать более подробно, и другие различные источники.
Ссылки на литературу и различные источники
Основное:
[1] Введение в алгебру. В 3 частях. Часть 1. Основы алгебры. Кострикин А.И.
Дополнительное:
[1] Введение в алгебру. В 3 частях. Часть 2. Линейная алгебра. Кострикин А.И.
[2] Линейная алгебра и геометрия, Кострикин А.И., Манин Ю.И.
Прочее:
Для создания графики использовался manimCE: https://github.com/manimCommunity/manim
Кому интересно, то вот видео к статье:
Умножение матриц
21 мая 2018
- Домашняя работа
- Ответы
Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.
Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.
Согласованные матрицы
Одна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=left[ mtimes n right]$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали. Сейчас важно другое.
Определение. Матрицы вида $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, в которых количество столбцов в первой матрице совпадает с количеством строк во второй, называются согласованными.
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
- Нам важен порядок матриц. Например, матрицы $A=left[ 3times 2 right]$ и $B=left[ 2times 5 right]$ являются согласованными (2 столбца в первой матрице и 2 строки во второй), а вот наоборот — матрицы $B=left[ 2times 5 right]$ и $A=left[ 3times 2 right]$ — уже не согласованы (5 столбцов в первой матрице — это как бы не 3 строки во второй).
- Согласованность легко проверить, если выписать все размеры друг за другом. На примере из предыдущего пункта: «3 2 2 5» — посередине одинаковые числа, поэтому матрицы согласованы. А вот «2 5 3 2» — не согласованы, поскольку посередине разные числа.
Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $left[ ntimes n right]$ согласованы всегда.
В математике, когда важен порядок перечисления объектов (например, в рассмотренном выше определении важен порядок матриц), часто говорят об упорядоченных парах. Мы встречались с ними ещё в школе: думаю, и ежу понятно, что координаты $left( 1;0 right)$ и $left( 0;1 right)$ задают разные точки на плоскости.
Так вот: координаты — это тоже упорядоченные пары, которые составляются из чисел. Но ничто не мешает составить такую пару из матриц. Тогда можно будет сказать: «Упорядоченная пара матриц $left( A;B right)$ является согласованной, если количество столбцов в первой матрице совпадает с количеством строк во второй».
Ну и что с того?
Определение умножения
Рассмотрим две согласованные матрицы: $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$. И определим для них операцию умножения.
Определение. Произведение двух согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой считаются по формуле:
[begin{align} & {{c}_{i;j}}={{a}_{i;1}}cdot {{b}_{1;j}}+{{a}_{i;2}}cdot {{b}_{2;j}}+ldots +{{a}_{i;n}}cdot {{b}_{n;j}}= \ & =sumlimits_{t=1}^{n}{{{a}_{i;t}}cdot {{b}_{t;j}}} end{align}]
Обозначается такое произведение стандартно: $C=Acdot B$.
По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]
У тех, кто впервые видит это определение, сразу возникает два вопроса:
- Что это за лютая дичь?
- А почему так сложно?
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?
Прежде всего заметим, что длинная строчка для расчёта ${{c}_{i;j}}$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:
- Берём $i$-ю строку в первой матрице;
- Берём $j$-й столбец во второй матрице;
- Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.
Данный процесс легко понять по картинке:
Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем ${{c}_{ij}}$. И так для всех $1le ile m$ и $1le jle k$. Т.е. всего будет $mtimes k$ таких «извращений».
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:
[begin{align} & vec{a}=left( {{x}_{a}};{{y}_{a}};{{z}_{a}} right); \ & overrightarrow{b}=left( {{x}_{b}};{{y}_{b}};{{z}_{b}} right). \ end{align}]
Тогда их скалярным произведением будет именно сумма попарных произведений:
[overrightarrow{a}times overrightarrow{b}={{x}_{a}}cdot {{x}_{b}}+{{y}_{a}}cdot {{y}_{b}}+{{z}_{a}}cdot {{z}_{b}}]
По сути, в те далёкие годы, когда деревья были зеленее, а небо ярче, мы просто умножали вектор-строку $overrightarrow{a}$ на вектор-столбец $overrightarrow{b}$.
Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.
Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.
Умножение квадратных матриц
Задача 1. Выполните умножение:
[left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]cdot left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]]
Решение. Итак, у нас две матрицы: $A=left[ 2times 2 right]$ и $B=left[ 2times 2 right]$. Понятно, что они согласованы (квадратные матрицы одинакового размера всегда согласованы). Поэтому выполняем умножение:
[begin{align} & left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]cdot left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]=left[ begin{array}{*{35}{r}} 1cdot left( -2 right)+2cdot 3 & 1cdot 4+2cdot 1 \ -3cdot left( -2 right)+4cdot 3 & -3cdot 4+4cdot 1 \end{array} right]= \ & =left[ begin{array}{*{35}{r}} 4 & 6 \ 18 & -8 \end{array} right]. end{align}]
Вот и всё!
Ответ: $left[ begin{array}{*{35}{r}}4 & 6 \ 18 & -8 \end{array} right]$.
Задача 2. Выполните умножение:
[left[ begin{matrix} 1 & 3 \ 2 & 6 \end{matrix} right]cdot left[ begin{array}{*{35}{r}}9 & 6 \ -3 & -2 \end{array} right]]
Решение. Опять согласованные матрицы, поэтому выполняем действия:[]
[begin{align} & left[ begin{matrix} 1 & 3 \ 2 & 6 \end{matrix} right]cdot left[ begin{array}{*{35}{r}} 9 & 6 \ -3 & -2 \end{array} right]=left[ begin{array}{*{35}{r}} 1cdot 9+3cdot left( -3 right) & 1cdot 6+3cdot left( -2 right) \ 2cdot 9+6cdot left( -3 right) & 2cdot 6+6cdot left( -2 right) \end{array} right]= \ & =left[ begin{matrix} 0 & 0 \ 0 & 0 \end{matrix} right]. end{align}]
Как видим, получилась матрица, заполненная нулями
Ответ: $left[ begin{matrix} 0 & 0 \ 0 & 0 \end{matrix} right]$.
Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.
В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.
Основные свойства матричного произведения
В двух словах. Умножение матриц:
- Некоммутативно: $Acdot Bne Bcdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $Acdot B=Bcdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
- Ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
- Дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$ и $left( A+B right)cdot C=Acdot C+Bcdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.
А теперь — всё то же самое, но более подробно.
Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.
Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:
[left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]cdot left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]=left[ begin{array}{*{35}{r}}4 & 6 \ 18 & -8 \end{array} right]]
Но если поменять матрицы местами, то получим совсем другой результат:
[left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]=left[ begin{matrix} -14 & 4 \ 0 & 10 \end{matrix} right]]
Получается, что $Acdot Bne Bcdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $left[ 2times 3 right]$ и $left[ 3times 5 right]$ вполне себе согласованы в указанном порядке, но те же матрицы $left[ 3times 5 right]$ и $left[ 2times 3 right]$, записанные в обратном порядке, уже не согласованы. Печаль.:(
Среди квадратных матриц заданного размера $n$ всегда найдутся такие, которые дают одинаковый результат как при перемножении в прямом, так и в обратном порядке. Как описать все подобные матрицы (и сколько их вообще) — тема для отдельного урока. Сегодня не будем об этом.:)
Тем не менее, умножение матриц ассоциативно:
[left( Acdot B right)cdot C=Acdot left( Bcdot C right)]
Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.
В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $left[ ntimes n right]$. Множество всех таких матриц обозначается ${{M}^{n}}$ (т.е. записи $A=left[ ntimes n right]$ и [Ain {{M}^{n}}] означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.
Определение. Единичная матрица размера $n$ — это такая матрица $E$, что для любой квадратной матрицы $A=left[ ntimes n right]$ выполняется равенство:
[Acdot E=Ecdot A=A]
Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.
Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:
[begin{align} & Acdot left( B+C right)=Acdot B+Acdot C; \ & left( A+B right)cdot C=Acdot C+Bcdot C. \ end{align}]
Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)
Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.
Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?
Случай прямоугольных матриц
А ничего — всё то же самое, что и с квадратными.
Задача 3. Выполните умножение:
[left[ begin{matrix} begin{matrix} 5 \ 2 \ 3 \end{matrix} & begin{matrix} 4 \ 5 \ 1 \end{matrix} \end{matrix} right]cdot left[ begin{array}{*{35}{r}} -2 & 5 \ 3 & 4 \end{array} right]]
Решение. Имеем две матрицы: $A=left[ 3times 2 right]$ и $B=left[ 2times 2 right]$. Выпишем числа, обозначающие размеры, в ряд:
[3; 2; 2; 2]
Как видим, центральные два числа совпадают. Значит, матрицы согласованы, и их можно перемножить. Причём на выходе мы получим матрицу $C=left[ 3times 2 right]$:
[begin{align} & left[ begin{matrix} begin{matrix} 5 \ 2 \ 3 \end{matrix} & begin{matrix} 4 \ 5 \ 1 \end{matrix} \end{matrix} right]cdot left[ begin{array}{*{35}{r}} -2 & 5 \ 3 & 4 \end{array} right]=left[ begin{array}{*{35}{r}} 5cdot left( -2 right)+4cdot 3 & 5cdot 5+4cdot 4 \ 2cdot left( -2 right)+5cdot 3 & 2cdot 5+5cdot 4 \ 3cdot left( -2 right)+1cdot 3 & 3cdot 5+1cdot 4 \end{array} right]= \ & =left[ begin{array}{*{35}{r}} 2 & 41 \ 11 & 30 \ -3 & 19 \end{array} right]. end{align}]
Всё чётко: в итоговой матрице 3 строки и 2 столбца. Вполне себе $=left[ 3times 2 right]$.
Ответ: $left[ begin{array}{*{35}{r}} begin{array}{*{35}{r}} 2 \ 11 \ -3 \end{array} & begin{matrix} 41 \ 30 \ 19 \end{matrix} \end{array} right]$.
Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?
Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
Задача 4. Найдите все возможные попарные произведения матриц:
[A=left[ begin{array}{*{35}{r}} begin{matrix} 1 \ 1 \end{matrix} & begin{array}{*{35}{r}} -1 \ 1 \end{array} & begin{matrix} 2 \ 2 \end{matrix} & begin{array}{*{35}{r}} -2 \ 2 \end{array} \end{array} right]]; $B=left[ begin{matrix} begin{matrix} 0 \ 2 \ 0 \ 4 \end{matrix} & begin{matrix} 1 \ 0 \ 3 \ 0 \end{matrix} \end{matrix} right]$; $C=left[ begin{matrix}0 & 1 \ 1 & 0 \end{matrix} right]$.
Решение. Для начала запишем размеры матриц:
[A=left[ 2times 4 right]; B=left[ 4times 2 right]; C=left[ 2times 2 right]]
Получаем, что матрицу $A$ можно согласовать лишь с матрицей $B$, поскольку количество столбцов у $A$ равно 4, а такое количество строк только у $B$. Следовательно, можем найти произведение:
[Acdot B=left[ begin{array}{*{35}{r}} 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end{array} right]cdot left[ begin{array}{*{35}{r}} 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end{array} right]=left[ begin{array}{*{35}{r}}-10 & 7 \ 10 & 7 \end{array} right]]
Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:
[A cdot B=left[ 2times 4 right]cdot left[ 4times 2 right]=left[ 2times 2 right]]
Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.
Какие ещё возможны варианты? Безусловно, можно найти $Bcdot A$, поскольку $B=left[ 4times 2 right]$, $A=left[ 2times 4 right]$, поэтому упорядоченная пара $left( B;A right)$ является согласованной, а размерность произведения будет:
[B cdot A=left[ 4times 2 right]cdot left[ 2times 4 right]=left[ 4times 4 right]]
Короче говоря, на выходе будет матрица $left[ 4times 4 right]$, коэффициенты которой легко считаются:
[Bcdot A=left[ begin{array}{*{35}{r}} 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end{array} right]=left[ begin{array}{*{35}{r}}1 & 1 & 2 & 2 \ 2 & -2 & 4 & -4 \ 3 & 3 & 6 & 6 \ 4 & -4 & 8 & -8 \end{array} right]]
Очевидно, можно согласовать ещё $Ccdot A$ и $Bcdot C$ — и всё. Поэтому просто запишем полученные произведения:
[Ccdot A=left[ begin{array}{*{35}{r}} 1 & 1 & 2 & 2 \ 1 & -1 & 2 & -2 \end{array} right]]
[Bcdot C=left[ begin{array}{*{35}{r}}1 & 0 \ 0 & 2 \ 3 & 0 \ 0 & 4 \end{array} right]]
Это было легко.:)
Ответ: $AB=left[ begin{array}{*{35}{r}} -10 & 7 \ 10 & 7 \end{array} right]$; $BA=left[ begin{array}{*{35}{r}} 1 & 1 & 2 & 2 \ 2 & -2 & 4 & -4 \ 3 & 3 & 6 & 6 \ 4 & -4 & 8 & -8 \end{array} right]$; $CA=left[ begin{array}{*{35}{r}} 1 & 1 & 2 & 2 \ 1 & -1 & 2 & -2 \end{array} right]$; $BC=left[ begin{array}{*{35}{r}}1 & 0 \ 0 & 2 \ 3 & 0 \ 0 & 4 \end{array} right]$.
Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.
Но на этом история не заканчивается. Переходим к частным случаям умножения.:)
Вектор-строки и вектор-столбцы
Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
Определение. Вектор-столбец — это матрица размера $left[ mtimes 1 right]$, т.е. состоящая из нескольких строк и только одного столбца.
Вектор-строка — это матрица размера $left[ 1times n right]$, т.е. состоящая из одной строки и нескольких столбцов.
На самом деле мы уже встречались с этими объектами. Например, обычный трёхмерный вектор из стереометрии $overrightarrow{a}=left( x;y;z right)$ — это не что иное как вектор-строка. С точки зрения теории разницы между строками и столбцами почти нет. Внимательными надо быть разве что при согласовании с окружающими матрицами-множителями.
Задача 5. Выполните умножение:
[left[ begin{array}{*{35}{r}} 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 \ 2 \ -1 \end{array} right]]
Решение. Перед нами произведение согласованных матриц: $left[ 3times 3 right]cdot left[ 3times 1 right]=left[ 3times 1 right]$. Найдём это произведение:
[left[ begin{array}{*{35}{r}} 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 \ 2 \ -1 \end{array} right]=left[ begin{array}{*{35}{r}} 2cdot 1+left( -1 right)cdot 2+3cdot left( -1 right) \ 4cdot 1+2cdot 2+0cdot 2 \ -1cdot 1+1cdot 2+1cdot left( -1 right) \end{array} right]=left[ begin{array}{*{35}{r}} -3 \ 8 \ 0 \end{array} right]]
Ответ: $left[ begin{array}{*{35}{r}}-3 \ 8 \ 0 \end{array} right]$.
Задача 6. Выполните умножение:
[left[ begin{array}{*{35}{r}} 1 & 2 & -3 \end{array} right]cdot left[ begin{array}{*{35}{r}} 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end{array} right]]
Решение. Опять всё согласовано: $left[ 1times 3 right]cdot left[ 3times 3 right]=left[ 1times 3 right]$. Считаем произведение:
[left[ begin{array}{*{35}{r}} 1 & 2 & -3 \end{array} right]cdot left[ begin{array}{*{35}{r}} 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end{array} right]=left[ begin{array}{*{35}{r}}5 & -19 & 5 \end{array} right]]
На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)
Ответ: $left[ begin{matrix} 5 & -19 & 5 \end{matrix} right]$.
Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).
Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.
Возведение матрицы в степень
Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.
Такие произведения всегда согласованы:
[Acdot A=left[ ntimes n right]cdot left[ ntimes n right]=left[ ntimes n right]]
И обозначаются точно так же, как и обычные степени:
[begin{align} & Acdot A={{A}^{2}}; \ & Acdot Acdot A={{A}^{3}}; \ & underbrace{Acdot Acdot ldots cdot A}_{n}={{A}^{n}}. \ end{align}]
На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Задача 7. Возведите матрицу в указанную степень:
${{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}$
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:
[begin{align} & {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{2}}=left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 1cdot 1+1cdot 0 & 1cdot 1+1cdot 1 \ 0cdot 1+1cdot 0 & 0cdot 1+1cdot 1 \end{array} right]= \ & =left[ begin{array}{*{35}{r}} 1 & 2 \ 0 & 1 \end{array} right] end{align}]
[begin{align} & {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}={{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 1 & 2 \ 0 & 1 \end{array} right]cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 1 & 3 \ 0 & 1 \end{array} right] end{align}]
Вот и всё.:)
Ответ: $left[ begin{matrix}1 & 3 \ 0 & 1 \end{matrix} right]$.
Задача 8. Возведите матрицу в указанную степень:
[{{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{10}}]
Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:
[begin{align} & {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{10}}={{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left( left[ begin{matrix} 1 & 3 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 3 \ 0 & 1 \end{matrix} right] right)cdot left( left[ begin{matrix} 1 & 3 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right] right)= \ & =left[ begin{matrix} 1 & 6 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 4 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{matrix} 1 & 10 \ 0 & 1 \end{matrix} right] end{align}]
Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.
Ответ: $left[ begin{matrix} 1 & 10 \ 0 & 1 \end{matrix} right]$.
Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:
[{{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{n}}=left[ begin{array}{*{35}{r}} 1 & n \ 0 & 1 \end{array} right]]
Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.
В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $left[ 3times 3 right]$.
Задача 9. Возведите матрицу в указанную степень:
[{{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{3}}]
Решение. Не будем искать закономерности. Работаем «напролом»:
[{{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{3}}={{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{2}}cdot left[ begin{matrix}0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]]
Для начала возведём эту матрицу в квадрат:
[begin{align} & {{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{2}}=left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]cdot left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end{array} right] end{align}]
Теперь возведём в куб:
[begin{align} & {{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{3}}=left[ begin{array}{*{35}{r}} 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end{array} right]cdot left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end{array} right] end{align}]
Вот и всё. Задача решена.
Ответ: $left[ begin{matrix} 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end{matrix} right]$.
Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)
На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.
Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.
Смотрите также:
- Определитель
- Обратная матрица
- Тест к уроку «Что такое логарифм» (средний)
- Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
- Координаты вершин правильного тетраэдра
- Нестандартная задача B5 на площадь круга
Умножение матриц: примеры, алгоритм действий, свойства произведения
Произведение двух матриц
Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C ⏟ m × n = A ⏟ m × p × B ⏟ p × n
- A = a ( i j ) размеров m × n ;
- B = b ( i j ) размеров p × n
Матрицу C , элементы c i j которой вычисляются по следующей формуле:
c i j = a i 1 × b 1 j + a i 2 × b 2 j + . . . + a i p × b p j , i = 1 , . . . m , j = 1 , . . . m
Вычислим произведения АВ=ВА:
А = 1 2 1 0 1 2 , В = 1 0 0 1 1 1
Решение, используя правило умножения матриц:
А ⏟ 2 × 3 × В ⏟ 3 × 2 = 1 2 1 0 1 2 × 1 0 0 1 1 1 = 1 × 1 + 2 × 0 + 1 × 1 1 × 0 + 2 × 1 + 1 × 1 0 × 1 + 1 × 0 + 2 × 1 0 × 0 + 1 × 1 + 2 × 1 = = 2 3 2 3 ⏟ 2 × 2
В ⏟ 3 × 2 × А ⏟ 2 × 3 = 1 0 0 1 1 1 × 1 2 1 0 1 2 = 1 × 1 + 0 × 0 1 × 2 + 0 × 1 1 × 1 + 0 × 2 0 × 1 + 1 × 0 0 × 2 + 1 × 1 0 × 1 + 1 × 2 1 × 1 + 1 × 0 1 × 2 + 1 × 1 1 × 1 + 1 × 2 = 1 2 1 0 1 2 1 3 3 ⏟ 3 × 3
Произведение А В и В А найдены, но являются матрицами разных размеров: А В не равна В А .
Свойства умножения матриц
Свойства умножения матриц:
- ( А В ) С = А ( В С ) — ассоциативность умножения матриц;
- А ( В + С ) = А В + А С — дистрибутивность умножения;
- ( А + В ) С = А С + В С — дистрибутивность умножения;
- λ ( А В ) = ( λ А ) В
Пример 1
Проверяем свойство №1: ( А В ) С = А ( В С ) :
( А × В ) × А = 1 2 3 4 × 5 6 7 8 × 1 0 0 2 = 19 22 43 50 × 1 0 0 2 = 19 44 43 100 ,
А ( В × С ) = 1 2 3 4 × 5 6 7 8 1 0 0 2 = 1 2 3 4 × 5 12 7 16 = 19 44 43 100 .
Проверяем свойство №2: А ( В + С ) = А В + А С :
А × ( В + С ) = 1 2 3 4 × 5 6 7 8 + 1 0 0 2 = 1 2 3 4 × 6 6 7 10 = 20 26 46 58 ,
А В + А С = 1 2 3 4 × 5 6 7 8 + 1 2 3 4 × 1 0 0 2 = 19 22 43 50 + 1 4 3 8 = 20 26 46 58 .
Произведение трех матриц
Произведение трех матриц А В С вычисляют 2-мя способами:
- найти А В и умножить на С : ( А В ) С ;
- либо найти сначала В С , а затем умножить А ( В С ) .
Пример 3
Перемножить матрицы 2-мя способами:
4 3 7 5 × — 28 93 38 — 126 × 7 3 2 1
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). А В = 4 3 7 5 × — 28 93 38 — 126 = 4 ( — 28 ) + 3 × 38 4 × 93 + 3 ( — 126 ) 7 ( — 28 ) + 5 × 38 7 × 93 + 5 ( — 126 ) = 2 — 6 — 6 21
2). А В С = ( А В ) С = 2 — 6 — 6 21 7 3 2 1 = 2 × 7 — 6 × 2 2 × 3 — 6 × 1 — 6 × 7 + 21 × 2 — 6 × 3 + 21 × 1 = 2 0 0 3 .
Используем формулу А В С = ( А В ) С :
1). В С = — 28 93 38 — 126 7 3 2 1 = — 28 × 7 + 93 × 2 — 28 × 3 + 93 × 1 38 × 7 — 126 × 2 38 × 3 — 126 × 1 = — 10 9 14 — 12
2). А В С = ( А В ) С = 7 3 2 1 — 10 9 14 — 12 = 4 ( — 10 ) + 3 × 14 4 × 9 + 3 ( — 12 ) 7 ( — 10 ) + 5 × 14 7 × 9 + 5 ( — 12 ) = 2 0 0 3
Ответ: 4 3 7 5 — 28 93 38 — 126 7 3 2 1 = 2 0 0 3
Умножение матрицы на число
Произведение матрицы А на число k — это матрица В = А k того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
b i , j = k × a i , j
Свойства умножения матрицы на число:
- 1 × А = А
- 0 × А = нулевая матрица
- k ( A + B ) = k A + k B
- ( k + n ) A = k A + n A
- ( k × n ) × A = k ( n × A )
Пример 4
Найдем произведение матрицы А = 4 2 9 0 на 5.
5 А = 5 4 2 9 0 5 × 4 5 × 2 5 × 9 5 × 0 = 20 10 45 0
Умножение матрицы на вектор
Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
А В = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а m 1 а m 2 ⋯ а m n b 1 b 2 ⋯ b 1 n = a 11 × b 1 + a 12 × b 2 + ⋯ + a 1 n × b n a 21 × b 1 + a 22 × b 2 + ⋯ + a 2 n × b n ⋯ ⋯ ⋯ ⋯ a m 1 × b 1 + a m 2 × b 2 + ⋯ + a m n × b n = c 1 c 2 ⋯ c 1 m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
А В = а а ⋯ а b b ⋯ b = a 1 × b 1 a 1 × b 2 ⋯ a 1 × b n a 2 × b 1 a 2 × b 2 ⋯ a 2 × b n ⋯ ⋯ ⋯ ⋯ a n × b 1 a n × b 2 ⋯ a n × b n = c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋯ ⋯ ⋯ ⋯ c n 1 c n 2 ⋯ c n n
Найдем произведение матрицы А и вектора-столбца В :
А В = 2 4 0 — 2 1 3 — 1 0 1 1 2 — 1 = 2 × 1 + 4 × 2 + 0 × ( — 1 ) — 2 × 1 + 1 × 2 + 3 × ( — 1 ) — 1 × 1 + 0 × 2 + 1 × ( — 1 ) = 2 + 8 + 0 — 2 + 2 — 3 — 1 + 0 — 1 = 10 — 3 — 2
Найдем произведение матрицы А и вектора-строку В :
А = 3 2 0 — 1 , В = — 1 1 0 2
А В = 3 2 0 1 × — 1 1 0 2 = 3 × ( — 1 ) 3 × 1 3 × 0 3 × 2 2 × ( — 1 ) 2 × 1 2 × 0 2 × 2 0 × ( — 1 ) 0 × 1 0 × 0 0 × 2 1 × ( — 1 ) 1 × 1 1 × 0 1 × 2 = — 3 3 0 6 — 2 2 0 4 0 0 0 0 — 1 1 0 2
Ответ: А В = — 3 3 0 6 — 2 2 0 4 0 0 0 0 — 1 1 0 2
Умножение матриц
Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.
Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.
Согласованные матрицы
Одна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=left[ mtimes n right]$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали. Сейчас важно другое.
Определение. Матрицы вида $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, в которых количество столбцов в первой матрице совпадает с количеством строк во второй, называются .
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
- Нам важен порядок матриц. Например, матрицы $A=left[ 3times 2 right]$ и $B=left[ 2times 5 right]$ являются согласованными (2 столбца в первой матрице и 2 строки во второй), а вот наоборот — матрицы $B=left[ 2times 5 right]$ и $A=left[ 3times 2 right]$ — уже не согласованы (5 столбцов в первой матрице — это как бы не 3 строки во второй).
- Согласованность легко проверить, если выписать все размеры друг за другом. На примере из предыдущего пункта: «3 2 2 5» — посередине одинаковые числа, поэтому матрицы согласованы. А вот «2 5 3 2» — не согласованы, поскольку посередине разные числа.
Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $left[ ntimes n right]$ согласованы всегда.
В математике, когда важен порядок перечисления объектов (например, в рассмотренном выше определении важен порядок матриц), часто говорят об упорядоченных парах. Мы встречались с ними ещё в школе: думаю, и ежу понятно, что координаты $left( 1;0 right)$ и $left( 0;1 right)$ задают разные точки на плоскости.
Так вот: координаты — это тоже упорядоченные пары, которые составляются из чисел. Но ничто не мешает составить такую пару из матриц. Тогда можно будет сказать: «Упорядоченная пара матриц $left( A;B right)$ является согласованной, если количество столбцов в первой матрице совпадает с количеством строк во второй».
Ну и что с того?
Определение умножения
Рассмотрим две согласованные матрицы: $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$. И определим для них операцию умножения.
Определение. $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой считаются по формуле:
Обозначается такое произведение стандартно: $C=Acdot B$.
По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]
У тех, кто впервые видит это определение, сразу возникает два вопроса:
- Что это за лютая дичь?
- А почему так сложно?
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?
Прежде всего заметим, что длинная строчка для расчёта $<_>$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:
- Берём $i$-ю строку в первой матрице;
- Берём $j$-й столбец во второй матрице;
- Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.
Данный процесс легко понять по картинке:
Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем $<_>$. И так для всех $1le ile m$ и $1le jle k$. Т.е. всего будет $mtimes k$ таких «извращений».
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:
Тогда их скалярным произведением будет именно сумма попарных произведений:
По сути, в те далёкие годы, когда деревья были зеленее, а небо ярче, мы просто умножали вектор-строку $overrightarrow$ на вектор-столбец $overrightarrow$.
Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.
Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.
Умножение квадратных матриц
[left[ begin<*<35>> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*<35>> -2 & 4 \ 3 & 1 \end right]]
Решение. Итак, у нас две матрицы: $A=left[ 2times 2 right]$ и $B=left[ 2times 2 right]$. Понятно, что они согласованы (квадратные матрицы одинакового размера всегда согласованы). Поэтому выполняем умножение:
[begin & left[ begin<*<35>> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*<35>> -2 & 4 \ 3 & 1 \end right]=left[ begin<*<35>> 1cdot left( -2 right)+2cdot 3 & 1cdot 4+2cdot 1 \ -3cdot left( -2 right)+4cdot 3 & -3cdot 4+4cdot 1 \end right]= \ & =left[ begin<*<35>> 4 & 6 \ 18 & -8 \end right]. end]
Задача 2. Выполните умножение:
[left[ begin 1 & 3 \ 2 & 6 \end right]cdot left[ begin<*<35>>9 & 6 \ -3 & -2 \end right]]
Решение. Опять согласованные матрицы, поэтому выполняем действия:[]
[begin & left[ begin 1 & 3 \ 2 & 6 \end right]cdot left[ begin<*<35>> 9 & 6 \ -3 & -2 \end right]=left[ begin<*<35>> 1cdot 9+3cdot left( -3 right) & 1cdot 6+3cdot left( -2 right) \ 2cdot 9+6cdot left( -3 right) & 2cdot 6+6cdot left( -2 right) \end right]= \ & =left[ begin 0 & 0 \ 0 & 0 \end right]. end]
Как видим, получилась матрица, заполненная нулями
Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.
В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.
Основные свойства матричного произведения
В двух словах. Умножение матриц:
- Некоммутативно: $Acdot Bne Bcdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $Acdot B=Bcdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
- Ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
- Дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$ и $left( A+B right)cdot C=Acdot C+Bcdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.
А теперь — всё то же самое, но более подробно.
Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.
Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:
[left[ begin<*<35>> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*<35>> -2 & 4 \ 3 & 1 \end right]=left[ begin<*<35>>4 & 6 \ 18 & -8 \end right]]
Но если поменять матрицы местами, то получим совсем другой результат:
[left[ begin<*<35>> -2 & 4 \ 3 & 1 \end right]cdot left[ begin<*<35>> 1 & 2 \ -3 & 4 \end right]=left[ begin -14 & 4 \ 0 & 10 \end right]]
Получается, что $Acdot Bne Bcdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $left[ 2times 3 right]$ и $left[ 3times 5 right]$ вполне себе согласованы в указанном порядке, но те же матрицы $left[ 3times 5 right]$ и $left[ 2times 3 right]$, записанные в обратном порядке, уже не согласованы. Печаль.:(
Среди квадратных матриц заданного размера $n$ всегда найдутся такие, которые дают одинаковый результат как при перемножении в прямом, так и в обратном порядке. Как описать все подобные матрицы (и сколько их вообще) — тема для отдельного урока. Сегодня не будем об этом.:)
Тем не менее, умножение матриц ассоциативно:
[left( Acdot B right)cdot C=Acdot left( Bcdot C right)]
Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.
В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $left[ ntimes n right]$. Множество всех таких матриц обозначается $<^>$ (т.е. записи $A=left[ ntimes n right]$ и [Ain <^>] означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.
Определение. размера $n$ — это такая матрица $E$, что для любой квадратной матрицы $A=left[ ntimes n right]$ выполняется равенство:
[Acdot E=Ecdot A=A]
Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.
Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:
Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)
Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.
Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?
Случай прямоугольных матриц
А ничего — всё то же самое, что и с квадратными.
[left[ begin begin 5 \ 2 \ 3 \end & begin 4 \ 5 \ 1 \end \end right]cdot left[ begin<*<35>> -2 & 5 \ 3 & 4 \end right]]
Решение. Имеем две матрицы: $A=left[ 3times 2 right]$ и $B=left[ 2times 2 right]$. Выпишем числа, обозначающие размеры, в ряд:
Как видим, центральные два числа совпадают. Значит, матрицы согласованы, и их можно перемножить. Причём на выходе мы получим матрицу $C=left[ 3times 2 right]$:
[begin & left[ begin begin 5 \ 2 \ 3 \end & begin 4 \ 5 \ 1 \end \end right]cdot left[ begin<*<35>> -2 & 5 \ 3 & 4 \end right]=left[ begin<*<35>> 5cdot left( -2 right)+4cdot 3 & 5cdot 5+4cdot 4 \ 2cdot left( -2 right)+5cdot 3 & 2cdot 5+5cdot 4 \ 3cdot left( -2 right)+1cdot 3 & 3cdot 5+1cdot 4 \end right]= \ & =left[ begin<*<35>> 2 & 41 \ 11 & 30 \ -3 & 19 \end right]. end]
Всё чётко: в итоговой матрице 3 строки и 2 столбца. Вполне себе $=left[ 3times 2 right]$.
Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?
Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
Задача 4. Найдите все возможные попарные произведения матриц:
Решение. Для начала запишем размеры матриц:
[A=left[ 2times 4 right]; B=left[ 4times 2 right]; C=left[ 2times 2 right]]
Получаем, что матрицу $A$ можно согласовать лишь с матрицей $B$, поскольку количество столбцов у $A$ равно 4, а такое количество строк только у $B$. Следовательно, можем найти произведение:
[Acdot B=left[ begin<*<35>> 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end right]cdot left[ begin<*<35>> 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end right]=left[ begin<*<35>>-10 & 7 \ 10 & 7 \end right]]
Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:
[A cdot B=left[ 2times 4 right]cdot left[ 4times 2 right]=left[ 2times 2 right]]
Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.
Какие ещё возможны варианты? Безусловно, можно найти $Bcdot A$, поскольку $B=left[ 4times 2 right]$, $A=left[ 2times 4 right]$, поэтому упорядоченная пара $left( B;A right)$ является согласованной, а размерность произведения будет:
[B cdot A=left[ 4times 2 right]cdot left[ 2times 4 right]=left[ 4times 4 right]]
Короче говоря, на выходе будет матрица $left[ 4times 4 right]$, коэффициенты которой легко считаются:
[Bcdot A=left[ begin<*<35>> 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end right]cdot left[ begin<*<35>> 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end right]=left[ begin<*<35>>1 & 1 & 2 & 2 \ 2 & -2 & 4 & -4 \ 3 & 3 & 6 & 6 \ 4 & -4 & 8 & -8 \end right]]
Очевидно, можно согласовать ещё $Ccdot A$ и $Bcdot C$ — и всё. Поэтому просто запишем полученные произведения:
[Ccdot A=left[ begin<*<35>> 1 & 1 & 2 & 2 \ 1 & -1 & 2 & -2 \end right]]
[Bcdot C=left[ begin<*<35>>1 & 0 \ 0 & 2 \ 3 & 0 \ 0 & 4 \end right]]
Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.
Но на этом история не заканчивается. Переходим к частным случаям умножения.:)
Вектор-строки и вектор-столбцы
Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
Определение. — это матрица размера $left[ mtimes 1 right]$, т.е. состоящая из нескольких строк и только одного столбца.
— это матрица размера $left[ 1times n right]$, т.е. состоящая из одной строки и нескольких столбцов.
[left[ begin<*<35>> 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end right]cdot left[ begin<*<35>> 1 \ 2 \ -1 \end right]]
Решение. Перед нами произведение согласованных матриц: $left[ 3times 3 right]cdot left[ 3times 1 right]=left[ 3times 1 right]$. Найдём это произведение:
[left[ begin<*<35>> 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end right]cdot left[ begin<*<35>> 1 \ 2 \ -1 \end right]=left[ begin<*<35>> 2cdot 1+left( -1 right)cdot 2+3cdot left( -1 right) \ 4cdot 1+2cdot 2+0cdot 2 \ -1cdot 1+1cdot 2+1cdot left( -1 right) \end right]=left[ begin<*<35>> -3 \ 8 \ 0 \end right]]
Задача 6. Выполните умножение:
[left[ begin<*<35>> 1 & 2 & -3 \end right]cdot left[ begin<*<35>> 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end right]]
Решение. Опять всё согласовано: $left[ 1times 3 right]cdot left[ 3times 3 right]=left[ 1times 3 right]$. Считаем произведение:
[left[ begin<*<35>> 1 & 2 & -3 \end right]cdot left[ begin<*<35>> 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end right]=left[ begin<*<35>>5 & -19 & 5 \end right]]
На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)
Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).
Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.
Возведение матрицы в степень
Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.
Такие произведения всегда согласованы:
[Acdot A=left[ ntimes n right]cdot left[ ntimes n right]=left[ ntimes n right]]
И обозначаются точно так же, как и обычные степени:
На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Задача 7. Возведите матрицу в указанную степень:
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:
[begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^<2>>=left[ begin 1 & 1 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*<35>> 1cdot 1+1cdot 0 & 1cdot 1+1cdot 1 \ 0cdot 1+1cdot 0 & 0cdot 1+1cdot 1 \end right]= \ & =left[ begin<*<35>> 1 & 2 \ 0 & 1 \end right] end]
[begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^<3>>= <<left[ begin1 & 1 \ 0 & 1 \end right]>^<3>>cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*<35>> 1 & 2 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*<35>> 1 & 3 \ 0 & 1 \end right] end]
Ответ: $left[ begin1 & 3 \ 0 & 1 \end right]$.
Задача 8. Возведите матрицу в указанную степень:
Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:
[begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^<10>>= <<left[ begin1 & 1 \ 0 & 1 \end right]>^<3>>cdot <<left[ begin1 & 1 \ 0 & 1 \end right]>^<3>>cdot <<left[ begin1 & 1 \ 0 & 1 \end right]>^<3>>cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left( left[ begin 1 & 3 \ 0 & 1 \end right]cdot left[ begin 1 & 3 \ 0 & 1 \end right] right)cdot left( left[ begin 1 & 3 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right] right)= \ & =left[ begin 1 & 6 \ 0 & 1 \end right]cdot left[ begin 1 & 4 \ 0 & 1 \end right]= \ & =left[ begin 1 & 10 \ 0 & 1 \end right] end]
Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.
Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:
Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.
В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $left[ 3times 3 right]$.
Задача 9. Возведите матрицу в указанную степень:
Решение. Не будем искать закономерности. Работаем «напролом»:
[ <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^<3>>= <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^<2>>cdot left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]]
Для начала возведём эту матрицу в квадрат:
[begin & <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^<2>>=left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]cdot left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]= \ & =left[ begin<*<35>> 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end right] end]
Теперь возведём в куб:
[begin & <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^<3>>=left[ begin<*<35>> 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end right]cdot left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]= \ & =left[ begin<*<35>> 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end right] end]
Вот и всё. Задача решена.
Ответ: $left[ begin 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end right]$.
Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)
На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.
Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.
learnopengl. Урок 1.7 — Трансформации
Теперь мы знаем как создавать объекты, раскрашивать их и накладывать на них текстуры, но они все еще довольно скучны, поскольку являются статическими объектами. Мы можем попробовать заставить их двигаться изменяя координаты вершин для каждого кадра, но это довольно муторно и требует процессорных вычислений. Есть гораздо более удобный способ для совершения трансформаций над объектом — это применение матриц. Но это не значит, что мы сейчас будем разговаривать про кунг фу и искусственный цифровой мир.
Часть 2. Базовое освещение
Часть 3. Загрузка 3D-моделей
Часть 4. Продвинутые возможности OpenGL
Часть 5. Продвинутое освещение
Матрицы — это очень мощные математические конструкции, которые поначалу пугают, но стоит к ним привыкнуть и они сразу станут крайне полезными. Во время обсуждения матриц требуется также немного углубиться в математику. Также для более склонных к математике читателей я оставлю ссылки на дополнительные ресурсы по этой теме.
Как бы то ни было, для полного понимания трансформаций мы, во первых, должны разобраться с векторами. Основная задача этой главы — дать вам основные математические знания, которые нам понадобятся позже.
Вектора
В самом простом определении, вектора — это не более чем направления. У вектора может быть направление и магнитуда (также иногда называется модулем или длиной). Вы можете представлять себе вектора в качестве направлений на карте сокровищ: “Сделайте 10 шагов налево, теперь 3 шага на север и теперь 5 шагов направо”. В данном примере “налево” — это направление, а “10 шагов” — это длина вектора. Направления на этой карте сокровищ составляются из 3 векторов. Вектора могут иметь любую размерность, но чаще всего используются двухкомпонентные и четырехкомпонентные вектора. Если вектор двухкомпонентный, то он описывает направление на плоскости (или на 2D графике), если вектор трехкомпонентный, то он описывает направление в трехмерном мире.
Ниже вы можете видеть 3 вектора, каждый из которых представлен в виде (x, y) в качестве стрелок на 2D графике. Поскольку более интуитивно представлять вектора в 2D (чем в 3D), то вы можете думать о 2D векторах, как о 3D векторах, но с нулевой z координатой. До тех пор, пока вектор описывает направление — позиция вектора не меняет его значения. На графике можно увидеть, что вектора v и w одинаковы, хотя из позиции отличаются:
Когда математики описывают вектора, они предпочитают использовать символы нижнего регистра с небольшой черточкой сверху. Пример:
Поскольку вектора зачастую описывают направление — то иногда их тяжело представить в виде позиции. Обычно мы визуализируем вектор следующим образом: мы устанавливаем центр в (0, 0, 0), а затем указываем направление, описанное точкой. Таким образом получается позиционный вектор (также мы можем взять за центр другую точку, а потом сказать “Этот вектор указывает на точку в пространстве из этой точки”). Позиционный вектор (3, 5) будет указывать на точку (3, 5) на графе с основанием (0, 0). С помощью векторов мы можем описывать как направления так и позиции в двухмерном и трехмерном пространствах.
Также мы можем производить над векторами некоторые математические действия.
Скалярные векторные операции
Скаляр — это одно число (или однокомпонентный вектор, если вы хотите продолжать работать с векторами). Во время сложения/вычитания/умножения или деления вектора на скаляр мы просто складываем/вычитаем/умножаем или делим каждый элемент вектора на этот скаляр. Пример:
Где вместо сложения может быть вычитание, умножение или деление.
Обратный вектор
Обращение (отрицание) вектора — это получение вектора, чье направление противоположно исходному. Обратный вектор для вектора, указывающего на северо-восток, будет вектор, указывающий на юго-запад. Для обращения вектора мы просто умножаем вектор на -1. Пример:
Сложение и вычитание
Сложение двух векторов производится покомпонентно. Пример:
Визуально сумма векторов v=(4,2) и k=(1,2) выглядит так:
Также как и с обычным сложением и вычитанием, вычитание векторов — это тоже сложение, но с обратным вторым вектором:
Вычитание векторов друг из друга порождают вектор, который является разницей в позициях операндов:
Длина
Для получения длины (модуля) вектора мы используем теорему Пифагора, которые вы, возможно, помните со школы. Вектор образует треугольник, если представить его компоненты в качестве сторон треугольника:
Поскольку длина сторон (x, y) известна, и мы хотим узнать длину гипотенузы — то мы делаем это следующим образом:
Где ||v|| — это длина вектора v. Такая формула легко расширяется в 3D добалением z^2. Пример расчета длины:
Вычисленное значение: 4.47
Также существует специальный вид векторов, называемый единичными векторами. Особенность таких векторов в том, что их длина всегда равна 1. Мы можем преобразовать любой вектор в единичный делением этого вектора на его длину:
Такой вектор называется нормализованным. Единичные векторы обозначаются с небольшой крышей над буквой. С ними, также, проще работать, поскольку нам приходится заботиться только о направлении такого вектора.
Умножение вектора на вектор
Умножение двух векторов выполняется довольно странно. Нормальное умножение не применимо, поскольку оно не имеет визуального смысла, но у нас есть 2 специфических подхода, из которых можно выбирать во время умножения: первый — скалярное произведение, которое изображается как точка, а второе — векторное произведение, которое изображается как крест.
Скалярное произведение
Скалярное произведение двух векторов эквивалентно скалярному произведению длин этих векторов, умноженное на косинус угла между ними. Если это предложение сбило вас с толку, то посмотрите на формулу:
Где угол между векторами описан как тета. Почему это может быть интересно? Что же, представим если вектора v и k являются единичными векторами. Соответственно формула сокращается до:
Теперь скалярное произведение определяет только угол между двумя векторами. Вы возможно помните, что функция cos становится 0, с углом в 90 градусов ну и 1 с углом 0. Это позволяет легко проверять ортогональны ли вектора или параллельны друг другу (ортогональность означает, что вектора прямоугольны). Если хотите узнать больше про sin или cosine, то рекомендую видео Khan Academy про базовую тригонометрию.
Вы также можете вычислить угол между двумя неединичными векторами, но для этого вам придется разделить результат на длины этих векторов, чтобы остаться только с cos.
Так как же считать скалярное произведение? Скалярное произведение — это умножение компонентов векторов и последующее сложение результатов. Пример:
Для вычисления угла между векторами нам потребуется обратить функцию косинуса (cos^-1) в данном случае — это 143.1 градуса. Таким образом мы эффективно вычислили угол между этими двумя векторами. Скалярное произведение очень полезно во время работы со светом.
Векторное произведение
Векторное произведение возможно только в трехмерном пространстве и принимает на вход два непараллельных вектора, а возвращает вектор, который ортогонален входным. Если входные вектора ортогональны друг другу, то векторное произведение создаст 3 ортогональных вектора. Далее вы узнаете, почему это может быть полезно. Следующее изображение показывает как это выглядит трехмерном пространстве:
В отличии от других операций, векторное произведение не очень интуитивно без углубления в линейную алгебру, так что лучше просто запомнить формулу. Ниже представлено векторное произведение между двумя ортогональными векторами A и B.
Как вы можете видеть, в этой формуле не очень много смысла. В любом случае после всех этих шагов вы получите вектор, который будет ортогонален входным.
Матрицы
Теперь, после того как мы обсудили почти все на счет векторов, настало время углубиться в матрицы. Матрица, обычно, это четырехугольних из набора чисел, символов и/или выражений. Вот пример матрицы 2х3:
Доступ к элементам матрицы осуществляется с помощью (i,j), где i — это строка, а j — это столбец. Вот почему матрица выше называется 2х3 (3 столбца и 2 строки). Такая система — обратна той, что используется в 2D графах (x, y). Для получения значения 4 из матрицы выше, мы должны указать индекс (2, 1) (вторая строка, первый столбец).
Матрицы, по факту, ничего более чем четырехугольные массивы математических выражений. Они также обладают очень приятным набором математических свойств и, также как и вектора, имеют несколько операций — сложение, вычитание и умножение.
Сложение и вычитание
Сложение матрицы со скаляром выполняется следующим образом:
Скаляр просто прибавляется во всем элементам матрицы. Тоже самое происходит и при вычитании:
Сложение и вычитание между двумя матрицами выполняется поэлементно. Таким образом операции сложения и вычитания могут быть применены только к матрицам одинакового размера. Пример:
Тоже самое, только с вычитанием:
Умножение матрицы на скаляр
Также как сложение и вычитание, умножение матрицы на скаляр производится умножением каждого элемента матрицы на скаляр. Пример:
Умножение матриц
Умножение матриц не очень сложное, но и не такое простое. Умножение имеет несколько ограничений:
- Вы можете умножать только матрицы, где число столбцов первой совпадает с числом строк второй матрицы.
- Умножение матриц не коммутативно. A * B != B * A.
Вот пример умножения двух матриц 2х2:
Сейчас, возможно вы пытаетесь понять, что же тут вообще происходит? Умножение матриц — это комбинация из нормального умножения и сложения с использованием строк левой матрицы со столбцами правой матрицы. Следующее изображение должно внести немного ясности:
В начале мы берем верхнюю строку левой матрицы и левый столбец правой матрицы. Выбранные нами строка и столбец определяет то, какой элемент результирующей матрицы мы собираемся рассчитать. Если бы мы взяли первую строку левой матрицы, то мы собираемся работать с верхней строкой результирующей матрицы, затем мы выбираем столбец в правой матрице, он определяет то, с каким столбцом результирующей матрицы мы работаем. Для вычисления нижнего-правого элемента мы должны выбрать нижнюю строку левой матрицы и правый столбец правой матрицы.
Для вычисления результирующего значения мы перемножаем элементы строки и столбца с помощью обычного умножения. Результаты умножения затем складываются и мы получаем результат. Вот оттуда и идет первое ограничение.
В результате получается матрица размером (n, m), где n — количество строк в левой матрице, а m — количество столбцов в правой матрице.
Если у вас возникла проблема — то не волнуйтесь. Просто продолжайте вычислять руками и возвращайтесь к этому уроку, когда возникают сложности. Вскоре умножение матриц будет на автомате.
Давайте закроем вопрос умножения матриц одним большим примером. Для представления алгоритма использованы цвета. Для тренировки попробуйте сами посчитать результат, а затем сравнить с результатом в примере.
Как вы можете видеть умножение матриц довольно муторный процесс с большим количеством мест, где можно ошибиться. И эти проблемы лишь растут при увеличении размеров. Если вы все еще жаждите больше математических свойств матриц я крайне рекомендую видео Khan Academy.
Умножение матрицы на вектор
Мы уже использовали вектора в прошлых уроках. Мы использовали их, чтобы представлять позиции, цвета и текстурные координаты. Теперь давайте немного углубимся в кроличью нору и расскажем, что вектор — это на самом деле просто Nx1 матрица, где N — это количество компонентов вектора. Если вы чуть подумаете об этом — это имеет смысл. Вектора, прямо как матрицы — массив чисел, но только с 1 колонкой. И как же нам поможет эта информация? Что же, если у нас есть матрица MxN мы сможем ее умножить на Nx1 вектор, так как количество столбцов матрицы равно количеству строк вектора.
Но зачем нам вообще уметь умножать матрицу на вектор? Довольно много различных 3D/2D трансформаций можно выполнить, умножая матрицу на вектор, получая измененный вектор. Если вы все еще не уверены в том, что полностью понимаете текст выше, то вот немного примеров:
Единичная матрица
В OpenGL обычно работают с матрицами трансформации размерами 4х4 по той причине, что большинство векторов имеет 4 компонента. Самая простая матрица трансформации которую можно обсудить — это единичная матрица. Единичная матрица — это NxN матрица, заполненная нулями, но с 1 по диагонали. Как мы можете заметить эта матрица совершенно не изменяет вектор:
Вектор выглядит нетронутым. Это становится очевидно из правил умножения: первый результирующий элемент — это каждый элемент первой строки матрицы, умноженные на каждый элемент вектора. Поскольку каждый элемент строки равен 0, кроме первого — то мы получаем 1 * 1 + 0 * 2 + 0 * 3 + 0 * 4 = 1. Тоже самое применяется и к остальным 3 элементам вектора.
Вы можете спросить, зачем вообще может понадобится матрица трансформации, которая ничего не трансформирует? Единичная матрица зачастую является отправной точкой для генерации других матриц трансформации и если мы углубимся в линейную алгебру, это также очень удобная матрица для доказательства теорем и решения линейных уравнений.
Матрица масштабирования
Когда мы масштабируем вектор — мы увеличиваем длину стрелки на величину масштабирования, сохраняя направление. Пока мы работаем в 2 или 3 размерностях мы можем определить масштабирование вектором из 2 или 3 величин, каждая из которых масштабирует одну из осей (x, y или z).
Давайте попробуем масштабировать вектор v = (3,2). Мы будем масштабировать вектор по оси x на 0.5, что сделает его в 2 раза уже; и масштабируем вектор по оси y на 2, что увеличит высоту в 2 раза. Давайте посмотрим как будет выглядеть если мы масштабируем вектор на (0.5, 2). Запишем результат в виде s.
Помните, что OpenGL зачастую работает в 3D пространстве, соответственно для 2D можно оставить Z координату, равную 1. Операция масштабирования, которую мы только что выполнили, является неоднородной, поскольку величина масштабирования для каждой оси различается. Если бы величина масштабирования была бы одинаковой — то такое преобразование называется однородным.
Давайте построим матрицу трансформации которая выполнит для нас масштабирование. Мы уже увидели на единичной матрице, что диагональный элемент будет умножен на соответствующий элемент вектора. Что если мы заменим единицы в единичной матрице на тройки? В таком случае мы умножим все элементы вектора на это значение. Соответственно если мы представим величины масштабирования как (S1, S2, S3) то мы сможем определить матрицу масштабирования для любого вектора (x, y, z):
Заметьте, что 4 элемент вектора равняется 1. Этот компонент обозначается как w и будет потом использован для других задач.
Матрица сдвига
Сдвиг — это процесс добавления одного вектора к другому для получения нового вектора с другой позицией, то-есть сдвиг вектора на основании вектора сдвига. Мы уже обсуждали сложение векторов, поэтому для вас это не будет чем-то новым.
Также как и с матрицей масштабирования в матрице 4х4 есть несколько позиций для выполнения требуемых операций, для сдвига — это верхние 3 элемента четвертой колонки. Если мы представим вектор сдвига как (Tx, Ty, Tz) — то мы можем определить матрицу сдвига следующим образом:
Это работает, потому что все значения вектора умножаются на w компонент вектора и складываются с начальным значениями. Это было бы невозможно при использовании матриц 3х3.
Гомогенные координаты
Компонента вектора w также называется гомогенной координатой. Для получения 3D вектора из гомогенной координаты мы делим x, y и z координаты на w. Обычно этого не замечают, так как w большую часть времени равна 1.0. Использование гомогенных координат имеет несколько преимуществ: они позволяют нам выполнять сдвиги на 3D векторах (без w компоненты это было бы невозможно) и в следующей главе мы используем значение w для создания 3D визуализаций.
Также когда гомогенная координата равна 0 — то вектор считается вектором направления, так как вектор с компонентой w равной 0 не может быть сдвинут.
С матрицей сдвига мы можем двигать объекты по всем 3 направлениям (x, y, z), что делает эту матрицу крайне полезной для наших задач.
Матрица вращения
Последние пару трансформаций были довольно просты для понимания и представления в 2D или 3D пространстве, но вращения немного более заковыристые. Если вы хотите узнать как же именно эти матрицы формируются — то я рекомендую видео Khan Academy про линейную алгебру.
Для начала давайте определим что вообще такое — вращение вектора. Вращение в 2D и 3D определяется углом. Угол может выражаться в углах или в радианах, в которых полный оборот — это 360 градусов или 2Pi соответственно. Я предпочитаю работать с градусами, поскольку они более логичны для меня.
Большинство вращательных функций требует угол в радианах, но благо преобразование из одной системы в другую выполнить довольно просто:
Градусы = радианы * (180.0f / PI)
Радианы = градусы * (PI / 180.0f)
Где PI примерно 3.14159265359
Вращение на половину круга — требует от нас вращения на 360/2 = 180 градусов. Вращение на 1/5 направо требует от нас вращение на 360/5 = 72 градуса направо. Вот пример обычного 2D вектора, где v повернут на 72 градуса направо от k.
Вращение в 3D описывается углом и осью вращения. Угол определяет то насколько вектор будет повернут относительно данной оси. При вращении 2D векторов в 3D мире, к примеру, мы установим ось вращения — Z.
С помощью тригонометрии мы можем преобразовывать вектора в повернутые на определенный угол. Обычно это делается хитрой комбинацией sin и cos функций. Обсуждение того, как генерируется матрицы трансформации — выходит за пределы нашего урока.
Матрица вращения определена для каждой оси в 3D пространстве, где угол показан как тета.
Матрица вращения вокруг оси X:
Матрица вращения вокруг оси Y:
Матрица вращения вокруг оси Z:
С помощью матриц вращения мы можем вращать наши вектора по одной из трех осей. Также можно совмещать их, например в начале повернуть по X оси, а потом по Y. Правда такой подход быстро приведет к проблеме, называемый проблемой шарнирного замка (Gimbal Lock). Мы не будем вдаваться в детали, но лучше использовать вращение по конкретной оси, например (0.662, 0.2, 0.722) (заметьте, что это единичный вектор), вместо того, чтобы совмещать вращения по конкретным осям. Матрица для таких преобразований существует и выглядит она следующим образом, где (Rx, Ry, Rz) — это ось вращения:
Математические обсуждения на счет генерации такой матрицы выходят за рамки этого урока. Просто держите в голове, что даже такая матрица не решает проблему шарнирного замка полность (ее просто сложнее получить). Для того, чтобы полностью решить эту проблему нам придется работать с вращениями с помощью кватернионов, которые не просто безопаснее, но еще и гораздо дружелюбнее с точки зрения вычислений. Как бы то ни было обсуждение кватернионов отведено в более поздний урок.
Комбинирование матриц
Для того, чтобы достичь максимальной полезности использования матриц для трансформаций мы должны комбинировать матрицы трансформации в одну матрицу. Давайте посмотрим, сможем ли мы сгенерировать матрицу трансформации, которая будет в себя включать несколько трансформаций. Например у нас есть вектор (x, y, z) и мы хотим масштабировать его в 2 раза и сдвинуть на (1, 2, 3). Для этого нам потребуются матрицы масштабирования и смещения. В результате мы получим что-то вроде:
Заметьте, что во время умножения матриц мы в начале выполняем сдвиг, а потом масштабирование. Умножение матриц не коммутативно, что означает, что порядок умножения важен. Во время умножения матриц правая матрица умножается на вектор, поэтому вам надо читать умножения справа налево. Рекомендуется в начале масштабировать, затем вращать и в конце сдвигать, во время объединения матриц, в ином случае они могут отрицать друг-друга. Например если вы в начале выполните сдвиг, а затем масштабирование, то матрица сдвига тоже будет масштабировать!
В итоге матрица трансформации применяется следующим образом:
Отлично, вектор масштабирован в 2 раза и смещен на (1, 2, 3).
На практике
После того, как мы обсудили всю теорию настало время применять ее на практике. OpenGL не имеет встроенной поддержки матричных или векторных преобразований, поэтому нам придется использовать собственные математические класса и функции. В этих уроках мы абстрагируемся от тонких математических деталей и просто используем готовые математические библиотеки. К счастью уже есть простая в использовании и заточенная под OpenGL математическая библиотека, под названием GLM.
GLM это аббревиатура от OpenGL Mathematics. Эта библиотека является заголовочной, что означает, что нам достаточно подключить требуемые заголовочные файлы. Не нужно заморачиваться ни с линковкой ни с компиляцией. GLM можно скачать с официального сайта. Скопируйте корневую директорию с заголовочными файлами в вашу папку includes и можно начинать.
Большая часть функциональности GLM можно найти в 3 заголовочных файлах:
Давайте посмотрим, сможем ли мы применить наши знания в преобразованиях для сдвига вектора (1, 0, 0) на (1, 1, 0) (заметьте, что мы обозначили из как glm::vec4 с гомогенной координатой равной 1.0):
В начале мы создали вектор названный vec с помощью встроенного в GLM векторного класса. Затем мы определяем mat4, которая является единичной матрицей 4х4. Затем мы создаем матрицу трансформации, передавая нашу единичную матрицу в функцию glm::translate, вместе с вектором сдвига.
Затем мы умножаем наш вектор на матрицу трансформации и выводим результат. Если вы все еще помните как работает матрица сдвига — то вы понимаете, что результирующий вектор должен быть (1+1, 0+1, 0+0), который равен (2, 1, 0). Код выше выводит 210, что означает, что матрица сдвига сделала свою работу.
Давайте попробуем сделать нечто более интересное и попробуем масштабировать, а затем повернуть объект из прошлого урока. В начале мы повернем контейнер на 90 градусов против часовой стрелки. Затем масштабируем его на 0.5 для того, чтобы уменьшить его в 2 раза. Давайте построим матрицу трансформации для этого.
В начале мы уменьшаем контейнер на 0.5, по каждой оси, а затем поворачиваем контейнер на 90 градусов по Z координате. Заметьте, что текстура также повернулась. Поскольку мы передаем матрицу в каждую из GLM функций, GLM автоматически перемножает матрицы, в результате получая матрицу трансформации.
Некоторые версии GLM принимают углы в радианах, а не в градусах. Если у вас такая версия — то преобразуйте градусы в радианы с помощью glm::radians(90.0f).
Следующий большой вопрос — это как передать матрицу трансформации в шейдер? Ранее мы уже говорили, что GLSL имеет тип mat4. Так что нам осталось принять mat4 в качестве uniform переменной и умножить вектор позиции на эту матрицу.
В GLSL также имеются типы mat2 и mat3, которые предоставляют такие же операции, что и вектора. Все затронутые в этой статье операции доступны в матричных типах.
Мы добавили uniform и умножили позиционный вектор на трансформационную матрицу перед тем как передать ее в gl_Position. Наш контейнер теперь должен стать меньше в 2 раза и повернуться на 90 градусов. Но нам все еще надо передать трансформационную матрицу в шейдер?
В начале мы получаем позицию uniform переменной и затем отправляем в нее данные матрицы с помощью функции glUniform с постфиксом Matrix4fv. Первый аргумент должен быть позицией переменной. Второй аргумент сообщает OpenGL сколько матриц мы собираемся отправлять, в нашем случае 1. Третий аргумент говорит требуется ли транспонировать матрицу. OpenGL разработчики часто используют внутренних матричный формат, называемый column-major ordering, который используется в GLM по умолчанию, поэтому нам не требуется транспонировать матрицы, мы можем оставить GL_FALSE. Последний параметр — это, собственно, данные, но GLM не хранит данные точно так как OpenGL хочет их видеть, поэтому мы преобразовываем их с помощью value_ptr.
Мы создали матрицу трансформации, объявили uniform в вершинном шейдере, и отправили матрицу в шейдере с помощью которой мы корректируем вершинные координаты. В результате должно получиться что-то вроде этого:
Отлично! Наш контейнер действительно повернут налево и стал в 2 раза меньше, так что трансформация прошла успешно. А теперь давайте заставим вращаться наш контейнер в реальном времени, а также передвинем его в нижний правый угол. Для того, чтобы это сделать придется производить вычисления при каждой итерации основного цикла. Мы используем функцию GLFW для получения времени, чтобы менять угол со временем:
Держите в голове, что раньше мы могли объявить матрицу трансформации где угодно, но теперь мы создаем ее при каждой итерации, чтобы мы могли обновлять вращение на каждый кадр. Это значит, что мы должны пересоздавать матрицу трансформации на каждой итерации игрового цикла. Обычно, когда на сцене несколько объектов, то их матрицы трансформации пересоздаются с новыми значениями при каждой итерации отрисовки.
Теперь мы вращаем объект вокруг центра (0, 0, 0), а после этого сдвигаем повернутую версию в нижний-правый угол экрана. Помните, что реальная последовательность применения трансформаций читается в обратном порядке: даже в коде мы в начале сдвигаем, а потом поворачиваем, то трансформации применяются в обратном порядке, в начале поворот, затем сдвиг. Понимание всех этих трансформаций и того как они влияют на объекты довольно затруднительно. Попробуйте поэкспериментировать с трансформациями и вы быстро с ними свыкнитесь.
Если вы все сделали правильно — то вы получите что-то вроде этого:
Вот и все. Сдвинутый контейнер, поворачивающийся с течением времени, и все это выполнено с помощью одной матрицы трансформации! Теперь вы можете видеть, почему матрицы настолько сильны в графическом мире. Мы можем определить безграничное количество трансформаций и совмещать их в одну матрицу для последующего повторного использования. Использование подобных трансформаций в вершинном шейдере позволяет нам не менять вершинные данные, что сохраняет нам процессорное время, поскольку нам не требуется отправлять данные в буфер.
Если вам не удалось получить правильный результат или вы где-то застряли — то взгляните на исходный код вместе с вершинным и фрагментным шейдерами.
В следующем уроке мы обсудим как использовать матрицы для определения различных координатных пространств для наших вершин. Это будет новым шагом в мир 3D графики в реальном времени!
http://www.berdov.com/works/matrix/umnozhenie-matric/
http://habr.com/ru/post/319144/
Умножение матрицы на вектор
Содержание:
- Примеры с решением
Каждый вектор можно рассматривать как одностолбцовую или однострочную матрицу. Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.
Если 











Примеры с решением
Пример 1.
Даны матрица 



Вычислить координаты векторов 

Свойства умножения матрицы на вектор (


Элемент новой матрицы, стоящий на пересечении 



По этой ссылке вы найдёте полный курс лекций по высшей математике:
Операция определена при условии, что число столбцов первой матрицы равно числу строк второй.
Произведением матрицы 





Матрица умножается на вектор в соответствии с правилом «строк на столбец». При умножении матрицы на вектор столбцов количество столбцов в матрице должно соответствовать количеству строк в векторе столбцов.
Пример 2.
Замечание 1. Используя знак сокращенного суммирования, формулу (1) можно записать в виде 
Замечание 2. Введем обозначение матрицы в виде 



Возможно вам будут полезны данные страницы:
Замечание 3. Порядок матриц-сомножителей существен. Поэтому говорят об умножении матрицы 










Замечание 4. Умножение единичной матрицы
на квадратную матрицу
не изменяет последней:
.
Замечание 5. Произведение двух ненулевых матриц может дать нулевую матрицу 

Лекции:
- Циркуляция векторного поля. Ротор вектора. Теорема Стокса
- Векторное произведение векторов
- Таблица производных полная: для студентов
- Функции двух переменных. Действия над случайными величинами
- Найти значение выражения
- Область значения функции
- Нормальное распределение
- Ранг матрицы: примеры решения
- Найдите объем тела ограниченного
- Разложение вектора по базису
| Элементы матрицы A |
| Элементы вектора b или c |
| Результат умножения вектора-строки на матрицу с*A |
| Результат умножения матрицы на вектор-столбец A*b |
Каждый вектор можно рассматривать как одностолбцовую или однострочную матрицу. Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.
Если A-матрица размера m*n, то вектор столбец b имеет размер n, а вектор строка b имеет размер m.
Таким образом, что бы умножить матрицу на вектор, надо рассматривать вектор как вектор-столбец. При умножении вектора на матрицу, его нужно рассматривать как вектор -строку.
Пример.
Умножить матрицу
(begin{pmatrix} 1+2i & 2+i & 1+3i \ 2 & 4+2i & 2+5i end{pmatrix})
на комплексный вектор
(begin{pmatrix} 2+2i \ 1+4i \ 2+2i end{pmatrix})
Получаем результат
Как видите при неизменной размерности вектора, у нас могут существовать два решения.
Хотелось бы обратить Ваше внимание на то что матрица в первом и втором варианте, несмотря на одинаковые значения, совершенно разные (имеют различную размерность)
В первом случае вектор считается как столбец и тогда необходимо умножать матрицу на вектор, а во втором случае у нас вектор-строка и тогда у нас произведение вектора на матрицу.
Свойства умножения матрицы на вектор
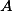



1. Произведение матрицы на сумму векторов-столбцов равна сумме произведений матрицы на каждый из векторов
2. Произведение суммы векторов-строк на матрицу равна сумме произведений векторов на матрицу
3. Общий множитель вектора можно вынести за пределы произведения матрицы на вектор/вектора на матрицу
4.Произведение вектора-строки на произведение матрицы и вектора столбца, равноценно произведению произведения вектора-строки на матрицу и вектора-столбца.
Удачных расчетов!!

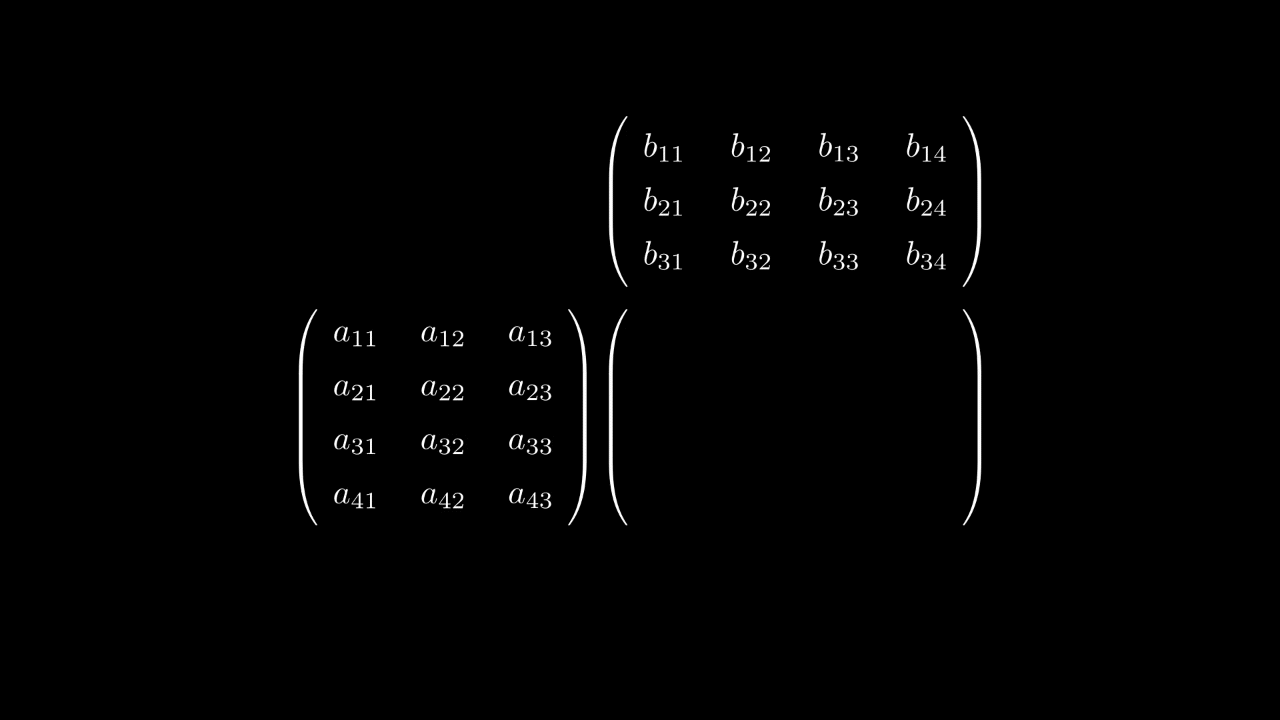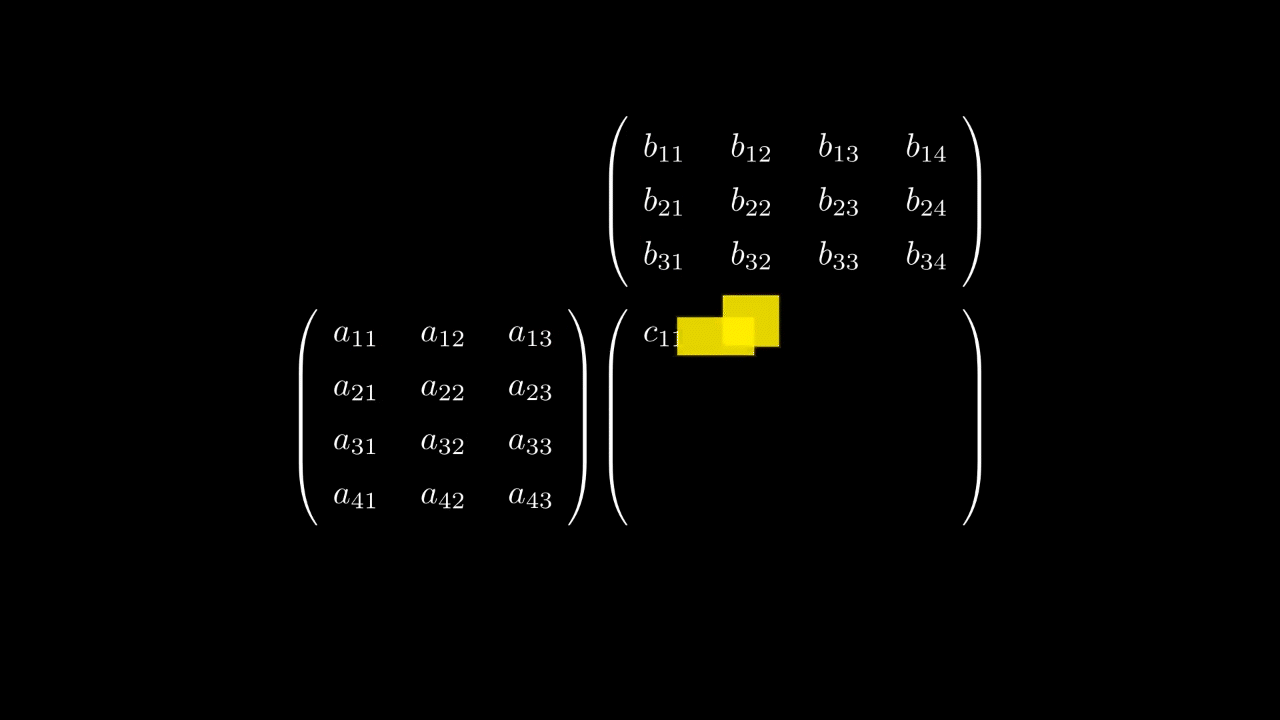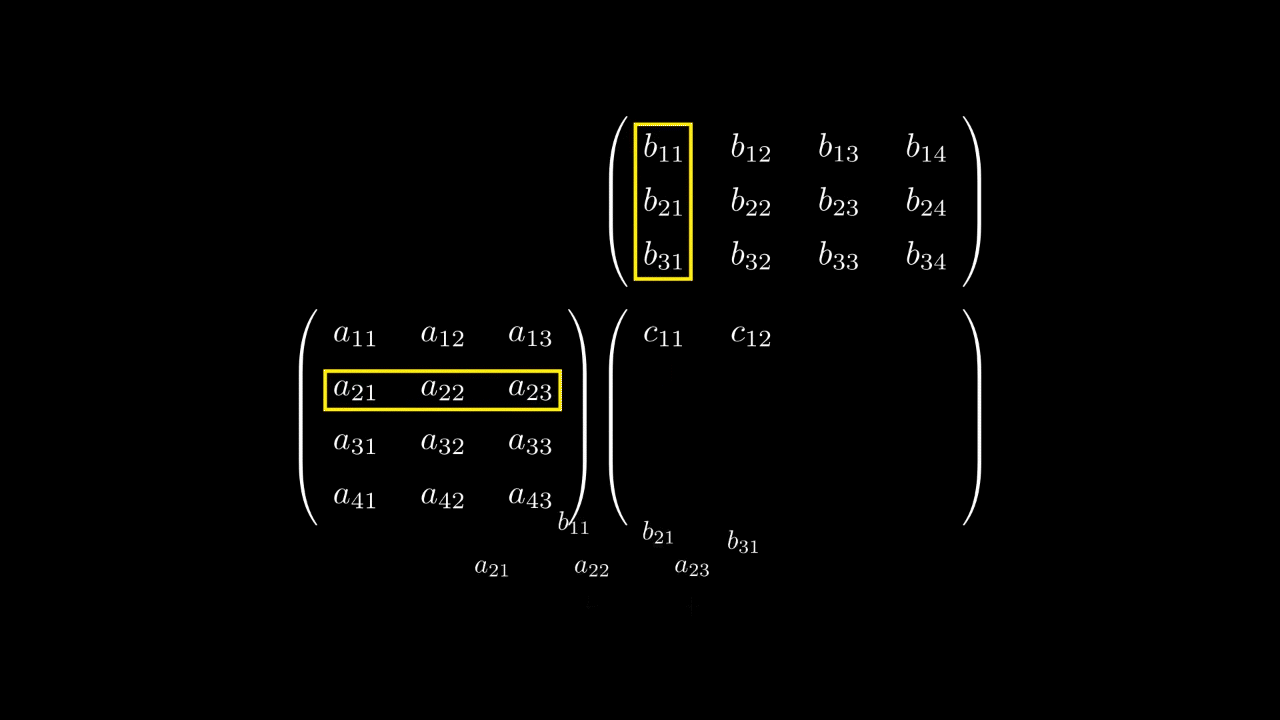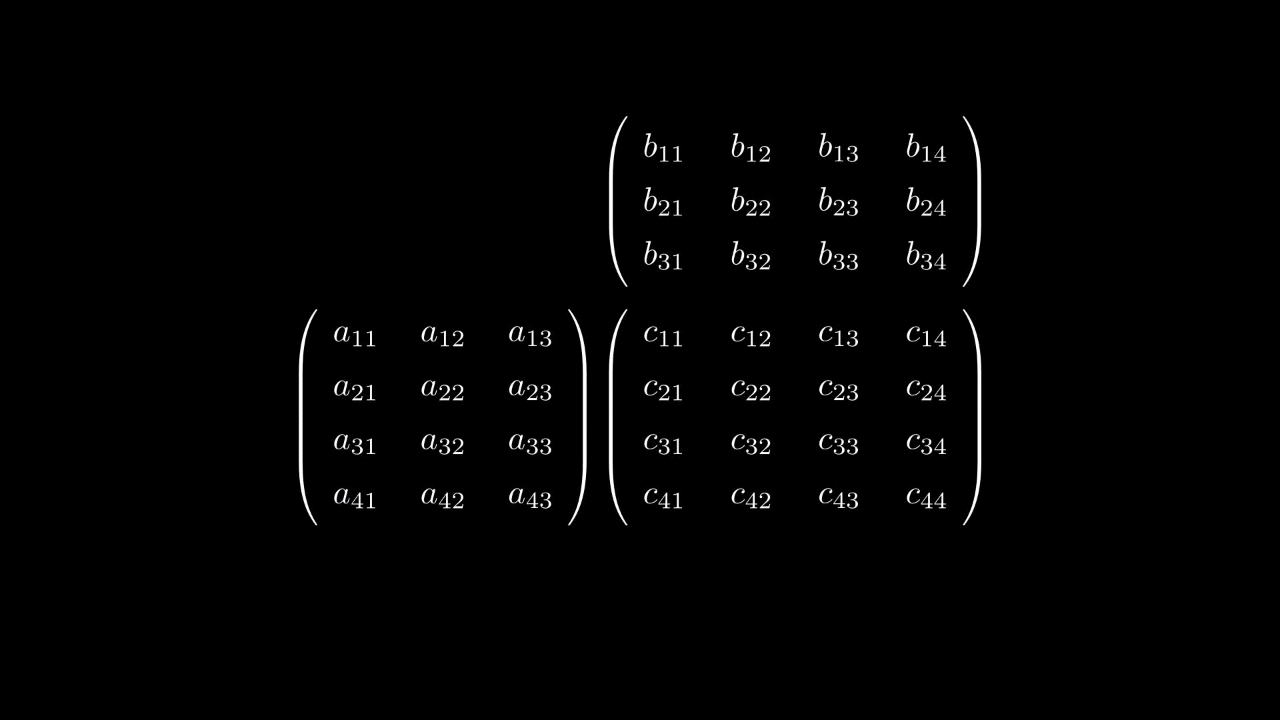
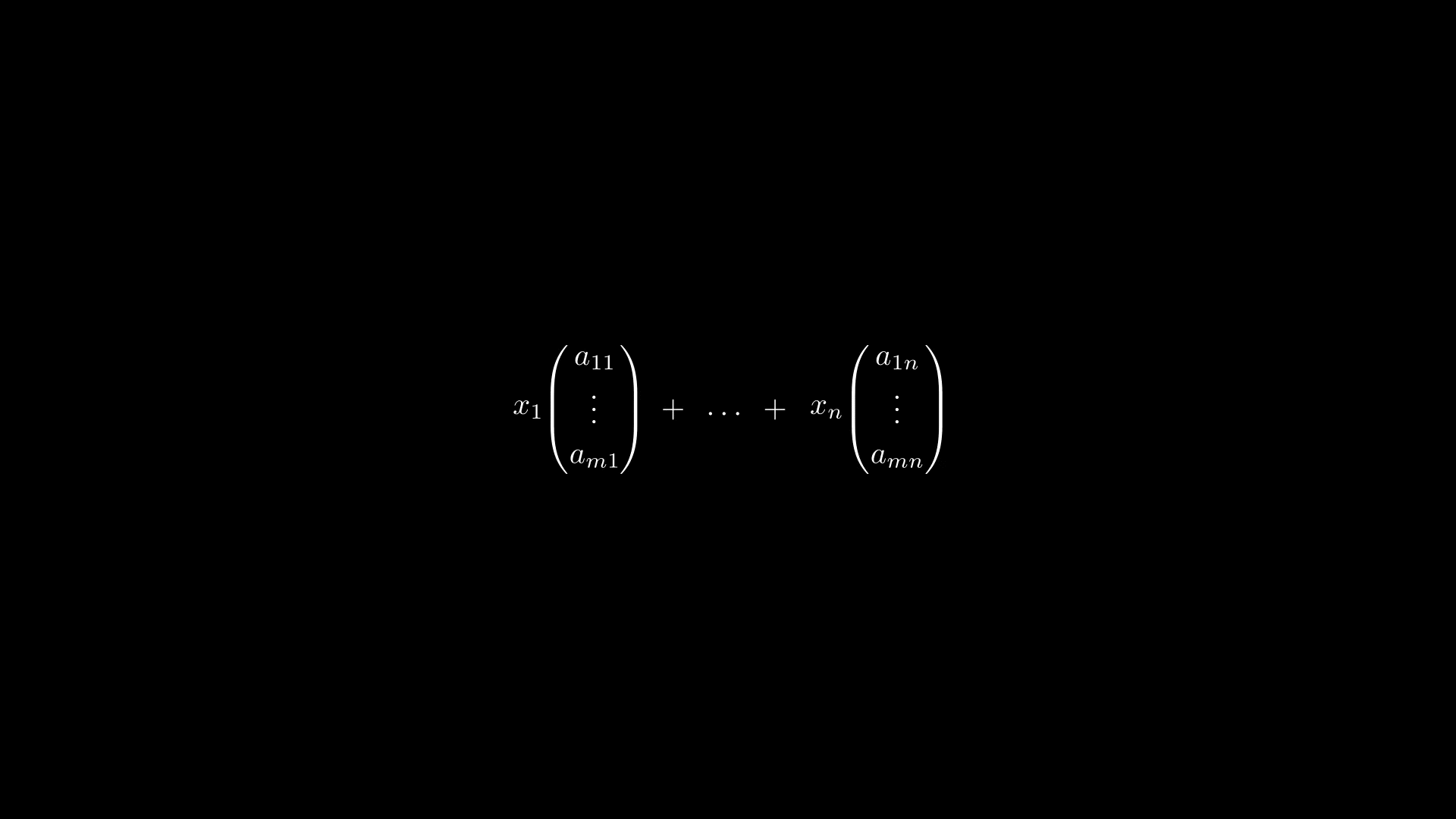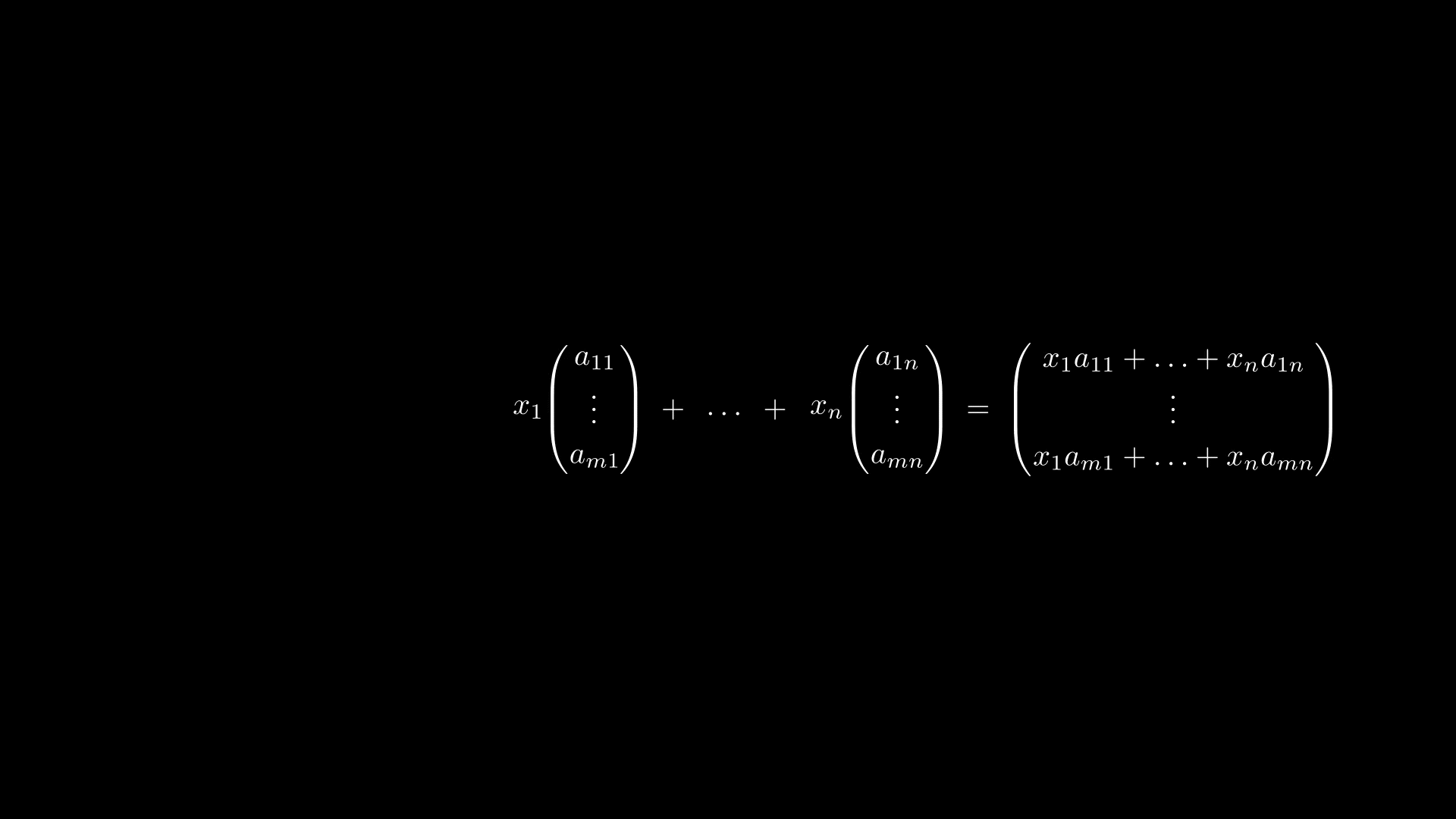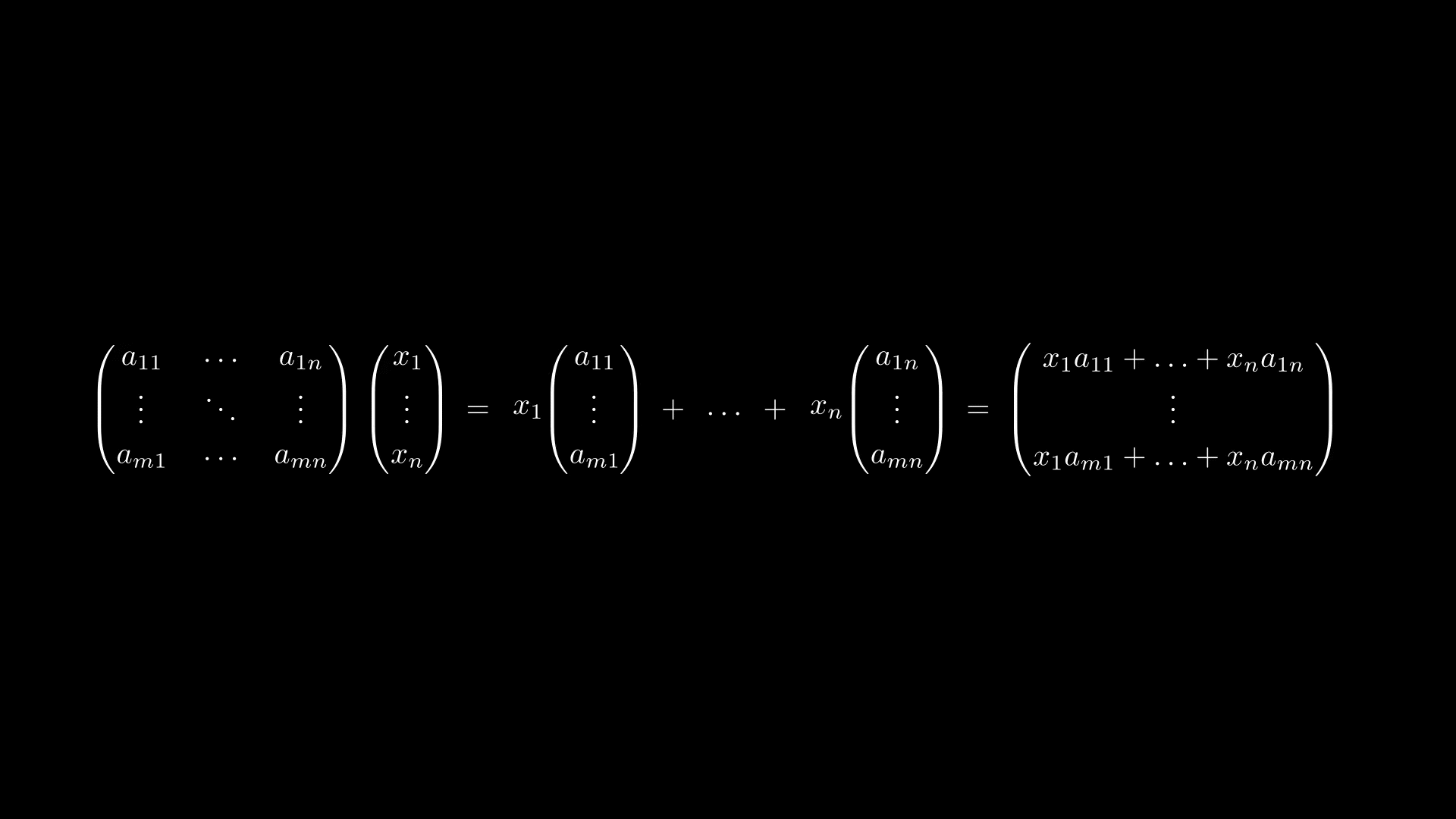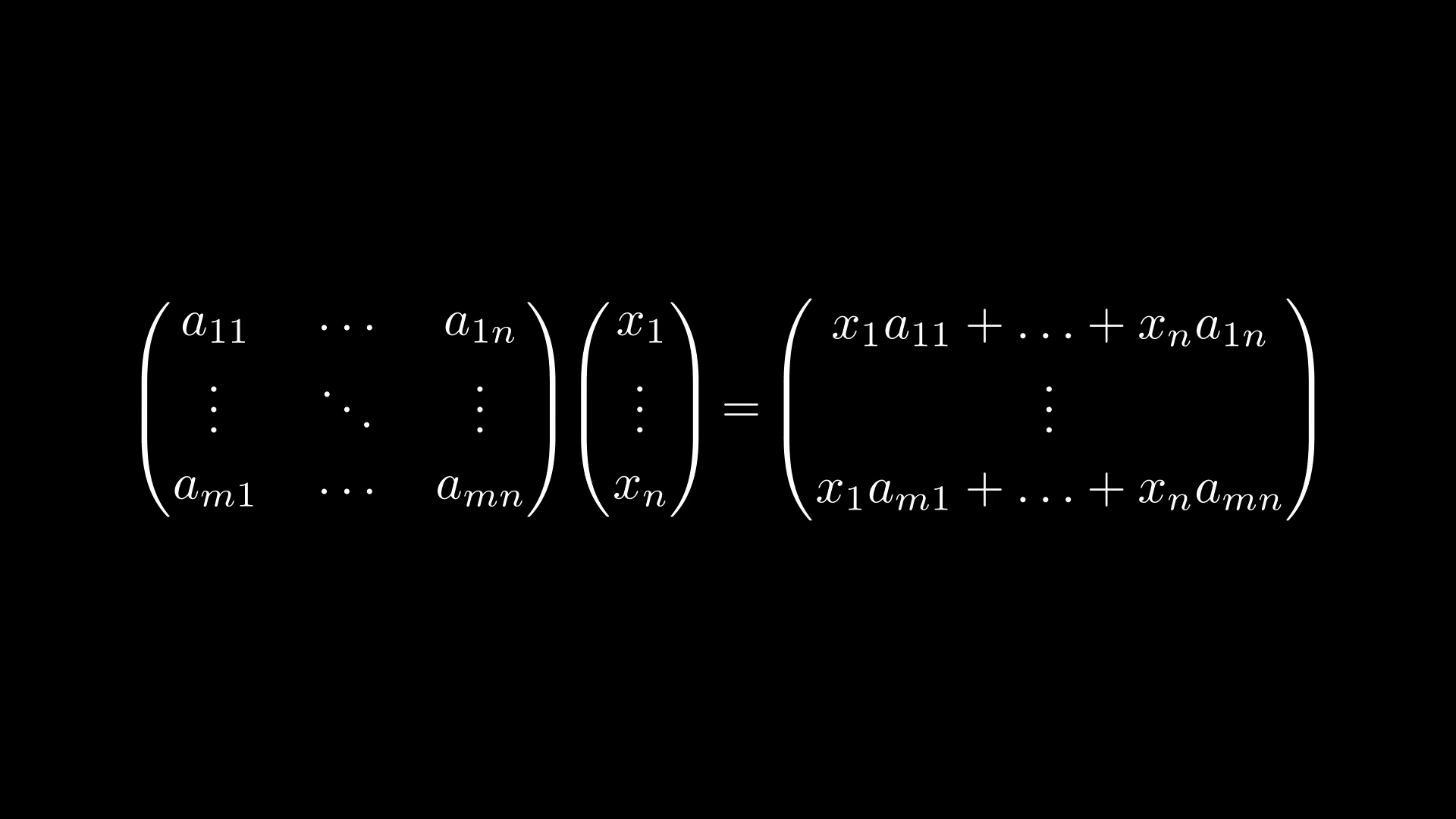
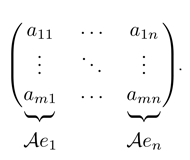
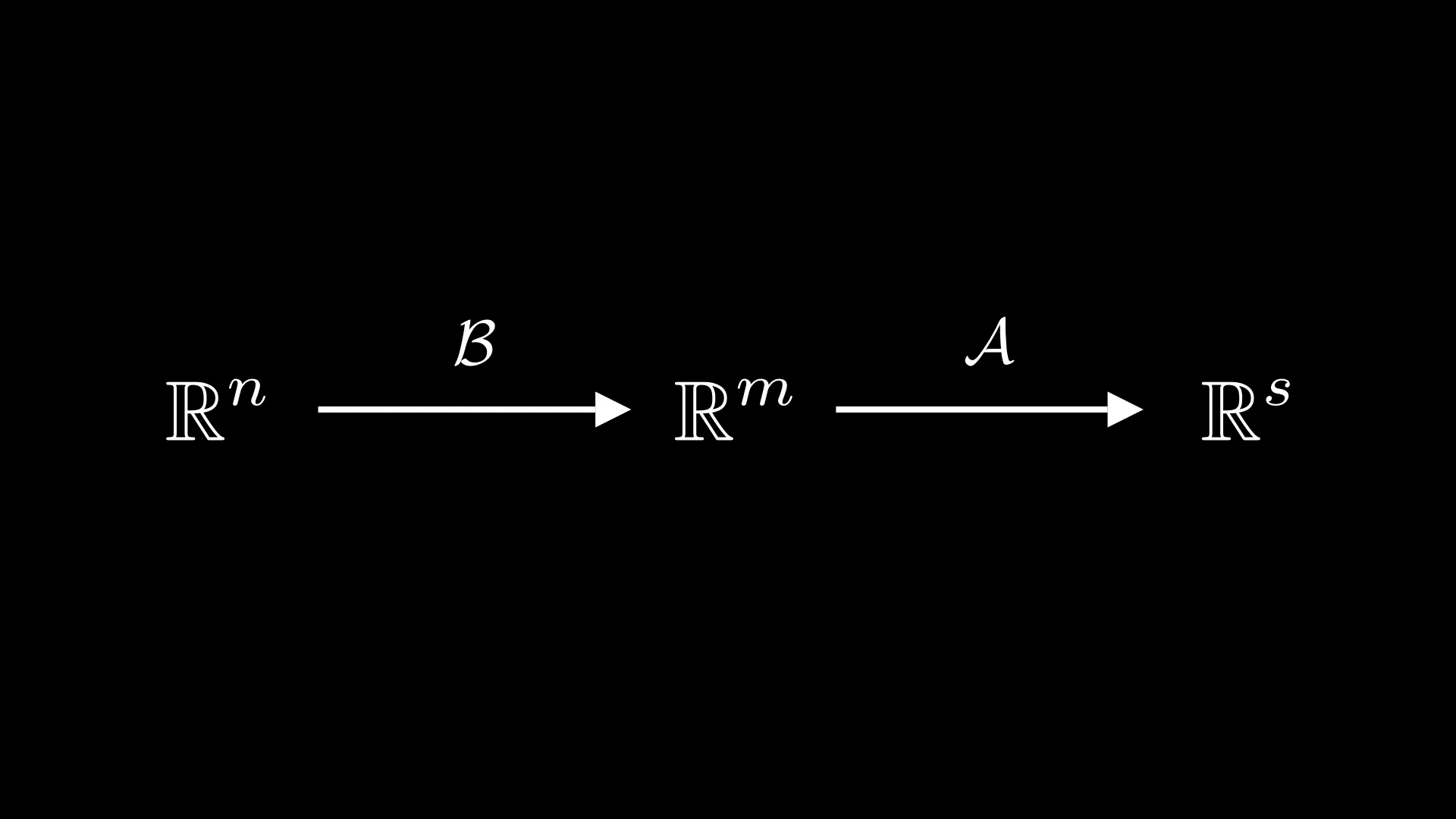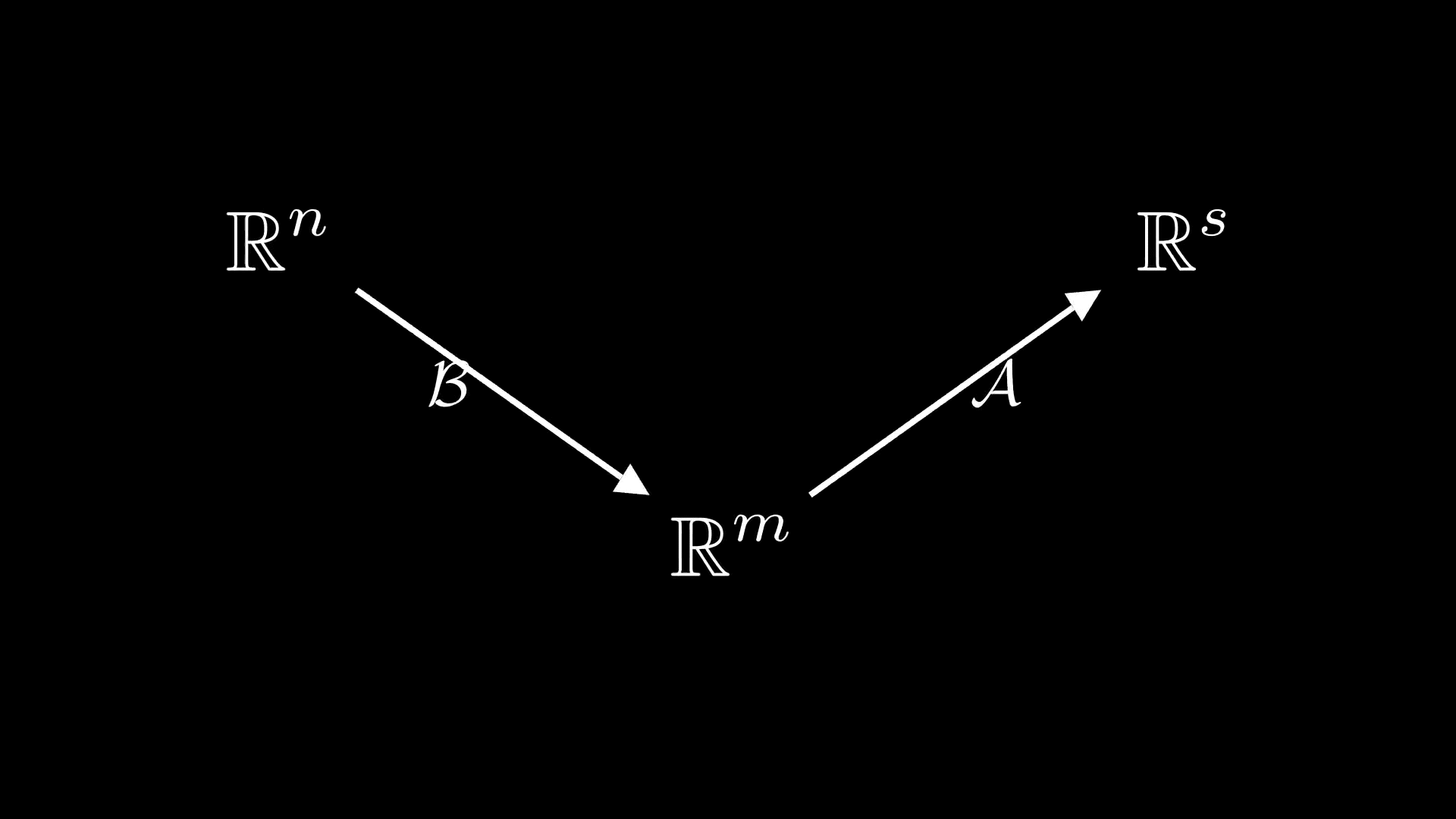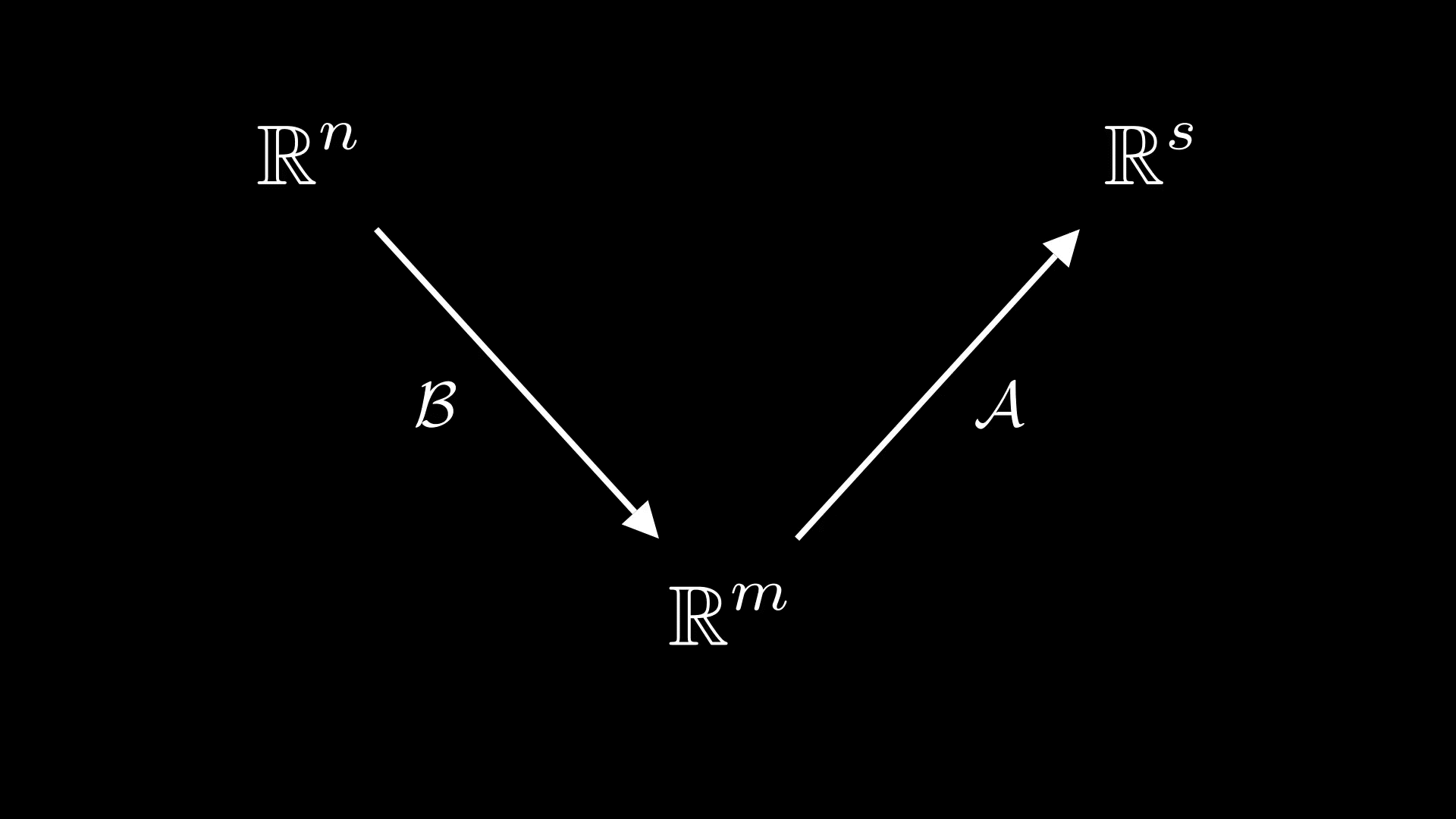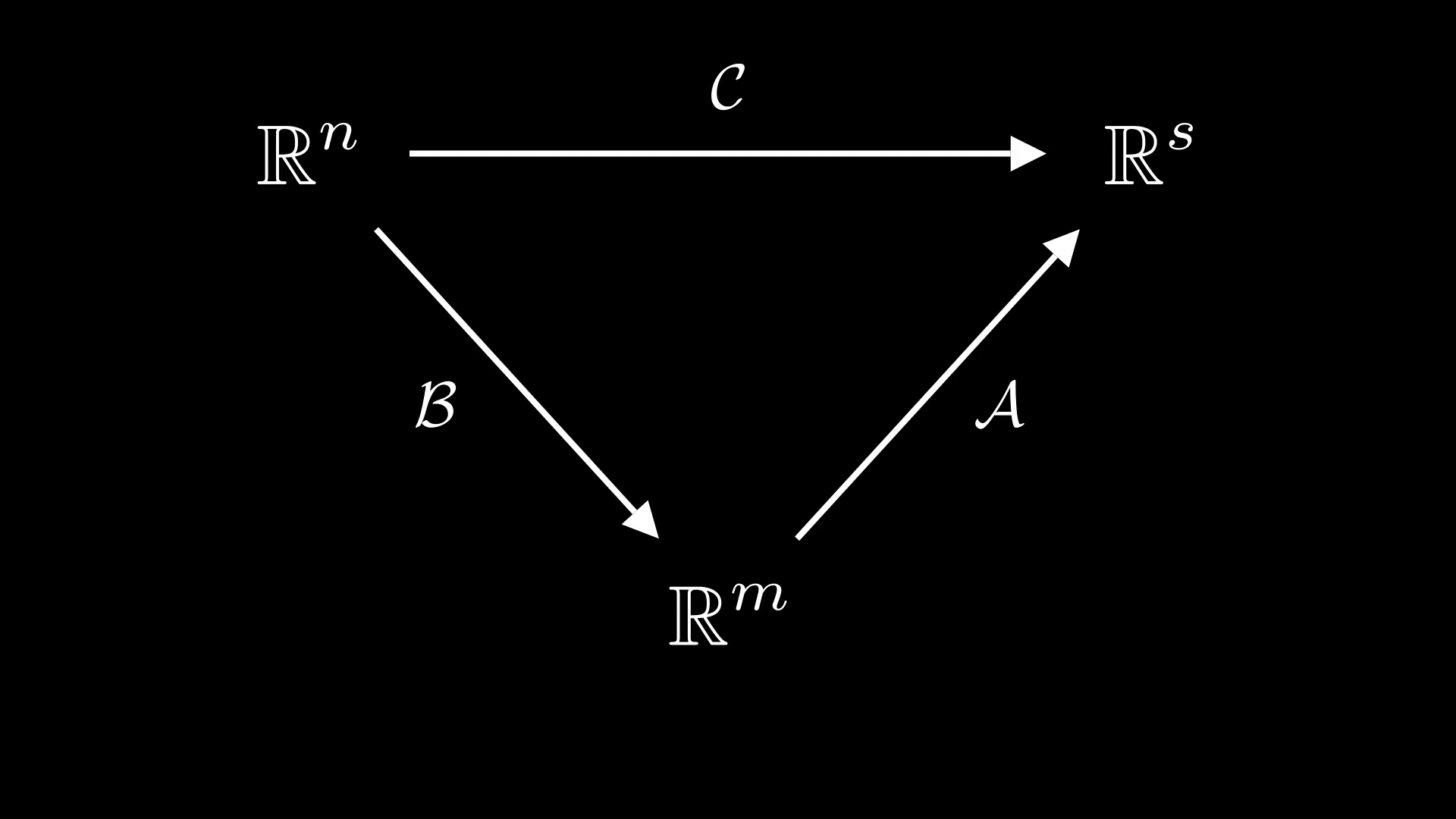
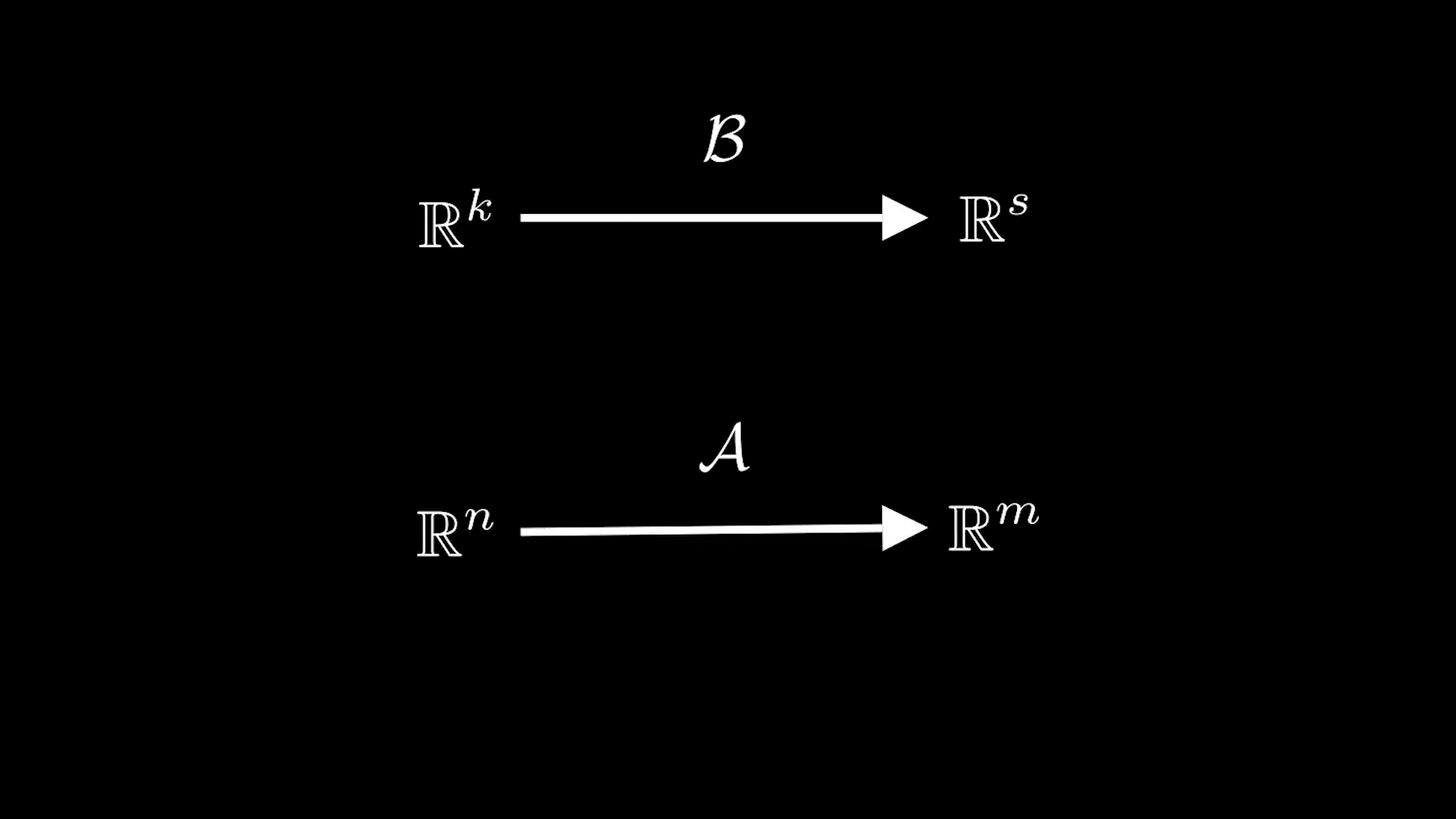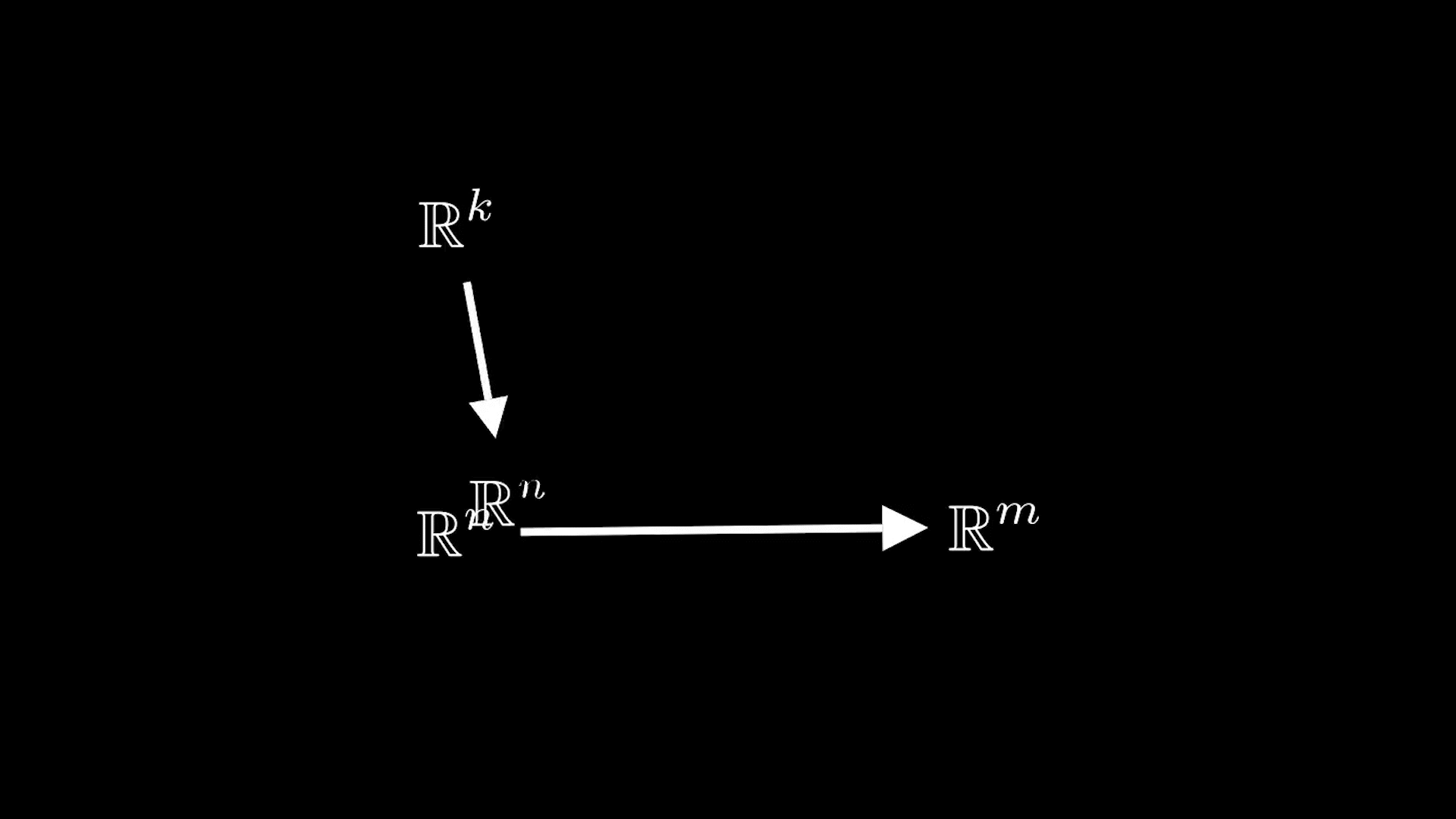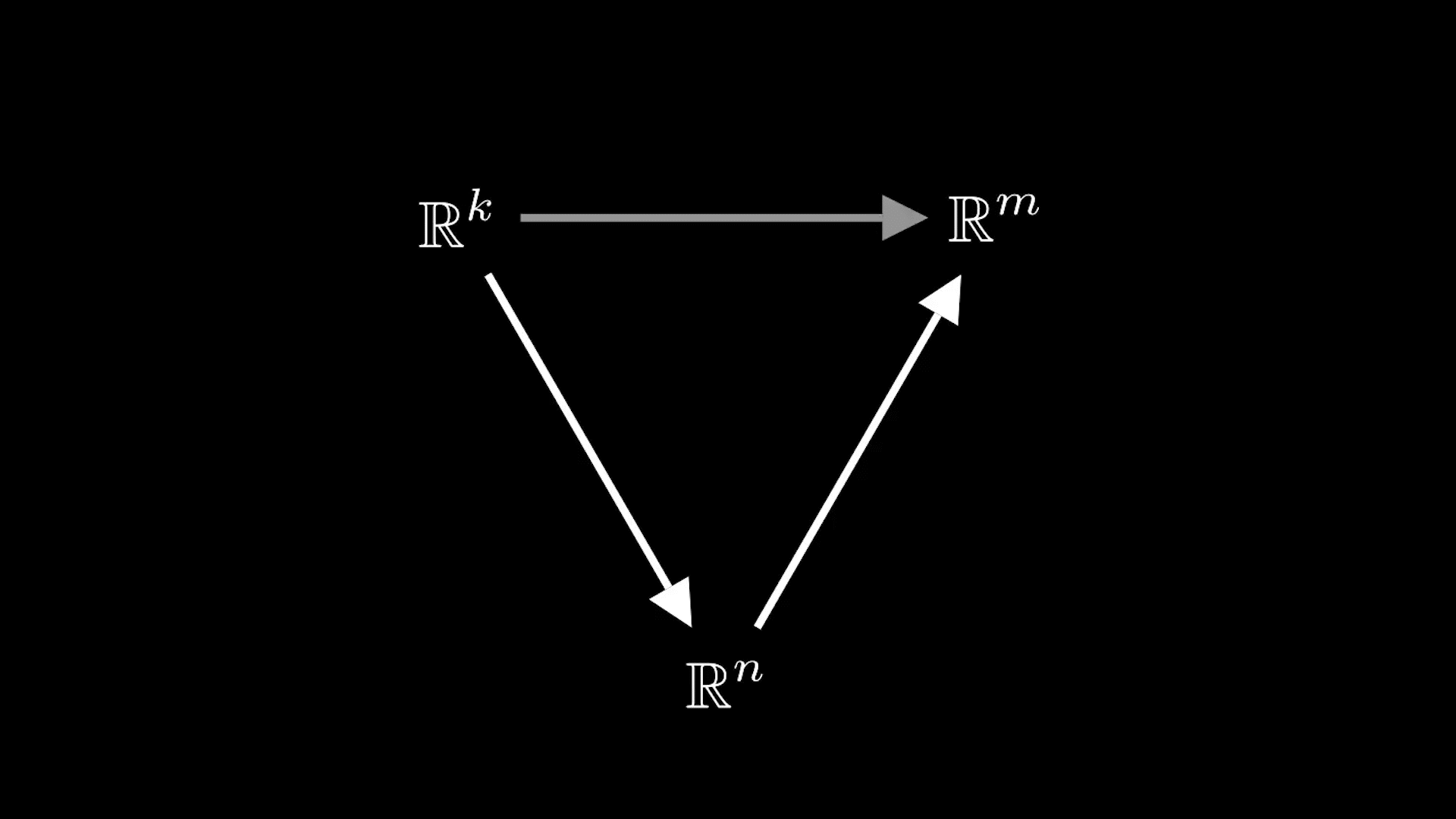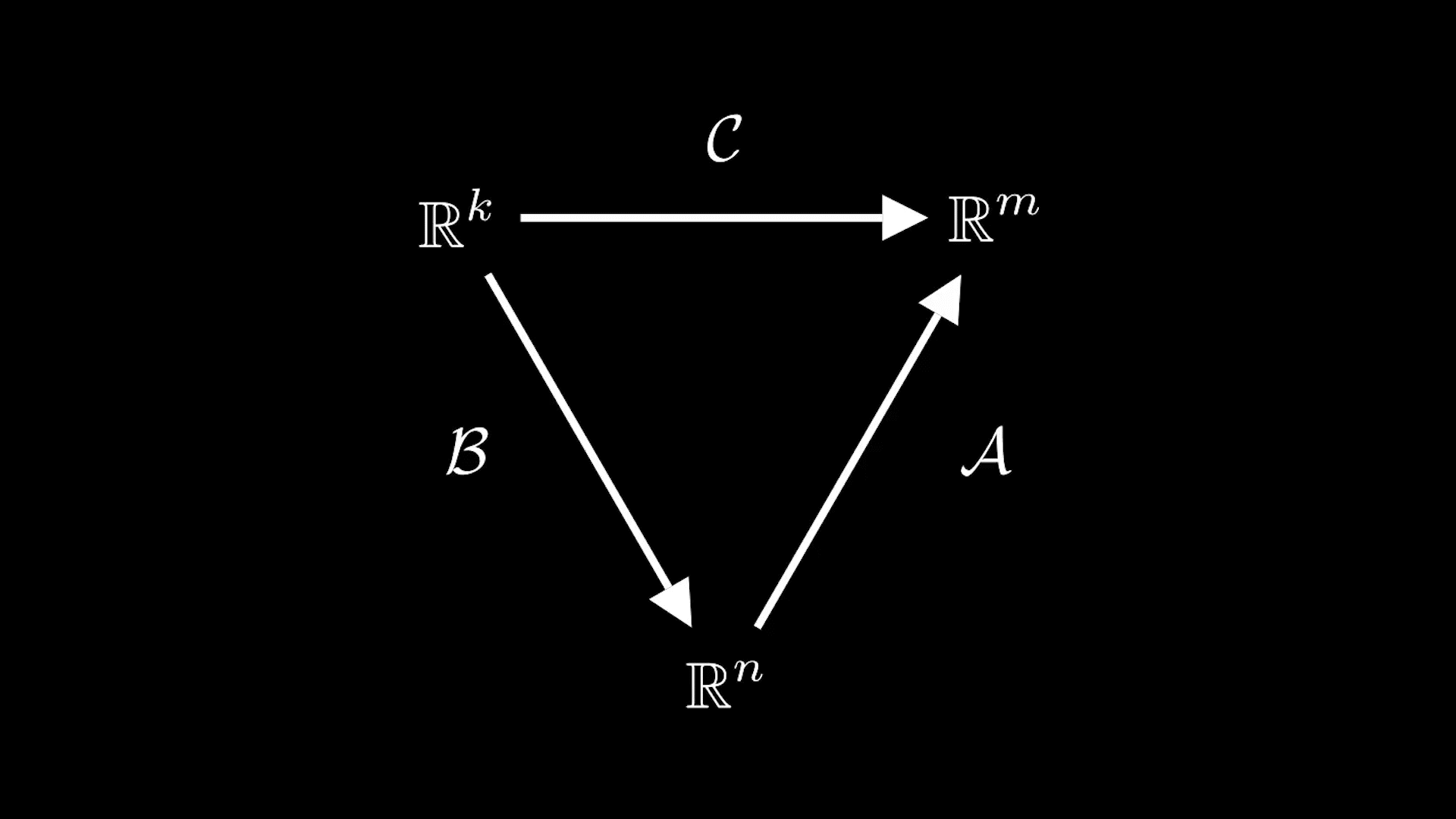



 на квадратную матрицу
на квадратную матрицу  .
.

=Ab_1+Ab_2)
A=c_1A+c_2A)
A=lambda{(cA)}\A(lambda{b})=lambda(Ab))
=(cA)b)