Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Вот смотри…
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Определение модуля:
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)
Свойства модуля:
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
( |mathbf{a}|,) (( a) — любое число).
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf{3} right|=mathbf{3})
( left| -mathbf{3} right|=mathbf{3}.)
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)
( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)
А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)
( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| text{ }le text{ } right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10}) | ( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Выражения также равны, если оба числа отрицательны:
| ( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10) | ( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4}) | ( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
или
| ( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4}) | ( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
( mathbf{4}<mathbf{10})
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
( {{left| x right|}^{2}}=?)
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
( {{left| x right|}^{2}}={{x}^{2}})
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
( {{left| 5 right|}^{2}}={{5}^{2}}=25)
( {{left| -5 right|}^{2}}=?)
Ну, и почему сомнения? Действуем смело!
( {{left| -5 right|}^{2}}={{5}^{2}}=25)
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
а) ( |3|text{ }+text{ }|-9|;)
б) ( |-5|text{ }-text{ }|6|;)
в) ( |15left| cdot right|-3|;)
г) ( displaystyle frac{|8|}{|-2|}).
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:
( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)
Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).
Решение:
( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)
( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)
( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb{R}):
- ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при text{ }c>0)
- ( {{left| x right|}^{2}}={{x}^{2}})
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Обратите внимание на картинку.
Для того чтобы узнать тему нашего урока, попробуйте отгадать ребус.
Эта информация доступна зарегистрированным пользователям
На этом уроке разберемся, что называют модулем числа, раскроем его геометрический смысл, рассмотрим основные свойства модуля, научимся находить модуль числа и применять эти знания при решении задач.
В переводе с латинского «модуль» (modulus) означает мера, размер.
Считается, что данный термин впервые ввел в пользование английский философ и математик Роджер Котс, друг и ученик Исаака Ньютона.
Многие ученые использовали в своих научных трудах понятие модуль, однако символьное обозначение он приобрел только в конце XIX века.
В 1841 году выдающийся немецкий ученый Карл Теодор Вильгельм Вейерштрасс ввел символьное обозначение модуля числа, которое используют и применяют по сегодняшний день.
В некоторых случаях вместо «модуль числа» говорят: «абсолютная величина», но надо понимать, что это тождественно равные понятия.
Эта информация доступна зарегистрированным пользователям
В математике модуль имеет несколько значений. Разберем, что в математике называют модулем числа (абсолютной величиной).
Эта информация доступна зарегистрированным пользователям
Рассмотрим понятие модуль с геометрической точки зрения.
Вам уже известно, что на координатной прямой мы отмечаем действительные числа, а каждому действительному числу на этой прямой соответствует определенная точка и наоборот, каждой точке на координатной прямой соответствует действительное число.
Точка задается некоторым расстоянием от начала координат.
Длина отрезка от начала координат до точки вмещает в себя определенное количество единичных отрезков координатной прямой.
Длина такого отрезка всегда неотрицательная величина.
Рассмотрим пример:
Два мяча катнули по одной прямой. Первый мяч откатился вправо от исходной точки на 4 м, второй мяч влево от исходной точки на 6 м.
Изобразим координатную прямую и отметим на ней координаты точек остановки этих двух мячей.
Эта информация доступна зарегистрированным пользователям
Точка О— это исходная точка мячей- точка начала отсчета.
Единичный отрезок координатной прямой равен 1 деление- 1 метр.
Вправо откладываем координату первого мяча А (+4)
Влево откладываем координату второго мяча В (-6)
Расстояние от точки А до начала отсчета 4 единичных отрезка.
Длина ОА = 4 единичных отрезка.
Расстояние от точки В до начала отсчета 6 единичных отрезков.
Длина ОВ = 6 единичных отрезков.
Расстояние ОА и ОВ называют абсолютной величиной, модулем числа, они всегда положительны.
Таким образом, модулем числа называют расстояние на координатной прямой от начала отсчета до заданной точки (выраженной в единичных отрезках).
Обозначается модуль двумя вертикальными чертами слева и справа от числа | |.
Запись |A| читается как «Модуль А» или «Модуль числа А».
Пример 1
|7|— модуль числа 7
Изобразим координатную прямую, отметим на ней точку с координатой 7
Эта информация доступна зарегистрированным пользователям
Зная определение модуля числа, мы можем утверждать, что |7| — это расстояние от точки с координатой 7 до точки начала отсчета О, что составляет 7 единичных отрезков.
Значит, модуль числа 7 равен самому числу 7
|7| = 7
Пример 2
|-5| — модуль числа (-5)
Изобразим координатную прямую, отметим на ней точку с координатой (-5).
Эта информация доступна зарегистрированным пользователям
Зная определение модуля числа, мы можем утверждать, что от точки с координатой (-5) до точки начала отсчета О помещается 5 единичных отрезков.
5 единичных отрезков — это и есть расстояние от точки с координатой (-5) до точки начала отсчета (модуль числа).
Значит, модуль числа (-5) равен 5
|-5| = 5
Пример 3
|-1|— модуль числа (-1)
В расстояние от точки с координатой (-1) до точки начала отсчета помещается только один единичный отрезок этой прямой, поэтому модуль (-1) равен 1.
|-1| = 1
Эта информация доступна зарегистрированным пользователям
Рассмотрим некоторые свойства модуля числа.
1. Модуль нуля равен нулю
Так как от нуля до начала отсчета нет никакого расстояния (0 единичных отрезков), модуль нуля и есть нуль.
|0| = 0
2. Модуль числа всегда число неотрицательное (т.е. положительное или нуль)
Модуль положителен, так как по определению модуль — это расстояние, а расстояние всегда является положительным числом.
Приведем пример:
Мяч катнули вдоль прямой на расстояние, равное 3 м вправо, мяч ударился о стену и покатился вдоль прямой в обратном направлении на 3 м и остановился.
Изобразим на координатной прямой координаты точек в момент каждой остановки мяча.
Эта информация доступна зарегистрированным пользователям
Точка О на координатной прямой- это точка откуда катнули мяч- точка начала отсчета.
Единичный отрезок координатной прямой равен 1 деление- 1метр.
Точка А с координатой А (+3) — момент удара мяча о стенку.
Точка В с координатой В (0) — совпадает с точкой отсчета.
Можно ли утверждать, что мяч не преодолевал никакого расстояния, оставаясь в исходной точке в состоянии покоя, ведь в конечном счете мяч оказался в точке 0 м (от точки ноль до начала отсчета О не помещается ни одного единичного отрезка)? Конечно же, нет!
Путь мяча был бы равен нулю, если бы его вообще никуда не пинали, и он оставался в состоянии покоя в точке О.
Но мы должны понимать, что путь (расстояние), которое преодолел мяч, состоит из 3 единичных отрезков в правую сторону и 3 единичных отрезков в левую сторону; сложив все единичные отрезки, получим:
3 единичных отрезка + 3 единичных отрезка = 6 единичных отрезков
6 единичных отрезков = 6 м
Для определения пути мы складывали только числовое значение без учета направления. Это числовое значение и есть модуль числа.
Таким образом, можно сказать, что любое число состоит из знака и абсолютного значения (модуля).
Поэтому, чтобы найти модуль числа, нужно записать это число без учета знака.
Эта информация доступна зарегистрированным пользователям
3. Модули противоположных чисел равны
Рассмотрим на примере данное утверждение:
Пусть модуль х равен 4, получим равенство |x| = 4
Отметим на координатной прямой точки, которые удовлетворяют этому равенству:
Эта информация доступна зарегистрированным пользователям
Точка О — начало отсчета координатной прямой х.
Модул ь- это расстояние от начала отсчета до точки в единичных отрезках, равное в данном случае четырем.
Откладываем 4 единичных отрезка вправо, получаем точку с координатой 4
Но такое же количество единичных отрезков можно отложить влево, тогда получим точку с координатой (-4)
Получим на координатной прямой две точки, которые удовлетворяют условию |x| = 4
В данном примере значение х может быть равным:
х = 4
х = —4
Числа 4 и —4 отличаются только знаками, поэтому смело можем сказать, что это противоположные числа.
На координатной прямой противоположные числа, хоть и по разные стороны от точки начала отсчета, но находятся на равных расстояниях от этой точки, т.е. по модулю равны.
4. Модуль произведения двух чисел равен произведению модулей этих чисел
В буквенном выражении это можно записать так:
(mathbf{|a cdot b| = |a| cdot |b|})
Пример: (mathbf{|5 cdot 6| = |5| cdot |6| = 5 cdot 6 = 30})
5. Квадрат модуля числа равен квадрату этого числа
(mathbf{|a|^2 = a^2 })
Пример:
(mathbf{|10|^2 = 10^2 = 100 })
(mathbf{|-2|^2 = 2^2 = 4})
6. Модуль частного двух чисел равен частному их модулей
(mathbf{Bigl| frac{x}{y}Bigr| = frac{|x|}{|y|} , y neq 0})(так как на нуль делить нельзя).
Пример:
(mathbf{Bigl| frac{8}{2}Bigr| = frac{|8|}{|2|}= frac{8}{2} = 4 })
(mathbf{Bigl| -frac{8}{2}Bigr| = frac{|-8|}{|2|}= frac{8}{2} = 4 })
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров таких задач.
Задача 1
Запишите все числа, имеющие модуль 142.
Решение:
Представим координатную прямую с началом отсчета в точке О
Эта информация доступна зарегистрированным пользователям
Нам известно, что модуль числа — это расстояние (количество единичных отрезков) от нуля до какой-либо точки.
142 единичных отрезка мы можем отложить на координатной прямой вправо и получим точку с координатой 142.
Также 142 единичных отрезка мы можем отложить влево от нуля, в этом случае получаем точку с координатой 142.
На координатной прямой находятся два числа, которые имеют модуль 142, а расстояние до этих точек содержат по 142 единичных отрезка.
|142| = 142
|-142| = 142
Ответ: числа 142 и —142 имеют модуль 142
Задача 2
Расположите числа —15; —1; 4; 7 в порядке возрастания модулей.
Решение:
Надо понимать, что в порядке возрастания будем располагать не сами числа —15; —1; 4; 7, а их модули.
Для этого найдем модули каждого из них:
|-15| = 15
|-1| = 1
|4| = 4
|7| = 7
Модули чисел получились: 15, 1, 4, 7
Расположим эти числа в порядке возрастания (от самого маленького к самому большому):
1, 4, 7, 15.
Получаем такую последовательность равенств,
|-1| = 1
|4| = 4
|7| = 7
|-15| = 15
Следовательно, числа в порядке возрастания их модулей должны располагаться так: -1, 4, 7, -15
Ответ: —1, 4, 7, —15
Задача 3
На координатной прямой отметили две точки -73 и 68. Модуль какого числа больше?
Решение:
Представим, что на координатной прямой на определенном расстоянии от точки О (налала отсчета) отмечены две точки.
Слева от точки начала отсчета расположена точка с координатой -73
Справа от точки начала отсчета расположена точка с координатой 68
Нам известно, что модуль — это расстояние от заданной точки до точки начала отсчета, выраженное в единичных отрезках.
Эта информация доступна зарегистрированным пользователям
Расстояние от точки О до точки с координатой -73 содержит больше единичных отрезков, чем расстояние от точки О до точки с координатой 68 (т.е. координата точки -73 находится дальше от начала координат, чем точка с координатой 68).
Значит, модуль числа -73 больше модуля числа 68
|-73| = 73
|68| = 68
73 > 68, а это значит:
|-73| > |68|
Ответ: |-73| > |68|
Задача 4
На координатной прямой точка А отмечена левее точки начала отсчета на 2 единицы и точка В — правее от точки начала отсчета на 6 единиц.
Чему равны координаты этих точек?
Чему равен модуль каждой координаты?
Решение:
Построим координатную прямую, за начала отсчета примем точку О
Единичный отрезок равен 1 деление- 1 единица.
На координатной прямой отметим точки А и В
Эта информация доступна зарегистрированным пользователям
Точка А имеет координату A (-2), так как она отодвинута влево от точки О на расстояние в два единичных отрезка.
Точка В имеет координату В (6), так как она отодвинута вправо от точки О на расстояние в шесть единичных отрезков.
Получили точки с координатами A (-2) и В (6)
Модуль-это расстояние в единичных отрезках от заданной точки до начала отсчета.
Таким образом:
Модуль —2 равен 2
|-2| = 2
Модуль 6 равен 6
|6| = 6
Ответ: Модули координат точек A (-2) и В (6) равны 2 и 6 соответственно.
Наверное, вы уже заметили, что значение координат может быть положительным и отрицательным, а модули только положительными.
Эта информация доступна зарегистрированным пользователям
Содержание материала
- Что такое модуль?
- Видео
- Решение более сложных примеров
- Основные свойства модуля
- Модуль числа
- Свойства модуля числа
- Уравнения и неравенства с модулем
- Уравнения
- Неравенства
- Расстояние между точками
- Свойства абсолютной величины
- Тест для закрепления материала
Что такое модуль?
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3
| 3 |= 3
|−3|= 3
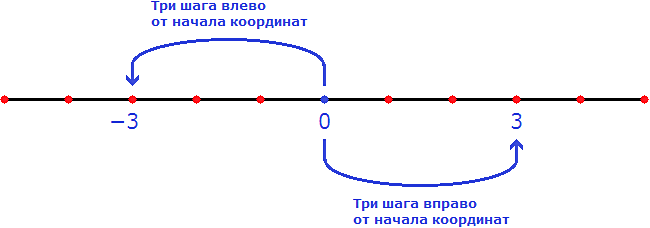
Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:
Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:
|x1 − x2|
Где x1 и x2 — числа на координатной прямой.
Например, отметим на координатной прямой числа 2 и 5.
Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:
|2 − 5| = |−3| = 3
Видим, что расстояние от числа 2 до числа 5 равно трём шагам:
Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3
То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:
|5 − 2| = | 3 | = 3
Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:
|x1 − x2| = |x2 − x1|
Это равенство можно прочитать так: Расстояние от x1 до x2 равно расстоянию от x2 до x1.
Видео
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
Модуль числа
Сформулируем на строгом языке математики наше интуитивное представление о «величине» числа, которое мы сформировали в предыдущем разделе.
О
Модуль или абсолютная величина вещественного числа x — само число x , если оно неотрицательно, иначе − x .
∣ x ∣ = { − x , если x ≥ − x , если x <
Допустим, мы хотим найти модуль какого-то числа a. Согласно определению, нам надо провести элементарную проверку. Если число a положительное или равно , то модулем a и является само a. Если же a меньше , то результатом модуля будет −a.
П
Примеры значений модуля
∣ 5 ∣ = 5 ∣ ∣ = ∣ − 1 2 ∣ = − ( − 1 2 ) = 1 2
Легко убедиться, что модуль числа полностью соответсвует по смыслу «величине» числа, рассмотренной в предыдущем разделе. Там мы утверждали, что по «величине» −1 больше 5, а −1 равно 1. И действительно:
∣−1∣=1∣−1∣=1∣5∣=5∣−1∣>∣5∣∣1∣=1∣−1∣=∣1∣
Т
Эквивалентное определение модуляПоложение знака нестрогого неравенства в определении модуля не имеет значения:
∣ x ∣ = { − x , если x ≥ − x , если x < = { − x , если x > − x , если x ≤ ДоказательствоОбозначим второе определение модуля числа x как ∣ x ∣ ′ . Покажем, что какой x не возьми, будет выполняться ∣ x ∣ = ∣ x ∣ ′ .
Пусть x > . По классическому определению ∣ x ∣ = x . По второму: ∣ x ∣ ′ = x . То есть ∣ x ∣ = ∣ x ∣ ′ .
Пусть x = . По классическому определению ∣ ∣ = . А вот во втором определении попадает уже под второе условие, то есть ∣ ∣ ′ = − = . Опять имеем ∣ ∣ = ∣ ∣ ′ .
Наконец, пусть x < . По классическому определению ∣ x ∣ = − x . У второго определения та же ситуация: ∣ x ∣ ′ = − x . Получается, что и в этом случае ∣ x ∣ = ∣ x ∣ ′ .
Итак, мы рассмотрели все возможные значения для x и во всех случаях ∣ x ∣ = ∣ x ∣ ′ . Это и означает, что между двумя определениями нет никакой разницы ■
Такое определение иногда бывает полезно. Например, если x лежит в следующих пределах: −1≤x≤, то можно сразу сказать, что ∣x∣=−x, даже несмотря на то, что для x= так выражаться будет некорректно, ведь ∣∣=, а не −.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
- |a| > 0
2. Модуль положительного числа равен самому числу.
- |a| = a, если a > 0
3. Модуль отрицательного числа равен противоположному числу.
- |−a| = a
4. Модуль нуля равен нулю.
- |0| = 0, если a = 0
5. Противоположные числа имеют равные модули.
- |−a| = |a| = a
6. Модуль произведения равен произведению модулей этих чисел.
- |a b| = |a| |b|, когда
a · b = 0
или
−(a · b), когда a · b < 0
7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:
Уравнения и неравенства с модулем
Перед тем, как перейти к этой части, повторите, как решаются обычные уравнения и неравенства с одной переменной.
Уравнения
Приступая к задачам с ( left|Mright| ), нужно все время помнить, что внутри знака может скрываться как положительное выражение, так и отрицательное.( left|3-xright|=5;Rightarrow;3-x=5;или;3-x=-5. ) Поэтому решить нужно оба варианта уравнения: x = 3 — 5 x = 3 — (- 5) x = — 2 x = 8Корни уравнения: — 2 и 8.Или посложнее: ( left|6-5xright|=2x+1 )Сразу напомним себе, что ( 2x+1geq0 ), следовательно, ( 2xgeq-1,;и;xgeq-frac12 ).Теперь два варианта для положительного и отрицательного выражения под знаком ( left|Mright| ):6 — 5x = 2x + 1 или 6 — 5x = — 2x — 1 7x = 5 3x = 7x = ( х=frac57 ) x = ( х=frac73 ) x = ( х=2frac13 )Все условия соблюдены, уравнение имеет два корня: ( frac57 ) и ( 2frac13 ).
Неравенства
Здесь тоже приходится учитывать двойственную природу ( left|Mright| ). Если в уравнениях мы обозначаем условие ( left|xright|=a;и;left|xright|=-a ), то в неравенствах помещаем содержимое модуля “меж двух огней” таким образом (табл. 1):
Таблица 1. Неравенства

Расстояние между точками
Представим числовую ось. Отметим на ней две точки, например 5 и 3. Какое между ними расстояние? Ничего сложного, скажете вы, расстояние равно 5−3=2. И это правильный ответ. Сразу заметим, что 3−5=(−1)(5−3)=−2, то есть при вычитании из меньшей точки большей получаем то же расстояние, но со знаком минус.
Расстояние между точками −2 и −4 равно −2−(−4)=2. И опять, если мы поменяем местами числа в разности, то получим отрицательное расстояние −4−(−2)=(−1)(−2−(−4))=−2
Общий посыл вы уловили. Для нахождения расстояния между двумя точками, надо из большей точки вычесть меньшую. Если сделать наоборот, то получим противоположное, отрицательное расстояние.
Вроде все ясно. Ну и причем здесь модуль? А вот представим, что у вас нет точных значений. Вам просто дали точки a и b, и попросили найти расстояние между ними. Какая-то из двух разностей ниже будет расстоянием:
a−bb−a
Но какая именно? Тут к нам и приходит на помощь модуль. Расстояние между a и b обозначим так:
∣a−b∣
Если a>b, то мы угадали с разностью и получим положительный результат. Взятие модуля никак на него не повлияет. Если a<b, то мы не угадали и получаем отрицательное расстояние. Но, по определению модуля, в результате все-равно получим положительное расстояние.
О
Расстоянием между двумя точками a и b на числовой оси называется модуль их разности: ∣ a − b ∣ .
Наконец, поговорим о модулях одного числа, например ∣5∣ или ∣−2∣. Их можно представить вот так:
∣5∣=∣5−∣∣−2∣=∣−2−∣
В этом смысле модуль одного числа можно понимать как расстояние от до этого числа (до 5 и до −2) на числовой оси.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
- Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
- Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
- Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
- Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
- Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
- Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
- Такое же правило распространяется и на показатель степени выражения.
Это интересно: что такое разность в математике?
Тест для закрепления материала
- 1 Модуль числа не может быть:
- Положительным
- Отрицательным
- Равным нулю
Вопрос 1 из 10
- 2 Модуль отрицательного числа равен:
- Самому числу
- Нулю
- Противоположному числу
Вопрос 2 из 10
- 3 Чему равен модуль числа — 3,82?
- 3,82
- — 3,82
Вопрос 3 из 10
- 4 Найдите расстояние (в единичных отрезках) от начала координат до точки А (7,8):
- 7,8
- — 7,8
Вопрос 4 из 10
- 5 Чему равен модуль точки, лежащей от начала отсчета влево на 3,3 единицы?
- 6,6
- — 3,3
- 3,3
Вопрос 5 из 10
- 6 Найди отрицательное число, модуль которого равен 25:
- — 50
- — 25
- 25
Вопрос 6 из 10
- 7 Выберите все числа, имеющие модуль 45:
- 45; — 45; 0
- — 45; 0; 45
- 45; — 45
Вопрос 7 из 10
- 8 Модуль какого из чисел расположен на координатной прямой правее 567 или — 765?
- 567
- — 765
- Никакого
Вопрос 8 из 10
- 9 Модуль какого из чисел 354 или — 289 больше:
- 354
- Равны
- — 289
Вопрос 9 из 10
- 10 Найдите значение выражения: |- 240| — |90|:
- — 330
- 150
- 330
Вопрос 10 из 10
Пройти тест заново
Теги
Ниже представлены основные свойства модуля действительного числа (т.е. положительного, отрицательного и нуля).
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
- Свойство 8
Свойство 1
Модуль числа представляет собой расстояние, которое не может быть отрицательным. Следовательно, и модуль не может быть меньше нуля.
|a| ≥ 0
Свойство 2
Модуль положительного числа равняется этому же числу.
|a| = a, при a > 0
Свойство 3
Модуль отрицательного числа равняется этому же числу, но с противоположным знаком.
|-a| = a, при a < 0
Свойство 4
Модуль числа ноль равняется нулю.
|a| = 0, при a = 0
Свойство 5
Модули противоположных чисел равны между собой.
|-a| = |a| = a
Свойство 6
Модуль числа a – это квадратный корень из a2.
Свойство 7
Модуль произведения равняется произведению модулей чисел.
|ab| = |a| ⋅ |b|
Свойство 8
Модуль частного равняется делению одного модуля на другой.
|a : b| = |a| : |b|
Тригонометрическая форма записи комплексного числа
Также, в зависимости от решаемой задачи, вы можете перевести комплексное число в алгебраическую или показательную форму.
Геометрическое представление комплексного числа
Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу можно сопоставить точку на этой плоскости с соответствующими координатами
, и радиус-вектор
комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу (рис. 1). Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.
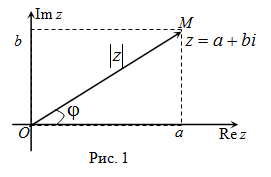
Модуль и аргумент комплексного числа
Если является действительным числом, то его модуль
равен абсолютной величине этого действительного числа.
Например.
Свойства модуля
в том и только том случае, если
, т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.
Свойства аргумента
- Для комплексного числа
аргумент определяется с точностью до
.
Длязначение аргумента не определено.
- Главным значением аргумента называется число
. Для обратного числа выполняется свойство:
.
Действия над комплексными числами в тригонометрической форме
Сравнение
Два комплексных числа и
называются равными, если
Умножение
Для произведения комплексных чисел в тригонометрической форме верно равенство:
Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.
Деление
Частное комплексных чисел в тригонометрической форме выполняется по формуле:
Возведение в степень
Для возведения в степень комплексных чисел в тригонометрической форме верна формула:
Подробнее про возведение в степень читайте в отдельной статье: Возведение в степень комплексного числа.
| Понравился сайт? Расскажи друзьям! | |






 Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.