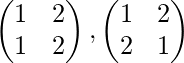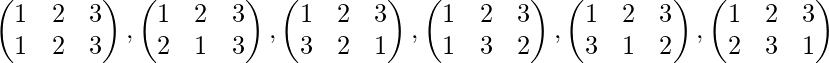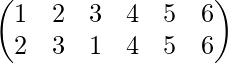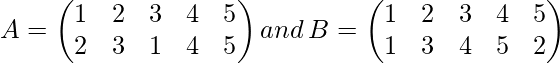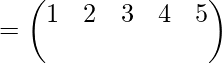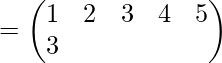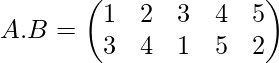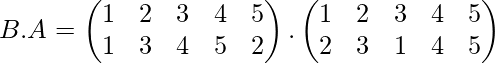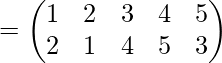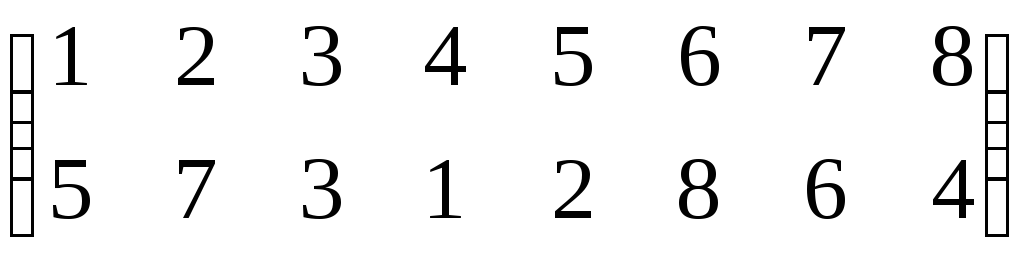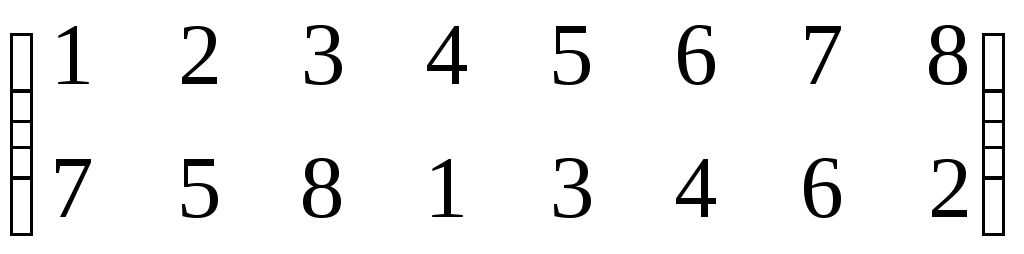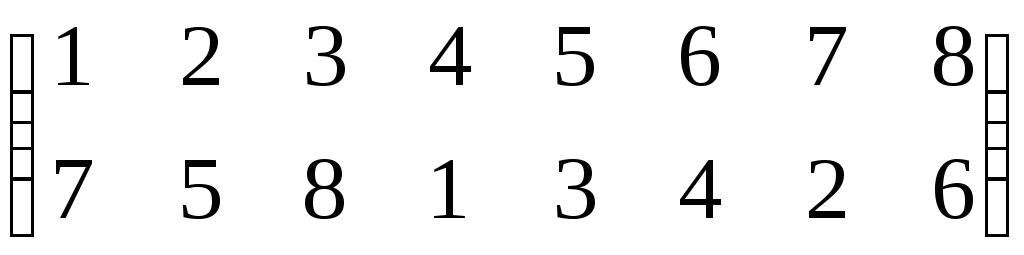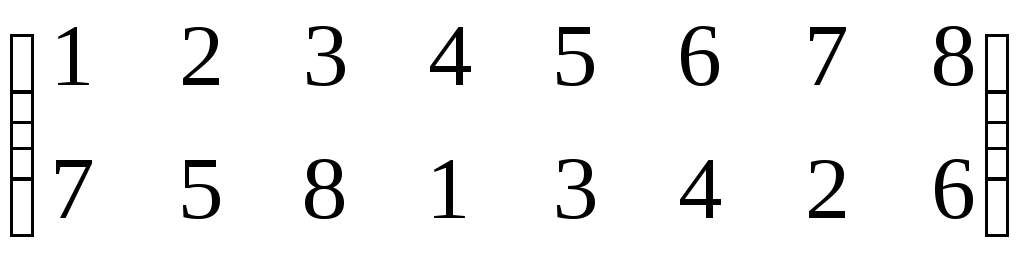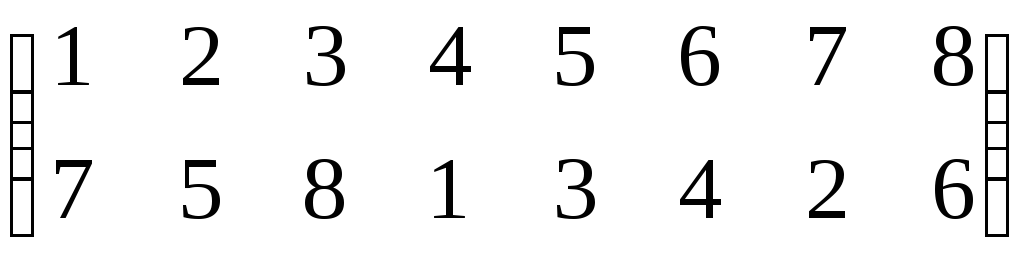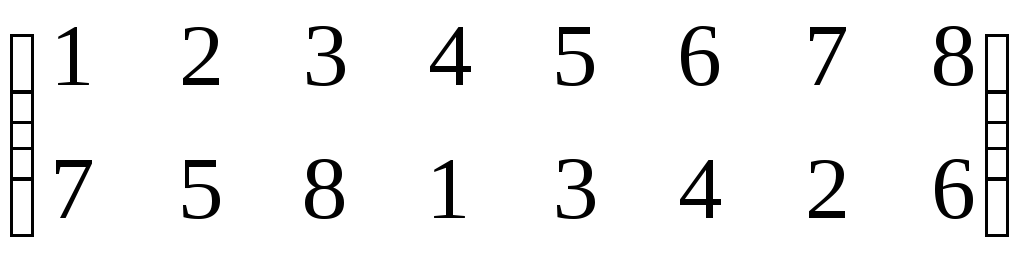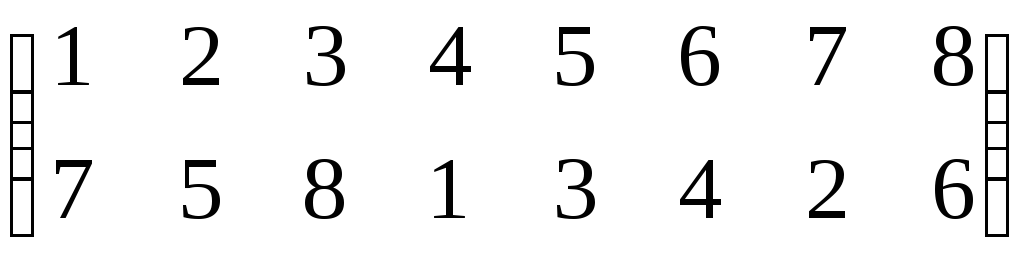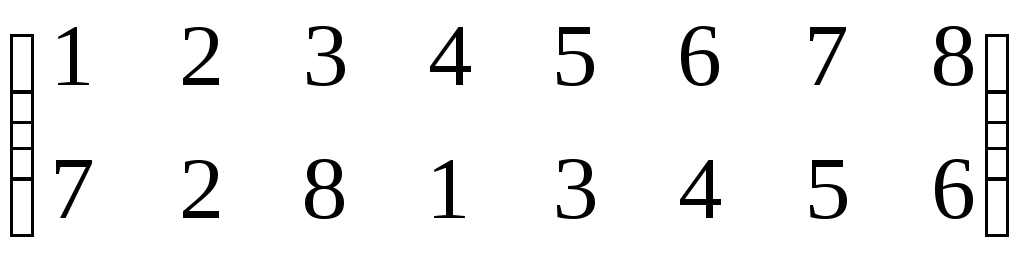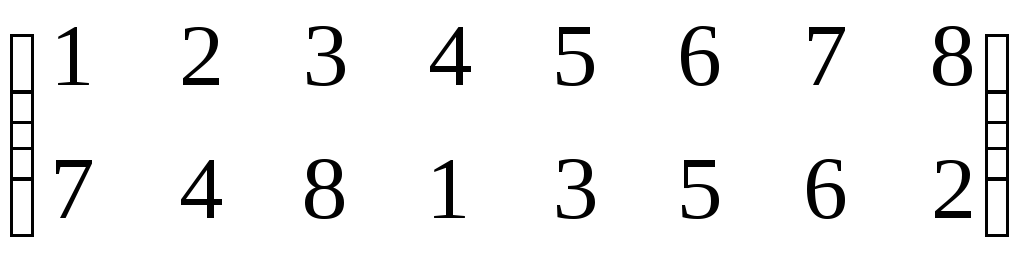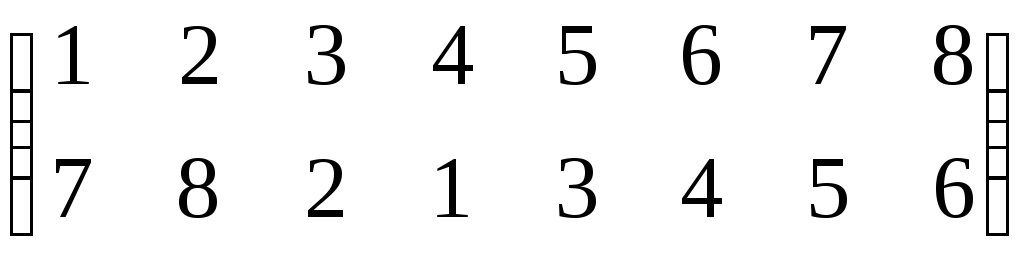Как найти произведение перестановок

Содержание

1 Умножение перестановок
- 1.1 Пример
2 Обратная перестановка
- 2.1 Получение обратной перестановки
3 Группа перестановок
4 Группа чётных перестановок
5 Группа подстановок
6 См. также
7 Источники информации

Умножение перестановок

Определение:

Умножением (англ. multiplication) или композицией (англ. composition) перестановок, представленных в виде целочисленных функций , где позиция элемента, а — его номер, называется перестановка, получаемая по следующему правилу:

Утверждение:

Умножение перестановок ассоциативно:

Доказывается простым раскрытием скобок.

Перед прочтением примера перемножения перестановок рекомендуем познакомиться с циклами в данной статье: Действие перестановки на набор из элементов, представление в виде циклов

Пример

или

Обратная перестановка

Определение:

Обратной перестановкой (англ. inverse permutation) к перестановке называется такая перестановка, что:

Утверждение:

Для каждой перестановки существует перестановка, обратная ей.

Пусть дана перестановка , построим обратную ей перестановку : если , то . Очевидно, что данная перестановка является обратной к .

Также обратная перестановка единственна. Это следует из того, что для каждой -ой позиций в исходной перестановке однозначно определяется -ая позиций в обратной перестановке, значение которой есть

Определение:

Перестановка, равная своей обратной, называется инволюцией (англ. involution):
, то есть её представление в виде циклов не содержит цикла, размер которого больше двух.

Утверждение:

Количество инволюционных перестановок длины может быть получено по формуле: , где

Докажем формулу по индукции. Базой являются . Предположим, что для всех , где , , формула верна. Рассмотрим перестановку длины и попробуем найти количество инволюций этой длины. Существует инволюций, при (у которых последний элемент представляет собой цикл длины ), а число инволюций длины , содержащих в своём представлении в виде циклов цикл , где , (так как при фиксированных и имеем перестановок оставшихся элементов, которые не нарушают свойств инволюции). Таким образом,

Определение:

Перестановка, содержащая чётное количество инверсий, называется чётной (англ. even permutation), в противном случае нечётной (англ. odd permutation).

Определение:

Перестановка, меняющая местами только два элемента, называется транспозицией (англ. transposition).

Лемма:

Если в перестановке, длина которой больше , поменять местами элемента, то её четность изменится.

Доказательство:

Для элементов, стоящих рядом, истинность утверждения очевидна: их взаимное расположение относительно других элементов не изменилось, а транспозиция этих чисел изменяет количество инверсий на единицу. Пусть теперь между перемещаемыми элементами и находятся элементов, то есть перестановка имеет вид: , . Сначала поменяем последовательно с числами , а затем число с рядом стоящими . В итоге мы выполним транспозиций рядом стоящих элементов, то есть чётность перестановки изменится.

Получение обратной перестановки

Пусть в массиве содержится перестановка, длины , тогда после выполнения алгоритма в массиве будет содержаться перестановка, обратная ей.

fun reversePerm(p : int[], rep : int[])
  for i = 1 to n
      rep[p[i]] = i;

Группа перестановок

Определение:

Группой (англ. group) называется множество с заданной на нём бинарной операцией , удовлетворяющей следующим свойствам:

— ассоциативность соответствующей бинарной операции.
Существование нейтрального элемента относительно операции , такого, что для любого
Для любого существует называемый обратным элементом, такой, что

Утверждение:

Множество перестановок с элементами с операцией умножения является группой (часто группу перестановок называют симметрической (англ. symmetric group), и обозначают ).

Свойства и (ассоциативность умножения и существование обратной перестановки для любой из перестановок) доказаны выше, а в качестве нейтрального элемента выступает тождественная перестановка ().

Мощность симметрической группы:

Теорема Кэли утверждает, что любая конечная группа изоморфна подгруппе некоторой группе перестановок.

Группа чётных перестановок

Определение:

Группа чётных перестановок (англ. alternating group) является подгруппой симметричной группы перестановок, образованной всеми чётными перестановками. Композиция не выводит из группы, так как если представить каждую перестановку группы в виде чётного числа транспозиций и перемножить их, чётность не изменится.

Утверждение:

Количество чётных перестановок длины равно количеству нечётных и равно

Пусть число число чётных перестановок , а нечётных . Сделаем транспозицию для всех чётных перестановок. Получим нечётных различных перестановок, то есть . Проделаем то же самое с нечётными перестановками. Получим, что , то есть и .

Группа подстановок

Определение:

Подстановкой (англ. substitution) называется всякое взаимно однозначное отображение множества первых натуральных чисел на себя.

Всякая подстановка может быть записана при помощи двух перестановок, подписанных одна под другой:

Где через обозначается то число, в которое при подстановке переходит число .

Определение:

Группой подстановок (англ. group of substitutions) называется некоторая совокупность подстановок, замкнутая относительно композиции отображений, определяющей бинарную операцию для подстановок на одном и том же множестве.

См. также

Теорема Кэли
Действие перестановки на набор из элементов, представление в виде циклов

Источники информации

Wikipedia — Involution

Источник

11:18

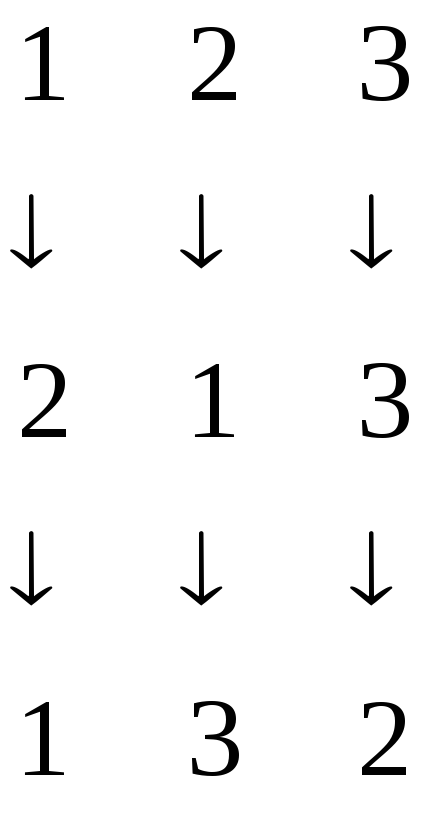
Произведение перестановок

Перестановка порядка n это биективное отображение конечного множества из n элементов в себя.

Таблица вида

$$begin{pmatrix} 1 & 2& 3& 4\ 2 & 4&1&3 end{pmatrix}$$, что означает перестановку $$1mapsto 2,2mapsto 4,3mapsto 1,4mapsto 3$$

Также можно для удобства переставлять столбцы местами:

$$begin{pmatrix} 1 & 2& 3& 4\ 2 & 4&1&3 end{pmatrix} =begin{pmatrix} 2 & 1& 3& 4\ 4 & 2&1&3 end{pmatrix}=begin{pmatrix} 4 & 3& 2& 1\ 3 & 1&4&2 end{pmatrix}$$

Для наглядности, ту же перестановку можно изобразить картинкой вида

Пример вычисления произведения перестановок: если

При помощи обычного определения удобно вычислять произведение так: в перестановке σ переставляем столбцы так, что первая строчка в σ совпадает с последней строчкой в τ . Тогда произведением будет перестановка, у которой первая строчка — стандартная, а вторая строчка — это вторая строчка из σ.

Пример 1:

Пример 2. Найти произведение перестановок можно и так

Первая перестановка переводит один в два, а вторая два в семь, значит произведение переводит один в семь и т.д.

Перестановки удобно перемножать и в том случае, когда они представлены в виде произведения непересекающихся циклов.

Например: στ= (1,2,4,3) · (1,3) = (2,4,3)

При этом произведение получается так: для каждого элемента от 1 до 4 надо пройти по циклам в левой части и проследить куда он переходит.

В частности, 3 сначала переходит в 1 (цикл (1 , 3)),

а затем 1 в 2 (цикл(1 , 2 , 4 , 3)).
Значит в произведении 3 будет переходить в 2.

Умножение перестановок некоммутативно: τσ ≠ στ.

Следовательно решение уравнений вида: τx = σ, xτ = σ

x = τ^-1σ, x = στ^-1

Категория: Комбинаторика | Просмотров: 13953 | | Теги: перестановки | Рейтинг: 3.5/2

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Let G be a non-empty set, then a one-one onto mapping to itself that is as shown below is called a permutation.

The number of elements in finite set G is called the degree of Permutation.
Let G have n elements then P_n is called a set of all permutations of degree n.
P_nis also called the Symmetric group of degree n.
P_n is also denoted by S_n.
The number of elements in P_n or S_ⁿ is

Examples:

Case1: Let G={ 1 } element then permutation are S_n or P_n = $begin{pmatrix} 1 \ 1 end{pmatrix}$

Case 2: Let G= { 1, 2 } elements then permutations are $begin{pmatrix} 1 & 2\ 1 &2 end{pmatrix} , begin{pmatrix} 1 & 2\ 2 &1 end{pmatrix}$

Case 3: Let G={ 1, 2, 3 } elements then permutation are 3!=6. These are,

$begin{pmatrix} 1 & 2 & 3\ 1 & 2 & 3 end{pmatrix} , begin{pmatrix} 1 & 2 & 3\ 2& 1& 3 end{pmatrix} , begin{pmatrix} 1 & 2 & 3\ 3 & 2 & 1 end{pmatrix} , begin{pmatrix} 1 & 2 & 3\ 1 & 3 & 2 end{pmatrix} , begin{pmatrix} 1 & 2 & 3\ 3 & 1 & 2 end{pmatrix} , begin{pmatrix} 1 & 2 & 3\ 2 & 3 & 1 end{pmatrix}$

Reading the Symbol of Permutation

Suppose that a permutation is $begin{pmatrix} 1 & 2 & 3 &4 &5&6\ 2&3&1&4&5&6 end{pmatrix}$

First, we see that in a small bracket there are two rows written, these two rows have numbers. The smallest number is 1 and the largest number is 6.
Starting from the left side of the first row we read as an image of 1 is 2, an image of 1 is 2, an image of 2 is 3, an image of 3 is 1, an image of 4 is 4 (Self image=identical=identity), an image of 5 is 6 and image of 6 is 5.
The above thing can be also read as: Starting from the left side of the first row 1 goes to 2, 2goes to 3, 3goes to,4 goes to 4,5 goes to 6, and 6 goes to 5.

A cycle of length 2 is called a permutation.

Example:

1) $begin{pmatrix} 4 & 5\ end{pmatrix}$

Length is 2, so it is a transposition.

2) $begin{pmatrix} 1 & 2 & 3\ end{pmatrix}$

Length is three, so it is not a transposition.

Multiplication of Permutation

Problem: If $A= begin{pmatrix} 1 & 2 & 3&4&5\ 2&3&1&4&5 end{pmatrix} and ,B= begin{pmatrix} 1 & 2 & 3 &4&5\ 1&3&4&5&2 end{pmatrix}$

Find the product of permutation A.B and B.A

Solution: $A= begin{pmatrix} 1 & 2 & 3&4&5\ 2&3&1&4&5 end{pmatrix} and ,B= begin{pmatrix} 1 & 2 & 3 &4&5\ 1&3&4&5&2 end{pmatrix}$

$A.B= begin{pmatrix} 1 & 2 & 3&4&5\ 2&3&1&4&5 end{pmatrix} . begin{pmatrix} 1 & 2 & 3 &4&5\ 1&3&4&5&2 end{pmatrix}$

$= begin{pmatrix} 1 & 2 & 3&4&5\ &&&& end{pmatrix}$

Here we can see that in first bracket 1 goes to 2 i.e. image of 1 is 2, and in second row 2 goes to 3 i.e. image of 2 is 3.

Hence, we will write 3 under 1 in the bracket shown below,

$= begin{pmatrix} 1 & 2 & 3&4&5\ 3&&&& end{pmatrix}$

Do above step with all elements of first row, answer will be

$A.B= begin{pmatrix} 1 & 2 & 3&4&5\ 3&4&1&5&2 end{pmatrix}$

Similarly,

$B.A= begin{pmatrix} 1 & 2 & 3&4&5\ 1&3&4&5&2 end{pmatrix} . begin{pmatrix} 1 & 2 & 3 &4&5\ 2&3&1&4&5 end{pmatrix}$

$= begin{pmatrix} 1 & 2 & 3&4&5\ 2&1&4&5&3 end{pmatrix}$

Last Updated :
18 May, 2022

Like Article

Save Article

Источник

Цель
работы

Целью
лабораторной работы является изучение
основных свойств перестановок, понятия
мощности множества, знакомство с понятием
нумерующей биекции.

Краткие
теоретические положения

Множество
натуральных чисел от 1 до
или множествоназывается начальным отрезкомнатурального ряда и обозначается.
Биективное отображениеназываетсяn_перестановкой
и задается таблицей вида
,
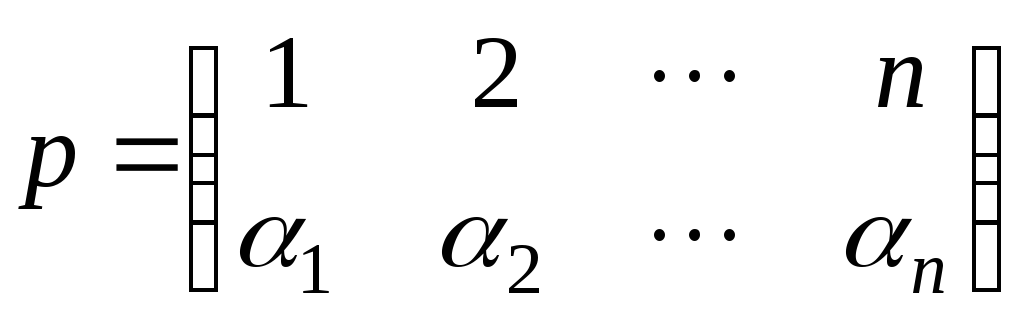
где.
Множество—
перестановок обозначается.
Таким образом,.
Произведениемдвух биекцийназывается биекциятакая, что

Таким
образом, произведение двух перестановок
– это перестановка, которая получается,
если сначала выполнить первую из
перемножаемых перестановок, а затем
вторую. Таким образом, имеем
,
то есть произведение перестановок, это
джойн перестановок как отображений.

Пример 2.1.
Найти произведение
и произведениеперестановок,
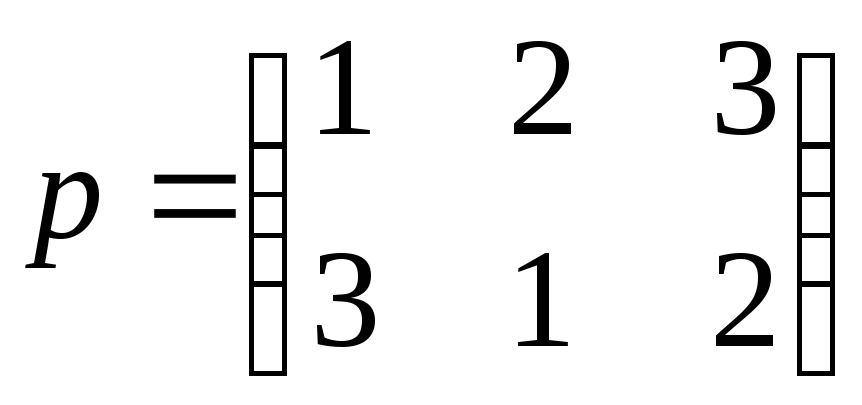
и.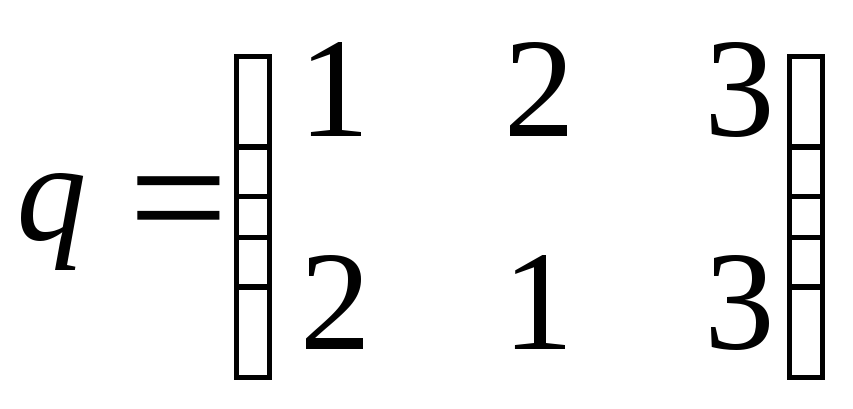

Решение.
Найдем
.
Процесс вычисления реализуем в виде
диаграммы:

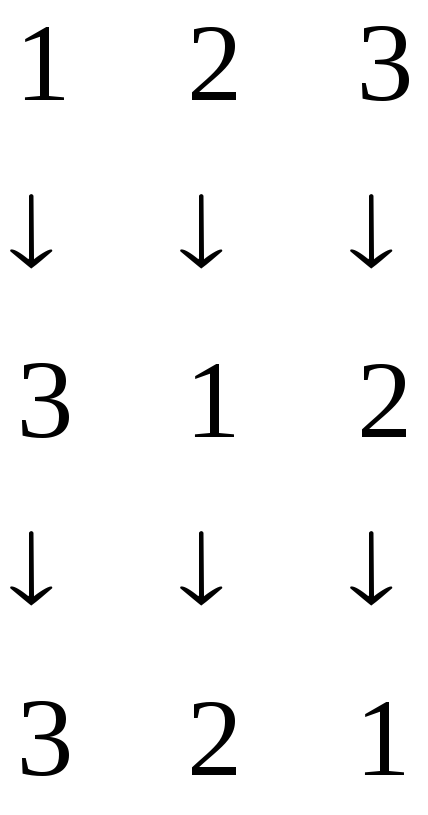
Таким
образом, получили перестановку
.

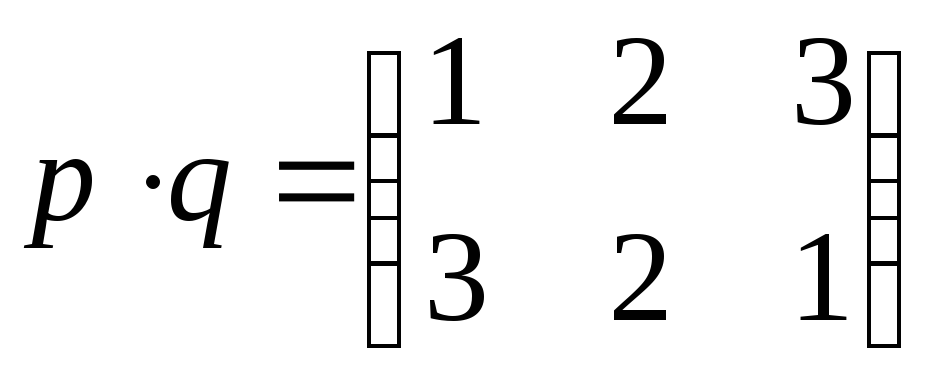
Аналогичным
образом находим
:

Получили:
.

Решение
задачи закончено.

Замечание.
Из данного примера видно, что, вообще
говоря,
,
то есть операция умножения перестановок
не является коммутативной.

Единичной
перестановкой
называется перестановка вида,
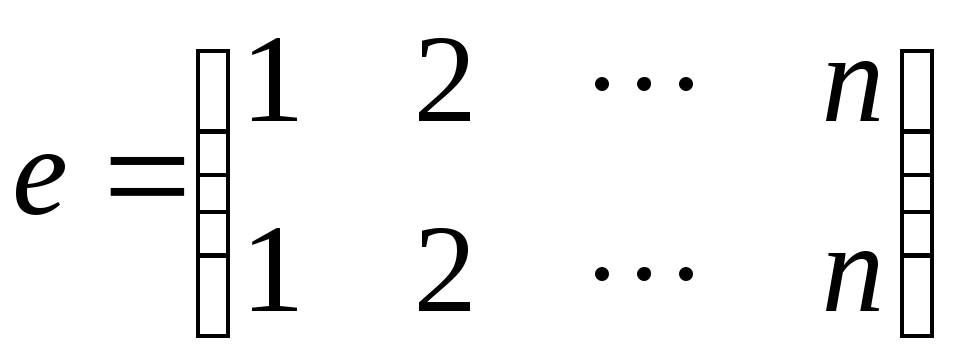
то есть эта перестановка удовлетворяет
соотношению.
Единичная перестановка обладает
свойством:.
то есть единичная перестановка играет
роль единицы при умножении перестановок.

Обратной
перестановкой

по отношению к перестановкеназывается однозначно определенная
перестановкатакая, что.

Пример 2.2.
Дана перестановка
.
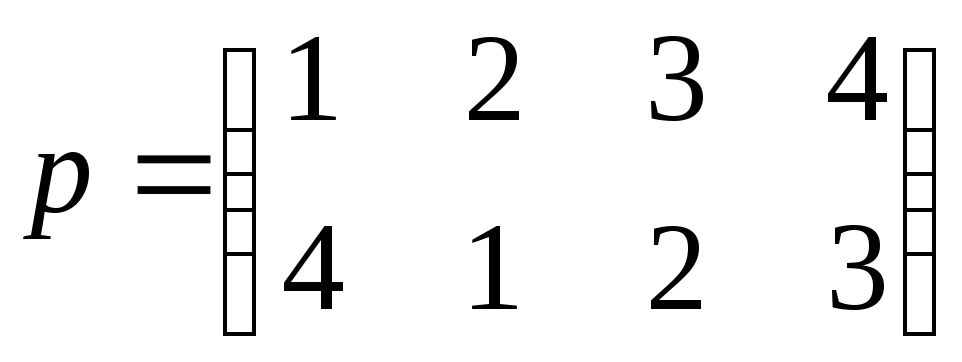
Найти обратную перестановку.

Решение.
Для нахождения обратной перестановки
достаточно поменять местами строки ее
таблицы:

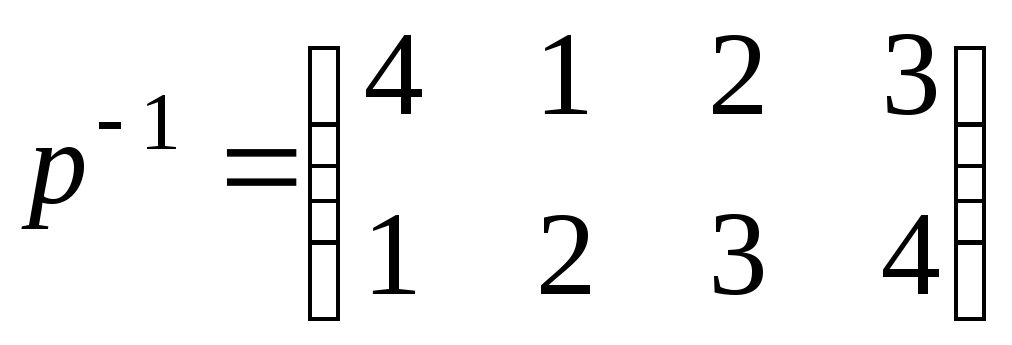
Данный
ответ является верным. Но его целесообразно
привести к каноническому виду (то есть
однозначно определенному) путем
перестановки столбцов полученного
ответа таким образом, чтобы в верхней
строке получилась стандартная
последовательность
.
Окончательный ответ имеет вид:

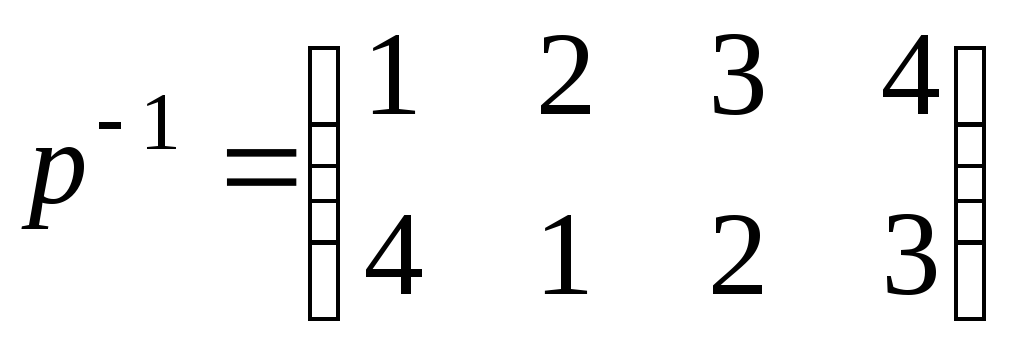
Перестановка
называется циклической
или
циклом длины
,
если при ее действии часть элементовмножестваостаются неподвижными, то есть,
а остальные элементы этого множествапереставляются по циклу в соответствии
с диаграммой

и
выполняется соотношение
.

Такая
перестановка записывается в виде
.

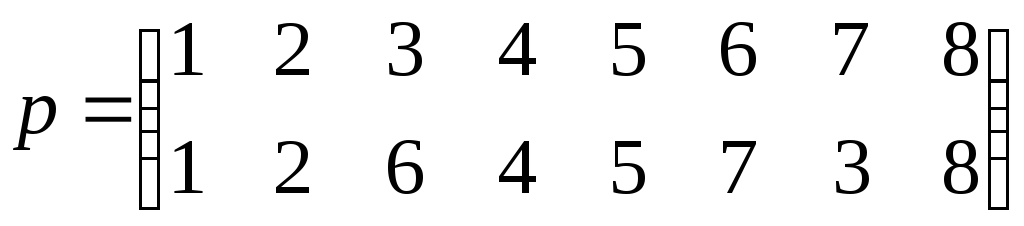
Пример 2.3.
Дан цикл
.
Записать эту перестановку в стандартном
виде.

Решение.
Элементы множества
остаются неподвижными при действии
данной перестановки, а элементы множествапереставляются по схеме:. Получаем перестановку

Всякая
перестановка, может быть представлена
в виде произведения непересекающихся,
то есть не имеющих общих элементов
циклов. Непересекающиеся циклы
коммутируют, то есть перестановочны,
поэтому порядок записи циклов в таком
разложении не существенен.

Пример 2.4. Перестановку 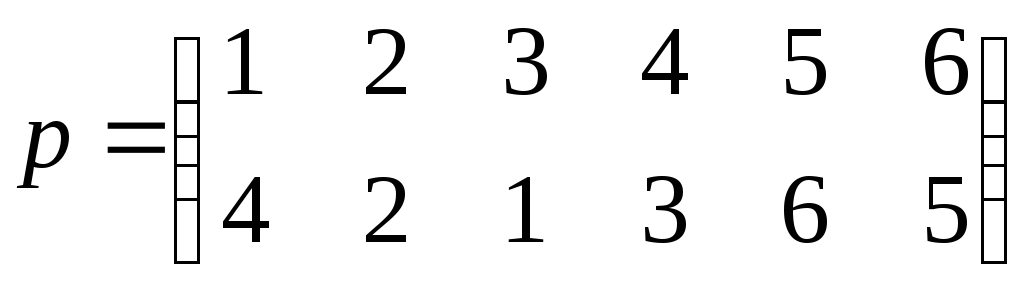представить в виде произведения циклов.

Решение.
Представим
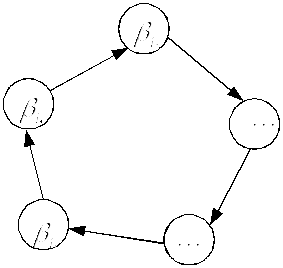
перестановку в виде ориентированного
графа на множестве вершин
.
Расположение вершин графа произвольно,
выбираем расположение по кругу. Образы
элементов изображаем ориентированными
ребрами. Получаем граф:

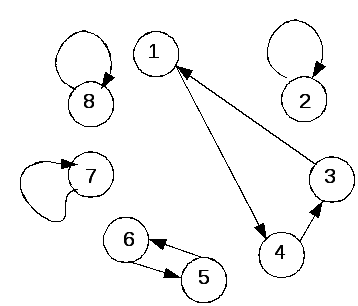
Из
визуального анализа данного графа
получаем, что в графе имеется ориентированный
цикл длины 3, орцикл длины 2 и 3
элементарных цикла-петли длины 1. Получаем
искомое разложение
в виде циклов. Порядок циклов в разложении
и выбор первого элемента каждого цикла
не существенен. Если порядокперестановки предполагается известным,
то полученное разложение на циклы можно
записать более кратко.

Порядком

перестановки
называется наименьшее положительное
целое числотакое,
что
.

Пусть
перестановка
разложена в произведениенепересекающихся цикловс длинами,.
Тогда порядок перестановки находится
по формуле.

Например,
для данной перестановки имеем
.
Отсюда.

Транспозицией
называется перестановка, являющаяся
циклом длины 2. То есть, транспозиция
фактически является перестановкой
некоторых двух элементов
.
Такая транспозиция записывается в виде.
Всякая перестановка может быть записана
как произведение транспозиций.

Пример 2.5.
Представить
перестановку
как произведение транспозиций.

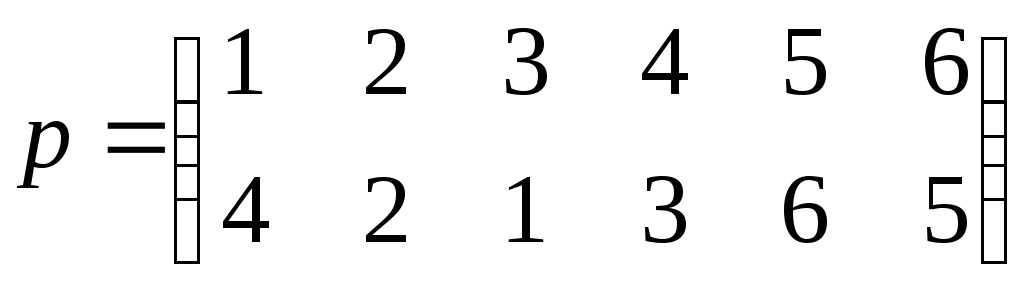
Решение.
Используем
результат предыдущего примера, в котором
было получено разложение данной
перестановки в произведение циклов:
.
В данном разложении первый циклуже является транспозицией, а второй
циклможно представить в виде произведения
двух перестановок,
то есть циклический сдвиг можно
реализовать серией двух последовательных
парных обменов, при которых первый
элемент«проталкивается» вдоль цикла.

Таким
же образом любой цикл
длиныможно представить в виде произведениятранспозиции в виде.

В
данном примере получаем разложение
перестановки на транспозиции:
=.
В этом разложении имеется три перестановки,
то есть нечетное число. Такая перестановка
называетсянечетной
и это записывается в виде
.
Если число транспозиций в разложении
перестановки четное, то перестановка
называется
четной
и
для нее выполняется свойство
.