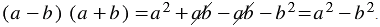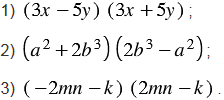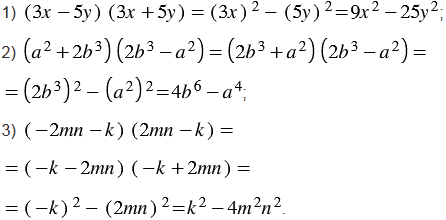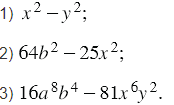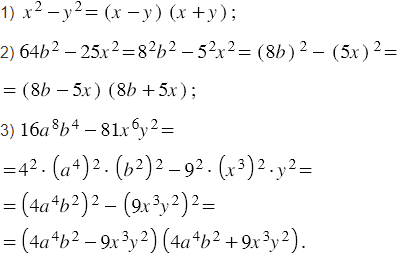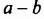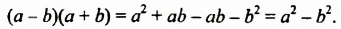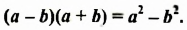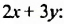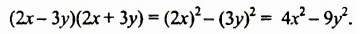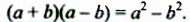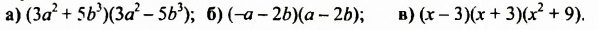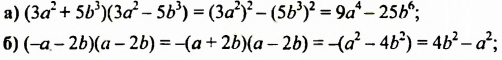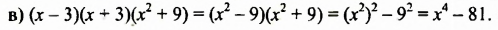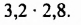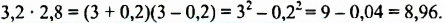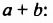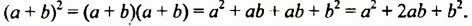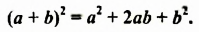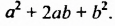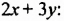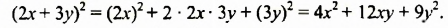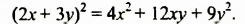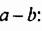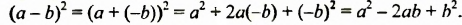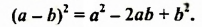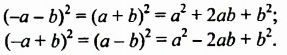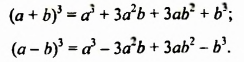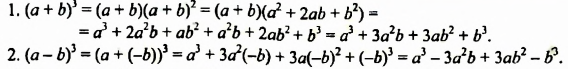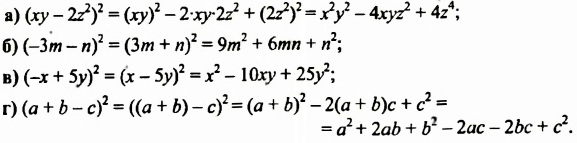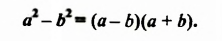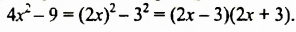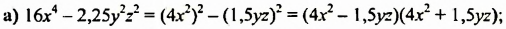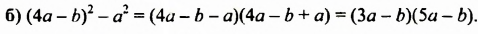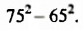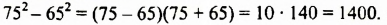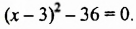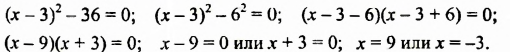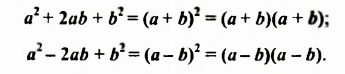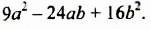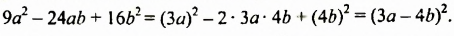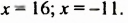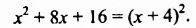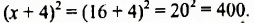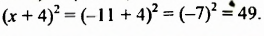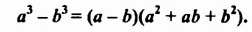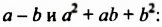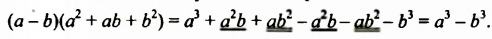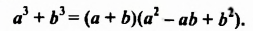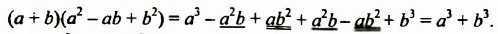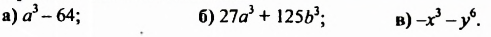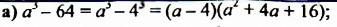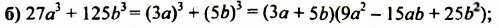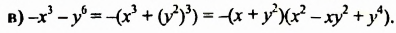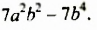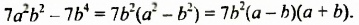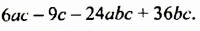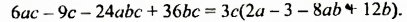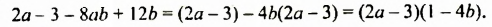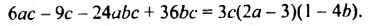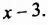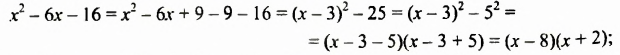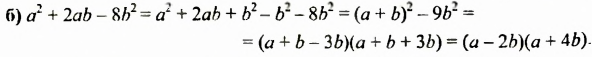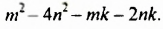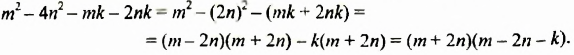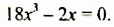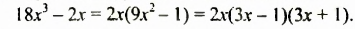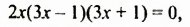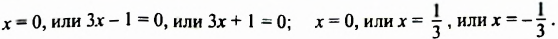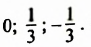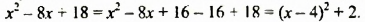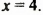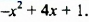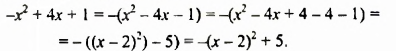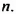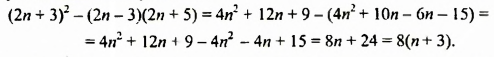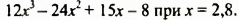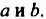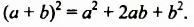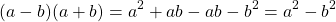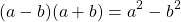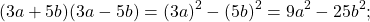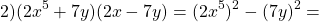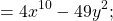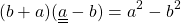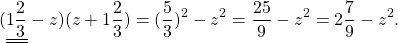Произведение суммы и разности
Произведение суммы и разности двух выражений можно найти как произведение многочленов. Для ускорения вычислений удобнее вывести формулу.
Найдем произведение суммы и разности двучленов непосредственным умножением:
-ab и +ab — противоположные слагаемые, поэтому их сумма равна нулю.
Вывод:
Произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Формула произведения суммы и разности:
Произведение суммы и разности двух выражений можно изобразить схематически так:
Рассмотрим на примерах, как находить произведение суммы и разности двух выражений с помощью схемы и с помощью формулы.
1)(3a+5b)(3a-5b)
Если все, что стоит до «+» и до «-«, заключить в квадрат, все, что после этих знаков — в круг, то произведение суммы (3a+5b) и разности (3a-5b) с помощью схемы можно представить так:
Чтобы применить форму произведения суммы разности, найдем a и b. В данном примере a=3a, b=3b:
Важно помнить — при возведении в квадрат произведения нескольких множителей, дроби или степени их обязательно следует записывать в скобках!
Как найти произведение суммы и разности, если слагаемые в скобках поменять местами?
От перестановки мест слагаемых сумма не меняется. Поэтому в разности квадратов на первое месте нужно поставить то выражение, которое стоит на первом месте в разности. Например,
Выражения вида (-a-b)(a-b) также можно упрощать по формуле произведения суммы и разности. Вынесем -1 и из первых скобок, и из вторых:
(-1)∙(-1)=1, получаем
Таким образом,
Например,
Произведение разности и суммы двух выражений. Разность квадратов двух выражений.
Мы уже знаем правило умножения многочлена на многочлен. Но существуют правила, которыми удобно пользоваться при умножении многочленов в частных случаях.
Одним из таких частных случаев является произведение двух многочленов, один из которых представляет собой разность двух выражений, а другой — их сумму.
Умножим разность 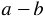
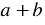
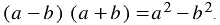
Следовательно, при умножении разности выражений на их сумму можно сразу записать результат — разность квадратов этих выражений. Поэтому полученное тождество называют формулой сокращенного умножения.
Правило:
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Обратите внимание, при возведении выражений в квадрат используем свойства степени с натуральным показателем.
Если выражение (1) переписать так
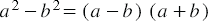
то мы получим тождество, которое называют формулой разности квадратов двух выражений.
Правило:
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
Разложите на множители:
Поделись с друзьями в социальных сетях:
Формулы сокращенного умножения с примерами решения
Содержание:
Формулы сокращенного умножения
Умножение разности двух выражений на их сумму
Умножим разность
Полученное тождество позволяет умножать разность двух выражений на их сумму не по правилу умножения двух многочленов, а сокращенно: сразу записывать произведение в виде 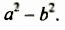
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Умножим по этому правилу разность 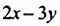
Из переместительного свойства умножения следует, что произведение суммы двух выражений и их разности равно разности квадратов этих выражений:
Примеры выполнения заданий:
Пример №135
Решение:
Пример №136
Вычислить
Решение:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений
Возведем в квадрат сумму
Полученное тождество называют формулой квадрата суммы. Оно является формулой сокращенного умножения, поскольку позволяет возводить в квадрат сумму любых двух выражений не по правилу умножения двух многочленов, а сокращенно: сразу записывать квадрат в виде трехчлена
Формулируют формулу квадрата суммы так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение этих выражений плюс квадрат второго выражения.
Возведем в квадрат сумму
При возведении суммы 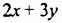
Квадрат разности двух выражений
Возведем в квадрат разность
Итак, получили такую формулу квадрата разности:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения.
Квадрат суммы и квадрат разности двух выражений еще называют квадратом двучлена.
Квадраты противоположных чисел равны: 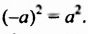
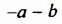
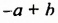
Для тех, кто хочет знать больше
Чтобы возвести сумму или разность двух выражений в куб, можно использовать формулы куба суммы или куба разности:
Докажем эти формулы.
Формулируют формулу куба суммы так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.
Формулу куба разности формулируют аналогично.
Примеры выполнения заданий:
Пример №137
Возвести в квадрат выражение:
Решение:
Разложение на множители разности квадратов двух выражений
В тождестве 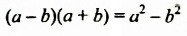
Полученное тождество называют формулой разности квадратов двух выражений. Формулируют ее так:
Разность квадратов двух выражении равна произведению разности этих выражений и их суммы.
Формула разности квадратов позволяет разложить на множители двучлена 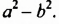
Примеры выполнения заданий:
Пример №138
Разложить на множители:
Решение:
Пример №139
Вычислить
Решение:
Пример №140
Решить уравнение
Решение:
Разложение многочленов на множители с использованием формул квадрата суммы и квадрата разности
Запишем формулы квадрата суммы и квадрата разности двух выражений (квадрата двучлена), поменяв в них левые и правые части:
Первая из этих формул дает разложение на множители трехчлена 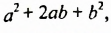
Примеры выполнения заданий:
Пример №141
Разложить на множители трехчлен
Решение:
Пример №142
Найти значение выражения 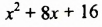
Решение:
Запишем сначала трехчлен 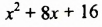
При 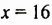
При 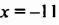
Разность и сумма кубов двух выражений
Разность квадратов двух выражений можно разложить на множители по формуле разности квадратов. При разложении на множители разности кубов двух выражений используют формулу разности кубов:
Докажем это тождество, перемножив выражения
В формуле разности кубов трехчлен 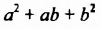
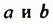
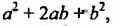
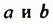
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
При разложении на множители суммы кубов двух выражений используют формулу суммы кубов:
Докажем это тождество:
Трехчлен 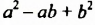
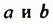
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Примеры выполнения заданий:
Пример №143
Разложить на множители:
Решение:
Применение нескольких способов для разложения многочленов на множители
Часто при разложении многочлена на множители нужно использовать несколько способов. Если это возможно, то разложение уместно начинать с вынесения общего множителя за скобки.
Рассмотрим несколько примеров:
1. Разложим на множители многочлен
Сначала вынесли общий множитель 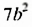
2. Разложим на множители многочлен
Все члены многочлена имеют общий множитель 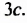
Многочлен 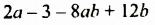
Примеры выполнения заданий:
Пример №144
Разложить на множители трехчлен:
Решение:
а) Если к выражению 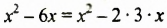
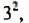
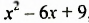
Поэтому, выделив квадрат этого двучлена, получим:
Пример №145
Разложить на множители многочлен
Решение:
Пример №146
Решить уравнение
Решение:
Разложим левую часть уравнения на множители:
откуда:
Ответ:
Применение преобразований выражений
Нам уже встречались задачи, при решении которых нужно было преобразовывать то или иное выражение. Чаще всего мы использовали преобразования выражений при решении уравнений, доказательстве тождеств, нахождении значений выражении. Рассмотрим еще некоторые задачи, решение которых связано с преобразованием выражений.
Сравнение значений многочлена с нулем
Пример №147
Доказать, что многочлен 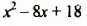
Решение:
Выделив из трехчлена 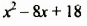
Мы представили многочлен в виде суммы двух слагаемых 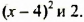
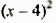
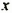
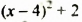
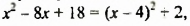
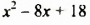
Нахождение наибольшего и наименьшего значений выражений
Исходя из равенства 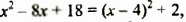
указать наименьшее значение многочлена 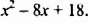
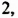
Пример №148
Найти наибольшее значение многочлена
Решение:
Преобразуем данный многочлен так:
Наибольшее значение многочлена равно 5.
Решение задач на делимость
Пример №149
Доказать, что значение выражения 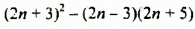
Решение:
Упростим данное выражение:
При любом целом значении 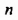
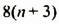
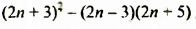
Нахождение значений многочлена с помощью микрокалькулятора
Пример №150
С помощью микрокалькулятора найти значение многочлена
Решение:
Значение данного многочлена искать удобнее, если его предварительно преобразовать так:
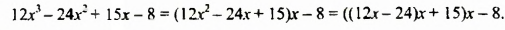
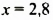
Выполнив вычисления, найдем значение многочлена. Оно равно 109,264.
Интересно знать
Античные математики использовали формулы сокращенного умножения задолго до нашей эры. В те времена формулы представлялись не в привычном нам символическом виде, а формулировались словами.
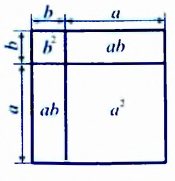
Ученые Древней Греции алгебраические утверждения, формулы, выражающие определенные зависимости между величинами, трактовали геометрически. Так, произведение 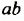
Приведем пример алгебраического утверждения, которое было известно древнегреческим ученым и в геометрической терминологии формулировалось так: площадь квадрата, построенного на сумме двух отрезков, равна сумме площади квадратов, построенных на каждом из этих отрезков, плюс удвоенная площадь прямоугольника, построенного на этих отрезках.
Нетрудно догадаться, что речь идет о формуле квадрата суммы, которую мы символически записываем так:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Разложение многочленов на множители
- Системы линейных уравнений с двумя переменными
- Рациональные выражения
- Квадратные корни
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены
- Многочлены
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Произведение суммы и разности
Произведение суммы и разности двух выражений можно найти как произведение многочленов. Для ускорения вычислений удобнее вывести формулу.
Найдем произведение суммы и разности двучленов непосредственным умножением:
-ab и +ab — противоположные слагаемые, поэтому их сумма равна нулю.
Произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Формула произведения суммы и разности:
Произведение суммы и разности двух выражений можно изобразить схематически так:
Рассмотрим на примерах, как находить произведение суммы и разности двух выражений с помощью схемы и с помощью формулы.
Если все, что стоит до «+» и до «-«, заключить в квадрат, все, что после этих знаков — в круг, то произведение суммы (3a+5b) и разности (3a-5b) с помощью схемы можно представить так:
Чтобы применить форму произведения суммы разности, найдем a и b. В данном примере a=3a, b=3b:
Важно помнить — при возведении в квадрат произведения нескольких множителей, дроби или степени их обязательно следует записывать в скобках!
Как найти произведение суммы и разности, если слагаемые в скобках поменять местами?
От перестановки мест слагаемых сумма не меняется. Поэтому в разности квадратов на первое месте нужно поставить то выражение, которое стоит на первом месте в разности. Например,
Выражения вида (-a-b)(a-b) также можно упрощать по формуле произведения суммы и разности. Вынесем -1 и из первых скобок, и из вторых:
http://www.evkova.org/formulyi-sokraschennogo-umnozheniya
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Формулы сокращенного умножения
- Произведение разности и суммы двух выражений. Разность квадратов двух выражений.
Мы уже знаем правило умножения многочлена на многочлен. Но существуют правила, которыми удобно пользоваться при умножении многочленов в частных случаях.
Одним из таких частных случаев является произведение двух многочленов, один из которых представляет собой разность двух выражений, а другой — их сумму.
Умножим разность 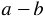
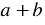
Получили тождество:
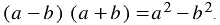
Следовательно, при умножении разности выражений на их сумму можно сразу записать результат — разность квадратов этих выражений. Поэтому полученное тождество называют формулой сокращенного умножения.
Правило:
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Примеры:
Выполните умножение многочленов:
Решение:
Обратите внимание, при возведении выражений в квадрат используем свойства степени с натуральным показателем.
Если выражение (1) переписать так
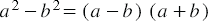
то мы получим тождество, которое называют формулой разности квадратов двух выражений.
Правило:
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
Примеры:
Разложите на множители:
Решение:
Советуем посмотреть:
Квадрат суммы и квадрат разности двух выражений
Сумма и разность кубов двух выражений
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 513,
Мерзляк, Полонский, Якир, Учебник
Номер 541,
Мерзляк, Полонский, Якир, Учебник
Номер 548,
Мерзляк, Полонский, Якир, Учебник
Номер 612,
Мерзляк, Полонский, Якир, Учебник
Номер 642,
Мерзляк, Полонский, Якир, Учебник
Номер 693,
Мерзляк, Полонский, Якир, Учебник
Номер 711,
Мерзляк, Полонский, Якир, Учебник
Номер 1178,
Мерзляк, Полонский, Якир, Учебник
Номер 1206,
Мерзляк, Полонский, Якир, Учебник
Номер 12,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 38,
Мерзляк, Полонский, Якир, Учебник
Номер 58,
Мерзляк, Полонский, Якир, Учебник
Номер 74,
Мерзляк, Полонский, Якир, Учебник
Номер 106,
Мерзляк, Полонский, Якир, Учебник
Номер 119,
Мерзляк, Полонский, Якир, Учебник
Номер 120,
Мерзляк, Полонский, Якир, Учебник
Номер 166,
Мерзляк, Полонский, Якир, Учебник
Номер 178,
Мерзляк, Полонский, Якир, Учебник
Номер 299,
Мерзляк, Полонский, Якир, Учебник
Номер 411,
Мерзляк, Полонский, Якир, Учебник
Произведение суммы и разности
Произведение суммы и разности двух выражений можно найти как произведение многочленов. Для ускорения вычислений удобнее вывести формулу.
Найдем произведение суммы и разности двучленов непосредственным умножением:
-ab и +ab — противоположные слагаемые, поэтому их сумма равна нулю.
Произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Формула произведения суммы и разности:
Произведение суммы и разности двух выражений можно изобразить схематически так:
Рассмотрим на примерах, как находить произведение суммы и разности двух выражений с помощью схемы и с помощью формулы.
Если все, что стоит до «+» и до «-«, заключить в квадрат, все, что после этих знаков — в круг, то произведение суммы (3a+5b) и разности (3a-5b) с помощью схемы можно представить так:
Чтобы применить форму произведения суммы разности, найдем a и b. В данном примере a=3a, b=3b:
Важно помнить — при возведении в квадрат произведения нескольких множителей, дроби или степени их обязательно следует записывать в скобках!
Как найти произведение суммы и разности, если слагаемые в скобках поменять местами?
От перестановки мест слагаемых сумма не меняется. Поэтому в разности квадратов на первое месте нужно поставить то выражение, которое стоит на первом месте в разности. Например,
Выражения вида (-a-b)(a-b) также можно упрощать по формуле произведения суммы и разности. Вынесем -1 и из первых скобок, и из вторых:
Умножение натуральных чисел
Я сперва покажу на примере, для чего нужно умножение, а после дам определение умножения и подробно расскажу об этом действии.
Допустим, мы хотим купить 14 тетрадей по 22 рубля каждая. Планируя покупку, нам нужно знать, сколько мы заплатим за всю покупку?
Чтобы ответить на этот вопрос, нам нужно сложить стоимость каждой тетради, которую мы хотим купить. А, так мы запланировали покупку 14 тетрадей, тогда мы складываем 22 рубля 14 раз, то есть, находим сумму 14 слагаемых, каждое из которых равно 22 :
22+22+22+22+22+22+22+22+22+22+22+22+22+22=308 (то есть, 308 рублей).
Если размер и количество одинаковых слагаемых небольшие, мы без особого труда можем найти их сумму. Но что же делать, если слагаемые многозначные и их количество велико?
Для ускорения подсчетов используется действие умножения .
Умножение – это арифметическое действие сложения определенного количества одинаковых слагаемых.
Действие умножение – это частный случай действия сложение.
Когда нам нужно сложить несколько одинаковых слагаемых, мы, вместо утомительного вычисления суммы одинаковых чисел, умножаем это слагаемое на количество его повторений. Если взять наш пример, то мы слагаемое 22 умножаем на количество – 14 .
Еще раз: умножить 22 на 14 – это означает, что нам нужно сложить 14 чисел, каждое из которых равно 22 .
Число, которое является повторяющимся слагаемым, называется множимое (то, что множится, умножается).
Число, которое указывает на количество одинаковых слагаемых, называется множитель.
Множимое и множитель имеют общее название – сомножители.
Результат действия умножения называется произведением.
Так, в нашем примере мы складываем цену одной тетради ( 22 рубля) столько раз, сколько тетрадей хотим купить ( 14 штук). Значит, 22 – это множимое , 14 – это множитель . Стоимость покупки, полученная в результате умножения 22 на 14 ( 308 рублей) – это произведение .
На записи действие умножения обозначается точкой ( ∙ ) или косым крестом ( x ), которые ставятся между сомножителями. В отдельных случаях допускается обозначение звездочкой ( * ). Результат действия умножение, то есть, найденное произведение записывается в виде равенства. Если, к примеру, нужно умножить 22 на 14 , то записать это действие и его результат можно так:
22 ∙14=308,
22x14=308,
22*14=308.
При записи от руки действие умножение принято обозначать при помощи точки, косой крест используется в основном при печати, а звездочка – в компьютерном наборе. Но даже и во время компьютерного набора грамотнее использовать точку или косой крест (букву х).
Прочитать действие умножения и результат можно такими способами:
- двадцать два умножить на четырнадцать будет триста восемь;
- двадцать два, умноженное на четырнадцать, равно триста восемь;
- двадцать два на четырнадцать – триста восемь;
- произведение двадцати двух и четырнадцати равно триста восемь.
Компоненты действия умножение для двух сомножителей:
Компоненты умножения для трех сомножителей и более:
Основные свойства умножения
Поскольку действие умножение является частным случаем действия сложение, то основные свойства сложения распространяются и на умножение.
Действие умножение , как и сложение, можно выполнить всегда , и при этом получается единственный результат этого действия .
Законы умножения и их следствия
Умножение обладает такими основными свойствами, называемые законами умножения, из которых вытекают остальные свойства и следствия:
- переместительный закон умножения;
- сочетательный закон умножения.
Переместительный закон умножения.
Произведение двух или нескольких сомножителей от изменения их порядка не меняется.
Это значит, что значение произведения не зависит от порядка перемножения сомножителей, то есть, от порядка выполнения действия умножение.
Для двух сомножителей мы можем записать переместительный закон умножения в общем виде так:
ab=ba.
Допустим, нам нужно подсчитать количество отделений в шкафу (рис. 1).
В верхнем ряду их 5 , в среднем и нижнем тоже по 5 отделений. Нетрудно посчитать, что всего во всех рядах их: 5+5+5=15 , или 5 ∙3=15 .
Но эти же самые отделения можно считать и по вертикали, по столбцам : в первом их 3 , во втором тоже 3 , в третьем, четвертом и пятом столбцах их также по 3 штуки. То есть, в каждом столбце по 3 отделения. Всего столбцов 5 , поэтому: 3+3+3+3+3=15 , или 3 ∙5=15 .
Это означает, что 5 ∙3=3 ∙5 .
Это свойство также верно для трех и более сомножителей.
К примеру, нам нужно подсчитать количество отделений в двух одинаковых шкафах (рис. 2).
В первом шкафу количество отделений, как мы уже выяснили, можно узнать, умножив количество отделений в одном ряду на количества рядов: 5 ∙3 .
Во втором шкафу количество отделений точно такое же ( 5 ∙3 ), поскольку два шкафа полностью одинаковые .
Общее количество отделений в двух шкафах можно найти, сложив количество отделений в каждом шкафу : 5 ∙3+5 ∙3 .
Выражение 5 ∙3 – это не что иное, как повторяющееся слагаемое , поэтому мы можем заменить эту сумму произведением , умножив слагаемое 5 ∙3 на количество его повторений, то есть, на 2 :
5 ∙3+5 ∙3 =5 ∙3 ∙2.
Найдя результаты левой и правой части этого равенства, мы убедимся, что они одинаковые , а значит, мы произвели замену суммы произведением верно :
15+15=15 ∙2,
30=30.
Но количество отделений в одном шкафу мы также можем найти, умножив количество рядов на количество отделений в одном ряду: 3 ∙ 5 . Тогда в двух шкафах у нас будет:
3 ∙5+3 ∙5=3 ∙5 ∙2,
15+15=15 ∙2,
30=30.
Значит, 5 ∙3 ∙2=3 ∙5 ∙2=30.
Также мы можем сразу умножить количество шкафов на количество отделений в одном шкафу. Тогда мы получим: 2 ∙5 ∙3=30 или 2 ∙3 ∙5=30 , в зависимости от того, каким способом мы посчитали, сколько отделений содержит один шкаф.
Поэтому, для трех сомножителей переместительный закон умножения в общем виде выглядит так:
abc=acb=bac=bca=cab=cba.
Сочетательный закон умножения.
Результат умножения трех и более чисел не изменяется, если любые из этих сомножителей заменить их произведением.
Следовательно, мы можем группировать множители между собой каким угодно образом, и выполнять действие умножения с этими группами.
В общем виде для трех сомножителей сочетательный закон умножения можно выразить так:
abc=a(bc)=(ab)c=b(ac).
Этот закон можно назвать следствием переместительного закона умножения.
Действительно, согласно переместительному закону, мы можем перенести множители , стоящие в конце выражения a ∙ b ∙ c ∙ d , в его начало, и объединить их в одну группу ( c ∙ d ) ∙ a ∙ b , то есть, найти их произведение c ∙ d . А так как при изменении порядка сомножителей, результат действия умножение не изменяется, то и изменение порядка групп сомножителей одного произведения, также не влияют на результат.
Так, при подсчете количества отделений в двух шкафах на рисунке 2, мы можем сперва найти число отделений в одном шкафу, а потом умножить результат на 2 :
(5 ∙3) ∙2=15 ∙2=30,
(3 ∙5) ∙2=15 ∙2=30,
а можем сперва найти общее количество рядов отделений в обоих шкафах, а после умножить их на количество отделений в ряду:
(3 ∙2) ∙5=6 ∙5=30.
Как видите, результат во всех случаях одинаковый.
Особые случаи умножения: умножение единицы и нуля
Если в произведении двух чисел один из сомножителей единица, то произведение равно второму сомножителю:
a ∙1=1 ∙a=a.
Действительно, при умножении любого числа на 1 , мы берем это число 1 раз, а значит, получаем только это число.
А при умножении единицы на любое число (например, 1 ∙ 7 ) мы находим сумму семи единиц, то есть, то количество единиц, из которых состоит данное число. Следовательно, сумма этих единиц равна самому данному числу :
1+1+1+1+1+1+1=7.
Если в произведении любого количества сомножителей одним из сомножителей является нуль, то и произведение равно нулю:
a∙b∙0=0∙a∙b=a∙0∙c=0.
Так, при умножении любого числа на 0 , мы берем это число 0 раз, то есть, не берем ни разу . А если ничего не брать, то ничего и не получится.
А при умножении нуля на любое число, мы находим сумму нулей , которая, как вам известно, равна 0 .
Умножение однозначных чисел
Умножение двух однозначных натуральных чисел a и b – это нахождения суммы b слагаемых, каждое из которых равно числу a, и при этом a и b являются натуральными числами.
Если a и b – числа, находящиеся в самом начале натурального ряда, то найти такую сумму особого труда не составляет: 1 ∙2=1+1=2 . Но если взять числа, которые замыкают первый десяток, например, 8 и 9 , то для вычисления 8 ∙9 , а именно, суммы 8+8+8+8+8+8+8+8+8=72 , то в этом случае вычисление результата потребует от нас определенного времени.
Для облегчения вычисления, были посчитаны результаты умножения всех однозначных чисел друг на друга, и сведены в специальные таблицы умножения.
Умножение однозначных чисел – это основа быстрого и точного вычисления произведений любых чисел, поэтому очень важно знать на память все таблицы умножения .
Умножение многозначного числа на однозначное
Допустим, нам нужно умножить 985 на 4 . Умножить 985 на 4 – это сложить 4 раза число 985 , то есть, 985+985+985+985 . Мы можем представить каждое из слагаемых 985 в виде суммы его разрядных слагаемых , а именно: 900+80+5 . Получится такое выражение:
900+80+5+900+80+5+900+80+5+900+80+5.
Воспользуемся законами сложения и сгруппируем одинаковые слагаемые этого выражения вместе:
900+900+900+900+80+80+80+80+5+5+5+5,
(900+900+900+900)+(80+80+80+80)+(5+5+5+5).
Суммы в скобках мы можем заменить на произведение одинаковых слагаемых и числа этих слагаемых в каждых скобках:
900 ∙4+80 ∙4+5 ∙4.
Таким образом, чтобы умножить многозначное число на однозначное, достаточно умножить это однозначное число на количество единиц в каждом разряде многозначного числа, и сложить полученные результаты.
Умножение в столбик многозначного числа на однозначное
Удобно и быстро умножить многозначное число на однозначное, и при этом не запутаться в расчете помогает запись вычисления в столбик .
Для этого пишем множимое 985 , и под цифрой его разряда единиц записываем множитель 4 . Проводим под множителем горизонтальную черту, ставим между сомножителями знак умножения (точку или косой крест), и получаем такую запись:
4 раза по 5 единиц – это будет 20 единиц, то есть, 2 десятка и 0 простых единиц. Поэтому, пишем под чертой в разряде единиц 0 , а 2 десятка запоминаем или записываем маленькую цифру 2 над разрядом десятков множимого 985 :
4 раза по 8 десятков – это 32 десятка. Прибавим к ним 2 десятка, которые получились после умножения однозначного числа на единицы, получим 32 десятка, то есть, 3 сотни и 2 десятка. Цифру 2 пишем под чертой в разряде десятков, а над разрядом сотен множимого 975 (в уме) ставим маленькую цифру 3 :

4 раза по 9 сотен – это 36 сотен. Прибавим к ним 3 сотни, которые держим в уме, получаем 39 сотен, или 3 тысячи и 9 сотен. Значит, пишем под горизонтальной чертой в разряде сотен цифру 9 и, поскольку в множимом 985 нет ни одной тысячи, то сразу запишем в результате под чертой цифру 3 в разряде тысяч:
Умножение многозначных чисел
Прежде чем рассказать, как в общем случае умножить одно многозначное число на другое, я расскажу о двух частных случаях умножения многозначных чисел:
- умножение на число, которое начинается на единицу, и заканчивается любым количеством нулей;
- умножение на число, которое начинается на любые, отличные от нуля, цифры, и заканчивается одним или несколькими нулями.
Умножение на число, состоящее из единицы и любого количества нулей
Пусть необходимо умножить 327 на 10 . Это означает, что мы должны 10 раз взять (сложить) число 327 . Известно, что если мы возьмем (сложим) одну единицу 10 раз, то мы получим 1 десяток, значит, взяв 327 единиц 10 раз, у нас будет 327 десятков, то есть, 3270 единиц. Значит:
327 ∙10 =3270
Рассмотрим еще один пример. Умножим 327 на 100 , то есть, 100 раз возьмем (сложим) число 327 . Если единицу повторить 100 раз, получится 100 единиц, или одна сотня . Значит, 327 единиц, повторенные 100 раз, дадут нам 327 сотен, что можно записать так: 32700 .
327 ∙100 =32700
Итак, чтобы умножить какое-нибудь число на другое, которое начинается на единицу, и заканчивается любым количеством нулей, достаточно к концу первого числа дописать столько нулей, сколько содержится во втором числе.
Умножение на число, которое начинается цифрами, и заканчивается любым количеством нулей
Например, умножим то же самое число 327 , но уже на 20 . Это означает, что мы должны сложить одно и то же число 327 друг с другом 20 раз:
327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327.
Воспользуемся сочетательным законом умножения , и представим эти слагаемые в виде 10 одинаковых групп, каждая из которых содержит два слагаемых 327 :
(327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327).
Сумму в скобках мы можем, согласно определению действия умножение, заменить на произведение , поскольку слагаемые суммы у нас одинаковые. Получим следующее:
(327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2).
Но здесь мы опять видим, что выражение состоит из десяти одинаковых слагаемых , каждое из которых представляет собой произведение. Значит, мы и это выражение можем представить в виде произведения :
(327 ∙2) ∙10.
Рассмотрим другой пример: 764 ∙300 .
Здесь нам нужно найти сумму 300 чисел, каждое из которых – это число 764 . Эти 300 слагаемых мы группируем в 100 групп, в каждой из которых содержится 3 слагаемых 764 . Можем ли мы узнать, какое число единиц содержит каждая из 100 групп? Да, можем. Для этого нам нужно найти сумму трех слагаемых 764 , или просто 764 умножить на 3 .
764 ∙3 =2292.
Зная, сколько единиц содержится в одной группе и количество этих одинаковых групп, мы можем найти, сколько единиц находится во всех этих группах. Групп у нас 100 , значит, мы находим сумму 100 слагаемых, каждое из которых – это найденное нами число 2292 . То есть, 2292 умножаем на 100 . Для этого достаточно просто приписать справа к числу 2292 два нуля:
2292 ∙100 =229200.
Итак, чтобы умножить какое-нибудь число на другое, начинающееся любыми цифрами и заканчивающееся нулями, достаточно умножить первое число на число, образованное первыми цифрами второго, а к результату приписать справа столько нулей, сколько их было в конце второго числа.
Иными словами: нужно от второго числа отбросить нули в конце, умножить получившиеся числа, а к результату приписать справа столько нулей, сколько изначально отбросили.
Общее правило умножения чисел
Допустим, необходимо найти произведение двух многозначных чисел 2834 и 168 . Это означает, что нам нужно сложить 168 одинаковых чисел, каждое из которых равно 2834 :
Количество слагаемых ( 168 ) мы можем разложить на разрядные слагаемые ( 100+60+8 ) и согласно сочетательному закону сложения сгруппировать их следующим образом : сто слагаемых плюс шестьдесят слагаемых плюс восемь слагаемых.
Исходя из определения умножения, выражения в скобках мы можем представить не в виде суммы большого количества слагаемых, а как сумму произведений:
Таким образом, чтобы умножить два многозначных числа, достаточно последовательно умножить одно из этих чисел на количество единиц каждого из разрядов второго числа, и сложить полученные результаты.
Частное произведение – это число, полученное после умножения одного из сомножителей на количество единиц какого-либо разряда другого сомножителя.
Умножение в столбик многозначных чисел
При записи действия умножения в столбик сомножители располагаются друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел ; под множителем проводим горизонтальную черту, и ставим между сомножителями знак действия умножения:
Далее, умножаем множимое 2834 последовательно на количество единиц каждого разряда множителя справа налево , то есть, начиная с младшего разряда.
Умножаем 2834 на 8 единиц, получается 22672 единиц. Результат умножения, то есть, первое частное произведение , записываем под горизонтальной чертой.
Далее, нам нужно умножить множимое на 6 десятков; для этого умножаем 2834 на 6 , а к результату приписываем 0 , получается 170040 .
В частных произведениях обычно не пишут (опускают) нули в конце числа для упрощения записи. При этом следует не забывать, что, первую полученную цифру частного произведения нужно писать в том разряде, цифру которого мы умножаем на множимое.
В нашем случае это выглядит так . Цифра 6 , которую мы умножаем на множимое 2834 , находится в числе 168 в разряде десятков , то есть, обозначает количество десятков . Следовательно, первую полученную цифру частного произведения нужно записать в разряде десятков , потому что сейчас мы именно количество десятков умножаем на множимое.
Итак, 6 ∙4 =24 , значит мы пишем в строке под первым частным произведением в разряде десятков цифру 4 , а 20 десятков, то есть, 2 сотни, запоминаем. Дальше считаем и записываем так же, как и любое другое умножение многозначного и однозначного чисел . После нахождения второго частного произведения , у нас получилась такая запись:
Теперь умножаем множимое на 1 сотню. Для этого достаточно умножить 2834 на 1 и приписать справа два нуля , получится 283400 . Но в записи мы нули не пишем , поэтому начинаем писать третье частное произведение с разряда сотен.
Нам осталось только сложить три полученные частные произведения .
Итак, результат умножения 2834 ∙168 = 476112 .
Некоторые особенности записи умножения в столбик
При записи нахождения произведения двух чисел в столбик существуют некоторые особенности, которые помогают сократить запись и упростить наглядность вычисления. Все они являются следствием свойств умножения.
Если у первого сомножителя количество цифр, составляющих его, меньше, чем у второго , то удобно при записи в столбик поменять сомножители местами, записав число с большим количеством цифр первым. Например, произведение 284 ∙12093 находят как 12093 ∙284 . Это делается, чтобы избавиться от необходимости находить много частных произведений.
Если в множителе некоторые цифры являются нулями, то можно не записывать соответствующие промежуточные произведения, которые, что очевидно, будут равняться также нулю . При этом промежуточное произведение, полученное от умножения следующей значащей цифры (то есть, отличной от нуля) на множимое, начинают записывать с разряда, соответствующего положению этой значащей цифры. Например:
Если один из сомножителей представляет собой число, которое оканчивается любым количеством нулей , то мы записываем сомножители в столбик так, как будто этих нулей нет, находим произведение, мысленно отбросив эти нули, а потом к получившемуся после умножения числу приписываем отброшенные нули и получаем окончательный результат.
Если оба сомножителя – это числа, оканчивающиеся любым количеством нулей , то мы записываем их в столбик так, как будто этих нулей нет, а после нахождения произведения чисел без нулей, приписываем к ним столько нулей, сколько их было изначально.
Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось ли это у вас или нет.
Изменение произведения чисел при изменении его сомножителей
Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения , а также переместительный и сочетательный законы сложения.
Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.
Рассмотрим пример 18 ∙2 . Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6 .
18 ∙2 =36
18 ∙6 =108.
Если мы увеличим 36 в 3 раза, то мы получим как раз 108 .
По-другому и быть не может, и вот почему.
Первое произведение представляет собой сумму двух слагаемых :
18+18.
Второе произведение – это сумма шести таких же слагаемых :
18+18+18+18+18+18.
Если мы, воспользовавшись сочетательным законом умножения, сгруппируем эти слагаемые по 2 , то получим следующее:
(18+18)+(18+18)+(18+18).
Как видите, у нас получилось 3 одинаковых слагаемых , каждый из которых равен первому произведению . А это значит, что полученное произведение состоит из трех, которые были даны изначально, то есть, в 3 раза больше начального. Что и требовалось доказать.
Для второго сомножителя справедливость этого свойства доказывается на основе переместительного закона умножения .
Если уменьшить один из сомножителей в несколько раз, произведение также уменьшится в это же число раз.
Попробуйте самостоятельно доказать правильность этого свойства. Пишите в комментариях, получилось ли это у вас?
Если увеличить один из сомножителей в несколько раз, а второй в это же число раз уменьшить, то произведение при этом не поменяется.
Действительно, при увеличении одного из сомножителей произведение увеличивается , а при уменьшении другого сомножителя произведение уменьшается . Поэтому, если увеличить одно и одновременно уменьшить другое число, то эти изменения компенсируют друг друга , и произведение останется неизменным :
32 ∙8 =256,
Увеличим первый сомножитель в 4 раза, а второй во столько же раз уменьшим:
128 ∙2 =256.
Теперь уменьшим первый сомножитель произведения 32 ∙8 в 4 раза, а второй уменьшим в это же число раз:
8 ∙32 =256.
Умножение произведения на число и числа на произведение
Если необходимо умножить произведение на число, нужно любой сомножитель этого произведения умножить на данное число, а результат умножить последовательно на оставшиеся сомножители.
(a ∙b ∙c) ∙d =(a ∙d) ∙b ∙c =(b ∙d) ∙a ∙c =(c ∙d) ∙a ∙b
Действительно, пусть требуется найти результат (7 ∙9 ∙2) ∙5 . Мы можем сперва вычислить произведение в скобках (оно равно 126 ), а потом умножить его на 5 (результат 630 ). А можем, чтобы быстрее вычислить результат в уме, сперва умножить 5 на 2 , чтобы получить круглое число 10 , и потом легко вычислить ещё два произведения, воспользовавшись частными правилами умножения, описанными выше:
10 ∙7 =70 (просто приписываем к семерке нуль),
70 ∙9 =630 (находим по таблице умножения 7 ∙9 =63 и приписываем в конце нуль).
То есть, мы видим, что (7 ∙9 ∙2) ∙5 = (5 ∙2) ∙7 ∙9 .
Когда я пишу «находим по таблице умножения», это означает, что мы вспоминаем эту строку из таблицы, а не ищем её там на самом деле. Таблицу умножения нужно знать наизусть!
Если необходимо умножить число на произведение, нужно умножить данное число на любой сомножитель, а результат умножить на оставшиеся сомножители.
a ∙(b ∙c ∙d) =(a ∙b) ∙c ∙d =(a ∙c) ∙b ∙d =(a ∙d) ∙b ∙c.
Рассмотрим такой пример: 6 ∙(3 ∙5 ∙2) . Если найти значение произведения в скобках ( 30 ), а потом умножить на него число 6 , результатом будет 180 . А можно сначала умножить число 6 на 5 (будет 30 ), а потом результат умножить с остальными сомножителями:
30 ∙3 =90,
90 ∙2 =180.
Оба эти свойства являются очевидными следствиями переместительного и сочетательного законов умножения .
Распределительный закон умножения (умножение суммы на число)
Когда мы рассматривали умножение многозначного и однозначного чисел, мы раскладывали число 975 на его разрядные слагаемые ( 900+70+5 ), а потом умножали на 4 отдельно каждое это слагаемое. Аналогично можно поступать при умножении числа на любую сумму.
Например, найдем произведение суммы 5+2+4+9 и числа 3 . Это означает, что нужно найти такую сумму:
(5+2+4+9)+(5+2+4+9)+ (5+2+4+9).
Все эти слагаемые представляют собой одну сумму чисел, сгруппированных в определенные группы. Запишем их без скобок:
5+2+4+9+5+2+4+9+5+2+4+9,
а затем, используя переместительный и сочетательный законы сложения, сгруппируем одинаковые слагаемые:
Основываясь на определении действия умножение, так как мы имеем в каждых скобках одинаковые слагаемые, переписываем это выражение следующим образом:
5 ∙3+2 ∙3+4 ∙3+9 ∙3.
Распределительный закон умножения: для умножения суммы на любое число, необходимо каждое слагаемое этой суммы умножить на данное число, а затем сложить полученные произведения.
Согласно переместительному закону умножения, это свойство справедливо и при умножении числа на сумму.
Для умножения числа на сумму, необходимо умножить данное число на каждое слагаемое этой суммы, а результаты полученных произведения сложить.
(a+b+c+d)∙z =z∙(a+b+c+d) =a ∙z+b ∙z+c ∙z+d ∙z.
Название распределительный происходит от того, что действие умножения на сумму распределяется между каждым из слагаемых этой суммы.
Что такое сумма, разность, произведение, частное в математике?
В каких ещё значениях, не связанных с математикой, употребляются эти слова?
I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.
Все определения даются здесь на множестве натуральных чисел.
Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.
Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.
СУММА есть результат сложения чисел-слагаемых.
Вычитание — это операция, обратная сложению. Она состоит в нахождении одного из слагаемых по сумме и другому слагаемому. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, а искомое слагаемое — РАЗНОСТЬЮ.
РАЗНОСТЬ — это число, являющееся результатом вычитания, остаток вычитания.
Каждой паре чисел можно поставить в соответствие число, которое состоит из стольких единиц, сколько их содержится в первом числе из пары, взятых столько раз, сколько единиц содержится во втором числе из пары. Это соответствующее таким образом паре чисел (они называются сомножителями) число называется ПРОИЗВЕДЕНИЕМ.
ПРОИЗВЕДЕНИЕ — это результат умножения.
Деление есть операция, обратная умножению.
Деление — это нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение называется делимым, данный сомножитель — делителем, а искомый сомножитель — это ЧАСТНОЕ, то есть число, полученное от деления одного числа на другое.
II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.
Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.
СУММА в переносном значении означает совокупность, общее количество чего-либо.
Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.
РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.
Например. Разность интересов намного хуже разницы в возрасте. Дружба может начаться с представления об общности взглядов , а вражда — с разности взглядов.
ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.
Например. Высокое художественное произведение заставляет человека думать над своей жизнью. На конкурсе юных пианистов мальчик играл произведение П.И. Чайковского. Эта шкатулка — настоящее произведение искусства.
ЧАСТНОЕ — это что-то личное, персональное, принадлежащее только одному человеку, это его собственность, его и только его достояние. И будь то самоличные мысли, будь то имущество или что-нибудь другое, но оно принадлежит только ему, частному лицу.
Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?
Как найти произведение суммы
Сложение и умножение — базовые математические операции, стоящие в одном ряду с вычитанием, делением, возведением в степень, и другими. Комбинируя эти операции между собой, можно получить новые, более сложные операции.

Инструкция
Чтобы умножить сумму на число, перемножьте каждое слагаемое с этим числом, полученные числа сложите между собой.Пример. (a+b+c)*p=a*p+b*p+c*p.Обратная операция — вынесение общего множителя за скобку: a*p+b*p+c*p=p(a+b+c).
Для перемножения двух скобок, содержащих в себе суммы каких-то переменных, существует определенная схема. Надо умножить сначала слагаемое первой скобки на каждое из слагаемых второй скобки, сложить полученные результаты, затем ту же операцию проделать со вторым и последующими слагаемыми первой скобки. Осталось сложить полученные числа между собой.Пример.(a+b)*(c+d)=a*c+a*d+b*c+b*d.Помните, что перемножаются также и знаки перед числами. Произведение одинаковых знаков дает плюс, разных знаков — минус. Например, (a-b)(c+d)=a*c+a*d-b*c-b*d; (a-b)(c-d)=a*c-a*d-b*c+b*d.Обратная операция — разложение суммы на множители.
Чтобы перемножить три скобки, являющиеся суммами некоторых переменных, надо перемножить сначала любые две скобки, затем полученный результат умножить на третью скобку. Умножение четырех и большего числа скобок происходит аналогично. Группируйте скобки так, чтобы считать было удобнее и проще.
Частный случай произведения сумм — возведение суммы в степень. Например, (a+b)^2, (c-d)^3, (p-k)^6. Можно представить возведение в степень в виде произведения нескольких одинаковых скобок и перемножать их по правилам, изложенным выше. А можно воспользоваться формулами сокращенного умножения, которые всегда полезно помнить.
Видео по теме
Полезный совет
Выведите самостоятельно формулы сокращенного умножения, последовательно перемножая скобки. Это позволит лучше понять суть происходящего, а заодно потренироваться в умножении сумм.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.