Как найти произведение векторов в трехмерном - Исправление недочетов и поиск решений вместе с Examum.ru

Время на прочтение
10 мин

Количество просмотров 12K

В настоящий момент появилось достаточно большое количество библиотек дополненной реальности с богатым функционалом (ARCore, ARKit, Vuforia). Тем не менее я решил начать свой открытый проект, попутно описывая как это работает изнутри. Если повезет, то позже получится добавить какой-то особый интересный функционал, которого нет в других библиотеках. В качестве целевых платформ пока возьмем Windows и Android. Библиотека пишется на C++, и сторонние библиотеки будут задействованы по минимуму, т.е. преимущественно не будет использовано ничего готового. Фокус в статьях будет направлен на алгоритмы и математику, которые постараюсь описать максимально доступно и подробно. В этой статье пойдет речь про основы векторной алгебры.

Дополненная реальность — это совмещение виртуального мира и реального. Для этого, нам нужно представить окружающее реальное пространство в виде математической модели, понимая закономерности которой, мы сможем получить данные для совмещения. Начнем с основ векторной алгебры.

Вектора — это частный случай матриц, состоящие либо из одного столбца, либо из одной строки. Когда мы говорим о векторе, обычно имеется вектор-столбец $vec v = begin{pmatrix}v_x \ v_y \ v_z \v_wend{pmatrix}$ . Но записывать вектор как столбец неудобно, поэтому будем его транспонировать — $vec v = begin{pmatrix}v_x & v_y & v_z & v_wend{pmatrix}^T$ .

Длина вектора

Первое, что мы рассмотрим — получение длины вектора — , где $l$ — значение длины, $vec v$ — наш вектор. Для примера возьмем двумерный вектор:

$vec v = begin{pmatrix}x & yend{pmatrix}^T$ , где $x$ и $y$ — компоненты вектора, значения проекций вектора на оси двумерных координат. И мы видим прямоугольный треугольник, где $x$ и $y$ — это длины катетов, а $l$ — длина его гипотенузы. По теореме Пифагора получается, что $l = sqrt{x^2 + y^2}$ . Значит $l = |vec v| = sqrt{x^2 + y^2}$ . Вид формулы сохраняется и для векторов большей размерности, например — $l = |vec v| = |begin{pmatrix} x & y & z & wend{pmatrix}^T| = sqrt{x^2 + y^2 + z^2 + w^2}$ .

Скалярное произведение

Скалярное произведение векторов — это сумма произведение их компонентов: . Но так как мы знаем, что вектора — это матрицы, то тогда удобнее записать это в таком виде: $s = vec{a}^T vec{b}$ . Это же произведение можно записать в другой форме: $s = {vec a}^T vec b = |vec a| cdot |vec b| cdot cos{delta}$ , где $delta$ — угол между векторами $vec a$ и $vec b$ (для двумерного случая эта формула доказывается через теорему косинусов). По этой формуле можно заключить, что скалярное произведение — это мера сонаправленности векторов. Ведь, если $delta = 0^{circ}$ , то , и $s$ — это просто произведение длин векторов. Так как — не может быть больше 1, то это максимальное значение, которые мы можем получить, изменяя только угол $delta$ . Минимальное значение будет равно -1, и получается при $delta = 180^{circ}$ , т.е. когда вектора смотрят в противоположные направления. Также заметим, что при $delta = 90^{circ}$ , а значит какие бы длины не имели вектора $vec a$ и $vec b$ , все равно $s = 0$ . Можно в таком случае сказать, что вектора не имеют общего направления, и называются ортогональными.
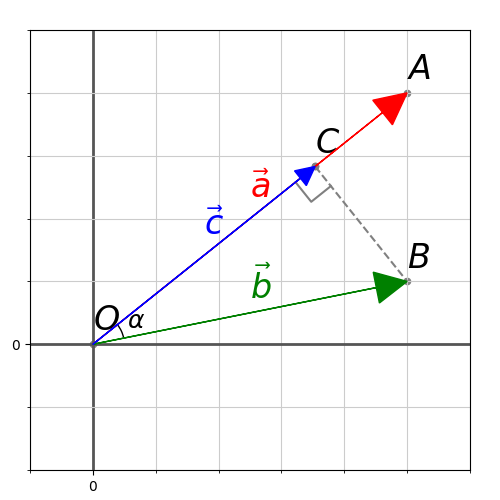
Также при помощи скалярного произведения, мы можем записать формулу длины вектора красивее: $|vec v| = sqrt{vec{v}^T vec v}$ , $|vec v|^2 = vec{v}^T vec{v}$ .

Проекция вектора на другой вектор

Возьмем два вектора: $vec a$ и $vec b$ .
Проекцию вектора на другой вектор можно рассматривать в двух смыслах: геометрическом и алгебраическом. В геометрическом смысле проекция вектора на ось — это вектор, а в алгебраическом – число.

Вектора — это направления, поэтому их начало лежит в начале координат. Обозначим ключевые точки: $O$ — начало координат, $A$ — конечная точка вектора $vec a$ , $B$ — конечная точка вектора $vec b$ .

В геометрическом смысле мы ищем такой $vec c$ , чтобы конечная точка вектора (обозначим ее как — $C$ ) была ближайшей точкой к точке $B$ , лежащей на прямой $OA$ .

Иначе говоря, мы хотим найти составляющую $vec b$ в $vec a$ , т.е. такое значение $t$ , чтобы и

Расстояние между точками $B$ и $C$ будет минимальным, если . Получаем прямоугольный треугольник — $OCB$ . Обозначим . Мы знаем, что $cos{alpha} = frac{|OC|}{|OB|}$ по определению косинуса через соотношение сторон прямоугольного треугольника
( $OB$ — гипотенуза, $OC$ — прилежащий катет).
Также возьмем скалярное произведение . Отсюда следует, что $cos{alpha} = frac {vec a cdot vec b } {|vec a| cdot |vec b|}$ . А значит $frac{|OC|}{|OB|} = frac {vec a cdot vec b } {|vec a| cdot |vec b|}$ .

Тут вспоминаем, что $OC$ — это искомый вектор $vec c$ , а $OB$ — $vec b$ , и получаем $frac{|vec c|}{|vec b|} = frac {vec a cdot vec b } {|vec a| cdot |vec b|}$ . Умножаем обе части на и получаем — $|vec c| = frac {vec a cdot vec b } {|vec a|}$ . Теперь мы знаем длину $vec c$ . Вектор $vec c$ отличается от вектора $vec a$ длинной, но не направлением, а значит через соотношение длин можно получить: $vec c = vec a cdot frac{|vec c|}{|vec a|}$ . И мы можем вывести финальные формулы:
$t = frac {vec a cdot vec b } {|vec a|^2} = frac {{vec a}^T vec b}{{vec a}^T vec a}$ и
$vec c = vec a t = vec a (frac {{vec a}^T vec b}{{vec a}^T vec a})$

Нормализованный вектор

Хороший способ упростить работу над векторами — использовать вектора единичной длины. Возьмем вектор $vec v$ и получим сонаправленный вектор единичной длины. Для этого вектор разделим на его длину: $vec{nv} = frac{vec v}{|vec v|}$ . Эта операция называется нормализацией, а вектор — нормализованным.
Зная нормализованный вектор и длину исходного вектора, можно получить исходный вектор: .

Зная нормализованный вектор и исходный вектор, можно получить его длину: $|vec v| = {vec v}^T vec{nv}$ .

Хорошим преимуществом нормализованных векторов является то, что сильно упрощается формула проекции (т.к. длина равна 1, то она сокращается). Проекция вектора $vec b$ на $vec a$ единичной длины:
$t = vec a cdot vec b = {vec a}^T vec b$
$vec c = vec a {(vec a}^T vec b)$

Матрица поворота двумерного пространства

Предположим у нас есть некая фигура:

Чтобы ее нарисовать, заданы координаты ее вершин, от которых строятся линии. Координаты заданы в виде набора векторов следующим образом $vec v_i = begin{pmatrix}{v_i}_x & {v_i}_y end{pmatrix}^T$ . Наша координатная сетка задана двумя осями — единичными ортогональными (перпендикулярными) векторами. В двумерном пространстве можно получить два перпендикулярных вектора к другому вектору такой же длины следующим образом: $perp vec v = begin{pmatrix}mp v_y & pm v_x end{pmatrix}^T$ — левый и правый перпендикуляры. Берем вектор, задающим ось $X$ — $vec{aX}=begin{pmatrix} 1 & 0 end{pmatrix}^T$ и ось $Y$ — левый к нему перпендикуляр — $vec{aY}=begin{pmatrix} 0 & 1 end{pmatrix}^T$ .
Выведем новый вектор, получаемый из наших базисный векторов:
$vec{v'} = vec{aX}^T cdot v_x + vec{aY}^T cdot v_y = begin{pmatrix} 1 & 0 end{pmatrix}^T cdot v_x + begin{pmatrix} 0 & 1 end{pmatrix}^T cdot v_y = begin{pmatrix} v_x & v_y end{pmatrix}^T = vec v$
Сюрприз — он совпадает с нашим исходным вектором.

Теперь попробуем как-то изменить нашу фигуру — повернем ее на угол $alpha$ . Для этого повернем векторы и , задающих оси координат. Поворот вектора $begin{pmatrix} 1 & 0 end{pmatrix}^T$ задается косинусом и синусом угла — $vec{aX}=rotate(begin{pmatrix} 0 & 1 end{pmatrix}^T, alpha) = begin{pmatrix} cos{alpha} & sin{alpha} end{pmatrix}^T$ . А чтобы получить вектор оси $Y$ , возьмем перпендикуляр к : $vec{aY}=perp vec{aX}=begin{pmatrix} -sin{alpha} & cos{alpha} end{pmatrix}^T$ . Выполнив эту трансформацию, получаем новую фигуру:
$vec{v_i'} = vec{aX} cdot {v_i}_x + vec{aY} cdot {v_i}_y$

Вектора и являются ортонормированным базисом, потому как вектора ортогональны между собой (а значит базис ортогонален), и вектора имеют единичную длину, т.е. нормированы.

Теперь мы говорим о нескольких системах координат — базовой системы координат (назовем ее мировой), и локальной для нашего объекта (которую мы поворачивали). Удобно объединить наш набор векторов в матрицу — $R = begin{pmatrix} vec{aX} & vec{aY} end{pmatrix} = begin{pmatrix} cos{alpha} & -sin{alpha} \ sin{alpha} & cos{alpha} end{pmatrix}$
Тогда $vec{v_i'} = vec{aX} cdot {v_i}_x + vec{aY} cdot {v_i}_y = begin{pmatrix} vec{aX} & vec{aY} end{pmatrix} vec{v_i} = R cdot vec{v_i}$ .

В итоге — $vec{v_i'} = R cdot vec{v_i}$ .

Матрица $R$ , составляющая ортонормированный базис и описывающая поворот, называется матрицей поворота.

Также матрица поворота имеет ряд полезных свойств, которые следует иметь ввиду:

При , где — единичная матрица, матрица соответствует нулевому повороту (угол ), и в таком случае локальные оси совпадают с мировыми. Как рассматривали выше, матрица никак не меняет исходный вектор.
— определитель матрицы равен 1, если у нас, как обычно бывает, правая тройка векторов. , если тройка векторов левая.
$R^T = R^{-1}$ .
$R^T R = R^{-1} R = I$ .
$R^T R = begin{pmatrix}vec{aX} & vec{aY}end{pmatrix}^T begin{pmatrix}vec{aX} & vec{aY}end{pmatrix} = begin{pmatrix}vec{aX}^Tvec{aX} & vec{aX}^Tvec{aY} \ vec{aY}^Tvec{aX} & vec{aY}^Tvec{aY}end{pmatrix} = begin{pmatrix} 1 & 0 \ 0 & 1 end{pmatrix}$ .
, поворот не меняет длины вектора.
зная и , можем получить исходный вектор — $vec v = R^{-1} vec{v'} = R^T vec{v'}$ . Т.е. умножая вектор на матрицу поворота мы выполняем преобразование координат вектора из локальной системы координат объекта в мировую, но также мы можем поступать и наоборот — преобразовывать мировые координаты в локальную систему координат объекта, умножая на обратную матрицу поворота.

Теперь попробуем повернуть наш объект два раза, первый раз на угол $alpha$ , второй раз на угол $beta$ . Матрицу, полученную из угла $alpha$ , обозначим как $R_a$ , из угла $beta$ — $R_b$ . Распишем наше итоговое преобразование:
$vec{{v'}_i} = R_b R_a vec{v_i}$ .

Обозначим , тогда $vec{{v'}_i} = R_c vec{v_i}$ . И из двух операций мы получили одну. Так как поворот — это линейное преобразование (описали ее при помощи одной матрицы), множество преобразований можно описать одной матрицей, что сильно упрощает над ними работу.

Масштабирование в двумерном пространстве

Масштабировать объект достаточно просто, нужно только умножить координаты точек на коэффициент масштаба: $vec{v_i'} = s cdot vec{v_i}$ . Если мы хотим масштабировать объект на разную величину по разным осям, то формула принимает вид: $vec{v_i'} = begin{pmatrix} s_x cdot {v_i}_x & s_y cdot {v_i}_y end{pmatrix}^T$ . Для удобства переведем операцию в матричный вид: $S = begin{pmatrix} s_x & 0 \ 0 & s_y end{pmatrix}, vec{v_i'} = S cdot vec{v_i}$ .

Теперь предположим, что нам нужно повернуть и масштабировать наш объект. Нужно отметить, что если сначала масштабировать, а затем повернуть, то результат будет отличаться, от того результата, где мы сначала повернули, а затем масштабировали:

Сначала поворот, а затем масштабирование по осям:

Сначала масштабирование по осям, а затем поворот:

Как мы видим порядок операций играет большое значение, и его нужно обязательно учитывать.
Также здесь мы также можем объединять матрицы преобразования в одну:
$vec{{v'}_i} = S R vec{v_i}, space T_a = S R space Rightarrow space vec{{v'}_i} = T_a vec{v_i}$
$vec{{v'}_i} = R S vec{v_i}, space T_b = R S space Rightarrow space vec{{v'}_i} = T_b vec{v_i}$

Хотя в данном случае, если , то . Тем не менее, с порядком преобразований нужно быть очень аккуратным. Их нельзя просто так менять местами.

Векторное произведение векторов

Перейдем в трехмерное пространство и рассмотрим определенное на нем векторное произведение.
Векторное произведение двух векторов в трёхмерном пространстве — вектор, ортогональный к обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.

Для примера возьмем два трехмерных вектора — $vec a$ , $vec b$ . И в результате векторного произведения получим $vec c = vec a times vec b = begin{pmatrix}a_y cdot b_z - a_z cdot b_y & a_z cdot b_x - a_x cdot b_z & a_x cdot b_y - a_y cdot b_x end{pmatrix}^T$

Визуализируем данную операцию:

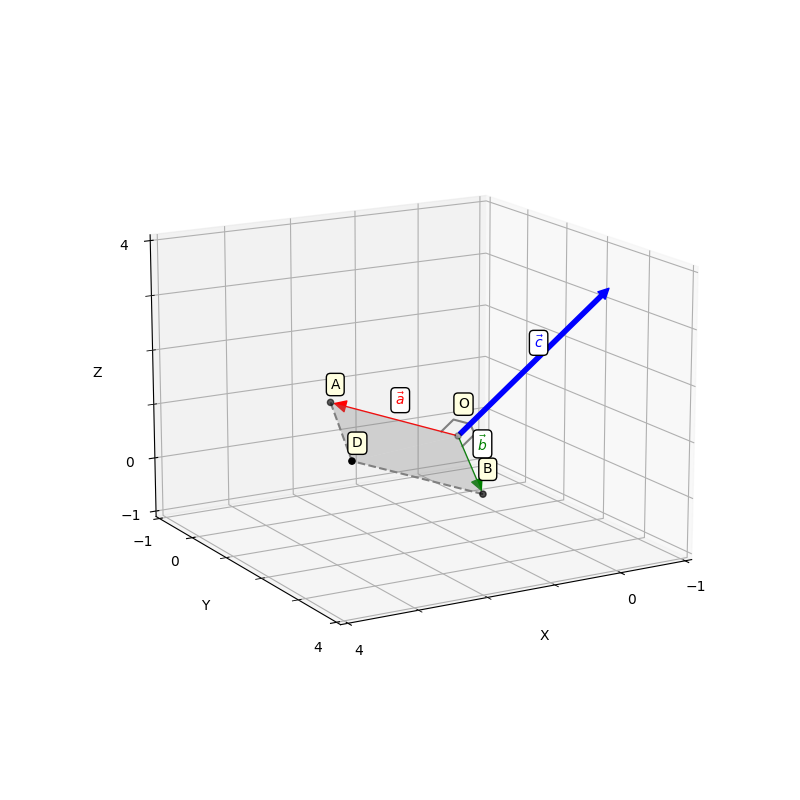
Здесь наши вектора $vec a$ , $vec b$ и $vec c$ . Вектора начинаются с начала координат, обозначенной точкой $O$ . Конечная точка вектора $vec a$ — точка $A$ . Конечная точка $vec b$ — точка $B$ . Параллелограмм из определения формируются точками $O$ , $A$ , $B$ , $D$ . Координаты точки $D$ находим как — . В итоге имеем следующие соотношения:

Два вектора образуют плоскость, а векторное произведение позволяет получить перпендикуляр к этой плоскости. Получившиеся вектора образуют образуют правую тройку векторов. Если берем обратный вектор, то получаем второй перпендикуляр к плоскости, и тройка векторов будет уже левой.

Для запоминания этой формулы удобно использовать мнемонический определитель. Пусть $i = begin{pmatrix} 1 & 0 & 0 end{pmatrix}^T, space j = begin{pmatrix} 0 & 1 & 0 end{pmatrix}^T, space k = begin{pmatrix} 0 & 0 & 1 end{pmatrix}^T$ , и мы раскладываем определить по строке как сумму определителей миноров исходной матрицы :
$vec c = vec a times vec b = begin{vmatrix} (i, j, k)^T & vec a & vec b end{vmatrix} = begin{vmatrix} i & a_x & b_x \ j & a_y & b_y \ k & a_z & b_z end{vmatrix} = i cdot begin{vmatrix} a_y & b_y \ a_z & b_z end{vmatrix} - j cdot begin{vmatrix} a_x & b_x \ a_z & b_z end{vmatrix} + k cdot begin{vmatrix} a_x & b_x \ a_y & b_y end{vmatrix} space Rightarrow$
$vec c = begin{pmatrix}a_y cdot b_z - a_z cdot b_y & a_z cdot b_x - a_x cdot b_z & a_x cdot b_y - a_y cdot b_x end{pmatrix}^T$

Некоторые удобные свойства данного произведения:

Если два вектора ортогональны и нормализованы, то вектор также будет иметь единичную длину. Параллелограмм, который образуется двумя исходными векторами, станет квадратом с длинной сторон равной единице. Т.е. площадь равна единице, отсюда длина выходного вектора — единица.

Матрица поворота трехмерного пространства.

С тем, как формировать матрицу в двумерном пространстве мы разобрались. В трехмерном она формируется уже не двумя, а тремя ортогональными векторами — . По свойствам, описанным выше, можно вывести следующие отношения между этими векторам:

Вычислить вектора этих осей сложнее, чем в матрице поворота двумерного пространства. Для примера получения этих векторов рассмотрим алгоритм, который в трехмерных движках называется lookAt. Для этого нам понадобятся вектор направления взгляда — $vec z$ и опорный вектор для оси $Y$ — $vec y$ . Сам алгоритм:

Обычно направление камеры совпадает с осью . Поэтому нормализуем и получаем ось — $vec aZ = frac{vec z}{|vec z|}$ .
Получаем вектор оси — $vec{aX} = frac{vec{y} times vec{aZ}}{|vec{y} times vec{aZ}|}$ . В итоге у нас есть два нормализованных ортогональных вектора и , описывающих оси и , при этом ось сонаправлена с входным вектором , а ось перпендикулярна к входному опорному вектору .
Получаем вектор оси из полученных и — .
В итоге

В трехмерных редакторах и движках в интерфейсах часто используются углы Эйлера для задания поворота. Углы Эйлера более интуитивно понятны — это три числа, обозначающие три последовательных поворота вокруг трех основных осей . Однако, работать с ними не очень то просто. Если попробовать выразить итоговый вектор напрямую через эти повороты, то получим довольно объемную формулу, состоящую из синусов и косинусов наших углов. Есть еще пара проблем с этими углами. Первая проблема — это то, что сами по себе углы не задают однозначного поворота, так как результат зависит от того, в какой последовательности происходили повороты — или или как-то еще. Углы Эйлера — это последовательность поворотов, а как мы помним, смена порядка трансформаций меняет итоговый результат. Вторая проблема — это gimbal lock.

Внутри же трехмерные движки чаще всего используют кватернионы, которых мы касаться не будем.

Существуют разные способы задания поворота в трехмерном пространстве, и каждый имеет свои плюсы и минусы:

Матрица поворота. С ней просто работать (т.к. это просто матрицы). Но есть логическая избыточность данных — все элементы матрицы связаны определенными условиями, так как количество элементов больше степеней свободы (12 элементов против трех степеней). Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота.
Углы Эйлера. Они интуитивно понятны, но работать с ними сложно.
Вектор оси вращения и угол порота вокруг нее. Любой возможный поворот можно описать таким образом. Поворота вектора вокруг заданной оси рассмотрим ниже.
Вектор поворота Родрига. Это трехмерный вектор, где нормализованный вектор представляет собой ось вращения, а длина вектора угол поворота. Этот способ задания поворота похож на предыдущий способ, но количество элементов здесь равно числу степеней свободы, и элементы не связаны между собой жесткими ограничениями. И мы можем взять трехмерный вектор с абсолютно случайными числами, и любой полученный вектор будет задавать какое-то возможное вращение.

Поворот вектора вокруг заданной оси

Теперь рассмотрим операцию, позволяющую реализовать поворот вектора вокруг оси.

Возьмем вектор $vec n$ — описывающий ось, вокруг которой нужно повернуть вектор $vec v$ на угол $alpha$ . Результирующий вектор обозначим как . Иллюстрируем процесс:

Вектор $vec n$ мы можем разложить сумму векторов: вектора, параллельный к вектору $vec n$ — $vec{v_parallel}$ , и вектора, перпендикулярному к вектору к вектору $vec n$ — $vec{v_{perp}}$ .
$vec v = vec{v_{parallel}} + vec{v_{perp}}$ .
Вектор $vec{v_parallel}$ — это проекция вектора $vec v$ на вектор $vec n$ . Т.к. $vec n$ — нормализованный вектор, то:
$vec{v_parallel} = vec{n} (vec{n}^T vec{v})$
Та часть $vec v$ , которая принадлежит оси вращения ( $vec{v_{parallel}}$ ) не измениться во время вращения. Повернуть нам нужно только $vec{v_{perp}}$ в плоскости перпендикулярной к $vec n$ на угол $alpha$ , Обозначим этот вектор как $vec{v_{perp rot}}$ . Тогда наш искомый вектор — $vec{v'} = vec{v_parallel} + vec{v_{perp rot}}$ .
Вектор $vec{v_{perp}}$ можем найти следующим образом:
$vec{v_{perp}} = vec v - vec{v_parallel}$
Для того, чтобы повернуть $vec{v_{perp}}$ , выведем оси $X$ и $Y$ в плоскости, в которой будем выполнять поворот. Это должны быть два ортогональных нормализованных вектора, ортогональных к $vec n$ . Один ортогональный вектор у нас уже есть — $vec{v_{perp}}$ , нормализуем его и обозначим как ось $X$ — $vec{aX} = frac{vec{v_{perp}}}{|vec{v_{perp}}|}$ .

Теперь получим вектор оси $Y$ . Это должен быть вектор, ортогональный к $vec n$ и (т.е. и к $vec{v_{perp}}$ ). Получить его можно через векторное произведение: $vec{d_y} = vec n times vec{v_{perp}}$ . Значит $vec{aY} = frac{vec{d_y}}{|vec{d_y}|}$ . По свойству векторного произведения $|vec{d_y}|$ будет равно площади параллелограмма, образуемого двумя исходными векторами ( $vec n$ и ). Так как вектора ортогональны, то у нас будет не параллелограмм, а прямоугольник, а значит $|vec{d_y}| = |vec{n}| cdot |vec{v_{perp}}|$ . $|vec{n}| = 1 space Rightarrow space |vec{d_y}| = |vec{v_{perp}}|$ . Значит $vec{aY} = frac{vec n times vec{v_{perp}}}{|vec{v_{perp}}|}$ .
Поворот двумерного вектора $vec v = begin{pmatrix} 1 & 0 end{pmatrix}^T$ на угол $alpha$ можно получить через синус и косинус — $rotate2D(vec v, alpha) = begin{pmatrix} cos{alpha} & sin{alpha} end{pmatrix}^T$ . Т.к. $vec{v_{perp}}$ в координатах полученной плоскости сонаправлен с осью $X$ , то он будет равен $begin{pmatrix} |vec{v_{perp}}| & 0 end{pmatrix}^T = begin{pmatrix} 1 & 0 end{pmatrix}^T cdot |vec{v_{perp}}|$ . Этот вектор после поворота — $rotate2D(begin{pmatrix} 0 & 1 end{pmatrix}^T, alpha) cdot |vec{v_{perp}}| = begin{pmatrix} cos{alpha} & sin{alpha} end{pmatrix}^T cdot |vec{v_{perp}}|$ . Отсюда можем вывести: $vec{v_{perp rot}} = (vec{aX} cdot cos{alpha} + vec{aY} cdot sin{alpha}) cdot |vec{v_{perp}}|$
$vec{v_{perp rot}} = (frac{vec{v_{perp}}}{|vec{v_{perp}}|} cdot cos{alpha} + frac{vec n times vec{v_{perp}}}{|vec{v_{perp}}|} cdot sin{alpha}) cdot |vec{v_{perp}}|$
$vec{v_{perp rot}} = vec{v_{perp}} cdot cos{alpha} + (vec n times vec{v_{perp}}) cdot sin{alpha}$
Теперь мы можем получить наш искомый вектор:
$vec{v'} = vec{v_{parallel}} + vec{v_{perp rot}} = vec{v_{parallel}} + vec{v_{perp}} cdot cos{alpha} + (vec n times vec{v_{perp}}) cdot sin{alpha}$

Мы разобрались с тем, как поворачивать вектор вокруг заданной оси на заданный угол, значит теперь мы умеем использовать поворот, заданный таким образом.

Получить вектор оси вращения и угол из вектора Родрига не составляет большого труда, а значит мы теперь умеем работать и с ним тоже.

Напоминаю, что матрица поворота представляет собой три базисных вектора , а углы Эйлера — три последовательных поворота вокруг осей $X$ , $Y$ , $Z$ . Значит мы можем взять единичную матрицу, как нулевой поворот , а затем последовательно поворачивать базисные вектора вокруг нужных нам осей. В результате получим матрицу поворота соответствующую углам Эйлера. Например:
$vec{aX'} = rotate((0, 0, 1)^T, angle_z, rotate((0, 1, 0)^T, angle_y, rotate((1, 0, 0)^T, angle_x, vec{aX})))$
$vec{aY'} = rotate((0, 0, 1)^T, angle_z, rotate((0, 1, 0)^T, angle_y, rotate((1, 0, 0)^T, angle_x, vec{aY})))$
$vec{aZ'} = rotate((0, 0, 1)^T, angle_z, rotate((0, 1, 0)^T, angle_y, rotate((1, 0, 0)^T, angle_x, vec{aZ})))$

Также можно отдельно вывести матрицы вращения по каждой из осей $X$ , $Y$ , $Z$ ( $R_x$ , $R_Y$ , $R_z$ соответственно) и получить итоговую матрицу последовательным их умножением:

Таким же образом можно перевести вектор поворота Родрига в матрицу поворота: также поворачиваем оси матрицы поворота, полученные от единичной матрицы.

Итак, с вращением объекта разобрались. Переходим к остальным трансформациям.

Масштабирование в трехмерном пространстве

Все тоже самое что и двумерном пространстве, только матрица масштабирования принимает вид: $S = begin{pmatrix} s_x & 0 & 0 \ 0 & s_y & 0 \ 0 & 0 & s_z end{pmatrix}$

Перемещение объекта

До этого момента точка начала локальных координат не смещалась в мировом пространстве. Так как точка начала координат нашего объекта — это его центр, то центр объект никуда не смещался. Реализовать это смещение просто: $vec{v'_i} = vec{v_i} + vec t$ , где $vec t$ — вектор, задающий смещение.

Теперь мы умеем масштабировать объект по осям, поворачивать его и перемещать.
Объединим все одной формулой: $vec{v'_i} = R cdot S cdot vec{v_i} + vec t$ :

$s_x = 0.5, space s_y = 0.5, space $$$

Чтобы упростить формулу, мы можем, как уже делали ранее, объединить матрицы $T = R cdot S space Rightarrow space vec{v'_i} = T cdot vec{v_i} + vec t$ . В итоге наше преобразование описывает матрица $T$ и вектор $vec t$ . Объединение вектора $vec t$ с матрицей $T$ еще более бы упростило формулу, однако сделать в данном случае не получится, потому как сложение здесь — это не линейная операция. Тем не менее сделать это возможно, и рассмотрим этот момент уже в следующей статье.

Заключение

Для какого-то покажется, что статья описывает очевидные вещи, кому-то может показаться наоборот немного запутанной. Тем не менее это базовый фундамент, на котором будет строиться все остальное. Векторная алгебра — является фундаментом для многих областей, так что статья может вам оказаться полезной не только в дополненной реальности. Следующая статья будет уже более узконаправленной.

Источник

Скалярное произведение

Скалярное произведение — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат. Используется в определении длины векторов и угла между ними.
$$ c = |overline a||overline b|cos(theta )$$

Обычно для скалярного произведения векторов $overline a$ и $overline b$ используется одно из следующих обозначений:

$$ c= (overline a,overline b) = overline acdotoverline b$$

Скалярным произведением двух векторов $overline a$ и $overline b$ будет скалярная величина, равная сумме попарного произведения координат векторов $overline a$ и $overline b$.

Для плоскости:
Скалярное произведение векторов $overline a = (a_x, a_y)$ и $overline b = (b_x, b_y)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y $$

Для пространства:
Скалярное произведение двух векторов в пространстве $overline a = (a_x, a_y, a_z)$ и $overline b = (b_x, b_y, b_z)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y + a_z b_z $$

Векторное произведение

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Определение:
Векторным произведением вектора $overline a$ на вектор $overline b$ в трёхмерном евклидовом пространстве называется вектор $overline c$, удовлетворяющий следующим требованиям:

длина вектора $overline c$ равна произведению длин векторов $overline a$ и $overline c$ на синус угла между ними (т. е. площади параллелограмма, образованного векторами $overline a$ и $overline b$
$$ | overline c| = | overline a| cdot | overline b|cdot sin (theta ),$$
вектор $overline c$ ортогонален каждому из векторов $overline a$ и $overline b$;
вектор $overline c$ направлен так, что тройка векторов $(overline a,overline b,overline c)$ является правой.

Понятие правой и левой тройки векторов:
Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов $(overline a,overline b,overline c)$ в трёхмерном пространстве называется правой, если с конца вектора $overline c$ кратчайший поворот от вектора $overline a$ к вектору $overline b$ виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.

Название правой и левой тройки пошло от определения направления тройки с помощью руки человека:

Правая тройка. Указательный палец к среднему пальцу двигается против часовой стрелки.

Векторное произведение обозначают:

$$overline c = overline a times overline b = [overline a, overline b]$$

Получение координат вектора $overline c$:
Если два вектора $overline a$ и $overline {b}$ представлены в правом ортонормированном базисе координатами $ overline a=(a_x,a_y,a_z), overline b=(b_x,b_y,b_z)$, то их векторное произведение имеет координаты:

$$ overline a timesoverline b = (a_yb_z — a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x).$$

Для запоминания этой формулы удобно использовать мнемонический определитель:
$$overline a timesoverline b = begin{vmatrix}
i & j & k \
a_x & a_y & a_z \
b_x & b_y & b_z \
end{vmatrix}, $$

где $i=(1,0,0), j=(0,1,0), k=(0,0,1)$.

Псевдоскалярное произведение двух векторов

Псевдоскалярным (или косым) произведением векторов $overline{a}$ и $overline{b}$ на плоскости называют число

$$c = | overline a| cdot | overline b|cdot sin (theta ),$$

где $theta$ — угол вращения (против часовой стрелки) от $overline{a}$ к $overline{b}$. Приставка «псевдо» означает, что объект может менять или не менять знак при отражениях пространства.

Псевдоскалярное произведение обозначают так:
$$c = overline a wedge overline b.$$

Если хотя бы один из векторов нулевой, то полагают $overline a wedge overline b = 0$.

Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.

С его помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.

Псевдоскалярное произведение существует только для 2-мерных векторов, его аналогом в трехмерном пространстве является смешанное произведение.

Основные свойства:

Линейность: $overline a wedge (lambda overline b + muoverline c ) = lambdaoverline awedgeoverline b + muoverline a wedge overline c$. Где $lambda, mu$ — произвольные вещественные числа.
Антикоммутативность: $overline a wedgeoverline b = -overline bwedgeoverline a$.
Ориентированная площадь треугольника ABC выражается формулой $S = (overline{AB}wedgeoverline{AC}) / 2$, а его площадь равна модулю этой величины.
$overline a wedge overline b = 0$ — необходимое и достаточное условие коллинеарности ненулевых векторов на плоскости.
Пусть заданы вектора $overline a = (a_1, a_2), overline b = (b_1, b_2)$. Тогда их псевдоскалярное произведение равно $overline a wedgeoverline b = a_1b_2 — a_2b_1$.

Использование в геометрических задачах

Пример 1. Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому достаточно посчитать косое произведение векторов $overline{P_1P_2}$ и $overline{P_1M}$ и по его знаку сделать вывод.

Пример 2. Определить, принадлежит ли точка отрезку.

Пусть точки $P_1(x_1, y_1), P_2(x_2, y_2)$ — концы заданного отрезка. Необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через $P_1, P_2$. Далее нужно определить лежит ли точка между точками $P_1$ и $P_2$. Для этого используем скалярное произведение векторов $overline{MP_1}, overline{MP_2}$. Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. $overline{P_1P_2} wedge overline{P_1M} = 0$ – косое произведение (точка лежит на прямой);
2. $(overline{MP_1}, overline{MP_2}) ≤ 0$ – скалярное произведение (точка лежит между $P_1$ и $P_2$).

Пример 3. Определить, пересекаются ли две прямые (прямые не совпадают).

Если прямые заданы точками $P_1(x_1, y_1), P_2(x_2, y_2), M_1(x_3, y_3), M_2(x_4, y_4)$, то условие их параллельности заключается в проверки косого произведения векторов $overline{P_1P_2}$ и $overline{M_1M_2}$: если оно равно нулю, то прямые параллельны, иначе — пересекаются.

Пример 4. Определить, пересекаются ли два отрезка.

Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Необходимо проверить, лежат ли концы каждого из отрезков по разные стороны относительного концов другого отрезка. Применим косое произведение векторов. Посмотрим на первый рисунок: $overline{P_1P_2}wedge overline{P_1M_2} * overline{P_1P_2}wedge overline{P_1M_1} < 0$ и $overline{M_1M_2}wedge overline{M_1P_1} * overline{M_1M_2}wedge overline{M_1P_2} < 0$. Важно обратить внимание на строгое неравенство, потому что возможен случай, при котором произведение равно нулю, но отрезки не пересекаются (отрезки лежат на одной прямой, но не имеют общих точек). Поэтому необходимо проверить, принадлежит ли хотя бы один конец каждого отрезка другому.

Еще примеры:

https://foxford.ru/wiki/informatika/primenenie-skalyarnogo-i-vektornogo-proizvedeniya
https://habr.com/en/post/147691/

Источник

Что такое произведение векторов

Определение

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.

Это одна из основных операций над векторами в векторной алгебре. Вектор, в отличие от обычного отрезка, имеет не только длину, но и направление в пространстве.

Основные типы перемножения векторов

В математике есть два основных вида умножения векторов: скалярное и векторное. Результатом первого является число, результатом второго — вектор. Оба произведения применяются к двум векторам. Также выделяют смешанное произведение векторов, которое является комбинацией двух вышеописанных. Оно применяется, когда необходимо узнать результат умножения трех векторов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Скалярное

Определение

Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Длина вектора является его модулем.

Записывается скалярное произведение двумя способами: ( (overline a,;overline b) ) или ( overline acdotoverline b.)

Алгебраические свойства скалярного произведения

Перестановочность. Произведение не меняется от перемены мест множителей: (overline acdotoverline b=overline bcdotoverline a.)
Сочетательность относительно числа. Умножение одного из векторов на число равносильно умножению обоих векторов на это число: ((lambdaoverline a)cdotoverline b=lambda(overline acdotoverline b)(lambdaoverline a)cdot(muoverline b)=(lambdamu)(overline acdotoverline b).)
Распределительный закон. Скалярное произведение суммы двух векторов на третий равносильно сумме скалярных произведений этих векторов на третий вектор: ((overline a+overline b)cdotoverline c=overline acdotoverline c+overline bcdotoverline c.)

Примечание

Таким образом, при выполнении алгебраических действий, связанных со скалярным произведением, с векторами можно обращаться как с числами.

Геометрические свойства скалярного умножения

Скалярное произведение вектора на него же равняется квадрату его модуля: (overline acdotoverline a=overline a^2=overline{left|aright|}cdotoverline{left|aright|}cdotcosleft(0right)=left|overline a^2right|.)
Если угол между векторами острый (меньше (90^circ)), то скалярное произведение этих векторов больше нуля.
Если угол между векторами тупой (больше (90^circ)), то их скалярное произведение меньше нуля.
Если вектора перпендикулярны (угол равен (90^circ)), то их скалярное произведение будет равняться нулю.
Если координаты перемножаемых векторов известны, то их скалярное произведение будет равняться сумме произведений соответствующих координат:( overline acdotoverline b=a_xcdot b_x+a_ycdot b_y+a_zcdot b_z.)

Геометрический смысл

Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго вектора на первый.

(overline acdotoverline b=left|overline aright|cdot пр_overline aoverline b=overline{left|bright|}cdot пр_overline boverline a)

(пр_overline boverline a=frac{overline acdotoverline b}{left|overline bright|})

Физический смысл

Скалярное произведение применяется для расчета работы, выполняемой при перемещении материальной точки вдоль вектора (overline s) под действием силы (overline F), приложенной под некоторым углом (varphi.)

Физический смысл скалярного произведения

Рисунок 1. Физический смысл скалярного произведения

Силу (overline F) необходимо разложить на ортогональные компоненты (overline{F_1}) и (overline{F_2}.) Тогда (overline{F_1}) будет являться проекцией силы (overline F) на вектор (overline s:)

(left|overline{F_1}right|=left|overline Fright|cdotcosleft(varphiright).)

В свою очередь, работа A вычисляется по формуле:

(A=left|overline{F_1}right|cdotleft|overline Sright|.)

Соединив данные формулы получим:

(A=left|overline Fright|cdotleft|overline Sright|cdotcosleft(varphiright),)

что является скалярным произведением векторов (overline F) и (overline s:)

(A=overline Fcdotoverline S.)

Векторное

Определение

Векторным произведением векторов overline a и overline b называют перпендикулярный им вектор overline c из правой тройки, модуль которого равняется произведению модулей векторов overline a и overline b на синус угла между ними.

Упорядоченная тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму совершается против часовой стрелки. В противном случае такая тройка называется левой.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Векторное произведение может выражаться в записи двумя способами: (overline atimesoverline b) и (lbrackoverline a,overline brbrack.)

Алгебраические свойства

Антиперестановочность. В отличие от скалярного произведения, в векторном при перемене мест множителей знак меняется на противоположный: (overline atimesoverline b=-(overline btimesoverline a))
Сочетательность относительно числа. Как и в случае со скалярным умножением, произведение числа на один из векторов равняется произведению его на другой или на оба вектора: ((lambdaoverline a)timesoverline b=overline atimes(lambdaoverline b)=lambda(overline atimesoverline b).)
Распределительный закон. Векторное произведение суммы двух векторов на третий равносильно сумме векторных произведений этих векторов на третий вектор: ((overline a+overline b)timesoverline c=overline atimesoverline c+overline btimesoverline c.)

Из этого следует, что при выполнении алгебраических действий, связанных с векторным произведением, скобки можно раскрывать так же, как при работе с числами, с поправкой на правило антиперестановочности.

Геометрические свойства

Если вектора (overline a) и (overline b) параллельны, то их векторное произведение равняется нулю.
Векторное произведение векторов с известными координатами выражается в матричном виде: (overline atimesoverline b=begin{vmatrix}i&j&k\a_x&a_y&a_z\b_x&b_y&b_zend{vmatrix}=left(begin{vmatrix}a_y&a_z\b_y&b_zend{vmatrix};;-begin{vmatrix}a_x&a_z\b_x&b_zend{vmatrix};;begin{vmatrix}a_x&a_y\b_x&b_yend{vmatrix}right).)

Геометрический смысл

Модуль векторного произведения двух векторов равняется площади параллелограмма, сторонами которого являются эти вектора.

Геометрический смысл векторного произведения

Рисунок 2. Геометрический смысл векторного произведения

Из определения векторного умножения следует, что модуль полученного вектора равняется произведению модулей исходных векторов на синус угла между ними:

Площадь параллелограмма вычисляется так:

(S=left|overline aright|cdot h, где h=left|overline bright|cdotsinleft(varphiright).)

Таким образом, получаем:

Отсюда следует формула для площади треугольника:

(S_bigtriangleup=frac12left|overline atimesoverline bright|)

Физический смысл

В физике векторное произведение применяется для расчета момента силы, приложенной к одной точке относительно другой:

(overline M=overline{AB}timesoverline F)

Смешанное умножение векторов

Фактически, смешанное произведение векторов представляется как скалярное умножение одного вектора на векторное произведение двух других. Результатом смешанного произведения является число.

Свойства смешанного умножения

((overline atimesoverline b)cdotoverline c=overline acdot(overline btimesoverline c)=overline acdotoverline bcdotoverline c.)
Если (overline acdotoverline bcdotoverline c) больше нуля, тройка векторов — правая.
Если( overline acdotoverline bcdotoverline c) меньше нуля, тройка векторов — левая.
Если вектора (overline a, overline b) и (overline c) компланарны, то их смешанное произведение равняется нулю.

Геометрический смысл

Если вектора overline a, overline b и overline c не компланарны, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах. Число будет положительным, если тройка векторов правая, и отрицательным, если тройка левая.

(V_{пар.}=overline acdotoverline bcdotoverline c)

Следствием этого является формула нахождения объема пирамиды:

(V_{пир.}=frac16left(overline acdotoverline bcdotoverline cright))

Произведение векторов, примеры и решения

Задача №1

Даны вектора (overline a=(-1,;0,;3) и overline b=(2,;-3,;1).)

Найти их скалярное произведение.

Решение

Возьмем формулу скалярного произведения для векторов с известными координатами:

(overline acdotoverline b=a_xcdot b_x+a_ycdot b_y+a_zcdot b_z) и подставим имеющиеся значения:

(overline acdotoverline b=(-1)cdot2+0cdot(-3)+3cdot1=1)

Задача №2

Найти площадь треугольника с известными координатами угловых точек

Задача №2

Координаты точек: (A(-1,;2,;3), B(0,;-2,;1), C(1,;2,;1))

Решение

Для решения этой простейшей задачи из геометрии воспользуемся следствием геометрического смысла векторного произведения:

(S_bigtriangleup=frac12left|overline atimesoverline bright|)

В данном случае треугольник построен на векторах( overline{AB}) и (overline{AC}). Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:

(overline{AB}=(0-(-1),;(-2)-2,;1-3)=(1,;-4,;-2))

(overline{AC}=(1-(-1),;2-2,;1-3)=(2,;0,;-2))

Векторное произведение векторов с известными координатами выполняется в матричном виде:

(overline atimesoverline b=begin{vmatrix}i&j&k\a_x&a_y&a_z\b_x&b_y&b_zend{vmatrix}=left(begin{vmatrix}a_y&a_z\b_y&b_zend{vmatrix};;-begin{vmatrix}a_x&a_z\b_x&b_zend{vmatrix};;begin{vmatrix}a_x&a_y\b_x&b_yend{vmatrix}right))

Подставляем значения векторов( overline{AB}) и (overline{AC}) в матрицу и производим вычисления:

(overline{AB}timesoverline{AC}=begin{vmatrix}i&j&k\1&-4&-2\2&0&-2end{vmatrix}=left(ibegin{vmatrix}-4&-2\0&-2end{vmatrix};;-jbegin{vmatrix}1&-2\2&-2end{vmatrix};;kbegin{vmatrix}1&-4\2&0end{vmatrix}right)=8i-2j+8k)

Подставляем полученное значение в формулу вычисления площади треугольника, учитывая, что в ней фигурирует модуль произведения:

(S_bigtriangleup=frac12left|overline{AB}timesoverline{AC}right|=frac12sqrt{8^2+{(-2)}^2+8^2}=sqrt{132}=11.49)

Источник

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.

Векторное Произведение Векторов. Свойства, определение

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

, где
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

Антикоммутативность
Свойство дистрибутивностиили
Сочетательное свойствоили, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.
По определению
и
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна. А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F]. Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до векторов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!

Смешанное произведение векторов: свойства примеры и решения, геометрический смысл смешанного произведения векторов

Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение.

В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.

Термин

Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.

Определение 1

Смешанным произведением a→, b→ и d→ является та величина, которая равняется скалярному произведению a→×b→ и d→ , где a→×b→ — умножение a→ и b→ . Операцию умножения a→, b→ и d→ зачастую обозначают a→·b→·d→ . Можно преобразовать формулу так:a→·b→·d→=(a→×b→,d→) .

Умножение в системе координат

Мы можем умножить вектора, если они указаны на координатной плоскости.
Возьмем i→, j→, k→
Произведение векторов в данном конкретном случае будет иметь следующий вид:a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

Из этого следует:
a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→
Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
a→×b→=( ayazbybz·i→-axazbxbz·j→+axaybxby·k→, dx·i→+dy·j→+dz·k→)==ayazbybz·dx-axazbxbz·dy+axaybxby·dz=axayazbxbybzdxdydz
Таким образом, можно сделать вывод, что:
a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz

Определение 3

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz .

Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.

(λ·a→)·b→·d→=a→·(λ·b→)·d→=a→·b→·(λ·d→)=λ·a→·b→·d→ λ∈R ;
a→·b→·d→=d→·a→·b→=b→·d→·a→; a→·d→·b→=b→·a→·d→=d→·b→·a→ ;
(a(1)→+a(2)→)·b→·d→=a(1)→·b→·d→+a(2)→·b→·d→a→·(b(1)→+b(2)→)·d→=a→·b(1)→·d→+a→·b(2)→·d→a→·b→·(d(1)→+d(2)→)=a→·b→·d(2)→+a→·b→·d(2)→

Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль. Результатом умножения также будет нуль в том случае, если два или больше множителей равны.

Действительно, если a→=b→ , то, следуя определению векторного произведения [a→×b→]=a→·b→·sin 0 =0 , следовательно, смешанное произведение равно нулю, так как ([a→×b→], d→)=(0→, d→)=0 .

Если же a→=b→ или b→=d→ , то угол между векторами [a→×b→] и d→ равен π2 . По определению скалярного произведения векторов ([a→×b→], d→)=[a→×b→]·d→·cosπ2=0 .

Свойства операции умножения чаще всего требуются во время решения задач. Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.

Пример 1

Докажите равенство ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→) , где λ — некоторое действительное число.

Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:

([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→) Мы разобрали, что (([a→×b→], b→)=0. Из этого следует, что ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)==([a→×b→], d→)+([a→×b→], λ·a→)+0=([a→×b→], d→)+([a→×b→], λ·a→)

Согласно первому свойству ([a⇀×b⇀], λ·a→)=λ·([a⇀×b⇀],a→) , а ([a⇀×b⇀], a→)=0 . Таким образом, ([a⇀×b⇀], λ·a→) . Поэтому,
([a⇀×b⇀], d→+λ·a→+b→)=([a⇀×b⇀], d→)+([a⇀×b⇀], λ·a→)==([a⇀×b⇀], d→)+0=([a⇀×b⇀], d→)

Равенство доказано.

Пример 2

Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.

Решение

Исходя из условия, можно представить пример в виде неравенства a→×b→, d→≤a→·b→·d→ .

По определению, преобразуем неравенство a→×b→, d→=a→×b→·d→·cos(a→×b→^, d→)==a→·b→·sin(a→, b→^)·d→·cos([a→×b→^], d)

Используя элементарные функции, можно сделать вывод, что 0≤sin(a→, b→^)≤1, 0≤cos([a→×b→^], d→)≤1 .

Из этого можно сделать вывод, что
(a→×b→, d→)=a→·b→·sin(a→, b→)^·d→·cos(a→×b→^, d→)≤≤a→·b→·1·d→·1=a→·b→·d→

Неравенство доказано.

Разбор типовых задач

Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz .

Пример 3

В прямоугольной системе координат представлены 3 вектора с такими координатами: a→=(1, -2, 3), b→(-2, 2, 1), d→=(3,-2, 5) . Необходимо определить, чему равно произведение указанных векторов a→·b→·d→ .

Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz=1-23-2213-25==1·2·5+(-1)·1·3+3·(-2)·(-2)-3·2·3-(-1)·(-2)·5-1·1·(-2)=-7

Пример 4

Необходимо найти произведение векторовi→+j→, i→+j→-k→, i→+j→+2·k→ , где i→,j→, k→ — орты прямоугольной декартовой системы координат.

Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i→+j→=(1, 1, 0)i→+j→-k→=(1, 1, -1)i→+j→+2·k→=(1, 1, 2)

Используем формулу, которая использовалась выше
i→+j→×(i→+j→-k→, (i→+j→+2·k→)=11011-1112=0i→+j→×(i→+j→-k→, (i→+j→+2·k→)=0

Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.

Пример 5

В прямоугольной системе координат расположены три вектора a→,b→ и d→ , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4, 2 и 3. Необходимо умножить вектора.

Обозначим c→=a→×b→ .

Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a→·b→·d→=([a→×b→], d→)=c→,d→=c→·d→·cos(c→, d→^) .

Используем длину вектора d→ , указанную в условии примера: a→·b→·d→=c→·d→·cos(c→, d→^)=3·c→·cos(c→, d→^) . Необходимо определить с→и с→, d→^ . По условию a→,b→^=π2, a→=4, b→=2 .

Вектор c→ найдем с помощью формулы: c→=[a→×b→]=a→·b→·sina→, b→^=4·2·sinπ2=8 Можно сделать вывод, что c→ перпендикулярен a→ и b→ . Вектора a→, b→, c→ будут являться правой тройкой, так использована декартовая система координат.

Векторы c→ и d→ будут однонаправленными, то есть, c→,d→^=0 . Используя выведенные результаты, решаем пример a→·b→·d→=3·c→·cos(c→, d→^)=3·8·cos 0=24 .

a→·b→·d→=24 .

Геометрический смысл

Используем множители a→, b→ и d→ .

Вектора a→, b→ и d→ исходят от одной точки. Используем их как стороны для построения фигуры.

Обозначим, что c→=[a→×b→]. Для данного случая можно определить произведение векторов как a→·b→·d→=c→·d→·cos(c→, d→^)=c→·npc→d→ , где npc→d→ — числовая проекция вектора d→ на направление вектора c→=[a→×b→] .

Абсолютная величина npc→d→ равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a→, b→ и d→ в качестве сторон. Исходя из этого, следует уточнить, что c→=[a→×b→] перпендикулярен a→ и вектору и вектору согласно определению умножения векторов. Величина c→=a→xb→ равняется площади параллелепипеда, построенного на векторах a→ и b→ .

Делаем вывод, что модуль произведения a→·b→·d→=c→·npc→d→ равен результату умножения площади основания на высоту фигуры, которая построена на векторах a→, b→ и d→ .

Определение 4

Абсолютная величина векторного произведения является объемом параллелепипеда: Vпараллелепипида=a→·b→·d→ .

Данная формула и является геометрическим смыслом.

Определение 5

Объем тетраэдра, который построен на a→,b→ и d→ , равняется 1/6 объема параллелепипеда Получаем, Vтэтраэда=16·Vпараллелепипида=16·a→·b→·d→ .

Источник

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

$vec{a}(x_{a};: y_{a};: z_{a})$

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

$vec{a}=vec{AB}(x_{B}-x_{A};: y_{B}-y_{A};: z_{B}-z_{A})$

Длина вектора vec{AB} в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

$|vec{a}|=sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}=sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}$ Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

$x_{M}=frac{x_{A}+x_{B}}{2};: : y_{M}=frac{y_{A}+y_{B}}{2};: : z_{M}=frac{z_{A}+z_{B}}{2}$

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

$vec{a}+vec{b}=vec{c}(x_{a}+x_{b};: y_{a}+y_{b};: z_{a}+z_{b})$

Разность векторов:

$vec{a}-vec{b}=vec{d}(x_{a}-x_{b};: y_{a}-y_{b};: z_{a}-z_{b})$

Произведение вектора на число:

$lambda cdot vec{a}=vec{p}(lambda x_{a};: lambda y_{a};:lambda z_{a} )$

Скалярное произведение векторов:

$vec{a}cdot vec{b}=|vec{a}|cdot |vec{b}|cdot cosvarphi =x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}$

Косинус угла между векторами:

$cosvarphi =frac{vec{a}cdot vec{b}}{|vec{a}|cdot vec{|b|}}=frac{x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}}{sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}cdot sqrt{x^{2}_{b}+y^{2}_{b}+z^{2}_{b}}}$

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами vec{AE} и vec{BK} . Для этого нужны их координаты.

$, \ A(0;0;0)\ B(1;0;0)\ E(frac{1}{2};0;1)\ K(1;frac{1}{2};1)$

Запишем координаты векторов:

$vec{AE}left (frac{1}{2};0;1 right )$

$vec{BK}left (0;frac{1}{2};1 right )$

и найдем косинус угла между векторами vec{AE} и vec{BK} :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

$Aleft ( frac{1}{2};-frac{1}{2};0 right )$

$Bleft ( frac{1}{2};frac{1}{2};0 right )$

$Cleft ( -frac{1}{2};frac{1}{2};0 right )$

Из прямоугольного треугольника AOS найдем $OS=frac{sqrt{2}}{2}.$

Координаты вершины пирамиды: $Sleft ( 0;0;frac{sqrt{2}}{2} right ).$

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

$Eleft ( frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

$Kleft ( -frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

Найдем координаты векторов и :

$overrightarrow{AE}left ( -frac{1}{4};frac{3}{4};frac{sqrt{2}}{4} right )$

$overrightarrow{BK}left ( -frac{3}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

и угол между ними:

$cosvarphi =frac{overrightarrow{AE}cdot overrightarrow{BK}}{left |overrightarrow{AE} right |cdot left |overrightarrow{BK} right |}=frac{1}{6}$

Покажем теперь, как вписать систему координат в треугольную призму.

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

$A_{1}(0;0;1)$

$B(frac{1}{2};frac{sqrt{3}}{2};0)$

$B_{1}(frac{1}{2};frac{sqrt{3}}{2};1)$

$C_{1}(-frac{1}{2};frac{sqrt{3}}{2};1)$

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

$D(frac{1}{4};frac{sqrt{3}}{4};1)$

Найдем координаты векторов и $overrightarrow{BC}_{1}$ , а затем угол между ними:

$overrightarrow{AD}(frac{1}{4};frac{sqrt{3}}{4};1)$

$overrightarrow{BC_{1}}(-1;0;1)$

$cosvarphi =frac{overrightarrow{AD}cdot overrightarrow{BC_{1}}}{left |overrightarrow{AD} right |cdot left |overrightarrow{BC_{1}} right |}=frac{3}{2sqrt{10}}$

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

$left{begin{matrix} A+C+D=0\ 2A-2B+D=0\ 4A+B+2C+D=0 end{matrix}right.$ .

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

$left{begin{matrix} A+C-2=0\ 2A-2B-2=0\ 4A+B+2C-2=0 end{matrix}right.$ ;

$left{begin{matrix} A+C=2\ A-B=1\ 4A+B+2C=2 end{matrix}right.$ .

Выразим C и B через A и подставим в третье уравнение:

$left{begin{matrix} C=2-A\ B=A-1\ 4A+A-1+4-2A=2 end{matrix}right.$ .

Решив систему, получим:

$, \ A=-frac{1}{3}\ , \ B=-frac{4}{3}\ , \ C=frac{7}{3}$

Уравнение плоскости MNK имеет вид:

$-frac{1}{3}x-frac{4}{3}y+frac{7}{3}z-2=0.$

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку $M(x_{0}, y_{0}, z_{0}),$ имеет вид:

$A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0.$

Угол между плоскостями равен углу между нормалями к этим плоскостям:

$cosvarphi =frac{left |vec{n}_{1}cdot vec{n}_{2} right |}{|vec{n}_{1}|cdot |vec{n}_{2}|}$

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть: $vec{n}_{1}=overrightarrow{AC}(1;1;0).$

Напишем уравнение плоскости AEF.

$, \ A(0;0;0)\ E(frac{1}{2};0;1)\ , \ F(0;frac{1}{2};1)$

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

$left.begin{matrix} A\ , \ E\ , \ F end{matrix}right|$ $, \ 0cdot A+0cdot B+0cdot C+D=0\ , \ frac{1}{2}cdot A+0cdot B+1cdot C+D=0\ , \ 0cdot A+frac{1}{2}cdot B+1cdot C+D=0$

Упростим систему:

$left{begin{matrix} D=0\ frac{1}{2}A+C=0\ , \ frac{1}{2}B+C=0 end{matrix}right.$ .

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

$cosvarphi =frac{|2+2|}{sqrt{2}cdot sqrt{9}}=frac{4}{sqrt{2}cdot 3}=frac{4}{sqrt{2}cdot 3}=frac{2sqrt{2}}{3}$

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор $vec{n_{1}}(1;0;0)$ .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

$B_{1}left ( 5;, 0;, sqrt{3} right )$

Координаты вектора $overrightarrow{B_{1}D}$ — тоже:

$overrightarrow{B_{1}D}left ( -5;, sqrt{33};, -sqrt{3} right )=overrightarrow{n}_{2}$

Находим угол между плоскостями, равный углу между нормалями к ним:

$cos, varphi =frac{5}{sqrt{25+33+3}}=frac{5}{sqrt{61}}$

Зная косинус угла, находим его тангенс по формуле

$1+tg^{2}varphi =frac{1}{cos^{2}varphi }$

Получим:
$tg, varphi =frac{6}{5}.$

Ответ: $frac{6}{5}.$

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

$sin, varphi =frac{left | overrightarrow{n}cdotoverrightarrow{a} right |}{left | overrightarrow{n} right |cdot |overrightarrow{a}|}$

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

$Eleft ( 1;, frac{1}{2};, 1 right )$

Находим координаты вектора $overrightarrow{AE}left ( 0;, frac{1}{2};, 1 right )$ .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

$sin, varphi =frac{left | overrightarrow{AC}cdot overrightarrow{AE} right |}{|overrightarrow{AC}|cdot|overrightarrow{AE}|}=frac{2}{2cdot sqrt{2}cdot sqrt{5}}=frac{1}{sqrt{10}}$

Ответ: $frac{1}{sqrt{10}}.$

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}$

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = $frac{6}{sqrt{5}}$ . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

$A_{1}left ( 0, ;0;, frac{6}{sqrt{5}} right )$

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

$left.begin{matrix} A_{1}\ B\ D end{matrix}right|$ $begin{matrix} frac{6}{sqrt{5}}C+D=0\ sqrt{10}A+D=0\ 3sqrt{10}B+D=0 end{matrix}$

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}=frac{6sqrt{10}}{sqrt{50+36+4}}=frac{6sqrt{10}}{sqrt{90}}=2.$

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник