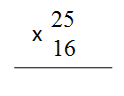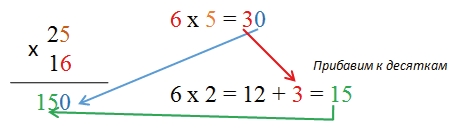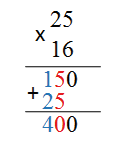Часто нужно с использованием закона умножения вычислить произведения натуральных чисел по порядку, начиная с (1).
Например,
1⋅2⋅3⋅4⋅5⋅6⋅7
и т. д. Не всегда важно вычислить числовое произведение. Чтобы можно было короче записать выражения такого вида, в математике используется знак «(!)».
Произведение всех натуральных чисел от 1 до (n) включительно называется факториалом числа n и записывается
n!
(читается как «эн факториал»).
Принято, что (0! = 1).
Пример:
1 задание.
Вычисли значение выражения.
a)
5!+4!=5⋅4⋅3⋅2⋅1+4⋅3⋅2⋅1=120+24=144
.
b)
7!−5!4!=7⋅6⋅5⋅4!−5⋅4!4!=5⋅4!(42−1)4!=5⋅41=205
((4!) выносится за скобки. В дроби равные факториалы можно сокращать).
c)
80!79!+59!58!=80⋅79!79!+59⋅58!58!=80+59=139
.
Каждый больший факториал можно выразить меньшим факториалом, т. е.
(n! = n(n-1)! = n(n-1)(n-2)! = n(n-1)(n-2)(n-3)!) и т. д.
Пример:
2 задание.
Сократи дробь:
.
3 задание.
Упрости выражение:
.
При увеличении значения (n) значение (n!) стремительно возрастает. Знак факториала удобно использовать, если нужно записывать большие числа.
Пример:
сколькими различными способами можно составить список учеников, если в нём должно быть (25) различных учеников?
1⋅2⋅3⋅…⋅24⋅25=25!
Ответ: список можно составить (25!) различными способами.
Содержание:
- Определение натурального числа
- Сложение натуральных чисел
- Умножение натуральных чисел
Определение натурального числа
Определение
Натуральными числами называются числа, которые используются при счете или для указания
порядкового номера предмета среди однородных предметов.
Например. Натуральными будут такие числа: $2,37,145,1059,24411$
Натуральные числа, записанные в порядке возрастания, образуют числовой ряд. Он начинается с наименьшего натурально числа 1.
Множество всех натуральных чисел обозначают $N={1,2,3, dots n, ldots}$. Оно бесконечно,
так как не существует наибольшего натурального числа. Если к любому натуральному числу прибавить единицу, то получаем натуральное число,
следующее за данным числом.
Пример
Задание. Какие из следующих чисел являются натуральными?
$$-89 ; 7 ; frac{4}{3} ; 34 ; 2 ; 11 ; 3,2 ; sqrt[3]{129} ; sqrt{5}$$
Ответ. $7 ; 34 ; 2 ; 11$
На множестве натуральных чисел вводится две основные арифметические операции —
сложение и
умножение.
Для обозначения этих операций используются соответственно символы » + « и
» • « (или » × «).
Сложение натуральных чисел
Каждой паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число $s$, называемое суммой. Сумма
$s$ состоит из стольких единиц, сколько их содержится в числах $n$ и $m$. О числе
$s$ говорят, что оно получено в результате сложения чисел $n$ и $m$, и пишут
$$n+m=s$$
Числа $n$ и $m$ называются при этом слагаемыми. Операция сложения натуральных чисел обладает следующими свойствами:
- Коммутативность: $n+m=m+n$
- Ассоциативность: $(n+m)+k=n+(m+k)$
Подробнее о сложении чисел читайте по ссылке.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму чисел:
$13+9 quad$ и $ quad 27+(3+72)$
Решение. $13+9=22$
Для вычисления
второй суммы, для упрощения вычислений, применим к ней вначале свойство ассоциативности сложения:
$$27+(3+72)=(27+3)+72=30+72=102$$
Ответ. $13+9=22 quad;quad 27+(3+72)=102$
Умножение натуральных чисел
Каждой упорядоченной паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число
$r$, называемое их произведением. Произведение $r$ содержит стольких единиц, сколько их содержится в числе
$n$, взятых столько раз, сколько единиц содержится в числе $m$. О числе
$r$ говорят, что оно получено в результате умножения чисел $n$ и $m$, и пишут
$n cdot m=r quad $ или $ quad n times m=r$
Числа $n$ и
$m$ называются множителями или сомножителями.
Операция умножения натуральных чисел обладает следующими свойствами:
- Коммутативность: $n cdot m=m cdot n$
- Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
Подробнее о умножении чисел читайте по ссылке.
Пример
Задание. Найти произведение чисел:
12$cdot 3 quad $ и $ quad 7 cdot 25 cdot 4$
Решение. По определению операции умножения:
$$12 cdot 3=12+12+12=36$$
Ко второму произведению применим свойство ассоциативности умножения:
$$7 cdot 25 cdot 4=7 cdot(25 cdot 4)=7 cdot 100=700$$
Ответ. $12 cdot 3=36 quad;quad 7 cdot 25 cdot 4=700$
Операция сложения и умножения натуральных чисел связаны законом дистрибутивности умножения относительно сложения:
$$(n+m) cdot k=n cdot k+m cdot k$$
Сумма и произведение любых двух натуральных чисел всегда есть число натуральное, поэтому множество всех натуральных чисел
замкнуто относительно операций сложения и умножения.
Так же на множестве натуральных чисел можно ввести операции
вычитания и
деления, как операции обратные к операциям
сложения и умножения соответственно. Но эти операции не будут однозначно определенны для любой пары натуральных чисел.
Свойство ассоциативности умножения натуральных чисел позволяет ввести понятие натуральной степени натурального числа:
$n$-й степенью натурального числа $m$ называется натуральное число
$k$, полученное в результате умножения числа $m$ самого на себя $n$ раз:
Для обозначения $n$-й степени числа $m$ обычно используется запись: $m^{n}$, в котором число
$m$ называется lt strong>основанием степени lt /strong>, а число $n$ — показателем степени.
Пример
Задание. Найти значение выражения $2^{5}$
Решение. По определению натуральной степени натурального числа это выражение можно записать следующим образом
$$2^{5}=2 cdot 2 cdot 2 cdot 2 cdot 2=32$$
Ответ. $2^{5}=32$
Читать дальше: что такое рациональное число.
Факториа́л числа n (лат. factorialis — действующий, производящий умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:
Например:
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Последовательность факториалов неотрицательных целых чисел начинается так:
- 1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, … (последовательность A000142 в OEIS)
Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция 
Содержание
- 1 Свойства
- 1.1 Рекуррентная формула
- 1.2 Комбинаторная интерпретация
- 1.3 Связь с гамма-функцией
- 1.4 Формула Стирлинга
- 1.5 Разложение на простые числа
- 1.6 Другие свойства
- 2 Обобщения
- 2.1 Двойной факториал
- 2.2 Кратный факториал
- 2.3 Убывающий факториал
- 2.4 Возрастающий факториал
- 2.5 Праймориал или примориал
- 2.6 Суперфакториалы
- 2.7 Субфакториал
- 3 Ссылки
- 4 См. также
- 5 Примечания
Свойства
Рекуррентная формула
Комбинаторная интерпретация
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:
ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA
Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.
Связь с гамма-функцией
Амплитуда и фаза факториала комплексного аргумента.
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.
Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как
Поскольку 

Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что
- 100! ≈ 9,33×10157;
- 1000! ≈ 4,02×102567;
- 10 000! ≈ 2,85×1035 659.
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые множители в степени
Таким образом,
где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.
Другие свойства
- Для натурального числа n
Обобщения
Двойной факториал
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,
По определению полагают 0!! = 1.
Последовательность значений n!! начинается так:
- 1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, … (последовательность A006882 в OEIS).
Кратный факториал
m-Кратный факториал числа n обозначается 
Пусть число n представимо в виде 


Двойной факториал является частным случаем m-кратного факториала для m = 2.
Кратный факториал связан с гамма-функцией следующим соотношением[2]:
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Убывающий факториал даёт число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Праймориал или примориал (англ. primorial) числа n обозначается n# и определяется как произведение всех простых чисел, не превышающих n. Например,
- 11# = 12# = 2 · 3 · 5 · 7 · 11 = 2310.
Последовательность праймориалов (включая 
- 1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, … (последовательность A002110 в OEIS).
Суперфакториалы
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен
(поскольку устоявшегося обозначения нет, используется функциональное).
В общем
Последовательность суперфакториалов чисел n⩾0 начинается так:
- 1, 1, 2, 12, 288, 34 560, 24 883 200, … (последовательность A000178 в OEIS).
Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:
- 1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000 … (последовательность A055462 в OEIS)
Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение первых n (m−1)-уровневых факториалов, то есть
где 

Субфакториал
Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.
Ссылки
- Онлайн Калькулятор Факториалов
См. также
- Факторион
Примечания
- ↑ «Энциклопедия для детей» Аванта+. Математика.
- ↑ wolframalpha.com.
| |
|---|
| Плюс ( + ) • Минус ( − ) • Знак умножения ( · или × ) • Знак деления ( : или / ) • Знак корня ( √ ) • Знак равенства ( =, ≈, ≡ и др.) • Знаки неравенства ( ≠, >, < и др.) • Бесконечность ( ∞ ) • Знак интеграла ( ∫ ) • Факториал ( ! ) • Вертикальная черта ( | ) • Знак градуса ( ° ) • Минута градуса ( ′ ) • Секунда градуса ( ″ ) • Штрих ( ′ ) • Звёздочка ( * ) • Обратная косая черта, бэкслеш ( ) • Процент ( % ) • Промилле ( ‰ ) • Тильда ( ~ ) • Циркумфлекс ( ^ ) • Плюс-минус ( ± ) • Обелюс ( ÷ ) • Десятичный разделитель ( , или . ) |
| Математика • История математических обозначений |
|
Факториал — это произведение всех натуральных чисел от единицы до данного числа включительно. Факториалы широко используются в комбинаторике. Факториал обозначается знаком «!». А вот формула факториала: 1 * 2 * 3 * 4 * … * n = n! автор вопроса выбрал этот ответ лучшим Факториал числа N есть количество всевозможных комбинаций каких-либо N объектов. Объясню на примере. Есть два шара. Первый помечен цифрой 4, второй цифрой 6. В данном случае, даны две цифры — 4 и 6, и возможно составить только две комбинации 46 и 64. Это и есть факториал числа 2, т.е. 2! = 2. Теперь посчитаем 3!. Даны 3 шара с тремя различными цифровыми пометками на каждом. Допустим, это цифры 8, 5, 3. Количество возможных комбинаций: 853, 538, 358, 385, 583, 835. Значит, 3! = 6. Факториал числа можно рассчитать по формуле: n! = 1*2*…*n Ксарфакс 6 лет назад Факториал — это термин, с которым сталкиваются уже в старших классах школы и на изучении высшей математики в институте. Это латинский термин. Он обозначается восклицательным знаком — !. Факториалом числа n называется произведение всех натуральных чисел от единицы до числа n включительно. Вот формула: n! = 1*2*…*(n-1)*n. То есть факториал имеет место только для тех чисел, которые >= 0 и являются целыми. Есть интересный момент — это факториал 0, он равен 1. Значения: 0! = 1 1! = 1 2! = 1*2 = 2 3! = 1*2*3 = 6 4! = 1*2*3*4 = 24 5! = 1*2*3*4*5 = 120 Суперфакториал Это произведение первых n факториалов. Например, sf(3) = 1! * 2! * 3! = 12. Этот термин был определён относительно недавно, в 1995 году. Это сделали: Применение факториала Комбинаторика, функциональный анализ, теория чисел. Dilyara K 5 лет назад Факториалом называют произведение всех чисел (натуральных) от единицы до n. Допустим факториал числа 6 будет записан так — 6!. Смысл факториала в том, что он дает число всех комбинаций, которые могут быть записаны для данного числа элементов. Например 6! будет равен 720, значит существует 720 комбинаций, которые можно сделать с 6 элементами (допустим есть шесть букв и из них можно составить 720 новых шестибуквенных слов, 2 буквы — только два двухбуквенных слова, из трех букв — 6 трехбуквенных слов, из 4х — 24 четырехбуквенных слова и т.д.) -Irinka- 4 года назад Факториалом называется математическая функция. Само слово происходит от латинского factorialis, в переводе обначающий производящий, умножающий. Факториал обозначают, как n! Для определения числа n нужно произвести умеюножение всех натуральных от 1 до n включительно. К примеру произведём расчет факториала: 6! = 1•2•3•4•5•6= 720 Galina7v7 7 лет назад Факториалом любого числа n называется произведение всех натуральных чисел , начиная с 1 ,продолжая 2 , 3 , и так далее , вплоть до самого числа n , и обозначается значком ! . То есть : n ! = 1 * 2 * 3 *….* (n — 2 ) * ( n — 1 ) * ( n ). Приведём примеры : 5 ! = 1 * 2 * 3 * 4 * 5 = 120 , и так с любым числом. KillNUR 5 лет назад В школе у меня был инженерный калькулятор. Там было много функци и среди них загадочный факториал. Опытным путем я выяснил, как он считается, а позже прочитал в книге для чего он нужен. Факториалом числа n называют произведение всех натуральнызхчисел от единицы до n. Записывают факториал так: n! Larchev 5 лет назад Факториал натурального числа N это произведение всех натуральных чисел от 1 до N Записывается это N! Читается эн факториал. Например, если мы хотим найти 10! то надо будет перемножить все натуральные числа от 1 до 10 друг на друга. 10! = 1*2*3*4*5*6*7*8*9*10 = 3628800₽ moreljuba 6 лет назад Под таким понятием как «факториал» подразумевается в матиматике произведение именно всех натуральных чисел, включая единицу и вплоть до того числа, которое было задано изначально, включая его. Факториал обозначают таким знаком как «!». Например: 5! = 1*2*3*4*5 Novasagova 6 лет назад Значение факториал, часто используют в математике и в математических задачах. Факториал, если говорить понятным языком — это произведение всех существующих натуральных чисел. Рассчитать факториал, можно по его специальной формуле: 1 * 2 * 3 * 4 * … * n = n! Красное облако 4 года назад Это функция, точнее значение всех чисел (имеются в виду произведение натуральных чисел). Натуральные числа от единицы (одного) и до «n». Суть, ну или смысл факториала это узнать (ну или высчитать) все возможные варианты числа во всех комбинациях. Игорь1997 10 лет назад Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно.Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе. Ольга84 10 лет назад Это что то из математики.Факториал-это произведение всех натуральных чисел.Его определяют,вроде как,для отрицательных чисел. Знаете ответ? |
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Умножение натуральных чисел
Определение
Умножение — одна из операций математики, предназначена для упрощения сложения одинаковых чисел.
Например: 4 + 4 + 4 = 4 · 3 = 12.
Умножение обозначают точкой «·» или крестиком «х».
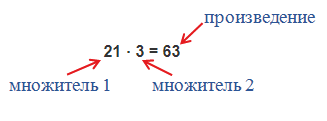
Числа, которые умножаются, называют «множителями», результат умножения, называют «произведением»
Пример:
Алгоритм умножения чисел
Разберем порядок умножения чисел на примере. Умножим число 25 на 16
1. Сначала записываем множители в столбик.
Второй множитель записывается под первым множителем так, что разряды второго множителя находились под соответствующими разрядами первого множителя, т.е. единицы второго множителя записываются под единицами первого, десятки под десятками и т.д. Снизу под записанными множителями проводится горизонтальная линия, а слева ставится знак умножения.
2. Производим последовательное умножение.
Сначала число, обозначающее разряд единиц класса единиц второго множителя последовательно умножаем на все разряды первого множителя.
Умножим цифру 6 на 5, получаем 30 — 3 десятка 0 единиц. 0 запишем под единицами, 3 «запомним». После этого 6 умножаем на цифру десятков первого множителя на 2, получаем 12. Прибавим к 12 получившиеся в предыдущем действии десятки, т.е. 3, в результате получаем 15. Поскольку разрядов в первом множителе больше нет., запишем число 15 под десятками. Первое неполное произведение 150.
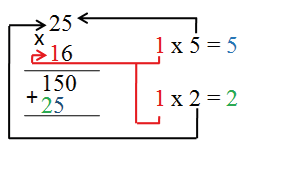
3. Найдем второе неполное произведение. Последовательно умножим десятки второго множителя — 1 на все разряды первого слагаемого. Сначала 1 умножим на 5, получаем 5, запишем полученное произведение под десятками. После этого 1 умножаем на 2, получим 2, записываем 2 впереди 5. Второе неполное произведение 25. Поскольку мы умножали десяток второго слагаемого на первое слагаемое, запись второго неполного произведения 25 будет находиться под разрядом десятков. Получается «смещение» числа влево.
4. Последовательно сложим цифры полученных неполных произведений по правилам сложения.
Свойства умножения натуральных чисел.
1. Переместительное свойство умножения.
a · b = b · a
От перемены мест множителей произведение не изменится.
12 · 4 = 4 · 12
12 · 4 = 48
4 · 12 = 48
2. Сочетательное свойство умножения.
a · (b · c) = (a · b) · c
Произведение не зависит от группировки сомножителей.
2 · (3 · 6) = (2 · 3) · 6
2 · (3 · 6) = 36
1) 3 · 6 = 18; 2) 18 · 2 = 36
(2 · 3) · 6 = 36
1) 2 · 3 = 6; 2) 6 · 6 = 36
3. Распределительное свойство умножения относительно сложения.
a · (b + c) = ab + ac
При умножении числа на сумму двух других чисел, можно данное число умножить на каждое из слагаемых, а полученные результаты сложить.
3 · (5 + 4) = 3 · 5 + 3 · 4
3 · (5 + 4) = 27
1) 5 + 4 = 9; 2) 9 · 3 = 27
3 · 5 + 3 · 4 = 27
1) 3 · 5 = 15; 2) 3 · 4 = 12; 3) 12 + 15 = 27
4. Распределительное свойство умножения относительно вычитания
a · (b — c) = ab — ac
При умножении числа на разность двух других чисел, можно данное число умножить на уменьшаемое и на вычитаемое, а полученные результаты вычесть.
6 · (7 — 5) = 6 · 7 — 6 · 5
6 · (7 — 5) = 12
1) 7 — 5 = 2; 2) 2 · 6 = 12
6 · 7 — 6 · 5 = 12
1) 6 · 7 = 42; 2) 6 · 5 = 30; 3) 42 — 30 = 12
5. Свойство умножения единицы на натуральное число
a · 1 = a
При умножении единицы на любое число, получим равное ему число.
1 · 76 = 76
6. Свойство умножения нуля на натуральное число
0 · a = 0
При умножении 0 на любое число, получим 0
0 · 123 = 0
Произведение всех натуральных чисел от 1 до 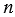
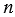
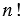
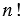
Пример:
3! = 1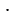
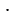
5! = 1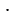
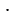
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 292 ,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 579,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 817,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 934,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1675,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1685,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 431,
Мерзляк, Полонский, Якир, Учебник
Номер 727,
Мерзляк, Полонский, Якир, Учебник
Номер 1036,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 70,
Мерзляк, Полонский, Якир, Учебник
Номер 110,
Мерзляк, Полонский, Якир, Учебник
Номер 196,
Мерзляк, Полонский, Якир, Учебник
Номер 1074,
Мерзляк, Полонский, Якир, Учебник
Номер 1197,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Задание 641,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1169,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1464,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1593,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 12,
Мерзляк, Полонский, Якир, Учебник
Номер 227,
Мерзляк, Полонский, Якир, Учебник
Номер 269,
Мерзляк, Полонский, Якир, Учебник
Номер 432,
Мерзляк, Полонский, Якир, Учебник
Номер 528,
Мерзляк, Полонский, Якир, Учебник
Номер 564,
Мерзляк, Полонский, Якир, Учебник
Номер 706,
Мерзляк, Полонский, Якир, Учебник
Номер 1006,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 67,
Мерзляк, Полонский, Якир, Учебник
Номер 265,
Мерзляк, Полонский, Якир, Учебник
Номер 485,
Мерзляк, Полонский, Якир, Учебник

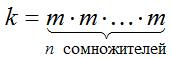



















![(n)_k = n^{underline{k}} = n^{[k]}= ncdot (n-1)cdot ldotscdot (n-k+1) = frac{n!}{(n-k)!}.](https://dic.academic.ru/dic.nsf/ruwiki/aca87691cf1194f991c519c26583be69.png)