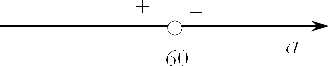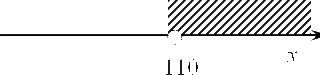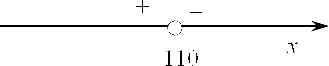Как найти производительность труда в задаче

Производительность труда в задаче 17

2 октября 2015

Задачи этого типа появились в ЕГЭ относительно недавно, но застали врасплох как учеников, так и многих учителей. А всё потому что решаются они с помощью производной — инструмента, совершенно непривычного для второй части экзамена.

Задача 17. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $3t$единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $4t$единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.

В приведённом условии есть важный момент, после осознания которого у вас вообще не будет проблем с решением подобных задач. Дело в том, что величина $t$, указанная для первого завода и для второго — это не одно и то же число! Другими словами, суммарное время рабочих на первом и другом заводе будет разным.

Для решения введём новые переменные: ${{a}^{2}}$ — суммарное время рабочих на первом заводе, ${{b}^{2}}$ — суммарное время на втором. С учётом производительности получим:

$begin{align}& {{a}^{2}}to 3a \& {{b}^{2}}to 4b \end{align}$

Таким образом, затратив суммарно ${{a}^{2}}+{{b}^{2}}$ часов времени, мы получим $3a+4b$ единиц продукции в неделю. Всё остальное — элементарная математика, подробно описанная в видеоуроке:

В прошлый раз мы рассматривали довольно «противные» задачи, связанные с вычислением времени в задачах про кредиты. Но это было очень просто по сравнению с тем, что мы будем рассматривать сегодня, а именно экономическую задачу 17 про производительность труда, в которой требуется применять производную. Эти задачи появились в ЕГЭ по математике относительно недавно, и те, кто уже с ними столкнулся, оценили, что, во-первых, условие таких задач довольно длинное, а, во-вторых, в каждой из таких задач есть неприятная зацепка, на которой «прогорели» очень многие ученики.

Думаю, вы уже догадались, что речь идет о той самой задачи 17, когда у Григория есть два завода, и еще указана производительность труда, и требуется оценить, какое наибольшее количество продукции можно произвести на этих двух заводах, если распределить нагрузку оптимально. Но на самом деле, в этих задачах 17 нет ничего сложного, даже чуть проще, чем многие задачи на кредиты. Поэтому сейчас мы рассмотрим одно из таких заданий, внимательно пробежимся по каждому пункту и посмотрим, как именно должно выглядеть идеальное ее решение.

Задача № 1

Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $3t$ единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $4t$. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.

Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Шаг первый: вводим переменные

Прежде всего, перед тем как переходить к непосредственному решению задачи 17 из ЕГЭ по математике, попытаться что-то посчитать, составить какие-то формулы, поймите одну простую вещь: величина ${{t}^{2}}$, данная и в первом, и во втором предложении, никак не связаны друг с другом. Коэффициент $t$ нам дан исключительно для того, чтобы сравнить производительность на разных заводах при одинаковом расходе времени. Думаю, это сравнение абсолютно очевидно: на первом производительность составляет $3t$, а на втором — $4t$, т.е. чуть побольше. На практике это означает следующее: давайте распишем, что происходит на каждом из них.

На первом заводе у нас расходуется ${{a}^{2}}$ времени (после замены) и производится $3a$ единиц продукции. На втором — ${{b}^{2}}$ времени и $4b$ продукции.

А теперь давайте сложим расходы времени и суммарный выпуск продукта.

Получим, что суммарный расход времени составляет ${{a}^{2}}+{{b}^{2}}$, а суммарный расход продукции — $3a+4b$. При этом еще раз обращаю ваше внимание: никто не говорил, что ${{a}^{2}}$ и ${{b}^{2}}$ должны быть равны. Ключевое слово здесь «если» и в первом, и во втором случае. Именно поэтому мы так смело меняем коэффициенты $t$ на $a$ в первом случае и на $b$ во втором случае.

Шаг второй: составляем и решаем уравнение

Давайте посмотрим, что у нас получилось. ${{a}^{2}}+{{b}^{2}}$ — это суммарный расход времени. Поскольку Григорий платит рабочему 500 рублей за каждый час работы, то всего он сможет заплатить такую сумму:

[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000]

Вот и первое уравнение.

На самом деле, основная сложность этой задачи 17 про производительность труда — вовсе не составление уравнения. Она состоит в том, что нужно понять, что на первом и на втором заводе время разное. Именно поэтому для первого мы везде заменили $t$ на $a$, а для второго — $t$ на $b$. В итоге как вы сейчас увидите, мы получим одно уравнение с двумя неизвестными, которое легко упрощается — одна неизвестная легко выражается через другую. И поэтому вся функция, выражающая количество произведенного товара, на самом деле зависит от одной-единственной переменной, в нашем случае это будет переменная $a$.

Далее, я думаю, все понятно: у нас есть функция, отрезок, на котором эта функция рассматривается, а все, что нам требуется найти — это наибольшее значение этой функции на данном отрезке. Вообщем, классическая задача для применения производных, в нашем случае новая задача 17 из ЕГЭ по математике.

Суммарный выпуск продукции ($S$) равен:

[S=3a+4bto max ]

Вот теперь задача и проявилась: имея ограничение на $a$ и $b$, нам нужно добиться того, чтобы $S$ принимала свое максимальное значение. Для начала давайте немножко поработаем с уравнением: $$

[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000left| :500 right.]

[{{a}^{2}}+{{b}^{2}}=10000]

Отсюда выразим $b$:

[{{b}^{2}}=10000-{{a}^{2}}]

[b=sqrt{10000-{{a}^{2}}}]

Конечно, тут следовало бы перед выражением поставить $pm $, однако у нас речь идет о времени, а оно не может быть отрицательным, поэтому мы берем положительное значение. Итого суммарный объем выпускаемого товара может быть выписан как функция от одной-единственной переменной $a$:

[S=3a+4sqrt{10000-{{a}^{2}}}]

Шаг третий: находим максимальное значение функции

Теперь нам нужно найти максимальное значение этой функции на всей области определения, а совершенно очевидно, что величину $a$, т.е. количество товара, выпущенного на первом заводе, увеличивать до бесконечности нельзя, просто потому что корень имеет конкретную область определения — величина, стоящая под корнем, не должна быть отрицательной. Давайте запишем это:

[10000-{{a}^{2}}ge 0]

[{{a}^{2}}le 10000]

[left| a right|le 100]

[ain left[ 0;100 right]]

Итого мы получили классическую задачу из первой части ЕГЭ по математике: у нас есть функция, есть интервал, соответственно, нужно найти максимальное значение этой функции на заданном интервале. Давайте считать производную:

[{S}’=3+4cdot frac{1cdot left( 10000-{{a}^{2}} right)}{2sqrt{10000-{{a}^{2}}}}=3+frac{4cdot left( -2a right)}{2sqrt{10000-{{a}^{2}}}}=]

[=3-frac{4a}{sqrt{10000-{{a}^{2}}}}]

[3-frac{4a}{sqrt{10000-{{a}^{2}}}}=0]

Решаем полученное уравнение:

[3=frac{4a}{sqrt{sqrt{10000-{{a}^{2}}}}}]

[3sqrt{10000-{{a}^{2}}}=4a]

[9left( 10000-{{a}^{2}} right)=16{{a}^{2}}]

[90000-9{{a}^{2}}=16{{a}^{2}}]

[25{{a}^{2}}=90000]

[5a=3cdot 100]

[a=frac{3cdot 100}{5}=60]

Теперь, зная, чему равно $a$, легко найти $b$:

[b=sqrt{10000-3600}=sqrt{6400}=80]

Однако для полного и обоснованного решения необходимо понять знак производной. Давайте начертим числовую прямую и отметим на ней $a=60$ и посмотрим, что происходит при $a gt 60$:

Например, если взять $a=99$ мы получим следующее:

[10000-{{99}^{2}}={{100}^{2}}-{{99}^{2}}=left( 100-99 right)left( 100+99 right)=199]

Если посмотрим на исходное выражение, то очевидно, что $sqrt{199} lt 99$, но посчитав его, получаем в ответе отрицательное число.

Отсюда следует, что$a=60$является точкой максимума, т.е. именно той, которую мы и хотели найти. Именно в ней наша исходная функция принимает исходное значение. Осталось подставить в $S$ полученное значение $a$ и $b$:

[S=3cdot 60+4cdot 80=180+320=500]

Окончательный ответ: 500 единиц товара.

Нюансы решения

Как видите, все оказалось не так уж и сложно. Единственно, что нам нужно запомнить — это то, что величина ${{t}^{2}}$, когда речь идет о первом заводе дает нам информацию о производительности труда именно на нем, т.е. связывает время, затраченное на производство и количество продукции в рамках только него.

Величина ${{t}^{2}}$, относящаяся ко второму заводу, говорит нам именно о нем и никак не связана с первым.

Более того, считать, что количество времени, затраченного рабочими на первом и на втором заводах, абсолютно одинаково — это вообще глупость, потому что в этом случае полученное уравнение оказалось бы намного проще и решалось бы как элементарное линейное: нам бы не потребовалось никаких производных, никаких доказательств, что мы получили точку максимума — мы просто бы разделили зарплату между рабочими первого и второго производств пополам.

Поэтому запомните: время, потраченное на первом и на втором заводах, разное, поэтому пусть на первом потрачено ${{a}^{2}}$ времени, а на втором — ${{b}^{2}}$. В этом случае задача действительно становится сложнее, при этом интересней и вполне достойной называться задачей 17 из ЕГЭ по математике.

Задача № 2

А в качестве десерта предлагаю решить еще одну такую же задачу 17 из ЕГЭ по математике, однако выкладки в этот раз будут минимальными, по возможности такими, какие и нужно делать на экзамене по математике.

Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $t$ единиц продукции. А если рабочие второго завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $2t$ единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час.

Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?

Шаг первый: вводим переменные

Если рабочие на первом заводе трудятся ${{x}^{2}}$, то это дает нам $x$ единиц товара. На втором ${{y}^{2}}$ времени дает нам $y$ товаров. Вновь складываем расходы времени — ${{x}^{2}}+{{y}^{2}}$ и отдельно складываем объем продукции — $x+2y$. Величина ${{x}^{2}}+{{y}^{2}}$ — это суммарный расход времени за неделю.

Шаг второй: составляем и решаем уравнение

Поскольку за каждый час работы платится 500 рублей, то суммарный расход денег за неделю составит:

[500cdot left( {{x}^{2}}+{{y}^{2}} right)=30250000]

[{{x}^{2}}+{{y}^{2}}=60500]

Таким способом, ограничения на ${{x}^{2}}$ и ${{y}^{2}}$ найдены.

Теперь необходимо записать сумму:

[S=x+2yto max ]

Опять же будем считать производную, но для этого сначала необходимо выразить $y$ через $x$:

[{{y}^{2}}=60500-{{x}^{2}}]

[y=sqrt{60500-{{x}^{2}}}]

Подставляем найденное значение $y$ в нашу формулу и получаем:

[S=x+2cdot sqrt{60500-{{x}^{2}}}]

Находим производную этой конструкции:

[{S}’=1+2frac{1left( -2x right)}{2sqrt{60500-{{x}^{2}}}}=1-frac{2x}{sqrt{60500-{{x}^{2}}}}]

Вновь приравниваем полученное выражение к нулю:

[1-frac{2x}{sqrt{60500-{{x}^{2}}}}=0]

[frac{1}{1}=frac{2x}{sqrt{60500-{{x}^{2}}}}]

[sqrt{60500-{{x}^{2}}}=2x]

[60500-{{x}^{2}}=4{{x}^{2}}]

[60500=5{{x}^{2}}]

[{{x}^{2}}=frac{60500}{5}=121cdot 100]

[x=11cdot 10=110]

Шаг третий: находим максимальное значение функции

Мы получили критическую точку функции $S$. Теперь необходимо доказать, что это точка максимума. Для этого начертим вновь прямую, отметим на ней полученную точку 110 и возьмем любое число, больше чем 110. Однако для упрощения дальнейших выкладок предлагаю взять не рандомное число как в прошлый раз, а посчитать его с помощью следующего метода. Для начала давайте найдем $y$. Запишем такое выражение:

[y=2x=220]

Очевидно, что 220 больше 110, и если мы поставим его в нашу функцию, то получим число на отмеченном интервале:

Давайте подставим:

${S}’left( 220 right)=1-frac{2cdot 220}{sqrt{60500-{{220}^{2}}}}=1-frac{440}{sqrt{60500-48400}}=$

$=1-frac{440}{sqrt{12100}}=1-frac{440}{110}=1-4=-3$

Следовательно, справа от числа 110 мы получаем отрицательную производную, а слева, естественно, будет положительная.

Итого 110 — точка максимума. Это является строгим обоснованием.

Теперь подставляем в выражение $x$ и $y$, которые мы нашли:

[S=110+2cdot 220=110+440=550]

Ответ: 550 единиц товара.

Ключевые моменты решения задач17 на производительность труда из ЕГЭ по математике

Все, что нам нужно знать — это:

1. Правило вычисления производных сложных функций.
2. Правила решения несложных уравнений.

Кроме того, хотел бы отметить, что не надо бояться работать с большими числами. Такие выражения, когда у нас появляются пятизначные и более числа, абсолютно типичны для последних задач 17 из ЕГЭ по математике, потому что они реально трудные. Но на самом деле, в этих задачах из ЕГЭ нет ничего трудного. Вам только нужно знать следующее:

• ${{a}^{2}}to a$ и ${{b}^{2}}to 2b$ — как связано затраченное время с объемом выпущенного товара;
• $S=a+2bto max $ — суммарный объем товара находится по несложной формуле.

Кроме того, необходимо понимать, как связано время, затраченное на первом производстве и на втором, т.е. каковы максимальны ограничения на это время.

А дальше дело техники: считаем производную, решаем уравнение, подставляем в исходное ограничение и получаем окончательный ответ.

Надеюсь, это видео поможет вам построить собственный завод, где вы будете платить рабочим по 30 млн. рублей в неделю, если такой суммы вам окажется недостаточно, заходите на наш сайт, подписывайтесь на паблик ВКонтакте и на канал в YouTube. До новых встреч!

Смотрите также:

1. Задачи на кредит с плавающим платежом
2. Задачи с экономическим содержанием — основные формулы
3. Тест к уроку «Что такое логарифм» (средний)
4. Решение задач B12: №440—447
5. Как решать задачу 18: графический подход
6. Нестандартные задачи B2: кредит в банке

Но, поскольку, нас интересует прирост, а не рост производительности труда, то

ΔПТ = 100,07% — 100% = 0,07%

Ответ:  Прирост производительности труда составил 0,07%

Задача 2. Изменение процентной производительности труда

Определить как изменится производительность труда. Если известно, что на предприятии внедрили три группы мероприятий, каждое из которых повлекло за собой изменение производительности труда.

Изменение производительности труда:

1 группа мероприятий — +2%

2 группа мероприятий — -4%

3 группа мероприятий — -12,5%

Решение:

Найдем индексы производительности труда после ввода мероприятий.

I первой группы мероприятий = (100+2)/100=1,02

I второй группы мероприятий = (100-4)/100=0,96

I третей группы мероприятий=(100-12,5)/100=0,875

Ответ: I-1=1,02; I-2=0,96; I-3=0,875.

Задача 3. Прирост производительности труда на основании изменения трудоемкости

Рассчитать рост производительности труда в условно-натуральном измерении на мыловаренном заводе, если известны данные о производстве мыла и отработанные человеко-дни.

Коэффициенты перевода в условное мыло: хозяйственного -1.0, туалетного — 1.8, мыльной стружки — 2.2.

Наименование показателя	Базовый период	Отчетный период
Отработано человеко-дней	160	170
Произведено хозяйственного мыла, т	100	200
Произведено туалетного мыла, т	75	65
Произведено мыльной стружки, т	90	95

Комментарий.

Суть данной задачи в оценке производительности труда в условиях меняющейся номенклатуры производства и фонда рабочего времени. Сначала мы обязаны привести всю производственную программу к некому условному изделию. После чего, выяснить, какое количество этих самых условных изделий производилось за единицу времени, что и будет выражать производительность труда в условно-натуральном измерении. Соотношение данных цифр и даст нам рост производительности труда.

 Решение.

Приведем производственную программу к единому измерителю — условным изделиям.

Производственная программа в условных изделиях для базового периода равна:

100 + 1,8 * 75 + 90 * 2,2 = 433

Производственная программа в условных изделиях в отчетном периоде равна:

200 + 1,8 * 65 + 2,2 * 95 = 526

Поскольку фонд рабочего времени различался, определим выработку за один человеко-день

в базовом периоде:

433 / 160 = 2,70625

в отчетном периоде:

526 / 170 = 3,09412

Рост производительности труда отчетного периода к базовому, соответственно, будет равен:

3,09412 / 2,70625 = 1,14332 или 14,3%

Ответ: рост производительности труда составил 14,3%

P.S. Догадайтесь, откуда я знаю, что на производстве были заняты 8 человек?

Задача 4. Изменение производительности при изменении объема производства

Определить как изменится производительность труда, если изменение объема производства равно +11% и изменение численности персонала равно +5.

Решение:

Чтобы найти объем производства нужно рассчитать индексы объема производства и численности персонала и подставить полученные значения в формулу:

I пт = I v /  I ч

I пт- индекс производительности труда.

I v- индекс объема производства.

I ч- индекс численности работников.

Решим задачу.

Iv= (100+11)/100=1,11

Iч=(100+5)/100=1,05

Iпт=1,11/1,05=1,057

Ответ: производительность труда увеличилась на 5,7%

Задача 5. Изменение производительности при снижении трудоемкости и численности персонала

Определить как изменится производительность труда в плановом году, если предполагается, что численность основных рабочих уменьшится с 450 да 430 человек. При этом планируется ряд мероприятий, которые позволят снизить трудоемкость на 9%, а также возможно увеличение производительности за счет организационных мероприятий на 7%.

Решение:

Найдем индекс численности рабочих.

Iч=430/450=0,955

Численность персонала снизилась на 4,5%.

Найдем изменение производительности труда за счет снижения трудоемкости.

∆пт=100*9/100-9=900/91=9,8%

Производительность труда выросло на 9,8% за счет снижения трудоемкости.

Найдем индекс объемов производства

Iv=(100+7)/100=1,07

Найдем индекс производительности труда а счет снижения трудоемкости

Iпт=(100+9,8)/100=1,098

Теперь найдем окончательный индекс производительности по формуле:

Iпт=1,07/0,955*1,098=1,12*1,098=1,22976

Ответ: производительность труда выросла на 22,976%

Задача 6. Изменение численности и объема производства

В базовом году численность рабочих составляла 330 рабочих. В плановом году планируется увеличить численность рабочих на 10%.

Объем произведенной товарной продукции составляет 4550 грн., в плановом году ожидается увеличение объема производства на 6%.

Определить производительность труда в базовом и плановом году, определить изменение производительности труда в абсолютном и относительном выражении.

Решение:

Найдем производительность труда в базовом году по формуле:

Пт = V / Ч

V –объем производства

Ч – численность рабочих

Пт – производительность труда

Пт=4550/330=13,788 грн./чел.

Найдем изменение численности рабочих и объема производства в плановом году. Умножим количество рабочих в базовом году на индекс. Аналогично с объемом производства.

Ч пл=330*1,1=363 рабочих

V пл=4550*1,06=4823 грн.

Теперь мы можем найти производительность труда в плановом году.

Пт пл=4823/363=13,286

Найдем изменение пт в относительном выражении

∆Пт=13,286/13,788=0,964

Производительность труда снизилась на 3,6%

Найдем снижение производительности труда в абсолютном выражении

∆Пт=13,788-13,286=0,502 грн.

Ответ: Пт б=13.788 грн/чел; Пт пл=13,286грн/чел; ∆пт=0,964; ∆пт=0,502грн.

Задача 7. Определить производительность труда по товарной продукции

Определить производительность труда рабочих, работающих на предприятии, если известно, что объем товарной продукции составляет 2950 тысяч грн., а численность рабочих равна 58 человек.

Решение.

Производительность труда – это показатель эффективности работы персонала. Производительность труда – это количество продукции, произведенной рабочим за единицу времени.

ПТ = V / Ч

V – Объем товарной продукции.

Ч – численность работников.

Найдем производительность труда.

Пт = 2 950 000 / 58 = 50 860 грн.

Ответ: производительность труда составила 50 860 грн. товарной продукции на одного человека

Задача 8. Изменение производительности труда в результате изменения численности и выпуска

В плановом году выпуск изделий Б увеличился на 30%. Численность рабочих увеличилась на 2 человека. В базовом году численность рабочих составляла 274 человека. Численность других категорий работающих не изменяется.

Определить, как изменится производительность труда основных рабочих, занятых на производстве изделия Б.

Решение.

Изменение производительности труда рабочих рассчитывается по формуле:

ΔПТ = Iv / Iч

Iv – индекс товарной продукции

Iч – индекс рабочих

В числителе учитывается изменение объема производства, а в знаменателе изменение количества рабочих. Эти значения используются в виде индекса.

Найдем изменение численности работников на предприятии

Iч = ( 274+2 )/ 274=1,0072

Индекс V(товарной продукции) равен 1,30

Найдем изменение производительности труда

∆Пт=1,30/1,0072=1,291

Производительность труда увеличилась на 29,1%

Ответ: производительность труда увеличилась на 29,1%

Задача 9. Изменение производительности труда в результате изменения выполнения норм выработки

На участке в базовом периоде рабочие в среднем выполняли нормы времени на 115%. После внедрения организационно-технических мероприятий нормы времени начали выполняться на 125%. Как изменилась при этом производительность труда.

Решение.

Наряду с показателем производительности труда существуют показатели выполнения норм времени и выполнения норм выработки.

Выполнение норм времени — время, необходимое на производство одного изделия.

Норма выработки – количество продукции, которое должно быть поизведено за единицу времени.

Процент выполнения норм определяется, как отношение фактических показателей к плановым показателям.

∆Пт = 125/115*100-100=8,7%

Ответ: производительность труда увеличилась на 8,7%

Задача 10. Изменение производительности труда при снижении трудоемкости изделия

Трудоемкость изделия снизилась на 15%. Определить, как изменится производительность труда.

Решение.

Показатель трудоемкости является обратным показателю производительности труда. Существуют обратно пропорциональные зависимости между производительностью труда и трудоемкостью изделия

∆Те – процент уменьшения трудоемкости изделия

∆Пт – процент увеличения производительности труда изделия

Найдем изменение производительности труда

∆ПТ =  15% / ( 100% — 15% ) х 100% = 17,65%

Ответ: за счет снижения трудоемкости на 15 процентов, производительность труда увеличилась на 17,65%

Задача 11. Изменение трудоемкости при изменении производительности труда

Определить, как изменится трудоемкость изготовленного изделия, если известно, что изменение производительности труда равно 20%

Решение.

Рассчитаем изменение трудоемкости по формуле:

∆Те = 20% / (100% — 20% ) х 100% = 25%

Ответ: трудоемкость уменьшилась на 25 процентов за счет увеличения производительности труда на 20%

Задача 12. Расчеты при изменении роста производительности и трудоемкости одновременно

В результате проведения организационных мероприятий производительность труда в бригаде увеличилась на 14,5%. Частичная модернизация оборудования позволила снизить трудоемкость на 7%. Определить рост по каждому мероприятию отдельно.

Решение.

Найдем изменение трудоемкости по первому мероприятию по формуле

∆Те = ∆Пт / (100% — ∆Пт ) х 100%

∆Те = 14,5% / (100% — 14,5% ) х 100% = 16,96%

Трудоемкость изделия уменьшилась на 16,96% за счет увеличения производительности труда на 14,5%

Найдем увеличение производительности труда по второму мероприятию по формуле

∆Пт = ∆Те / (100% — ∆Те ) х 100%

∆Пт = 7% / (100% — 7% ) х 100% = 7,53%

Производительность труда увеличилась на 7,53% за счет снижения трудоемкости изделия на 7%.

Ответ: первое мероприятие привело к уменьшению трудоемкости изделия на 16,96%, второе мероприятие привело к увеличению производительности труда на 7,53%.

Задача 13. Определить снижение трудоемкости за счет увеличения производительности труда

Производительность труда на участке увеличилась на 16%, численность персонала осталась неизменной. Определить снижение трудоемкости продукции на участке и изменение объем производства.

Решение.

Так как численность рабочих осталась неизменной, объем производства вырос на 16%.

Найдем снижение трудоемкости

∆Те = ∆Пт / (100% — ∆Пт ) х 100%

∆Те = 16 / ( 100 — 16 ) х 100% = 19,05%

Трудоемкость уменьшилась на 19,05%

Ответ: снижение трудоемкости составило 19,05%, объем производства вырос на 16%.

Задача 14. Рост производительности труда за счет нескольких мероприятий

Рост производительности труда с помощью первой группы мероприятий составил 17%,а с помощью второй на 7%. Определите общее изменение производительности труда.

Решение.

Производительность труда изменяется за счет внедрения различных мероприятий на предприятии. Для того чтобы узнать суммарное увеличение производительности труда за счет нескольких мероприятий нужно умножить индексы роста (или снижения) производительности труда между собой.

Найдем изменение производительности труда

∆Пт=1,17*1,07=1,2519

Ответ: производительность труда увеличилась на 25,19% в целом с помощью все мероприятий.

Задача 15. Определить уровень производительности труда на основании производственных показателей

На основе исходных данных, приведенных в таблице ниже, определить уровень производительности труда в расчетном и отчетном годах, а также численность персонала в расчетном году.

Показатели	Значения
Среднесуточная численность промышленно-производственного персонала в отчетном году, чел.	300
Объем выпуска товарной продукции, млн. грн.:
Отчетный год	16,5
Расчетный год	17
Плановое повышение производительности труда в расчетном году, %	7

Решение.

Найдем уровень производительности труда в расчетном и отчетном годах. Это можно сделать по формуле:

ПП = ТП / ЧР

ПП – уровень производительности труда.

ТП – годовой объем товарной продукции.

ЧР – среднегодовая численность работников.

Найдем уровень производительности труда в отчетном году

Подставим значения в формулу.

ПП_отч.=16,5/300=0,055=55 тыс. грн./чел.

Найдем уровень производительности труда в расчетном году.

Так как плановое повышение производительности труда в расчетном году составляет 7% нам нужно уровень производительности труда в отчетном году умножить на коэффициент 1,07.

ПП_расч.=55 000*1,07=58 850 грн./чел.

Теперь мы можем найти среднесуточную численность промышленно-производственного персонала в расчетном году по формуле:

ЧР = ПП / ТП

Подставим значения в формулу.

ЧР_расч.=17 000 000/58 850=289 человек

2-й способ решения — без таблицы

Как обойтись без составления таблицы?

Сразу составить уравнение.

Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.

Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.

Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.

А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.

Во-первых, сравним формулы:

Движение	Работа
( displaystyle v=frac{S}{t})	( displaystyle P=frac{A}{t})
Скорость движения	Скорость выполнения работы, т.е. производительность
Пройденный путь	Выполненная работа
Потраченное на движение время	Потраченное на работу время

Теперь рассмотрим задачу:

Пример №1

Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.

Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?

Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).

Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:

( displaystyle frac{112}{x}=frac{112}{x+1}+2).

То же самое уравнение! Вот и получается, что работа и движение – одно и то же.

Как решать задачи на совместную работу

Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).

Пример №2

Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).

За какое время они заполнят бассейн, работая вместе?

Решение

Во-первых, давай придумаем аналогию с движением.

Придумал?

Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).

А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.

Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!

Тогда что нас просят найти? Время, через которое они встретятся.

Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.

Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).

Итак,

( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).

Тогда время, за которое с такой производительностью будет выполнена работа ( A):

( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)

Итак, правило:

При совместной работе производительности складываются

А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.

Пример 8

На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?

Решение:

Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).

Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).

Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).

( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.

То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).

Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:

Примеры решения задач.

1. На сколько процентов изменится показатель производительности труда в плановом периоде, если за отчетный период продукции выработано на сумму 2500тыс.руб. Численность работающих составляла 1350 человек, в плановом периоде объем вырабатываемой продукции должен возрасти на 6% численность останется без изменения.

РЕШЕНИЕ.

Расчет можно произвести на основании изменений показателя выработки.

Выработка на одного рабочего за отчетный период составит:

В = Q / N = 2500 / 1350 = 1,85 тыс.руб./ чел.

По условию объем вырабатываемой продукции увеличивается на 6% и будет составлять 2650 тыс.руб.

При сохранении численности в плановом периоде показатель выработки будет составлять: Вп = 2650 / 1350 = 1,96 тыс.руб. /чел.

Рост производительности труда составит:

∆В = 1,96 – 1,85 = 0,11 тыс.руб. или 6%.

ОТВЕТ: Рост производительности труда составит 6%.

2. Определить показатели производительности труда: среднегодовой, среднедневной и среднечасовой, если за год продукции выработано на сумму 10000 тыс.руб., среднесписочная численность рабочих – 380 человек, количество рабочих дней в году 204, эффективная продолжительность рабочего дня – 8 ч.

РЕШЕНИЕ.

Среднегодовая выработка на одного рабочего может быть найдена по формуле: Вг = Q / Nр = 10000 / 380 = 26,3 тыс.руб.

Одним рабочим в течении года произведено продукции на сумму 26,3 тыс.руб., продолжительность года ,по условию 204 дня, следовательно среднедневная выручка на одного рабочего будет составлять: Вдн = 26,3 / 204 = 0,13 тыс.руб..

При продолжительности рабочей смены 8 часов, часовая выработка рабочего составит: Вч = 0,13 / 8 = 0,02тыс.руб..

ОТВЕТ: Вг =26,3 тыс.руб., Вдн = 0,13 тыс. руб., Вч = 0,02 тыс.руб..

3. Общий объем трудозатрат на годовой выпуск продукции (ДСП) – 650000 нормо – часов. Плановый объем выпуска ДСП –220000куб.м. Фактические трудозатраты на выпущенную продукцию – 645000 чел.-ч. Фактически выпущено плит – 195000 куб.м. Определить плановую и фактическую трудоемкость 1 куб.м плит. Сделать вывод.

РЕШЕНИЕ.

Трудоемкость продукции представляет собой затраты живого труда на производство единицы продукции, и может быть найдена по формуле: Тр = Т / Q

Плановая трудоемкость составляет:

Тр п = 650000 / 220000 = 2,95 чел./час

Фактическая трудоемкость равна:

Тр ф = 645000 / 195000 = 3,3 чел./ час.

ОТВЕТ: Фактическая трудоемкость производства ДСП выше плановой, что является причиной невыполнения плана по производству ДСП.