Как найти производную 15х - Исправление недочетов и поиск решений вместе с Examum.ru

Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.

Калькулятор производных

Производная функции

Допустимые операции: + — / * ^
Константы: pi
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

Показать детали вычисления

Показать шаги вычисления производной и упрощения формулы

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Синтаксис описания формул

В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, — — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.

Таблица синтаксиса математических выражений

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Вычисление производной

Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…

Правила дифференцирования

1) производная суммы:

2) производная произведения:

3) производная частного:
$(frac{u}{v})'=frac{u'v-v'u}{v^2}$
4) производная сложной функции равна произведению производных:

Таблица производных

Производная степенной функции:
$(x^{n})'=nx^{n-1}$
Производная показательной функции:
$(a^{x})'=a^{x}ln(a)$
Производная экспонециальной функции:
$(e^{x})'=e^{x}$
Производная логарифмической функции:
$(ln(x))'=frac{1}{x}$
Производные тригонометрических функций:
,
,
$(tan(x))'=frac{1}{cos^2(x)}$ ,
$(cot(x))'=-frac{1}{sin^2(x)}$
Производные обратных тригонометрических функций:
$(arcsin(x))'=frac{1}{sqrt{1-x^2}}$ ,
$(arccos(x))'=-frac{1}{sqrt{1-x^2}}$ ,
$(arctg(x))'=frac{1}{1+x^2}$ ,
$(arcctg(x))'=-frac{1}{1+x^2}$
Производные гиперболических функций:

Источник

Производная функции/
15/x

Функция f()
— производная -го порядка
в точке

⚟

График:

от
до

Кусочно-заданная:

{ кусочно-заданную функцию ввести здесь

Решение

Вы ввели
[src]

15
--
x

$$frac{15}{x}$$

d /15
--|--|
dxx /

$$frac{d}{d x} frac{15}{x}$$

Преобразовать

Подробное решение

Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
1. В силу правила, применим: получим
Таким образом, в результате:

Ответ:

График

Построить график f(x)

Построить график f'(x)

Первая производная
[src]

-15 
----
  2 
 x

$$- frac{15}{x^{2}}$$

Упростить

Вторая производная
[src]

30
--
 3
x

$$frac{30}{x^{3}}$$

Упростить

Третья производная
[src]

-90 
----
  4 
 x

$$- frac{90}{x^{4}}$$

Упростить

График

Источник

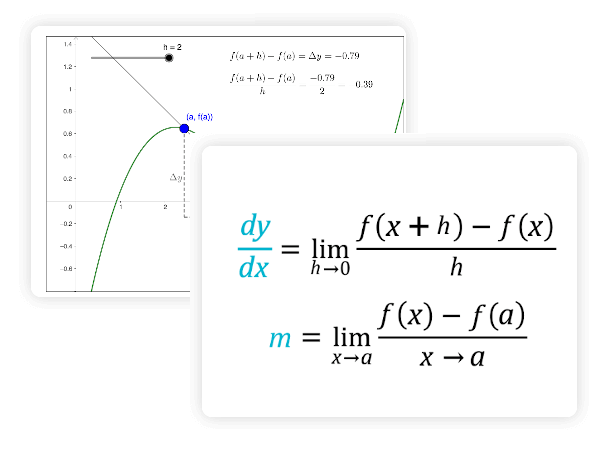
Что такое производная в математике

Производная функции — это понятие дифференциального исчисления, которое характеризует скорость изменения функции в данной точке. Он определяется как предел отношения приращения функции к приращению ее аргумента, когда приращение аргумента стремится к нулю, если такой предел существует. Функция, имеющая конечную производную (в некоторой точке), называется дифференцируемой (в этой точке).

Процесс вычисления производной называется дифференцированием. Обратный процесс — поиск оригинала — интеграция.

Почему вам может понадобиться рассчитать производную

На первый взгляд производные нужны, чтобы набить головы уже перегруженным школьникам, но это не так. Рассмотрим машину, которая ездит по городу. Иногда стоит, иногда едет, иногда тормозит, иногда ускоряется.

Допустим, он ехал 3 часа и проехал 60 километров. Затем, используя формулу из начальной школы, мы делим 60 на 3 и говорим, что она ехала со скоростью 20 км / ч. Мы правы? Что ж, отчасти верно. Получили «среднюю скорость». Но что от этого толку? На этой скорости машина может ехать 5 минут, а в остальное время ехать медленнее или быстрее. Что я должен делать?

А зачем нам знать скорость на все 3 часа маршрута? Разделим маршрут на 3 части по часу и рассчитаем скорость на каждом участке. Давайте. Допустим, у вас скорость 10, 20 и 30 км/ч. Вот. Ситуация уже более ясная — в последний час машина ехала быстрее, чем в предыдущие.

Но это опять же в среднем. Что, если он просто ехал медленно полчаса за последний час, а затем внезапно ускорился и начал быстро двигаться? Да, может быть так.

Как мы видим, чем больше мы разбиваем наш 3-часовой интервал, тем точнее мы получим результат. Но нам не нужен «более точный» результат — нам нужен совершенно точный результат. Это означает, что время нужно делить на бесконечное количество частей. А сама деталь — значит, будет бесконечно маленькой.

Если мы разделим на это время расстояние, которое машина преодолела за бесконечно малый период времени, мы также получим скорость. Но уже не средний, а «моментальный». И таких мгновенных скоростей тоже будет бесконечно много.

Если вы понимаете все вышеперечисленное, тогда вы понимаете значение производной. Производная — это скорость, с которой что-то меняется. Например, в нашем случае скорость — это скорость, с которой «пройденное расстояние» изменяется во времени. А может быть «скорость изменения температуры при изменении долготы к северу». Или «скорость исчезновения конфет из вазы на кухне». В общем, если есть что-то, определенное значение «Y», которое зависит от некоторого значения «X», то, скорее всего, есть является производной, которая записывается как dy / dx. И это просто показывает, как значение y изменяется при бесконечно малом изменении значения x — как наше расстояние изменилось при бесконечно малом изменении во времени.

Источник

Данный онлайн калькулятор вычисляет производную функции. Программа не только вычисляет ответ, она производит пошаговое решение. Выбирается порядок дифференцирования.
Как пользоваться калькулятором для нахождения производных онлайн:
1. Введите математическое выражение с переменной x, в выражении используйте стандартные операции: + сложение, —
вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции.
2. Выберите порядок дифференцирования (решения производных от первого до пятого порядка включительно).
3. Нажмите кнопку — Вычислить производную.
4. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями.

При помощи нашего калькулятора вы можете найти производную онлайн как от элементарной функции, так и от сложной, не имеющей решения в аналитическом виде.
Калькулятор поможет найти производную функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

Основные функции

$x^{a}$ : x^a

модуль x: abs(x)

Производные

Для того, чтобы найти производную функции f(x)
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции напишите в окне гаджета: f[x, y, z,…,t], j, где
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где означает тоже, что и Выше.

Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.

Примеры

x*E^x, x;
x^3*E^x, {x,17};
x^3*y^2*Sin[x+y], x;
x^3*y^2*Sin[x+y], y,
x/(x+y^4), {x,6}.

Источник

Онлайн калькулятор. Вычисление производных.

Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам.

Также универсальный калькулятор умеет вычислять производные любого порядка (дифференцирование).

Онлайн калькулятор производных

Перенос?

f»left(log left(frac{1-x^2}{1+x^2}right)right)

$$textbf{Вычисление производной 2-го порядка:} newline f»(x) = {{2xleft(-{{2x}over{x^2+1}}-{{2xleft(1-x^2right)}over{left(x^2+1right)^2}}right)}over{1-x^2}}+{{2xleft(x^2+1right)left(-{{2x}over{x^2+1}}-{{2xleft(1-x^2right)}over{left(x^2+1right)^2}}right)}over{left(1-x^2right)^2}}+{{left(x^2+1right)left(-{{2}over{x^2+1}}+{{8x^2}over{left(x^2+1right)^2}}-{{2left(1-x^2right)}over{left(x^2+1right)^2}}+{{8x^2left(1-x^2right)}over{left(x^2+1right)^3}}right)}over{1-x^2}} =newline -{{4left(3x^4+1right)}over{left(x-1right)^2left(x+1right)^2left(x^2+1right)^2}} =newline -{{12x^4+4}over{x^8-2x^4+1}}$$

Пояснения к калькулятору

Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
⌫ — удалить в поле ввода символ слева от курсора.
C — очистить поле ввода.
При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
Ввод числа в n-ой степени и квадратного корня прозводится кнопками a^b и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.

Вычисление производных

Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке «x». Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
f'(x) — производная первого порядка;
f»(x) — производная второго порядка;
f»'(x) — производная третьего порядка.
fⁿ(x) — производная любого n-о порядка.

Источник