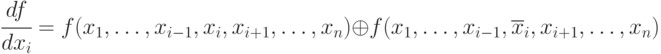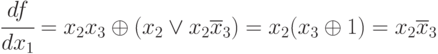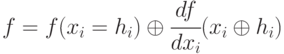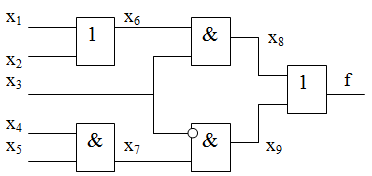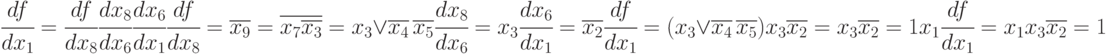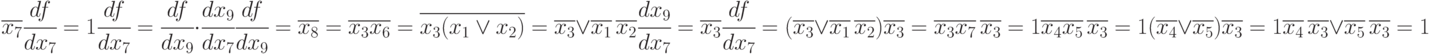Как найти производную булевой функции - Исправление недочетов и поиск решений вместе с Examum.ru

Производная
первого порядка
от булевой функцииf
по переменной x_i
определяется следующим образом [9]:

=f(х₁,х₂,…,х_i_-1,1,x_i₊₁,…,x_n)Åf(x₁,x₂,…,x_i_-1,0,x_i₊₁,…,x_n),

где
f(х₁,х₂,…,х_i_-1,1,x_i₊₁,…,x_n)
– единичная остаточная функция,
получаемая в результате подстановки
вместо х_i
константы 1, а f(х₁,х₂,…,х_i_-1,0,x_i₊₁,…,x_n)
– нулевая остаточная функция, получаемая
в результате подстановки вместо x_i
константы 0.

Пример.
f=х₁Úх₂.

Пример.

Булева
производная по x_i=0,
если f
не зависит от x_i,
булева производная по x_i=1,
если f
зависит только от x_i.

Булева
производная первого порядка определяет
условия, при которых функция изменяет
свое значение при изменении значения
переменной x_i
.

В
нашем примере функция f(х₁х₂х₃)
изменяет свое значение при изменении
х₁,
если истинна конъюнкция х₂х₃,
т.е. х₂=1,
х₃=1.

Пример.
Определим все булевы производные функции

Итак,
значение функции изменяется (функция
переключается) при изменении х₁,
если х₂=1
или х₃=0
;
при изменении х₂,
если х₁=х₃=1
(х₁х₃=1);
при изменении х₃,
если х₁=1;
х₂=0
.

Смешанная
булева производная k-го
порядка определяется путем вычисления
k
раз булевых производных первого порядка
от булевых производных первого порядка,
например [9]:

Булева
производная k-го
порядка равна сумме по модулю 2 всех
производных первых, вторых, третьих,
…, k-х
смешанных производных, и определяет
условия, при которых функция изменяет
значение при одновременном изменении
соответствующих переменных, например:

Таким
образом, f
переключается при одновременном
переключении х₁,
х₂,
когда х₃=0,
либо независимо от х₃
при переключении х₁
и х₂
с 1,1 на 0,0 или с 0,0 на 1,1.

При
синтезе методом каскадов оптимальное
исключение переменных достигается
путем анализа веса производных [9]. Вес
производной по данной переменной –
число конституент соответствующей
переключательной функции. То есть,
сначала исключается переменная,
производная которой имеет максимальный
вес, что означает максимальное изменение
функции при изменении переменной.

9.6. Элементарные автоматы памяти на основе комбинационного автомата и задержки

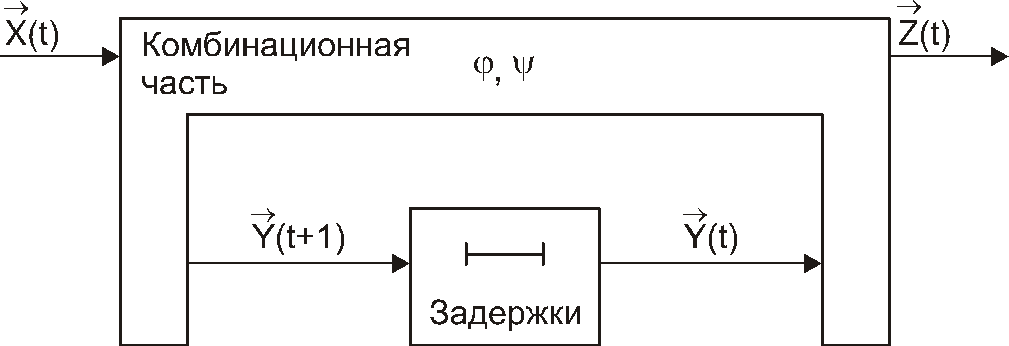
Последовательностный
автомат может быть синтезирован как
композиция комбинационного автомата,
реализующего функции переходов j
и выходов y
и элементарных автоматов памяти [10, 19],
например, задержек на один такт (рис.
64).

Рис.
64. Задержка на один такт

Физически
элементарный автомат памяти типа
«задержка на один такт» реализуется
линией задержки, которая может быть
выполнена в виде специальных элементов
– линий задержки или в виде соединения
логических элементов, не инверсирующего
сигнал, либо, в частных случаях, линией
связи, поскольку передача сигнала по
ней имеет некоторую конечную длительность,
не превышающую длительность такта.

Рассмотрим
синтез элементарных автоматов памяти
на основе задержек на один такт. Пусть
требуется синтезировать автомат, выход
которого устанавливается в состояние
логической единицы при поступлении
сигнала логической единицы на вход
установки (обычно он обозначается S
– «Set»)
и хранящий это состояние до поступления
сигнала логической единицы на вход
сброса (обычно он обозначается R
– «Reset»).
Таким образом, требуется создать автомат,
имеющий два входа R
и S
и один выход, который обозначим z
(рис. 65). Иногда добавляют и инверсный
выход
.

Рис.
65. Элементарный автомат памяти

Ясно,
что синтезируется последовательностный
автомат, так как его выходной сигнал
зависит от последовательности поступления
сигналов на входы:

Видно,
что при одинаковых входных сигналах на
входах SR,
выходной сигнал может быть как 0, так и
1.

В
таком случае опишем функционирование
автомата первичной таблицей
переходов-выходов (табл. 55).

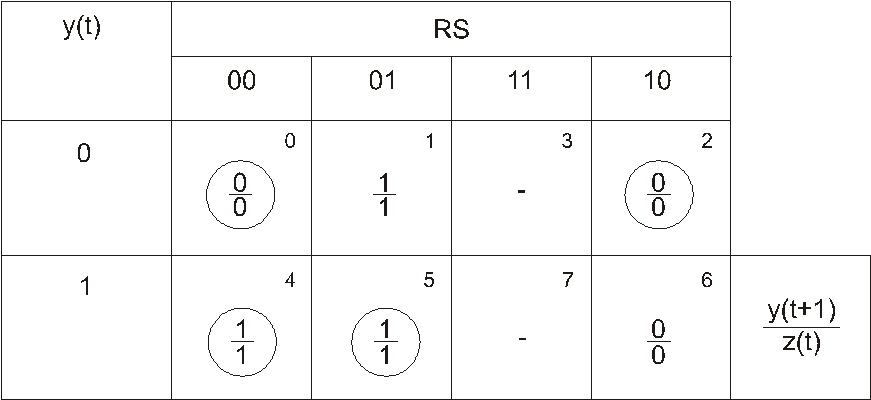
Таблица
55

Первичная
таблица переходов-выходов

Итак,
в исходном состоянии автомат находится
в строке с номером 1, в клетке, соответствующей
нулевому состоянию RS.
При поступлении набора сигналов 01
(начинается установка) автомат начинает
переходить в состояние 2 (возникает
неустойчивый такт 2), затем происходит
перемещение во вторую строку – в
устойчивый такт 2, обведенный кружком,
при этом на выходе возникает сигнал 1.
При поступлении сигнала 10 в первой
строке и сигналов 00, 01 во второй строке
состояние автомата не меняется, состояние
11 считается невозможным.

Очевидно,
что сокращение числа строк табл. 55
невозможно, иначе мы имели бы комбинационный
автомат (у которого одно состояние –
одна строка).

Приступим
к кодированию состояний. Оно в данном
случае тривиально: исходное состояние
сопоставим с состоянием 0 (1 строка),
другое состояние сопоставим с 1.

Получим
таблицы переходов-выходов для автомата
Мили (табл. 56) и автомата Мура (табл. 57).

Таблица
56

Таблица
переходов-выходов элементарного автомата
памяти Мили

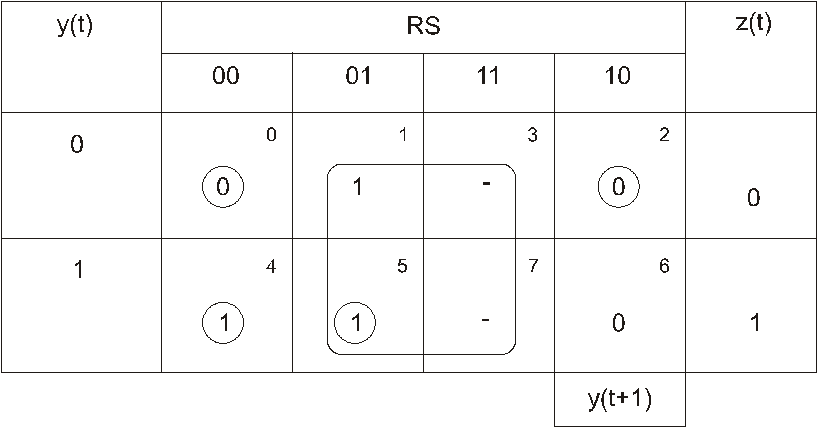
Таблица
57

Таблица
переходов-выходов элементарного автомата
памяти Мура

Таким
образом, для автомата Мура (табл. 57)
z(t)=y(t).

Построим
автомат Мура. Получим функции переходов
y(t+1)
и выходов z(t):

Минимизируя
y(t+1)
по карте Карно, какой и является табл.
57, получаем:

Реализуем
эту функцию в виде переключательной
схемы (рис. 66).

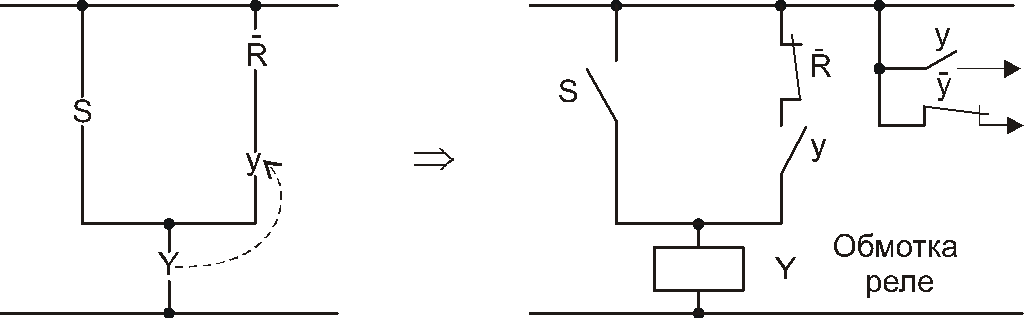
Рис.
66. Переключательные схемы элементарного
автомата памяти Мура

На
рис. 66 Y
– хранитель состояния автомата (например,
обмотка реле), обратная связь, указанная
пунктиром реализует так называемую
самоблокировку. Задержка на один такт
осуществляется следующим образом:
сначала срабатывает Y,
затем замыкается его контакт y.
Технически предполагается, что к моменту
размыкания S,
y
уже замкнут.

Построим
схему на функциональных элементах в
базисе И-НЕ:

Таким
образом, один элемент 2И-НЕ реализует
функцию
,
второй –
.

Соответствующая
схема показана на рис. 67.

Рис.
67. Реализация элементарного автомата
памяти

на
функциональных элементах 2И-НЕ

Можно
заметить, что выход второго элемента в
цепи R
при R=0
соответствует значению
.
Эту схему часто изображают в несколько
другом виде, полагая, что задержка
реализуется в линии связи (рис. 68).

Рис.
68. Элементарный автомат памяти RS
триггер

Это
известная схема так называемого RS
триггера.

Его
условное графическое обозначение
приведено на рис. 69.

Рис.
69. Условное графическое обозначение RS
триггера

Для
описания работы элементарных автоматов
памяти применяются таблицы возбуждения,
указывающие условия перехода от текущего
к последующему внутреннему состоянию.
Такая таблица для RS
триггера – табл. 58.

Таблица
58

Таблица
возбуждения RS
триггера

y(t)	y(t+1)
	0	1
0	0 ~	1 0
1	0 1	~ 0	S R

Аналогично
выглядит таблица и для такого элементарного
автомата памяти как дистанционный
переключатель, который имеет механическую
обратную связь (механическую фиксацию
состояния) и широко применяется в
автоматике – рис. 70.

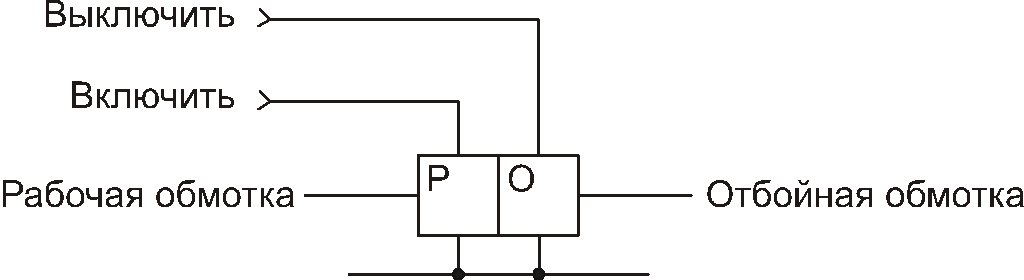
Рис.
70. Условное графическое обозначение

дистанционного
переключателя

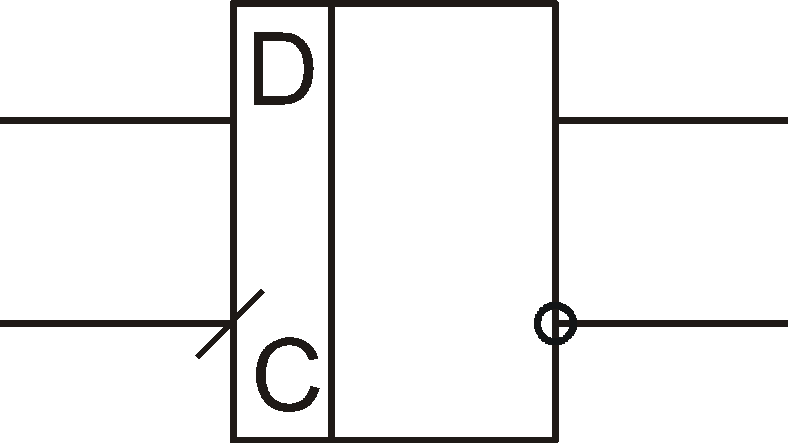
Задержка
на один такт может быть реализована и
так называемым D
триггером, устанавливающимся в состояние,
определяемое его входом D
по специальному разрешающему сигналу
– синхроимпульсу. Это уже синхронный
автомат в отличие от рассмотренных выше
асинхронных (рис. 71, табл. 59).

Рис.
71. Условное графическое обозначение
синхронного D
триггера

Косая
черта с наклоном вперед на входе
синхронизации обозначает срабатывание
по фронту синхроимпульса.

Таблица
59

Таблица
возбуждения D
триггера

y(t)	y(t+1)
	0	1
0	0	1
1	0	1	D(t)

D
триггер без синхронизации – аналог
обычного реле (рис. 72).

Рис.
72. Условное графическое обозначение
реле

и
временная диаграмма работы

Имеются
и другие элементарные автоматы памяти,
например, асинхронный RS
триггер с инверсным управлением (нулями,
а не единицами, рис. 73, табл. 60), синхронный
JK
триггер (рис. 74, табл. 61).

Рис.
73. Условное графическое обозначение

RS
триггера с инверсным управлением

Таблица
60

Таблица
возбуждения RS
триггера с инверсным управлением

y(t)	y(t+1)
	0	1
0	1 ~	0 1
1	1 0	~ 1	S R

Рис.
74. Условное графическое обозначение
синхронного JK
триггера,

срабатывающего
по заднему фронту импульса

Таблица
61

Таблица
возбуждения синхронного JK
триггера,

срабатывающего
по заднему фронту импульса

y(t)	y(t+1)
	0	1
0	0 ~	1 ~
1	~ 1	~ 0	J K

При
синтезе сложных последовательностных
автоматов на основе элементарных
автоматов памяти (элементов памяти) для
получения функций, описывающих управление
ими комбинационной частью автомата,
строится таблица возбуждения элементарных
автоматов памяти (таблица возбуждения
элементов памяти).

Соседние файлы в папке Дискретная математика

Источник

Производная первого порядка от булевой функции F по переменной XI Есть сумма по модулю 2 соответствующих остаточных функций:

Где – единичная остаточная функция;

– нулевая остаточная функция

Производная первого порядка от булевой функции Определяет условия, при которых эта функция изменяет значение при переключении переменной Xi (при переменной значения Xi на противоположное).

Пример

Вычислим производную От булевой функции.

. Согласно определению

Смешанной производной От булевой функции F по переменным ( называется выражение вида

Смешанную производную K-го порядка вычисляют, определяя производную первого порядка K Раз фиксацией переменных (порядок фиксации переменных не имеет значения); количество упорядочиваний равно K!

Производная K-го порядка От булевой функции по переменным Определяет условия, при которых эта функция изменяет значение при одновременном изменении значений переменных .

Упражнения

1. Проверить приведенные в теории равносильности путем построения таблиц истинности.

2. Построить СДНФ для Х1 | х2, х1 ¯ х2.

3. Минимизировать булеву функцию F(X1, X2, X3) = Ø(X1 Ú X1ØX2) ® ØX1X2X3, используя равносильности, операции склеивания и поглощения.

4. Минимизировать следующие функции с помощью диаграмм Вейча: F(X1, X2) = ØX1X2 ® X2, F(X1, X2, X3) = X1 ® ØX2 Ú ØX1ØX2(X3 Å ØX1), F(X1, X2, X3, X4) = ØX1X2 ® (X4 ¯ X3).

5. Проверить принадлежность классам Т0, Т1, T*, T<, ТL Функций ¯, |, Ú, ®, Å.

6. Определить

для функции F(X1, X2, X3) = X1 ® ØX1ØX2(X3 Å ØX1).

< Предыдущая		Следующая >

Источник

Дифференцирование и интегрирование булевых функций
f ( x1, x2 ,…, xn )
 f ( x1, x2 ,…, xi 1,1,…, xn )  f ( x1, x2 ,…, xi 1,0,…, xn )
xi
f ( x1, x2 , x3 )  x1x2  x1 x3
единичная остаточная
функция
нулевая остаточная
функция
f ( x1, x2 , x3 )
 f (1, x2 , x3 )  f (0, x2 , x3 )  1 x2  1 x3   0  x2  0  x3   x2  x3
x1
(условие переключения)
f ( x1, x2 , x3 ) изменит свое значение при изменении x1 при условии — x2  x3  1
f
 x1  x1 x3   x1 x3  x11  x3   x1x3
x2
условие переключения f при переключении x2
f
 x1x2  x1  x1 x2
x3
x1x3 =1
x1 x2 =1 условие переключения f при переключении x3
k

f ( x1, x2 ,…, xn )

Смешанная производная

xi1 xi2 …xik
xik
  k 1 f ( x , x ,…, x ) 
1 2
n 

 xi xi …xi


1 2
k 1 
Производная k-го порядка
 k f ( x1, x2 ,…, xn )
f
2 f

 


 xi1 , xi2 ,…, xik

x

x

x
iI i i, jI ,i  j i j i, j , sI ,


I  {i1, i2 ,…,ik }
i  j ,i  s, s  j
3 f
k f
 … 
xi x j xs
xi1 xi2 …xik
f
 x2  x3
x1
f ( x1, x2 , x3 )  x1x2  x1 x3
f  x x
f
 x1x3
1 2
x2
x3
2 f
  f   1  x   0  x   1  x



3
3
3  x3
x1x2 x2  x1 
x1 0 0 0 0 1 1 1 1
x2 0 0 1 1 0 0 1 1
2 f
 x2  x3    x1x3   x3  x3  x1x2  x1 x2
x3 0 1 0 1 0 1 0 1
  x1, x2 
11101011
условие переключения f при одновременном переключении x1 и x2
2 f
f
f
2 f



 x1, x2  x1 x2 x1x2
x3  x1x2  x1 x2  1
f переключается при одновременном переключении x1, x2
с 00 на 11 и с 11 на 00
3 f
f
f
f
2 f
2 f
2 f
3 f







 x1, x2 , x3  x1 x2 x3 x1x2 x1x3 x2x3 x1x2x3
2 f
  f 

  x2

x1x3 x3  x1 
2 f
  f 

  x1

x2x3 x3  x2 
3 f
   2 f 

1


x1x2x3 x1  x2x3 
3 f
 x1 x 2 x3  x1x2 x3  x1x2 x3  x1 x 2 x3  x1 x 2 x3  x1x2 x3
 x1, x2 , x3 
f переключается при переключении входных переменных
100↔011, 110↔001, 111↔000
Интеграл
 f ( X )dxi  {F j  X , xi },
F j  X , xi 
xi
f ( x1, x2 )  x1 & x2
X  ( x1, x2 ,…,xi 1, xi 1,…,xn )
 f (X )
 f ( x1, x2 )dx3  {F j  x1, x2 , x3 }
F j  x1, x2 , x3 
x3
{F j ( X , xi )}  2
 f ( x1, x2 )  x1 & x2
F j  x1, x2 , x3 
 F j  x1, x2 ,0  F j  x1, x2 ,1  x1 & x2
x3
x1 & x2  1  x1  1,

 x2  1
 F j 1,1,0  F j 1,1,1  1
x1 & x2  0  x1  1,
 F j 1,0,0  F j 1,0,1  0

x

 2
24  16
 F j 1,1,0   0,
 F j 1,1,0   1,
или 

 F j 1,1,1  1
 F j 1,1,1  0
F j 1,0,0  F j 1,0,1  1
F j 1,0,0  F j 1,0,1  0
или
 x1  0,
F j 0,1,0  F j 0,1,1  1 или






F
,
1
,

F
,
1
,
1

j
j
F j 0,1,0  F j 0,1,1  0
 x2  1
 x1  0,
 F j 1,0,0  F j 1,0,1  0 F j 0,0,0  F j 0,0,1  1 или

F j 0,0,0  F j 0,0,1  0
 x2  0
2
X
x1
 F j 1,1,0   0,
 F j 1,1,0   1,
или 

 F j 1,1,1  1
 F j 1,1,1  0
x2
f ( x1, x2 ) x3 F j ( x1, x2 , x3 )
1
1
1
1
1
F j 1,0,0  F j 1,0,1  1
или
F j 1,0,0  F j 1,0,1  0
F j 0,1,0  F j 0,1,1  1
или
F j 0,1,0  F j 0,1,1  0
…
…
…
…
…
1
1
1
1
1
1
1
1
1
1
1
1
1
…
1
…
…
16
или F j 0,0,0  F j 0,0,1  0
F j 0,0,0  F j 0,0,1  1
Многомерное интегрирование
 f ( X )dxi1 dxi2 …dxik  F j X , xi1 , xi2 ,…,xik ,



 k F j X , xi1 , xi2 ,…, xik
 f (X )
 xi1 , xi2 ,…, xik

F j X , xi1 , xi2 ,…,xik   2
k 2
X
Разложение булевой функции в заданной точке
Теорема. Любая булева функция f ( x1, x2 ,…, xn ) представима
своим значением в точке 00…0 и значениями всех производных
в этой точке:



 n f
  n
2

f


f ( x1, x2 ,…, xn )  f (0,0,…,0)  
& xi1   
& xi1 xi2   …




x
x x
 i1 1 i1 00…0
  i1,i2 1 i1 i2 00…0

 i1 i2





k
n
n

f

f

…  
&
x
x
…
x

…

& x1x2 …xn

i1 i2 ik
 i ,i ,…,i 1 xi xi …xi

x1x2 …xn
1 2
k 00…0
00…0
 i1 2i …ki

1 2

k
f ( x1, x2 , x3 )  x1x2  x1 x3
f
 x1 x2
0,0,0  0
x3
3 f
1
x1x2x3
0,0,0
f
 x2  x3 0,0,0  1
x1
2 f  x
3 0,0,0  0
x1x2
f
 x1x3 0,0,0  0
x2
2 f
 x1
0,0,0  0
x2x3
2 f
 x 2 0,0,0  1
x1x3
f ( x1, x2 , x3 ) 0,0,0  x1  x1x3  x1x2 x3
f ( x1, x2 , x3 ) 0,0,0  f (0,0,0) 
2 f

x1x2
f (0,0,0)  0
2 f
& x1x2 
x1x3
f
f
f
& x1 
& x2 
& x3 
x1 0,0,0
x2 0,0,0
x3 0,0,0
0,0,0
2 f
& x1x3 
x2x3
0,0,0
3 f
& x2 x3 
x1x2x3
& x1x2 x3
0,0,0
Разложение булевой функции в точке
(1, 2 ,…, n )
(0,0,…,0)
xi   i
xi
f ( x1, x2 , x3 )  x1x2  x1 x3
f (1,0,1)  1
f
 x2  x3 1,1,0  1
x1
2 f  x
3 1,1,0  0
x1x2
f ( x1, x2 , x3 ) 1,1,0  f (1,1,0) 
2 f

x1x2
1,1,0
3 f

x1x2x3
f
 x1x3 1,1,0  0
x2
2 f
 x 2 1,1,0  0
x1x3
(1,1,0)
f
 x1 x2
1,1,0  0
x3
2 f
 x1
1,1,0  1
x2x3
3 f
1
x1x2x3
f
f
f
&  x1  1 
&  x2  1 
&  x3  0  
x1 1,1,0
x2 1,1,0
x3 1,1,0
2 f
&  x1  1 x2  1 
x1x3
1,1,0
2 f
&  x1  1 x3  0  
x2x3
&  x1  1 x2  1 x3  0   1  x1  x 2 x3  x1 x 2 x3
1,1,0
(1, 2 ,…, n )
&  x2  1 x3  0  
1,1,0
Проблема порождения ложного значения функции
— транспортное запаздывание значений переменных
Трасса T(Xa,Xb) булевой функции f(X) – цепь интервала J(Xa,Xb):
X i  J , X i  X a , X i  X b X a  X i  X b
f  X a   f  X b , f  X i   f  X a 
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
x1
x2
x3
x4
f
0000000011
0000111100
0011001100
0101010101
1 11 0 01 0 00 0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1111
0000-0100-0110-0111-1111 — трасса длины 4
0111
0011
1011
1101
1110
0101
0110
1001
1010
0001
0010
0100
1000
0000
0000-1000-1100 — трасса длины 2
0100-1100-1101 — трасса длины 2
1100
Чем больше трасс, тем больше
возможность порождения ложной
информации
Вес производной – число конституент
  k f ( x , x ,…, x ) 
1 2
n 
P
  xi , xi ,…, xi 

1 2
k 


Чем больше вес производной, тем сильнее функция зависит от
переменных по которым она была продифференцирована
Оптимальное разложение функции по k переменным
  k f ( x , x ,…, x ) 
1 2
n 
1) Находят max P
  xi , xi ,…, xi  — определяют исключаемые переменные.

1 2
k 


2) Для единичной и нулевой остаточных функций повторяют шаг 1),
пока они не будут иметь простой вид
Взаимно ортогональные
функции f & f   0
Переключательные функции
f ( x1 , x2 ,…, xn ) : {0,1,…,k1  1}  {0,1,…,k2  1}  … {0,1,…,kn  1}  {0,1,…,k f  1}
x1 {0,1,2}, x2 {0,1}, x3 {0,1}, f {0,1,2,3}
x1
x2
x3
f ( x1, x2 , x3 )
Гиперкуб
210
1
0 110
3
3
3
001
000011112222
001100110011
010101010101
331023011103
211
111
101
1
1
010
201
011
1
2
200
100
3
000
k1  k2  …  kn  k f  k
k-значные переключательные функции
x1
1
2
3  2  2  12
Таблица Вейча
x2 x3
00 01 10
3
3
1
2
3
1
1
11
1
3
Отрицание
x  x  1(mod k )
1. Циклический сдвиг или отрицание Поста:
2. Зеркальное отображение или отрицание Лукашевича: Nx  k  1  x
1 при x  i,
3. Характеристическая функция: ji ( x)  
i  0,1,…,k  1
при
x

i

k  1 при x  i,
i  0,1,…,k  1
4. Ii ( x)  
при
x

i

Свойства операций
Конъюнкция x1x2
Дизъюнкция x1  x2
1. ассоциативность
5. min( x1, x2 )
7. max( x1, x2 )
2. коммутативность
3. дистрибутивность
6. x1  x2 (mod k )
8. x1  x2 (mod k )
4. Правила спуска символа I вглубь формулы
k  1 при c   ,
I (c)  
c,  0,1,…,k  1
при
c



 I 0 ( x)  …  I 1( x)  I 1( x)  …  I k 1( x) при   0,

I ( I ( x))  0 при 0    k  1,
 I ( x) при   k  1

I ( x1x2 )  I ( x1)( I ( x2 )  …  I k 1( x2 ))  I ( x2 )( I ( x1)  …  I k 1( x1))
I ( x1  x2 )  I ( x1)( I0 ( x2 )  …  I ( x2 ))  I ( x2 )( I 0 ( x1)  …  I ( x1))
5. Правило исключения «чистых» вхождений переменной
x  1 I1( x)  2  I 2 ( x)  …  (k  1) I k 1( x)
6. Правило введения переменной
7. Правила упрощений
x1  x1( I 0 ( x2 )  …  I k 1( x2 ))

Источник

Определение. Булева функция fP_n существенно зависит от переменной x_i, если существует такой набор значений a₁, …, a_i_-1, a_i₊₁, …, a_n, что

В этом случае x_i называют существенной переменной, в противном случае x_i называют несущественной переменной.

Определение. Производная первого порядка от булевой функции f по переменной x_i есть сумма по модулю 2 соответствующих остаточных функций:

где f(x₁, x₂, …, x_i_-1, 1, x_i₊₁, …, x_n) – единичная остаточная функция; f(x₁, x₂, …, x_i_-1, 0, x_i₊₁, …, x_n) – нулевая остаточная функция; — сумма по модулю 2.

Единичная остаточная функция получается в результате приравнивания переменной x_i единице, нулевая – приравниванием x_i нулю.

Определение. Весом производной от булевой функции называется число конституент этой производной.

Утверждение. Чем больше вес производной , тем больше функция f зависит от переменной x_i.

Пример 50.

Определить переменную x_i, по которой производная функции

имеет минимальный (максимальный) вес, т. е. функция f(x₁, x₂, x₃, x₄, x₅) зависит от нее менее (более) существенно.

Решение.

Определим вес каждой переменной, найдя сначала соответствующую производную.

Имеем

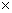
Для вычисления веса производной зависящей от четырех переменных х₂, х₃, х₄, х₅, представим 4-мерное пространство с образующими {x₂, x₃, x₄, x₅} в виде декартова произведения двух двумерных пространств {x₂, x₃} {x₄, x₅} с образующими {x₂, x₃} и {x₄, x₅} соответственно. Тогда производную можно задать в виде двумерной таблицы (табл. 2.61). Вес производной равен числу единиц в этой таблице.

Таблица 2.61 Вычисление веса производной (df/dx₁) для примера 50

х₂х₃	х₄х₅
00	01	10	11
00	0	0	1	1
01	1	0	1	0
10	0	0	0	0
11	1	0	1	1

Итак,

Аналогично вычислим вес производных (i = 2, 3, 4, 5) (табл. 2.62, 2.63, 2.64, 2.65). Имеем:

Таблица 2.62 Вычисление веса производной (df/dx₂) для примера 50

*х₁х₃*	*х₄х₅*
00	01	10	11
00	0	0	0	0
01	0	1	0	1
10	0	0	1	1
11	0	1	0	0

Таблица 2.63 Вычисление веса производной (df/dx₃) для примера 50

*х₁х₂*	*х₄х₅*
00	01	10	11
00	0	0	1	0
01	0	1	1	1
10	1	0	1	1
11	0	1	0	0

Таблица 2.64 Вычисление веса производной (df/dx₄) для примера 50

*х₁х₂*	*х₃х₅*
00	01	10	11
00	1	0	0	0
01	1	0	0	0
10	0	1	0	0
11	1	0	0	1

Таблица 2.65 Вычисление веса производной (df/dx₅) для примера 50

*х₁х₂*	*х₃х₄*
00	01	10	11
00	1	0	1	1
01	1	0	0	0
10	1	0	0	0
11	1	0	1	0

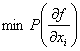
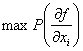
Выяснили, что минимальное значение получено при дифференцировании функции f по переменным х₂ и х₄, максимальное значение получено при дифференцировании функции f по переменной х₃.

Источник

Аннотация: В лекции рассматривается задача построения п проверяющего теста для конкретной заданной неисправности. Изложены аналитические методы построения тестов для комбинационных схем, которые основаны на символьных вычислениях. К ним относятся метод различающей функции и булевых производных. Описан структурный метод активизации одномерных путей.

17. 1 Метод различающей функции

Задача построения проверяющего теста для данной неисправности в комбинационной схеме может быть решена аналитически, если функционирование схемы в исправном и неисправном состояниях задано с помощью аналитических выражений функций выходов.

Пусть f(X) — булева функция, реализуемая исправной комбинационной схемой, а — булева функция, реализуемая неисправной схемой.

Назовем различающей функцией следующее выражение [17.1]:

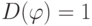
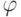
Очевидно, что наборы значений входных переменных , на которых , являются проверяющими тестами для данной неисправности varphi .

Для примера рассмотрим схему, изображенную на рис. 17.1.

Рис.
17.1.
Пример схемы для метода различающей функции

Применим метод различающей функции для построения проверяющего входного набора для константной неисправности 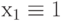$х_{1}equiv 1$ . В этом случае имеем:

функцию, реализуемую исправной схемой
$f(x)=(x_1&x_2)vee(x_2&overline{x}_3)$ ;
функцию, которая реализуется неисправной схемой,
$varphi(x)=x_2vee(x_2&overline{x}_3)=x_2$ .

Тогда различающая функция равна: 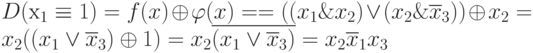$D(х_{1}equiv 1)=f(x)oplus varphi(x)= =((x_1&x_2)vee(x_2&overline{x}_3)) oplus x_{2}=x_{2}((x_{1}veeoverline{x}_3)oplus 1)=x_2overline{(x_{1}veeoverline{x}_3)}=x_2overline{x}_1x_3$ .

Очевидно, что равенство $D(x_{1}equiv 1)=1$ обеспечивает набор значений входных переменных $x_{1}=0$ , $x_{2}=1$ , $x_{3}=1$ , который и является проверяющим тестом для данной неисправности. Для больших схем этот метод становится слишком громоздким и требует больших вычислительных ресурсов. Однако следует отметить, что современные методы символьных вычислений (над булевыми выражениями) позволяют расширить его возможности.

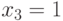
17.2 Метод булевых производных

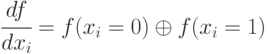
Булева производная функции f(X) по переменной $x_{i}$ определяется следующим выражением: $cfrac{df}{dx_i}=f(x_i=0)oplus f(x_i=1)$ [17.2]. Существует и другое, эквивалентное приведённому, определение булевой производной: $cfrac{df}{dx_i}=f(x_1,ldots,x_{i-1},x_i,x_{i+1},ldots,x_n)oplus f(x_1,ldots,x_{i-1},overline{x}_i,x_{i+1},ldots,x_n)$
.

Например, для булевой функции 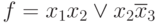$f=x_1x_2vee x_2overline{x}_3$ , булева производная
$cfrac{df}{dx_1}= x_2x_3oplus(x_2vee x_2overline{x}_3) = x_{2}(x_{3}oplus 1) = x_2overline{x}_3$
.

При вычислении булевых производных сложных функций полезны следующие свойства булевых производных:

Важны следующие частные случаи этих формул для функции , не зависящей от переменной $x_{i}$ :

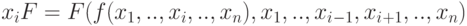
На практике важным является дифференцирование сложных функций, когда функция явно не зависит от переменной $x_{i}F = F(f(x_{1},..,x_{i},..,x_{n}),x_{1},..,x_{i}_{-1},x_{i}_{+1},..,x_{n})$ .

В этом случае имеет место 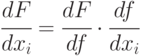$cfrac{dF}{dx_i}=cfrac{dF}{df}cdotcfrac{df}{dx_i}$ .

Для булевых функций справедливо следующее разложение Тейлора по переменной $x_{i}$ в точке $x_{i}=h_{i}$ с использованием булевой производной:

$f=f(x_i=h_i)opluscfrac{df}{dx_i}(x_ioplus h_i)$

Тогда различающая функция неисправности для 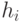$h_{i}$ может быть представлена следующим образом:

, где $h_{i} =0,1$ .

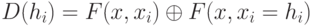
Используя разложение Тейлора функции по переменной $x_{i}$ в точке $h_{i}$ , получаем:

$D(h_i)=F(X,x_i=h_i)opluscfrac{dF}{dx_i}(x_ioplus h_i)oplus F(X,x_i=h_i)= cfrac{dF}{dx_i}(x_ioplus h_i)$

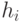
Здесь второй сомножитель даёт условие различения сигналов $x_{i}$ и $h_{i}$ в исправной и неисправной схеме на линии . Первый же сомножитель определяет условие распространения рассогласования сигнала в исправной и неисправной схеме до выхода схемы . Это соотношение является основой для метода булевых производных.

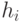
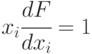
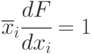
Таким образом, для построения теста для константной неисправности $h_{i}equiv 0$ необходимо решить булево уравнение (найти значения входных переменных) $x_icfrac{dF}{dx_i}=1$ , а для неисправности $h_{i}equiv 1$ — уравнение $overline{x}_icfrac{dF}{dx_i}=1$ .

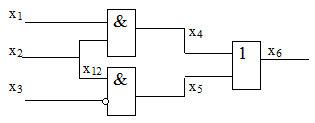
Рассмотрим метод булевых производных на примере построения теста неисправности 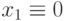$x_{1}equiv 0$ для схемы рис. 17.2. Для построения теста нам необходимо решить уравнение $x_1cfrac{df}{dx_1}=1$ .

Рис.
17.2.
Иллюстрация метода булевых производных

При вычислениях используем приведенные выше свойства булевых производных и получаем:

$cfrac{df}{dx_1}=cfrac{df}{dx_8}cfrac{dx_8}{dx_6}cfrac{dx_6}{dx_1}\ cfrac{df}{dx_8}=overline{x_9}=overline{x_7overline{x_3}}=x_3veeoverline{x_4},overline{x_5}\ cfrac{dx_8}{dx_6}=x_3\ cfrac{dx_6}{dx_1}=overline{x_2}\ cfrac{df}{dx_1}=( x_3veeoverline{x_4},overline{x_5})x_3overline{x_2}= x_3overline{x_2}=1\ x_1cfrac{df}{dx_1}=x_1x_3overline{x_2}=1$

Из этого выражения следует, что набор значений входов $x_{1}=1$ , $x_{2}=0$ , $x_{3}=1$ является проверяющим тестом для данной неисправности.

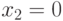
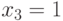
Рассмотрим построение теста для неисправности $x_{7}equiv 1$ внутренней линии той же схемы.

$overline{x_7}cfrac{df}{dx_7}=1\ cfrac{df}{dx_7}=cfrac{df}{dx_9}cdotcfrac{dx_9}{dx_7}\ cfrac{df}{dx_9}=overline{x_8}=overline{x_3x_6}=overline{x_3(x_1vee x_2)}=overline{x_3}veeoverline{x_1},overline{x_2}\ cfrac{dx_9}{dx_7}=overline{x_3}\ cfrac{df}{dx_7}=(overline{x_3}veeoverline{x_1},overline{x_2})overline{x_3}=overline{x_3}\ overline{x_7},overline{x_3}=1\ overline{x_4x_5},overline{x_3}=1\ (overline{x_4}veeoverline{x_5})overline{x_3}=1\ overline{x_4},overline{x_3}veeoverline{x_5},overline{x_3}=1$

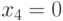
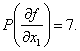
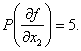
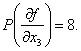
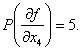
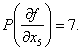
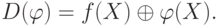
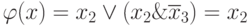Таким образом, для проверки данной неисправности можно использовать наборы $x_{4}=0$ , $x_{3}=0$ или $x_{5}=0$ , $x_{3}=0$ , что следует из последнего выражения для различающей функции.

Источник