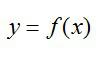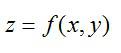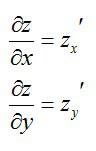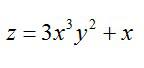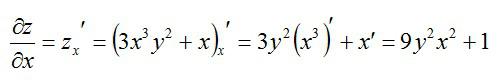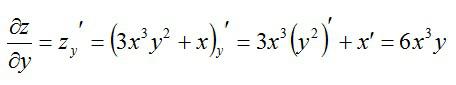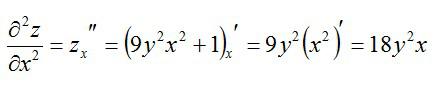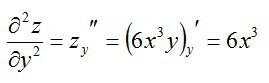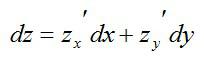Как найти производную частного формула

При дифференцировании функций нахождение производной частного обычно вызывает наибольшие затруднения. Лучший способ разобраться и понять, как находится производная частного, — рассмотреть конкретные примеры с подробными пояснениями.

Именно этим мы сейчас и займемся. Для дифференцирования нам понадобится таблица производных. Напишем еще раз правило, по которому берется производная частного:

   

(Поначалу неплохо его выписать на листочек и держать перед глазами). В отличие от производной произведения, затруднений с определением, где здесь u,  а где — v, в производной частного нет: понятно, что все, что вверху, в числителе — это u, а все что внизу, в знаменателе — v. Если u и v — табличные функции, производная частного может быть найдена легко: достаточно расписать все по формуле, найти каждую из производных, и упростить.

Пример. Найти производную частного:

   

Здесь u=2-4x, v=3x+7

   

Производную линейной функции полезно помнить: (kx+b)’=k, где k и b — числа, причем k — число, стоящее перех x. А можно найти как производную суммы: (kx+b)’=k·x’+b’=k·1+0=k. Таким образом, (2-4x)’=-4, (3x+7)’=3, и знак умножения перед скобкой и перед буквой обычно не пишется

   

   

   

   

   

Общий множитель в числителе выносим за скобку, затем дробь сокращаем:

   

   

u=2x³+7x-5, v=6x-8. Расписываем по формуле производной частного:

   

здесь числитель представляет собой сумму и разность функций. Как находить производную суммы и разности, мы уже знаем.

   

   

   

   

Здесь u=2lnx+1, v=2√x. Значит, производная частного равна

   

   

   

   

Примеры для самопроверки. Найти производную частного:

   

Показать решение

Пока что мы рассмотрели только самые простые примеры на производную частного. В более сложных примерах числитель и знаменатель дроби могут быть сложными функциями, либо являться, в свою очередь, производными произведения и частного. Такие примеры мы обсудим чуть позже.

Частные производные

Частные производные применяются в заданиях с функциями нескольких переменных. Правила нахождения точно такие же как и для функций одной переменной, с разницей лишь в том, что одну из переменных нужно считать в момент дифференцирования константой (постоянным числом).

Формула

Частные производные для функции двух переменных $ z(x,y) $ записываются в следующем виде $ z’_x, z’_y $ и находятся по формулам:

Частные производные первого порядка

$$ z’_x = frac{partial z}{partial x} $$

$$ z’_y = frac{partial z}{partial y} $$

Частные производные второго порядка

$$ z»_{xx} = frac{partial^2 z}{partial x partial x} $$

$$ z»_{yy} = frac{partial^2 z}{partial y partial y} $$

Смешанная производная

$$ z»_{xy} = frac{partial^2 z}{partial x partial y} $$

$$ z»_{yx} = frac{partial^2 z}{partial y partial x} $$

Частная производная сложной функции

а) Пусть $ z (t) = f( x(t), y(t) ) $, тогда производная сложной функции определяется по формуле:

$$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$

б) Пусть $ z (u,v) = z(x(u,v),y(u,v)) $, тогда частные производные функции находится по формуле: 

$$ frac{partial z}{partial u} = frac{partial z}{partial x} cdot frac{partial x}{partial u} + frac{partial z}{partial y} cdot frac{partial y}{partial u} $$

$$ frac{partial z}{partial v} = frac{partial z}{partial x} cdot frac{partial x}{partial v} + frac{partial z}{partial y} cdot frac{partial y}{partial v} $$

Частные производные неявно заданной функции

а) Пусть $ F(x,y(x)) = 0 $, тогда $$ frac{dy}{dx} = -frac{f’_x}{f’_y} $$

б) Пусть $ F(x,y,z)=0 $, тогда $$ z’_x = — frac{F’_x}{F’_z}; z’_y = — frac{F’_y}{F’_z} $$

Примеры решений

Пример 1

Найти частные производные первого порядка $ z (x,y) = x^2 — y^2 + 4xy + 10 $

Решение

Для нахождения частной производной по $ x $ будем считать $ y $ постоянной величиной (числом): $$ z’_x = (x^2-y^2+4xy+10)’_x = 2x — 0 + 4y + 0 = 2x+4y $$ Для нахождения частной производной функции по $ y $ определим $ y $ константой: $$ z’_y = (x^2-y^2+4xy+10)’_y = -2y+4x $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ z’_x = 2x+4y; z’_y = -2y+4x $$

Пример 2

Найти частные производные функции второго порядка $ z = e^{xy} $

Решение

Сперва нужно найти первый производные, а затем зная их можно найти производные второго порядка. Полагаем $ y $ константой: $$ z’_x = (e^{xy})’_x = e^{xy} cdot (xy)’_x = ye^{xy} $$ Положим теперь $ x $ постоянной величиной: $$ z’_y = (e^{xy})’_y = e^{xy} cdot (xy)’_y = xe^{xy} $$ Зная первые производные аналогично находим вторые. Устанавливаем $ y $ постоянной: $$ z»_{xx} = (z’_x)’_x = (ye^{xy})’_x = (y)’_x e^{xy} + y(e^{xy})’_x = 0 + ye^{xy}cdot (xy)’_x = y^2e^{xy} $$ Задаем $ x $ постоянной: $$ z»_{yy} = (z’_y)’_y = (xe^{xy})’_y = (x)’_y e^{xy} + x(e^{xy})’_y = 0 + x^2e^{xy} = x^2e^{xy} $$ Теперь осталось найти смешанную производную. Можно продифференцировать $ z’_x $ по $ y $, а можно $ z’_y $ по $ x $, так как по теореме $ z»_{xy} = z»_{yx} $ $$ z»_{xy} = (z’_x)’_y = (ye^{xy})’_y = (y)’_y e^{xy} + y (e^{xy})’_y = ye^{xy}cdot (xy)’_y = yxe^{xy} $$

Ответ

$$ z’_x = ye^{xy}; z’_y = xe^{xy}; z»_{xy} = yxe^{xy} $$

Пример 3

Найти частную производную сложной функции $ z = x^2 + y^2, x = sin t, y = t^3 $

Решение

Находим $ frac{partial z}{partial x} $: $$ frac{partial z}{partial x} = (x^2+y^2)’_x = 2x $$ Находим $ frac{partial z}{partial y} $: $$ frac{partial z}{partial y} = (x^2+y^2)’_y = 2y $$ Теперь ищем $ frac{dx}{dt} $ и $ frac{dy}{dt} $: $$ frac{dx}{dt} = frac{d(sin t)}{dt} = cos t $$ $$ frac{dy}{dt} = frac{d(t^3)}{dt} = 3t^2 $$ Подставляем всё это в формулу и записываем ответ: $$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$ $$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$

Ответ

$$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$

Пример 4

Пусть $ 3x^3z — 2z^2 + 3yz^2-4x+z-5 = 0 $ задаёт неявную функцию $ F(x,y,z) = 0 $. Найти частные производные первого порядка.

Решение

Записываем функцию в формате: $ F(x,y,z) = 3x^3z — 2z^2 + 3yz^2-4x+z-5 = 0 $ и находим производные: $$ z’_x (y,z — const) = (x^3 z — 2z^2 + 3yz^2-4x+z-5)’_x = 3 x^2 z — 4 $$ $$ z’_y (x,y — const) = (x^3 z — 2z^2 + 3yz^2-4x+z-5)’_y = 3z^2 $$

Ответ

$$ z’_x = 3x^2 z — 4; z’_y = 3z^2; $$

Производная произведения и производная частного

3 февраля 2015

В этом уроке мы продолжаем изучать производные функций и переходим к более сложной теме, а именно, к производным произведения и частного. Если вы смотрели предыдущий урок, то наверняка поняли, что мы рассматривали лишь самые простые конструкции, а именно, производную степенной функции, суммы и разности. В частности, мы узнали, что производная суммы равна их сумме, а производная разности равна, соответственно, их разности. К сожалению, в случае с производными частного и произведения формулы будут гораздо сложнее. Начнем мы именно с формулы производной произведения функций.

Производные тригонометрических функций

Для начала позволю себе небольшое лирическое отступление. Дело в том, что помимо стандартной степенной функции — $y={{x}^{n}}$, в этом уроке будут встречаться и другие функции, а именно, $y=sin x$, а также $y=cos x$ и прочая тригонометрия — $y=tgx$ и, разумеется, $y=ctgx$.

Если производную степенной функции мы все прекрасно знаем, а именно $left( {{x}^{n}} right)=ncdot {{x}^{n-1}}$, то, что касается тригонометрических функций, нужно упомянуть отдельно. Давайте запишем:

[begin{align} {{left( sin x right)}^{prime }} &=cos x \ {{left( cos x right)}^{prime }} &=-sin x \ {{left( tgx right)}^{prime }} &=frac{1}{{{cos }^{2}}x} \ {{left( ctgx right)}^{prime }} &=frac{1}{{{cos }^{2}}x} \end{align}]

Но эти формулы вы прекрасно знаете, давайте пойдем дальше.

Что такое производная произведения?

Для начала самое главное: если функция представляет собой произведение двух других функций, например, $fcdot g$, то производная этой конструкции будет равна следующему выражению:

[{{left( fcdot g right)}^{prime }}={f}’cdot g+fcdot {g}’]

Как видите, эта формула значительно отличается и является более сложной, нежели те формулы, которые мы рассматривали ранее. Например, производная суммы считается элементарно —${{left( f+g right)}^{prime }}={f}’+{g}’$, либо производная разности, которая тоже элементарно считается ― ${{left( f-g right)}^{prime }}={f}’-{g}’$.

Давайте попробуем применить первую формулу для вычисления производных двух функций, которые нам даны в задаче. Начнем с первого примера:

[y={{x}^{3}}left( x-5 right)]

Очевидно, что в качестве произведения, точнее, в качестве множителя, выступает следующая конструкция: ${{x}^{3}}$, мы можем рассматривать в качестве $f$, а $left( x-5 right)$ мы можем рассматривать в качестве $g$. Тогда их произведение как раз и будет произведением двух функций. Решаем:

[begin{align}& {{left( {{x}^{3}}cdot left( x-5 right) right)}^{prime }}={{left( {{x}^{3}} right)}^{prime }}cdot left( x-5 right)+{{x}^{3}}cdot {{left( x-5 right)}^{prime }}= \& =3{{x}^{2}}cdot left( x-5 right)+{{x}^{3}}cdot 1 \end{align}].

Теперь давайте внимательно посмотрим на каждое из наших слагаемых. Мы видим, что и в первом, и во втором слагаемом присутствует степень $x$: в первом случае это ${{x}^{2}}$, а во втором — ${{x}^{3}}$. Давайте вынесем наименьшую степень за скобки, в скобке останется:

[begin{align}& 3{{x}^{2}}cdot left( x-5 right)+{{x}^{3}}cdot 1={{x}^{2}}left( 3cdot 1left( x-5 right)+x right)= \& ={{x}^{2}}left( 3x-15+x right)={{x}^{2}}(4x-15) \end{align}]

Все, мы нашли ответ.

Возвращаемся к нашим задачам и попробуем решить:

[fleft( x right)=xleft( sqrt[3]{x}-1 right)]

Итак, переписываем:

[fleft( x right)=xcdot left( sqrt[3]{x}-1 right)]

Опять же замечаем, что речь идет о произведении произведения двух функций: $x$, которую можно обозначить за $f$, и $left( sqrt[3]{x}-1 right)$, которую можно обозначить за $g$.

Таким образом, перед нами вновь произведение двух функций. Для нахождения производной функции $fleft( x right)$ вновь воспользуемся нашей формулой. Получим:

[begin{align}& {f}’=left( x right)’cdot left( sqrt[3]{x}-1 right)+xcdot {{left( sqrt[3]{x}-1 right)}^{prime }}=1cdot left( sqrt[3]{x}-1 right)+xfrac{1}{3sqrt[3]{x}}= \& =sqrt[3]{x}-1+sqrt[3]{x}cdot frac{1}{3}=frac{4}{3}sqrt[3]{x}-1 \end{align}]

Ответ найден.

Зачем раскладывать производные на множители?

Только что мы использовали несколько очень важных математических фактов, которые сами по себе не имеют отношения к производным, однако без их знания все дальнейшее изучение этой темы просто не имеет смысла.

Во-первых, решая самую первую задачу и, уже избавившись от всех знаков производных, мы зачем-то начали раскладывать это выражение на множители.

Во-вторых, решая следующую задачу, мы несколько раз переходили от корня к степени с рациональным показателем и обратно, при этом используя формулу 8-9-го класса, которую стоило бы повторить отдельно.

По поводу разложения на множители ― зачем вообще нужны все эти дополнительные усилия и преобразования? На самом деле, если в задаче просто сказано «найти производную функции», то эти дополнительные действия не требуются. Однако в реальных задачах, которые ждут вас на всевозможных экзаменах и зачетах, просто найти производную зачастую недостаточно. Дело в том, что производная является лишь инструментом, с помощью которой можно узнать, например, возрастание или убывание функции, а для этого требуется решать уравнение, раскладывать его на множители. И вот здесь этот прием будет очень уместен. Да и вообще, с функцией, разложенной на множители, гораздо удобней и приятней работать в дальнейшем, если требуются какие-то преобразования. Поэтому правило № 1: если производную можно разложить на множители, именно так и стоит поступать. И сразу правило № 2 (по сути, это материал 8-9-го класса): если в задаче встречается корень n-ной степени, причем, корень явно больше двух, то этот корень можно заменить обычной степенью с рациональным показателем, причем в показателе появится дробь, где n― та самая степень ― окажется в знаменателе этой дроби.

Разумеется, если под корнем присутствует какая-то степень (в нашем случае это степень k), то она никуда не девается, а просто оказывается в числителе этой самой степени.

А теперь, когда вы все это поняли, давайте вернемся к производным произведения и посчитаем еще несколько уравнений.

Но прежде чем переходить непосредственно к вычислениям, хотел бы напомнить такие закономерности:

[begin{align}& {{left( sin x right)}^{prime }}=cos x \& {{left( cos x right)}^{prime }}=-sin x \& left( tgx right)’=frac{1}{{{cos }^{2}}x} \& {{left( ctgx right)}^{prime }}=-frac{1}{{{sin }^{2}}x} \end{align}]

Считаем первый пример:

[y={{x}^{4}}cdot sin x]

У нас опять произведение двух функций: первая ― $f$, вторая ― $g$. Напомню формулу:

[{{left( fcdot g right)}^{prime }}={f}’cdot g+fcdot {g}’]

Давайте решим:

[begin{align}& {y}’={{left( {{x}^{4}} right)}^{prime }}cdot sin x+{{x}^{4}}cdot {{left( sin x right)}^{prime }}= \& =3{{x}^{3}}cdot sin x+{{x}^{4}}cdot cos x={{x}^{3}}left( 3sin x+xcdot cos x right) \end{align}]

Переходим ко второй функции:

[y=left( 3x-2 right)cos x]

Опять же, $left( 3x-2 right)$ ― это функция $f$, $cos x$ ― это функция $g$. Итого производная произведения двух функций будет равна:

[begin{align}& {y}’={{left( 3x-2 right)}^{prime }}cdot cos x+left( 3x-2 right)cdot {{left( cos x right)}^{prime }}= \& =3cdot cos x+left( 3x-2 right)cdot left( -sin x right)=3cos x-left( 3x-2 right)cdot sin x \end{align}]

Вот такое решение.

Идем далее и переходим к более сложным примерам. Для экономии времени я буду пропускать очевидные действия и буду писать лишь ключевые шаги. Итак:

[y={{x}^{2}}cos x+4xsin x]

Запишем:

[{y}’={{left( {{x}^{2}}cdot cos x right)}^{prime }}+{{left( 4xsin x right)}^{prime }}]

Выпишем по отдельности:

[begin{align}& {{left( {{x}^{2}}cdot cos x right)}^{prime }}=left( {{x}^{2}} right)’cos x+{{x}^{2}}cdot {{left( cos x right)}^{prime }}= \& =2xcdot cos x+{{x}^{2}}cdot left( -sin x right)=2xcdot cos x-{{x}^{2}}cdot sin x \end{align}]

На множители мы это выражение не раскладываем, потому что это еще не окончательный ответ. Сейчас нам предстоит решить вторую часть. Выписываем ее:

[begin{align}& {{left( 4xcdot sin x right)}^{prime }}={{left( 4x right)}^{prime }}cdot sin x+4xcdot {{left( sin x right)}^{prime }}= \& =4cdot sin x+4xcdot cos x \end{align}]

А теперь возвращаемся к нашей изначальной задаче и собираем все в единую конструкцию:

[begin{align}& {y}’=2xcdot cos x-{{x}^{2}}cdot sin x+4sin x+4xcos x=6xcdot cos x= \& =6xcdot cos x-{{x}^{2}}cdot sin x+4sin x \end{align}]

Все, это окончательный ответ.

Переходим к последнему примеру ― он будет самым сложным и самым объемным по вычислениям. Итак, пример:

[y={{x}^{2}}tgx-2xctgx]

Считаем:

[{y}’={{left( {{x}^{2}}cdot tgx right)}^{prime }}-{{left( 2xctgx right)}^{prime }}]

Считаем каждую часть отдельно:

[begin{align}& {{left( {{x}^{2}}cdot tgx right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}cdot tgx+{{x}^{2}}cdot {{left( tgx right)}^{prime }}= \& =2xcdot tgx+{{x}^{2}}cdot frac{1}{{{cos }^{2}}x} \end{align}]

[begin{align}& {{left( 2xcdot ctgx right)}^{prime }}={{left( 2x right)}^{prime }}cdot ctgx+2xcdot {{left( ctgx right)}^{prime }}= \& =2cdot ctgx+2xleft( -frac{1}{{{sin }^{2}}x} right)=2cdot ctgx-frac{2x}{{{sin }^{2}}x} \end{align}]

Возвращаясь к исходной функции, посчитаем ее производную в целом:

[begin{align}& {y}’=2xcdot tgx+frac{{{x}^{2}}}{{{cos }^{2}}x}-left( 2ctgx-frac{2x}{{{sin }^{2}}x} right)= \& =2xcdot tgx+frac{{{x}^{2}}}{{{cos }^{2}}x}-2ctgx+frac{2x}{{{sin }^{2}}x} \end{align}]

Вот, собственно, и все, что я хотел рассказать по производным произведения. Как видите, основная проблема формулы состоит не в том, чтобы ее заучить, а в том, что получается довольно большой объем вычислений. Но это нормально, потому что сейчас мы переходим к производной частного, где нам придется очень сильно потрудиться.

Что представляет собой производная частного?

Итак, формула производной частного. Пожалуй, это самая сложная формула в школьном курсе производных. Допустим, у нас есть функция вида $frac{f}{g}$, где $f$ и $g$ ― также функции, с которых тоже можно снять штрих. Тогда она будет считаться по следующей формуле:

[{{left( frac{f}{g} right)}^{prime }}=frac{{f}’cdot g-fcdot {g}’}{{{g}^{2}}}]

Числитель чем-то напоминает нам формулу производной произведения, однако между слагаемыми стоит знак «минус» и еще в знаменателе добавился квадрат исходного знаменателя. Давайте посмотрим, как это работает на практике:

[fleft( x right)=frac{{{x}^{2}}-1}{x+2}]

Попытаемся решить:

[{f}’={{left( frac{{{x}^{2}}-1}{x+2} right)}^{prime }}=frac{{{left( {{x}^{2}}-1 right)}^{prime }}cdot left( x+2 right)-left( {{x}^{2}}-1 right)cdot {{left( x+2 right)}^{prime }}}{{{left( x+2 right)}^{2}}}]

Предлагаю выписать каждую часть отдельно и записать:

[begin{align}& {{left( {{x}^{2}}-1 right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}-{1}’=2x \& {{left( x+2 right)}^{prime }}={x}’+{2}’=1 \end{align}]

Переписываем наше выражение:

[begin{align}& {f}’=frac{2xcdot left( x+2 right)-left( {{x}^{2}}-1 right)cdot 1}{{{left( x+2 right)}^{2}}}= \& =frac{2{{x}^{2}}+4x-{{x}^{2}}+1}{{{left( x+2 right)}^{2}}}=frac{{{x}^{2}}+4x+1}{{{left( x+2 right)}^{2}}} \end{align}]

Мы нашли ответ. Переходим ко второй функции:

[y=frac{1}{{{x}^{2}}+4}]

Судя по тому, что в ее числителе стоит просто единица, то здесь вычисления будут чуть проще. Итак, запишем:

[{y}’={{left( frac{1}{{{x}^{2}}+4} right)}^{prime }}=frac{{1}’cdot left( {{x}^{2}}+4 right)-1cdot {{left( {{x}^{2}}+4 right)}^{prime }}}{{{left( {{x}^{2}}+4 right)}^{2}}}]

Посчитаем каждую часть примера отдельно:

[begin{align}& {1}’=0 \& {{left( {{x}^{2}}+4 right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}+{4}’=2x \end{align}]

Переписываем наше выражение:

[{y}’=frac{0cdot left( {{x}^{2}}+4 right)-1cdot 2x}{{{left( {{x}^{2}}+4 right)}^{2}}}=-frac{2x}{{{left( {{x}^{2}}+4 right)}^{2}}}]

Мы нашли ответ. Как и предполагалось, объем вычисления оказался существенно меньше, чем для первой функции.

В чем разница между обозначениями?

У внимательных учеников наверняка уже возник вопрос: почему в одних случаях мы обозначаем функцию как $fleft( x right)$, а в других случаях пишем просто $y$? На самом деле, с точки зрения математики нет абсолютно никакой разницы ― вы вправе использовать как первое обозначение, так и второе, при этом никаких штрафных санкций на экзаменах и зачетах не последует. Для тех, кому все-таки интересно, поясню, почему авторы учебников и задач в одних случаях пишут $fleft( x right)$, а в других (гораздо более частых) ― просто $y$. Дело в том, что записывая функцию в виде[fleft( x right)=frac{{{x}^{2}}-1}{x+2}], мы неявно намекаем тому, кто будет читать наши выкладки, что речь идет именно об алгебраической интерпретации функциональной зависимости. Т. е., есть некая переменная $x$, мы рассматриваем зависимость от этой переменной и обозначаем ее $fleft( x right)$. При этом, увидев вот такое обозначение, тот, кто будет читать ваши выкладки, например, проверяющий, будет подсознательно ожидать, что в дальнейшем его ждут лишь алгебраические преобразования ― никаких графиков и никакой геометрии.

С другой стороны, используя обозначения вида[y=frac{1}{{{x}^{2}}+4}], т. е., обозначая переменную одной единственной буквой, мы сразу даем понять, что в дальнейшем нас интересует именно геометрическая интерпретация функции, т. е., нас интересует, в первую очередь, ее график. Соответственно, столкнувшись с записью вида[y=frac{1}{{{x}^{2}}+4}], читатель вправе ожидать графических выкладок, т. е., графиков, построений и т. д., но, ни в коем случае, не аналитических преобразований.

Еще хотел бы обратить ваше внимание на одну особенность оформления задач, которые мы сегодня рассматриваем. Многие ученики считают, что я привожу слишком подробные выкладки, и многие из них можно было бы пропустить или просто решить в уме. Однако именно такая подробная запись позволит вам избавится от обидных ошибок и значительно увеличит процент правильно решенных задач, например, в случае самостоятельной подготовки к контрольным или экзаменам. Поэтому если вы еще неуверенны в своих силах, если вы только начинаете изучать данную тему, не спешите ― подробно расписывайте каждый шаг, выписывайте каждый множитель, каждый штрих, и очень скоро вы научитесь решать такие примеры лучше, чем многие школьные учителя. Надеюсь, это понятно. Давайте посчитаем еще несколько примеров.

Несколько интересных задач

На этот раз, как мы видим, в составе вычисляемых производных присутствует тригонометрия. Поэтому напомню следующее:

[begin{align}& {(sin x)}’=cos x \& {{left( cos x right)}^{prime }}=-sin x \end{align}]

Конечно, нам не обойтись и без производной частного, а именно:

[{{left( frac{f}{g} right)}^{prime }}=frac{{f}’cdot g-fcdot {g}’}{{{g}^{2}}}]

Считаем первую функцию:

[fleft( x right)=frac{sin x}{x}]

Запишем:

[begin{align}& {f}’={{left( frac{sin x}{x} right)}^{prime }}=frac{{{left( sin x right)}^{prime }}cdot x-sin xcdot left( {{x}’} right)}{{{x}^{2}}}= \& =frac{xcdot cos x-1cdot sin x}{{{x}^{2}}}=frac{xcos x-sin x}{{{x}^{2}}} \end{align}]

Вот мы и нашли решение этого выражения.

Переходим ко второму примеру:

[y=frac{xsin x}{cos x}]

Очевидно, что ее производная будет более сложной уже хотя бы потому, что и в числителе, и в знаменателе данной функции присутствует тригонометрия. Решаем:

[{y}’={{left( frac{xsin x}{cos x} right)}^{prime }}=frac{{{left( xsin x right)}^{prime }}cdot cos x-xsin xcdot {{left( cos x right)}^{prime }}}{{{left( cos x right)}^{2}}}]

Заметим, что у нас возникает производная произведения. В этом случае она будет равна:

[begin{align}& {{left( xcdot sin x right)}^{prime }}={x}’cdot sin x+x{{left( sin x right)}^{prime }}= \& =sin x+xcos x \end{align}]

Возвращаемся к нашим вычислениям. Записываем:

[begin{align}& {y}’=frac{left( sin x+xcos x right)cos x-xcdot sin xcdot left( -sin x right)}{{{cos }^{2}}x}= \& =frac{sin xcdot cos x+x{{cos }^{2}}x+x{{sin }^{2}}x}{{{cos }^{2}}x}= \& =frac{sin xcdot cos x+xleft( {{sin }^{2}}x+{{cos }^{2}}x right)}{{{cos }^{2}}x}=frac{sin xcdot cos x+x}{{{cos }^{2}}x} \end{align}]

Вот и все! Мы посчитали.

Как свести производную частного к простой формуле производной произведения?

И вот тут хотелось бы сделать одно очень важное замечание, касающееся именно тригонометрических функций. Дело в том, что наша исходная конструкция содержит в себе выражение вида $frac{sin x}{cos x}$, которую легко можно заменить просто $tgx$. Таким образом, мы сведем производную частного к более простой формуле производной произведения. Вот давайте посчитаем этот пример еще раз и сравним результаты.

Итак, теперь нам нужно учесть следующее:

[frac{sin x}{cos x}=tgx]

Перепишем нашу исходную функцию $y=frac{xsin x}{cos x}$ с учетом этого факта. Получим:

[y=xcdot tgx]

Давайте посчитаем:

[begin{align}& {y}’={{left( xcdot tgx right)}^{prime }}{x}’cdot tgx+x{{left( tgx right)}^{prime }}=tgx+xfrac{1}{{{cos }^{2}}x}= \& =frac{sin x}{cos x}+frac{x}{{{cos }^{2}}x}=frac{sin xcdot cos x+x}{{{cos }^{2}}x} \end{align}]

Теперь, если мы сравним полученный результат с тем, что мы получили ранее, при вычислении по другому пути, то мы убедимся, что получили одно и то же выражение. Таким образом, каким бы путем мы не шли при вычислении производной, если все посчитано верно, то ответ будет одним и тем же.

Важные нюансы при решении задач

В заключении хотел бы рассказать вам еще одну тонкость, связанную с вычислением производной частного. То, что я вам сейчас расскажу, не было в изначальном сценарии видеоурока. Однако за пару часов до съемок я занимался с одним из своих учеников, и мы как раз разбирали тему производных частного. И, как выяснилось, этот момент многие ученики не понимают. Итак, допустим, нам нужно посчитать снять штрих следующей функции:

[y=frac{48}{x}+3{{x}^{2}}+100]

В принципе, ничего сверхъестественного на первый взгляд в ней нет. Однако в процессе вычисления мы можем допустить много глупых и обидных ошибок, которые я бы хотел сейчас разобрать.

Итак, считаем эту производную. Прежде всего, заметим, что у нас присутствует слагаемое $3{{x}^{2}}$, поэтому уместно вспомнить следующую формулу:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

Кроме того, у нас присутствует слагаемое $frac{48}{x}$ ― с ним мы будем разбираться через производную частного, а именно:

[{{left( frac{f}{g} right)}^{prime }}=frac{{f}’cdot g-fcdot {g}’}{{{g}^{2}}}]

Итак, решаем:

[{y}’={{left( frac{48}{x} right)}^{prime }}+{{left( 3{{x}^{2}} right)}^{prime }}+10{0}’]

С первым слагаемым никаких проблем, смотрите:

[{{left( 3{{x}^{2}} right)}^{prime }}=3cdot {{left( {{x}^{2}} right)}^{prime }}=3k.2x=6x]

А вот с первым слагаемым, $frac{48}{x}$, нужно поработать отдельно. Дело в том, что многие ученики путают ситуацию, когда нужно найти ${{left( frac{x}{48} right)}^{prime }}$и когда нужно найти ${{left( frac{48}{x} right)}^{prime }}$. Т. е., они путаются, когда константа стоит в знаменателе, и когда константа стоит в числителе, соответственно, когда переменная стоит в числителе, либо в знаменателе.

Для начала проработаем первый вариант:

[{{left( frac{x}{48} right)}^{prime }}={{left( frac{1}{48}cdot x right)}^{prime }}=frac{1}{48}cdot {x}’=frac{1}{48}cdot 1=frac{1}{48}]

С другой стороны, если мы попробуем аналогично поступить и со второй дробью, то получим следующее:

[begin{align}& {{left( frac{48}{x} right)}^{prime }}={{left( 48cdot frac{1}{x} right)}^{prime }}=48cdot {{left( frac{1}{x} right)}^{prime }}= \& =48cdot frac{{1}’cdot x-1cdot {x}’}{{{x}^{2}}}=48cdot frac{-1}{{{x}^{2}}}=-frac{48}{{{x}^{2}}} \end{align}]

Однако тот же самый пример можно было посчитать и иначе: на этапе, где мы переходили к производной частного, можно рассмотреть $frac{1}{x}$ как степень с отрицательным показателем, т. е., мы получим следующее:

[begin{align}& 48cdot {{left( frac{1}{x} right)}^{prime }}=48cdot {{left( {{x}^{-1}} right)}^{prime }}=48cdot left( -1 right)cdot {{x}^{-2}}= \& =-48cdot frac{1}{{{x}^{2}}}=-frac{48}{{{x}^{2}}} \end{align}]

И так, и так мы получили один и тот же ответ.

Таким образом, мы еще раз убедились в двух важных фактах. Во-первых, одну и ту же производную можно посчитать совершенно различными способами. Например, ${{left( frac{48}{x} right)}^{prime }}$ можно рассматривать и как производную частного, и как производную степенной функции. При этом если все вычисления выполнены верно, то ответ всегда получится одним и тем же. Во-вторых, при вычислении производных, содержащих и переменную, и константу, принципиально важным является то, где находится переменная ― в числителе или в знаменателе. В первом случае, когда переменная находится в числителе, мы получаем простую линейную функцию, которая элементарно считается. А в случае, если переменная стоит в знаменателе, то мы получаем более сложное выражение с сопутствующими выкладками, приведенными ранее.

На этом урок можно считать законченным, поэтому если вам что-то непонятно по производным частного или произведения, да и вообще, если у вас есть любые вопросы по этой теме, не стесняйтесь ― заходите на мой сайт, пишите, звоните, и я обязательно постараюсь вам помочь.

Сами по себе производные ― тема отнюдь не сложная, но очень объемная, и то, что мы сейчас изучаем, будет использоваться в будущем при решении более сложных задач. Именно поэтому все недопонимания, связанные с вычислениями производных частного или произведения, лучше выявить немедленно, прямо сейчас. Не когда они представляют собой огромный снежный ком недопонимания, а когда представляют собой маленький теннисный шарик, с которым легко разобраться.

Смотрите также:

1. Вводный урок по вычислению производных степенной функции
2. Простое определение производной функции
3. Основное тригонометрическое тождество
4. Как быстро извлекать квадратные корни
5. Проценты в задачах на наибольшее-наименьшее значение используем пропорции
6. Сложная задача B14: работа трех исполнителей

Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.

Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями.

Функция двух и более переменных

Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной: 

Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.

А что, если добавить еще одну переменную? Получится такая функция:

Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так:

Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.

Частная производная первого порядка

Запоминаем главное правило:

При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.

То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:

Сначала возьмем частную производную по иксу, считая игрек обычным числом:

Теперь считаем частную производную по игреку, принимая икс за константу:

Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.

Частная производная второго порядка

Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.

По иксу:

По игреку:

Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:

1. При дифференцировании по одной независимой переменной, вторая принимается за константу.
2. Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.

Частные производные и полный дифференциал функции

Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.

Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:

Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.

Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.

Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!