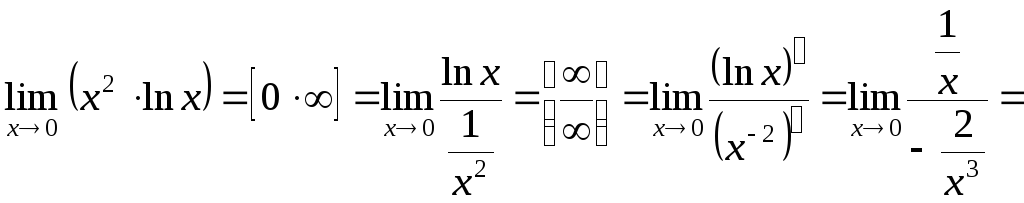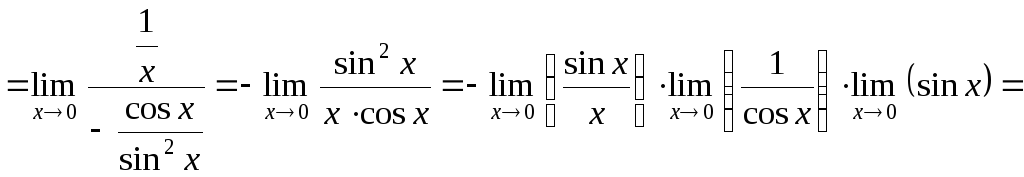Как найти производную через логарифмирование

Содержание:

• Суть метода логарифмического дифференцирования
• Производная показательно-степенной функции

Для функций вида $y(x)=frac{u_{1}(x) cdot u_{2}(x) cdot ldots cdot u_{k}(x)}{v_{1}(x) cdot v_{2}(x) cdot ldots cdot v_{m}(x)}$ для упрощения нахождения
производной рациональнее использовать логарифмическое дифференцирование.

Суть метода логарифмического дифференцирования

Суть такого дифференцирования заключается в следующем: вначале находится
логарифм заданной функции, а уже затем
вычисляется от него производная. Пусть задана некоторая функция
$y=f(x)$. Прологарифмируем левую и правую части данного выражения:

$$ln y=ln f(x)$$

Далее продифференцируем полученное равенство при условии, что
$y$ является функцией от $x$, то есть найдем
производную сложной функции:

$$(ln y)^{prime}=(ln f(x))^{prime} Rightarrow frac{1}{y} cdot y^{prime}=(ln f(x))^{prime}$$

А тогда, выражая искомую производную $y^{prime}$, в
результате имеем:

$$y^{prime}=y cdot(ln f(x))^{prime}$$

Производная показательно-степенной функции

Рационально использовать логарифмическое дифференцирование и при нахождении
производной показательно-степенной
(или степенно-показательной) функции или «функции в степени функция», то есть в случае, когда заданная функция имеет
вид $y(x)=u(x)^{v(x)}$. Логарифмируем левую и правую часть:

$$ln y(x)=ln u(x)^{v(x)}$$
$$ln y(x)=v(x) cdot ln u(x)$$

Тогда

$$(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime}$$

Производную в левой части равенства находим как производную сложной функции, а в правой — как производную произведения:

$$begin{array}{c}
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)} Rightarrow \
Rightarrow y^{prime}(x)=y(x) cdotleft(v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)}right)
end{array}$$

Читать дальше: производная степенно-показательной функции.

Простое объяснение принципов решения логарифмического дифференцирования и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

From Wikipedia, the free encyclopedia

In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formula

where is the derivative of f.^[1] Intuitively, this is the infinitesimal relative change in f; that is, the infinitesimal absolute change in f, namely scaled by the current value of f.

When f is a function f(x) of a real variable x, and takes real, strictly positive values, this is equal to the derivative of ln(f), or the natural logarithm of f. This follows directly from the chain rule:^[1]

Basic properties[edit]

Many properties of the real logarithm also apply to the logarithmic derivative, even when the function does not take values in the positive reals. For example, since the logarithm of a product is the sum of the logarithms of the factors, we have

So for positive-real-valued functions, the logarithmic derivative of a product is the sum of the logarithmic derivatives of the factors. But we can also use the Leibniz law for the derivative of a product to get

Thus, it is true for any function that the logarithmic derivative of a product is the sum of the logarithmic derivatives of the factors (when they are defined).

A corollary to this is that the logarithmic derivative of the reciprocal of a function is the negation of the logarithmic derivative of the function:

just as the logarithm of the reciprocal of a positive real number is the negation of the logarithm of the number.^{[citation needed]}

More generally, the logarithmic derivative of a quotient is the difference of the logarithmic derivatives of the dividend and the divisor:

just as the logarithm of a quotient is the difference of the logarithms of the dividend and the divisor.

Generalising in another direction, the logarithmic derivative of a power (with constant real exponent) is the product of the exponent and the logarithmic derivative of the base:

just as the logarithm of a power is the product of the exponent and the logarithm of the base.

In summary, both derivatives and logarithms have a product rule, a reciprocal rule, a quotient rule, and a power rule (compare the list of logarithmic identities); each pair of rules is related through the logarithmic derivative.

Computing ordinary derivatives using logarithmic derivatives[edit]

Logarithmic derivatives can simplify the computation of derivatives requiring the product rule while producing the same result. The procedure is as follows: Suppose that and that we wish to compute . Instead of computing it directly as , we compute its logarithmic derivative. That is, we compute:

Multiplying through by ƒ computes f′:

This technique is most useful when ƒ is a product of a large number of factors. This technique makes it possible to compute f′ by computing the logarithmic derivative of each factor, summing, and multiplying by f.

For example, we can compute the logarithmic derivative of to be .

Integrating factors[edit]

The logarithmic derivative idea is closely connected to the integrating factor method for first-order differential equations. In operator terms, write

and let M denote the operator of multiplication by some given function G(x). Then

can be written (by the product rule) as

where now denotes the multiplication operator by the logarithmic derivative

In practice we are given an operator such as

and wish to solve equations

for the function h, given f. This then reduces to solving

which has as solution

with any indefinite integral of F.^{[citation needed]}

Complex analysis[edit]

The formula as given can be applied more widely; for example if f(z) is a meromorphic function, it makes sense at all complex values of z at which f has neither a zero nor a pole. Further, at a zero or a pole the logarithmic derivative behaves in a way that is easily analysed in terms of the particular case

zⁿ

with n an integer, n ≠ 0. The logarithmic derivative is then

and one can draw the general conclusion that for f meromorphic, the singularities of the logarithmic derivative of f are all simple poles, with residue n from a zero of order n, residue −n from a pole of order n. See argument principle. This information is often exploited in contour integration.^{[2][3][verification needed]}

In the field of Nevanlinna theory, an important lemma states that the proximity function of a logarithmic derivative is small with respect to the Nevanlinna characteristic of the original function, for instance .^{[4][verification needed]}

The multiplicative group[edit]

Behind the use of the logarithmic derivative lie two basic facts about GL₁, that is, the multiplicative group of real numbers or other field. The differential operator

is invariant under dilation (replacing X by aX for a constant). And the differential form

is likewise invariant. For functions F into GL₁, the formula

is therefore a pullback of the invariant form.^{[citation needed]}

Examples[edit]

• Exponential growth and exponential decay are processes with constant logarithmic derivative.^{[citation needed]}
• In mathematical finance, the Greek λ is the logarithmic derivative of derivative price with respect to underlying price.^{[citation needed]}
• In numerical analysis, the condition number is the infinitesimal relative change in the output for a relative change in the input, and is thus a ratio of logarithmic derivatives.^{[citation needed]}

See also[edit]

• Generalizations of the derivative – Fundamental construction of differential calculus
• Logarithmic differentiation – Method of mathematical differentiation
• Elasticity of a function

References[edit]

Логарифмическое дифференцирование

При
вычислении производной от логарифма
произведения, частного, степени или
корня, для упрощения нахождения
производной проводят предварительное
преобразование (см. Пример 10(и)).

В
ряде случаев для нахождения производной
целесообразно заданную функцию сначала
прологарифмировать (по умолчанию имеется
в виду натуральный логарифм). Затем
найти производную от этого логарифма
и по ней отыскать производную от заданной
функции. Такой прием называется
логарифмическим
дифференцированием.

Метод логарифмического
дифференцирования позволяет легко
найти производную показательно-степенной
функции вида

,

где

и
– дифференцируемые функции аргумента
.

Пример 14.

Найти
производную функции
.

Решение.

Прологарифмируем
обе части функции и преобразуем выражение:

.

Теперь дифференцируем
уравнение, как неявно заданную функцию:

;

;

;

;

Так
как
,
то окончательно получаем:

.

Производные высших порядков

Производной
2-го порядка от функции

называется производная от её первой
производной, т.е.

.

Аналогично,
производной 3-го порядка от функции
называется
производная от её второй производной,
т.е.

.

Таким
образом, производной
-го
порядка от функции

называется производная от производной
-го
порядка, т.е.

.

Следовательно,
для нахождения производной
-го
порядка необходимо последовательно
найти производную первого, затем второго,
затем третьего и т.д. до-го
порядка.

Пример 15.

Найти
третью производную
функции
.

Решение.

;

;

.

2.3. Дифференциал функции

Из определения
производной и свойств пределов следует,
что если

то ,

где
–
бесконечно малая величина ().

Выражаем
и получаем, что:.
Так как,
то в дальнейшем ее можно не учитывать
и мы получим:

Главная
часть приращения функции, линейная
относительно приращения независимой
переменной
,
называется дифференциалом
функции
и обозначаетсяили:

.

Т.
к. дифференциал
,
то дифференциал
функции равен произведению производной
функции на дифференциал аргумента:

.

Таким
образом, для нахождения дифференциала
функции, необходимо найти производную

и умножить её
на дифференциал независимой переменной
.

Пример
16.

Найти
дифференциал функции
.

Решение.

.

2.4. Применение дифференциального исчисления функции одной переменной

2.4.1. Применение производной при вычислении пределов.

Правило Лопиталя

При
вычислении предела функции подстановка
предельного значения аргумента часто
приводит к неопределенностям вида
,,
от которых невозможно избавиться при
помощи ранее изученных приемов. Теорема,
известная под названиемправило
Лопиталя,
является одним из основных инструментов
для раскрытия таких неопределенностей.

Правило
Лопиталя:
Пусть в некоторой окрестности точки
функцииидифференцируемы и.
Еслииодновременно являются бесконечно малыми
или бесконечно большими функциями при
,
то

,

при условии, что
предел отношения производных существует.

Эта
теорема справедлива также и для
односторонних пределов, и в случае,
когда
.

В
некоторых случаях раскрытие
неопределенностей вида
может потребовать неоднократного
применения правила Лопиталя.

Неопределенности

,,,,,

сводятся к
неопределенностям вида
путем алгебраических преобразований.

Пример 17.

Вычислить с помощью
правила Лопиталя пределы:

а); б); в).

Решение.

а)

.

б)

.

в)
.

Обозначим
искомый предел через
и прологарифмируем выражение:

;

или

.

Тогда:

.

Так
как
,
то искомый предел.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Её получают следующим образом (используя формулу вычисления производной сложной функции):