Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Пример:
Решение:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
О производных / Habr
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие. Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. А что мне с производной? Ну, знаю я «предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует» — и что? В общем, не понимал я это дело. И не любил.
И только значительно позже, уже в ВУЗе, когда оказалось, что ни одна мало-мальски важная задача по физике, электротехнике, системам автоматического управления, мат.анализу и многим другим предметам без производных не решается — я понял, какая это важная вещь — знание не только текущего положения дел, но и динамики их изменения. Казалось бы, и что статья с таким началом может делать в этом блоге?
А вот что. Представьте себе двух людей. Пусть их будут звать Коля и Петя.
Коля и Петя — одного возраста, пола, с одинаковым образованием и работают в одной и той же фирме, на должностях одного уровня и получают одинаковую зарплату.
Какие на основании данной вводной можно сделать выводы? Можно ли сказать, что их жизнь складывается одинаково? Можно ли утверждать, что они одинаково довольны в финансовом и личном плане? Можно ли сказать, что их карьеры строятся схожим образом?
Конечно же, нифига подобного!
Дело в том что Коля — всегда был очень умён, трудолюбив и раньше, до наблюдаемого нами момента, его карьера шла очень хорошо. Он был начальником начальника Пети и зарабатывал раз в 25 больше. Но потом в его жизни что-то поменялось — может жена ушла, может в секту попал, а может пить начал. Или всё вместе. Блеск в глазах пропал, после двух сорванных проектов в должности его понизили и на горизонте замаячил злорадный силуэт увольнения.
А вот Петя — гением никогда не был. Он был обычным неглупым трудягой, который честно работал. Без героических свершений и позорных провалов. Его карьера медленно и плавно двигалась в гору и кресло начальника отдела уже, в принципе, было готово принять в себя его попу.
Вот это и есть важность понимания динамики процесса. Глянем для закрепления материала на еще одну ситуацию.
У нас есть Маша, Даша и Наташа.
Они, как и их друзья Коля и Петя, полностью идентичны в своём текущем состоянии (возраст, работа, зарплата, семейное положение ну и т.д.). Более того, мы даже кое-что знаем об их прошлом. Никто из них никогда не забирался выше текущего места в жизни, никаких форс-мажоров у них не было, и у нас есть еще одна важная вещь — информация о некотором моменте в прошлом (скажем, год назад). И согласно этой информации — опять таки, все объективные параметры этих девушек были равны. Вернёмся к нашим вопросам. Как на счёт оценки положения дел у этих дам? Можно ли говорить об одном уровне карьерного роста, амбициях, достижениях и о том, где каждая из них будет через 5 лет?
И, конечно же, опять — нифига подобного!
Глянем вот на этот график:
Даша — стабильный середнячок. Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Наташа — пока еще справляется, но уже без былого энтузиазма. Большего, чем сейчас, ей не хочется и не светит. Это почти её предел.
Маша — сильная и амбициозная личность. Текущая точка — просто досадное недоразумение, первая ступенька в лестнице её карьеры. Ну просто времени еще было мало и выше забраться пока не удалось. Но обязательно удастся и на это будут брошены все силы.
К чему это я?
1. Частенько в разговорах между давно не встречавшимися или только познакомившимися людьми проскакивают фразы в духе:
- А где работаешь?
- А кем?
- Сколько получаешь?
и т.д.
Люди получают ответы на эти вопросы и судят по ним о собеседнике. А ведь это всего лишь «положение дел в данной точке», которое, как мы уже выяснили, информации несёт мало. Не судите поспешно.
2. Иногда человек смотрит сам на себя со стороны и приходит к выводу, что, мол «я ничтожество, нищий и убогий, а еще дурак и бездарь» или наоборот «я всего добился, я крут, бел и пушист». В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.
3. Посмотрите на графики сверху. Где Ваш? А Вы уверены? А почему? А Вы по нему двигаетесь? А на Вашей должности и в Вашей компании вообще по нему можно двигаться? Что Вас останавливает? Хотите ли Вы через 5 лет быть в той же точке? А на том же графике?
Каков знак Вашей производной?
habr.com
Объясните, что такое производная, чтобы понял школьник : Вопросы преподавания
Что такое производная в данной точке :
1)для простоты начертите параболу , её производная ;
2)возьмите точку на положительной части параболы, т.е. справа от нуля,
3)теперь через эту точку прочертите касательную к параболе и
4)обозначьте точку пересечения касательной с осью как ;
5)теперь опустите перпендикуляр из точки на ось ;
6)Вы должны наблюдать прямоугольный треугольник ;
7)обозначьте угол ;
8)так вот производная в точке , т.е. будет тангенсом .
, иначе говоря производная — это тангенс угла наклона касательной,
ведь косательная — это по сути прямая, т.е. имеет формулу , а это и есть .
dxdy.ru
Как брать производную? Высшая математика, производная.
На самом деле брать производную не так уж и трудно, главное хорошенько проработать алгоритм.
Кстати если после просмотра материала у вас будут трудности пишите МНЕ, я дешево помогу вам решить примеры.
Итак, без чего мы не сможем обойтись? Конечно же таблица производных!
Таблица производных
в данной таблице указаны значения производной простейших функций, внимательно изучите таблицу производных, после чего можно приступать к решению заданий.
Данная таблица поможет нам брать производные от тригонометрических и логарифмических функций.
Теперь разберем поэтапно как брать производную, начиная с самых простых и элементарных функций.
Сперва разберем самые простые производные.
Если вы еще не поняли смотрим более легкие уроки.
matematikaprosta.ru
Что такое производная. Практический смысл производной
Геометрический смысл производной
|
ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К КРИВОЙ Касательной к кривой y=ƒ(x) в точке М называется предельное положение секущей, проведенной через точку М и соседнюю с ней точку М1 кривой, при условии, что точка М1 неограниченно приближается вдоль кривой к точке М. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ Производная функции y=ƒ(x) в точке х0 численно равна тангенсу угла наклона к оси Ох касательной, проведенной к кривой y=ƒ(x) в точке М (х0; ƒ(x0)). |
ВИЗНАЧЕННЯ ДОТИЧНОЇ ДО КРИВОЇ Дотичною до кривої y=ƒ(x) в точці М називається граничне положення січної, проведеної через точку М і сусідню з нею точку М1 кривої, за умови, що точка М1 необмежено наближається вздовж кривої до точки
ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇ Похідна функції y=ƒ(x) в точці х0 чисельно дорівнює тангенсу кута нахилу до осі Ох дотичної, проведеної до кривої y=ƒ(x) в точці М (х0; ƒ(x0)). |
Практический смысл производной
Рассмотрим, что практически означает величина, найденная нами как производная от некоторой функции.
Прежде всего, производная — это основное понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке.
Что такое «скорость изменения»? Представим себе функцию f(x) = 5. Вне зависимости от значения аргумента (х) ее значение никак не изменяется. То есть, скорость ее изменения равна нулю.
Теперь рассмотрим функцию f(x) = x. Производная х равна единице. Действительно, легко заметить, что на каждое изменение аргумента (х) на единицу, значение функции прирастает также на единицу.
С точки зрения полученной информации теперь посмотрим в таблицу производных простых функций. Исходя из этого сразу же становится понятен физический смысл нахождения производной функции. Такое понимание должно облегчить решение практических задач.
Соответственно, если производная показывает скорость изменения функции, то двойная производная показывает ускорение.
Дифференциальное исчисление |
Описание курса
| Правила дифференцирования
profmeter.com.ua
Ответы@Mail.Ru: Объясните производную по-человечески, пожалуйста!
Производная — это скорость: движения, старения, глупения, выздоровления, ожирения и т. д.
Начнём с функции. Так:
Функция — это любая зависимость чего-нибудь от чего-нибудь.
Например, вес портфеля зависит от количества учебников в нём.
Тяжесть похмелья по утрам зависит от объёма выпитого.
Количество волос на голове зависит от возраста.
Величина, которая зависит, называется функцией, а то, от чего она зависит, называется аргументом.
Т. е. возраст — аргумент (и довольно часто) , а количество волос на голове — функция.
Любому значению аргумента соответствует своё значение функции — так, например, в 25 лет у человека 100 тысяч волос, а в 55 лет (у того же человека) — их всего 100.
Понятно, что функция (пышность шевелюры) должна как-то изменяться при изменении её аргумента (число подаренных на 23 февраля галстуков, дезодорантов и бритв с носками) .
Волосы у человека выпадают каждый день по десятку штук.
Вот эта скорость изменения функции — минус 10 штук в день — и есть производная.
У разных людей своя собственная функция, заложенная природой, — волосы выпадают по-разному, кто-то лысеет в двадцать, а кто-то не лысеет в семьдесят, поэтому очевидно, что производная зависит от функции — у каждой функции она своя.
В математике значением производной в данной точке считается отношение изменения функции к изменению аргумента. Причём изменения аргумента должно быть как можно меньше (стремиться к нулю) .
Именно это записывается формулой:
<img src=»//content.foto.my.mail.ru/list/roga_i_kopyta/_answers/i-72.jpg» >
Производная тоже может меняться в разных точках.
Например, испугался человек — и быстро облысел, или, наоборот, витаминов налопался — лишние волосы повылазили.
В первом случае производная (одной и той же функции) отрицательная (число волос убывает) и большая (выпало много) , а во втором — положительная (растут новые волосы) и маленькая (выросло мало) .
Поэтому, в принципе, производная — это тоже функция.
Кроме механического смысла (скорость) у производной есть геометрический смысл — касательная к графику функции.
Если мы нарисуем график изменения числа волос у человека во времени, то получим что-то вроде этого (по горизонтальной оси время, по вертикальной — мохнатость) :
<img src=»//content.foto.my.mail.ru/list/roga_i_kopyta/_answers/i-71.jpg» >
Человек родился с каким-то количеством волос, потом они у него растут (производная положительна — количество волос увеличивается) , затем почему-то выпадают (наверное, попал под кислотный дождь) , а потом снова отрастают, а к старости уже выпадают.
Видно, что производная меняется.
Если мы проведём касательную к этому графику в какой-то точке, то получим график производной в этой точке (вернее, получим прямую, тангенс угла наклона которой численно равен значению производной в точке касания). <img src=»//content.foto.my.mail.ru/list/roga_i_kopyta/_answers/i-73.jpg» >
Производная — обратное первообразной.
<a rel=»nofollow» href=»http://mgyie.ru/index.php?option=com_remository&Itemid=30&func=fileinfo&id=1370″ target=»_blank»>http://mgyie.ru/index.php?option=com_remository&Itemid=30&func=fileinfo&id=1370</a>
Основы высшей математики для чайников
Скорость изменения чего-то.
На графике это будет наклоном кривой, изображающей процесс, в заданной точке времени. Поэтому для графика любой функции можно нарисовать график ее производной, то есть график скорости, с которой меняется значение функции в каждой точке, а в алгебраической записи — по определенным правилам получить из формулы для функции формулу для скорости ее изменения, то есть производной.
touch.otvet.mail.ru
Производная функции — это… Что такое Производная функции?
У этого термина существуют и другие значения, см. Производная.
Иллюстрация понятия производной
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
История
В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления.
Русский термин «производная функции» впервые употребил В. И. Висковатов.[1]
Определение
Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности можно представить в виде
если существует.
Определение производной функции через предел
Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,
Общепринятые обозначения производной функции в точке
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).
Дифференцируемость
Производная функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна:
Для дифференцируемой в функции в окрестности справедливо представление
- при
Замечания
Геометрический и физический смысл производной
Тангенс угла наклона касательной прямой
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией
Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.
Скорость изменения функции
Пусть — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени
Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью
Производные высших порядков
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
Если функция дифференцируема в , то производная первого порядка определяется соотношением
Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда
Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).
- или
- или
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,
Способы записи производных
В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:
- Лагранжа , при этом для малых n часто используют штрихи и римские цифры:
- и т. д.
Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.
- Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):
- Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:
- — производная первого порядка по при , или — вторая производная по в точке и т. д.
- , или иногда .
- В вариационном исчислении и математической физике часто применяется обозначение , ; для значения производной в точке — . Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.
Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:
Примеры
- Пусть . Тогда
- Пусть . Тогда если то
где обозначает функцию знака. Если то а следовательно не существует.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
, то
- Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
- где — биномиальные коэффициенты.
Следующие свойства производной служат дополнением к правилам дифференцирования:
Доказательство
Таблица производных некоторых функций
Производная вектор-функции по параметру
Определим производную вектор-функции по параметру:
- .
Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут .
Свойства производной вектор-функции (всюду предполагается, что производные существуют):
См. также
Примечания
Литература
- В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
- В. А. Гусев, А. Г. Мордкович «Математика»
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
- В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1
dic.academic.ru
Что такое производная?
Производной функции называется базовый элемент в дифференциальном исчислении. Этот элемент и является определенным результатом применения какой-то определенной операции дифференцирования по отношению к исходной функции.
Определение производной
Для того, чтобы понять, что такое производная, необходимо знать, что название функции происходит непосредственно от слова «произведенная», то есть образовавшаяся от другой какой-либо величины. При этом сам процесс определения производной какой-то определенной функции имеет название — «дифференцирование».
Наиболее распространенный метод представления и определения, при использовании теории пределов, несмотря на то, что она появилась гораздо позже дифференциальных исчислений. По определению данной теории, производной называется предел в отношении приращения функций к приращению аргумента, в случае если таковой предел имеется, и при условии, что данный аргумент стремится к нулевому значению.
Принято считать, что, впервые, термин и понятие «производная» употребил в своих трудах известный русский математик по имени В.И.Висковатов.
Рассмотренный ниже небольшой пример поможет наглядно понять, что такое производная.
- Для поиска производной функции f в точке х, нам нужно определить значения данной функции непосредственно в точке х, а так же в точке х+Δх. Причем Δx – это приращения аргумента х.
- Найти приращение для функции у приравненное к f(х+Δх) – f(х).
- Записать производную при помощи предела отношения f’ = lim(f(x+Δх) – f(x))/Δх, исчислить при Δх → 0.
Обычно производная обозначается знаком апострофа — «’» непосредственно над дифференцируемой функцией. Обозначение в виде одного апострофа обозначает первую производную, в виде двух – вторую. Производную наивысшего порядка принято задавать соответствующей цифрой, к примеру f^(n) – что означает производную n-го порядка, где буква «n» – целое число , которое ? 0. Производная нулевого порядка — это и есть сама дифференцируемая функция.
С целью облегчения дифференцирования усложненных функций, были разработаны и приняты определен
elhow.ru
Производная функции
Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.
Как найти?
Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования:
- Вынос константы за знак производной: $$ (Cu)’ = C(u)’ $$
- Производная суммы/разности функций: $$ (u pm v)’ = (u)’ pm (v)’ $$
- Производная произведения двух функций: $$ (u cdot v)’ = u’v + uv’ $$
- Производная дроби: $$ bigg (frac{u}{v} bigg )’ = frac{u’v — uv’}{v^2} $$
- Производная сложной функции: $$ ( f(g(x)) )’ = f'(g(x)) cdot g'(x) $$
Примеры решения
| Пример 1 |
| Найти производную функции $ y = x^3 — 2x^2 + 7x — 1 $ |
| Решение |
|
Производная суммы/разности функций равна сумме/разности производных: $$ y’ = (x^3 — 2x^2 + 7x — 1)’ = (x^3)’ — (2x^2)’ + (7x)’ — (1)’ = $$ Используя правило производной степенной функции $ (x^p)’ = px^{p-1} $ имеем: $$ y’ = 3x^{3-1} — 2 cdot 2 x^{2-1} + 7 — 0 = 3x^2 — 4x + 7 $$ Так же было учтено, что производная от константы равна нулю. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = 3x^2 — 4x + 7 $$ |
| Пример 2 |
| Найти производную функции $ y = sin x — ln 3x $ |
| Решение |
|
По правилу производной разности: $$ y’ = (sin x — ln 3x)’ = (sin x)’ — (ln 3x)’ = $$ По таблице интегрирования находим: $$ (sin x)’ = cos x $$ $$ (ln x)’ = frac{1}{x} $$ С учетом того, что аргумент натурального логарифма отличен от $ x $, то нужно домножить ещё на производную самого аргумента: $$ y’ = (sin x)’ — (ln 3x)’ = cos x — frac{1}{3x} cdot (3x)’ = $$ После упрощения получаем: $$ = cos x — frac{1}{3x} cdot 3 = cos x — frac{1}{x} $$ |
| Ответ |
| $$ y’ = cos x — frac{1}{x} $$ |
| Пример 3 |
| Найти производную функции $ y = (3x-1) cdot 5^x $ |
| Решение |
|
В данном примере стоит произведение двух функций, а производная произведения находится по формуле номер 3: $$ (u cdot v)’ = u’v + uv’ $$ $$ y’ = ( (3x-1) cdot 5^x )’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = $$ Производная первой функции вычисляется как разность фунций: $$ (3x-1)’ = (3x)’ — (1)’ = 3(x)’ — (1)’ = 3 $$ Вторая функция является показательной, производная которой находится по формуле: $ (a^x)’ = a^x ln a $: $$ (5^x)’ = 5^x ln 5 $$ Продолжаем решение с учетом найденных производных: $$ y’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = 3 cdot 5^x + (3x-1) 5^x ln 5 $$ |
| Ответ |
| $$ y’ = 3cdot 5^x + (3x-1) 5^x ln 5 $$ |
| Пример 4 |
| Найти производную функции $ y = frac{ln x}{sqrt{x}} $ |
| Решение |
|
Производную дроби найдем по четвертой формуле. Положим $ u = ln x $ и $ v = sqrt{x} $. Тогда их производные по таблице основных элементарных функций равны: $$ u’ = (ln x)’ = frac{1}{x} $$ $$ v’ = (sqrt{x})’ = frac{1}{2sqrt{x}} $$ Используя формулу №4 получаем: $$ y’ = bigg ( frac{ln x}{sqrt{x}} bigg )’ = frac{ frac{1}{x} cdot sqrt{x} — ln x cdot frac{1}{2sqrt{x}} }{x} = $$ Выносим множитель $ frac{1}{2sqrt{x}} $ в числителе за скобку: $$ y’ = frac{2-ln x}{2xsqrt{x}} $$ |
| Ответ |
| $$ y’ = frac{2-ln x}{2xsqrt{x}} $$ |
| Пример 5 |
| Найти производную функции $ y = ln sin 3x $ |
| Решение |
|
Данная функция является сложной, потому производную будем брать по цепочке. Сначала от внешней функции, затем от внутренней. При этом выполняя их перемножение. $$ y’ = (ln sin 3x )’ = frac{1}{sin 3x} cdot (sin 3x)’ = $$ Заметим, что аргумент синуса отличен от $ x $, поэтому тоже является сложной функцией: $$ = frac{1}{sin 3x} cdot cos 3x cdot (3x)’ = frac{1}{sin 3x} cdot cos 3x cdot 3 $$ Учитывая определение котангенса $ ctg x = frac{cos 3x}{sin 3x} $ перепишем полученную производную в удобном компактном виде: $$ y’ = 3ctg 3x $$ |
| Ответ |
| $$ y’ = 3ctg 3x $$ |
Производная и интеграл — проще некуда
Время на прочтение
12 мин
Количество просмотров 58K
19 декабря 2020 г. на Хабре вышла статья «Интуитивное объяснение интеграла».
В комментариях к ней некоторые пользователи указали, что объяснение получилось не очень интуитивным, например:
“Тема сама по себе интересная, недавно снова повторял курс, но должен сказать, что на мой взгляд, в материале нет изюминки. Автор прав, что в современных изданиях часто даются темы без описания их прикладного применения, из-за чего непонятен смысл их изучения.
Но конкретно интегралы это такая тема, которую надо описать или короче, чем у вас, или намного дольше.
Иначе и школьник не поймет, и те, кто знает, ничего нового не откроют.»
Я попробую изложить материал максимально коротко и просто. Так, чтобы школьники, наконец, поняли, пусть и с помощью родителей. Итак:
Я живу на плоскости, и мой мир выглядит так:
Все мои перемещения ограничиваются прямой линией, которую я называю «ось абсцисс» и обозначаю ее латинской буквой х. Таким образом, я могу гулять от точки, обозначенной цифрой ноль (там находится мой дом), вправо до бесконечности и назад, до нуля. Цифры на оси абсцисс позволяют мне понять, как далеко я от дома. Сейчас я нахожусь в 10 делениях от него.
Да, я слышал, что есть миры, в которых можно перемещаться и влево от нуля, и там расстояния обозначаются отрицательными числами: -1, -2 и т. д., до бесконечности. Кроме того, в тех мирах можно опуститься ниже оси абсцисс, но мой мир максимально прост.
Как-то раз, летящие птицы навели меня на мысль, что по нашему миру можно перемещаться не только влево или вправо, но и «вверх». Потом я узнал, что есть некие люди, умеющие строить дороги, ведущие в наши плоские небеса. Было бы неплохо бы с ними переговорить. И вот я общаюсь со специалистом (С), по строительству таких дорог:
Я: Здравствуйте, вы занимаетесь строительством дорог в небо?
С: Добрый день, да.
Я: А какие дороги вы умеете строить?
С: Самые простые варианты — прямые дороги различной крутизны.
Я: А что такое «крутизна»? Я всегда жил на горизонтальной прямой, и понятия не имею, что это слово может значить.
С: «Крутизна» показывает то, насколько трудно будет вам подниматься (или опускаться) по данной дороге. Чем круче дорога, тем тяжелее подъем или спуск. Давайте нарисуем на нашей плоскости еще одну ось — вертикальную. Мы назовем ее осью ординат, и обозначим латинской буквой у. На этой оси есть цифры, обозначающие «высоту» — расстояние до оси х.
Чтобы нам было проще ориентироваться в нашем двухмерном мире, нанесем на его плоскость линии, идущие от цифр, расположенных на осях х и у:
Теперь любое место (точку) на плоскости мы можем обозначить двумя цифрами. Первая цифра будет обозначать расстояние от нуля до проекции этой точки на ось х…
Я: Простите, а что такое «проекция»?
С: Видите внизу, на оси абсцисс, тень от летящей птицы? Она находится в точке, обозначенной цифрой 6 на оси х. Эта тень и есть проекция тела птицы на ось х. А если бы Солнце находилось справа от птицы, мы бы увидели ее тень на оси у, в районе цифры 8. Это есть проекция тела птицы на ось ординат. Она показывает, на какой высоте летит птица. То есть, расстояние от «земли» (от оси х) до нее.
Мы можем обозначить положение птицы двумя цифрами (6, 8). Первая цифра — проекция на ось х, вторая — проекция на ось у. Эти две цифры мы называем координатами птицы.
Вместо запятой между целой и дробной частями чисел, я буду ставить точку (т.е., не 13,5 а 13.5) для того, чтобы не путать с запятыми между соседними числами.
Я: Отлично, что дальше?
С: Дальше мы отгоним птицу и нарисуем дорогу:
Вы можете заметить, что эта дорога поднимается на одну клеточку вверх, при перемещении проекции на ось х на одну клеточку вправо.
Когда человек перемещается из точки с координатами (4, 4) в точку с координатами (10, 10), его проекция на ось х меняется на 6 цифр. То есть, его тень перемещается вправо на 6 единиц (клеточек). Такое же изменение проекции происходит по оси у. То есть, он одновременно поднимается вверх также на 6 единиц.
Изменение какого-либо параметра (например, проекции на ось х или у), мы обозначаем буквой d (дельта). Изменение высоты мы запишем как dy, а изменение проекции на ось х — как dx. То есть, в данном случае, dу = 6, и dx также = 6.
Разделив изменение высоты на изменение положение тени человека при его перемещении (dy/dx), мы узнаём крутизну данного участка дороги: 6 / 6 = 1.
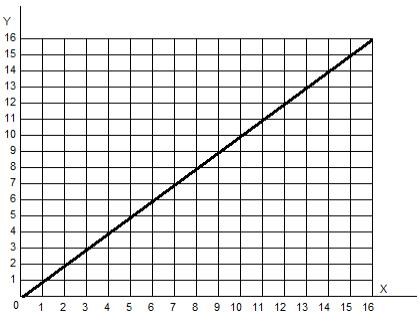
В нашей проектной документации мы используем очень краткое описание маршрута прокладываемой дороги. В данном случае оно будет выглядеть как математическая формула у = 1*х.
Это значит, что у всегда равен х, и это справедливо для любой точки дороги. Если человек будет находиться, например, в точке, тень от которой падает на ось х в точке 15, он будет находиться на высоте 15. Два параметра — положение тени человека на оси абсцисс и высота, на которой он находится, жестко связаны между собой вышеуказанной формулой.
Разумеется, можно было просто указать крутизну дороги одно цифрой, в данном случае, единицей, но проблема в том, что во-первых, дороги не всегда начинаются у вашего дома — в точке с координатами (0, 0). Во-вторых, существуют дороги, крутизна которых не постоянна. Но о них позже. А пока давайте нарисуем еще пару прямых дорог:
Мы видим, что верхняя дорога поднимается круче, чем та, которую мы рассмотрели ранее. А нижняя дорога — наоборот, более пологая. Высота (проекция на ось у), на которой находится человек, идущий по верхней дороге, равна 10. То есть, перемещаясь от начала координат до точки, в которой он находится сейчас, он изменил свою проекцию на ось у на 10 единиц. В то же самое время, его тень (проекция на ось х) переместилась вправо всего на 5 единиц. Разделив 10 на 5, мы получаем цифру 2. Эта цифра — соотношение высоты и удаленности от нуля по оси х — есть показатель крутизны дороги. Понятно?
Я: Да, я понял это еще на первом примере. А если мы разделим проекцию перемещения человека, идущего по нижней дороге на ось у, на перемещение его тени по оси х, (5/10), мы получим цифру 0.5, или 1/2. Это и есть показатель крутизны нижней дороги?
С: Совершенно верно! Между каждой из дорог и осью х (горизонталью) есть некоторый угол. Чем больше этот угол, тем круче поднимается дорога. Соотношение координаты любой точки дороги (если дорога прямая) по оси у и координаты этой же точки по оси х, называют тангенсом этого угла. Для каждого угла — свой тангенс. Тангенс угла верхней дороги равен 2, тангенс угла нижней, более пологой дороги, равен 0.5. Соответственно, формулы, которыми мы опишем две последние дороги будут выглядеть как у = 2х и у = 0.5х.
Эти формулы мы называем функциями. Мы говорим, что у — функция от х, где х независимая переменная (мы ее задаём), а у — зависимая переменная, так как мы ее вычисляем, исходя из заданного значения х. И она жестко зависит от значения х. Например, задав х = 12 для дороги, описываемой формулой у = 0.5х, мы, подставляя цифру 12 вместо х, узнаём, что у в этой точке равен 6.
В математике функции обозначают, например, так: f(x) = x. Эта функция справедлива для дороги, рассмотренной нами в самом первом примере. Для второй и третьей дорог, функции будут выглядеть соответственно, как f(x) = 2x и f(x) = 0.5x. Не очень сложно, да?
Я: Не очень. Что еще мне нужно знать о дорогах?
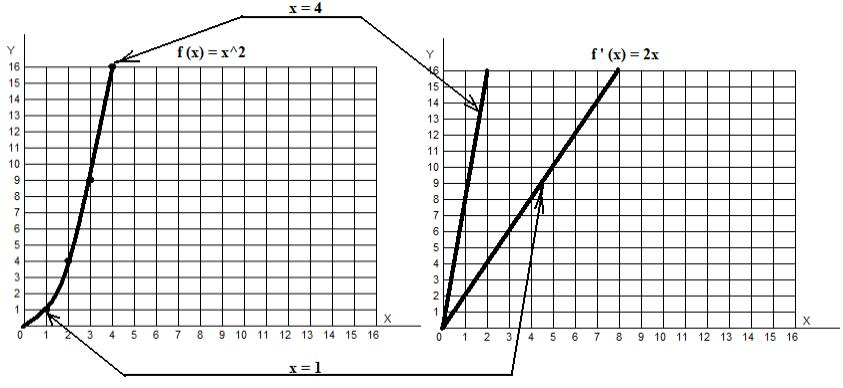
С: Мы делаем не только прямые дороги. Например, мы можем построить дорогу, которая описывается формулой (функцией) у = x2, или f(x) = x2. Крутизна этой дороги будет увеличиваться, по мере ее удаления от оси у.
Чтобы построить рисунок этой дороги, мы найдем (вычислим) координаты нескольких ее точек. Для этого мы подставим в формулу у = x2 вместо х сначала 1, потом 2, затем 3 и т.д. И рассчитаем значение у для всех этих точек. Сначала подставим 1:
y = х2 = 12 = 1.
Это значит, что для точки, с координатой по х равной 1, ее координата по у также равна 1. Нанесем эту точку на график:
Теперь рассчитаем координату по у для точки, с координатой по х равной 2:
y = x2 = 22 = 4.
Таким образом, наша вторая точка будет иметь координаты (2, 4). Рассчитав у для точек с координатами по х 3 и 4, получим их полные координаты (3, 9) и (4, 16) соответственно. Нанесем эти точки на график:
Теперь соединим все точки линией, обозначающей дорогу:
Для любой точки этой дороги справедлива формула y = x2. Например, для точки, с координатой по х = 1,5, мы получим ее координату по у, возведя 1,5 в квадрат. То есть, ее координаты (1.5, 2.25). Таким образом, мы можем узнать высоту любой точки дороги, задавая ее абсциссу (положение ее тени на оси х).
Но возникает проблема: мы не можем посчитать крутизну какой-либо точки дороги, так как она меняется постоянно. Не получится просто взять две точки дороги сверху и снизу от исследуемой и посмотреть, насколько изменится высота при прохождении пути между ними, разделив перемещение проекции на ось у на перемещение тени по оси х. Точнее, мы можем это сделать, но полученная цифра не будет соответствовать крутизне в средней точке между ними. Смотрите:
Допустим, мы хотим узнать крутизну нашей кривой дороги на участке от начала координат (точки с координатами (0, 0)), до точки с координатами (3, 9). На этом участке дорога поднимается на 9 единиц, в то время, как удаление от начала координат по х составляет 3 единицы. Считаем крутизну так же, как мы считали ее для прямой дороги: 9 / 3 = 3. То есть, крутизна на этому участке, вроде бы, равна 3. Но если мы проведем прямую с крутизной, равной 3, то увидим, что на самом деле дорога в самом низу идет гораздо более полого, чем прямая, а в точке пересечения прямой и дороги, крутизна дороги уже больше крутизны прямой! Крутизна кривой в центре между этими точками также не совпадает с крутизной прямой. Засада. Что же делать? Как нам узнать крутизну каждой точки в ситуации, когда первая постоянно меняется, и нет ни единого прямого участка? Вот для таких случаев господин Ньютон и придумал дифференцирование.
Дифференцирование преобразует нашу функцию в другую функцию, которая как раз-таки позволяет точно вычислить крутизну дороги в данной точке. Мы не будем вдаваться в то, как он пришел к своему решению, а просто воспользуемся результатом его работы — таблицей дифференциалов. Я не буду ее приводить, в Сети такого добра навалом. Можно просто ввести в строку поиска формулу, которую нужно дифференцировать.
Для нашей функции f(x) = x2 дифференцирование будет выглядеть таким образом: нам нужно перенести двойку из показателя степени влево, перед х, и уменьшить степень х на единицу. То есть, в данном случае степень х станет равна 1: f ‘(x) = 2x.
Обратите внимание на штрих после буквы f: f ‘(x) — так обозначается функция, которая произошла от нашей оригинальной функции. Поэтому ее называют производной функцией.
Но что нам теперь делать с этой производной? Как с ее помощью найти крутизну какой-либо точки оригинальной функции f(x) = x2? Очень просто. Мы подставляем в производную значение проекции на ось х, точки дороги, крутизна которой нас интересует. Допустим, мы хотим узнать, насколько круто поднимается дорога в точке, находящейся над цифрой 1 по оси х. Мы подставляем эту единицу в производную, и вычисляем значение:
f ‘(x) = 2x = 2*1 = 2.
Эта двойка и показывает нам крутизну дороги над точкой 1 по оси х.
А какова крутизна дороги в точке с абсциссой 4 (проекцией на ось х = 4)? Подставляем эту четверку в производную функцию f ‘(x) = 2x = 2*4 и получаем цифру 8.
Эта восьмерка означает, что крутизна дороги в точке с абсциссой 4 равна 8. То есть, в этой точке дорога поднимается так же круто, как верхняя прямая на правом графике. Вот и весь смысл дифференцирования (нахождения производной).
Слева — график самой дороги, а справа — прямые, крутизна которых соответствует крутизне дороги в указанных точках. То есть, в указанных точках дороги подниматься так же тяжело, как по соответствующим этим точкам прямым. «Здесь так же круто, как там».
Давайте найдем производную нашей самой первой функции f (x) = x.
Мы проделаем такой же трюк: перенесем степень переменной вперед, перед х (это ничего не изменит, так как степень х была равна 1). Кроме того, мы уменьшим степень х на единицу. При этом степень станет равна нулю, и х превратится в единицу (потому, что любое число (кроме нуля) в нулевой степени равно 1).
Мы получили производную функции f(x) = x. Она выглядит так: f ‘(x) = 1. Что это значит? Это значит, что крутизна данной дороги на любом ее участке равна 1. То есть, при изменении абсциссы на dx, dy изменится ровно на такую же величину. В принципе, мы это знали и раньше, но теперь мы вычислили крутизну дороги через производную.
В учебниках пишут, что производная постоянной (некоторого числа) равна нулю. Почему это так?
Давайте построим дорогу, которая описывается функцией f(x) = 5. Это означает, что высота (проекция на ось у) любой точки данной дороги всегда равна 5, следовательно, dy (изменение высоты) равно нулю.
Поэтому эта дорога идет параллельно оси абсцисс, то есть, никакого изменения высоты не будет, на сколько бы мы не перемещались вправо. А раз крутизна дороги равна нулю, то и производная данной функции равна нулю (dy/dx = 0/dx = 0).
Повторим: производная отображает крутизну функции (графика, дороги), а в данном случае никакой крутизны нет. Что и имеется ввиду, когда говорят, что производная постоянной равна нулю.
Я: Хорошо, я все понял: по оригинальной функции я могу вычислить высоту дороги в любой ее точке, а по производной — крутизну в любой ее точке. Но дорога не может висеть в воздухе, она же должна опираться на ось х?
С: Совершенно правильный вопрос. Под дорогой нам придется сделать насыпь. И чем больше материала (клеточек) мы потратим на данный участок дороги, тем больше вам придется заплатить.
Я: А как вы посчитаете, сколько клеточек вам понадобится? Для участка прямой дороги, параллельной оси абсцисс f(x) = 5, все просто:
У нас получается прямоугольник, высота которого равна постоянной 5, а длину мы можем посчитать, вычитая координату по х левой стороны прямоугольника из координаты его правой стороны: 10 — 3 = 7. То есть, ширина прямоугольника равна 7, соответственно, его площадь равна 5 * 7 = 35 клеточек. Я буду вам должен за 35 клеточек.
Нет проблем и с дорогой, которая поднимается (или опускается) по прямой.
Как и в предыдущем случае, ширину основания мы узнаём, вычитая координаты границ по оси х друг из друга: 9 — 3 = 6.
Высоту найти немного сложнее: нам придется вычислить ее среднее значение. Для этого мы берем высоту (проекцию на ось у) левой верхней точки закрашенной фигуры, прибавляем к ней высоту правой верхней точки и делим пополам:
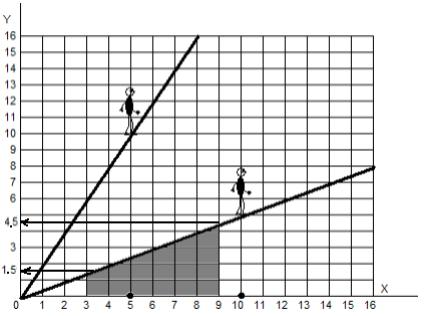
(1.5 + 4.5) : 2 = 3. Эта тройка — средняя высота фигуры. Мы умножаем ее на ширину фигуры и получаем цифру 18. То есть, на данный участок дороги потрачено 18 клеток, верно? Но как узнать, сколько клеток потребует участок дороги типа y = x2?
С протяженностью участка дороги слева направо разобраться легко, она равна 4 — 1 = 3 клетки, но как быть с высотой? Ведь мы не можем в данном случае сложить 1 и 16, затем разделить пополам и получить среднюю высоту фигуры? Как нам посчитать площадь этой насыпи?
С: Господин Ньютон предусмотрел и это. Метод подсчета площади криволинейных фигур называется «интегрирование». Нам придется вспомнить то, как мы находили производную функции f (x) = x2 Она выглядит так: f ‘(x) = 2x.
Эту, как и многие другие математические операции, можно производить и в обратную сторону. Если нам известна производная функции, мы можем восстановить эту изначальную функцию, называемую первообразной. То есть, имея функцию, показывающую изменение крутизны дороги, мы можем восстановить функцию, показывающую саму дорогу — высоту любой ее точки.
Если для нахождения производной мы переносили вперед показатель степени переменной (двойку), и уменьшали степень переменной х на единицу
f(x) = x2 => f ‘(x) = 2x,
то теперь нам следует поступить ровно наоборот: двойку, стоящую перед х следует перенести наверх, в степень: f ‘(x) = 2x => f(x) = x2 .Так мы получаем первообразную функцию. То есть, ту функцию, от которой производная произошла.
Но не все так просто, давайте рассмотрим дорогу, описываемую функцией
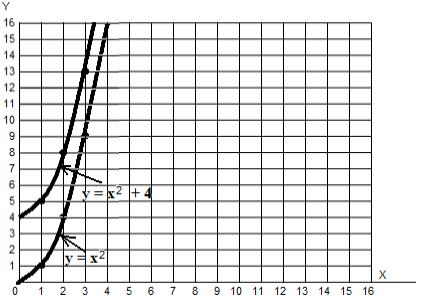
f (x) = x2 + 4:
Она выглядит точно так же, как дорога f (x) = x2 , но располагается выше. Если мы найдем производную этой функции, то обнаружим, что она выглядит точно так же, как производная от функции f (x) = x2 ! То есть, как f ‘(x) = 2x. Ибо при нахождении производной четверка (постоянная) будет отброшена.
Я: Почему?
С: Потому, что она не влияет на крутизну графика. Вы же помните, что производная описывает крутизну оригинального (первообразного) графика на каждом его участке? А теперь посмотрите на точки обоих графиков, расположенные, к примеру над цифрой 3 на оси х. Крутизна верхнего и нижнего графиков в этих точках одинакова! То же самое касается любых двух точек этих графиков, расположенных друг под другом. Эти две дороги идут параллельно друг другу, поэтому, их крутизна везде совпадает. Отличается только высота.
Но производная — это не про высоту, а про крутизну дороги. Потому и получается, что обе функции f (x) = x2 и f (x) = x2 + 4 приводят к одной и той же производной f ‘(x) = 2x.
Я: Погодите, но тогда получается, что функции, к примеру, f (x) = x2 + 5 или f (x) = x2 + 1.3 и даже f (x) = x2 — 2 также приводят к одной и той же производной? Ведь они все параллельны друг другу, и их крутизна в точках, расположенных друг под другом, совпадает?
С: Да, наша производная имеет бесконечный набор первообразных. Поэтому первообразную функции f (x) = 2x записывают как F (x) = x2 + C, где буква С может быть любым числом. От этого числа зависит только высота, на которой проходит дорога. Точнее, разница высот между данной дорогой, и дорогой, у которой С = 0. Если Вы снова посмотрите на графики выше, то увидите, что любая точка верхнего графика ровно на 4 клетки выше аналогичной точки нижнего графика.
Обратите внимание также на то, что буква F в первообразной — заглавная (большая), Первообразная является «матерью» производной, поэтому мы относимся к ней с уважением, и пишем ее имя заглавной буквой.
Все множество функций, описываемых формулой F (x) = x2 + C, называется неопределенным интегралом. Самая распространенная формула для нахождения неопределенного интеграла выглядит так:
По этой формуле мы можем найти неопределенный интеграл нашей функции f (x) = x2. Для этого мы увеличиваем степень переменной на единицу, а в знаменатель просто ставим получившуюся степень переменной. Степень нашей переменной была 2, увеличив ее на единицу, получаем x3. Эту же тройку мы ставим в знаменатель (под дробную черту). Получается выражение F (x) = x3/3 + С.
Теперь вернемся к нашей криволинейной фигуре.
Чтобы узнать ее площадь, в полученный нами неопределенный интеграл нужно подставить абсциссу ее правой границы — цифру 4 (при этом постоянная С отбрасывается):
F (x) = x3/3 = 43/3 = 21 1/3 (двадцать одна целая и одна треть)
То же самое проделаем с левой границей фигуры:
F (x) = x3/3 = 13/3 = 1/3 (одна треть)
Теперь нам остается вычесть из первого числа второе: 21 1/3 — 1/3 = 21
Искомая площадь равна 21 клетке. Для проверки вы можете примерно посчитать закрашенные клетки на картинке.
Давайте подытожим все вышесказанное. Итак, у нас есть некоторая формула (функция) f(x), описывающая некую линию на графике.
Чтобы найти крутизну этой линии (функции) в какой-либо ее точке, мы находим производную данной функции f ‘(x), затем подставляем в полученную производную проекцию на ось х интересующей нас точки оригинальной функции, и вычисляем искомый параметр. Полученная цифра будет показывать тангенс угла наклона прямой, которая поднимается (или опускается) так же круто, как исходный график в исследуемой точке.
А чтобы найти площадь под участком графика исходной функции, следует найти ее первообразную F, затем, в эту первообразную по очереди подставить координаты по х правой и левой границы фигуры, площадь которой мы хотим найти, а затем вычесть два полученных числа друг из друга. Результат вычитания и есть искомая площадь.
Я: А почему вы отбросили постоянную С? Разве это не приведет к тому, что площадь под участками кривых f (x) = x2 и f (x) = x2 + 4, находящимися друг под другом, будут одинаковыми?
С: Не беспокойтесь, при нахождении интеграла второй функции, постоянная 4 в ее первообразной превратится в 4х, поэтому, к площади под ней добавится прямоугольник высотой 4 клеточки и ошибки не будет. Ну так что, какую дорогу Вы выбираете?