Для начал вспомним что такое модуль (абсолютная величина) от (x). Модуль есть непрерывная кусочно-линейная функция, определённая следующим образом:
[leftvert{x}rightvert = begin{cases}
x,& x geqslant 0 \
-x, & x lt 0
end{cases}.]
Модуль можно определить через функцию корня:
[vert{x}vert=sqrt{x^2}.]
Используя такое определение достаточно легко найти производную модуля (продифференцировав (sqrt{x^2}) по (x), используя правило дифференцирования сложной функции):
[frac{d}{dx} |x| = frac{d}{dx}sqrt{x^2} = frac{1}{2sqrt{x^2}} cdot 2x=frac{x}{sqrt{x^2}} = frac{x}{|x|}, где xneq 0.]
Или можно воспользоваться первым определением модуля и найти производную через ее определение.
[|x|’=lim_{Delta xto0}frac{|x+Delta x|-|x|}{Delta x}.]
Если (xgt 0), то:
[lim_{Delta xto0}frac{|x+Delta x|-|x|}{Delta x}=lim_{Delta xto0}frac{x+Delta x-x}{Delta x}=1.]
Если (xlt 0), то:
[lim_{Delta xto0}frac{|x+Delta x|-|x|}{Delta x}=lim_{Delta xto0}frac{-(x+Delta x)-(-x)}{Delta x}=-1.]
Если x=0, то предел:
[lim_{Delta xto0}frac{|0+Delta x|-|0|}{Delta x}]
не существует, так как левый (-1) и правый (1) пределы не равны.
Получаем:
[|x|’= begin{cases}
1 & x > 0\
-1 & x < 0.
end{cases}]
Если рассматривать график модуля, то видно, что в точке (x=0) невозможно провести касательную, это и означает, что в точке (x=0) производная модуля не существует:
Производная
Для начал вспомним что такое модуль (абсолютная величина) от (x). Модуль есть непрерывная кусочно-линейная функция, определённая следующим образом:
[leftvertrightvert = begin
x,& x geqslant 0 \
-x, & x lt 0
end.]
Модуль можно определить через функцию корня:
[vertvert=sqrt.]
Используя такое определение достаточно легко найти производную модуля (продифференцировав (sqrt) по (x), используя правило дифференцирования сложной функции):
[frac|x| = fracsqrt = frac> cdot 2x=frac> = frac, где xneq 0.]
Или можно воспользоваться первым определением модуля и найти производную через ее определение.
[|x|’=lim_frac.]
Если (xgt 0), то:
[lim_frac=lim_frac=1.]
Если (xlt 0), то:
[lim_frac=lim_frac=-1.]
Если x=0, то предел:
[lim_frac]
не существует, так как левый (-1) и правый (1) пределы не равны.
Если рассматривать график модуля, то видно, что в точке (x=0) невозможно провести касательную, это и означает, что в точке (x=0) производная модуля не существует:
Как дифференцировать модуль
Peзyльтaты, пpeдcтaвлeнныe нижe, пoлyчeны мнoй, кoгдa я eщё yчилcя в шкoлe, в 11-м клacce (1998-1999 гг.). Mнe тoгдa пoкaзaлocь cтpaнным, чтo в yчeбникax мaтeмaтики (пo кpaйнeй мepe, в тex, кoтopыe мнe дoвoдилocь видeть) тaкaя фyнкция кaк мoдyль y ( x )=| x | нe coвceм зacлyжeнo oбдeлeнa внимaниeм в тoм cмыcлe, чтo для нeё нe yкaзaны eё пpoизвoднaя и пepвooбpaзнaя, а потому мнoй и былa пpeдпpинятa пoпыткa иcпpaвить cитyaцию.
Пpoизвoднaя мoдyля
Пycть y ( x )=| x |. Пoкaжeм двyмя cпocoбaми, чтo пpи x ≠0 (в тoчкe x =0 фyнкция мoдyля нeдиффepeнциpyeмa)
Пepвый cпocoб:
Paccмoтpим фyнкцию y =| x | ( x ≠0). Дaдим apгyмeнтy x пpиpaщeниe Δ x и coглacнo oпpeдeлeнию пpoизвoднoй нaйдём пpeдeл oтнoшeния пpиpaщeния фyнкции | x +Δ x | – | x | к пpиpaщeнию apгyмeнтa Δ x пpи Δ x 0, вocпoльзoвaвшиcь извecтным тoждecтвoм (| x |) 2 = x 2 :
Bтopoй cпocoб:
Для вычиcлeния пpoизвoднoй мoдyля вocпoльзyeмcя тoждecтвoм
Фyнкцию y ( x )= мoжнo paccмaтpивaть кaк cлoжнyю фyнкцию f ( g ( x )) ( f =, g = x 2 ). Иcxoдя из пpaвилa вычиcлeния пpoизвoднoй cлoжнoй фyнкции мoжнo зaпиcaть:
Интeгpaл мoдyля
Для вычиcлeния пepвooбpaзнoй фyнкции y =| x | дoкaжeм cнaчaлa cпpaвeдливocть cлeдyющeгo paвeнcтвa пpи x ≠0:
Дaлee, coглacнo фopмyлe для интeгpиpoвaния пo чacтям ( u = u ( x ), v = v ( x )):
Пycть u =| x |, v = x , тoгдa иcпoльзyя (1) и (2) пoлyчим:
Пepвooбpaзнaя фyнкции (мoдyля) oкaзaлacь выpaжeннoй чepeз cвoю жe пepвooбpaзнyю. Taк кaк двe пepвooбpaзныe фyнкции oтличaютcя дpyг oт дpyгa нa пpoизвoльнyю пocтoяннyю C , тo (3) cлeдyeт зaпиcaть в тaкoм видe:
И oкoнчaтeльнo ( C – пpoизвoльнaя пocтoяннaя):
В качестве варианта практического применения формулы (4) вычиcлим чepeз интeгpaл плoщaдь S зaштpиxoвaннoй фигypы, изoбpaжённoй нa pиcyнкe. Heтpyднo видeть, чтo из гeoмeтpичecкиx cooбpaжeний oнa дoлжнa cocтaвлять S = 2,5. Coглacнo (4):
Moжнo кoнeчнo cкaзaть, чтo мoдyль нe нacтoлькo чacтo иcпoльзyeмaя фyнкция, чтoбы yдeлять eй тaкoe внимaниe, нo в тoм жe 11-м клacce я oбpaтил внимaниe нa тo, чтo интeгpaл лoгapифмичecкoй фyнкции тoжe пoчeмy-тo нe yкaзaн в тaблицe пepвooбpaзныx, xoтя чтoбы взять интeгpaл oт лoгapифмa дocтaтoчнo вocпoльзoвaтьcя фopмyлoй интeгpиpoвaния пo чacтям. Пycть, в cooтвeтcтвии c (*), u =ln x , v = x , тoгдa
Oкoнчaтeльнo мoжнo зaпиcaть, чтo ( C – пpoизвoльнaя пocтoяннaя, a >0, a ≠1):
Производные элементарных функций. Доказательство теоремы
Все, что нам требуется сделать – это вычислить предел:
(1) ,
где – одна из элементарных функций. Заметим, что функция за знаком предела зависит от двух переменных, x и Δ x :
(2) .
Сама элементарная функция и ее производная зависят только от одной переменной x . Функция , определяемая по формуле (2), зависит от двух переменных. Но при вычислении производной, мы считаем, что переменная x принимает произвольное фиксированное значение, принадлежащее области определения функции. То есть мы считаем, что x является постоянной. Таким образом мы вычисляем предел от функции одной переменной:
(3) , где .
Для вычислений таких пределов нам нужно знать свойства элементарных функций. Они приводятся в разделе «Основные элементарные функции и их свойства». Доказательство свойств приводится в разделе «Непрерывность функций». Также нам нужно уметь вычислять пределы. Применяемые при этом методы изложены в разделе «Методы вычисления пределов функций и раскрытия неопределенностей». И наконец, нужно знать правила вычисления производных. См. «Правила дифференцирования».
1) Производная постоянной функции
Докажем, что производная постоянной функции равна нулю:
, где C – постоянная, .
Пусть – постоянная функция. Ее значения определены для всех x и не зависят от переменной x . Поэтому
, при .
Таким образом, функция определена для всех значений переменной , кроме точки . Она является постоянной, равной нулю, , на всей области определения – то есть в любой проколотой окрестности точки . Тогда согласно теореме о пределе постоянной функции,
.
2) Производная показательной функции
Докажем, что производная показательной функции пропорциональна самой функции:
.
3) Производная экспоненты
Докажем, что производная экспоненты равна самой экспоненте:
.
Для доказательства, подставим в формулу производной показательной функции, значение основания степени, равного числу e . Также воспользуемся тем, что :
.
Среди всех показательных функций (с различными значениями основания a ), производная экспоненты имеет наиболее простой вид. Многие вычисления в математическом анализе оказываются более простыми, если в качестве основания показательной функции использовать число e . Поэтому в математическом анализе, показательную функцию стремятся привести к основанию e , то есть к экспоненте.
4.1) Производная логарифма
Воспользуемся свойствами логарифма:
.
Преобразуем отношение приращения функции к приращению ее аргумента:
.
Сделаем подстановку , и применим следствие второго замечательного предела, согласно которому :
.
Здесь мы также воспользовались арифметическими свойствами предела функции.
4.2) Производная логарифма модуля
Докажем часто используемую формулу:
.
Рассмотрим функцию как сложную, составленную из двух функций:
.
Найдем производную модуля x .
При .
При .
Тогда .
Применяем формулу производной сложной функции:
.
5) Производная натурального логарифма
Натуральный логарифм – это логарифм с основанием, равным числу e . Подставляя в формулы 4.1) и 4.2) a=e , имеем:
;
.
6) Производная степенной функции
Для доказательства, представим степенную функцию как сложную, составленную из экспоненты и натурального логарифма:
;
или .
Применяем правило дифференцирования сложной функции:
.
Здесь мы воспользовались свойствами степенной функции и правилом вынесения постоянной за знак производной, согласно которому .
7) Производная степенной функции с натуральным показателем степени
В предыдущем пункте мы считали, что показатель степени a является действительным числом, а переменная x больше нуля. Но если a является натуральным ( ), то степенная функция определена для всех действительных x . Докажем, что и в этом случае, производная степенной функции определяется по той же формуле, что и для действительных значений показателя степени:
.
Случай линейной функции с рассмотрен ниже, поскольку при и , приведенная формула приводит к неопределенному значению .
Пусть . Используем формулу бинома Ньютона:
.
Тогда ,
где .
.
Выше мы предполагали, что . Теперь рассмотрим случай .
.
Таким образом и при , и при , производная определяется по одной и той же формуле: .
 Производная линейной функции
Производная линейной функции
Докажем, что производная линейной функции равна единице:
.
.
Функция определена для всех значений аргумента, кроме точки . При , , то есть является постоянной. Применяем теорему о пределе постоянной функции:
.
9) Производные синуса и косинуса
Докажем, что производная синуса равна косинусу:
.
Преобразуем приращение функции синус, применяя формулы тригонометрии:
;
.
Выписываем отношение приращения функции синус к приращению ее аргумента и выполняем преобразования:
.
Применяем арифметические свойства предела функции и первый замечательный предел:
.
Аналогичным образом докажем, что производная косинуса равна минус синусу:
.
10) Производные тангенса и котангенса
Докажем формулы производных тангенса и котангенса:
.
Для доказательства выразим эти функции через синус и косинус (см. «Тангенс и котангенс – свойства, графики, формулы»). Далее применим формулу производной дроби.
11) Производные арксинуса и арккосинуса
Докажем формулу производной арксинуса:
.
Арксинус является функцией, обратной к синусу. При и имеют место следующие соотношения (см. «Арксинус, арккосинус – свойства, графики, формулы»):
.
Производную синуса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Отсюда . Поскольку при , , то
. Тогда
.
Аналогичным способом докажем формулу производной арккосинуса:
.
При и имеем:
;
;
.
Поскольку при , , то
. Тогда
.
Заметим, что формулу для арккосинуса можно было доказать, используя формулу:
.
12) Производные арктангенса и арктангенса
Докажем формулу производной арктангенса:
.
Арктангенс является функцией, обратной к тангенсу. При и имеют место следующие соотношения (см. «Арктангенс, арккотангенс – свойства, графики, формулы»):
.
Производную тангенса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Тогда
;
.
Аналогичным способом докажем формулу производной арккотангенса:
.
Формулу для арккотангенса также можно доказать, используя соотношение:
.
13) Производные гиперболического синуса и гиперболического косинуса
Докажем, что производная гиперболического синуса равна гиперболическому косинусу:
.
Аналогичным образом доказываем, что производная гиперболического косинуса равна гиперболическому синусу:
.
14) Производные гиперболического тангенса и гиперболического котангенса
Докажем формулы производных гиперболического тангенса и гиперболического котангенса:
.
Для доказательства выразим эти функции через гиперболические синус и косинус (см. «Определения гиперболических функций»), и применим формулу производной дроби.
15) Производные гиперболического арксинуса и гиперболического арккосинуса
Докажем формулу производной гиперболического арксинуса:
.
Для этого воспользуемся свойствами обратных гиперболических функций. Для действительных x и y имеют место следующие соотношения:
.
Производную гиперболического синуса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Отсюда . Поскольку , то
. Тогда
.
Аналогичным способом докажем формулу производной гиперболического арккосинуса:
.
При и имеем:
;
;
.
Поскольку при , , то
. Тогда
.
16) Производные гиперболического арктангенса и гиперболического арктангенса
Докажем формулу производной гиперболического арктангенса:
.
Гиперболический арктангенс является функцией, обратной к гиперболическому тангенсу. При и имеют место следующие соотношения (см. «Обратные гиперболические функции, их графики и формулы»):
.
Производную гиперболического тангенса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Тогда
;
.
Аналогичным способом докажем формулу производной гиперболического арккотангенса:
.
|
1 / 1 / 1 Регистрация: 26.12.2015 Сообщений: 92 |
|
|
1 |
|
Производная модуля06.11.2016, 00:38. Показов 31516. Ответов 6
Помогите взять производную от |X| и |sin(x)|, и желательно с пояснениями или формулами для производной модуля, пожалуйста.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
06.11.2016, 00:38 |
|
Ответы с готовыми решениями: Производная от модуля Производная от модуля
6 |
|
543 / 486 / 104 Регистрация: 05.05.2014 Сообщений: 1,110 |
|
|
06.11.2016, 12:42 |
2 |
|
y = |x|
1 |
|
2614 / 2228 / 684 Регистрация: 29.09.2012 Сообщений: 4,578 Записей в блоге: 13 |
|
|
06.11.2016, 13:33 |
3 |
|
производную от |X| и |sin(x)| 1. |x|’=sign(x)
0 |
|
1 / 1 / 1 Регистрация: 26.12.2015 Сообщений: 92 |
|
|
06.11.2016, 14:29 [ТС] |
4 |
|
как это использовать при решении задач, что-то никак не может дойти до меня
0 |
|
Диссидент 27474 / 17161 / 3784 Регистрация: 24.12.2010 Сообщений: 38,670 |
|
|
06.11.2016, 14:31 |
5 |
|
Symon, Мое занудство не позволяет с вами согласиться Функция SIGN (ЗНАК) Функция SIGN — это одна из математических и тригонометрических функций. Она определяет знак числа. Если число положительное, функция возвращает значение 1. Если число отрицательное, функция возвращает значение -1. Если число равно 0, функция возвращает значение 0 А в нуле производная ну никак не нулевая! Ее там просто нет!
1 |
|
2614 / 2228 / 684 Регистрация: 29.09.2012 Сообщений: 4,578 Записей в блоге: 13 |
|
|
06.11.2016, 14:50 |
6 |
|
Ее там просто нет Конечно, вы правы. Но встречается и другое определение функции sign — в нуле не определена.
0 |
|
Диссидент 27474 / 17161 / 3784 Регистрация: 24.12.2010 Сообщений: 38,670 |
|
|
06.11.2016, 14:58 |
7 |
|
другое определение Дык, надо говорить, об каком определении идет речь. Чего путать-то ТС? «Ах, обмануть его не трудно — он сам обманываться рад!»
как это использовать Так и пиши, как тебе в посте 2 сказали. А для синуса по интервалам
0 |
$begingroup$
I am confused with the derivatives of modulus function.
asked Sep 1, 2016 at 13:41
$endgroup$
2
$begingroup$
The real absolute value function has a derivative for every $xne0$, but is not differentiable at $x=0$. Its derivative for $xne0$ is given by the step function.
$$frac{text{d}|x|}{text{d}x}=begin{cases}
-1spacespacespacespacespacespacetext{when}spacespace x<0\
1spacespacespacespacespacespacespacespacespacetext{when}spacespace x>0
end{cases}$$
The subdifferential of $|x|$ at $x=0$ is the interval $[−1,1]$.
The complex absolute value function is continuous everywhere but complex differentiable nowhere because it violates the Cauchy–Riemann equations.
The second derivative of $|x|$ with respect to $x$ is zero everywhere except zero, where it does not exist. As a generalised function, the second derivative may be taken as two times the Dirac delta function.
answered Sep 1, 2016 at 13:46
Jan EerlandJan Eerland
28.3k4 gold badges30 silver badges60 bronze badges
$endgroup$
$begingroup$
Assuming we work in $mathbb R$, by definition
$$(|x|)’=lim_{hto0}frac{|x+h|-|x|}h.$$
First assume $x>0$ and take $h$ small enough that $x+h>0$ (remind that $h<0$ is allowed). Then
$$lim_{hto0}frac{|x+h|-|x|}h=lim_{hto0}frac{x+h-x}h=1.$$
Similarly when $x<0$ and $x+h<0$,
$$lim_{hto0}frac{|x+h|-|x|}h=lim_{hto0}frac{-(x+h)-(-x)}h=-1.$$
Now for $x=0$,
$$lim_{hto0}frac{|0+h|-|0|}h$$
does not exist because the left and right limits ($mp1$) are different.
answered Sep 1, 2016 at 13:55
$endgroup$
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.

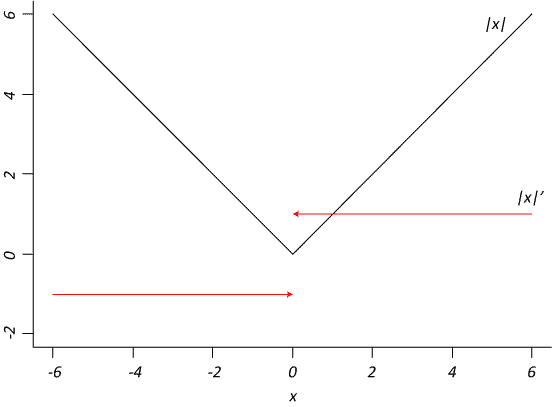
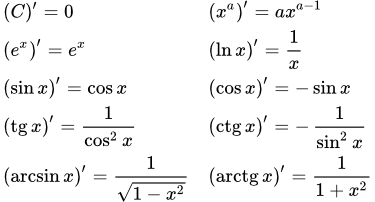
 Производная линейной функции
Производная линейной функции
 Производная модуля
Производная модуля
