Производная дроби – что это такое
Определение
Производная дроби – это значение, которое получается, если производную числителя умножить на знаменатель и прибавить числитель, умноженный на производную знаменателя, а затем все это разделить на квадрат знаменателя.
Формула производной от дроби
Формула ПД имеет следующий вид:
(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{v^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.
Приведем доказательство данной формулы. Рассмотрим выражение y=fracupsilonnu. Все представленные переменные – это функции от х. Умножим их на (nu). Получим (ytimesnu=upsilon).
Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:
(left(upsilontimesnuright)’=upsilon’timesnu+upsilontimesnu’)
Тогда выводим:
(y’timesnu+ytimesnu’=upsilon’)
Из этого вычисляем нужную нам производную:
(y’timesnu=upsilon’-ytimesnu’=upsilon’-fracupsilonnutimesnu’=frac{upsilon’v-upsilonnu’}nu;;y’=frac{upsilon’v-upsilonnu’}{nu^2})
Что и требовалось доказать.
Следует также привести таблицу с производными часто встречающихся функций:
Как решать производные функции с дробями, примеры
Чтобы понять, как решать ПФ с дробями, приведем несколько примеров.
Пример 1
Найти производную дроби (y=frac x{In;x}.)
Решение
Из формулы следует, что числитель (upsilon=х), а знаменатель (nu=In;х). Найдем их производные:
(upsilon’=left(хright)’=1,;nu’=left(In;xright)’=frac1x)
Подставляем решенные (upsilon’;и;nu’) в формулу и получаем:
( y’=left(frac x{In;x}right)’=frac{left(xright)’In;x-xleft(In;xright)’}{left(In;xright)^2}=frac{In;x;-x{displaystylefrac1x}}{In^2x}=frac{In;x-1}{In^2x})
Ответ: (y’=frac{In;x-1}{In^2x}.)
Пример 2
Найти производную дроби, равную (y=frac{cos;x}x).
Решение
По формуле производной частного:
(y’=left(frac{cos;x}xright)=frac{left(cos;xright)’x-cos;xleft(xright)’}{left(xright)^2})
Производная косинуса дает нам синус с минусом:
(left(cos;xright)’=-sin;x)
В таком случае:
(y’=frac{-x;sin;x-cos;x}{x^2}=-frac{x;sin;x+cos;x}{x^2})
Ответ: (y’=-frac{x;sin;x+cos;x}{x^2}.)
Пример 3
Найти производную дроби (yleft(xright)=frac{e^x-1}{e^x+1}.)
Решение
Из таблицы производных находим:
(left(e^xright)’=e^x)
Применяем правила дифференцирования постоянной и суммы:
(left(e^x-1right)’=left(e^xright)’-left(1right)’=e^x-0=e^x;;left(e^x+1right)’=left(e^xright)’+left(1right)’=e^x-0=e^x)
Используем формулу производной дроби:
(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{nu^2};left(frac{e^x-1}{e^x+1}right)’=frac1{left(e^x+1right)^2}timeslbrackleft(e^x-1right)’left(e^x+1right)-left(e^x-1right)left(e^x+1right)’rbrack=frac1{left(e^x+1right)^2}timeslbrack e^xleft(e^x+1right)-left(e^x-1right)e^xrbrack=frac{2e^x}{left(e^x+1right)^2})
Ответ: (y’=frac{2e^x}{left(e^x+1right)^2}.)
Формула производной от дроби, примеры
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Формула производной от дроби
Раздел о производных является отдельным самостоятельным разделом в математическом анализе. Условимся, что читателю известно понятия предела, производной, дифференциала, а также ряд свойств производной.
В данной статье рассмотрим одно из свойств производной, а именно формулу производной от дроби. Приведём эту формулу. Пусть функция $v(x)$ имеет производную в точке $x$ и $v(x)neq0$, тогда:
$(frac{u}{v})’=frac{u’v-uv’}{v^2}.$
Напомним формулы производных элементарных функций:
Рисунок 1. Формулы производных элементарных функций. Автор24 — интернет-биржа студенческих работ
Примеры
Решим примеры. Преобразования, позволяющие применить другие свойства производной, мы применять не будем. В решениях будем использовать только формулу производной от дроби.
По условию даются функции. Нужно найти производные.
Пример 1
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ
Пример 2
Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ
Пример 3
Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ
Пример 4
Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 10. Пример. Автор24 — интернет-биржа студенческих работ
Пример 5
Рисунок 11.
Рисунок 12. Пример. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 15.05.2023
III.3. Дифференцирование функции одной переменной
Глава III. Введение в математический анализ и основы дифференциального исчисления функции одной переменной >
(схема 30)
При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.
Пусть явно задана функция y=f (x). Функция,
зависящая непосредственно от переменной x, называется
простой.
Рассмотрим для простой функции точку x, принадлежащую ее области определения. Дадим
приращение аргументу ∆x в точке x. Функция
получит при этом соответствующее (3.9) приращение ∆y=f(x+∆x)—f(x).
Производной функции y=f (x) по переменной x в некоторой точке называется предел отношения
приращения функции
к приращению аргумента, когда
последнее стремится к нулю, то есть
. (3.15)
Функция, имеющая в точке конечную производную,
называется дифференцируемой в этой точке. Процесс нахождения производной называется
дифференцированием и обозначается .
Производная
характеризует скорость изменения функции в достаточно малой окрестности заданной
точки.
Приведем таблицу производных основных элементарных
функций (без доказательства), которые рассматриваются нами как функции простые
и явно заданные.
Теорема 3.9. Если функция
дифференцируема в некоторой точке, то она в этой точке непрерывна
Следствие. В точках разрыва функция производной не имеет
Существуют такие точки, в которых функция непрерывна,
но не дифференцируема.
точке к графику функции можно провести бесконечное множество
касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к
теореме 3.9 неверно.
Среди явных
функций особое место занимают обратные функции, производная
которых находится с помощью следующей теоремы.
Теорема 3.10. Если
строго монотонная функция y=f (x) дифференцируема на некотором интервале Х, причем ее производная не
обращается в нуль на Х, то обратная к ней функция
x=φ(y) также
дифференцируема на этом интервале, при этом:
(3.
Доказательство. Дадим функции
y=f (x) в точке x бесконечно малое приращение аргумента ∆x→0, функция при этом получит соответствующее приращение
∆y. Так как по условию теоремы функция
дифференцируема в каждой точке интервала Х, то в каждой точке этого
интервала функция непрерывна (по теореме 3.9). Следовательно, по определению
непрерывности функции выполняется: , это означает, что
при ∆x
→0; ∆y→0.
По
определению производной можно записать:
, теорема доказана
Среди явных функций выделяют класс сложных функций.
Функция называется
сложной, если она представляет собой композицию нескольких функций: y=f (φ(x)). Функция f называется внешней, а φ — внутренней функцией, выступающей в качестве
независимого переменного.
Теорема 3.11.
Чтобы
продифференцировать сложную
функцию необходимо сначала продифференцировать внешнюю функцию по внутренней,
считая внутреннюю функцию независимой переменной, затем
продифференцировать внутреннюю функцию по независимому переменному и результаты
дифференцирования перемножить, то есть
(3.31)
Пример 3.8. Найти
производную функции .
Решение. Согласно формуле (3.31) и с учетом табличных формул
(3.17), (3.19), (3.29) имеем:
.
К явным функциям можно отнести функции, заданные
параметрически, вида:,
где t –
параметр. Производную такой функции несложно получить:
. (3.
Пример 3.9. Найти
производную функции .
Решение. Согласно
формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Примечание.
Функция,
заданная в примере 3.9, представляет собой параметрическое уравнение окружности
радиуса a. Действительно, возведем оба уравнения в квадрат и сложим
их почленно, получим:
Помимо таблицы производных
имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме
производных этих функций:
(3.33)
Данная теорема может быть обобщена для произвольного
конечного числа функций-слагаемых.
Пример 3.10.
Найти производную функции.
Решение. Согласно
формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:
Теорема 3.13. Производная произведения двух дифференцируемых функций равна
произведению производной первой функции-сомножителя на вторую функцию плюс
произведение первой функции на производную
второй функции–сомножителя, то есть
(3.34)
Пример 3.11.
Найти производную функции .
Решение. Согласно формуле (3.34) и с учетом табличных формул
(3.22), (3.24) имеем:
Теорема 3.14.
Производная частного двух функций
равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а
числитель есть разность между
произведением знаменателя на производную числителя и произведением
числителя на производную знаменателя, то есть
(3.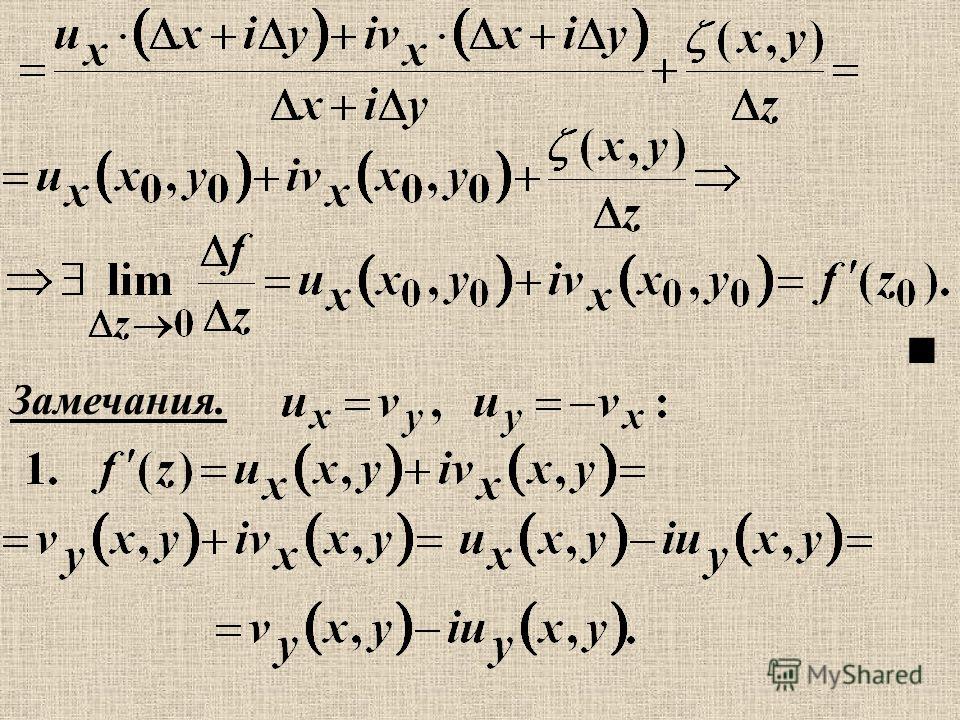
Пример 3.12.
Найти производную функции.
Решение. Согласно формуле (3.35) и с учетом табличных формул
(3.17), (3.29) имеем:
Все рассмотренные выше при дифференцировании функции
были заданы в явном виде, то есть уравнением y=f (x),
разрешенным относительно y.
Функция называется неявно заданной, если она
имеет вид F (x;y)=0.
Неявный способ задания к свойствам функции отношения не имеет. В этом случае
любое выражение, содержащее переменную y, нужно
рассматривать как функцию сложную. Следовательно, при нахождении производной неявных функций следует применять теорему о
дифференцировании сложной функции. В процессе отыскания
все слагаемые,
содержащие , оставляют в левой части равенства и выносят из них за скобки как общий
множитель. Слагаемые, не содержащие , переносят в правую часть, и полученное уравнение разрешают
относительно искомой .
Пример 3.13.
Найти производную неявной
функции .
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной
произведения, с учетом табличных формул (3.17) и (3.18)
имеем:
Иногда для упрощения процесса дифференцирования
громоздких функций применяют их предварительное логарифмирование (логарифмическое
дифференцирование). Данный метод целесообразен в тех случаях, когда
функция представляет собой произведение и (или) частное различных функций,
таких как показательные и степенные выражения (особенно иррациональные).
Логарифмическое дифференцирование используется также для нахождения производных
показательно-степенных функций, которые без предварительного логарифмирования
вообще не дифференцируются. При использовании данного метода в левой части получают производную от натурального
логарифма
y, которая равна . После этого обе части умножают на y, при этом в правой части заменяют y на заданную по
условию функцию.
Пример 3.14.
Найти производную функции .
Решение.
Прологарифмируем заданную функцию .
По свойству логарифма степени имеем:. Согласно формуле
(3.31) дифференцирования сложной функции
и (3.34) производной произведения, с учетом табличных формул (3.19) и (3.29)
можно записать
.
После умножения обеих частей последнего равенства на
y
окончательно получим:. Заметим, что без предварительного логарифмирования
производную заданной функции найти невозможно, так как нельзя обосновать
использование формул дифференцирования (3.17) или (3.22)
Пусть функция y=f (x)
дифференцируема в некоторой текущей точке x и при этом . Тогда по определению производной и формуле (3.15) можно
записать: . Иначе: приращение функции имеет вид
. (3.
Дифференциалом функции y=f (x) в точке x называется главная часть приращения этой
функции, равная произведению производной функции на приращение аргумента:
. (3.37)
Найдем дифференциал независимой переменной x, то есть
дифференциал функции y=x. Так
как , то по формуле (3.37) имеем dy=dx=∆x. Тогда формула (3.37) для вычисления дифференциала
функции может быть записана в виде:
. (3.38)
Если в формуле
(3.36) отбросить бесконечно малую величину α∙∆x, то
получим приближенное равенство .
.
(3.39)
Формула (3.39) применяется для вычисления приближенных
значений функций.
Пример
3.15. Вычислить приближенно значение .
Решение.
Рассмотрим функцию . По формуле (3.39)
имеем:
.
Так как x+∆x=0,95, то при x=1 и ∆x=-0,05
получаем:
Процесс дифференцирования может быть многократным. Производная от первой
производной называется второй производной функции или производной 2-го порядка.
Производная от последней, в свою очередь, является производной 3-го порядка и
так далее.
порядка заданной функции, то есть
. (3.40)
Вопросы для самопроверки
9
Основные
правила дифференцирования. Сумма.
Выведем
несколько правил вычисления производных,
В этом пункте значения функций u и v и
их производных в точке х0
обозначаются для краткости так: u(х0)
= u, v(х0)
= v, u'(х0)
= u’, v'(х0)=v`.
Если
функции u и v дифференцируемы в точке
х0,
то их сумма дифференцируема в этой
точке и
(u+v)’
= u’ + v’.
Коротко
говорят: производная
суммы равна сумме производных.
1) Для доказательства
вычислим сначала приращение суммы
функций в рассматриваемой точке: Δ(u+v)
= u (х0+Δx)+
v(х0+Δx)
– (u(х0)+v(х0))
= (u(х0+Δx)-u(х0))
+ (v(х0+Δx)-v(х0))
= Δu + Δv
2)
3)
Функции u и v дифференцируемы в точке
х0,
т. е. при Δх→0
Тогда
при
Δх→0 (см. правило 3, а) предельного
перехода),
т. е. (u+v)’ = u’+v’
Основные
правила дифференцирования. Произведение.
Если
функции и и v дифференцируемы в точке
х0,
то их произведение дифференцируемо в
этой точке и
(uv)’
= u’v+uv’.
1)
Найдем сначала приращение произведения:
Δ(uv)
= u(х0+Δx)v(х0+Δx)-u(х0)v(х0)=(u(х0)+
Δu)(v(х0)+
Δv)-u(х0)v(х0)
=
=u(х0)v(х0)+
Δuv(х0)+u(х0)
Δv+ΔuΔv-u(х0)v(х0)=
Δuv(х0)+u(х0)
Δv+ΔuΔv
2)
3)
В силу дифференцируемости функций u и
v в точке х0
при Δx→0 имеем
Поэтому
т.
е. (uv)’ = u’v+uv’, что и требовалось доказать.
Следствие. Если
функция u дифференцируема в х0,
а С — постоянная, то функция Сu
дифференцируема в этой точке и
(Сu)’
= Сu’.
Коротко
говорят: постоянный
множитель можно выносить за знак
производной.
Для доказательства
воспользуемся правилом 2 и известным
из пункта о производной,
фактом С’ = 0:
(Сu)’
= Сu’ + С’u = Cu’ + 0⋅u
= Cu’.
Пример.
Продифференцировать
функцию .
Решение.
В
данном примере .
Применяем правило производной
произведения:
Обращаемся
к таблице производных основных
элементарных функций и получаем ответ:
Основные
правила дифференцирования. Частное
Если
функции u и v дифференцируемы в точке
x0
и функция v не равна нулю в этой точке,
то частное u/v также дифференцируемо в
x0
и
Выведем
сначала формулу
1)
найдем приращение функции 1/v:
2)
Отсюда
3)
При Δx→0 имеем Δv/Δx→v’ (в силу
дифференцируемости v в точке x0),
Δv→0 (по
доказанной лемме).
Поэтому
Теперь,
пользуясь правилом нахождения производной
произведения функций, находим производную
частного:
Пример.
Выполнить
дифференцирование функции .
Решение.
Исходная
функция представляет собой отношение
двух выражений sinx и 2x+1.
Применим правило дифференцирования
дроби:
Не
обойтись без правил дифференцирования
суммы и вынесения произвольной постоянной
за знак производной:
Производная
сложной функции.
Если
функция f имеет производную в точке х0,
а функция g имеет производную в точке
y0=f(x0)y
то сложная функция h(х) = g(f(х)) также имеет
производную в точке х0,
причем
h’(x0)
= g’(f(x0))•f’(x0)
(1)
Для
доказательства формулы (1) надо (как и
раньше) при Δx≠0 рассмотреть дробь Δh/Δx
и установить, что
при
Δx→0.
Δy
= f(x0+Δx)-f(x0)=
Δf
Тогда
Δh = h(х0
+ Δх) — h(x0)
= g(f(x0
+Δx)) — g(f(x0))
= g(y0
+ Δy) — g(y0)
= Δg.
Δy→0 при Δx→0, так как f дифференцируема
в точке x0.
Далее доказательство мы проведем
только для таких функций f, у которых
Δf≠0 в некоторой окрестности точки х0.
Тогда
при
Δx→0, так как Δf/Δx→f’(x0)
при Δx→0, а Δg/Δy→g’(y0)
при Δy→0, что выполнено при Δx→0.
Пример.НА
ВСЯКИЙ СЛУЧАЙ !! ! ! !!!
http://www.mathelp.spb.ru/book1/proizvodnaya.htm
Производная
обратной функции.
Пусть
функция
дифференцируема
и строго монотонна на
.
Пусть также в точке
производная
.
Тогда в точке
определена дифференцируемая функция
,
которую называют обратной к
,
а ее производная вычисляется по формуле
.
Примеры.
Найти
производную обратной тригонометрической
функции y = arcsinx. Обратная функция x
= siny и ,
по формуле для обратной функции .
Найдем функции
y = arctgx.
Обратная функция x = tgy,
Производная
суммы, производная разности.
Для
доказательства второго правила
дифференцирования воспользуемся
определением производной и свойством
предела непрерывной функции.
Подобным
образом можно доказать, что производная
суммы (разности) n функций
равна сумме (разности) n производных
Пример.
Найти
производную функции
Решение.
Упростим
вид исходной функции
Используем
правило производной суммы (разности):
В
предыдущем пункте мы доказали, что
постоянный множитель можно выносить
за знак производной, поэтому
Осталось
воспользоваться таблицей производных:
Производная e в степени x и показательной функции. Удивительная особенность производной e в степени х
Содержание
- Производные простых функций
- Что такое предел
- Виды логарифмов
- Как находить производные сложных логарифмических функций?
- Общая формула производной логарифма
- Случай отрицательных значений y
- Внутренняя и внешняя функции
- Понятие производной сложной функции
- Правила нахождения производных
- Некоторые свойства и практические примеры
- Сложные производные
- Синтаксис описания формул
- Производная натурального логарифма
- Прикладное использование производной
- Таблица производных
- Некоторые интересные факты о числе е
- Что такое логарифмическое дифференцирование?
- Производная экспоненты
Производные простых функций
1.
с´ = 0
Пример:
5´ = 0
Пояснение:
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение:
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение:
В данном случае, при каждом изменении аргумента функции (х) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с.
Откуда следует, что
(cx + b)’ = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|’ = x / |x| при условии, что х ≠ 0
Пояснение:
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x < 0 оно равно (-1), а когда x > 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
( xc )’= cxc-1, при условии, что xc и сxc-1,определены а с ≠ 0
Пример:
(x2 )’ = 2x
(x3)’ = 3x2
Для запоминания формулы:
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу.
6. Производная дроби 1/х
(1/х)’ = – 1 / x2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)’ = (x-1 )’ , тогда можно применить формулу из правила 5 таблицы производных
(x-1 )’ = -1x-2 = – 1 / х2
7. Производная дроби с переменной произвольной степени в знаменателе
( 1 / xc )’ = – c / xc+1
Пример:
( 1 / x2 )’ = – 2 / x3
8. Производная корня (производная переменной под квадратным корнем)
( √x )’ = 1 / ( 2√x ) или 1/2 х-1/2
Пример:
( √x )’ = ( х1/2 )’ значит можно применить формулу из правила 5
( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)
9.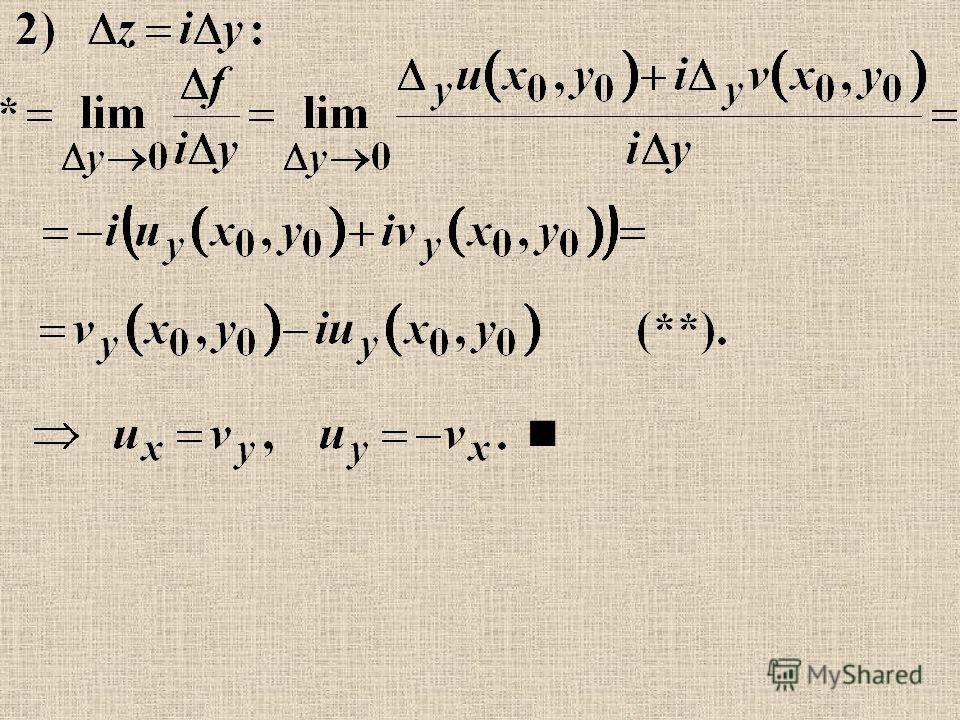
( n√x )’ = 1 / ( n n√xn-1 )
.
Приведенная здесь таблица производных простых функций содержит только основные преобразования, которые (по большому счету) следует запомнить наизусть.
Что такое предел
Вначале разберемся с понятием предела. Рассмотрим какое-нибудь математическое выражение, например, i = 1/n. Можно увидеть, что при увеличении «n «, значение «i «будет уменьшаться, а при стремлении «n» к бесконечности (которая обозначается значком ∞), «i» будет стремиться к предельному значению (называемого чаще просто пределом), равному нулю. Выражение предела (обозначаемого как lim) для рассматриваемого случая можно записать в виде lim n →∞ (1/ n) = 0 .
Существуют различные пределы для различных выражений. Одним из таких пределов, вошедших в советские и российские учебники как второй замечательный предел, является выражение lim n →∞ (1+1/ n) n .
К первому же замечательному пределу относят выражение lim n →∞ (Sin n / n) = 1.
Как найти производную ex – в этом видео.
Виды логарифмов
Прежде, чем перейти к формулам производных, напомним, что для некоторых логарифмов предусмотрены отдельные названия:
1. Десятичный логарифм (lg x)
lg x = log10x
Т.е. это логарифм числа x основанию 10.
2. Натуральный логарифм (ln x)
ln x = loge x
Т.е. это логарифм числа x по основанию e (экспонента).
Как находить производные сложных логарифмических функций?
Что можно сказать о производной логарифмической функции y = lnx на основании таблицы производных? Можно сказать, что она существует и выражается формулой
(1)
Однако в большинстве задач математического анализа, с которыми придётся столкнуться в дальнейшем, присутствует сложная логарифмическая функция.
В случае сложной логарифмической функции y = lnu, где u – дифференцируемая функция аргумента x, формула (1) примет вид
(2)
Пользуясь формулой (2), найдём производную логарифмической функции с произвольным положительным основанием a. Пусть
В результате применения свойств логарифмов:
Так как – постоянный множитель, то – постоянный множитель, то
или
(3)
Пример 1. Найти производную функции
Решение. Применяя правило дифференцирования дроби (частного), а затем формулу (3), получим
Пример 2. Найти производную функции
Решение. Используя свойства логарифмов, данную функцию можно записать проще:
Это сложная логарифмическая функция.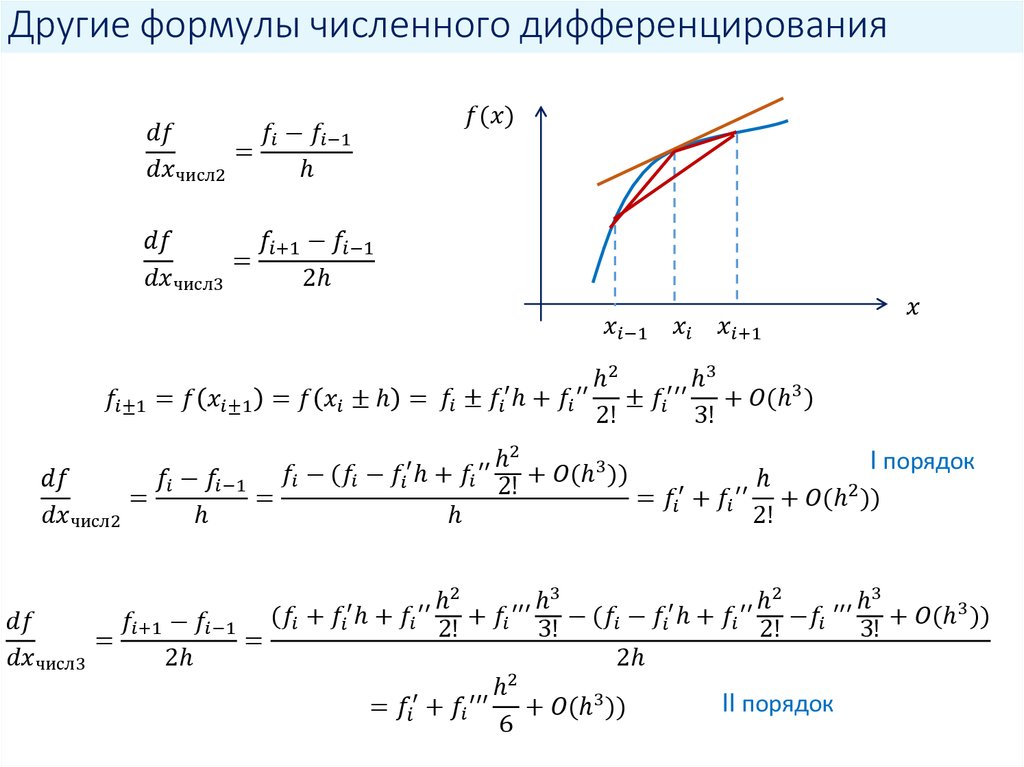
получаем
Нет времени вникать в решение? Можно заказать работу!
Общая формула производной логарифма
Производная логарифма x по основанию a равняется числу 1, разделенному на произведение натурального логарифма a и числа x.
Случай отрицательных значений y
Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:
.
Отсюда
(3) .
То есть, в общем случае, нужно найти производную от логарифма модуля функции .
Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .
Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x, отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:
.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.
Внутренняя и внешняя функции
Зачем же нам нужно разбираться во вложенности функций? Что нам это дает? Дело в том, что без такого анализа мы не сможем надежно находить производные разобранных выше функций.
И для того, чтобы двигаться дальше, нам будут нужны еще два понятия: внутренняя и внешняя функции. Это очень простая вещь, более того, на самом деле мы их уже разобрали выше: если вспомнить нашу аналогию в самом начале, то внутренняя функция – это «пакет», а внешняя – это «коробка». Т.е. то, во что икс «заворачивают» сначала – это внутренняя функция, а то, во что «заворачивают» внутреннюю – уже внешняя.
Выполни последнюю практику анализа сложных функций, и перейдем, наконец, к тому, ради чего всё затевалось – будем находить производные сложных функций:
Заполни пропуски в таблице:
Понятие производной сложной функции
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные – машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
Посмотрите на формулу 9 в таблице производных.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии – приготовлении запечёных яблок, фаршированных ягодами.
Итак, “яблоко” – это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x, в свою очередь, является “фаршем” (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на “яблоко”, поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме.
Пример 1.Найти производную функции
Сначала определим, где здесь “яблоко”, то есть функция по промежуточному аргументу u, а где “фарш”, то есть промежуточный аргумент u по независимой переменной x. Определяем: возведение в степень – это функция по промежуточному аргументу, то есть “яблоко”, а выражение в скобках (разность двух тригонометрических функций) – это промежуточный аргумент, то есть “фарш”.
Тогда
Далее по таблице производных (производная суммы или разности, производные синуса и косинуса) находим:
Требуемая в условии задачи производная (готовое “фаршированое яблоко”):
Нахождение производной сложной логарифмической функции имеет свои особенности, поэтому у нас есть и урок “Производная логарифмической функции”.
Пример 2.Найти производную функции
Неправильное решение:вычислять натуральный логарифм каждого слагаемого в скобках и искать сумму производных:
Правильное решение:опять определяем, где “яблоко”, а где “фарш”. Здесь натуральный логарифм от выражения в скобках – это “яблоко”, то есть функция по промежуточному аргументу u, а выражение в скобках – “фарш”, то есть промежуточный аргумент u по независимой переменной x.
Тогда (применяя формулу 14 из таблицы производных)
Во многих реальных задачах выражение с логарифмом бывает несколько сложнее, поэтому и есть урок “Производная логарифмической функции”.
Пример 3.Найти производную функции
Неправильное решение:
Правильное решение.В очередной раз определяем, где “яблоко”, а где “фарш”. Здесь косинус от выражения в скобках (формула 7 в таблице производных)- это “яблоко”, оно готовится в режиме 1, воздействующем только на него, а выражение в скобках (производная степени – номер 3 в таблице производных) – это “фарш”, он готовится при режиме 2, воздействующей только на него.
Производная сложной логарифмической функции – частое задание на контрольных работах, поэтому настоятельно рекомендуем посетить урок “Производная логарифмической функции”.
Первые примеры были на сложные функции, в которых промежуточный аргумент по независимой переменной был простой функцией. Но в практических заданиях нередко требуется найти производную сложной функции, где промежуточный аргумент или сам является сложной функцией или содержит такую функцию. Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования. Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы. Ниже – два примера, как это делается.
Кроме того, полезно знать следующее. Если сложная функция может быть представлена в виде цепочки из трёх функций
,
то её производную следует находить как произведение производных каждой из этих функций:
.
Для решения многих ваших домашних заданий может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Пример 4.Найти производную функции
Применяем правило дифференцирования сложной функции, не забывая, что в полученном произведении производных промежуточный аргумент по независимой переменной x не меняется:
Готовим второй сомножитель произведения и применяем правило дифференцирования суммы:
Второе слагаемое – корень, поэтому
Таким образом получили, что промежуточный аргумент, являющийся суммой, в качестве одного из слагаемых содержит сложную функцию: возведение в степень – сложная функция, а то, что возводится в степень – промежуточный аргумент по независимой переменной x.
Поэтому вновь применим правило дифференцирования сложной функции:
Степень первого сомножителя преобразуем в корень, а дифференцируя второй сомножитель, не забываем, что производная константы равна нулю:
Теперь можем найти производную промежуточного аргумента, нужного для вычисления требуемой в условии задачи производной сложной функции y:
Тогда
Пример 5.Найти производную функции
Сначала воспользуемся правилом дифференцирования суммы:
Получили сумму производных двух сложных функций. Находим первую из них:
Здесь возведение синуса в степень – сложная функция, а сам синус – промежуточный аргумент по независимой переменной x. Поэтому воспользуемся правилом дифференцирования сложной функции, попутно вынося множитель за скобки:
Теперь находим второе слагаемое из образующих производную функции y:
Здесь возведение косинуса в степень – сложная функция f[g(x)], а сам косинус – промежуточный аргумент по независимой переменной x.
Результат – требуемая производная:
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим (cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной хcos(x) по независимой переменной х . Таким образом, получим y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
.
.
В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции
.
Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
Учитывая, что , будем иметь
Но , откуда
, откуда
.
Пример 4. Найти производную функции y=xex
Решение.
.
Некоторые свойства и практические примеры
- Приведем правило для нахождения производной обратной функции.
Пусть дана функция
y=f(x)y=f(x)
y=f(x), в которой переменная x является аргументом. Полагая теперь аргументом переменную y, получим функцию в виде
x=g(y)x=g(y)
x=g(y).
f′(x)=(ln(x2+2x))′=(x2+2x)′⋅x2+2×1=x2+2x2x+2
Найти производную функции
f(x)=sin(ln2x)
Решение
Полагаем
ln2x=v
Тогда:
f′(x)=(sinv)v′⋅v′=cosv⋅(ln2x)′=cos(ln2x)⋅(2x)′⋅2×1=xcos(ln2x)
Сложные производные
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Пример 2
Найти производную функции
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях.
1) Сначала нам нужно вычислить выражение , значит, сумма , значит, сумма – самое глубокое вложение.
2) Затем необходимо вычислить логарифм:
3) Далее косинус:
4) Потом косинус возвести в куб:
5) На пятом шагу разность:
6) И, наконец, самая внешняя функция – это квадратный корень:
Формула дифференцирования сложной функции применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
Вроде без ошибок….
(1) Берем производную от квадратного корня.
(2) Берем производную от разности, используя правило
(3) Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба).
(4) Берем производную от косинуса.
(5) Берем производную от логарифма.
(6) И, наконец, берем производную от самого глубокого вложения .
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Пример 3
Найти производную функции
Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, а трёх функций. Как найти производную от произведения трёх множителей?
Пример 4
Найти производную функции
Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки.
В таких случаях необходимо последовательно применить правило дифференцирования произведения два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций: , а за «вэ» – логарифм: , а за «вэ» – логарифм: . Почему так можно сделать? А разве – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
Теперь осталось второй раз применить правило к скобке к скобке :
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде – легче будет проверять.
Готово.
Рассмотренный пример можно решить вторым способом:
Оба способа решения абсолютно равноценны.
Пример 5
Найти производную функции
Это пример для самостоятельного решения, в образце он решен первым способом.
Рассмотрим аналогичные примеры с дробями.
Пример 6
Найти производную функции
Здесь можно пойти несколькими путями:
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного , приняв за , приняв за весь числитель:
В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить? Приведём выражение числителя к общему знаменателю и избавимся от трёхэтажности дроби:
Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:
Пример 7
Найти производную функции
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
Пример 8
Найти производную функции
Тут можно пойти длинным путём, используя правило дифференцирования сложной функции:
Но первый же шаг сразу повергает в уныние – предстоит взять неприятную производную от дробной степени , а потом ещё и от дроби , а потом ещё и от дроби .
Поэтому перед тем как брать производную от «навороченного» логарифма, его предварительно упрощают, используя известные школьные свойства:
! Если под рукой есть тетрадь с практикой, перепишите эти формулы прямо туда. Если тетради нет, перерисуйте их на листочек, поскольку оставшиеся примеры урока буду вращаться вокруг этих формул.
Само решение можно оформить примерно так:
Преобразуем функцию:
Находим производную:
Предварительное преобразование самой функции значительно упростило решение. Таким образом, когда для дифференцирования предложен подобный логарифм, то его всегда целесообразно «развалить».
А сейчас пара несложных примеров для самостоятельного решения:
Пример 9
Найти производную функции
Пример 10
Найти производную функции
Все преобразования и ответы в конце урока.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.
Производная натурального логарифма
Производная от натурального логарифма числа x равняется единице, разделенной на x.
Данная формула получена следующим образом:
Сокращение ln e в данном случае возможно благодаря свойству логарифма:
Производная натурального логарифма сложной функции u = u (x):
Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Таблица производных
Производная степенной функции:
Производная показательной функции:
Производная экспонециальной функции:
Производная логарифмической функции:
Производные тригонометрических функций:
,
,
,
Производные обратных тригонометрических функций:
,
,
,
Производные гиперболических функций:
Некоторые интересные факты о числе е
С этим числом связаны фамилии таких ученых, как Непер, Отред, Гюйгенс, Бернулли, Лейбниц, Ньютон, Эйлер, и другие. Последний собственно и ввел обозначение е для этого числа, а также нашел первые 18 знаков, используя для расчета открытый им ряд е = 1 + 1/1! + 2/2! + 3/3! …
Число e встречается в самых неожиданных местах.
Что такое логарифмическое дифференцирование?
Если функция дана в виде
,
то перед тем, как находить её производную, часто бывает выгодно прологарифмировать эту функцию.
Это прежде всего случаи, когда требуется найти производную произведения или частного функций, а также степенной функции, когда основание и степень – функции.
На основании свойств сложных функций доказано, что производная функции, вид которой приведён выше, может быть найдена по формуле
Пример 3. Найти производную функции
Решение. Логарифмируем обе части равенства и находим:
Решение. Окончательно находим производную данной функции:
Пример 4.
.
Решение. Логарифмируем обе части равенства:
Дифференцируем:
Выражаем и находим производную данной функции:
Производная экспоненты
Экспонентой называется показательная функция, в качестве основания которой находится число е. Она обычно отображается в виде F (x) = ex, где показатель степени x является переменной величиной. Данная функция обладает полной дифференцируемостью во всем диапазоне вещественных чисел. С ростом x она постоянно возрастает и всегда больше нуля. Обратная к ней функция — логарифм.
Известный математик Тейлор сумел разложить эту функцию в ряд, названный его именем ex = 1 + x/1! + x 2 /2! + x 3 /3! + … в диапазоне x от — ∞ до + ∞.
Закон, базирующийся на этой функции, называется экспоненциальным.
- возрастание сложных банковских процентов;
- увеличение популяции животных и населения планеты;
- время окоченения трупа и многое другое.
Повторим еще раз замечательное свойство данной зависимости — значение ее производной в любой точке всегда равно значению функции в этой точке, то есть (ex)’ = ex .
Приведем производные для наиболее общих случаев экспоненты:
- (eax)’ = a ∙ eax
- (ef (x))’ = f'(x) ∙ ef (x).
Используя данные зависимости, несложно найти производные для других частных видов этой функции.
Источники
- https://profmeter.com.ua/communication/learning/course/course17/lesson251/
- https://LivePosts.ru/articles/education-articles/matematika/udivitelnaya-osobennost-proizvodnoj-e-v-stepeni-h
- https://MicroExcel.ru/proizvodnye-logarifmov/
- https://function-x.ru/proizvodnaya_logarifmicheskoi_funkcii.
html
- https://1cov-edu.ru/mat_analiz/proizvodnaya/nayti/logarifmicheskaya/
- http://cos-cos.ru/math/254/
- https://function-x.ru/derivative2.html
- https://math.semestr.ru/math/diff.php
- https://studwork.org/spravochnik/matematika/proizvodnye/proizvodnaya-naturalnogo-logarifma
- http://www.mathprofi.ru/slozhnye_proizvodnye_logarifmicheskaja_proizvodnaja.html
- https://planetcalc.ru/675/?thanks=1
- https://planetcalc.ru/675/
Пример 3
f(x)=sin(ln2x)f(x)= sin {(ln {2x})}
ln2x=vln {2x}=v
f′(x)=(sinv)v′⋅v′=cosv⋅(ln2x)′=cos(ln2x)⋅(2x)′⋅12x=cos(ln2x)xf'(x)=(sin {v})’_v cdot v’ = cos {v} cdot (ln {2x})’ =cos{(ln {2x})} cdot (2x)’ cdot dfrac {1} {2x} = dfrac {cos(ln{2x})} {x}
SavePearlHarbor
Опубликовано 16.09.2022 автором admin
Разработка софта это не только про код. Разработка софта это во многом про Toolchain(ы). Прежде чем начать исполняться исходники проходят гигантский путь и с каждым годом выходят все более и более массивные системы сборки. Современные технологии разработки софта настолько многостадийные, что понять их не просто.
Toolchain это как длинный конвейер.
По-настоящему разобраться как варятся артефакты сложно. Как же это сделать?
Надо прибегнуть к народной
Читать далее →
Рубрика: Без рубрики
|
Добавить комментарий
Опубликовано 16.09.2022 автором admin
Давние читатели “crawl” могут вспомнить, что у меня никогда не хватало терпения для идеи “Искусственный Интеллект просто хочет жить”.
“Эксперты-свидетели защиты, включая умный гель онлайн из Ратгерского университета, показали, что в культурах нейронов отсутствуют примитивные структуры среднего мозга, необходимые для того, чтобы испытывать боль и страх или стремиться к самосохранению. Защита же утверждала, что концепция “права” предназначена для защиты отдельных лиц от необоснованных страданий. Поскольку умные гели лишены возможности морального или физического страдания, то у них нет права на защиту, независимо от уровня их самосознания. Защита красноречиво резюмировала это рассуждение во время заключительного выступления: “Сами гели не заботятся о своей жизни и смерти. Почему тогда мы должны?” Приговор ещё находится на стадии обжалования.“
— который должен был служить противовесом для
Читать далее →
Рубрика: Без рубрики
|
Добавить комментарий
Опубликовано 16.
Краткое описание проекта
В данном проекте перед нами стояла задача – с помощью чат-бота разгрузить КЦ, а также оперативно и качественно отвечать на вопросы студентов и школьников группы образовательных организаций.
В группе состоят 9 образовательных учреждений, у каждого из которых есть свой сайт с виджетом и бот в Telegram. Конечные каналы общения подключены к омниканальной платформе Helpdeskeddy.
В качестве платформы для low-code создания бота и настройки интеграции с Helpdeskeddy была выбрана чат-бот платформа chatme.ai.
Интеграция с Helpdeskeddy
На платформе chatme.ai нет встроенного коннектора к Helpdeskeddy. Поэтому интеграция к Helpdeskeddy реализована внутри бота через HTTP-запросы, а на стороне Helpdeskeddy настроены правила отправки вебхуков. Интеграционные возможности конструктора платформы позволили быстро реализовать подобную интеграцию и в отсутствие встроенного коннектора.
Создание бота
На старте нам был предоставлен набор интентов и
Читать далее →
Рубрика: Без рубрики
|
Добавить комментарий
Опубликовано 16.
Компания Honeywell решила свернуть свой существующий бизнес и операции в России и Беларуси. Для многих нефтегазовых предприятий России это стало неприятным событием. Дело в том, что на опасных производственных объектах для обучения персонала обязаны использоваться компьютерные имитационные тренажеры и да, большинство компьютерных имитационных тренажеров в нефтегазовой промышленности создавалось именно на базе программного обеспечения Honeywell Unisim. Спустя некоторое время начался процесс остановки таких программных и программно-аппаратных комплексов, т.к. необходима актуальная лицензия на Unisim, а продлить ее невозможно.
На рынке РФ, к сожалению, практически отсутствуют компании, ведущие разработку аналогичных тренажеров для нефтегазовых объектов, не используя UniSim. Причина достаточна проста, сейчас на рынке нет
Читать далее →
Рубрика: Без рубрики
|
Добавить комментарий
Опубликовано 16.
Продолжаю дорабатывать небольшой скрипт на языке PowerShell для работы в программах-оболочках «Windows PowerShell» версии 5.1 и «PowerShell» версии 7 (я работаю в операционной системе «Windows 10»). Скрипт разбирает заданный файл с кодом на языке HTML с помощью методов библиотеки «HTML Agility Pack» и выводит в консоль HTML-дерево HTML-страницы из файла. При выводе в консоль HTML-дерева внимание пользователя с помощью цвета фокусирую на значениях атрибутов «class» HTML-элементов. Далее выполняю анализ названий БЭМ-сущностей на соответствие методологии БЭМ («Блок, Элемент, Модификатор»). Скрипт может быть полезен при изучении методологии БЭМ, схем именования в БЭМ и так далее.
Про визуализацию HTML-дерева я писал в статье «PowerShell: обход и визуализация HTML-дерева из файла». Про методологию БЭМ и соглашениях по именованию, использующихся в рамках этой методологии, я писал в статье «PowerShell: классическая схема именования в БЭМ и регулярные выражения».
В данной статье
Читать далее →
Рубрика: Без рубрики
|
Добавить комментарий
Формулы и правила дифференцирования в математике с примерами решения и образцами выполнения
Оглавление:
Формулы дифференцирования
Выгодно иметь такие правила, которые позволяли бы находить производные проще, с минимальной затратой времени. Действительно, такие правила имеются, причем они выводятся из основного правила дифференцирования.
Производная постоянной
Пусть С — постоянная величина; тогда равенство
у = С
можно рассматривать как выражение функции, не меняющей своего значения с изменением аргумента. В справедливости этого можно убедиться, представив это равенство графически, т. е. в виде прямой линии АВ, параллельной оси Ох (рис. 85).
Действительно, с изменением абсциссы точек этой прямой ординаты их остаются постоянными.
Для нахождения производной функции у = С применим основное правило дифференцирования:
т. е. производная постоянной равна нулю.
Не следует производную постоянной смешивать с пределом постоянной, который, как известно, равен самой постоянной.
Производная функции у = х
Применяя основное правило дифференцирования, получим:
т. е. производная функции у = х равна единице, или: производная независимой переменной равна единице.
Производная алгебраической суммы функций
Возьмем функцию
где — функции от х и имеющие производные по х. Если аргументу х дать приращение то и функции и, v и w получат приращения, соответственно равные , и , а потому у также получит приращение . По основному правилу находим:
Слагаемые правой части последнего равенства являются производными функций . Указанное равенство можно переписать:
или
т.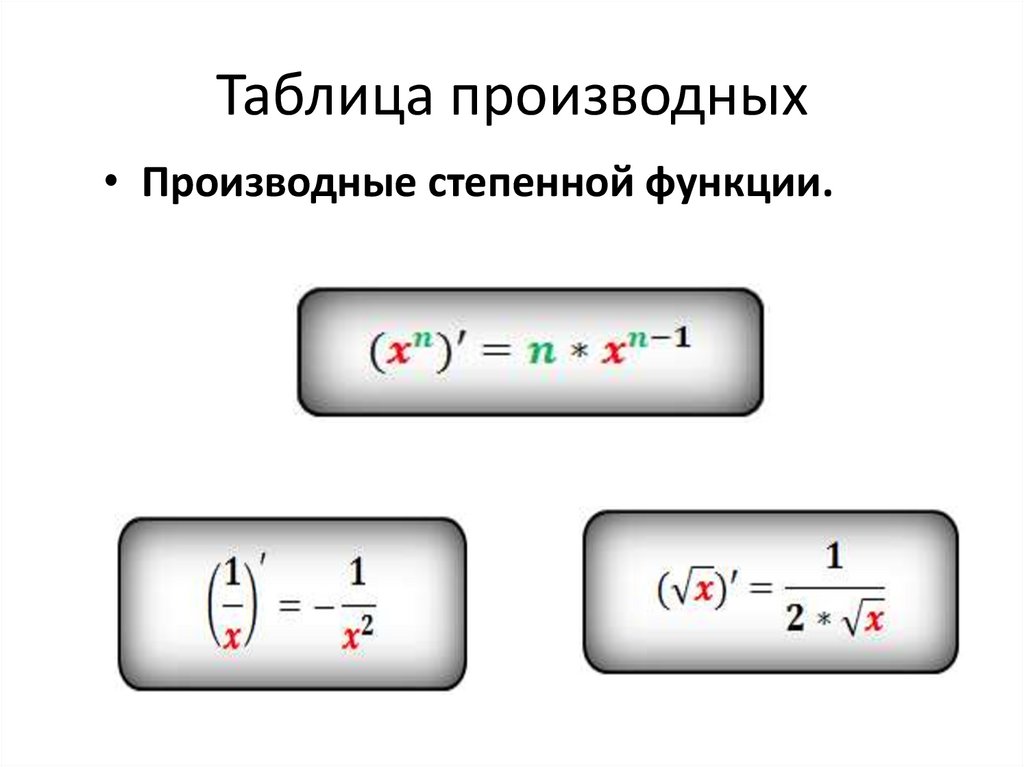
Производная произведения двух функций
Пусть дана функция
где и и v — функции от х имеющие производные по x. Дадим аргументу х приращение тогда согласно основному правилу будем иметь:
Но и и v не зависят от , а потому их нужно считать постоянными *)
*) Это можно иллюстрировать на рис. 86. Здесь
при ; согласно следствию 1 теоремы IV можем написать:
Приращение же функции и меняется с изменением , поэтому согласно теореме IV имеем:
Таким образом,
Но
Далее, так как и дифференцируема, то она непрерывна, следовательно.
Если то не меняется.
Поэтому
Итак,
т. е. производная произведения двух функций равна сумме произведений первой функции на производную второй и второй функции на производную первой.
Производная произведения постоянной на функцию
Возьмем функцию
где
причем функция и имеет производную по х. Применяя правило (IV), получим:
т. е. производная произведения постоянной на функцию равна произведению постоянной на производную функции.
Производная степени с целым положительным показателем
Возьмем сначала функцию
Представив ее в виде произведения и применяя правило (IV), получим:
Найдем производную новой функции:
Заменив ее произведением и опять применяя то же правило (IV), найдем:
Поступив точно так же с функцией
найдем:
Если продолжать дифференцирование функций и т. д. этим способом, то получим результаты, подчиняющиеся одной и той же формуле:
Таким образом, производная степени , где т— целое положительное число, равна произведению показателя степени на основание х в степени, на единицу меньшей чем данная.
Однако выведенное правило справедливо для любого показателя т, что мы и докажем.
Производная функции . Представив функцию в виде степени с дробным показателем и применяя правило (VI), получим:
Таким образом,
т. е. производная функции равна единице, деленной на удвоенную функцию.
Производная функции .
Заменив на и дифференцируя по правилу (VI), получим:
т. е. производная дроби равна отрицательной дроби, равной единице, деленной на квадрат знаменателя.
Производная частного
Возьмем функцию
где и и v — функции от х, имеющие производные по x, причем при значении х, при котором находится производная. Применим основное правило дифференцирования.
4-й шаг: применяя теоремы V, III, II и следствие 1 теоремы IV , находим:
Здесь, как и при выводе формулы (IV), нужно считать и и v не зависящими от , а .
Итак,
т. е. производная частного равна дроби, знаменатель которой есть квадрат делителя, л числитель есть разность между произведением делителя на производную делимого и произведением делимого на производную делителя.
Применение формул дифференцирования
Рассмотрим несколько примеров на применение выведенных правил.
Пример:
Продифференцировать функцию
Решение:
По правилу (III) имеем:
Применяя к первым трем слагаемым правило (V), а к последнему— правило (I), получим:
Согласно правилам (VI) и (II) будем иметь:
Пример:
Продифференцировать функцию
Решение:
По правилу (IV) имеем:
По правилу (III):
По правилам (V), (II). (I) и (VI):
Этот пример можно решить иначе: сначала перемножить выражения в скобках, а затем продифференцировать полученную сумму:
Пример:
Продифференцировать функцию
Решение:
Преобразуем данную функцию следующим образом:
Применяя правила (V) и (VI), будем иметь:
Пример:
Продифференцировать функцию
Решение:
Представим данную функцию в следующем виде:
Применяя правила (III) и (V), получим:
По правилам (VIII), (VII) и (VI) имеем:
По правилам (VIII), (VII) и (VI) имеем:
Пример:
Продифференцировать функцию
Решение:
По правилу (IX) имеем:
Дифференцируя сумму по правилу (III), получим:
Наконец, по правилам (VI), (II), (I) и (V) найдем:
Можно иначе продифференцировать данную функцию, разделив в правой части данного уравнения почленно числитель на знаменатель, получим:
или
отсюда
Функция от функции (сложная функция)
Пусть нам даны две функции:
и
Если в (1) заменить и его выражением из (2), то получим:
Из уравнений (1) и (2) видно, что у есть функция от и, но и в свою очередь функция от х таким образом, функция у зависит от функции
Функцию (3) называют функцией от функции или слоэюной функцией.
Всякую сложную функцию можно представить в виде нескольких простых. Разберем примеры.
Пример:
Представить функцию
в виде двух простых.
Решение:
Положим
тогда
Мы получили две функции и и у более простого вида, чем данная.
Пример:
То же для функции
Решение:
Положим
тогда
Производная сложной функции
Возьмем функцию
причем
Пусть функция (2) имеет производную при данном х; тогда при и , Пусть также и функция (1) имеет производную при значении и, соответствующем тому же значению х. Напишем тождество
Применяя к правой части тождества (3) теорему о пределе произведения, получим:
Но, как известно,
Поэтому равенство (4) можно переписать:
Формула (5) служит для дифференцирования сложной функции, составленной из двух простых.
Пример:
Продифференцировать функцию
Решение:
Представим данную функцию в виде следующих двух:
Найдем сначала (т. е. производную функции у по аргументу и), а затем и (т. е. производную функции и по аргументу х):
Искомая производная будет:
или, заменяя и его значением,
Как видно из формулы (5), производная сложной функции выражается произведением производных простых функций и, конечно, перестановка сомножителей не изменит результата. Однако удобней находить эти сомножители в одной определенно выбранной последовательности, которую полезно запомнить как правило. Так, например, для разобранного случая степенной функции это правило можно высказать следующим образом:
для дифференцирования сложной степенной функции*) нужно взять производную сначала от степени по основанию (принимая основание за аргумент), а потом от выражения, стоящего в основании, по независимой переменной и результаты перемножить.
*) Под сложной степенной функцией будем разуметь степень, основание которой есть функция от х.
Если — сложная степенная функция, то ее производная согласно этому правилу запишется так:
Пусть, например, требуется найти производную функции
Положив
и, применяя правило (6), будем иметь:
В дальнейшем для каждого особого случая будут даваться аналогичные правила, устанавливающие свою последовательность дифференцирования.
Разберем еще пример. Пусть требуется найти производную функции
Разбив ее на две простые функции, получим:
отсюда
Следовательно,
И здесь можно установить последовательность в нахождении производной, которая выразится следующим правилом: для дифференцирования сложной функции нужно сначала взять производную от этой функции по подкоренному выражению и (считая и аргументом), а потом от подкоренного выражения по независимой переменной и результаты перемножить; таким образом, считая и функцией от x получаем:
Так, например, производная функции
но вышеуказанному правилу найдется так:
Если дан корень другой степени, то его нужно предварительно преобразовать в степень с дробным показателем и применить правило для дифференцирования сложной степенной функции.
Производные тригонометрических функций
По общему правилу дифференцирования находим:
1-й шаг:
2-й шаг:
Преобразуя разность синусов, будем иметь:
3-й шаг:
После деления числителя и знаменателя дроби на 2 получим:
4-й шаг:
Но
поэтому
Следовательно
2.
По формуле приведения можно написать:
отсюда
Для дифференцирования сложной функции представим ее в виде двух простых:
Согласно формуле (5) имеем:
Следовательно,
3.
Заменив tg x отношением и применяя правило дифференцирования частного, получим:
Итак, имеем:
4.
Как и в случае 3, имеем:
Таким образом,
В п. 2 настоящей лекции мы дифференцировали сложную функцию , пользуясь формулой (5) .
Однако эту операцию можно произвести и по следующему правилу:
для дифференцирования сложной тригонометрической функции *) нужно сначала взять производную от тригонометрической функции по выражению, стоящему под ее знаком (принимая его за аргумент), а потом от этого выражения по независимой переменной и результаты перемножить;
*) Под сложной тригонометрической функцией будем понимать тригонометрическую функцию сложного аргумента.
поэтому, считая и функцией от х, получаем:
Пользуясь правилом (1), процесс дифференцирования функции sin можно записать таким образом:
Пример:
Продифференцировать функцию
Решение:
Согласно правилу (2) настоящей лекции найдем:
Пример:
Продифференцировать функцию
Решение:
Переписав функцию в виде найдем по правилу (6)
Но сложная тригонометрическая функция, а потому согласно правилу (1) настоящей лекции имеем:
Следовательно,
Процесс дифференцирования данной функции можно записать следующим образом:
Производная логарифмической функции
Пусть дана функция
Для ее дифференцирования применим общее правило.
или
Положим
отсюда
Подставив значения и в равенство (1), получим:
или, после потенцирования
Из равенства (2) следует, что, если
4-й шаг.
Множитель не зависит от n поэтому его можно считать постоянным при ; следовательно,
В подробных курсах анализа доказывается теорема: предел логарифма переменной величины равен логарифму предела этой же переменной величины; поэтому
Но, согласно,
Равенство (4) будет иметь вид
Следовательно,
т. е. производная натурального логарифма равна единице, деленной на аргумент.
Если дан десятичный логарифм, то его нужно предварительно выразить через натуральный. Мы знаем, что
Дифференцируя обе части последнего равенства, получим:
или
т. е. производная десятинного логарифма равна произведению производной натурального логарифма на постоянный множитель 0,4343.
Пример:
Продифференцировать функцию
Решение:
Данная функция сложная; положим
тогда
Отсюда согласно формуле (5) имеем:
Производную сложной логарифмической функции *) можно найти и по следующему правилу:
для дифференцирования сложной логарифмической функции нужно сначала взять производную от логарифма по выражению, стоящему под знаком логарифма (принимая его за аргумент), а потом от выражения, стоящего под знаком логарифма, по независимой переменной и результаты перемножить;
*) То-есть логарифмической функции сложного аргумента.
поэтому, считая и функцией х получаем:
Пример:
Продифференцировать функцию
Решение:
Согласно правилу (5) найдем:
Но cos ( 1—х) — сложная тригонометрическая функция; применяя к ней правило (2) , получим:
или
Пример:
Продифференцировать функцию
Решение:
Преобразуем сначала данную функцию, применив правила логарифмирования корня и дроби:
Продифференцировав полученную функцию [ln х по правилу (XIV), а ln (1 + x) по правилу (5)], найдем:
Производная степени при любом показателе
Мы вывели формулу
для m целого положительного. Докажем теперь справедливость этой формулы для любого показателя. Положим, что в равенстве
m имеет любое постоянное значение; логарифмируя это равенство по основанию е, получим:
Приняв во внимание, что ln у — сложная функция ( ln у зависит от у, а у зависит от x), дифференцируем обе части равенства (1) по х:
отсюда
Следовательно,
Производная показательной функции
Дана показательная функция
Прологарифмировав равенство (1) по основанию е, получим:
Дифференцируем это равенство по х, считая )ln у сложной функцией:
отсюда
Следовательно,
т.
Если дана показательная функция
где е — основание натурального логарифма, то производная ее найдется по формуле (XVI):
или
т. е. производная показательной функции равна самой функции.
Пример:
Продифференцировать функцию
Решение:
Заменив данную сложную функцию двумя простыми, получим:
Согласно формуле (5) имеем:
Данную функцию можно дифференцировать и по следующему правилу:
для дифференцирования сложной показательной функции *) нужно сначала взять производную от показательной функции по выражению, стоящему в показателе (считая его аргументом), а потом от выражения, стоящего в показателе, по независимой переменной и результаты перемножить;
*) То-есть показательной функции сложного аргумента.
поэтому, считая и функцией от х, получаем:
Пример:
Продифференцировать функцию
Решение:
По правилу (3) настоящей лекции
Но согласно правилу (3)
Следовательно,
Производные обратных тригонометрических функций
1.
В силу определения арксинуса получаем:
Здесь sin у представляет сложную функцию (sin y зависит от у, а у зависит от х; дифференцируя обе части этого равенства по х, напишем):
или
откуда
Приняв во внимание, что
*) Здесь радикал берется с плюсом, так как значения arcsin х заключены между и , а в этом промежутке cos у имеет положительные значения.
а также равенство (1), получим:
или
2.
Согласно определению арккосинуса имеем:
Дифференцируя обе части этого равенства по x, считая cos у сложной функцией, найдем:
или
отсюда
Но
**) И здесь радикал берется с плюсом, так как значения arccos х заключены между 0 и ; в этом же промежутке sin у имеет положительные значения.
поэтому
или
*) Здесь радикал берется с плюсом, так как значения arcsin х
К .
заключены между — у и +у,ав этом промежутке cos у имеет
положительные значения.
**) И здесь радикал берется с плюсом, так как значения arccos х заключены между 0 и я; в этом же промежутке sin у имеет положительные значения.
3.
Согласно определению арктангенса имеем:
Дифференцируя обе части этого равенства по х, как и в предыдущих случаях, получим:
или
отсюда
Но
Приняв во внимание равенство (2), получим:
Следовательно,
4.
Для данной функции имеем:
После дифференцирования этого равенства получим:
или
отсюда
Но
Следовательно,
т. е.
Пример:
Продифференцировать функцию
Решение:
Заменим данную сложную функцию двумя простыми:
Согласно формуле (5) имеем:
Для дифференцирования этой функции можно воспользоваться и следующим правилом:
для дифференцирования сложной обратной тригонометрической функции*) нужно сначала взять производную от обратной тригонометрической функции по выражению, стоящему под ее знаком (принимая его за аргумент), а потом от этого же выражения по независимой переменной и результаты перемножить;
*) То-есть обратной тригонометрической функции сложного аргумента.
таким образом, считая и функцией от х, получаем:
Пример:
Продифференцировать функцию .
Решение:
Данная функция — обратная тригонометрическая и притом сложная; применяя вышеуказанное правило для производной аrсsin u, найдем:
Но тоже сложная функция; согласно правилу (7) имеем:
Следовательно,
Производная неявной функции
Пусть неявная функция у задана уравнением
Найдем производную у’, полагая, что она существует. Для этого дифференцируем обе части уравнения (1), применяя правило для производной алгебраической суммы, получим:
Так как ху — произведение переменных величин, то:
Таким образом, равенство (2) примет вид
или
Решая последнее уравнение относительно у’, найдем
Для дифференцирования данной функции можно было бы сначала выразить у через х, а потом уже найти производную от явной функции.
откуда
По внешнему виду этот результат отличается от найденного ранее, но если мы в равенстве (3) подставим значение у, то получим:
Таким образом, результаты дифференцирования в обоих случаях оказались одинаковыми. Однако переход от неявной к явной функции можно делать только в простейших случаях. Встречаются неявные функции, которые обратить в явные очень трудно и даже невозможно. Например, функцию у, заданную уравнением
ху + х = sin у, явно выразить нельзя. Поэтому приходится дифференцировать такие функции как неявные.
Разберем другой пример. Пусть требуется найти производную неявной функции у, заданной уравнением
Применяя правило дифференцирования алгебраической суммы, имеем:
Но сложная функция ( зависит от у, а у зависит от х). По правилу дифференцирования сложной степенной функции имеем:
Следовательно, равенство (4) примет вид
или
откуда
Производная второго порядка
Пусть функция у = f(x) имеет производную у’ = f'(x).
Вторую производную функции у = f(x) принято обозначать так:
Пример:
Найти вторую производную функции
Решение:
Механический смысл второй производной
Пусть тело движется прямолинейно по закону
Мы установили, что скорость v движения тела в данный момент t определяется как производная пути по времени, т. е.
Если тело движется неравномерно, то скорость v с течением времени изменяется и за промежуток времени ät получает приращение . В этом случае величина отношения показывающая изменение скорости в единицу времени, называется средним ускорением в промежутке времени от t до t + .
Положим, что , тогда среднее ускорение
стремится к величине, которая называется ускорением в данный момент времени t.
Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента.
Пример:
Точка движется прямолинейно по закону
Найти скорость и ускорение точки в момент t = 5.
Решение:
Для определения скорости нужно найти первую производную данной функции при t = 5. Таким образом:
и
Ускорение j равно второй производной функции при t = 5, т. е.
Величина ускорения оказалась постоянной для любого значения t, значит, движение точки по заданному закону происходит с постоянным ускорением.
Дополнение к формулам дифференцирования
Смотрите также:
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Производная частного двух функций (производная дроби).
|
Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника |
⇐ ПредыдущаяСтр 5 из 89Следующая ⇒
Докажем правило дифференцирования частного двух функций (дроби) . По определению производной Пример. Выполнить дифференцирование функции . Решение. Исходная функция представляет собой отношение двух выражений sinx и 2x+1. Применим правило дифференцирования дроби: Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной: В заключении, давайте соберем все правила в одном примере. Пример. Найти производную функции , где a – положительное действительное число. Решение. А теперь по порядку. Первое слагаемое . Второе слагаемое Третье слагаемое Собираем все вместе: 4.Вопрос.Производные Основных элементарных функций. Задание. Найти производную функции Решение. Используем правила дифференцирования и таблицу производных: Ответ. 5.Вопрос.Производная сложной функции примеры Все примеры этого раздела опираются на таблицу производных и теорему о производной сложной функции, формулировка которой такова: Пусть 1) функция u=φ(x) имеет в некоторой точке x0 производную u′x=φ′(x0), 2) функция y=f(u) имеет в соответствующей точке u0=φ(x0) производную y′u=f′(u). Тогда сложная функция y=f(φ(x)) в упомянутой точке также будет иметь производную, равную произведению производных функций f(u) и φ(x): (f(φ(x)))′=f′u(φ(x0))⋅φ′(x0) или, в более короткой записи: y′x=y′u⋅u′x. В примерах этого раздела все функции имеют вид y=f(x) (т.е. рассматриваем лишь функции одной переменной x). В примерах №1, №2 и №3 изложен подробный процесс нахождения производной сложных функций. Пример №4 предназначен для более полного понимания таблицы производных и с ним имеет смысл ознакомиться. Желательно после изучения материала в примерах №1-3 перейти к самостоятельному решению примеров №5, №6 и №7. Примеры №5, №6 и №7 содержат краткое решение, чтобы читатель мог проверить правильность своего результата. Пример №1 Найти производную функции y=ecosx. Решение Нам нужно найти производную сложной функции y′. Так как y=ecosx, то y′=(ecosx)′. Чтобы найти производную (ecosx)′ используем формулу №6 из таблицы производных. Дабы использовать формулу №6 нужно учесть, что в нашем случае u=cosx. Дальнейшее решение состоит в банальной подстановке в формулу №6 выражения cosx вместо u: Итак, y′=(ecosx)′=ecosx⋅(cosx)′(1. Теперь нужно найти значение выражения (cosx)′. Вновь обращаемся к таблице производных, выбирая из неё формулу №10. Подставляя u=x в формулу №10, имеем: (cosx)′=−sinx⋅x′. Теперь продолжим равенство (1.1), дополнив его найденным результатом: y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)(1.2) Так как x′=1, то продолжим равенство (1.2): y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)=ecosx⋅(−sinx⋅1)=−sinx⋅ecosx(1.3) Итак, из равенства (1.3) имеем: y′=−sinx⋅ecosx. Естественно, что пояснения и промежуточные равенства обычно пропускают, записывая нахождение производной в одну строку, – как в равенстве (1.3). Итак, производная сложной функции найдена, осталось лишь записать ответ. Ответ: y′=−sinx⋅ecosx. Пример №2 Найти производную функции y=9⋅arctg12(4⋅lnx). Решение Нам необходимо вычислить производную y′=(9⋅arctg12(4⋅lnx))′. Для начала отметим, что константу (т. y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′(2.1) Теперь обратимся к выражению (arctg12(4⋅lnx))′. Чтобы выбрать нужную формулу из таблицы производных было легче, я представлю рассматриваемое выражение в таком виде: ((arctg(4⋅lnx))12)′. Теперь видно, что необходимо использовать формулу №2, т.е. (uα)′=α⋅uα−1⋅u′. В эту формулу подставим u=arctg(4⋅lnx) и α=12: Дополняя равенство (2.1) полученным результатом, имеем: y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′(2.2) Примечание: показатьскрыть Теперь нужно найти (arctg(4⋅lnx))′. Используем формулу №19 таблицы производных, подставив в неё u=4⋅lnx: (arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′ Немного упростим полученное выражение, учитывая (4⋅lnx)2=42⋅(lnx)2=16⋅ln2x. (arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′=11+16⋅ln2x⋅(4⋅lnx)′ Равенство (2. y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′(2.3) Осталось найти (4⋅lnx)′. Вынесем константу (т.е. 4) за знак производной: (4⋅lnx)′=4⋅(lnx)′. Для того, чтобы найти (lnx)′ используем формулу №8, подставив в нее u=x: (lnx)′=1x⋅x′. Так как x′=1, то (lnx)′=1x⋅x′=1x⋅1=1x. Подставив полученный результат в формулу (2.3), получим: y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′==108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅4⋅1x=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x). Напомню, что производная сложной функции чаще всего находится в одну строку, – как записано в последнем равенстве. Поэтому при оформлении типовых расчетов или контрольных работ вовсе не обязательно расписывать решение столь же подробно. Ответ: y′=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x). Пример №3 Найти y′ функции y=sin3(5⋅9x)−−−−−−−−−√7. Решение Для начала немного преобразим функцию y, выразив радикал (корень) в виде степени: y=sin3(5⋅9x)−−−−−−−−−√7=(sin(5⋅9x))37. Теперь приступим к нахождению производной. Так как y=(sin(5⋅9x))37, то: y′=((sin(5⋅9x))37)′(3.1) Используем формулу №2 из таблицы производных, подставив в неё u=sin(5⋅9x) и α=37: ((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))37−1(sin(5⋅9x))′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′ Продолжим равенство (3.1), используя полученный результат: y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′(3.2) Теперь нужно найти (sin(5⋅9x))′. Используем для этого формулу №9 из таблицы производных, подставив в неё u=5⋅9x: (sin(5⋅9x))′=cos(5⋅9x)⋅(5⋅9x)′ Дополнив равенство (3.2) полученным результатом, имеем: y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′(3.3) Осталось найти (5⋅9x)′. Для начала вынесем константу (число 5) за знак производной, т. y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′=37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅5⋅9x⋅ln9==15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x. Можно вновь от степеней вернуться к радикалам (т.е. корням), записав (sin(5⋅9x))−47 в виде 1(sin(5⋅9x))47=1sin4(5⋅9x)−−−−−−−−−√7. Тогда производная будет записана в такой форме: y′=15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7. Ответ: y′=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7. Пример №4 Показать, что формулы №3 и №4 таблицы производных есть частный случай формулы №2 этой таблицы. Решение В формуле №2 таблицы производных записана производная функции uα. (u−1)′=−1⋅u−1−1⋅u′=−u−2⋅u′(4.1) Так как u−1=1u и u−2=1u2, то равенство (4.1) можно переписать так: (1u)′=−1u2⋅u′. Это и есть формула №3 таблицы производных. Вновь обратимся к формуле №2 таблицы производных. Подставим в неё α=12: (u12)′=12⋅u12−1⋅u′=12u−12⋅u′(4.2) Так как u12=u−−√ и u−12=1u12=1u−−√, то равенство (4.2) можно переписать в таком виде: (u−−√)′=12⋅1u−−√⋅u′=12u−−√⋅u′ Полученное равенство (u−−√)′=12u−−√⋅u′ и есть формула №4 таблицы производных. Как видите, формулы №3 и №4 таблицы производных получаются из формулы №2 подстановкой соответствующего значения α. Пример №5 Найти y′, если y=arcsin2x. Решение Нахождение производной сложной функции в данном примере запишем без подробных пояснений, которые были даны в предыдущих задачах. Ответ: y′=2xln21−22x−−−−−−√. Пример №6 Найти y′, если y=7⋅lnsin3x. Решение Как и в предыдущем примере, нахождение производной сложной функции укажем без подробностей. Желательно записать производную самостоятельно, лишь сверяясь с указанным ниже решением. Ответ: y′=21⋅ctgx. Пример №7 Найти y′, если y=9tg4(log5(2⋅cosx)). Решение 6 Вопрос. Производная обратной функции примеры. Производная обратной функции Формула Известно свойство степеней, что тогда Используя производную степенной функции: будем иметь: Доверь свою работу ✍️ кандидату наук! Имя Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности ⇐ Предыдущая12345678910111213141516Следующая ⇒ Поиск по сайту: |
2 = 8 $ описывает «наклонный» эллипс (см.
Заметим, что $ (10x + 6y) + (6x + 10y)·frac{dy}{dx} = 0 $ можно рассматривать как линейное уравнение с $ frac{dy}{dx} $ как «неизвестное». Итак, если вам даны координаты точки на эллипсе, вы можете вставить их в уравнение и найти $\frac{dy}{dx}$ напрямую. (На самом деле вам нужно написать выражение $ frac{-10x-6y}{6x+10y} $, только если домашнее задание или экзаменационная задача требуют этого.) Если вам 9 лет0007, учитывая наклон касательной линии и запрашивая точки, в которых происходит этот наклон, вы можете вставить это значение для $ frac{dy}{dx} $ в то же уравнение, чтобы получить уравнение для линии, которая пересекает эллипс в этих точках.
[Обратите внимание, что точки касания по горизонтали и вертикали расположены симметрично относительно линии $ y = -x ; $ это потому, что большая ось эллипса лежит на этой линии.
Также, как и следовало ожидать, соотношения $ frac{dy}{dx} = -frac{10x+6y}{6x+10y} $ и $ frac{dx}{dy } = -frac{6x+10y}{10x+6y} $ обратны друг другу.
Чтобы вернуться к предыдущей точке, вертикальные точки касания «делят» эллипс на две части, которые являются кривыми неявной функции $ x . $ Мы можем получить их, применив квадратичную формулу к уравнению эллипса: 92} . $
Дробное дифференцирование – обзор
ScienceDirect
РегистрацияВход
Подробно обсуждается концепция дробного дифференцирования и интегрирования, предложенная Капуто и Фабрицио.
Из: Дробные операторы с постоянным и переменным порядком с приложением к геогидрологии, 2018 г.
PlusAdd to Mendeley
Абдон Атангана, Седа Игрет Араз, в новой числовой схеме с многочленом Ньютона, 2021 г.
Abstract
Дробное дифференцирование и интегрирование с обобщенным ядром Миттаг-Леффлера были предложены в 2016 году и привлекли внимание многих исследователей из всех научных областей. Было признано, что эти дифференциальные и интегральные операторы обладают многими свойствами, наблюдаемыми в задачах реального мира, например, перекрестным поведением. Обыкновенные дифференциальные уравнения с этими производными очень сложны для аналитического решения, поэтому численные схемы являются адекватными инструментами для решения этих уравнений. Были предложены некоторые числовые схемы с некоторыми преимуществами и недостатками. В этой главе мы используем двухшаговый многочлен Ньютона для получения численной схемы, которая будет использоваться также для решения дифференциальных и интегральных уравнений с дробными производными Атанганы-Балеану.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780323854481000135
Abdon Atangana, в приложении к операторам Geo с постоянными и дробными порядками -Гидрология, 2018
Реферат
В этой главе представлены различные виды дробного дифференцирования и интегрирования. Он начинается с краткого генезиса концепции дробного исчисления, затем представляет концепцию дробного дифференцирования со степенным ядром, известным как производные Римана-Лиувилля и Капуто с дробным порядком, и их свойства. Таким образом, понятие локальной производной дробного порядка представлено с его различными свойствами. Подробно обсуждается концепция дробного дифференцирования и интегрирования, введенная Капуто и Фабрицио. Дробные дифференциальные операторы с ядром Миттаг-Леффлера, введенные Атанганой и Балеану, анализируются вместе с их соответствующими свойствами.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780128096703000059
Abdon Atangana, в приложении к операторам Geo с постоянными и дробными порядками -Hydrology, 2018
8.4 Ограничение дробной производной для модели загрязнения подземных вод
Хотя концепции дробной дифференциации и интегрирования кажутся лучшими математическими инструментами для описания движения потока подземных вод внутри геологической формации, называемой водоносным горизонтом, обратите внимание, что эта концепция имеет свои ограничения. Сообщим, что полевые и численные эксперименты по транспорту растворенных веществ через неоднородные пористые и трещинные водоносные горизонты показывают, что движение шлейфов загрязняющих веществ может не иметь постоянного масштабирования; тем не менее, вместо этого переходные диффузионные состояния, то есть, демонстрируют сложную диффузию, такую как супердиффузия, субдиффузия и фиковская диффузия, которые происходят в нескольких транспортных масштабах.


Просмотреть книгу Глава покупки
Читать полная глава
URL: https://www.sciendirect.com/science/article/pii/b9780128096703000084
в математике в науке и инженерном. Линейность
Подобно дифференцированию целого порядка, дробное дифференцирование является линейной операцией:
(2.
где D p обозначает любую мутацию дробного дифференцирования, рассматриваемую в этой книге.
Линейность дробного дифференцирования непосредственно следует из соответствующего определения. Например, для дробных производных Грюнвальда–Летникова, определяемых формулой (2.43), имеем:
0Dtp(λf(t)+μg(t))=lim h→0nh=t−ah−p∑r=0n(−1)r(pr)(λf(t−rh)+μg(t−rh )) = ΛLim H → 0NH = T -AH -P∑R = 0N (−1) r (pr) f (t -rh)+мклм H → 0nh = t -a -p∑r = 0n (−1) r (pr) g (t -rh) = λAdtpf (t)+µAdtpg (t).
Аналогично, для дробных производных Римана–Лиувилля 9-го порядка0007 p ( k −1 ≤ p < k ), определяемое формулой (2.103), имеем
0Dtp(λf(t)+µg(t))=1Γ(k−p)dkdtk∫at(t−τ)k−p−1(λf(τ)+µg(τ))dτ=λΓ(k −p)dkdtk∫at(t−τ)k−p−1f(τ)dτ+µΓ(k−p)dkdtk∫at(t−τ)k−p−1g(τ)dτ=λaDtpf(t)+ μaDtpg(t).
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.
-Гидрология, 2018
7.5.2 Единственность решения
Однако нам нужно показать, что решение единственно. Пусть h и h2 — два возможных решения нашей начальной краевой задачи. Затем, используя уравнение (7.66) будем иметь
(7.68)h(r,t)−h′(r,t)=2(1−α)(2−α)M(α)[K(r,t,h )−K(k,t,h′)]+2α(2−α)M(α)∫0t[K(k,t,h)−K(k,t,h′)]ds.
Применяя норму к обеим сторонам, имеем
‖h(r,t)−h′(r,t)‖=‖2(1−α)(2−α)M(α)[K(r ,t,h)−K(r,t,h′)]+2α(2−α)M(α)∫0t[K(r,t,h)−K(r,t,h′)]ds ‖⩽2(1−α)(2−α)M(α)‖K(r,t,h)−K(r,t,h′)‖+2α(2−α)M(α)∫0t ‖K(r,t,h)−K(r,t,h′)‖dс использованием условия Липшица оператора kernelundefinedK⩽2(1−α)L(2−α)M(α)‖h−h′ ‖+2αL(2−α)M(α)∫0t‖h−h′‖ds
Тогда имеем
(7.69)‖h(r,t)−h′(r,t)‖⩽(2(1−α)L(2−α)M(α)+2αL(2−α )M(α))‖h(r,t)−h′(r,t)‖.
Отсюда следует, что ′(r,t)‖⩽0.
Если предположить, что
(1−2(1−α)L(2−α)M(α)+2αL(2−α)M(α))≠0,
, то
‖h(r ,t)−h′(r,t)‖=0.
Отсюда следует, что
h(r,t)=h′(r,t).
Делаем вывод, что решение единственное.
Здесь мы представляем численное решение уравнения. (7.62). Для этого представление первого приближения локальной производной и производных Капуто–Фабрицио показано вместе со вторым приближением.
(7.71)∂S∂x=12[(si+1n+1−si−1n+1)−(si+1n−si−1n)2(Δx)]
(7.72)∫0t∂s∂ zexp(−α1−α(t−z))dz=12∑k=0n(sik+1−sik)di,n,k1
(7.73)di,n,k1=exp(−kα1−α (n−j+1))−exp(−kα1−α(n−j)).
Кроме того,
(7,74)∫0t∂s∂zexp(−α1−α(t−z))dz=12∑k=0n(sik+1−sik)di,n,k2
(7,75 )di,n,k2=exp(−kD(n−j+1))−exp(−kD(n−j)).
Тогда со вторым приближением для локальной производной имеем следующее si−1n)2(∆x)2.
Таким образом, составляя уравнения. (7.76), (7.74), (7.72) и (7.71) в уравнение. (7.62) дает:
(7.77)T((si+1n+1−2sin+1+si−1n+1)+(si+1n−2sin+si−1n)2(∆x)2+1ri(12 [(si+1n+1−si−1n+1)−(si+1n−si−1n)2(∆x)]))=S(12∑k=0n(sik+1−sik)di,n, k1)+DSy(12∑k=0n(sik+1−sik)di,n,k2)
Переставляя, получаем следующее:
(7.
(7,79)=(T(∆x)2−Sdi,n,n12−DSydi,n,n22)sin−−1ri(12[(si+1n+1−si −1n+1)−(si+1n−si−1n)2(∆x)])+S(12∑k=0n(βik)di,n,k1)+DSy(12∑k=0n−1(βik )di,n,k2)βik=sik+1−sik.
Приведенную выше рекурсивную формулу можно использовать для численного решения уравнения подземных вод для безнапорного водоносного горизонта с дробной производной Капуто–Фабрицио.
Подземные воды, протекающие в безнапорном водоносном горизонте с дробной производной Атангана-Балеану
В этом разделе поток подземных вод в безнапорном водоносном горизонте рассматривается с использованием вновь установленной дробной дифференциации, основанной на нелокальном и несингулярном ядре. Эта модификация мотивирована тем, что не все природные явления могут быть смоделированы с использованием концепции степенного закона, которая является основным предположением при использовании Капуто и производной Римана–Лиувилля с дробным порядком. Поэтому в этом разделе ядро, основанное на степени x−α, будет заменено обобщенной функцией Миттаг–Леффлера.
(7.80)T(∂2s∂r2+∂sr∂r)=S(Dtα0ABC(s))+DSy∫0t∂s∂zexp(−D(t−z))dz,
, где производная по времени заменяется производной Атанганы-Балеану в смысле Капуто. Анализ будет состоять из представления сначала о существовании единственного решения с использованием некоторой теоремы о неподвижной точке, а затем с последующим выводом приближенного решения с использованием некоторого рекурсивного метода.
(7.81)αAB(α)Γ(α)∫0t(t−y)1−α(T(∂2s∂r2+∂sr∂r)−DSy∫0t∂s∂zexp (−D(t−z))dz)dy
(7.82)+1−αAB(α)(T(∂2s∂r2∂sr∂r)−DSy∫0t∂s∂zexp(−D(t−z))dz)=Ss(r,t )−Ss(r,0).
Для простоты рассмотрим следующее отображение ))дз.
Просмотр книги Глава Чита
Читать полная глава
URL: https://www.sciendirect.com/science/article/pii/b9780128096703000072
в математике в науке и инженерном. коэффициенты
Для реализации метода дробных разностей вычисления дробных производных необходимо вычислить коэффициенты
(7.22)wk(α)=(−1)k(αk),undefinedk=0,1,2,….
, где α — порядок дробного дифференцирования.
Одним из возможных подходов является использование рекуррентных соотношений
(7.23)w0(α)=1;undefinedwk(α)=(1−α+1k)wk−1(α),undefinedk=1,2,3,…
Этот подход подходит для фиксированного значения α.
Однако в некоторых задачах (например, при идентификации системы) необходимо найти наиболее подходящее значение α; это означает, что рассматриваются различные значения α, и для каждого конкретного значения α коэффициенты
wk(α) необходимо вычислять отдельно. В таком случае рекуррентные соотношения (7.23) не очень подходят. Вместо этого можно использовать метод быстрого преобразования Фурье [105].
Коэффициенты
wk(α) можно рассматривать как коэффициенты степенного ряда для функции (1 − z ) α :
(7.24)(1−z)α=∑k=0∞(−1)k(αk)zk=∑k=0∞wk(α)zk.
Замена
z=e−iφ имеем
(7.25)(1−e−iφ)α=∑k=0∞wk(α)e−ikφ,
и коэффициенты
wk(α) выражаются через преобразование Фурье:
(7.26)wk(α)=12πi∫02πfα(φ)eikφdφ, undefinedfα(φ)=(1−e−iφ)α.
Технически коэффициенты
wk(α) можно вычислить с помощью любой реализации быстрого преобразования Фурье.
wk(α) метод быстрого преобразования Фурье всегда следует сочетать с принципом «короткой памяти» (см. раздел 7.3).
Просмотр книги Глава Чита
Читать полная глава
URL: https://www.sciencerect.com/science/article/pii/s00765300265
в математике в науке и технике, 1999 3 9 3
. Теорема единственности как метод решения
В некоторых случаях. Теорему 3.4 можно использовать непосредственно как метод решения дифференциальных уравнений дробного порядка. Мы проиллюстрируем это ниже на двух примерах.
Пример 3.1
Рассмотрим начальную задачу в терминах последовательных дробных производных (обозначения те же, что и в теореме 3.4):
(3.33)0Dtσny(t)=λy(t)
(3.34)[0Dtσk−1y(t)]t=0=bk, k=1,….,n.
В этом случае мы имеем f ( t, y ) = λ y .
(3.35)y0(t)=∑i=1nbitσi−1Γ(σi),
(3.36)ym(t)=y0(t)+λΓ(σi)∫0t(t−τ)σn−1ym− 1 (τ) dτ = y0 (t)+λ0dt — σnym — 1 (t), m = 1,2,3,….
Используя (3.35) и (3.36) и применяя формулу дробного дифференцирования степенной функции (2.117), получаем:
y1(t)=y0(t)+λ 0Dt−σn{∑i=1nbitσi−1Γ(σi)}=y0(t)+λ∑i=1nbitσn+σi−1Γ(σn+σi),y2( t)=y0(t)+λ 0Dt−σny1(t)=y0(t)+λ 0Dt−σn{y0(t)+λ∑i=1nbitσn+σi−1Γ(σn+σi)}=y0(t )+λ∑i=1nbitσn+σi−1Γ(σn+σi)+λ2∑i=1nbit2σn+σi−1Γ(2σn+σi)=∑i=1nbi∑k=02λktkσn+σi−1Γ(kσn+σi),
и по индукции можно показать, что
(3.37)ym(t)=∑i=1nbi∑k=0mλktkσn+σi−1Γ(kσn+σi), m=1,2,3,….
Принимая предел (3.37) в виде м → ∞, получаем решение задачи (3.33) (3.34):
(3.38)y(t)=∑i=1nbi∑k=0∞λktkσn+σi−1Γ(kσn+σi)=∑i=1nbitσi−1Eσn,σi(λtσn),
, где E α ,β ( z ) — функция Миттаг-Леффлера (см.
Если n = 1 и α 1 = 1, то начальная задача (3.33)–(3.34) принимает вид
(3.39)y′(t)=λy(t), y(0)=b1,
и с учетом соотношения (1.57) формула (3.38) дает классическое решение задачи ( 3.39):
y(t)=b1E1,1(λt)=eλt.
Пример 3.2
[4] Рассмотрим следующую начальную задачу в терминах дробных производных Римана–Лиувилля:
(3.40)0Dtαy(t)=tαy(t), [0Dtα−1y(t)]t=0=b,
где 0 < α < 1.
В данном случае f ( т, у ) = т α у . В соответствии с доказательством теоремы 3.4 возьмем
(3.41)y0(t)=btα−1Γ(α),
(3.42)ym(t)=btα−1Γ(α)+1Γ(α)∫0t(t−τ)α−1ταym−1 (τ)dτm=1,2,3….
Используя (3.35) и (3.36) и применяя формулу дробного дифференцирования степенной функции (2.
ym(t)=btα−1Γ(α)+b∑k=1mΓ(2α)Γ(4α)….Γ(2kα)Γ(α)Γ(3α)….Γ(2kα+α)tα( 2k+1)−1,m=1,2,3….
и принятие предела м → ∞ дает решение:
(3.43)y(t)=btα−1Γ(α)+b∑k=1∞Πj=1kΓ(2jα)Πj=1kΓ(2jα+α)tα(2k+1)−1.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/S00765300228
-Гидрология, 2018
12.2 Моделирование с помощью переменных Капуто Порядок
Доказано, что концепция переменного порядка с дифференциацией является очень мощным математическим инструментом для моделирования анонимных диффузионных процессов благодаря их способности включать в математическую модель эффект неоднородности геологической формации, по которой перемещается загрязнение. Для очень сложной системы было показано, что использование концепции дробного дифференцирования с постоянным дробным порядком нельзя применять только при однородной неоднородности.

(12.1)D∂2C∂x2−v∂C∂x−λRC=R∂C∂t+f(x,t),
при начальных и граничных условиях:
(12.2)C(x ,0)=0,undefinedC(0,t)=c0exp(−αt),undefinedCx(∞,t)=0.
Для данного уравнения параметр D – коэффициент дисперсии, V – скорость миграции загрязнения в пределах геологической формации, R – замедление, обусловленное свойствами матричной почвы, λ приходится на константу радиоактивного распада, c0 считается начальным входом концентрации, α — положительная константа, и, наконец, f(x,t) — любой источник и сток в системе. С другой стороны, для модели движения загрязнений подземных вод пренебрегается f(x,t), так как предполагается, что в исследуемой системе отсутствует стоковая функция. Следовательно, в этом разделе также пренебрегается функцией стока. Имея в виду, что неоднородность геологической формации может быть включена в математическую формулировку с использованием концепции дифференциации переменного порядка, в этом разделе классическая дифференциация адвективной модели будет заменена дифференциацией переменного порядка в смысле Капуто.
(12.3)f(x,t)+D∂2C∂x2−v∂C∂x−λRC=RD0α(t,x)C,
при начальных и граничных условиях:
(12.4)C (x,0)=0,не определеноC(0,t)=c0exp(−γt),не определеноCx(∞,t)=0.
В этом уравнении также α(t,x) является непрерывной функцией в (0,1), которую можно измерить по фактам полевых наблюдений. В этой новой модели или модифицированной модели аналитическое решение было введено только в [187]; также здесь представлено существование точного решения.0003
Read full chapter
URL: https://www.sciencedirect.com/science/article/pii/B9780128096703000126
In Mathematics in Science and Engineering, 1999
10.8 Fractional Multipoles
Recently N. Энгета [60] предложил определение мультиполей дробного порядка плотности электрического заряда. Понятие мультиполей дробного порядка служит интерполяцией между случаями точечных мультиполей целого порядка, таких как точечные монополи, точечные диполи, точечные квадруполи и т.
Поскольку термины монополь, диполь, квадруполь, и т. д. связаны со степенью двойки (а именно, 2 0 , 2 1 , 2 2 и т. д.), мультиполи дробного порядка называется 2 α -полюса.
В трехмерном случае Н. Энгета обнаружил, что потенциальная функция точечного мультиполя с полюсом 2 α вдоль оси z , 0 < α < 1, может быть выражена через уравнение Римана-Лиувилля дробная производная с нижним выводом т = -∞:
(10.92)Φ2α,z(x,y,z)=qlα4π∈ −∞Dtα(1×2+y2+z2),
, где q – так называемый электрический монопольный момент, а ∈ – известный физический постоянная (диэлектрическая проницаемость однородного изотропного пространства).
Постоянная, которая принимается в виде л α, , где л имеет размерность длины, вводится для получения традиционной размерности результирующей объемной плотности заряда как Кулон/м 3 .
Оценка дробной производной (10.92) дает [60]
где P α ( z ) — функция Лежандра первого рода нецелой степени α [63].
Очевидно, что электростатический потенциал действует на монополь,
Φ1(x,y,z)=q4π∈1×2+y2+z2,
и для диполя
Φ2(x,y,z)=q4π∈cosθx2+y2+z2, cosθ=zx2+y2+z2,
являются частными случаями функции
Φ2α,z(x,y,z) при α = 0 и α = 1.
В этом примере применения дробного исчисления интересно, что рассматривается статический объект, а дробная производная с нижней конечной t = −∞ применяется по отношению к пространственной переменной.
В другой статье [61] Н. Энгета приводит примеры структур, содержащих клинья и конусы, потенциалы которых можно описать как электростатические потенциалы наборов распределений заряда, которые ведут себя как мультиполи дробного порядка.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/S00765300290
L. Zheng, X. Zhang, in Modeling and Analysis of Modern Fluiding Проблемы, 2017
7.6.1 Основное уравнение
Определяющие уравнения несжимаемого обобщенного Олдройда-Б: μ(1+θDβDtβ)A1,
, где T denotes the Cauchy stress tensor, − p I is the indeterminate spherical stress, S is the extra-stress tensor, A 1 = L + L T is первый тензор Ривлина–Эриксена с градиентом скорости L = град V , μ динамическая вязкость жидкости, λ и θ – времена релаксации и торможения, α 7
08 и
β параметры дробного исчисления такие, что 0 ≤ α ≤ β ≤ 1, и
(7.
DtβA1+(V·∇)A1−LA1-A1LT,
, в котором Dtα и Dtβ — операторы дробного дифференцирования порядка α и β на основе определения Римана–Лиувилля, определяется как (Miller and Ross, 1993; Samko и др., 1993):
(7,165)Dtp[f(t)]=1Γ(1−p)ddt∫0tf(τ)(t−τ)pdτ,0≤p≤1.
Γ(·) обозначает гамма-функцию. Эта модель сводится к обычной модели Олдройда-Б, когда α = β = 1.
Далее мы определим поле скоростей и дополнительное напряжение вида: y,z,t),0,0),S=S(y,z,t),
где u ( y , z , t ) скорость в x -координатное направление.
Подставляя уравнение (7.166) в (7.162) и с учетом начального условия S ( Y , Z , 0) = 0 (жидкость находится в состоянии покоя до момента T = 0), мы получаем S YY = S YY = S yz = S zz = 0 (Havlin and Ben-Avraham, 2002; Tan and Masuoka, 2005a) и соответствующие уравнения в частных производных: (1+θDtβ)∂yu(y,z,t),
(7.
, в котором τ 1 = S XY и τ 2 = S xz — касательные.
Баланс линейного количества движения в отсутствие объемных сил сводится к (Havlin and Ben-Avraham, 2002): yp=∂zp=0,
, где ρ — постоянная плотность жидкости, а ∂ p /∂ x — градиент давления вдоль x — ось. Исключая τ 1 и τ 2 между уравнениями. (7.167) и (7.168) и предполагая наличие постоянного градиента давления в направлении потока, находим определяющее уравнение в виде:
(7.171)(1+λDtα)∂u(y,z,t)∂t =ν(1+θDtβ)(∂2∂y2+∂2∂z2)u(y,z,t)−1ρ(1+λDtα)∂p∂x,
, в котором ν = μ / ρ – кинематическая вязкость жидкости.
Посмотреть главуКнига покупок
Читать главу 9 полностью0003
URL: https://www.
Частичные дроби
Способ «разбиения» дробей, содержащих многочлены.
Что такое частичные дроби?
Мы можем сделать это напрямую:
Вот так:
2
х-2 + 3
х+1 =
2(х+1) + 3(х−2)
(х-2)(х + 1)
Который можно упростить с помощью Rational Expressions до:
=
2x+2 + 3x−6
x 2 +x−2x−2
=
5x−4
x 2 −x−2
… но как нам двигаться в обратном направлении?
Вот что мы собираемся открыть:
Как найти «части», из которых состоит одна дробь
(« частичных дробей »).
Зачем они нам?
Во-первых… зачем они нам?
Потому что каждая неполная дробь на проще .
Это может помочь решить более сложную дробь.
Разложение на неполные дроби
Итак, позвольте мне показать вам, как это сделать.
Метод называется «Разложение на частичные дроби» и выглядит следующим образом:
Шаг 1: Фактор дна
Шаг 2: Напишите по одной частичной дроби для каждого из этих множителей
Шаг 3: Умножьте на низ, чтобы у нас больше не было дробей
Теперь найдите константы 907 1 и A 2
Замена корней или «нулей» (x−2)(x+1) может помочь:
И у нас есть ответ: 3
3
Это было просто! … почти слишком просто …
… потому что может быть намного сложнее !
Теперь подробно рассмотрим каждый шаг.
Правильные рациональные выражения
Во-первых, это работает только для правильных рациональных выражений, где степень верхней на меньше нижней на .
Степень является наибольшим показателем степени , который имеет переменная.
Если ваше выражение неверно, сначала выполните полиномиальное деление в длину.
Разложение нижнего многочлена на множители
Факторирование нижнего многочлена зависит от вас. См. Факторинг в алгебре.
Но не разлагайте их на комплексные числа… вам может понадобиться остановить некоторые множители на квадратичных (называемых неприводимыми квадратичными числами, потому что любое дальнейшее разложение на множители приводит к комплексным числам):
Пример: (x
2 −4)( x 2 +4)
- x 2 −4 можно разложить на (x−2)(x+2)
- Но х 2 +4 делит на комплексные числа, так что не делайте этого
Таким образом, лучшее, что мы можем сделать, это:
(x−2)(x+2)(x 2 +4)
Таким образом, множители могут быть комбинацией
- 5 множителей.
- неприводимые квадратичные множители
Если у вас есть квадратичный множитель, вам необходимо включить эту частичную дробь:
B 1 x + C 1 (Ваш квадрат)
Факторы с показателями степени
Иногда вы можете получить множитель с показателем степени, например (x−2) 3 …
Вам нужна частичная дробь для каждого показателя степени из 1 вверх.
Like this:
Example:
1 (x−2) 3
Has partial fractions
A 1 x−2 + A 2 (х−2) 2 + А 3
(x — 2) 3
То же самое может также произойти с квадратиками:
Пример:
1 (x 2 +2x +3) 2
. :
B 1 x +C 1 x 2 +2x +3 + B 2 x +C 2 (X 2 9010 +2 +2 +2 9015 +2 9015 +2 9010 +2 9010 +2 9010 +2 (x 903 2
Иногда использование корней не решает проблему
Даже после использования корней (нулей) основания вы можете получить неизвестные константы.
Итак, следующее, что нужно сделать, это:
Собрать все степени х вместе, а затем решить это как систему линейных уравнений.
Боже мой! Это много, чтобы справиться! Итак, пример, который поможет вам понять:
Большой пример, объединяющий все это
Вот хороший большой пример для вас!
x 2 +15 (x+3) 2 (x 2 +3)
- Поскольку (x+3) 2 имеет показатель степени 2, требуется два члена (A 1 и A 2 ).
- And (x 2 +3) является квадратичным, поэтому потребуется Bx + C:
x 2 +15 (x +3) 2 (x 2 +3) = A 1 x +3 + A x +3 + A0315 2 (x +3) 2 + BX +C x 2 +3
Теперь умножьте по (x +3) 2 (x 2 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3 +3.
x 2 +15 = (x+3)(x 2 +3)A 1 + (x 2 +3)A 2 + (x+3) 2 (Bx + C)
На x = −3 стоит ноль (поскольку x+3=0), поэтому попробуем:
(−3) 2 +15 = 0 + ( (−3) 2 +3) A 2 + 0
и упростите его до:
24 = 12A 2
SO 2 = 2
Дайте нам заменить A 2 2:
. Дайте нам заменить A 2 2:
.
x 2 +15 = (x+3)(x 2 +3)A 1 + 2x 2 +6 + (x+3) 2 (Bx + C)
Теперь разверните всего:
x 2 +15 = (x 3 +3x+3x 2 +9)A 1 + 2x 2 +6 + (x 3 9)0105 +6x 2 +9x)B + (x 2 +6x+9)C
Суммировать степени x вместе:
x 2 +15 = x 3 (A 6 +B 1 )+x 2 (3A 1 +6B+C+2)+x(3A 1 +9B+6C)+(9A 1 +6+9C)
Разделить степени и записать как Системы линейных уравнений:
| x 3 : | 0 | = | А 1 +Б | |
| х 2 : | 1 | = | 3А 1 +6В+С+2 | |
| х: | 0 | = | 3А 1 +9В+6С | |
| Константы: | 15 | = | 9А 1 +6+9С |
Упростите и организуйте аккуратно:
| 0 | = | А 1 | + | Б | ||
| −1 | = | 3А 1 | + | 6Б | + | С |
| 0 | = | 3А 1 | + | 9Б | + | 6С |
| 1 | = | А 1 | + | С |
Теперь решите.
Вы можете выбрать свой способ решения этого… Решил для начала вычесть 4-е уравнение из 2-го:
| 0 | = | А 1 | + | Б | ||
| −2 | = | 2А 1 | + | 6Б | ||
| 0 | = | 3А 1 | + | 9Б | + | 6С |
| 1 | = | А 1 | + | С |
Затем вычесть 2 раза 1-е уравнение из 2-го:
| 0 | = | А 1 | + | Б | ||
| −2 | = | 4Б | ||||
| 0 | = | 3А 1 | + | 9Б | + | 6С |
| 1 | = | А 1 | + | С |
Теперь я знаю, что B = −(1/2) .
Мы куда-то движемся!
И из 1-го уравнения я могу вычислить, что A 1 = +(1/2) .
И из 4-го уравнения я могу вычислить, что C = +(1/2) .
Окончательный результат:
| A 1 =1/2 | А 2 =2 | Б=-(1/2) | С=1/2 |
Теперь мы можем записать наши дроби:
х 2 +15
(х+3) 2 (х 2 +3)
знак равно
1
2(х+3)
+
2
(х+3) 2
+
−x + 1
2(х 2 +3)
Фу! Много работы. Но это может быть сделано.
(Примечание: на это у меня ушло почти
час , потому что
Пришлось исправлять
2 глупые ошибки на этом пути!)
Резюме
- Начните с Правильных Рациональных выражений (если нет, сначала выполните деление)
- Разложите нижнюю часть на:
- линейные коэффициенты
- или «неприводимые» квадратичные множители
- Запишите частичную дробь для каждого множителя (и каждого показателя степени каждого)
- Умножить все уравнение на нижнюю часть
- Решите для коэффициентов по
- подставляя нули снизу
- составить систему линейных уравнений (в каждой степени) и решить
- Запиши свой ответ!
Воздействие на миомиР с помощью богатой токотриенолом фракции для стимулирования дифференцировки миобластов | Гены и питание
- Исследования
- Открытый доступ
- Опубликовано: 29 ноября 2018 г.
- Азраул Мумтазах Разак 1 ,
- Шай Циан Хор 1 ,
- Файзул Джаафар 1 ,
- Норвахида Абдул Карим 1 и
- …
- Сюзана Макпол
ORCID: orcid.org/0000-0002-5239-6196 1
Гены и питание
том 13 , номер статьи: 31 (2018)
Процитировать эту статью
-
1886 доступов
-
6 цитирований
-
1 Альтметрика
-
Сведения о показателях
Abstract
Background
Некоторые специфичные для мышц микроРНК (myomiR) по-разному экспрессируются во время клеточного старения.
Результаты
Индекс слияния и площадь поверхности мышечной трубки были выше ( p < 0,05) на 3-й и 5-й дни, чем на 1-й день дифференцировки. Старение снижает скорость дифференцировки, о чем свидетельствует снижение как индекса слияния, так и площади поверхности мышечных трубок в стареющих клетках ( p < 0,05). Лечение TRF значительно увеличивало дифференцировку молодых и стареющих миобластов на 1, 3 и 5 дни. В стареющих миобластах TRF увеличивал экспрессию miR-206 и miR-486 и сниженная экспрессия PTEN и PAX7 .
Вывод
TRF потенциально может способствовать дифференцировке миобластов путем модулирования экспрессии myomiR, которые регулируют экспрессию миогенных генов.
История вопроса
Сателлитные клетки, расположенные между базальной пластинкой и сарколеммой, действуют как жизненно важные компоненты ткани скелетных мышц, поскольку обладают способностью к регенерации. Эти сателлитные клетки находятся в состоянии митотического покоя и останавливаются в фазе G 0 . Эти клетки экспрессируют ограниченное количество генов и белков [1]. В ответ на стресс, такой как повреждение мышц или физиологические изменения, сателлитные клетки активируются и подвергаются миогенезу, который включает ряд процессов [2].
Миогенная программа контролируется различными семействами факторов транскрипции, такими как семейство парных генов box, состоящее из PAX3 и PAX7, и семейство миогенных регуляторов, включающее MYOD1, MYOG, Myf5 и Myf6 [1, 3]. Транскрипционный фактор PAX7 необходим для биогенеза мышечных сателлитных клеток и спецификации линии миогенных предшественников [5]. Функционируя выше семейства MYOD, PAX7 экспрессируется в пролиферирующих миобластах, но быстро подавляется во время дифференцировки.
МикроРНК (миРНК) привлекли огромное внимание и открывают новые возможности для понимания механизма регуляции развития скелетных мышц. miRNAs представляют собой эволюционно консервативные малые РНК, которые были идентифицированы как посттранскрипционные регуляторы для подавления экспрессии генов-мишеней. Подавление экспрессии генов опосредуется связыванием микроРНК с 3′-нетранслируемой областью (UTR) мРНК-мишени [11].

Выяснение участия миомиР во время дифференцировки сателлитных клеток человека дает текущую информацию о возможных взаимодействиях между факторами транскрипции, миомиР и их мРНК-мишенями, особенно при модулировании пищевыми соединениями. Мы предложили витамин Е в качестве многообещающего агента для модуляции экспрессии миомиР. Витамин Е состоит из α-, β-, γ- и δ-токоферола и α-, β-, γ- и δ-токотриенола, которые являются мощными жирорастворимыми антиоксидантами. Было обнаружено, что добавки витамина Е предотвращают повреждение мышц [13]. Однако молекулярный механизм воздействия витамина Е на здоровье мышц остается неясным. Помимо изомера токоферола, смесь токотриенолов, в частности известная как богатая токотриенолом фракция (TRF), которая менее изучена, показывает лучший эффект по сравнению с одиночным изомером токоферола [14]. TRF обычно извлекают из пальмового масла и состоят из α-токоферола и α-, β-, γ- и δ-токотриенола. Сообщается, что он защищает от окислительного повреждения и подавляет выработку активных форм кислорода (АФК) [15].
Материалы и методы
Клеточная культура и серийное пассирование
Система клеток Clonetics® Skeletal Muscle Myoblast Cell System, содержащая нормальные человеческие миобласты скелетных мышц (HSMM; каталожный номер CC-2580, партия 0000257384), полученные из четырехглавой мышцы 17 труп женщины в возрасте 1 года, приобретенный в компании Lonza, США. Клетки поддерживали в ростовой среде, среде для роста скелетных мышц-2 (среда SkGM™-2), которая состояла из базальной среды SkBM™-2.
Индукция дифференцировки
Среду для дифференцировки готовили путем добавления 2% лошадиной сыворотки к среде DMEM-F12. Для индуцирования дифференцировки обе группы клеток высевали при плотности 20 000 клеток/см 9 .
Определение миогенной чистоты
Миогенную чистоту культур контролировали путем определения экспрессии десмина, белка цитоскелета, который экспрессируется только в миогенных клетках, но не в фибробластах. Количество десмин-позитивных клеток, представленное в процентах от общего числа ядер, определяли как миогенную чистоту культуры клеток, и подсчитывали не менее 500 клеток. Иммуноцитохимию проводили с использованием антител, специфичных к десмину, в разведении 1:50 (клон D33; DAKO, Дания). Клетки промывали × 1 фосфатно-солевым буфером (PBS) и фиксировали 100% этанолом в течение 10 мин. Фиксирующий агент удаляли путем трехкратной промывки × 1 PBS в течение 5 мин. Сайты неспецифического связывания блокировали 1% FBS, разведенным в PBS, в течение 30 мин. Затем клетки инкубировали с первичными антителами против десмина. Специфическое связывание антител определяли с помощью Alexa Fluor 488 (Invitrogen, США), непосредственно связанного со вторичным антителом в разведении 1:500. Ядра выявляли флуоресцентно методом Hoechst (Sigma, США) в разведении 0,0001% с / с . Все изображения были оцифрованы с помощью программного обеспечения ImageJ.
Количественное определение площади поверхности миотрубочек и миоядер
Оценивали положительные флуоресцентные области пяти случайно выбранных полей из трех отдельных экспериментов. Для каждой обработки использовали среднюю площадь необработанной группы для расчета процентного увеличения или уменьшения площади мышечных трубочек.
Количественное определение индекса слияния
Для расчета индекса слияния подсчитывали количество ядер, включенных в мышечные трубки (> 2 ядер), и определяли отношение этого числа к общему количеству ядер.
Подготовка и обработка TRF
В этом исследовании использовали Gold Tri E 70 (Sime Darby Bioganic Sdn. Bhd., Малайзия). Этот Gold Tri E 70 состоит из 25% α-токоферола и 75% токотриенола. Кроме того, ВЭЖХ-анализ Gold Tri E 70 показал, что он состоит из 173,6 мг/г α-токоферола, 193,4 мг/г α-токотриенола, 26,2 мг/г β-токотриенола, 227,7 мг/г γ-токотриенола и 98,2 мг/мг δ-токотриенол. Исходный раствор TRF готовили в темноте путем растворения 1 г Gold Tri E 70 (Sime Darby Bioganic Sdn. Bhd., Малайзия) в 1 мл 100% этанола (1:1) и хранили при - 20 °C в течение более 1 месяца. TRF активировали путем инкубации 45 мкл исходного раствора TRF (1 г/1 мл) с 60 мкл FBS в течение ночи при 37 °C. Чтобы приготовить TRF в концентрации 50 мкг/мл, 9К активированному TRF добавляли 0 мкл DMEM с 10% FBS и 105 мкл 100% этанола, после чего добавляли 600 мкл смеси, содержащей FBS и 100% этанол (1:1). Раствор TRF (50 мкг/мл) готовили с использованием культуральной среды. Миобласты обрабатывали 50 мкг/мл TRF в течение 24 ч, а необработанные миобласты инкубировали со средой SKGM-2 (Lonza, США) для анализа пролиферации и со средой DMEM-F12 (Lonza, США) для анализа дифференцировки. Серия титрований доз, проведенная в предыдущем исследовании, показала, что обработка 50 мкг/мл TRF в течение 24 часов приводит к наибольшему проценту жизнеспособных молодых и стареющих миобластов [16]. Кроме того, клетки миобластов, используемые в настоящем исследовании, аналогичны клеткам в нашем предыдущем исследовании [16]. Среду как для необработанных, так и для TRF-клеток меняли одновременно, и обе группы клеток собирали в один и тот же день.
Дизайн праймеров
Прямые праймеры для микроРНК были разработаны в соответствии с последовательностями микроРНК, перечисленными в базе данных miRBase (http://www.mirbase.org). Для miR-486 для синтеза прямого праймера была выбрана форма miR-486-5p . В таблице 1 показаны последовательности прямых праймеров для проверенных микроРНК. Праймеры для человека GAPDH , PAX7 , IGF1R и PTEN были разработаны из перечисленных баз данных NIH GenBank с использованием программного обеспечения Primer 3 и обработаны последовательностями в базе данных GenBank для подтверждения специфичности. Эффективность и специфичность каждого набора праймеров подтверждали оценкой профиля плавления. Последовательности праймеров для количественного анализа экспрессии генов показаны в таблице 2.
Таблица 1 Последовательности праймеров проверенных микроРНК
Полная таблица
Таблица 2 Последовательности праймеров для количественного анализа экспрессии генов
Полная таблица
Экстракция РНК Центр молекулярных исследований, Цинциннати, США) в соответствии с инструкциями производителя. К каждому экстрагированному образцу добавляли полиакриловый носитель (Molecular Research Center, Cincinnati, USA) для осаждения суммарной РНК. Осадок экстрагированной РНК промывали 75% этанолом и сушили перед растворением в дистиллированной воде без РНКазы. Аликвоты тотальной РНК хранили при температуре - 80 °C сразу после экстракции. Выход и чистоту выделенной суммарной РНК определяли нанокапельном спектрофотометре (Thermo Scientific, США).
qRT-PCR в реальном времени
Для количественного анализа микроРНК сначала выполняли обратную транскрипцию (ОТ) с 10 нг общей РНК с использованием набора Taqman microRNA Reverse Transcription Kit (Applied Biosystems, США) в соответствии с инструкциями производителя. Затем проводили реакции ПЦР для количественного определения уровней экспрессии миомиР (миР-206, миР-133b и миР-486) с использованием Taqman Universal PCR Master Mix No AmpErase UNG (Applied Biosystems, США) в соответствии с инструкциями производителя и анализа микроРНК Taqman. набор (Applied Biosystems, США) использовали для выявления интересующих миомиР. ПЦР-амплификацию проводили на приборе iQ5 Multicolor Real-Time PCR iCycler (Bio-Rad, США) при 9{ mathrm {Ct} mathrm {value} mathrm {of} mathrm {RNU} 6 mathrm {B} — mathrm {Ct} mathrm {value} mathrm {of} mathrm{miRNA}} $$
Экспрессию генов PAX7 , IGF1R и PTEN анализировали с использованием набора KAPA SYBR Fast One Step qRT-PCR kit (KAPA Biosystems, США) и iQ5 Multicolor Real-Time PCR iCycler ( Био-Рад, США). Каждая смесь qRT-PCR содержала 11,7 мкл воды, свободной от нуклеаз, 10 мкл мастер-микса KAPA SYBR Fast, 0,3 мкл фермента RT, 1 мкл 100 мкМ прямого праймера, 1 мкл 100 мкМ обратного праймера и 1 мкл общей РНК (50–100 нг). Реакции проводили на iQ5 Multicolor Real-Time PCR iCycler (Bio-Rad, США) при 42°C в течение 5 мин и 9{ mathrm {Ct} mathrm {value} mathrm {of} mathrm {GAPDH} — mathrm {Ct} mathrm {value} mathrm {of} mathrm {} mathrm{gene} mathrm{of} mathrm{interest}} $$
Определение профиля клеточного цикла
Необработанные контрольные и обработанные TRF миобласты субкультивировали в 10 см 2 чашках для тканевых культур. После 24 часов инкубации клетки собирали и готовили для анализа клеточного цикла с использованием набора реагентов ДНК CycleTEST PLUS (Becton Dickinson, США) в соответствии с инструкциями производителя. Состояние клеточного цикла анализировали на проточном цитометре FACS Calibur (Becton Dickinson, США) с использованием иодида пропидия (PI) в качестве специфического флуоресцентного красителя. Для каждого образца измеряли интенсивность флуоресценции PI 15000 клеток.
Статистический анализ
Данные представлены в виде среднего ± SD. Эксперименты проводили не менее трех раз, данные анализировали с помощью критерия Стьюдента t и однофакторного дисперсионного анализа (ANOVA). Значимость была принята на уровне 90 691 p 90 692 < 0,05.
Результаты
Влияние TRF на морфологию и миогенную чистоту миобластов скелетных мышц
Молодые миобласты (PD 14) имели нормальную веретенообразную форму с круглыми ядрами (рис. 1a, b, c), в то время как стареющие миобласты были крупнее и уплощеннее и состоял из выступающих промежуточных филаментов (рис. 1г, д). Стареющие миобласты проявляли различные морфологические особенности при обработке TRF. Большинство клеток имели веретенообразную форму (рис. 1f), что напоминало молодые миобласты, обработанные TRF (рис. 1c). Миогенность миобластов составила более 90% в обеих группах лечения (таблица 3). Сравнение между различными группами лечения показало, что миогенность была одинаковой во всех группах лечения.
Рис. 1
Морфология молодых и стареющих миобластов для контрольных и обработанных TRF клеток. Наблюдение проводили в условиях фазово-контрастной ( а , d ) и флуоресцентной микроскопии ( b , с , е , f ) (увеличение × 40). Клетки миобластов окрашивали антителом против десмина (зеленый), а ядра окрашивали Hoechst (синий). Контрольные стареющие миобласты казались более крупными и плоскими с наличием более заметных промежуточных филаментов (9).0746 d , e ) по сравнению с контрольными молодыми миобластами ( a , b ). Некоторые стареющие миобласты, обработанные TRF ( f ), оставались веретенообразными, что напоминало молодой контроль, в то время как некоторые демонстрировали более плоскую и крупную морфологию. В молодых миобластах, обработанных TRF ( c ) морфологических изменений не наблюдалось
Таблица 3. Миогенная чистота миобластов в культуре
Полноразмерная таблица
0049
Индекс слияния (рис. 2) и площадь поверхности мышечной трубки (рис. 3) были больше на 3-й и 5-й дни, чем на 1-й день дифференцировки. Старение вызывает значительное снижение скорости дифференцировки стареющих миобластов на 3-й и 5-й дни по сравнению с молодыми миобластами (контроль) ( p < 0,05), что наблюдается по уменьшению индекса слияния и площади поверхности миотрубочек. Лечение TRF значительно увеличивало скорость дифференцировки с увеличением индекса слияния и площади поверхности миотрубочек на 1, 3 и 5 день как в молодых, так и в стареющих миобластах (9).0691 р < 0,05).
Рис. 2
Влияние TRF на дифференцировку миобластов. Индекс слияния измеряли как индекс дифференцировки. A обозначает P <0,05 по сравнению с молодым контролем, B P <0,05 по сравнению с контролем старения, C P <0,05 по сравнению с молодым обработкой, D 1. 1-й день того же лечения и e p < 0,05 по сравнению с 3-м днем того же лечения. Данные представлены как среднее ± SD, n = 3
Изображение полного размера
Рис. 3
Влияние TRF на дифференцировку миобластов, измеренное по площади поверхности миотуба. A обозначает P <0,05 по сравнению с молодым контролем, B P <0,05 по сравнению с контролем старения, C P <0,05 по сравнению с молодым обработкой, D 1. 1-й день того же лечения и e p < 0,05 по сравнению с 3-м днем того же лечения. Данные представлены как среднее ± SD, n = 3
Изображение полного размера
Обработка TRF модулирует экспрессию myomiR
Изменения экспрессии микроРНК наблюдались во всех группах миобластов. Экспрессия miR-133b была значительно снижена в стареющих миобластах во время фазы пролиферации (рис. 4a). Однако наблюдалось значительное увеличение экспрессии miR-133b в молодых миобластах при обработке TRF ( p < 0,05). Во время фазы дифференцировки miR-133b 9Экспрессия 0692 была снижена в стареющих миобластах ( p < 0,05). Не наблюдалось значительных изменений в экспрессии miR-133b , когда молодые и стареющие миобласты обрабатывали TRF во время дифференцировки по сравнению с контрольной группой (рис. 4b).
Рис. 4
Влияние TRF на экспрессию микроРНК при пролиферации и дифференцировке молодых и стареющих миобластов. Экспрессия miR-133b ( a , b ), miR-206 ( c , d ) и miR-486 ( e , f ) в молодых контрольных миобластах, TRF-обработанных молодых миобластах, стареющих контрольных миобластах. a Обозначает p < 0,05 по сравнению с молодым контролем, b p < 0,05 по сравнению со стареющим контролем и c p 0,5 по сравнению с молодым Foбластом, обработанным моими TRобластами 0,5 по сравнению с молодыми Данные представлены в виде относительного значения экспрессии (REV), нормализованного до Экспрессия RNU6B (среднее ± SD, n = 3)
Полноразмерное изображение
Экспрессия miR-206 была значительно снижена в стареющих миобластах во время фазы пролиферации (рис. 4c). После обработки TRF экспрессия miR-20 6 значительно увеличилась в молодых миобластах ( p < 0,05). Во время фазы дифференцировки экспрессия miR-206 в стареющих миобластах значительно снизилась ( p < 0,05). Однако при лечении TRF экспрессия miR-206 значительно увеличивалась в молодых миобластах с 1-го по 3-й день фазы дифференцировки и увеличивалась только в 1-й день фазы дифференцировки в стареющих миобластах (рис. 4d).
Экспрессия miR-486 была значительно снижена в стареющих миобластах во время фаз пролиферации и дифференцировки (рис. 4e, f). Однако при обработке TRF наблюдалось значительное увеличение экспрессии miR-486 в стареющих миобластах в фазе пролиферации и на 1-й и 5-й дни в фазе дифференцировки (9).0691 р < 0,05).
Обработка TRF модулирует экспрессию генов-мишеней и вышестоящих регуляторов миомиР
Стареющие миобласты показали значительное снижение экспрессии PAX7 во время фазы пролиферации ( p < 0,05) (рис. 5a). После обработки TRF экспрессия PAX7 значительно увеличивалась в молодых миобластах во время пролиферации. Во время фазы дифференцировки наблюдалось значительное снижение экспрессии PAX7 в стареющих миобластах (9).0691 р < 0,05). Обработка TRF во время фазы дифференцировки вызывала значительное снижение экспрессии PAX7 в молодых миобластах на 3 и 5 день и на 1 и 5 день в стареющих миобластах (рис. 5b).
Рис. 5
Влияние TRF на экспрессию нижестоящих генов. Экспрессия PAX7 ( A , B ), PTEN ( C , D ) и IGF1 R ( E , FRISED My , , ). миобласты, стареющие контрольные миобласты и стареющие миобласты, обработанные TRF. a Обозначает p < 0,05 по сравнению с молодым контролем, b p < 0,05 по сравнению со стареющим контролем и c p < 0,05 обработанных миобластов по сравнению с молодыми. Данные представлены в виде относительного значения экспрессии (REV), нормализованного к экспрессии GAPDH (среднее значение ± SD, n = 3)0691 p < 0,05) (рис. 5в, г). Обработка TRF вызывала значительное снижение экспрессии PTEN в молодых и стареющих миобластах во время фазы пролиферации. Во время фазы дифференцировки обработка TRF снижала экспрессию PTEN в стареющих миобластах в 1-й день дифференцировки (рис. 5d).
Стареющие миобласты демонстрируют значительно сниженную экспрессию IGF1R во время фазы пролиферации и на 3-й день фазы дифференцировки ( p < 0,05) (рис. 5д, е). Обработка TRF вызывала значительное увеличение экспрессии IGF1R в молодых и стареющих миобластах во время фазы пролиферации. Во время фазы дифференцировки обработка TRF вызывала значительное увеличение экспрессии IGF1R в стареющих миобластах на 1-й день, которая снижалась на 5-й день (рис. 5f).
Влияние TRF на профиль клеточного цикла
Анализ профиля клеточного цикла в день 0 показал, что популяция миобластов в G 0 /G 1 была значительно выше, а в фазе S популяция стареющих клеток была значительно ниже, чем в молодых клетках ( p < 0,05) (рис. 6). Лечение TRF вызвало значительное снижение доли стареющих миобластов в фазе G 0 /G 1 и значительное увеличение доли молодых и стареющих миобластов в фазе S ( p < 0,05) (рис. . 6д).
Рис. 6
Профиль клеточного цикла молодых и стареющих миобластов в день 0 дифференцировки. Проточная цитометрия анализ прогрессии клеточного цикла молодых контрольных миобластов ( a ), молодых миобластов, обработанных TRF ( b ), стареющих контрольных миобластов ( c ) и стареющих миобластов, обработанных TRF ( d ). Количественный анализ развития клеточного цикла молодых и стареющих миобластов ( и ). a Обозначает p < 0,05 по сравнению с молодым контролем. b p < 0,05 по сравнению со стареющим контролем и c p < 0,05 по сравнению с молодой обработанной группой. Данные выражены в виде среднего ± SD ( n = 6)
Полноразмерное изображение
На 1-й день дифференцировки процент миобластов в фазе G 0 /G 1 был значительно выше в стареющих клетках, чем что в молодых клетках ( p < 0,05), тогда как процент клеток в S и G 2 /M фазы было значительно снижено в обеих группах миобластов (рис. 7). Сравнение профиля клеточного цикла между 0-м и 1-м днями дифференцировки показало достоверную разницу в процентном содержании клеток в фазах G 0 /G 1 , S и G 2 /M в обеих группах ( пк). < 0,05).
Рис. 7
Профиль клеточного цикла молодых и стареющих миобластов в 1-й день дифференцировки. Проточная цитометрия анализ прогрессии клеточного цикла молодых контрольных миобластов ( a ), обработанные TRF молодые миобласты ( b ), стареющие контрольные миобласты ( c ) и стареющие миобласты, обработанные TRF ( d ). Количественный анализ развития клеточного цикла молодых и стареющих миобластов ( и ). a Обозначает p < 0,05 по сравнению с молодым контролем и d p < 0,05 по сравнению с тем же лечением в 0-й день дифференцировки. Данные выражены как среднее ± SD ( n = 6)
Увеличенное изображение
Обсуждение
Целостность клеточной структуры миобластов, а также формирование миотрубок поддерживают цитоскелет, клеточная мембрана и внеклеточный матрикс (ВКМ) [21]. Молодые миобласты морфологически представляют собой веретенообразные и удлиненные структуры. Напротив, стареющие миобласты проявляют морфологические изменения с уплощенной структурой и большей цитоплазмой. После индукции дифференцировки миобласты сливаются вместе, образуя многоядерную мышечную трубку. Молодые миобласты образуют миотубы с крупными разветвлениями, тогда как стареющие миобласты образуют более мелкие миотубы [16]. По мере старения клеток уровень активных форм кислорода (АФК) пропорционально увеличивается. Кроме того, уровень антиоксидантов обратно пропорционален уровню АФК на протяжении всего процесса старения. Накопление АФК в клетках вызывает окислительный стресс, который вызывает окислительное повреждение макромолекул, таких как ДНК, РНК, белки и липиды [22]. Следовательно, некоторые пути и клеточный метаболизм изменяются, что приводит к изменениям в цитоскелете, клеточной мембране и ВКМ [23], что приводит к фенотипическим изменениям в стареющих миобластах, как наблюдается в настоящем исследовании.
Следовательно, предполагается, что введение антиоксидантов в измененную систему уменьшит окислительный стресс, тем самым задержав старение миобластов.
Витамин Е, особенно TRF, играет ключевую роль в удалении пероксильных радикалов и предотвращает перекисное окисление макромолекул, тем самым улучшая окислительный статус клеток [24]. Витамин Е состоит из двух изомеров: токоферола и токотриенола. Сообщается, что токотриенол обладает лучшей антиоксидантной активностью и эффективно снижает окислительный стресс в липофильной среде [25]. В этом исследовании лечение TRF улучшило морфологическую структуру стареющих миобластов и показало черты, сходные с молодыми миобластами. Предыдущее исследование показало, что обработка TRF стареющих фибробластных клеток изменяет морфологическую структуру с образованием молодых фибробластов [26]. Точно так же в предыдущем исследовании Khor et al. сообщалось, что стареющие миобласты, обработанные TRF, по-видимому, имеют сходные морфологические особенности с молодыми миобластными клетками [16]. Это наблюдение может быть связано с модуляцией экспрессии белка, который участвует в поддержании клеточной структуры. Матриксная металлопротеиназа (ММР), ответственная за деградацию проколлагена, высоко экспрессируется в стареющих клетках. Этот белок изменяет поддержание клеточной структуры в стареющих клетках [27]. Однако TRF увеличивает экспрессию проколлагена в стареющих фибробластных клетках [28], тем самым улучшая морфологическую структуру стареющих клеток, как это наблюдалось в этом исследовании.
Гомеостаз между пролиферацией и дифференцировкой клеток миобластов во время миогенеза жестко регулируется для предотвращения неконтролируемой пролиферации [29]. В настоящем исследовании процент популяции стареющих клеток миобластов был выше в фазе G 0 /G 1 и ниже в фазе S, чем у молодых клеток, во время пролиферации. Аналогичный результат наблюдался и в дифференцированных стареющих миобластах. Интересно, что обработка TRF как пролиферирующих молодых, так и стареющих клеток миобластов усиливала прогрессирование клеточного цикла, поскольку клеточная популяция в G 0 /G 1 и S фазы уменьшены и увеличены соответственно. Однако во время индукции дифференцировки TRF способствует прерыванию клеточного цикла в молодых клетках миобластов. Как и у других соматических клеток, способность клеток миобластов к пролиферации ограничивается репликативным старением из-за прогрессирующей потери длины теломер [30]. Чтобы предотвратить прогрессирование опухоли, контрольные точки клеточного цикла действуют как барьеры для предотвращения репликации поврежденной ДНК, в результате чего клетки останавливаются на уровне G9.0315 0 /G 1 фаза [29].
Все контрольные точки клеточного цикла регулируются несколькими циклин-зависимыми киназами (CDK) и циклиновыми белками. В зависимости от раздражителей или клеточной среды, таких как реакция на повреждение ДНК (укорочение теломер), ингибиторы CDK, такие как p16 или p21, экспрессируются для ингибирования образования комплекса CDK/циклин, тем самым останавливая прогрессирование клеточного цикла на уровне G 0 /G . 1 фаза [31]. Предыдущие исследования показали, что обработка стареющими фибробластными клетками TRF повышает экспрессию теломеразы и увеличивает удлинение теломер [26]. Кроме того, обработка стареющих клеток γ-токотриенолом подавляет p16, циклин D1 и гипофосфорилированный Rb, все из которых участвуют в остановке клеточного цикла [32]. Таким образом, постулируется, что TRF модулирует экспрессию теломеразы, увеличивает экспрессию белков, участвующих в клеточном цикле, для предотвращения остановки клеточного цикла и способствует пролиферации миобластов. Лечение TRF увеличивало процент клеток миобластов в G9.0315 0 /G 1 Фаза 1-го дня индукции дифференцировки, указывающая на стимуляцию остановки клеточного цикла и ингибирование клеточной пролиферации для возникновения дифференцировки. Это может быть связано с TRF, который зависит от клеточной среды или стимулов. Предыдущие исследования показали, что γ- и δ-токотриенолы стимулируют дифференцировку остеобластов, которые, в свою очередь, усиливают формирование кости [33]. Кроме того, предыдущее исследование показало, что комбинированная активность TRF намного лучше способствует дифференцировке миобластов, чем однократное лечение α-токотриенолом [16].
Однако полное понимание механизма TRF в стимулировании пролиферации и дифференцировки миобластов остается неуловимым.
На молекулярном уровне регуляция пролиферации и дифференцировки клеток миобластов в процессе миогенеза связана с несколькими генами и миомиР (миР) [11]. Во время обновления клеток покоящиеся сателлитные клетки усиливают экспрессию PAX7 и подавляют экспрессию его целевых генов миогенного регуляторного фактора (MRF), MYOD1, и MYOG. Экспрессия PAX7 способствует повторному включению покоящихся сателлитных клеток в ход клеточного цикла и усиливает пролиферацию миобластов [6]. В настоящем исследовании выражение 9Ген 0691 PAX7 был увеличен в дифференцированных миобластах, и эта повышенная экспрессия оставалась постоянной после нескольких дней индукции дифференцировки. Однако обработка TRF увеличивала экспрессию гена PAX7 во время пролиферации и снижала его экспрессию во время дифференцировки. Сообщалось, что повышенная экспрессия PAX7 с последующим подавлением ингибиторов миогенеза Id2 и Id3 повышает экспрессию MYOD1 и MYOG [34]. MYOD1 непосредственно вовлечен в активацию экспрессии p21, циклина D3 и Rb, которые имеют решающее значение для необратимого выхода клеток миобластов из G 9 в клеточном цикле.0315 0 /G 1 в фазе дифференцировки и терминальной фазе дифференцировки [35].
Экспрессия PAX7 регулируется миР-206 и миР-486. По мере увеличения экспрессии MYOD1 этот транскрипционный фактор, который имеет сайт связывания в промоторных областях miR-206 и miR-486 , облегчает экспрессию этих двух myomiR [5]. Интересно, что обработка TRF повышала экспрессию miR-206 во время пролиферации, и эта экспрессия дополнительно повышалась во время дифференцировки. Еще один миомиР, miR-486 повышалась при обработке TRF в пролиферирующих и дифференцированных миобластах. Напротив, обработка TRF не повышала экспрессию miR-486 во время дифференцировки. Предыдущие исследования показали, что супрессия гена PAX7 с помощью miR-206 и miR-486 усиливала приверженность клеток миобластов к дифференцировке [5]. Однако сверхэкспрессия PAX7 способствует неконтролируемой пролиферации [36]. Следовательно, в настоящем исследовании TRF может играть роль в поддержании пролиферации и дифференцировки миобластов, модулируя экспрессию гена PAX7 , miR-206 и miR-486 , не нарушая гомеостаза миогенеза.
Различные модуляторы, которые регулируют активность сателлитных клеток и используют различные сигнальные пути, включая путь IGF1R/P13K, контролируют миогенез. Этот путь опосредует функции IGF, поскольку и IGF-1, и IGF-2 связываются с IGF1R. IGF1R был подавлен на поздней стадии дифференцировки из-за присутствия ответного элемента (MRE) miR-133 , расположенного в 3’UTR [9]., 37]. Это могло бы объяснить прямое влияние miR-133 на IGF1R как на негативный регулятор PI3K/Akt. miR-133 подавляет фосфорилирование Akt посредством ингибирования белка IGF1R, который отвечает за метаболизм глюкозы, пролиферацию клеток и апоптоз [37, 38]. Снижение фосфорилирования Akt наблюдалось во время дифференцировки миобластов C2C12. miR-133 важен для регулирования и балансировки активности IGF в мышечных клетках. Было обнаружено, что IGF1R не регулируется при рабдомиосаркоме (RMS), где его экспрессия постоянно увеличивалась, и, следовательно, предполагается, что он является первоначальным фактором, ответственным за онкогенную трансформацию мышечных клеток [39].]. Длительная и последовательная экспрессия IGF1R приводила к усилению пролиферации и предотвращению фазы дифференцировки [37].
Активация Akt также активирует mTOR и ингибирует GSK3B, негативный регулятор синтеза белка и роста мышц. PTEN представляет собой фосфатазу PI3K, которая деактивирует Akt, ингибируя рост и выживание мышечных клеток [40]. Снижение экспрессии PTEN стимулирует путь PI3K/Akt для продвижения и экспрессии миогенных факторов транскрипции, таких как MYOD1, MYOG и Myf5, во время пролиферации и дифференцировки миобластов. В предыдущем исследовании сообщалось о снижении экспрессии miR-486 при мышечной дистрофии Дюшенна [41] и старении [42]. miR-486 действует как медиатор для MYOD1 и регулирует путь PI3K/Akt. miR-486 транскрибируется с интрона гена Ank1 , состоящего из 39а экзона, кодирующего специфичный для мышц белок Ank1, который соединяет саркомер с саркоплазматическим ретикулумом [43]. Экспрессия транскрипта гена Ank1 контролируется промоторным сайтом, содержащим два консервативных Е-бокса, взаимодействующих с MYOD [43]. Увеличение экспрессии miR-486 TRF показывает, что TRF обладает способностью задерживать фенотип старения и саркопению во время старения.
В настоящем исследовании также было показано, что лечение TRF увеличивает экспрессию myomiR в молодых и стареющих миобластах как в фазах пролиферации, так и в фазах дифференцировки. Таким образом, TRF может прямо или косвенно играть роль в биогенезе миомиР, который включает несколько процессов [11]. Первоначально myomiR транскрибируется в ядре как первичный транскрипт или pri-myomiR со структурой ствол-петля. Здесь процесс транскрипции модулируется различными транскрипционными факторами. Затем pri-myomiR подвергается процессингу с образованием pre-myomiR путем удаления обеих концевых цепей. Позже в цитоплазме петля pre-myomiR отщепляется и раскручивается геликазой с образованием одноцепочечной зрелой myomiR. В эти процессы модификации вовлечены различные белки, и они могут быть одной из прямых или косвенных мишеней TRF. На транскрипционном уровне miR-206 регулируется транскрипционным фактором FOXO3a [11]. Предыдущее исследование показало, что лечение TRF увеличивает экспрессию гена FOXO3a [44]. В другом открытии также сообщалось, что γ- и δ-токотриенол увеличивали экспрессию гена FOXO3a [45]. Следовательно, предполагается, что TRF модулирует биогенез myomiR посредством регуляции его фактора транскрипции.
Поскольку наблюдалось снижение экспрессии myomiRs в стареющих миобластах, мы предложили другой механизм TRF-опосредованной регуляции myomiRs, который может быть связан с его эффектом удаления радикалов. Фермент RNase III, Dicer, отвечает за отщепление петли от pre-miRNA (главный шаг в процессе биогенеза) с образованием двухцепочечных зрелых miRNAs [11]. Этот фермент ингибируется различными стрессорными факторами, в том числе АФК, которые накапливаются при старении [46]. Другое открытие показало, что экспрессия Dicer снижалась с повышенным уровнем окислительного стресса и повреждения ДНК. Поскольку TRF эффективно снижает уровни ROS, особенно в стареющих клетках, предполагается, что TRF модулирует myomiRs путем снижения окислительного стресса, что, в свою очередь, повышает активность и экспрессию Dicer. Следовательно, TRF может быть вовлечен в биогенез myomiRs посредством модуляции экспрессии Dicer. Следовательно, чтобы проверить специфичность ответа TRF на экспрессию Dicer, необходимы дальнейшие исследования с использованием других антиоксидантов или путем ингибирования функции miRNA анти-miR олигонуклеотидами.
TRF в природе существует в виде смеси различных форм витамина Е; все формы токотриенолов присутствуют в TRF в высокой концентрации. Однако каждая клетка по-своему предпочитает различные формы витамина Е. Предыдущее исследование показало, что концентрация α- и δ-токотриенола была самой высокой в миобластах [18], тогда как γ- и δ-токотриенола были наиболее распространенными формами. в фибробластах [47]. Как описано ранее, обработка TRF продемонстрировала лучший эффект, чем обработка одним изомером. Следовательно, предпочтительное и избирательное поглощение формы витамина Е клеткой представляет собой наилучший синергетический эффект между формами витамина Е и пригодностью, которая зависит от клеточной среды. На рисунке 8 суммировано модулирующее влияние TRF на экспрессию myomiR и миогенных регуляторных факторов. Наши результаты показали, что TRF является потенциальным агентом дифференцировки мышц, который модулирует экспрессию myomiRs и его генов-мишеней, участвующих в дифференцировке миобластов во время миогенеза.
Рис. 8
Модулирующие эффекты TRF на экспрессию миомиР и миогенных регуляторных факторов
Изображение в натуральную величину экспрессию myomiRs, в частности, miR-133b , miR-206 и miR-486 , тем самым модифицируя экспрессию их генов-мишеней, которые участвуют в миогенезе, чтобы способствовать дифференцировке мышц в молодых и стареющих миобластах.
Ссылки
-
Инь Х, Прайс Ф, Рудницкий М.А. Сателлитные клетки и ниша мышечных стволовых клеток. Physiol Rev. 2013; 93 (1): 23–67.
КАС
Статья
Google ученый -
Сакияма К., Абэ С., Тамацу Ю., Идэ Ю. Влияние растягивающих усилий на белки мышечного сокращения миобластов скелетных мышц. Биомед Рез. 2005;26(2):61–8.
КАС
Статья
Google ученый -
Дюмон Н.А., Ван Ю.С., Рудницкий М.А. Внутренние и внешние механизмы регуляции функции сателлитных клеток. Разработка. 2015;142(9):1572–81.
КАС
Статья
Google ученый -
Соуза-Виктор П., Муньос-Кановес П. Регенеративное снижение стволовых клеток при саркопении. Мол Асп Мед. 2016;50:109–17.
КАС
Статья
Google ученый -
Zammit PS, Relaix F, Nagata Y, Ruiz AP, Collins CA, Partridge TA, et al. Pax7 и миогенная прогрессия в сателлитных клетках скелетных мышц. Дж. Клеточные науки. 2006; 119(9):1824–32.
КАС
Статья
Google ученый -
Yamaguchi A, Sakuma K, Fujikawa T, Morita I. Экспрессия специфических IGFBP связана с маркерами пролиферации и дифференциации в регенерирующей подошвенной мышце крысы. J Physiol Sci. 2013;63(1):71–7.
КАС
Статья
Google ученый -
Баузер М., Херберг С., Арунлейт П., Ши Х., Фулзеле С., Хилл В.Д. и др. Влияние системы активин А-миостатин-фоллистатин на старение костных и мышечных клеток-предшественников.
Опыт Геронтол. 2013;48(2):290–7.
КАС
Статья
Google ученый -
Spangenburg EE, Booth FW. Множественные сигнальные пути опосредуют индуцированную LIF пролиферацию сателлитных клеток скелетных мышц. Am J Physiol Cell Physiol. 2002; 283(1):C204–C11.
КАС
Статья
Google ученый -
Возняк А.С., Андерсон Дж.Е. Зависимость от оксида азота активации и покоя сателлитных стволовых клеток в нормальных волокнах скелетных мышц. Дев Дин. 2007;236(1):240–50.
КАС
Статья
Google ученый -
Horak M, Novak J, Bienertova-Vasku J. Мышечно-специфические микроРНК в развитии скелетных мышц. Дев биол. 2016;410(1):1–13.
КАС
Статья
Google ученый -
Маккарти Дж.Дж.
Сеть MyomiR в пластичности скелетных мышц. Exerc Sport Sci Rev. 2011;39(3):150.
Артикул
Google ученый -
Сантос С.А., Сильва Э.Т., Карис А.В., Лира Ф.С., Туфик С., Дос Сантос Р.В. Добавка витамина Е подавляет повреждение мышц и воспаление после умеренных физических упражнений в условиях гипоксии. Диета J Hum Nutr. 2016;29(4):516–22.
КАС
Статья
Google ученый -
Али С.Ф., Вудман О.Л. Богатый токотриенолом экстракт пальмового масла более эффективен, чем чистые токотриенолы, в улучшении эндотелий-зависимой релаксации при окислительном стрессе. Оксидативный Мед Селл Лонгев. 2015;2015:10.
Артикул
Google ученый -
Будин С.Б., Хан К.Дж., Джаюсман П.А., Тайб И.С., Газали А.Р., Мохамед Дж. Антиоксидантная активность богатой токотриенолом фракции предотвращает вызванное фенитротионом повреждение почек у крыс.
J Токсикол Патол. 2013;26(2):111–8.
Артикул
Google ученый -
Khor SC, Razak AM, Wan Ngah WZ, Mohd Yusof YA, Abdul Karim N, Makpol S. Богатая токотриенолом фракция превосходит токоферол в продвижении миогенной дифференцировки в предотвращении репликативного старения миобластов. ПЛОС Один. 2016;11(2):e0149265.
Артикул
Google ученый -
Gwee Sian Khee S, Mohd Yusof YA, Makpol S. Экспрессия связанных со старением микроРНК и генов-мишеней при клеточном старении и модуляция богатой токотриенолом фракцией. Оксидативный Мед Селл Лонгев. 2014;2014:12.
Артикул
Google ученый -
Khor SC, Ngah W, Zurinah W, Yusof M, Anum Y, Abdul Karim N, et al. Обогащенная токотриенолом фракция улучшает механизмы антиоксидантной защиты и улучшает окислительный стресс, связанный с репликативным старением, в миобластах человека.
Оксидативный Мед Селл Лонгев. 2017;2017:17.
-
Щесны Б., Олах Г., Уокер Д.К., Вольпи Э., Расмуссен Б.Б., Сабо С. и др. Дефицит восстановления митохондриального генома делает пролиферирующие миобласты чувствительными к окислительному повреждению. ПЛОС Один. 2013;8(9):e75201.
КАС
Статья
Google ученый -
Моккегиани Э., Костарелли Л., Джаккони Р., Малавольта М., Бассо А., Пьяченца Ф. и др. Взаимодействие витамина Е с генами при старении и воспалительных возрастных заболеваниях: значение для лечения. Систематический обзор. Aging Res Rev. 2014; 14:81–101.
КАС
Статья
Google ученый -
Адамс JC, Watt FM. Регуляция развития и дифференцировки внеклеточным матриксом. Разработка. 1993;117(4):1183–98.
КАС
пабмед
Google ученый -
Huang X, Chen L, Liu W, Qiao Q, Wu K, Wen J и др. Участие окислительного стресса и нарушения цитоскелета в индуцированном микроцистином апоптозе в клетках CIK. Аква токсикол. 2015; 165:41–50.
КАС
Статья
Google ученый -
Ники Е. Роль витамина Е в качестве жирорастворимого поглотителя пероксильных радикалов: данные in vitro и in vivo. Свободный Радик Биол Мед. 2014;66:3–12.
КАС
Статья
Google ученый -
Виола В., Пиллоли Ф., Пиродди М., Пьерпаоли Э., Орландо Ф., Провинсиали М. и др. Почему токотриенолы работают лучше: взгляд на противораковый механизм витамина Е in vitro. Genes Nutr.
2012;7(1):29.
КАС
Статья
Google ученый -
Макпол С., Дюрани Л.В., Чуа К.Х., Юсоф М., Анум Ю., Нгах В. и др. Обогащенная токотриенолом фракция предотвращает остановку клеточного цикла и удлиняет длину теломер в стареющих диплоидных фибробластах человека. Биомед Рез Инт. 2011;2011(11):506171.
Google ученый
-
Хияма А., Сакаи Д., Рисбуд М.В., Танака М., Араи Ф., Абэ К. и др. Усиление старения клеток межпозвонкового диска за счет экспрессии матриксной металлопротеиназы, индуцированной передачей сигналов WNT/β-катенина. Ревмирующий артрит. 2010;62(10):3036–47.
КАС
Статья
Google ученый -
Макпол С., Джам Ф.А., Хор С.С., Исмаил З., Юсоф М., Анум Ю. и др. Сравнительное влияние биодинов, богатой токотриенолом фракции и токоферола на усиление синтеза коллагена и ингибирование деградации коллагена в модели преждевременного старения диплоидных фибробластов человека, вызванного стрессом.
Оксидативный Мед Селл Лонгев. 2013;2013:8.
-
Уолш К., Перлман Х. Выход из клеточного цикла при миогенной дифференцировке. Curr Opin Genet Dev. 1997;7(5):597–602.
КАС
Статья
Google ученый -
Zhu CH, Mouly V, Cooper RN, Mamchaoui K, Bigot A, Shay JW, et al. Клеточное старение в миобластах человека преодолевается человеческой теломеразной обратной транскриптазой и циклинзависимой киназой 4: последствия старения мышц и терапевтические стратегии при мышечных дистрофиях. Стареющая клетка. 2007;6(4):515–23.
КАС
Статья
Google ученый -
Harley CB, Futcher AB, Greider CW. Теломеры укорачиваются при старении фибробластов человека. Природа. 1990;345(6274):458.
КАС
Статья
Google ученый -
Zainuddin A, Chua K-H, Tan J-K, Jaafar F, Makpol S.
γ-Токотриенол предотвращает остановку клеточного цикла в старых клетках фибробластов человека через путь p16INK4a. J Physiol Biochem. 2017;73(1):59–65.
КАС
Статья
Google ученый -
Чин К.Ю., Има-Нирвана С. Влияние добавок токотриенола, полученного из аннато, на остеопороз, вызванный дефицитом тестостерона у крыс. Clin Interv Старение. 2014;9:1247.
Артикул
Google ученый -
Кумар Д., Шадрах Д.Л., Вейджерс А.Дж., Лассар А.Б. Id3 является прямой мишенью транскрипции Pax7 в покоящихся сателлитных клетках. Мол Биол Селл. 2009 г.;20(14):3170–7.
КАС
Статья
Google ученый -
Cenciarelli C, De Santa F, Puri PL, Mattei E, Ricci L, Bucci F, et al. Критическая роль, которую играет циклин D3 в опосредованной MyoD остановке клеточного цикла во время дифференцировки миобластов.
Мол Селл Биол. 1999;19(7):5203–17.
КАС
Статья
Google ученый -
Риуцци Ф., Сорчи Г., Сагедду Р., Сидони А., Аладжио Р., Нинфо В. и др. Дефицит передачи сигналов RAGE в клетках рабдомиосаркомы вызывает активацию PAX7 и неконтролируемую пролиферацию. Дж. Клеточные науки. 2014;127(8):1699–711.
КАС
Статья
Google ученый -
Хуан М.Б., Сюй Х., Се С.Дж., Чжоу Х., Цюй Л.Х. Рецептор инсулиноподобного фактора роста-1 регулируется микроРНК-133 во время скелетного миогенеза. ПЛОС Один. 2011;6(12):e29173.
КАС
Статья
Google ученый -
Скьяффино С., Маммукари С. Регуляция роста скелетных мышц с помощью пути IGF1-Akt/PKB: выводы из генетических моделей. Скелетная мышца. 2011;1(1):4.
КАС
Статья
Google ученый -
Crackower MA, Oudit GY, Kozieradzki I, Sarao R, Sun H, Sasaki T, et al. Регуляция сократимости миокарда и размера клеток с помощью различных сигнальных путей PI3K-PTEN. Клетка. 2002; 110(6):737–49..
КАС
Статья
Google ученый -
Александр М.С., Касар Дж.К., Мотохаши Н., Виейра Н.М., Айзенберг И., Маршалл Дж.Л. и др. Зависимая от микроРНК-486 модуляция сигнальных путей DOCK3/PTEN/AKT улучшает симптомы, связанные с мышечной дистрофией. Джей Клин Инвест. 2014;124(6):2651–67.
КАС
Статья
Google ученый -
Lai CY, Wu YT, Yu SL, Yu YH, Lee SY, Liu CM, et al.
Модулированная экспрессия микроРНК периферической крови человека от младенчества до взрослой жизни и ее роль в старении. Стареющая клетка. 2014;13(4):679–89.
КАС
Статья
Google ученый -
Смолл Э.М., О’Рурк Дж.Р., Мореси В., Сазерленд Л.Б., МакЭналли Дж., Джерард Р.Д. и др. Регуляция передачи сигналов PI3-киназы/Akt с помощью обогащенной мышцами микроРНК-486. Proc Natl Acad Sci. 2010;107(9):4218–23.
КАС
Статья
Google ученый -
Durani L, Jaafar F, Tan J, Tajul Arifin K, Mohd Yusof Y, Wan Ngah W. Нацеливание на гены инсулин-ассоциированного сигнального пути, повреждение ДНК, пути пролиферации и дифференцировки клеток с помощью богатой токотриенолом фракции в предотвращении клеточное старение диплоидных фибробластов человека. Клин Тер. 2015;166:e365–e73.
КАС
пабмед
Google ученый -
Смит-Викос Т., Слэк Ф.Дж. МикроРНК и их роль в старении. Дж. Клеточные науки. 2012;125(1):7–17.
КАС
Статья
Google ученый -
Джаафар Ф., Абдулла А., Макпол С. Клеточное поглощение и биодоступность богатой токотриенолом фракции в ингибированных SIRT1 диплоидных фибробластах человека. Научный доклад 2018; 8 (1): 10471.
Артикул
Google ученый
Ссылки на скачивание
Благодарности
Данное исследование выполнено при финансовой поддержке Министерства высшего образования в рамках Схемы грантов для фундаментальных исследований FRGS/2/2014/SKK01/UKM/01/1 и гранта Университета Кебангсаан Малайзии UKM-FF -2014-301. Авторы хотели бы выразить благодарность всем исследователям и сотрудникам кафедры биохимии медицинского факультета Малайзийского медицинского центра Университета Кебангсаан.
Информация об авторе
Авторы и организации
-
Кафедра биохимии, медицинский факультет, уровень 17, доклинический корпус Малайзийского медицинского центра Университета Кебангсаан (UKMMC), Джалан Яакоб Латиф, Бандар Тун Разак, Черас, 56000, Куала-Лумпур , Малайзия
Azraul Mumtazah Razak, Shy Cian Khor, Faizul Jaafar, Norwahidah Abdul Karim и Suzana Makpol
Авторы
- Azraul Mumtazah Razak
Посмотреть публикацию автора0003
Вы также можете искать этого автора в
PubMed Google Scholar - Shy Cian Khor
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Faizul Jaafar
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Norwahidah Abdul Karim
Посмотреть публикации автора
Вы также можете искать этого автора в
PubMed Google Scholar - Suzana Makpol
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar
Вклады
AMR провела эксперименты, проанализировала данные и подготовила рукопись. SCK и FJ проанализировали данные и составили рукопись. SM и NAK разработали исследование, интерпретировали данные и отредактировали рукопись. Все авторы читали и одобрили окончательный вариант рукописи.
Автор, ответственный за переписку
Переписка с
Сюзанна Макпол.
Заявление об этике
Конкурирующие интересы
Авторы заявляют, что у них нет конкурирующих интересов.
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Права и разрешения
Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 4.0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение, и воспроизведение на любом носителе, при условии, что вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения. Отказ Creative Commons от права на общественное достояние (http://creativecommons.org/publicdomain/zero/1.0/) применяется к данным, представленным в этой статье, если не указано иное.
Перепечатки и разрешения
Об этой статье
Анализ внеклеточной объемной доли миокарда для дифференциации обратимого и необратимого повреждения миокарда и прогнозирования неблагоприятного ремоделирования левого желудочка после инфаркта миокарда с подъемом сегмента ST
Сохранить цитату в файл
Формат:
Резюме (текст)PubMedPMIDAbstract (текст)CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Не удалось загрузить вашу коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Не удалось загрузить делегатов из-за ошибки
Повторите попытку
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл. адрес:
(изменить)
Который день?
Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день
Который день?
воскресеньепонедельниквторниксредачетвергпятницасуббота
Формат отчета:
SummarySummary (text)AbstractAbstract (text)PubMed
Отправить максимум:
1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
Полнотекстовые ссылки
Спрингер
Полнотекстовые ссылки
. 2021 Январь; 31 (1): 504-514.
doi: 10.1007/s00330-020-07117-9.
Epub 2020 12 августа.
Бин-Хуа Чен #
1
, Донг-Аолей Ан #
1
, Цзе Хэ
2
, Чун-Вэнь Ву
1
, Тин Юэ
1
, Руй Ву
1
, Руо-Ян Ши
1
, Халид Этир
3
, Бобби Джозеф
3
, Джиани Ху
3
, Цзянь-Ронг Сюй
4
, Лянь-Мин Ву
5
, Июн Пу
6
Принадлежности
- 1 Отделение рентгенологии, больница Ренджи, медицинский факультет Шанхайского университета Цзяо Тонг, № 160 Пуцзянь-роуд, Шанхай, 200127, Китайская Народная Республика.
- 2 Отделение кардиологии, больница Рэндзи, медицинский факультет Шанхайского университета Цзяо Тонг, № 160 Пуцзянь-роуд, Шанхай, 200127, Китайская Народная Республика.
- 3 Кафедра радиологии, Государственный университет Уэйна, Детройт, Мичиган, 48201, США.
- 4 Отделение рентгенологии, больница Ренджи, медицинский факультет Шанхайского университета Цзяо Тонг, № 160 Пуцзянь-роуд, Шанхай, 200127, Китайская Народная Республика. [email protected].
- 5 Кафедра радиологии, Больница Ренджи, Медицинский факультет Шанхайского университета Цзяо Тонг, № 160 PuJian Road, Шанхай, 200127, Китайская Народная Республика. [email protected].
- 6 Отделение кардиологии, больница Ренджи, медицинский факультет Шанхайского университета Цзяо Тонг, № 160 Пуцзянь Роуд, Шанхай, 200127, Китайская Народная Республика.
[email protected].
# Внесли поровну.
-
PMID:
32785772 -
DOI:
10.1007/s00330-020-07117-9
Бин-Хуа Чен и др.
Евро Радиол.
2021 янв.
. 2021 Январь; 31 (1): 504-514.
дои: 10.1007/s00330-020-07117-9.
Epub 2020 12 августа.
Авторы
Бин-Хуа Чен #
1
, Донг-Аолей Ан #
1
, Цзе Хэ
2
, Чун-Вэнь Ву
1
, Тин Юэ
1
, Руй Ву
1
, Руо-Ян Ши
1
, Халид Этир
3
, Бобби Джозеф
3
, Джиани Ху
3
, Цзянь-Ронг Сюй
4
, Лянь-Мин Ву
5
, Июн Пу
6
Принадлежности
- 1 Кафедра радиологии, Больница Ренджи, Медицинский факультет Шанхайского университета Цзяо Тонг, № 160 PuJian Road, Шанхай, 200127, Китайская Народная Республика.
- 2 Отделение кардиологии, больница Рэндзи, медицинский факультет Шанхайского университета Цзяо Тонг, № 160 Пуцзянь-роуд, Шанхай, 200127, Китайская Народная Республика.
- 3 Кафедра радиологии, Государственный университет Уэйна, Детройт, Мичиган, 48201, США.
- 4 Отделение рентгенологии, больница Ренджи, медицинский факультет Шанхайского университета Цзяо Тонг, № 160 Пуцзянь-роуд, Шанхай, 200127, Китайская Народная Республика. [email protected].
- 5 Кафедра радиологии, Больница Ренджи, Медицинский факультет Шанхайского университета Цзяо Тонг, № 160 PuJian Road, Шанхай, 200127, Китайская Народная Республика. [email protected].
- 6 Отделение кардиологии, больница Рэндзи, медицинский факультет Шанхайского университета Цзяо Тонг, № 160 Пуцзянь-роуд, Шанхай, 200127, Китайская Народная Республика.
[email protected].
# Внесли поровну.
-
PMID:
32785772 -
DOI:
10.1007/s00330-020-07117-9
Абстрактный
Цели:
Наше исследование было направлено на изучение прогностической ценности радиометрической ТА (анализ текстуры) при количественном картировании фракции ECV (внеклеточный объем) для дифференциации обратимого и необратимого повреждения миокарда и прогнозирования неблагоприятного ремоделирования левого желудочка у пациентов с реперфузированным ИМпST (инфаркт миокарда с подъемом сегмента ST). ).
Методы:
Это обсервационное проспективное когортное исследование выявило 70 пациентов (62 ± 9 лет, 62 мужчины [85,70%)] с ИМпST по поводу ТА, которым последовательно выполняли нативное и контрастное Т1-картирование. Особенности текстуры были извлечены из каждого набора карт ECV на основе анализа ROI (области интереса).
Полученные результаты:
После выбора признаков текстуры и уменьшения размеров пять выбранных признаков текстуры оказались статистически значимыми для дифференциации степени повреждения миокарда. Анализ кривой ROC (рабочей характеристики приемника) для дифференциации инфаркта, подлежащего восстановлению, и миокарда, подлежащего спасению, продемонстрировал значительно более высокую AUC (площадь под кривой) (0,9).1 [95% ДИ, 0,86–0,96], p < 0,0001) для горизонтальной фракции, чем для других характеристик текстуры (p < 0,05). LVAR (неблагоприятное ремоделирование левого желудочка) можно было предсказать по этим выбранным признакам. Различия в качественных и количественных исходных параметрах и горизонтальных фракциях были достоверными между пациентами с LVAR и без него. LGE (позднее усиление гадолинием) и характеристики горизонтальной фракции инфарктного миокарда при остром ИМпST были единственными двумя параметрами, выбранными для формирования оптимальной общей многофакторной модели для LVAR через 6 месяцев.
Выводы:
Рентгенологический анализ ECV может отличить обратимое от необратимого повреждения миокарда после ИМпST. LGE, а также радиомика TA (анализ текстуры) ECV может предоставить альтернативу для прогнозирования LVAR и функционального восстановления.
Ключевые моменты:
• Количественная оценка ECV позволила отличить инфарктный миокард от неинфарктного миокарда. • Рентгенологический анализ ECV может отличить обратимое повреждение миокарда от необратимого. • Анализ Radiomics TA показывает многообещающее сходство с результатами LGE, которые могут помочь в прогнозировании пациентов с инфарктом миокарда.
Ключевые слова:
Внеклеточный матрикс; магнитно-резонансная томография; Инфаркт миокарда; Ремоделирование желудочков.
Похожие статьи
-
Объемная доля внеклеточного объема миокарда позволяет дифференцировать обратимое и необратимое повреждение миокарда и прогнозировать неблагоприятное ремоделирование левого желудочка при инфаркте миокарда с подъемом сегмента ST.
Chen BH, An DA, He J, Xu JR, Wu LM, Pu J.
Чен Б.Х. и др.
J Magn Reson Imaging. 2020 авг; 52 (2): 476-487. doi: 10.1002/jmri.27047. Epub 2020 14 января.
J Magn Reson Imaging. 2020.
PMID: 31943526 -
CMR Native T1 Mapping позволяет дифференцировать обратимое и необратимое повреждение миокарда при инфаркте миокарда с подъемом сегмента ST: исследование OxAMI (Оксфордский острый инфаркт миокарда).
Лю Д., Борлотти А., Вилиани Д., Йерош-Херольд М., Алхалил М., Де Мария Г.Л., Фарни Г., Докинз С., Виджесурендра Р., Фрэнсис Дж., Феррейра В., Печник С., Робсон М.Д., Баннинг А., Чоудхури Р., Нойбауэр С., Чэннон К., Харбанда Р., Далл’Армеллина Э.
Лю Д. и др.
Циркулярная кардиоваскулярная визуализация. 2017 авг;10(8):e005986. doi: 10.1161/ОБЪЕМНОЕ ИЗОБРАЖЕНИЕ.116.005986.
Циркулярная кардиоваскулярная визуализация. 2017.
PMID: 28798137
Бесплатная статья ЧВК. -
Оценка внеклеточного объема миокарда с помощью CMR позволяет прогнозировать функциональное восстановление после острого инфаркта миокарда.
Кидамби А., Мотвани М., Уддин А., Рипли Д.П., МакДиармид А.К., Свобода П.П., Бродбент Д.А., Муса Т.А., Эрхайем Б., Лидер Дж., Круазиль П., Кларисс П., Гринвуд Д.П., Плейн С.
Кидамби А. и др.
JACC Cardiovasc Imaging. 2017 сен; 10 (9): 989-999. doi: 10.1016/j.jcmg.2016.06.015. Epub 2016 19 октября.
JACC Cardiovasc Imaging. 2017.
PMID: 27771398
Бесплатная статья ЧВК. -
Повышенная оксигенация связана с воспалением миокарда и неблагоприятным регионарным ремоделированием после острого инфаркта миокарда с подъемом сегмента ST.
Ши К., Ма М., Ян М.С., Ся К.С., Пэн В.Л., Хе И., Ли З.
Л., Го Ю.К., Ян З.Г.
Ши К. и др.
Евро Радиол. 2021 Декабрь; 31 (12): 8956-8966. doi: 10.1007/s00330-021-08032-3. Epub 2021 18 мая.
Евро Радиол. 2021.
PMID: 34003352 -
T 1 — Картирование и оценка внеклеточного объема у детей с мышечной дистрофией Дюшенна и у здоровых лиц контрольной группы при 3T.
Мафоро Н.Г., Маграт П., Мулен К., Шао Дж., Ким Г.Х., Проспер А., Ренелла П., Ву Х.Х., Халнон Н., Эннис Д.Б.
Мафоро Н.Г. и соавт.
J Cardiovasc Magn Reson. 2020 10 декабря; 22 (1): 85. дои: 10.1186/с12968-020-00687-з.
J Cardiovasc Magn Reson. 2020.
PMID: 33302967
Бесплатная статья ЧВК.
Посмотреть все похожие статьи
Цитируется
-
[Искусственный интеллект и радиомика: значение в МРТ сердца].
Рау А., Сощинский М., Тарон Дж., Рюйл П., Шлетт К.Л., Бамберг Ф., Краусс Т.
Рау А и др.
Радиология (Хайдельб). 2022 г., 25 августа. doi: 10.1007/s00117-022-01060-0. Онлайн перед печатью.
Радиология (Хайдельб). 2022.
PMID: 36006439Обзор.
Немецкий. -
Прогнозирование функции миокарда после коронарного шунтирования с использованием радиомикроскопических функций МРТ и алгоритмов машинного обучения.
Ариан Ф., Амини М., Мостафаи С., Резаи Калантари К., Хаддади Аввал А., Шахбази З., Касани К., Битарафан Раджаби А., Чаттерджи С., Овейси М., Шири И., Заиди Х.
Ариан Ф. и др.
J цифровое изображение. 2022 г., 22 августа. doi: 10.1007/s10278-022-00681-0. Онлайн перед печатью.
J цифровое изображение. 2022.
PMID: 35995896 -
Качество научных данных и отчетность по радиомике в исследованиях магнитно-резонансной томографии сердца: систематический обзор.
Чанг С., Хань К., Су Ю.Дж., Чой Б.В.
Чанг С. и др.
Евро Радиол. 2022 июль; 32 (7): 4361-4373. doi: 10.1007/s00330-022-08587-9. Epub 2022 1 марта.
Евро Радиол. 2022.
PMID: 35230519 -
Магнитно-резонансный анализ текстуры при инфаркте миокарда.
Пэн Ф., Чжэн Т., Тан С., Лю Ц., Сунь З., Фэн З., Чжао Х., Гун Л.
Пэн Ф. и др.
Front Cardiovasc Med. 2021 28 окт;8:724271. doi: 10.3389/fcvm.2021.724271. Электронная коллекция 2021.
Front Cardiovasc Med. 2021.
PMID: 34778395
Бесплатная статья ЧВК.
Обзор.
использованная литература
-
-
Mehta RH, Harjai KJ, Cox D et al (2003)Клинические и ангиографические корреляты и результаты субоптимального коронарного кровотока у пациентов с острым инфарктом миокарда, подвергающихся первичному чрескожному коронарному вмешательству.
Дж. Колл Кардиол 42: 1739–1746
—
DOI
-
Mehta RH, Harjai KJ, Cox D et al (2003)Клинические и ангиографические корреляты и результаты субоптимального коронарного кровотока у пациентов с острым инфарктом миокарда, подвергающихся первичному чрескожному коронарному вмешательству.
-
- Rodriguez-Palomares JF, Gavara J, Ferreira-Gonzalez I et al (2019)Прогностическое значение исходного ремоделирования левого желудочка у пациентов с реперфузионным ИМпST. JACC Cardiovasc Imaging. https://doi.org/10.1016/j.jcmg.2019.02.025
-
-
Кэррик Д., Хейг С., Раухаламми С. и др. (2015)Патофизиология ремоделирования ЛЖ у выживших после ИМпST: воспаление, отдаленный миокард и прогноз. JACC Cardiovasc Imaging 8: 779–789
—
DOI
-
Кэррик Д., Хейг С., Раухаламми С. и др. (2015)Патофизиология ремоделирования ЛЖ у выживших после ИМпST: воспаление, отдаленный миокард и прогноз. JACC Cardiovasc Imaging 8: 779–789
-
-
Пфеффер М.
А., Браунвальд Э. (1990)Ремоделирование желудочков после инфаркта миокарда. Экспериментальные наблюдения и клинические последствия. Тираж 81: 1161–1172.
—
DOI
-
Пфеффер М.
-
-
Bulluck H, Rosmini S, Abdel-Gadir A et al (2016)Остаточное миокардиальное железо после внутримиокардиального кровоизлияния во время фазы выздоровления реперфузированного инфаркта миокарда с подъемом сегмента ST и неблагоприятного ремоделирования левого желудочка. Circ Cardiovasc Imaging 9: 1–10
—
DOI
-
Bulluck H, Rosmini S, Abdel-Gadir A et al (2016)Остаточное миокардиальное железо после внутримиокардиального кровоизлияния во время фазы выздоровления реперфузированного инфаркта миокарда с подъемом сегмента ST и неблагоприятного ремоделирования левого желудочка. Circ Cardiovasc Imaging 9: 1–10
термины MeSH
вещества
Грантовая поддержка
- 81873886 / Национальный фонд естественных наук Китая
- 81873887 / Национальный фонд естественных наук Китая
- 2017YQ031 / Муниципальная комиссия Шанхая по здравоохранению и планированию семьи, отличная программа для молодых талантов
- SHDC12018X21 / Шанхайский центр развития больницы Шэнькан, проект клинических исследований и развития
- YG2017QN44 / Проект медицинского кросса Шанхайского университета Цзяо Тонг
- 19DZ2203800 / Шанхайский план действий по инновациям в области науки и техники, стандартный технологический проект
- 2019–1904 Шанхайский университет Цзяо Тонг, медицинский факультет, проект «Двойная сотня выдающихся людей»
Полнотекстовые ссылки
Спрингер
Укажите
Формат:
ААД
АПА
МДА
НЛМ
Отправить по телефону
Разложение на неполные дроби: повторяющиеся и неприводимые факторы
Вернуться к
Указатель уроков | Делайте уроки
в заказе | Подходит для печати
страница
Неполная дробь
Разложение: как обращаться с повторяющимися и неприводимыми факторами (стр.
2 из 3)
Разделы: Общие
методики, Как справляться с повторяющимися и неустранимыми факторами, Примеры
Иногда встречается множитель в знаменателе
больше одного. Например, в дроби
13 / 24 , знаменатель
24
факторы как 2223.
Фактор 2 происходит
три раза. Чтобы получить 13 / 24 ,
может быть 1 / 2
или 1 / 4 или
а 1 / 8
который был включен в оригинальное дополнение. Вы не можете сказать, глядя
по конечному результату.
Таким же образом, если рациональное выражение
имеет повторяющийся множитель в знаменателе, вы не можете сказать, просто взглянув,
какие знаменатели могли быть включены в первоначальное дополнение.
Вы должны учитывать каждую возможность.
- Найдите неполную дробь
разложение следующего выражения:
Фактор x
1 встречается в знаменателе три раза.
Я учту это, составив дроби, содержащие возрастающие степени
этого множителя в знаменателе, вот так:
Теперь умножаю на общее
знаменатель, чтобы получить:
Я мог бы использовать систему уравнений, чтобы
решить для A , B ,
С и Д ,
но другой метод казался более легким. Два числа обнуления x
= 1 и х
= 0: так
х = 1: 1 + 1 = 0 +
0 + С + 0, значит С
= 2
х
= 0: 1 = 0 + 0 + 0 Д ,
поэтому D = 1
Но что мне теперь делать? у меня есть два других
переменные, а именно A и
Б ,
для которых мне нужны значения. Но так как у меня есть значения для C и
Д ,
Я могу выбрать любые два других значения x ,
подключите их и получите систему уравнений, которую я могу решить для A и
Б .
Конкретные значения x
Я выбираю неважные, поэтому выберу поменьше:
х = 2:
Авторские права
Элизабет Стапель 2006-2011 Все права защищены
(2) 2 + 1
= А (2)(2 1) 2 + В (2)(2 1) +
(2)(2) + (1)(2 1) 3
4 + 1 = 2 А
+ 2 Б + 4 1
5 = 2 А + 2 В
+ 3
1
= А + В
х = 1:
(1) 2 + 1 = А (1)(1)
1) 2 + В (1)(1 1) + (2)(1) + (1)(1 1) 3
1 + 1 = 4 А
+ 2 Б 2 + 8
2
= 4 А + 2 В + 6
2 А В
= 2
Я все еще не могу решить систему уравнений,
но используя более простой метод решения для C и
Д ,
Теперь у меня есть более простая система для решения. Складывая два уравнения, я получаю
3 А = 3,
так А = 1.
Тогда B = 0 (так что
этот член в разложении «исчезает»), а полное разложение
это:
В приведенном выше примере один из коэффициентов
оказался нулевым. Это случается не часто (на уроках алгебры,
в любом случае), но не удивляйтесь, если вы получите ноль или даже дроби для
некоторые из ваших коэффициентов. Учебники обычно придерживаются довольно близко
к красивым аккуратным целым числам, но не всегда. Не думайте, что дробь
или ноль — неправильный ответ. Например:
…раскладывается как:
Примечание. Вы также можете обрабатывать дроби
вот так:
Если знаменатель вашего рационального выражения
имеет нефакторизуемый квадратичный, то у вас есть
для учета возможного «размера» числителя. Если
знаменатель содержит множитель второй степени, то числитель может не
быть просто числом; она может быть первой степени. Таким образом, вы будете иметь дело с
квадратичный множитель в знаменателе путем включения линейного выражения в
числитель.
- Найдите неполную дробь
разложение следующего:
Факторизируя знаменатель, я получаю x ( x 2
+ 3). Я не могу факторизовать квадратное
бит, поэтому моя расширенная форма будет выглядеть так:
Обратите внимание, что числитель для » x 2
+ 3″ дробь является линейным многочленом,
не просто постоянный срок.
Умножение на общий знаменатель,
Я получаю:
Единственный ноль в исходном знаменателе
х = 0,
так:
Затем А
= 1. Так как у меня нет другого полезного
x — значения для работы, я думаю, что возьму одно значение, которое я решил
ибо приравняем оставшиеся коэффициенты и посмотрим, что мне это даст:
(Нет единственного «правильного» пути
решить значения коэффициентов. Используйте любой метод, который «чувствует»
право на данное упражнение.)
Тогда разложение:
<< Предыдущая
Топ | 1
| 2 | 3 | Возвращаться
к индексу Далее >>
Заказать задачи по любым предметам можно здесь от 10 минут
Производная дроби
Производная дроби равна произведению производной числителя на знаменатель минус произведение числителя на производную знаменателя и всё делить на квадрат знаменателя:
$$ bigg (frac{u}{v} bigg )’ = frac{u’v-uv’}{v^2} $$
Следует понимать, что производная дроби НЕ РАВНА отношению производных числителя и знаменателя!
Примеры с решением
| Пример 1 |
| Найти производную дроби $ y = frac{x}{ln x} $ |
| Решение |
|
Из формулы следует, что числитель $$ u = x $$ а знаменатель $$ v = ln x $$ Находим их производные: $$ u’ = (x)’ = 1 $$ $$ v’ = (ln x)’ = frac{1}{x} $$ Подставляем найденные $ u’ $ и $ v’ $ в формулу производной дроби: $$ y’=bigg (frac{x}{ln x} bigg )’ = frac{(x)’ln x — x(ln x)’}{(ln x)^2} = $$ $$ = frac{ln x — x frac{1}{x}}{ln^2 x} = frac{ln x — 1}{ln^2 x} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = frac{ln x — 1}{ln^2 x} $$ |
| Пример 2 |
| Найти производную от дроби $ y = frac{cos x}{x} $ |
| Решение |
|
По формуле производной частного: $$ y’=bigg (frac{cos x}{x} bigg ) = frac{(cos x)’x-cos x (x)’}{(x)^2} = $$ Производная косинуса равна отрицательному синусу: $$ (cos x)’ = -sin x $$ Тогда: $$ y’ = frac{-xsin x — cos x}{x^2} = -frac{xsin x + cos x}{x^2} $$ |
| Ответ |
| $$ y’ = -frac{xsin x + cos x}{x^2} $$ |
урок 3. Математика ЕГЭ
Как найти производную от функции
Как считать производные?
Никто не использует определение производной, чтобы ее вычислить. Как же тогда ее посчитать?
Оказывается, существуют специальные формулы, с помощью которых производная от функции вычисляется достаточно просто.
Формулы производной
Выпишем теперь все формулы производной функции и порешаем примеры.
Производная от константы
Производная от любого числа всегда равна (0):
$$(const)^{/}=0;$$
Пример 1
$$(5)^{/}=0;$$
Производная от (x)
Производная просто от (x) равна (1):
$$x^{/}=1;$$
Производная от степени
$$(x^n)^{/}=n*x^{n-1};$$
Пример 2
$$(x^4)^{/}=4*x^{4-1}=4*x^{3};$$
$$(x^{10})^{/}=10*x^{10-1}=10*x^{9};$$
$$(x^{-3})^{/}=-3*x^{-3-1}=-3*x^{-4};$$
$$(x^{frac{1}{3}})^{/}=frac{1}{3}*x^{1-frac{1}{3}}=frac{1}{3}*x^{frac{2}{3}};$$
Производная от квадратного корня
$$(sqrt{x})^{/}=frac{1}{2sqrt{x}};$$
Тут полезно заметить, что формулу производной от квадратного корня можно не учить. Она сводится к формуле производной от степени:
$$(sqrt{x})^{/}=(x^{frac{1}{2}})^{/}=frac{1}{2}*x^{frac{1}{2}-1}=frac{1}{2}*x^{-frac{1}{2}}=frac{1}{2sqrt{x}};$$
Производная от синуса
$$sin(x)^{/}=cos(x);$$
Производная от косинуса
$$cos(x)^{/}=-sin(x);$$
Производная от тангенса
$$tg(x)^{/}=frac{1}{cos^{2}(x)};$$
Производная от котангенса
$$tg(x)^{/}=frac{-1}{sin^{2}(x)};$$
Производная от экспоненты
$$(e^x)^{/}=e^x;$$
Производная от показательной функции
$$(a^x)^{/}=a^x*ln(a);$$
Пример 3
$$(2^x)^{/}=2^{x}*ln(2);$$
Производная от натурального логарифма
$$(ln(x))^{/}=frac{1}{x};$$
Производная от логарифма
$$(log_{a}(x))^{/}=frac{1}{x*ln(a)};$$
Свойства производной
Помимо формул по вычислению производной еще есть свойства производной, их тоже надо выучить.
Вынесение константы за знак производной
$$(alpha*f(x))^{/}=alpha*(f(x))^{/};$$
Пример 4
$$(3*x^5)^{/}=3*(x^5)^{/}=3*5x^4=15x^4;$$
$$(10sin(x))^{/}==10*(sin(x))^{/}=10*cos(x);$$
Производная от суммы и разности двух функций
$$(f(x) pm g(x))^{/}=(f(x))^{/} pm (g(x))^{/};$$
Пример 5
$$(2x^4+x^3)^{/}=?$$
Тут (f(x)=2x^4), а (g(x)=x^3). Тогда по формуле производной от суммы:
$$(2x^4+x^3)^{/}=(2x^4)^{/}+(x^3)^{/}=2*(x^4)^{/}+(x^3)^{/}=2*4x^3+3x^2=8x^3+3x^2;$$
Пример 6
$$(ln(x)+cos(x))^{/}=(ln(x))^{/}+(cos(x))^{/}=frac{1}{x}-sin(x);$$
Пример 7
$$(x^6-e^x)^{/}=(x^6)^{/}-(e^x)^{/}=6x^5-e^x;$$
Производная от произведения двух функций
$$(f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/};$$
Пример 8
$$(x^2*sin(x))^{/}=?$$
$$(x^2*sin(x))^{/}=(x^2)^{/}*sin(x)+x^2*(sin(x))^{/}=2x*sin(x)+x^2*cos(x);$$
Пример 9
$$(ln(x)*e^x)^{/}=(ln(x))^{/}*e^x+ln(x)*(e^x)^{/}=frac{1}{x}*e^x+ln(x)*e^x;$$
Производная от частного двух функций
$$left(frac{f(x)}{g(x)}right)^{/}=frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2};$$
Пример 10
$$left(frac{x^3}{sin(x)}right)^{/}=frac{(x^3)^{/}*sin(x)-x^3*(sin(x))^{/}}{(sin(x))^2}=frac{3x^2*sin(x)-x^3*cos(x)}{(sin(x))^2};$$
Примеры нахождения производной
Рассмотрим несколько примеров нахождения производной, чтобы разобраться, как применяются свойства и формулы производной на практике.
Пример 11
$$(5x^3+2cos(x))^{/}=(5x^3)^{/}+(2cos(x))^{/}=$$
$$=5*(x^3)^{/}+2*(cos(x))^{/}=5*3*x^2+2*(-sin(x))=15x^2-2sin(x);$$
Пример 12
$$left(-frac{3x^2}{2x^4+5x}right)^{/}=-frac{(3x^2)^{/}*(2x^4+5x)-3x^2*(2x^4+5x)^{/}}{(2x^4+5x)^2}=$$
$$=-frac{6x*(2x^4+5x)-3x^2*(8x+5)}{(2x^4+5x)^2}=-frac{12x^5-24x^3+15x^2}{(2x^4+5x)^2};$$
Пример 13
$$(2xsqrt{x})^{/}=(2x)^{/}*sqrt{x}+2x*(sqrt{x})^{/}=$$
$$=2*sqrt{x}+2x*frac{1}{2sqrt{x}}=2*sqrt{x}+frac{2x}{2sqrt{x}}=2*sqrt{x}+sqrt{x}=3sqrt{x};$$
Производная сложной функции
Сложная функция — это функция не от аргумента (x), а от какой-то другой функции: (f(g(x))). Например, функция (sin(x^2)) будет сложной функцией: «внешняя» функция синуса берется от «внутренней» функции степени ((x^2)). Так как под синусом стоит аргумент не (x), а (x^2), то такая функция будет называться сложной.
Еще примеры сложных функций:
-
$$ln(3x^4);$$
Внешняя функция: натуральный логарифм; Внутренняя функция: ((3x^4)). -
$$cos(ln(x));$$
Внешняя функция: косинус; Внутренняя функция: ((ln(x))). -
$$e^{2x^2+3};$$
Внешняя функция: экспонента; Внутренняя функция: ((2x^2+3)). -
$$(sin(x))^3;$$
Внешняя функция: возведение в третью степень; Внутренняя функция: (sin(x)).
Чтобы посчитать производную от такой функции, нужно сначала найти производную внешней функции, а затем умножить результат на производную внутренней функции. В общем виде формула выглядит так:
$$f(g(x))^{/}=f^{/}(g(x))*g^{/}(x);$$
Скорее всего, выглядит непонятно, поэтому давайте разберем на примерах.
Пример 14
$$((cos(x))^4)^{/}=?$$
Внешней функцией тут будет возведение в четвертую степень, поэтому сначала считаем производную от степени по формуле ((x^n)^{/}=n*x^{n-1}). А потом умножаем результат на производную внутренней функции, у нас это функция косинуса, по формуле (cos(x)^{/}=-sin(x)):
$$((cos(x))^4)^{/}=underset{text{внешняя производная}}{underbrace{4*(cos(x))^3}}*underset{text{внутренняя производная}}{underbrace{(cos(x))^{/}}}=$$
$$=4*(cos(x))^3*(-sin(x))=-4*(cos(x))^3*sin(x);$$
Пример 15
$$(e^{2x^3+5})^{/}=?$$
Внешняя функция — это экспонента ((e^x)^{/}=e^x), а внутренняя функция — квадратный многочлен ((2x^3+5)):
$$(e^{2x^3+5})^{/}=e^{2x^3+5}*(2x^3+5)^{/}=e^{2x^3+5}*((2x^3)^{/}+5^{/})=e^{2x^3+5}*6x^2.$$
Пример 16
$$(ln((2x^2+3)^6))^{/}=?$$
Внешняя функция — это натуральной логарифм, берем производную от него по формуле ((ln(x))^{/}=frac{1}{x}), и умножаем на производную внутренней функции, у нас это шестая степень: ((x^n)^{/}=n*x^{n-1}). Но и на этом еще не все: под шестой степенью стоит не просто (x), а квадратный многочлен, значит еще нужно умножить на производную от этого квадратного многочлена:
$$ln((2x^2+3)^6)=frac{1}{(2x^2+3)^6}*((2x^2+3)^6)^{/}*(2x^2+3)^{/}=$$
$$=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*(4x+0)=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*4x=$$
$$=frac{6*(2x^2+3)^5*4x}{(2x^2+3)^6}=frac{24x*(2x^2+3)^5}{(2x^2+3)^6}=frac{24x}{(2x^2+3)^6}.$$
Вывод формул производной функции
Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись (f(x)) означает, что функция берется от аргумента (x). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента (x) может стоять все что угодно, например выражение (2x+3). Обозначение такой функции будет (f(2x+3)), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента (x) мы пишем (2x+3).
И несколько важных замечаний про (Delta f(x)) и (Delta x). Напомню, что значок (Delta) означает изменение некоторой величины. (Delta x) — изменения координаты (x) при переходе от одной точки на графике функции к другой; (Delta f(x)) — разница координат (y) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем (Delta x) для двух близких точек на графике функции (O) и (B):
$$Delta x=x_B-x_O;$$
Отсюда можно выразить (x_B):
$$x_B=x_O+Delta x;$$
Абсцисса (координата точки по оси (x)) точки (B) получается путем сложения абсциссы точки (O) и (Delta x).
Кстати, функцию (f(x)=x^3+sin(x)) от аргумента (x_B=x_O+Delta x) можно расписать:
$$f(x_B)=f(x_O+Delta x)=(x_O+Delta x)^3+sin(x_O+Delta x);$$
Рис.1. График произвольной функции
И распишем (Delta f):
$$Delta f(x)=f(x_B)-f(x_O)=f(x_O+Delta x)-f(x_O);$$
Тогда определение производной можно записать в виде:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x_O+Delta x)-f(x_O)}{Delta x} quad при quad Delta x to 0;$$
За (x_O) обычно обозначают точку, в окрестности которой берут производную. То есть, получается (x_O) — это абсцисса начальной точки, а (x_O+Delta x) — абсцисса конечной точки.
Нам это пригодится при выводе формул производной.
Производная квадратичной функции
Выведем теперь формулу производной от (f(x)=x^2), воспользовавшись определением производной:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
Распишем числитель (f(x+Delta x)-f(x)) с учетом, что (f(x)=x^2):
$$f(x+Delta x)-f(x)=(x+Delta x)^2-x^2=x^2+2xDelta x+(Delta x)^2-x^2=2xDelta x+(Delta x)^2;$$
Подставим в определение производной:
$$f^{/}(x)=frac{2xDelta x+(Delta x)^2}{Delta x}=frac{Delta x*(2x+Delta x)}{Delta x}=2x+Delta x;$$
Напоминаю, что (Delta x) это бесконечно малая величина:
$$(Delta x)^2 ll 0;$$
Поэтому этим слагаемым можно пренебречь. Вот мы и получили формулу для производной от квадратной функции:
$$f^{/}(x)=(x^2)^{/}=2x;$$
Производная от третьей степени
Аналогичные рассуждения можно провести для функции третьей степени:
$$f(x)=x^3;$$
Воспользуемся определением производной:
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
$$f(x+Delta x)-f(x)=(x+Delta x)^3-x^3=(x+Delta x-x)((x+Delta x)^2+(x+Delta x)*x+x^2)=$$
$$=Delta x*(x^2+2x*Delta x+(Delta x)^2+x^2+x*Delta x+x^2)=Delta x*(3x^2+3xDelta x);$$
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x}=frac{Delta x*(3x^2+3xDelta x)}{Delta x}=3x^2+3xDelta x;$$
Так как при умножении на бесконечно малую величину получается бесконечно малая величина, то слагаемым (3xDelta x) можно пренебречь:
$$f^{/}(x)=(x^3)^{/}=3x^2;$$
Точно таким же способом можно вывести формулы производных для любых степеней:
$$(x^4)^{/}=4x^3;$$
$$(x^5)^{/}=5x^4;$$
$$…$$
$$(x^n)^{/}=n*x^{n-1};$$
Кстати, эта формула справедлива и для дробных степеней.
Вывод остальных формул делается похожим образом, только там может понадобиться знание пределов. Вывод всех формул разбирается в университетском курсе математического анализа.
Что такое производная функции простыми словами? Для чего нужна производная? Определение производной
Как решать задания №7 из ЕГЭ по математике. Анализ графиков при помощи производной. Графики производной и графики функции
Исследуем функцию с помощью производной. Находим точки минимума и максимума, наибольшее и наименьшее значение функции. Точки экстремума. Промежутки возрастания и убывания.
Связь коэффициента наклона и тангенса угла наклона касательной к функции и производной функции в точке касания. Задание №7 в ЕГЭ по математике.

















 html
html
 Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.
Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.
 Соответственно, во всех примерах производная y′ берётся по переменной x. Чтобы подчеркнуть то, что производная берётся по переменной x, часто вместо y′ пишут y′x.
Соответственно, во всех примерах производная y′ берётся по переменной x. Чтобы подчеркнуть то, что производная берётся по переменной x, часто вместо y′ пишут y′x. 1)
1) е. число 9) можно вынести за знак производной:
е. число 9) можно вынести за знак производной: 2) теперь станет таким:
2) теперь станет таким: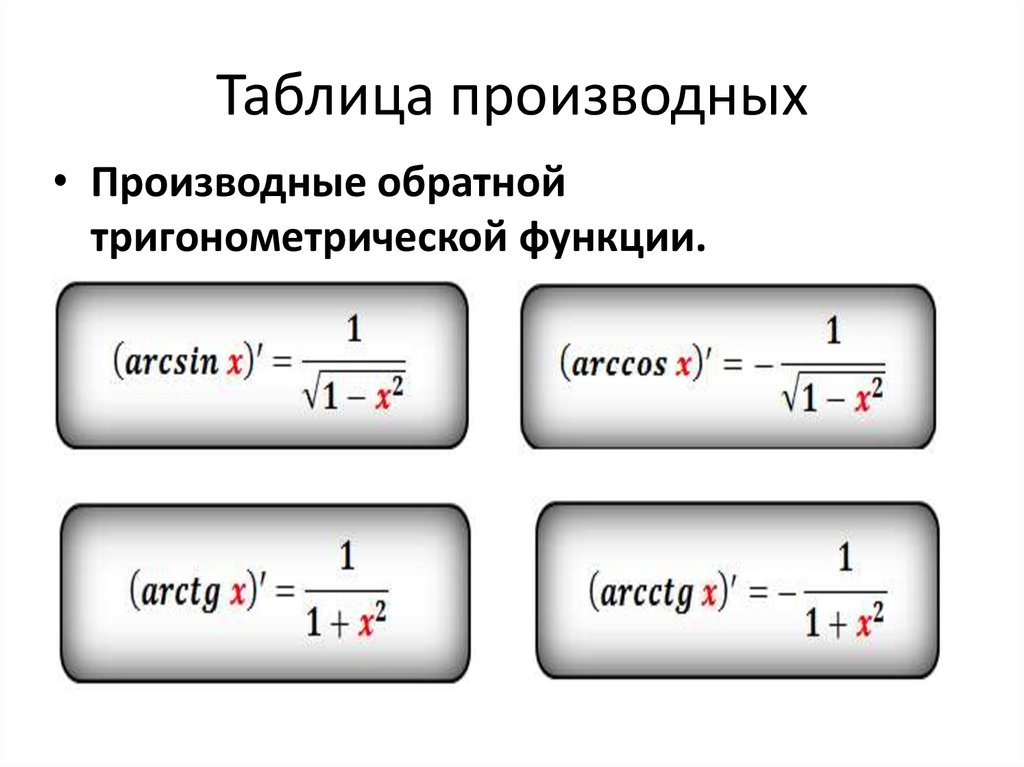
 е. (5⋅9x)′=5⋅(9x)′. Для нахождения производной (9x)′ применим формулу №5 таблицы производных, подставив в неё a=9 и u=x: (9x)′=9x⋅ln9⋅x′. Так как x′=1, то (9x)′=9x⋅ln9⋅x′=9x⋅ln9. Теперь можно продолжить равенство (3.3):
е. (5⋅9x)′=5⋅(9x)′. Для нахождения производной (9x)′ применим формулу №5 таблицы производных, подставив в неё a=9 и u=x: (9x)′=9x⋅ln9⋅x′. Так как x′=1, то (9x)′=9x⋅ln9⋅x′=9x⋅ln9. Теперь можно продолжить равенство (3.3): Подставляя α=−1 в формулу №2, получим:
Подставляя α=−1 в формулу №2, получим:


