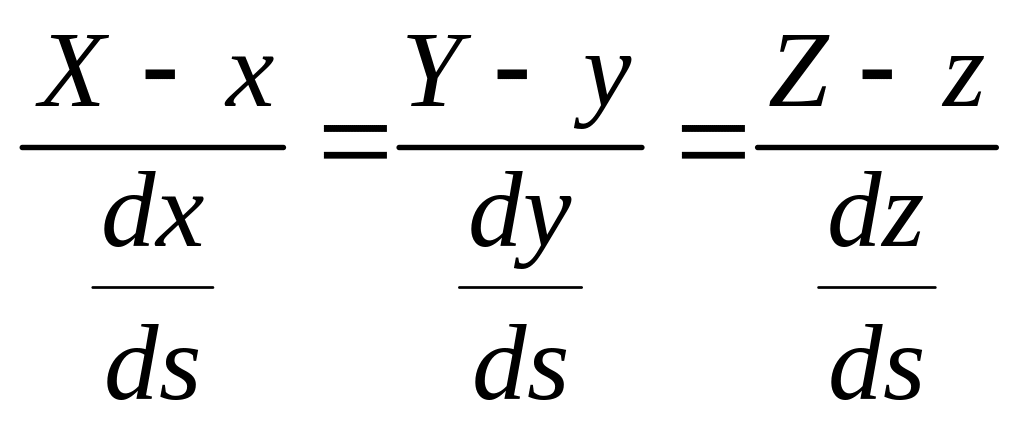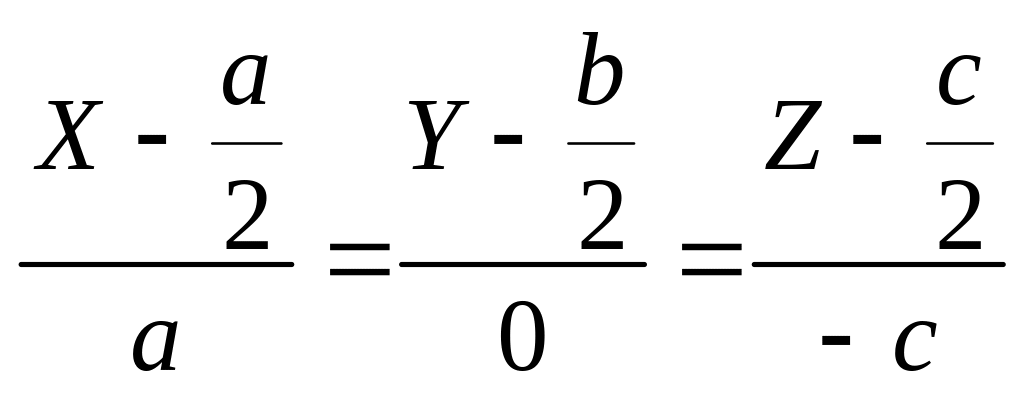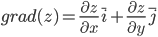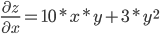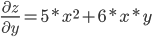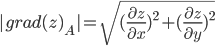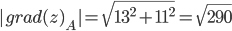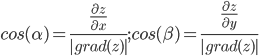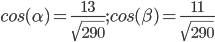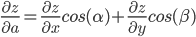Как найти производную единичного вектора

Напишем основные
правила дифференцирования векторных
функций.

1.

,

− постоянный вектор;

2.

;

3.

,
где т
= т(t)
− скалярная функция;

4

;

5.

.

Пример.
Найти производную скалярного произведения
векторов

и

.

□ Имеем

+


=

=
−6 + 6 = 0.

Полученный
результат объясняется тем, что скалярное
произведение заданных векторов

,
т.е. является постоянной величиной.
■

По аналогии с
дифференциалом скалярной функции
дифференциал векторной функции

есть вектор

,
определяемы равенством

,

где

− приращение скалярного аргумента t.

Дифференциал
вектора

,
как и производная

вектора

,
лежит на касательной к годографу.
Направление

на этой касательной зависит от знака

:
при

вектор

направлен в сторону возрастания
аргумента t,
при

,
наоборот, в сторону его убывания.

Дифференциал
векторной функции в проекциях:

или

,

где

− дифференциалы скалярных функций

.

Модуль дифференциала
векторной функции :

.

В
частности, для дифференциала радиус-вектора
точки

и его модуля имеем

и

.

С
другой стороны, дифференциал длины дуги
кривой

определяется формулой

.

Следовательно,

,

т.е.
модуль дифференциала радиус-вектора
точки равен дифференциалу длины дуги,
описываемой этой точкой.

Рассмотрим единичный
вектор

,
изменяющийся при изменении скаляра t
только по направлению. В этом случае

и
модуль вектора приращения

определяется из равенства

,

где

− угол смежности векторов

и

.
Отсюда следует, что

.

Рассматривая
аргумент t
как время, можно интерпретировать
производную

как угловую скорость вращения единичного
вектора.

Производная
от единичного вектора

есть вектор, перпендикулярный к нему,
модуль которого равен угловой скорости
вращения.

Отсюда
следует, что производная единичного
вектора, вообще говоря, не есть единичный
вектор; она будет таковым, если вращение
первоначального вектора происходит
равномерно.

Пусть векторная
функция

скалярного аргумента t
изменяется как по величине, так и по
направлению. Вектор

можно представить как произведение его
модуля

и единичного вектора его направления

:

.

Тогда

.

Вектор

,
как производная единичного вектора,
перпендикулярен вектору

и тем самым вектору

.
Следовательно, первое слагаемое

есть вектор, перпендикулярный вектору

,
а слагаемое

− вектор, ему параллельный. Таким
образом, последняя формула дает разложение
производной

от вектора

по направлению первоначального вектора

и к нему перпендикулярному.

Когда вектор

изменяется только по модулю, то вектор

сохраняет постоянное направление и

= 0. Если же вектор

имеет постоянный модуль, то

= 0. В этом случае

образует с вектором

прямой угол.

§ 4. Некоторые приложения векторных функций скаляроного аргумента

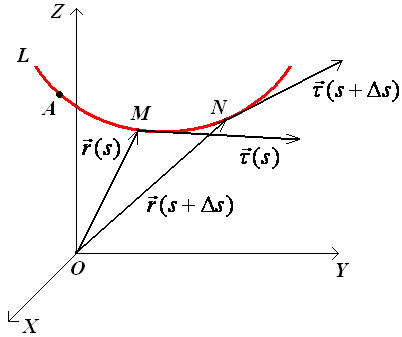
Пусть точка М(х,
y,
z)
описывает кривую L
в пространстве. Параметром, определяющим
положение точки М
на кривой, будем считать длину s
дуги АМ
кривой, отсчитываемую от определенной
точки А
кривой до точки М.
Радиус-вектор

точки М
будет функцией скалярного аргумента
s:

.

В
проекциях радиус-вектор точки запишется
как

,

где

− скалярные функции длины дуги s.
При этом величина s
считается положительной, если она
отложена в определенную сторону от
точки А,
которую мы примем за положительную, и
отрицательной, если она отложена в
другую сторону.

Продифференцируем
вектор

по скаляру s.
Получим вектор

,

направленный
по касательной к кривой в сторону
возрастания s.
Модуль этого вектора

.

Следовательно,
вектор

есть единичный вектор касательной к
кривой, направленный в сторону возрастания
s.

В проекциях

(1)

и

.

Так как единичный
вектор касательной

лежит на самой касательной, то уравнения
касательной к кривой в точке М,
как известно из аналитической геометрии,
напишутся так:

,
(2)

где
X,
Y,
Z
− текущие координаты точки на касательной,
а x,
y,
z
− координаты точки касания, причем
значения производных

берутся
в точке касания.

Плоскость,
перпендикулярная касательной и проходящая
через точку касания, называется
нормальной
плоскостью.

Любая
прямая, лежащая в этой плоскости и
пересекающая кривую в точке касания
М,
будет нормалью кривой.

Уравнение нормальной
плоскости можно получить, используя
условия перпендикулярности прямой и
плоскости. В результате получим

,
(3)

где
X,
Y,
Z
− текущие координаты точки на нормальной
плоскости.

Вектор

,
как производная единичного вектора

,
перпендикулярен к последнему. Поэтому
вектор

лежит в нормальной плоскости и определяет
некоторую нормаль, называемую главной
нормалью.

Модуль

называют кривизной
кривой.
Обозначим ее через К
=

,
где R
− радиус
кривизны
:

К
=

=

.

В
проекциях

.
(4)

Тогда
кривизна найдется по формуле

К
=

.
(5)

В
соответствии с (4) уравнения главной
нормали имеют вид

,
(6)

где
X,
Y,
Z
− текущие координаты точки на главной
нормали.

Плоскость,
перпендикулярная главной нормали и
проходящая через точку касания, называется
спрямляющей
плоскостью
кривой. Она
определяется уравнением

.
(7)

Плоскость, проходящая
через касательную и главную нормаль,
называется соприкасающейся
плоскостью.
Эту плоскость можно определить как
предельное положение плоскости,
проходящей через три точки кривой, когда
эти точки стремятся слиться в одну.

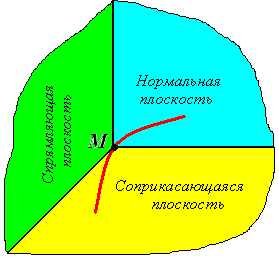
Если кривая –
плоская, то касательные ко всем ее точкам
находятся в одной плоскости – плоскости
кривой. В этом случае соприкасающаяся
плоскость совпадает с плоскостью кривой
и будет одна и та же для всех ее точек.
Главная нормаль кривой будет совпадать
с нормалью, определенной на плоскости.

Пример.
Составить уравнения касательной и
нормальной плоскости к кривой

в
точке

.

□ Имеем

уравнения
касательной:

;

уравнение
нормальной плоскости:

.

Находим

,

,

.
При

имеем

,

,

,

,

,

.

Уравнения
касательной:

.

Уравнение
нормальной плоскости:

или

.
■

Пример.
Составить уравнения винтовой линии,
если радиус основания цилиндра R
= 4, шаг h
=

,
и найти дифференциал ее дуги.

□ Параметрические
уравнения винтовой линии имеют вид

.

Согласно
условию задачи получим

,

т.к.

при

.

Дифференциал дуги
можно найти по формуле

=

.

Находим

,

,

.

Следовательно,

=

.
■

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Заказать задачи по любым предметам можно здесь от 10 минут

Производная функции по направлению

Как найти?

Постановка задачи

Найти производную функции $ u(x,y,z) $ в точке $ M (x_1,y_1,z_1) $ по направлению вектора $ overline{l} = (l_x,l_y,l_z) $

План решения

Если для функции $ u(x,y,z) $ существует производная в точке $ M(x_1,y_1,z_1) $, то значит в этой точке существует производная по любому направлению $ overline{l} $ и находится по формуле:

$$ frac{partial u}{partial l} = frac{partial u}{partial x} bigg |_M cdot cos alpha + frac{partial u}{partial y} bigg |_M cdot cos beta + frac{partial u}{partial z} bigg |_M cdot cos gamma $$

1. Находим частные производные первого порядка:
   $$ frac{partial u}{partial x}; frac{partial u}{partial y}; frac{partial u}{partial z} $$
2. Вычисляем полученные производные в точке $ M(x_1,y_1,z_1) $:
   $$ frac{partial u}{partial x} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial y} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial z} bigg |_{M(x_1,y_1,z_1)} $$
3. Получаем направляющие косинусы по формулам:
   $$ cos alpha = frac{l_x}{|overline{l}|}; cos beta = frac{l_y}{|overline{l}|}; cos gamma = frac{l_z}{|overline{l}|} $$
4. Подставляем все полученные данные в формулу и записываем ответ

Примеры решений

Пример 1

Найти производную функции $ u = x+ln(z^2+y^2) $ в точке $ M (2,1,1) $ по направлению вектора $ overline{l} = (-2,1,-1) $

Решение

Находим частные производные первого порядка и вычисляем их начение в точке $ M $: $$ frac{partial u}{partial x} = 1; frac{partial u}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial u}{partial y} = frac{2y}{z^2+y^2}; frac{partial u}{partial y} bigg |_{M(2,1,1)}=1 $$ $$ frac{partial u}{partial z} = frac{2z}{z^2+y^2}; frac{partial u}{partial z} bigg |_{M(2,1,1)} = 1 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{-2}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{-2}{sqrt{6}} $$ $$ cos beta = frac{1}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{1}{sqrt{6}} $$ $$ cos gamma = frac{-1}{sqrt{(-2)^2+1^2+(-1)^2}} = — frac{1}{sqrt{6}} $$ Подставляем полученные частные производные в точке $ M $ и направляющие косинусы в формулу: $$ frac{partial u}{partial l} = 1 cdot (-frac{2}{sqrt{6}}) + 1 cdot frac{1}{sqrt{6}} + 1 cdot (-frac{1}{sqrt{6}}) = -frac{2}{sqrt{6}} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ frac{partial u}{partial l} = -frac{2}{sqrt{6}} $$

Пример 2

Найти производную $ u = xy — frac{x}{z} $ в точке $ M(-4,3,-1) $ по направлению вектора $ overline{l} = (5,1,-1) $

Решение

Берем частные производные первого порядка от функции в точке $ M(-4,3,-1) $: $$ frac{partial u}{partial x} = y — frac{1}{z}; frac{partial u}{partial x} bigg |_{M(-4,3,-1)} = 4 $$ $$ frac{partial u}{partial y} = x; frac{partial u}{partial y} bigg |_{M(-4,3,-1)} = -4 $$ $$ frac{partial u}{partial z} = frac{x}{z^2}; frac{partial u}{partial z} bigg |_{M(-4,3,-1)} = -4 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{5}{sqrt{5^2+1^2+(-1)^2}} = frac{5}{sqrt{27}} $$ $$ cos beta = frac{1}{sqrt{5^2+1^2+(-1)^2}} = frac{1}{sqrt{27}} $$ $$ cos gamma = frac{-1}{sqrt{5^2+1^2+(-1)^2}} = frac{-1}{sqrt{27}} $$ По формуле производной по направлению получаем ответ: $$ frac{partial u}{partial l} = 4 cdot frac{5}{sqrt{27}} + (-4) cdot frac{1}{sqrt{27}} + (-4) cdot frac{-1}{sqrt{27}} = frac{20}{sqrt{27}} $$

Ответ

$$ frac{partial u}{partial l} = frac{20}{sqrt{27}} $$

Дифференцирование единичного вектора

Дифференцирование единичного вектора

• Вычислить производную единичного вектора по скалярному аргументу. В точечной кинематике скалярным аргументом обычно является время и расстояние вдоль пути. В качестве единичного вектора выберите m, ориентированный по касательной траектории, и рассчитайте его производную по времени. Производная dx / dr перпендикулярна единичному вектору m. Чтобы доказать это, используйте тождество t-t = l. Различая обе части этой идентичности по времени, 2-м = 0. PhD. Поскольку каждый фактор в этом уравнении не равен нулю, векторы di’dr и m перпендикулярны друг другу.

С помощью построения фазовой плоскости найдено периодическое движение системы, которое приводит к переходу в устойчивое состояние движения, зависящее от различных параметров и начальных условий движения. Людмила Фирмаль

Это верно для всего остального Вектор с постоянным числовым значением (модулем). Получает единичный вектор n вдоль вектора dt / dr. Тогда dx / dz =] dx / dz | p. (14) Поскольку единичный вектор изменяется только в направлении, годограф вектора m представляет собой кривую на сфере единичного радиуса (рисунок 16). Определяя модуль векторных производных, «= лим. dr d (-. o | Dg | Длина шнура до небольшого значения старшего порядка, равного длине дуги, которая соединяет шнур, т. Е. | При | = 1 | НЧ | Где Af — угол этой дуги. Используйте это выражение, чтобы получить = Lim Lim. Доктор Д> -. о! Dg | A / —O IDGIIdrl.

• Подставляя это значение в (14), используя уравнение радиуса кривизны и переменную s, получим dtp n = dtp ds d7 d.v df. Радиус кривизны p считается положительным. Единичные векторы, которые соответствуют вектору dt / dr и направлению, ориентированы параллельно ограничивающему положению вектора Am, поскольку Ar стремится к нулю. То есть он размещен на изогнутой контактной поверхности. Единичный вектор n перпендикулярен вектору m, ориентированному по касательной кривой.

В результате ограниченное положение вектора Am ориентируется в этом направлении, поэтому вектор n ориентируется вдоль основной нормали кривой в направлении его вогнутой поверхности. Если существует другой вектор B с постоянным модулем, все, что получено для единичного вектора, является действительным, и только радиус годографа заменяется модулем b. получить (15 ‘) Где n — единичный вектор, ориентированный перпендикулярно вектору b и параллельно дБлдт.

Сила трения скольжения расположена на общей касательной плоскости контактной поверхности объекта и направлена в направлении, противоположном направлению возможного или фактического скольжения тела под действием приложенной силы. Людмила Фирмаль

Уравнение (15 ‘) можно выразить как векторное произведение: LBI df = ωx B, Где ω — вектор угловых скоростей вращения вектора B и его модуль ||> | = | dcp / d / |. Вектор угловой скорости ω должен быть ориентирован перпендикулярно плоскости, в которой расположены векторы b и n, и, используя эту стрелку, поворот вектора b к n в этой плоскости против часовой стрелки под углом 90 ° Должны видеть Понятие вектора угловой скорости более подробно показано при рассмотрении жесткого поворота деревни вокруг неподвижной оси и других случаях его движения.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Вектор-функции

Предел и непрерывность вектор-функции.

Понятие вектор-функции.

Если каждому значению (tin E), где (Esubsetmathbb), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).

Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.

В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.

Предел вектор-функции.

Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_>r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_> |r(t)-a|=0,label
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).

Рис. 20.1

Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_<1>,a_<2>,a_<3>)), то
$$
lim_>r(t)=alabel
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label
$$

Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref, то выполняется условие eqref.

Обратно: если выполняются условия eqref, то из равенства eqref следует, что выполнено условие eqref. (bullet)

При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox <при> trightarrow t_<0>.nonumber
$$

Свойства пределов вектор-функций.

(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$

Если (r(t)rightarrow a) при (trightarrow t_<0>), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_<0>), то (f(t)r(t)rightarrow Aa) при (trightarrow t_<0>), то есть
$$
lim_f(t)r(t)=lim_>f(t)lim_r(t).label
$$

(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref. (bullet)

(circ) По условию (r_(t)=a_+alpha_), где (a_i(t)rightarrow 0) при (trightarrow t_<0> (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_<1>(t)+alpha_2(t)rightarrow 0) при (trightarrow t_<0>), откуда следует eqref. Докажем формулу eqref. В силу свойств скалярного произведения
$$
(r_<1>(t),r_2(t))-(a_1,a_2)=(alpha_<1>(t),a_<2>)+(alpha_<2>(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_<1>(t),alpha_<2>(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).

Аналогично доказывается формула eqref, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)

Непрерывность вектор-функции.

Вектор-функцию (r(t)) называют непрерывной при (t=t_<0>), если
$$
lim_>r(t)=r(t_0).label
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_<0>) в силу эквивалентности условий eqref и eqref означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_<0>).

Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_<0>). Тогда условие eqref означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label
$$

Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_<0>), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_<0>).

Производная и дифференциал вектор-функции.

Производная вектор-функции.

Если существует (displaystyle lim_<Delta trightarrow 0>frac<Delta r><Delta t>) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot(t_0)).

Таким образом,
$$
r'(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r(t_<0>)><Delta t>.label
$$
Аналогично вводится понятие второй производной
$$
r″(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r'(t_<0>)><Delta t>nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_<0>)=(x'(t_0),y'(t_0),z'(t_0))label
$$
Утверждение eqref следует из определения eqref и свойств пределов вектор-функций.

Аналогично, если существует (r″(t_<0>)), то
$$
r″(t_<0>)=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref, то есть вектор-функция (r(t)), имеющая производную в точке (t_<0>), непрерывна при (t=t_<0>).

(circ) Формулы eqref-eqref справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref. Пусть (Delta r_) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin
(r_<1>,r_<2>)’=displaystylelim_<Delta trightarrow 0>frac<(r_<1>(t+Delta t),r_<2>(t+Delta t))-(r_<1>(t),r_<2>(t))><Delta t>=\
=lim_<Delta trightarrow 0>left[left(r_<1>(t),frac<Delta r_<2>(t)><Delta t>right)+left(frac<Delta r_<1>(t)><Delta t>,r_2(t)right)+left(frac<Delta r_<1>(t)><Delta t>,Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
endnonumber
$$
так как (displaystyle frac<triangle mathrm_><triangle t>rightarrow r_‘(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)

Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).

Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.

(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^<2>)’=(C^<2>)’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$

Дифференциал вектор-функции.

Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_<0>), называют дифференцируемой при (t=t_<0>), если ее приращение (Delta r=r(t_<0>+Delta t)-r(t_<0>)) в точке (t_<0>) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).

Полагая (dt=Delta t), запишем равенство eqref в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac

.label (21)
$$

Замена переменного.

Если функция (t=t(s)) дифференцируема при (s=s_<0>, t(s_<0>)=t_<0>), а вектор-функция (r(t)) дифференцируема в точке (t_<0>), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_<0>), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_'(t_<0>)t_‘(s_<0>),label
$$

где индекс указывает, по какому переменному производится дифференцирование.

(circ) Функция (alpha(Delta(t))) в формуле eqref не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).

Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_<0>+Delta s)-t(s_<0>)rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref на (Delta sneq 0), получим
$$
frac<Delta r><Delta s>=r'(t_0)frac<Delta t><Delta s>+alpha(Delta t)frac<Delta t><Delta s>.label
$$
Правая часть eqref имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref, и справедливо равенство eqref. Формулу eqref запишем кратко в виде равенства
$$
r_’=r_’t_’,label
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)

Теорема Лагранжа и локальная формула Тейлора для вектор-функции.

Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label
$$
для вектор-функции, вообще говоря, неверна.

(circ) В самом деле, пусть формула eqref верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)

Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label
$$

(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label
$$
Преобразуем левую часть неравенства eqref:
$$
begin
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
endnonumber
$$
Тогда равенство eqref примет вид
$$
|r(beta)-r(alpha)|^<2>=(r(beta)-r(alpha),r'(xi))(beta-alpha).label
$$
Если (r(beta)=r(alpha)), то неравенство eqref справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref получим
$$
|r(beta)-r(alpha)|^<2>leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref. (bullet)

Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_^frac(t_<0>)>(t-t_<0>)^+varepsilon(t-t_<0>),label
$$
где (varepsilon(t-t_0)=o((t-t_<0>)^)) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_<0>)^varepsilon_<1>(t-t_<0>)), где (varepsilon_<1>(t-t_<0>)rightarrow 0) при (trightarrow t_<0>).Эта формула справедлива в предположении, что существует (r^<(n)>(t_0)). Для доказательства формулы eqref достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).

Векторное дифференцирование

В дальнейшем в различных главах будет использовано векторное дифференцирование, которое позволяет использовать более компактную и наглядную запись. Поэтому в этом параграфе кратко рассмотрим определения и свойства векторного дифференцирования (символ *= f обозначает равенство по определению).

1) Производная вектора х = (х Х2 . х_п) Т по скаляру t:

2) Производная скалярной функции 5 = s (х) по вектору х = = (х Х2 . х_п) Т :

3) Производная векторной функции f (х) (f = (Д . /_п) т ) по вектору х = (si Х2 . х_п) Т :

Используя приведенные определения и обычные правила дифференцирования, можно получить следующие правила векторного дифференцирования.

1°. Производная скалярного произведения по скаляру t:

Если у = х, то имеем

2°. Производная произведения матрицы и вектора по скаляру t:

А — (т х п)-матрица, зависящая от t.

3°. Производная скалярного произведения по вектору х =

Если у = z, то имеем

4°. Производная квадратичной формы по вектору х = = (Xj Х2 • • • &п) •

Q — симметрическг^я (тг х п)-матрица, не зависящей от х.

5°. Производная сложной векторной функции по скаляру t:

источники:

http://univerlib.com/mathematical_analysis/derivative/vector_functions/

http://studme.org/270187/tehnika/vektornoe_differentsirovanie