Как найти производную если число в степени

Как считать производную степенной функции

3 февраля 2015

Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.

В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.

Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.

Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.

Что такое производная?

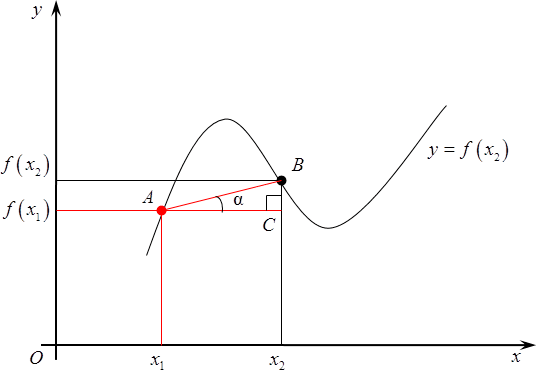
Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=fleft( x right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $fleft( {{x}_{1}} right)$.

Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $fleft( {{x}_{2}} right)$.

Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.

А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:

1. прямая $AC$параллельна оси $Ox$ по построению,
2. прямая $AB$ пересекает $AC$ под $alpha $,
3. следовательно, $AB$ пересекает $Ox$под тем же самым $alpha $.

Что мы можем сказать об $text{ }!!alpha!!text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:

[tg=frac{BC}{AC}]

Разумеется, $AC$ в данном случае легко считается:

[AC={{x}_{2}}-{{x}_{1}}]

Точно также и $BC$:

[BC=fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)]

Другими словами, мы можем записать следующее:

[operatorname{tg}text{ }!!alpha!!text{ }=frac{fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)}{{{x}_{2}}-{{x}_{1}}}]

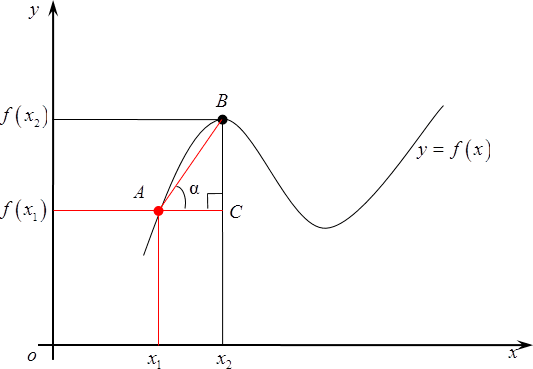
Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $fleft( {{x}_{2}} right)$.

Вновь рассмотрим наш маленький треугольник $ABC$и $text{ }!!alpha!!text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.

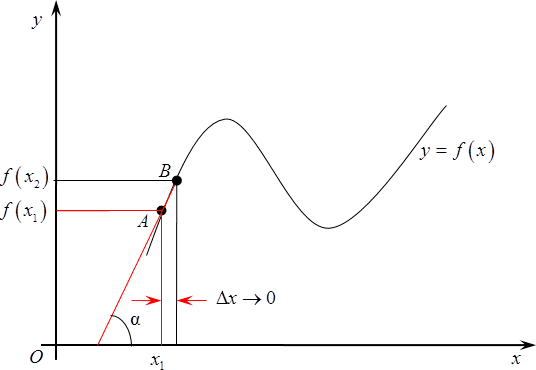
Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.

 

В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $text{ }!!alpha!!text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.

И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:

[{f}’left( {{x}_{1}} right)=operatorname{tg}text{ }!!alpha!!text{ }]

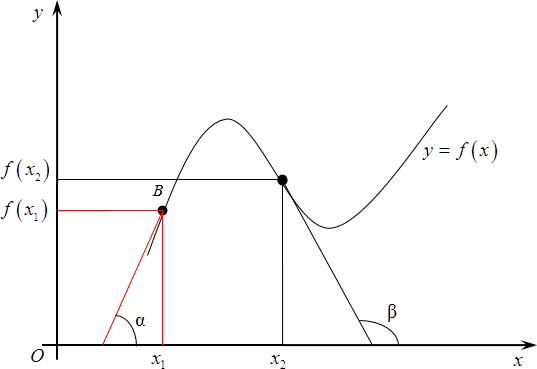
Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке. 

Угол между касательной и положительным направлением оси назовем $beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $beta $.

[{f}’left( {{x}_{2}} right)=tgtext{ }!!beta!!text{ }]

В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.

Производная степенной функции

К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.

Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}’=ncdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:

[begin{align}& y={{x}^{2}} \& {y}’=2cdot {{x}^{2-1}}=2x \end{align}]

А вот другой вариант:

[begin{align}& y={{x}^{1}} \& {y}’={{left( x right)}^{prime }}=1cdot {{x}^{0}}=1cdot 1=1 \& {{left( x right)}^{prime }}=1 \end{align}]

Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:

[fleft( x right)={{x}^{6}}]

Итак, мы получаем:

[{{left( {{x}^{6}} right)}^{prime }}=6cdot {{x}^{5}}=6{{x}^{5}}]

Теперь решим второе выражение:

[begin{align}& fleft( x right)={{x}^{100}} \& {{left( {{x}^{100}} right)}^{prime }}=100cdot {{x}^{99}}=100{{x}^{99}} \end{align}]

Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.

Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:

[{{left( f+g right)}^{prime }}={f}’+{g}’]

Аналогично, производная разности двух функций равна разности производных:

[{{left( f-g right)}^{prime }}={f}’-{g}’]

Пример:

[{{left( {{x}^{2}}+x right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}+{{left( x right)}^{prime }}=2x+1]

Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:

[{{left( ccdot f right)}^{prime }}=ccdot {f}’]

Пример:

[{{left( 3{{x}^{3}} right)}^{prime }}=3{{left( {{x}^{3}} right)}^{prime }}=3cdot 3{{x}^{2}}=9{{x}^{2}}]

Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:

[{{left( c right)}^{prime }}=0]

Пример решения:

[{{left( 1001 right)}^{prime }}={{left( frac{1}{1000} right)}^{prime }}=0]

Еще раз ключевые моменты:

1. Производная суммы двух функций всегда равна сумме производных: ${{left( f+g right)}^{prime }}={f}’+{g}’$;
2. По аналогичным причинам производная разности двух функций равна разности двух производных: ${{left( f-g right)}^{prime }}={f}’-{g}’$;
3. Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: ${{left( ccdot f right)}^{prime }}=ccdot {f}’$;
4. Если вся функция представляет собой константу, то ее производная всегда ноль: ${{left( c right)}^{prime }}=0$.

Давайте посмотрим, как все это работает на реальных примерах. Итак:

[y={{x}^{5}}-3{{x}^{2}}+7]

Записываем:

[begin{align}& {{left( {{x}^{5}}-3{{x}^{2}}+7 right)}^{prime }}={{left( {{x}^{5}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{7}’= \& =5{{x}^{4}}-3{{left( {{x}^{2}} right)}^{prime }}+0=5{{x}^{4}}-6x \end{align}]

В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.

Переходим ко второй функции:

[fleft( x right)=3{{x}^{2}}-2x+2]

Записываем решение:

[begin{align}& {{left( 3{{x}^{2}}-2x+2 right)}^{prime }}={{left( 3{{x}^{2}} right)}^{prime }}-{{left( 2x right)}^{prime }}+{2}’= \& =3{{left( {{x}^{2}} right)}^{prime }}-2{x}’+0=3cdot 2x-2cdot 1=6x-2 \end{align}]

Вот мы и нашли ответ.

Переходим к третьей функции — она уже посерьезней:

[y=2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5]

Решаем:

[begin{align}& {{left( 2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5 right)}^{prime }}={{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{{left( frac{1}{2}x right)}^{prime }}-{5}’= \& =2{{left( {{x}^{3}} right)}^{prime }}-3{{left( {{x}^{2}} right)}^{prime }}+frac{1}{2}cdot {x}’=2cdot 3{{x}^{2}}-3cdot 2x+frac{1}{2}cdot 1=6{{x}^{2}}-6x+frac{1}{2} \end{align}]

Ответ мы нашли.

Переходим к последнему выражению — самому сложному и самому длинному:

[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1]

Итак, считаем:

[begin{align}& {{left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 right)}^{prime }}={{left( 6{{x}^{7}} right)}^{prime }}-{{left( 14{{x}^{3}} right)}^{prime }}+{{left( 4x right)}^{prime }}+{5}’= \& =6cdot 7cdot {{x}^{6}}-14cdot 3{{x}^{2}}+4cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \end{align}]

Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:

[{y}’left( -1 right)=42cdot 1-42cdot 1+4=4]

Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.

Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:

[begin{align}& sqrt{x}={{x}^{frac{1}{2}}} \& {{left( sqrt{x} right)}^{prime }}={{left( {{x}^{frac{1}{2}}} right)}^{prime }}=frac{1}{2}cdot {{x}^{-frac{1}{2}}}=frac{1}{2}cdot frac{1}{sqrt{x}}=frac{1}{2sqrt{x}} \end{align}]

Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:

[y=sqrt{x}+sqrt[3]{x}+sqrt[4]{x}]

Записываем решение:

[begin{align}& left( sqrt{x}+sqrt[3]{x}+sqrt[4]{x} right)={{left( sqrt{x} right)}^{prime }}+{{left( sqrt[3]{x} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }} \& {{left( sqrt{x} right)}^{prime }}=frac{1}{2sqrt{x}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot {{x}^{-frac{2}{3}}}=frac{1}{3}cdot frac{1}{sqrt[3]{{{x}^{2}}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}{{x}^{-frac{3}{4}}}=frac{1}{4}cdot frac{1}{sqrt[4]{{{x}^{3}}}} \end{align}]

Возвращаемся к нашему примеру и записываем:

[{y}’=frac{1}{2sqrt{x}}+frac{1}{3sqrt[3]{{{x}^{2}}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}]

Вот такое сложное решение.

Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.

[y={{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x}]

Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:

[begin{align}& {{left( {{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}}cdot sqrt[3]{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{3}}cdot {{x}^{frac{2}{3}}} right)}^{prime }}= \& ={{left( {{x}^{3+frac{2}{3}}} right)}^{prime }}={{left( {{x}^{frac{11}{3}}} right)}^{prime }}=frac{11}{3}cdot {{x}^{frac{8}{3}}}=frac{11}{3}cdot {{x}^{2frac{2}{3}}}=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}} \& {{left( {{x}^{7}}cdot sqrt[3]{x} right)}^{prime }}={{left( {{x}^{7}}cdot {{x}^{frac{1}{3}}} right)}^{prime }}={{left( {{x}^{7frac{1}{3}}} right)}^{prime }}=7frac{1}{3}cdot {{x}^{6frac{1}{3}}}=frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x} \end{align}]

Оба слагаемых посчитаны, осталось записать окончательный ответ:

[{y}’=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}}+frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x}]

Мы нашли ответ.

Производная дроби через степенную функцию

Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.

Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

С другой стороны мы знаем, что выражение вида $frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,

[left( frac{1}{{{x}^{n}}} right)’={{left( {{x}^{-n}} right)}^{prime }}=-ncdot {{x}^{-n-1}}=-frac{n}{{{x}^{n+1}}}]

Пример:

[{{left( frac{1}{x} right)}^{prime }}=left( {{x}^{-1}} right)=-1cdot {{x}^{-2}}=-frac{1}{{{x}^{2}}}]

Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.

Итак, первая функция:

[fleft( x right)=frac{1}{{{x}^{2}}}]

Считаем:

[{{left( frac{1}{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{-2}} right)}^{prime }}=-2cdot {{x}^{-3}}=-frac{2}{{{x}^{3}}}]

Первый пример решен, переходим ко второму:

[y=frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}]

Решаем:

[begin{align}& {{left( frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} right)}^{prime }}= \& ={{left( frac{7}{4{{x}^{4}}} right)}^{prime }}-{{left( frac{2}{3{{x}^{3}}} right)}^{prime }}+{{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{4}} right)}^{prime }} \& {{left( frac{7}{4{{x}^{4}}} right)}^{prime }}=frac{7}{4}{{left( frac{1}{{{x}^{4}}} right)}^{prime }}=frac{7}{4}cdot {{left( {{x}^{-4}} right)}^{prime }}=frac{7}{4}cdot left( -4 right)cdot {{x}^{-5}}=frac{-7}{{{x}^{5}}} \& {{left( frac{2}{3{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( frac{1}{{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( {{x}^{-3}} right)}^{prime }}=frac{2}{3}cdot left( -3 right)cdot {{x}^{-4}}=frac{-2}{{{x}^{4}}} \& {{left( frac{5}{2}{{x}^{2}} right)}^{prime }}=frac{5}{2}cdot 2x=5x \& {{left( 2{{x}^{3}} right)}^{prime }}=2cdot 3{{x}^{2}}=6{{x}^{2}} \& {{left( 3{{x}^{4}} right)}^{prime }}=3cdot 4{{x}^{3}}=12{{x}^{3}} \end{align}]…

Теперь собираем все эти слагаемые в единую формулу:

[{y}’=-frac{7}{{{x}^{5}}}+frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}]

Мы получили ответ.

Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $fleft( x right)=…$, во втором: $y=…$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $fleft( x right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $fleft( x right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.

Сложные задачи с производными

В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.

Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:

[y={{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x}]

Считаем:

[begin{align}& {{left( {{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}} right)}^{prime }}-{{left( frac{1}{{{x}^{3}}} right)}^{prime }}+left( sqrt[3]{x} right) \& {{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}} \& {{left( frac{1}{{{x}^{3}}} right)}^{prime }}={{left( {{x}^{-3}} right)}^{prime }}=-3cdot {{x}^{-4}}=-frac{3}{{{x}^{4}}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot frac{1}{{{x}^{frac{2}{3}}}}=frac{1}{3sqrt[3]{{{x}^{2}}}} \end{align}]

Производная функции равна:

[{y}’=3{{x}^{2}}-frac{3}{{{x}^{4}}}+frac{1}{3sqrt[3]{{{x}^{2}}}}]

Первый пример решен. Рассмотрим вторую задачу:

[y=-frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}}]

Во втором примере действуем аналогично:

[{{left( -frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( -frac{2}{{{x}^{4}}} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }}+{{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}]

Посчитаем каждое слагаемое отдельно:

[begin{align}& {{left( -frac{2}{{{x}^{4}}} right)}^{prime }}=-2cdot {{left( {{x}^{-4}} right)}^{prime }}=-2cdot left( -4 right)cdot {{x}^{-5}}=frac{8}{{{x}^{5}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}cdot {{x}^{-frac{3}{4}}}=frac{1}{4cdot {{x}^{frac{3}{4}}}}=frac{1}{4sqrt[4]{{{x}^{3}}}} \& {{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( frac{4}{xcdot {{x}^{frac{3}{4}}}} right)}^{prime }}={{left( frac{4}{{{x}^{1frac{3}{4}}}} right)}^{prime }}=4cdot {{left( {{x}^{-1frac{3}{4}}} right)}^{prime }}= \& =4cdot left( -1frac{3}{4} right)cdot {{x}^{-2frac{3}{4}}}=4cdot left( -frac{7}{4} right)cdot frac{1}{{{x}^{2frac{3}{4}}}}=frac{-7}{{{x}^{2}}cdot {{x}^{frac{3}{4}}}}=-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}} \end{align}]

Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:

[{y}’=frac{8}{{{x}^{5}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}}]

И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные. 

Смотрите также:

1. Производная произведения и частного
2. Правила вычисления производных
3. Теорема Виета
4. Преобразование уравнений
5. Тест по методу интервалов для строгих неравенств
6. Тест по задачам B14: средний уровень, 2 вариант

Производная степени встречается в большинстве примеров на дифференцирование. Само правило нахождения производной степени простое. При дифференцировании степени с натуральным показателем проблем, как правило, не возникает. А вот найти производную степени с отрицательным или дробным показателями несколько сложнее. Легче всего понять, как найти производную степени, на примерах.

Открываем таблицу производных и правила дифференцирования.

Основная формула, по которой  может быть найдена производная любой степени —

   

Примеры. Найти производную степени:

   

   

Поскольку при дифференцировании число выносится за знак производной, то множитель, стоящий перед степенью, при нахождении производной просто переписываем:

   

   

Нахождение производной степени, стоящей в знаменателе дроби, немного сложнее. Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.

   

   

   

   

   

   

Производная степени используется и для дифференцирования корней. Предварительно корень приводится к степени, а в найденной производной снова возвращаемся к корню.

Например,

   

   

   

   

   

   

Если корень в знаменателе, сначала преобразовываем его в степень, затем — поднимаем наверх с отрицательным показателем, а  далее — как обычно, производная степени.

Например,

   

   

   

   

   

   

   

   

Примеры для самопроверки. Найти производную степени:

   

Показать решение

Содержание:

• Формула
• Примеры вычисления производной степенной функции

Формула

Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.

Заметим, что в качестве степени 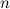может быть как
натуральное число,
то есть 1, 2, 3, …; так и любое отрицательное число: — 1, — 2 и т.д., а также и любое дробное, например, 2,34; — 4,1 или $frac{3}{4}$ , $-frac{5}{6}$ .

Заметим, что если аргумент у степенной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто $x$, то производную нужно находить по следующей формуле:

$$left(u^{n}right)^{prime}=n u^{n-1} cdot u^{prime}$$

Примеры вычисления производной степенной функции

Читать дальше: производная обратной функции (1/x)’.

2

2.7. Производная показательно-степенной функции

Функция
называется показательной, если независимая
переменная входит в показатель степени,
и степенной, если переменная является
основанием. Если же и основание и
показатель степени зависят от переменной,
то такая функция будет показательно –
степенной.

Пусть u = f(x)
и v = g(x)
– функции, имеющие производные в точке
х, f(x)>0.

Найдем
производную функции y =
u^v.
Логарифмируя, получим:

lny = vlnu

Пример.
Найти производную функции
.

По полученной
выше формуле получаем:

Производные
этих функций:

Окончательно:

2.8. Производная обратных функций

Пусть требуется
найти производную функции у = f(x

)
при условии, что обратная ей функция
x = g(y)
имеет производную, отличную от нуля в
соответствующей точке.

Для решения
этой задачи дифференцируем функцию x
= g(y) по х:

т.к. g(y)

0

т.е. производная
обратной функции обратна по величине
производной данной функции.

Пример.
Найти формулу для производной функции
arctg.

Функция arctg
является функцией, обратной функции
tg, т.е. ее производная
может быть найдена следующим образом:

Известно,
что

По приведенной
выше формуле получаем:

Т.к.
то можно записать окончательную формулу
для производной арктангенса:

Таким
образом получены все формулы для
производных арксинуса, арккосинуса и
других обратных функций, приведенных
в таблице производных.

2.9. Дифференциал функции

Пусть функция
y = f(x)
имеет производную в точке х:

Тогда можно записать:
,
где 0, при х0.

Следовательно:
.

Величина x-
бесконечно малая более высокого порядка,
чем f(x)x,
т.е. f(x)x
— главная часть приращения у.

Определение.
Дифференциалом функции f(x)
в точке х называется главня линейная
часть приращения функции.

Обозначается
dy или df(x).

Из определения
следует, что dy = f(x)x
или

dy
= f(x)dx

.

Можно также
записать:

2.10. Геометрический смысл дифференциала

y

f(x)

K

dy

M
y

L



x x + x
x

Из треугольника
MKL:
KL = dy
= tgx
= yx

Таким образом,
дифференциал функции f(x)
в точке х равен приращению ординаты
касательной к графику этой функции в
рассматриваемой точке.

2.11. Свойства дифференциала

Если u
= f(x)
и v = g(x)-
функции, дифференцируемые в точке х, то
непосредственно из определения
дифференциала следуют следующие
свойства:

1. d(u
   
   v) = (u 
   v)dx
   = udx
   
   vdx
   = du 
   dv

1. d(uv)
   = (uv)dx
   = (uv
   + vu)dx
   = vdu + udv

1. d(Cu) = Cdu

2.12. Дифференциал сложной функции. Инвариантная форма записи дифференциала

Пусть y
= f(x),
x = g(t),
т.е у- сложная функция.

Тогда
dy =
f(x)g(t)dt
= f(x)dx.

Видно, что форма записи
дифференциала dy не зависит
от того, будет ли х независимой переменной
или функцией какой- то другой переменной,
в связи с чем эта форма записи называется
инвариантной формой записи дифференциала.

Однако, если х-
независимая переменная, то

dx
= x,
но

если х зависит от t,
то х
 dx.

Таким
образом форма записи dy =
f(x)x
не является инвариантной.

Пример.
Найти производную функции
.

Сначала
преобразуем данную функцию:

Пример.
Найти производную функции
.

Пример.
Найти производную функции

Пример.
Найти производную функции

Пример.
Найти производную функции

Производная констант в переменных степенях

ПРОИЗВОДНАЯ ПОСТОЯННЫХ В ПЕРЕМЕННЫХ СТЕПЕНЯХ

В этом разделе две формы константы к переменной
власть будет представлена. Две экспоненциальные функции будут
и
, где х
— переменная, a — любая константа, а e равно
2,71828….

Вспоминая наше изучение логарифмов в математике,
Том 2-А, так как В и е являются обратными функциями, то

и

Если

, затем

ДОКАЗАТЕЛЬСТВО: Поскольку y = In x дифференцируемо, то и его
обратный, у =
. К
получить производную от y =
, мы
продифференцируем обе части уравнения (5.10) по x, что дает

Умножая обе части уравнения (5.12) на
дает

Дифференциация по цепному правилу и уравнение (5.11) дают

РЕШЕНИЕ.

РЕШЕНИЕ.

Если

, затем

ДОКАЗАТЕЛЬСТВО. Применение логарифмических правил,

Дифференцирование обеих частей уравнения (5.14) дает

ПРИМЕЧАНИЕ. In a является константой.

РЕШЕНИЕ:

Дифференциация по цепному правилу и уравнение (5.13) дают

РЕШЕНИЕ:

ПРАКТИКА
ЗАДАЧИ: Найдите d из следующего:

ОТВЕТА:

ОБЗОР

Ниже приведены основные темы, затронутые в этом
глава: 1. Производная константы:

Теорема 1. Производная константы равна нулю.

2. Производная переменной в степени:

Теорема 2. Производная функции
дан кем-то
, если n равно
любое действительное число.

3. Производная суммы двух или более функций:

Теорема 3. Производная суммы двух или более
дифференцируемых функций от x равна сумме их производных.

Если даны две функции от x, такие что u = g(x) и v = h(x), а также y = u + v = g(x) + h(x), то

4. Производная произведения двух или более функций:

Теорема 4. Производная произведения двух дифференцируемых
функций от x равно первой функции, умноженной на производную от
вторая функция плюс вторая функция, умноженная на производную от
первая функция.

Эту теорему можно распространить на три или более функций.

5. Производная частного двух функций:

Теорема 5. В точке, где знаменатель
не равна нулю, производная от отношения двух дифференцируемых
функции x равен знаменателю, умноженному на производную
числитель минус числитель, умноженный на производную от знаменателя, все
разделить на квадрат знаменателя.

6. Производная функции в степени:

Теорема 6. Производная любой
дифференцируемая функция от x, возведенная в степень n, где n — любое действительное число,
равен n умноженному на полиномиальную функцию от x в (n — ]) степени, умноженной на
производная от самого многочлена.

Если у =
, где ты
любая дифференцируемая функция от x, то

7. Производная функции в радикальной форме: To
дифференцировать функцию, содержащую радикал, заменить радикал на дробную часть
экспонента; затем найдите производную, применяя соответствующие теоремы.

8. Производная функции по цепному правилу:

, где переменная y = f(u) — дифференцируемая функция
u и u = g(x) является дифференцируемой функцией x.

9. Производная обратной функции:

Теорема 7. Производная обратной
функция равна обратной производной прямой функции.

10. Производная неявной функции: в уравнениях
содержащий x и y, если уравнение y не решено, то y называется неявным
функция х. Производная каждого члена, содержащего y, будет
с последующим

11. Производная тригонометрических функций:

12. Производная натуральных логарифмических функций:

Теорема 8. Натуральный логарифм y = In x имеет
производная

Если u — положительная дифференцируемая функция от x, то

13.